Как найти высоту предмета основание которого недоступно

Вернуться к содержанию учебника

Вопросы для повторения к главе 11. Страница 266

---

Вернуться к содержанию учебника

---

Как определить высоту предмета, основание которого неизвестно

При ориентировании на местности, например, в туристическом походе, иногда требуется определить высоту того или иного удаленного предмета или объекта. Если расстояние до него известно, то выполнить расчеты не составляет труда. А как быть, когда до основания нужного объекта не добраться, а измерить расстояние нет возможности? На помощь приходит знание геометрии.

Вам понадобится

• – шест;
• – астролябия.

Инструкция

При определении высоты удаленного предмета, основание которого недоступно, а расстояние до него нельзя измерить непосредственно, используйте простые вычисления с приемением подручных предметов или специальных приспособлений. Первый этап – определение расстояния до объекта.

Допустим, что от предмета с неизвестной вам высотой (точка Х) вас отделяет непреодолимое препятствие, например, река. Выберите на своей стороне точку А, располагающуюся примерно напротив нужного вам объекта.

Теперь повернитесь под прямым углом вправо и сделайте 15-20 шагов. В этом месте воткните в землю ветку или палочку. Это будет точка О. Проделайте точно такое же число шагов в том же направлении. Вы получили точку В; отметьте ее также каким-либо предметом.

От точки В двигайтесь под прямым углом, удаляясь от берега. В тот момент, когда точка вашего нахождения будет располагаться между объектом (точка Х) и точкой О, остановитесь. Расстояние от вас до точки В будет равно расстоянию от первой точки (А) до точки Х, обозначаемой нужный вам объект. Измерить расстояние теперь можно шагами, а затем перевести их в метры.

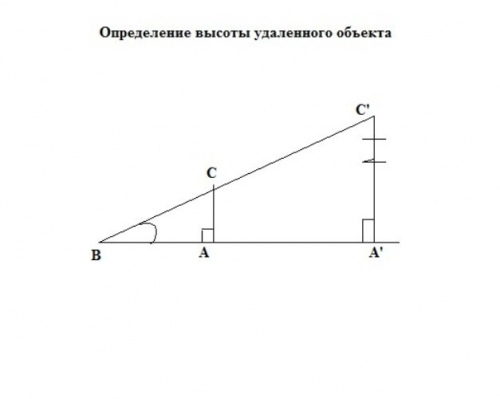
Теперь, когда расстояние до объекта известно, переходите к определению его высоты. Для этого вам понадобится длинный шест или палка с вращающейся планкой. Поставьте на удалении от измеряемого объекта шест АС с вращающейся планкой и направьте ее на верхнюю точку объекта (точка С’).

Отметьте на поверхности земли точку В, чтобы в этой точке прямая АА’ пересекалась бы с поверхностью земли. Треугольники А’С’В и АСВ будут подобными, поскольку имеют общий угол и по углу, равному 90 градусов. Из этого следует, что:
А’С’ / АС = ВА’ / ВА или

Высота предмета, таким образом, будет равняться:
А’С’ = АС х ВА’ / ВА.

Следующий способ предполагает более сложные вычисления. Допустим, вам требуется определить высоту АН удаленного предмета. Отметьте на определенном расстоянии от основания Н точку В и измерьте при помощи астролябии угол АВН, а затем по этим данным из прямоугольного треугольника АНВ найдите высоту объекта по формуле:

АН = НВ х tgАВН.

Источники:

• определение высоты предмета

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как определить высоту предмета,
основание которого неизвестно

При ориентировании
на местности, например, в туристическом походе, иногда требуется определить
высоту того или иного удаленного предмета или объекта. Если расстояние до него
известно, то выполнить расчеты не составляет труда. А как быть, когда до
основания нужного объекта не добраться, а измерить расстояние нет возможности?
На помощь приходит знание геометрии.

Вам понадобится

·        
–
шест;

·        
–
астролябия.

Инструкция

1

При определении
высоты удаленного предмета, основание которого недоступно, а расстояние до него
нельзя измерить непосредственно, используйте простые вычисления с приемением
подручных предметов или специальных приспособлений. Первый этап – определение
расстояния до объекта.

2

Допустим, что от
предмета с неизвестной вам высотой (точка Х) вас отделяет непреодолимое
препятствие, например, река. Выберите на своей стороне точку А, располагающуюся
примерно напротив нужного вам объекта.

3

Теперь повернитесь
под прямым углом вправо и сделайте 15-20 шагов. В этом месте воткните в землю
ветку или палочку. Это будет точка О. Проделайте точно такое же число шагов в
том же направлении. Вы получили точку В; отметьте ее также каким-либо
предметом.

4

От точки В
двигайтесь под прямым углом, удаляясь от берега. В тот момент, когда точка
вашего нахождения будет располагаться между объектом (точка Х) и точкой О,
остановитесь. Расстояние от вас до точки В будет равно расстоянию от первой
точки (А) до точки Х, обозначаемой нужный вам объект. Измерить расстояние
теперь можно шагами, а затем перевести их в метры.

5

Теперь, когда
расстояние до объекта известно, переходите к определению его высоты. Для этого
вам понадобится длинный шест или палка с вращающейся планкой. Поставьте на
удалении от измеряемого объекта шест АС с вращающейся планкой и направьте ее на
верхнюю точку объекта (точка С’).

6

Отметьте на
поверхности земли точку В, чтобы в этой точке прямая АА’ пересекалась бы с
поверхностью земли. Треугольники А’С’В и АСВ будут подобными, поскольку имеют
общий угол и по углу, равному 90 градусов. Из этого следует, что:
А’С’ / АС = ВА’ / ВА или 

Высота предмета, таким образом, будет равняться: А’С’ = АС х ВА’ / ВА.

7

Следующий способ
предполагает более сложные вычисления. Допустим, вам требуется определить высоту
АН удаленного предмета. Отметьте на определенном расстоянии от основания Н
точку В и измерьте при помощи астролябии угол АВН, а затем по этим данным из
прямоугольного треугольника АНВ найдите высоту объекта по формуле:
АН = НВ х tgАВН.

По линейным размерам. Чтобы определить расстояние
этим способом, надо:

держать перед собой линейку на
расстоянии вытянутой руки (50-60 см от глаза) и измерить по ней в миллиметрах
видимую ширину или высоту предмета, до которого требуется определить расстояние;

– действительную высоту (ширину)
предмета, выраженную в сантиметрах, разделить на видимую высоту (ширину) в
миллиметрах, и результат умножить на б (постоянное число) , получим расстояние.

Например, если столб высотой 4 м
(400 см) закрывается по линейке 8 мм, то расстояние до него будет 400 х 6 =
2400; 2400: 8 = 300 м (действительное расстояние). Чтобы определять расстояния
таким способом, требуется хорошо знать линейные размеры различных объектов,
либо иметь эти данные под рукой .
ЛИБО:
Инструкция
1
Самый нехитрый способ определить
расстояние на местности связан с использованием глазомера. Главное тут –
натренированная зрительная память и умение мысленно отложить на видимой
местности постоянную меру длины, например, 50 или 100 м. Закрепите в памяти
эталоны и при необходимости сравните с ними то расстояние, которое вам
необходимо измерить на местности. Один из самых простых эталонов – расстояние
между столбами линии электропередач, которое составляет обычно около 50 м.

2
Измеряя расстояние посредством
мысленного откладывания постоянной меры, учитывайте, что местные предметы будут
казаться уменьшенными в зависимости от их удаления. Иными словами, при удалении
в два раза предмет покажется в два раза меньше.

3
При использовании глазомера имейте ввиду,
что в условиях недостаточной видимости (в тумане, в сумерки, пасмурную погоду,
при дожде и т. п. ) предметы кажутся расположенными дальше, чем есть на самом
деле. Точность такого способа, прежде всего, зависит от тренированности
наблюдателя. Обычная ошибка на расстоянии в километр составляет около 15%.

4
Используйте способ определения
расстояний по линейным размерам. Для этого возьмите линейку и держите ее на
расстоянии вытянутой руки. Измерьте по линейке в миллиметрах видимую ширину
(высоту) объекта, до которого измеряете расстояние. Действительную ширину
(высоту) предмета, известную вам, переведите в сантиметры, затем разделите на
видимый размер в миллиметрах, а результат умножьте на 6 (постоянная величина) .
Получившийся результат будет искомым расстоянием до объекта.

5
Третий способ определить расстояние
на местности – по угловой величине. Для этого требуется знать линейную величину
объекта (длину, высоту или ширину) , а также угол в тысячных, под которым виден
наблюдаемый объект. Располагая такими данными, определите расстояние до объекта
по формуле:

D = L х 1000 / A;

где D — расстояние до объекта; L —
линейная величина объекта; A — угол, под которым видна линейная величина
объекта; 1000 — постоянная величина.

6
Для определения угловой величины
следует знать, что отрезку длиной 1 мм, расположенному на расстоянии 50 см от
глаза, будет соответствовать угол в 2 тысячных. Соответственно, для отрезка в 1
см угловая величина будет равна 20 тысячных и так далее. Запомните угловые
величины (в тысячных) некоторых подручных средств:

Большой палец руки (толщина) – 40;
Мизинец (толщина) – 25;
Карандаш – 10-11;
Спичечная коробка (ширина) – 50;
Спичечная коробка (высота) – 30
Спичка (толщина) – 2.

Определение высоты некоторых предметов

Определение
расстояний и высоты предметов

В
войсковой практике, где при вычислениях постоянно приходится пользоваться
соотношениями между угловыми и линейными величинами, вместо градусной системы
мер применяется артиллерийская (линейная), более простая и удобная для быстрых
приближепных вычислений. За единицу угловых мер артиллеристы принимают
центральный угол круга, стянутого дугой, равной длины окружности. Этот угол
называется делением угломера (так как используется во всех артиллерийских
угломерных приборах). Иногда этот/угол называют тысячной. Это название
объясняется тем, что длина дуги такого угла по окружности равна приближенно
тысячной доле ее радиуса. Это очень важное обстоятельство.

Следовательно, при наблюдении окружающих нас объектов (целей,
ориентиров и т. п.) мы находимся как бы в центре концентрических окружностей,
радиусы которых равны расстояниям до объектов. И мерой центральных углов будут
служить линейные отрезки, равные тысячной доле расстояния до
объектов. Так, если дом длиной 5 м расположен на удалении от наблюдателя
на 1000 м, то он укладывается в центральный угол, равный пяти
тысячным. Такой угол записывается на бумаге так: 0—05 (читается: ноль, ноль
пять). Если длина забора равна 100 м, то он укладывается в центральный угол,
равный 100 тысячным (одно большое деление угломерного прибора). Записывается
этот угол на бумаге так: 1—00 (и читается: один, ноль). Из этих примеров видно,
что углы позволяют очень быстро и легко посредством простейших арифметических
действий переходить из угловых измерений к линейным и обратно.

Так, например, если рядом с домом, находящимся от наблюдателя на
расстоянии Д-1500 м (Д — дистанция) находится  дерево  и 
угол  между  ними  укладывается в пятьдесят пять тысячных — У =
0—55 (У — угол) и требуется
определить расстояние от дома до дерева — В (В — расстояние), то из пропорции В
: Д = У : 1000 вытекает формула для определения линейных размеров.

Решим
пример. У столба высотой 6 м вы видите человека. Требуется определить
расстояние до него.

Вначале
определяем, в какой угол укладывается высота столба. Допустим, что высота
столба укладывается в угол У=0—05 (пять тысячных). Использование двух
вышеприведенных формул позволяет определять быстро и точно любые линейные и
угловые величины на местности.

Между
делениями угломера (в тысячных) и обычной градусной системой угловых мер
существуют соотношения: одна тысячная 0—01 равна 3,6′ (минуты), а большое
деление угломера (1—00) =6°. Эти соотношения позволяют при необходимости
осуществлять переход от одной системы измерений к другой.

Рассмотрим
простейшие способы измерения углов на местности.

Их
можно измерять с помощью полевого бинокля, линейки и подручных предметов.

В поле зрения бинокля (рис. 13)
имеются две взаимно-перпендикулярные угломерные шкалы для измерения
горизонтальных и вертикальных углов. Величина одного большого деления этих шкал
соответствует 0—10, а малого 0—05 тысячных. Для измерения угла между двумя
направлениями надо, глядя в бинокль, совместить какой-либо штрих угломерной
шкалы с одним из этих направлений и подсчитать число делений до второго
направления. Так, например, на рисунке 13 отдельное дерево (пулемет противника)
расположено влево от дороги на угол 0—30.

Вертикальной
шкалой пользуются при определении вертикальных углов; в случае их больших
размеров можно пользоваться и горизонтальной шкалой (повернув бинокль
вертикально).

При
отсутствии бинокля углы можно измерять обычной линейкой с миллиметровыми
делениями. Если такую линейку держать перед собой на расстоянии 50 см от глаз
(рис. 14), то одно деление ее (1 мм) будет соответствовать углу в две тысячных
(0—02).

Точность
измерения углов таким способом зависит от навыка в вынесении линейки точно на
50 см от глаза. Этого можно достигнуть, привязав к линейке ниточку и закусив ее
зубами на расстоянии 50 см.

С
помощью линейки можно измерять углы и в градусах. В этом случае ее следует
выносить на расстояние 60 см от глаза. Тогда 1 см на линейке будет
соответствовать углу в Г.

При отсутствии линейки с делениями можно использовать пальцы, ладонь
или любой небольшой предмет (спичечную коробку, карандаш), размер
которых в миллиметрах, а следовательно, и в тысячных известен (рис. 15). Такая
мерка выносится на расстояние 50 см от глаза и по ней путем сравнения
определяется искомая величина угла.

Для
приближенного определения расстояний на местности используются следующие
простейшие способы: глазомерный, по измеренным угловым величинам местных
предметов, промером шагами, по времени движения, по звуку и вспышке от
выстрела, на слух.

Глазомерный
способ — основной, самый простой и быстрый, наиболее доступный каждому в любых
условиях. Однако точный глазомер приобретается не сразу; он вырабатывается
путем систематической тренировки, проводимой в разнообразных условиях
местности, в различное время года и суток.

Чтобы
развить свой глазомер, необходимо как можно чаще упражняться в определении на
глаз расстояний с обязательной проверкой их шагами, по карте или другим
способом.

Тренировку
надо начинать с коротких расстояний (10, 50, 100 м). Хорошо освоив эти
дистанции, можно переходить последовательно к большим (200, 400, 800, 1000 м).
Потом можно легко определять расстояния и большие.

На
точность глазомерного способа указывают такие побочные явления, как:

—  
более крупные предметы кажутся всегда ближе мелких, расположенных на том же
расстоянии;

—  
чем меньше промежуточных предметов находится между глазом и наблюдаемым
предметом, тем этот предмет кажется ближе;

—  
при наблюдении снизу вверх, от подошвы горы к вершине, предметы кажутся ближе,
а при наблюдении сверху вниз — дальше.

Глазомерная
оценка расстояний может контролироваться, когда несколько человек измеряют одну
и ту же дистанцию независимо друг от друга. Беря среднее из всех этих
определений, получают наиболее точный замер.

Для
грубой оценки расстояний иногда пользуются примерными данными, приведенными в
таблице 1.

	Объекты и признаки	Расстояние, с которого они становятся видимыми (различимыми)
1	Отдельный небольшой дом, изба	5 км
2	Труба на крыше	3 км
3	Самолет на земле, танк на месте	1,2 км
4	Стволы деревьев, километровые стол-
	бы и столбы линий связи	1,0 км
5	Движение ног и рук бегущего или
	идущего человека	700 м
С	Переплеты оконных рам	500 м
7	Лицо человека, части его одежды	250—300 м
8	Черепица на крышах, листья на де-
	ревьях	200 м
9	Пуговицы и пряжки, подробности
	вооружения	150—170 м
10	Черты лица человека, кисти рук	100 м

Каждый
может уточнить и дополнить эту таблицу применительно к своим наблюдениям.

Точность
глазомерного способа зависит от натренированности наблюдателя, от величины
определяемых расстояний и от условий наблюдения. Для расстояний до 1000 м надо
добиться тренировкой определения величин с ошибкой не более 10—15%.

Если
известна линейная величина наблюдаемого предмета (высота, ширина или длина), то
для определения расстояния до него необходимо измерить угол (в тысячных), под
которым виден этот предмет. И по соотношению линейной (известной заранее) и
угловой (измеренной) величин этого предмета, по вышеуказанной формуле можно
определить расстояние до него.

При
измерении расстояний шагами надо натренироваться в ходьбе ровным шагом,
особенно в неблагоприятных условиях (на подъемах и спусках, при движении по
кочковатому лугу, в кустарнике и т. д.). Кроме того, надо знать длину своего
шага в метрах; она определяется из промера шагами линии, длина которой известна
заранее и должна быть не менее 200—300 м.

При
измерении расстояний шаги считают парами (обычно под левую ногу). После каждой
сотни пар шагов счет начинается снова. Чтобы не сбиться со счета, полезно
каждую пройденную сотню пар шагов отмечать на бумаге или же загибать
последовательно пальцы рук.

Ошибки
определения расстояний шагами, при ровном хорошо выверенном шаге, в среднем
достигают 2—4% измеренного расстояния.

Определять
расстояния можно по времени движения, если вы приблизительно знаете свою
среднюю скорость движения. Так, например, если средняя скорость движения
походным шагом равна 5 км/час (когда подъемы д спуски не более 5°), то, пройдя
45 минут по времени, можно ориентировочно сказать, что вами пройдено 3,75 км.

Определение
расстояний до стреляющих орудий основано на обнаружении, в момент выстрела,
вспышки и образования дыма. Затем, зная, что скорость распространения звука в
воздухе равна 330 м/сек, то есть округленно 1 км за 3 сек, отсчитываем время в
секундах от момента вспышки до момента слухового восприятия звука выстрела (или
взрыва) и, поделив его на три, определяем расстояние до орудий в километрах.
При отсутствии часов отсчитывать секунды можно путем порядкового счета «про
себя» двухзначных чисел (21, 22, 23, 24…), начиная с момента вспышки от
выстрела до прихода звука от нее. Отсчет каждого из этих чисел занимает
примерно одну секунду. Навыки такого счета, соразмерного ходу секундной
стрелки, довольно быстро приобретаются уже после 2— 3 тренировок в отсчете
двухзначных чисел.

Ночью
в условиях плохой видимости расстояния часто приходится оценивать на слух. Для
этого надо уметь определять по характеру звуков их источники и знать, с каких
примерно расстояний можно услышать эти звуки.

При нормальном
слухе и благоприятных акустических условиях дальность слышимости можно
приближенно считать такой, какой она дана в таблице 2.

Эти данные меняются в
зависимости от конкретных условий, в которых производится наблюдение, поэтому
должны учитываться каждым наблюдателем на основе его личного опыта.

Расскажем
о некоторых прикладных измерениях на местности: дальность видимого горизонта,
определение высоты дерева, определение ширины реки.

Для
того чтобы лучше развить глазомер, необходимо знать, как далеко лежит от
наблюдателя горизонт.

где h — высота наблюдателя (в км).

Сидя
в лодке и возвышаясь над водой только на 1 м, человек может обозревать
окружающую местность на дальности

Высоту дерева или любого
предмета можно определить по тени, шесту, лужице или зеркальцу и треугольнику
(рис. 16 а, б, в, г).

Если
на ровном месте измерить шагами длину своей тени (рис. 16, а), а затем длину
тени, отбрасываемой деревом (предметом), то искомую высоту легко вычислить из
пропорции:

где АК
— высота дерева (В); КЕ — тень дерева (D);
ак — ваш рост
(6);                     
ке — ваша тень (d).

Пример.
Длина вашей тени d равна трем шагам, тень дерева Д равна 9 шагам, то есть тень
дерева длиннее вашей тени в три раза. Если принять ваш рост 1,5 м, то высота
дерева будет В = 1,5 X 3 = 4,5 м.

Этот же способ можно применить при пасмурной погоде, когда тени от
предметов не видны. В этом случае для измерения нужно взять шест, равный длине
вашего роста (рис. 16, б). Шест этот надо установить на таком расстоянии от
дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с
верхней точкой шеста. Тогда высота дерева равна расстоянию от вашей
головы до основания дерева, как это видно из рисунка, то есть АС = ВС.

По
лужице и зеркальцу высоту дерева (предмета) можно измерять следующим образом.
Станьте так, чтобы лужица поместилась между вами и деревом (В). Найдите точку,
из которой видна отраженная в воде вершина дерева. Измеряемое дерево будет во
столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше
расстояния от лужицы до вас (АО). Вместо лужицы можно воспользоваться
зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.

С
помощью прямоугольного треугольника с двумя острыми углами по 45° высоту дерева
(предмета) определяют так. Отходя от дерева на некоторое расстояние и
прикладывая треугольник к глазам так, чтобы один из его катетов был параллелен
оси дерева, второй — параллелен земной поверхности, а гипотенуза представляла
собой

линию
визирования, добиваются такого положения, чтобы линия визирования прошла через
вершину дерева (рис. 16, г). В этом случае высота дерева Д равна расстоянию от
наблюдателя до дерева и плюс рост наблюдателя.

Ширину реки определяют следующим образом. Наблюдатель становится на
берегу реки в точке А (рис. 17, а) и выбирает на противоположном берегу
какой-либо хорошо заметный ориентир (куст, камень, дерево и
т. п.). После этого, идя в направлении, перпендикулярном к линии АБ, переходит
в точку В, удаленную от точки А больше, чем предполагаемая ширина реки. В точке
В устанавливает веху (палку, колышек и т. п.), затем, идя по тому же
направлению, переходит в точку С, которая находится от точки В на таком же
расстоянии, как и точка В от точки А. Далее от точки С идет
под прямым углом к линии АС до точки Д, то есть до тех пор, пока веха,
установленная в точке В, не окажется в створе с выбранным ориентиром (деревом)
на противоположном берегу. Из равенства тре-

угольников
ВДС = ВБА видно, что отрезок СД = АБ, то есть ширине реки. В нашем примере на
рисунке он равен 45 м.

Ширина
реки может быть определена и с помощью травинки. Сорвите ее и выберите на
противоположном берегу реки два заметных предмета. Встаньте лицом к этим
предметам, вытяните руки с травинкой и отмерьте с помощью ее расстояние между
предметами, смотря на них одним глазом (любым). После этого сложите травинку
пополам (вдвое) и отходите от берега до тех пор, пока расстояние между
выбранными предметами не закроется (не уложится) сложенной вдвое травинкой.
Замерьте это расстояние шагами, переведите его в метры — это и будет
расстояние, равное ширине реки (рис. 17, б).

Определить
крутизну скатов в полевых условиях очень важно при оценке проходимости
местности.

Для
того чтобы оценивать крутизну скатов на глаз, надо изучить на местности и
закрепить в зрительной памяти крутизну нескольких типичных 
скатов   (15°,  30°, 45°,

60°),
а затем путем мысленного сравнения с ними определять крутизну других скатов.

Следует всегда помнить, что снизу, от подошвы возвышенности, скат всегда
кажется круче, чем в действительности.

Более точные результаты
получаются, если, зайдя сбоку ската, сравнить его на глаз с величиной
какого-либо имеющегося целлулоидного треугольника, величины углов которого
известны.

Измерив
заранее углы между расставленными возможно шире большим, указательным и средним
пальцами руки, можно пользоваться и этими углами для оценки на глаз крутизны
скатов.

Крутизну
ската можно определять и промером шагов по приближенной формуле:

где ПШ — протяженность
ската, измеренная парами шагов.

Для
определения по этой формуле крутизны скатов наблюдатель становится в точке А
(рис. 18, а) и, держа на уровне глаз горизонтально папку или книжку, смотрит
вдоль нее и замечает на скате точку С, равную по высоте наблюдателя до уровня
глаз. Затем, двигаясь по направле-

нию к
этой точке, измеряют число пар шагов и по формуле определяют крутизну ската.

Пример.
От точки А до точки С отсчитано 4 пары шагов.

Крутизну
скатов можно замерять с помощью эклиметра — угломерного прибора для измерения
наклона линий местности к горизонту (рис. 18, б).

Чтобы
определить крутизну ската с помощью эклиметра, его держат на уровне глаз так,
чтобы линия основания АВ была параллельна направлению ската (обычно ставят на определенном
расстоянии веху с отметкой высоты расположения глаз наблюдателя). Тогда нить
отвеса эклиметра покажет угол, равный углу крутизны ската. Самодельный эклиметр
можно выполнить с помощью простого транспортира. К полочке транспортира в
центре (посредине) привязывают ниточку с грузиком и, переворачивая транспортир
вверх полочкой, направляют ее ребро параллельно боковой поверхности ската.
Ниточка с грузом отклоняется от деления 90° на шкале транспортира на угол,
равный крутизне ската.

Простые способы измерения расстояний
и высот на местности

Прямые методы определения линейных расстояний 

Точные измерения производятся с помощью мерной рулетки или стальной ленты,
длиной 10 или 20 метров. Иногда, применяют длинный шнур (в виде толстого
провода), на котором ставятся метки: белые – через каждые 2м и красные – через
10м, с закреплёнными, на концах, шпильками (стальными штырями или деревянными
кольями). Важно, чтобы измерительные приспособления не растягивались и были
точно отмерены, выверены по эталону. 

При обмерах полей и промеров по извилистым контурам, на местности, до сих пор
применяют полевой землемерный циркуль-измеритель «Ковылёк»
(“двухметровка”, старое название – «Сажень»),
в виде буквы А. Это раскладывающаяся деревянная вилка, с постоянным раствором
ножек, равным 2 метра. 

Во время работ по топографической съёмке местности – ведут журнал измерений,
составленный по стандартной форме, куда сразу заносятся номера точек стояния и
результаты текущих измерений. Дополнительно, составляют, от руки – абрис
(схематический чертёж снимаемой, в данный момент, местности). 

Приблизительные, грубые измерения с невысокой точностью, производят шагомерно –
парами своих шагов (равных, примерно, вашему росту, минус 10-20 сантиметров, в
зависимости от темпа ходьбы, степени пересечённости местности и угла наклона
земной поверхности). Результаты счёта – последовательно заносятся, записываются
в блокнот, в виде таблицы данных для дальнейшего пересчёта пройденных дистанций
и отрезков пути в метры.

Дистанционные визуальные методы определения расстояний 

Дистанционно-визуальные способы измерений длин – они применяются в тех случаях,
когда существует непреодолимая преграда, препятствие (река, болото, озеро,
глубокий овраг, горное ущелье), но сохраняется прямая видимость, достаточная
для производства измерений. 

Ширину реки можно определить геометрическим глазомерным способом, путём
построения вдоль её берега двух равных прямоугольных треугольников. Выбрав на
противоположном берегу (в направлении, перпендикулярном руслу) какой-нибудь
заметный предмет “А” (дерево, большой камень и т.п.), расположенный у
самой кромки воды, вбивают напротив него колышек “В” (рисунок 1).
Вдоль берега, перпендикулярно к линии АВ, отмеряют рулеткой или шагами,
например 20м и вбивают колышек “С”. На продолжении линии ВС в
расстоянии, равном также 20 м, вбивают еще один колышек “Д”. От
колышка “Д” в направлении ДЕ, перпендикулярном (направления задаются
при разведении рук в стороны и сведении их ладонями, прямо перед собой или с
помощью крестообразного эккера) к линии ДВ, надо идти от реки до тех пор, пока
колышек “С” не окажется на одной линии с предметом “А”. Так
как треугольники ABC и ЕДС абсолютно и полностью равны, то ширина реки будет
равна расстоянию ДЕ минус ВК (интервал до уреза воды). Если плечи ДС и СВ не
равны (нет возможности пройти вдоль берега; мешают густые заросли), то  AB = DE*BC/CD 

 
Рис.1 

Определить ширину реки можно и не отходя от воды, построением на местности
прямоугольного равнобедренного треугольника АДВ (рис. 2). Построив на точке
“А” прямой угол, отходят в направлении АС до такой точки
“Д”, из которой предмет “В” будет засекаться под углом 45°
(в этом случае, АВ=АД). Для разбивки углов применяется самодельный
крестообразный эккер (в виде квадратного листа бумаги с загнутыми, кверху,
уголками или, установленной на подставку, плоской деревянной крестовины с
четырьмя вбитыми, по квадрату, шпильками), с помощью которого строят углы 45° и
90° от ходовой линии (основной магистрали). На точке “А”, для лучшей
её видимости при расстановке вешек в створе, ставится хорошо заметный
“макет” (например, крепится белый лист бумаги, обращённый в сторону
пункта “Д”). 

Экспресс-метод, без установки эккера на штативе – две перекрещенных прямых
веточки, одинаковой длины, держать горизонтально на уровне глаз так, чтобы одна
ветка была параллельна течению реки и направлена на точку “А”
(смотреть, прикрыв один глаз). Тогда, линия угла-сорокапятки, проходящая через
концы веточек – смотрится-визируется закрыв другой глаз и слегка наклонив
голову. Можно визировать и с помощью шкалы компаса или циферблата наручных
часов (в качестве направляющей можно использовать измерительную линейку,
прикладывая её ребром через центр лимба). 

Имея возможность провести на местности триангуляцию (померить угломером или по
лимбу компаса) и посчитать тангенс угла (в полевых условиях, это возможно
проделать без калькулятора и точных математических таблиц Брадиса, при помощи
транспортира, линейки и циркуля), можно визировать под любым углом, а затем –
считать по формуле: 
АВ = АД * tg АДВ. 

Если угол равен 45 градусов, тогда tg(45°)=1  и, соответственно, АВ=АД 
tg(64°) = 2 и АВ=АД*2 
tg(72°) = 3 и АВ=АД*3 

 
Рис.2 

Достаточно точно ширина реки может быть установлена способом прямой засечки
(рис. 3). Для этого на противоположном берегу выбирают приметный предмет
“С”, а вдоль берега, на котором находится исследователь, прокладывают
базис АВ и измеряют длину его. Из точек “А” и “В” делают
засечки на точку “С”, т. е. измеряют углы CAB и ABC. Построив с
помощью мерной линейки и транспортира треугольник ABC, можно получить в
принятом для базиса АВ масштабе искомую ширину реки. 

Тем же способом ширина реки может быть определена и без непосредственного
измерения углов CAB и ABC, с помощью графических засечек на планшете. Надо
отложить на бумаге длину базиса AB в выбранном масштабе, затем из концов
базиса, ориентировав, стоя на угловых точках, планшетку, прочертить направления
на какой-нибудь видимый предмет “С” противоположного берега. Тогда,
ширину реки можно определить графически – на чертеже, пересчитав по его
масштабу. 

 
Рис.3 

Весьма прост и удобен приближенный прием определения ширины реки при помощи
травинки или нитки. Стоя на берегу реки в точке “А”, замечают на
противоположном ее берегу два приметных предмета (например лодку В и дерево
“С”), расположенных близ уреза (рис. 4). Затем, взяв травинку (нитку)
за ее концы вытянутыми перед собой руками, замечают ее длину “d”,
которой закрывается промежуток ВС между выбранными предметами (смотреть надо
одним глазом). Затем, сложив травинку пополам, отходят от реки до тех пор
(точка “D”), пока промежуток ВС не будет закрыт травинкой. Пройденное
расстояние AD будет равно ширине реки. 

 
Рис.4 

Существует и такой, самый быстрый, но весьма приближённый способ определения
ширины реки – закрывают правый глаз и направляют поднятый вверх большой палец
вытянутой горизонтально руки (рис. 5) в направлении приметного предмета
“А” противоположного берега. Затем, поменяв открытый глаз (так
появляется стереоскопический эффект в виде стереопары изображений из двух
различных точек наблюдения), замечают, что палец как бы отскочил вбок от
наблюдаемого предмета в точку “В”. Оценив на глаз расстояние АВ, в
метрах (предполагая, примерно, высоту или ширину предметов), и умножив его на
10, получают примерную ширину реки. Человек при таких измерениях – выступает
как стереофотограмметрический прибор. 

 
Рис.5

Определение расстояний по угловой величине известных
предметов

Пример (рис. 6). Расстояние между телеграфными столбами линии
связи, равное 55м (у старых, деревянных, обычно – 50-60 метров интервала, с
высотой 6м от земли), покрывается 34 миллиметровыми делениями линейки (3.4см),
удаленной от глаз на 50
сантиметров (рука вытянута
прямо перед собой). Тогда, расстояние до телеграфной линии, по уравнению
соотношения сторон подобных треугольников, равно: 
Д = 55м * ( 50см / 3.4см ) =
809 м. 

Если столбы видны не под прямым углом, а сбоку, тогда, чтобы исключить
завышение расстояния до них – надо результат счёта умножить ещё и на
поправочный коэффициент: 
для 45 градусов – 0.7 
30° – 0.9 

Например, для рассмотренного примера, при расположении линии столбов под углом
45 градусов относительно наблюдателя – реальное расстояние будет: 
809 * 0.7 = 566 метров (между 2-мя измеренными столбами). При больших углах –
расст-е определяется по высоте опор. 

Стандартное расстояние между опорами электросети высокого напряжения (ЛЭП) –
100 метров. Высота заводских труб – 30 м 

Если нет линейки, то для измерений можно использовать подручные предметы,
например – спичечный коробок (5 сантиметров – максимум, 2.5см – до середины). 

Точность определения дистанции по угловым величинам составляет 5-10% длины
измеряемого расстояния. 

 
Рис.6

Определение высоты столба с помощью вращающейся планки

Нужно поставить на некотором расстоянии от столба А’С’ шест АС
с вращающейся планкой и направить планку на верхнюю точку С’ столба (рис.7). С
противоположной стороны, прицелившись по рейке – отметить на поверхности земли
точку В. 

Из подобия треугольников А’С’В и АСВ следует: 
A'C' = AC * BA' / BA 
то есть, чтобы определить высоту А’С’ столба, дастаточно будет знать высоту АС
шеста и длину двух отрезков ВА’ и ВА 

Можно померить и без дополнительных приспособлений. Один человек, лёжа на
земле, смотрит на вершину объекта – по макушке головы стоящего помощника. Рост
известен, горизонтальные расстояния – промеряются шагомерно. Данный способ
применялся ещё во времена СССР, при проведении военно-патриотических и
спортивных игр среди молодёжи (учащихся средних и старших классов
общеобразовательных школ), с элементами военных учений, при участии кадровых
офицеров вооруженных сил. У советских пионеров эти спортивно-массовые
мероприятия назывались «Зарница», у старшеклассников – «Орлёнок». У зарубежных
бой-скаутов, наверно, тоже могло быть что-то похожее. 

 
Рис.7 

Определение высоты дерева с помощью тени 

В солнечную погоду, измерить длину тени от дерева и от человека. Используя
подобие треугольников, составить численную пропорцию (схема и формула показаны
на рисунке 8) или построить графически, в выбранном масштабе. 

В пасмурный день, когда не видно солнца на небе, поставленная задача решается
другими методами. Например, можно определить высоту с помощью способа,
изображённого на рисунке 2 (построение прямоугольного равнобедренного
треугольника), используя, дополнительно, современную лазерную указку, ориентированную
по эккеру на 45° относительно земной поверхности – для визирования вершины
предмета. Эккерная рамка ставится в вертикальной плоскости, а прямой угол между
поверхностью земли и стороной квадрата крестовины – выставляется по отвесу. 

Если произвольный угол A’B’C’ мерить при помощи угломера, тогда придётся
смотреть в таблицах тангенсы угла и считать. 

 
Рис.8 

Определение высоты дерева с помощью зеркала 

Если имеется зеркало, расположенное на земле горизонтально или лужа с дождевой
водой, можно использовать оптическое свойство – равенство углов падения и
зеркального отражения светового луча. Для этого, нужно встать на точке, из
которой, в середине зеркала видна вершина предмета. Зная свой рост (на уровне
глаз), расстояние до центра зеркала и от него до предмета, используя подобие
треугольников, составить численную пропорцию (как на рисунке 8) или построить
схему графически, в выбранном масштабе. 

Дистанционное определение высоты предмета 

Например, нужно определить высоту предмета (рис. 9), не подходя к нему
(невозможно преодолеть препятствия в виде реки или глубокого оврага).
Измеряются углы в точках А (DАС) и В (DВС), а так же расстояние АВ
между ними. В примере на картинке: 
DАС = 28°
DВС = 36°
АВ = 15 метров 

тогда, высота предмета: 
CD = АВ / ( 1/tg(DАС) - 1/tg(DВС) ) =
= 15 / ( 1/tg(28°) -
1/tg(36°) ) = 
= 15 / ( 1/0.53 - 1/0.73
) = 
= 15 / ( 1.89 - 1.38 ) = 
= 15 / 0.51 = 29 метров,
с общей суммарной ошибкой измерений - до 10-20% 

 
Рис.9 

Примеры, разобранные на этой Интернет-странице, можно бесплатно скачать,
сохранить на жёсткий диск своего компьютера или распечатать на принтере, чтобы
удобнее было осваивать практические методы измерения расстояний и эффективнее
тренироваться в реальных, полевых условиях. Правильное и точное определение
ширины реки или водоёма – обязательно необходимо проводить перед форсированием
водной преграды.

Высокоточные измерения расстояний

При наличии дальномера (лазерные, свето- и радиодальномеры),
получается довольно высокая точность, которая требуется при проведении
геодезических работ, где эти приборы и применяют профессионалы. Туристам, в их
походах и путешествиях, такие миллиметровые погрешности не нужны.

ПРИЛОЖЕНИЯ 

Таблица синусов, косинусов, тангенсов и котангенсов углов от 0° до 90° 
Точность вычислений – до третьего знака после запятой. Расчёт был проведён
в электронных таблицах Excel по формулам, вида: 
TAN(A1*pi()/180)
Пример: tg(60°) = 1.732 

a	sin a	cos a	tg a	ctg a
0	0,000	1,000	0,000
1	0,017	1,000	0,017
2	0,035	0,999	0,035
3	0,052	0,999	0,052
4	0,070	0,998	0,070
5	0,087	0,996	0,087
6	0,105	0,995	0,105
7	0,122	0,993	0,123
8	0,139	0,990	0,141
9	0,156	0,988	0,158
10	0,174	0,985	0,176	5,671
11	0,191	0,982	0,194	5,145
12	0,208	0,978	0,213	4,705
13	0,225	0,974	0,231	4,331
14	0,242	0,970	0,249	4,011
15	0,259	0,966	0,268	3,732
16	0,276	0,961	0,287	3,487
17	0,292	0,956	0,306	3,271
18	0,309	0,951	0,325	3,078
19	0,326	0,946	0,344	2,904
20	0,342	0,940	0,364	2,747
21	0,358	0,934	0,384	2,605
22	0,375	0,927	0,404	2,475
23	0,391	0,921	0,424	2,356
24	0,407	0,914	0,445	2,246
25	0,423	0,906	0,466	2,145
26	0,438	0,899	0,488	2,050
27	0,454	0,891	0,510	1,963
28	0,469	0,883	0,532	1,881
29	0,485	0,875	0,554	1,804
30	0,500	0,866	0,577	1,732
31	0,515	0,857	0,601	1,664
32	0,530	0,848	0,625	1,600
33	0,545	0,839	0,649	1,540
34	0,559	0,829	0,675	1,483
35	0,574	0,819	0,700	1,428
36	0,588	0,809	0,727	1,376
37	0,602	0,799	0,754	1,327
38	0,616	0,788	0,781	1,280
39	0,629	0,777	0,810	1,235
40	0,643	0,766	0,839	1,192
41	0,656	0,755	0,869	1,150
42	0,669	0,743	0,900	1,111
43	0,682	0,731	0,933	1,072
44	0,695	0,719	0,966	1,036
45	0,707	0,707	1,000	1,000
46	0,719	0,695	1,036	0,966
47	0,731	0,682	1,072	0,933
48	0,743	0,669	1,111	0,900
49	0,755	0,656	1,150	0,869
50	0,766	0,643	1,192	0,839
51	0,777	0,629	1,235	0,810
52	0,788	0,616	1,280	0,781
53	0,799	0,602	1,327	0,754
54	0,809	0,588	1,376	0,727
55	0,819	0,574	1,428	0,700
56	0,829	0,559	1,483	0,675
57	0,839	0,545	1,540	0,649
58	0,848	0,530	1,600	0,625
59	0,857	0,515	1,664	0,601
60	0,866	0,500	1,732	0,577
61	0,875	0,485	1,804	0,554
62	0,883	0,469	1,881	0,532
63	0,891	0,454	1,963	0,510
64	0,899	0,438	2,050	0,488
65	0,906	0,423	2,145	0,466
66	0,914	0,407	2,246	0,445
67	0,921	0,391	2,356	0,424
68	0,927	0,375	2,475	0,404
69	0,934	0,358	2,605	0,384
70	0,940	0,342	2,747	0,364
71	0,946	0,326	2,904	0,344
72	0,951	0,309	3,078	0,325
73	0,956	0,292	3,271	0,306
74	0,961	0,276	3,487	0,287
75	0,966	0,259	3,732	0,268
76	0,970	0,242	4,011	0,249
77	0,974	0,225	4,331	0,231
78	0,978	0,208	4,705	0,213
79	0,982	0,191	5,145	0,194
80	0,985	0,174	5,671	0,176
81	0,988	0,156		0,158
82	0,990	0,139		0,141
83	0,993	0,122		0,123
84	0,995	0,105		0,105
85	0,996	0,087		0,087
86	0,998	0,070		0,070
87	0,999	0,052		0,052
88	0,999	0,035		0,035
89	1,000	0,017		0,017
90	1,000	0,000		0,000

При отсутствии таблиц Брадиса, инженерного калькулятора и
компьютера, значения тригонометрических функций можно посчитать, с произвольно
высокой точностью, и на простейшем арифмометре, с помощью арифметических
операций сложения, вычитания, умножения и деления по формулам рядов: 

sin x = x - x^3/1*2*3 + x^5/1*2*3*4*5 - x^7/1*2*3*4*5*6*7 +
x^9/1*2*3*4*5*6*7*8*9 -... 

cos x = 1 - x^2/1*2 +
x^4/1*2*3*4 - x^6/1*2*3*4*5*6 + x^8/1*2*3*4*5*6*7*8 -...

tg x = x + (1/3 * x^3) +
(2/15 * x^5) + (17/315 * x^7) + ... 

В степень – число возводится с помощью многократного перемножения. 
Например, аргумент в кубе:  x^3 = x*x*x   На калькуляторе, после набора
числа, последовательно нажимаются кнопки: * = =  

Главные формулы из геометрии, использовавшиеся в
разобранных примерах 

Теорема Пифагора: a^2 + b^2 = c^2 

В прямоугольном треугольнике ABC (рис.10) – отношение двух его сторон, например
катета a к гиптенузе c, зависит от величины одного из острых углов, например A. 

Основные тригонометрические функции для прямоугольного треугольника: 

Синус: sin A = a / c  (отношение противолежащего катета к гипотенузе) 
Косинус: cos A = b / c 
Тангенс: tg A = a / b 
Котангенс: ctg A = b / a 

A + B = 90° 
B = 90° – A 

a = c * sin A = c * cos B 
a = b * tg A 

 
Рис.10 Основные тригонометрические формулы для прямоугольного треугольника.

Обновлено: 18.05.2023

Как-то в юности я занимался альпинизмом и ориентированием на местности, и не знаю как сейчас, но в то время нужно было обязательно знать раздел “Выживание в экстремальных условиях”, чтобы сдать экзамен и получить какой-либо разряд!

Собственно, решил поделиться с Вами и написать вкратце данную статью, полагая, что это будет очень познавательно и интересно! На самом деле способов еще гораздо больше, чем описано здесь, но они практически схожи, и вы в процессе чтения, вникнув в суть – сможете сами моделировать ситуации, и понять, что всё не так уж и сложно.

Ну что же, поехали.

Конечно не часто, но бывают в нашей жизни ситуации и обстоятельства, когда нужно знать высоту или расстояние до какого-либо объекта, например дома, дерева, да или похвастаться перед подругой))). Возможно придется строить траекторию для установки спутниковой тарелки, чтобы сигнал “стрелял” обходя высотки и не мешали кроны деревьев. ))) А мало ли, что еще.

Как ни парадоксально, но не забираясь с рулеткой на объект – расчет сделать не сложно, при том, что каждый метод может дать довольно точный результат. Конечно, с точностью до миллиметров не вычислить искомое значение, но погрешность будет точно уж небольшой.

Высота по отбрасываемой тени

Если погода солнечная и четко прослеживается тень, выбираем на объекте нижнюю контрольную точку от которой берет начало отбрасываемая тень будь-то дома, дерева, столба и пр.

Далее, ищем конец тени и производим замер длины тени.
После чего фиксируем в вертикальном положении любой предмет (на фото ниже – это обычный колышек) и аналогично замеряем длину его тени, а потом еще и высоту от точки начала тени до верхушки предмета.

Надеюсь, что у вас нет сомнения, что на фотографии треугольники с катетами Х1, Y1 и X2, Y2 подобны? Расчет строится на геометрическом свойстве подобных треугольников в которых отношения сторон равны и искомая высота объекта Y1 находится так:

При ориентировании на местности, например, в туристическом походе, иногда требуется определить высоту того или иного удаленного предмета или объекта. Если расстояние до него известно, то выполнить расчеты не составляет труда. А как быть, когда до основания нужного объекта не добраться, а измерить расстояние нет возможности? На помощь приходит знание геометрии.

• Как определить высоту предмета, основание которого неизвестно
• Как просто определить высоту дерева
• Как определить высоту пирамиды

При определении высоты удаленного предмета, основание которого недоступно, а расстояние до него нельзя измерить непосредственно, используйте простые вычисления с приемением подручных предметов или специальных приспособлений. Первый этап – определение расстояния до объекта.

Допустим, что от предмета с неизвестной вам высотой (точка Х) вас отделяет непреодолимое препятствие, например, река. Выберите на своей стороне точку А, располагающуюся примерно напротив нужного вам объекта.

Теперь повернитесь под прямым углом вправо и сделайте 15-20 шагов. В этом месте воткните в землю ветку или палочку. Это будет точка О. Проделайте точно такое же число шагов в том же направлении. Вы получили точку В; отметьте ее также каким-либо предметом.

От точки В двигайтесь под прямым углом, удаляясь от берега. В тот момент, когда точка вашего нахождения будет располагаться между объектом (точка Х) и точкой О, остановитесь. Расстояние от вас до точки В будет равно расстоянию от первой точки (А) до точки Х, обозначаемой нужный вам объект. Измерить расстояние теперь можно шагами, а затем перевести их в метры.

Теперь, когда расстояние до объекта известно, переходите к определению его высоты. Для этого вам понадобится длинный шест или палка с вращающейся планкой. Поставьте на удалении от измеряемого объекта шест АС с вращающейся планкой и направьте ее на верхнюю точку объекта (точка С’).

Отметьте на поверхности земли точку В, чтобы в этой точке прямая АА’ пересекалась бы с поверхностью земли. Треугольники А’С’В и АСВ будут подобными, поскольку имеют общий угол и по углу, равному 90 градусов. Из этого следует, что:
А’С’ / АС = ВА’ / ВА или

Высота предмета, таким образом, будет равняться:
А’С’ = АС х ВА’ / ВА.

Следующий способ предполагает более сложные вычисления. Допустим, вам требуется определить высоту АН удаленного предмета. Отметьте на определенном расстоянии от основания Н точку В и измерьте при помощи астролябии угол АВН, а затем по этим данным из прямоугольного треугольника АНВ найдите высоту объекта по формуле:

Григорию Владимировичу понадобилось определить высоту дерева, находящегося на приусадебном участке. Дерево подверглось нападению жука типографа и его нужно срочно спилить. При этом нужно выбрать, в какую сторону оно должно упасть в результате спиливания, чтобы не повредить строения и насаждения на участке. Дерево было очень высокое, и он никак не мог найти возможность измерить его известными ему методами.

Затем Ангелина попросила отца произвести три замера:

расстояние от дерева до зеркала

расстояние от зеркала до того места, где стоит Ангелина

рост самой Ангелины.

Отец произвёл измерения. Расстояние от дерева до зеркала составило 10,3 м, от зеркала до Ангелины – 1,4 м, а рост Ангелины составил 1,65 м.

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

Как определить высоту предмета, основание которого неизвестно

При ориентировании на местности, например, в туристическом походе, иногда требуется определить высоту того или иного удаленного предмета или объекта. Если расстояние до него известно, то выполнить расчеты не составляет труда. А как быть, когда до основания нужного объекта не добраться, а измерить расстояние нет возможности? На помощь приходит знание геометрии.

При определении высоты удаленного предмета, основание которого недоступно, а расстояние до него нельзя измерить непосредственно, используйте простые вычисления с приемением подручных предметов или специальных приспособлений. Первый этап – определение расстояния до объекта.

Допустим, что от предмета с неизвестной вам высотой (точка Х) вас отделяет непреодолимое препятствие, например, река. Выберите на своей стороне точку А, располагающуюся примерно напротив нужного вам объекта.

Теперь повернитесь под прямым углом вправо и сделайте 15-20 шагов. В этом месте воткните в землю ветку или палочку. Это будет точка О. Проделайте точно такое же число шагов в том же направлении. Вы получили точку В; отметьте ее также каким-либо предметом.

От точки В двигайтесь под прямым углом, удаляясь от берега. В тот момент, когда точка вашего нахождения будет располагаться между объектом (точка Х) и точкой О, остановитесь. Расстояние от вас до точки В будет равно расстоянию от первой точки (А) до точки Х, обозначаемой нужный вам объект. Измерить расстояние теперь можно шагами, а затем перевести их в метры.

Теперь, когда расстояние до объекта известно, переходите к определению его высоты. Для этого вам понадобится длинный шест или палка с вращающейся планкой. Поставьте на удалении от измеряемого объекта шест АС с вращающейся планкой и направьте ее на верхнюю точку объекта (точка С’).

Отметьте на поверхности земли точку В, чтобы в этой точке прямая АА’ пересекалась бы с поверхностью земли. Треугольники А’С’В и АСВ будут подобными, поскольку имеют общий угол и по углу, равному 90 градусов. Из этого следует, что:
А’С’ / АС = ВА’ / ВА или

Высота предмета, таким образом, будет равняться: А’С’ = АС х ВА’ / ВА.

Следующий способ предполагает более сложные вычисления. Допустим, вам требуется определить высоту АН удаленного предмета. Отметьте на определенном расстоянии от основания Н точку В и измерьте при помощи астролябии угол АВН, а затем по этим данным из прямоугольного треугольника АНВ найдите высоту объекта по формуле:
АН = НВ х tgАВН.

По линейным размерам. Чтобы определить расстояние этим способом, надо:

держать перед собой линейку на расстоянии вытянутой руки (50-60 см от глаза) и измерить по ней в миллиметрах видимую ширину или высоту предмета, до которого требуется определить расстояние;
– действительную высоту (ширину) предмета, выраженную в сантиметрах, разделить на видимую высоту (ширину) в миллиметрах, и результат умножить на б (постоянное число) , получим расстояние.
Например, если столб высотой 4 м (400 см) закрывается по линейке 8 мм, то расстояние до него будет 400 х 6 = 2400; 2400: 8 = 300 м (действительное расстояние). Чтобы определять расстояния таким способом, требуется хорошо знать линейные размеры различных объектов, либо иметь эти данные под рукой .
ЛИБО:
Инструкция
1
Самый нехитрый способ определить расстояние на местности связан с использованием глазомера. Главное тут – натренированная зрительная память и умение мысленно отложить на видимой местности постоянную меру длины, например, 50 или 100 м. Закрепите в памяти эталоны и при необходимости сравните с ними то расстояние, которое вам необходимо измерить на местности. Один из самых простых эталонов – расстояние между столбами линии электропередач, которое составляет обычно около 50 м.

2
Измеряя расстояние посредством мысленного откладывания постоянной меры, учитывайте, что местные предметы будут казаться уменьшенными в зависимости от их удаления. Иными словами, при удалении в два раза предмет покажется в два раза меньше.

3
При использовании глазомера имейте ввиду, что в условиях недостаточной видимости (в тумане, в сумерки, пасмурную погоду, при дожде и т. п. ) предметы кажутся расположенными дальше, чем есть на самом деле. Точность такого способа, прежде всего, зависит от тренированности наблюдателя. Обычная ошибка на расстоянии в километр составляет около 15%.

4
Используйте способ определения расстояний по линейным размерам. Для этого возьмите линейку и держите ее на расстоянии вытянутой руки. Измерьте по линейке в миллиметрах видимую ширину (высоту) объекта, до которого измеряете расстояние. Действительную ширину (высоту) предмета, известную вам, переведите в сантиметры, затем разделите на видимый размер в миллиметрах, а результат умножьте на 6 (постоянная величина) . Получившийся результат будет искомым расстоянием до объекта.

5
Третий способ определить расстояние на местности – по угловой величине. Для этого требуется знать линейную величину объекта (длину, высоту или ширину) , а также угол в тысячных, под которым виден наблюдаемый объект. Располагая такими данными, определите расстояние до объекта по формуле:

где D — расстояние до объекта; L — линейная величина объекта; A — угол, под которым видна линейная величина объекта; 1000 — постоянная величина.

6
Для определения угловой величины следует знать, что отрезку длиной 1 мм, расположенному на расстоянии 50 см от глаза, будет соответствовать угол в 2 тысячных. Соответственно, для отрезка в 1 см угловая величина будет равна 20 тысячных и так далее. Запомните угловые величины (в тысячных) некоторых подручных средств:

Большой палец руки (толщина) – 40;
Мизинец (толщина) – 25;
Карандаш – 10-11;
Спичечная коробка (ширина) – 50;
Спичечная коробка (высота) – 30
Спичка (толщина) – 2.

Читайте также:

  

• Что такое токсичность обж кратко

  

• 951 пп об утверждении примерного положения об организации деятельности семейного детского сада

  

• Анализ школьного атласа по географии 7 класс

  

• Что такое автоматизация кратко

  

• Как будут работать школы в свердловской области с 15 ноября

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Решение прямоугольных треугольников с формулами и примерами вычисления

Содержание:

В этой лекции вы ознакомитесь со знаменитой теоремой Пифагора. Вы научитесь по известным сторонам и углам прямоугольного треугольника находить его неизвестные стороны и углы.

Метрические соотношения в прямоугольном треугольнике

На рисунке 173 отрезок CD — высота прямоугольного треугольника ABC

Отрезки AD и DB называют проекциями катетов АС и СВ соответственно на гипотенузу.

Лемма. Высота прямоугольного треугольника, проведенная к гипотенузе делит треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Докажите лемму самостоятельно.

Теорема 15.1. Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

Доказательство. На рисунке 173 отрезок CD — высота прямоугольного треугольника ABC

Докажем, что

• Поскольку Отсюда
• Поскольку Отсюда
• Поскольку Отсюда

Если длины отрезков на рисунке 173 обозначить так:

АС = Ь, то доказанные соотношения принимают вид:

Эти равенства называют метрическими соотношениями в прямоугольном треугольнике.

Пример:

Даны два отрезка, длины которых равны а и b (рис. 174). Постройте третий отрезок, длина которого равна

Решение:

Рассмотрим треугольник ADC в котором отрезок DB является высотой (рис. 175). Имеем: Если обозначить

Проведенный анализ показывает, как провести построение.

На произвольной прямой отметим точку А и отложим последовательно отрезки АВ и ВС так, чтобы АВ = а, ВС = b. Построим окружность с диаметром АС. Через точку В проведем прямую, перпендикулярную прямой АС (рис. 175).

Докажем, что отрезок DB искомый. Действительно, как вписанный угол, опирающийся на диаметр АС. Тогда по теореме 15.1

Теорема Пифагора

Теорема 16.1 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство. На рисунке 176 изображен прямоугольный треугольник ABC Докажем, что
Проведем высоту CD. Применив теорему 15.1 для катетов АС и ВС, получаем:
Сложив почленно эти равенства, получим:

Далее имеем:

Если в прямоугольном треугольнике длины катетов равны а и b, а длина гипотенузы равна с, то теорему Пифагора можно выразить следующим равенством:

Теорема Пифагора позволяет по двум сторонам прямоугольного треугольника найти его третью сторону:

Из равенства также следует, что отсюда то есть гипотенуза больше любого из катетов 1 .

1 Другим способом этот факт был установлен в курсе геометрии 7 класса.

Пифагор:

Вы изучили знаменитую теорему, которая носит имя выдающегося древнегреческого ученого Пифагора.

Исследования древних текстов свидетельствуют о том, что утверждение этой теоремы было известно задолго до Пифагора. Почему же ее приписывают Пифагору? Скорее всего потому, что именно Пифагор нашел доказательство этого утверждения.

О жизни Пифагора мало что известно достоверно. Он родился на греческом острове Самос. По преданиям, он много путешествовал, приобретая знания и мудрость.

Поселившись в греческой колонии Кротон (на юге Италии), он окружил себя преданными учениками и единомышленниками. Так возник пифагорейский союз (или кротонское братство). Влияние этого союза было столь велико, что даже спустя столетия после смерти Пифагора многие выдающиеся математики Древнего мира Пифагор называли себя пифагорейцами.

Тригонометрические функции острого угла прямоугольного треугольника

На рисунке 180 изображен прямоугольный треугольник АВС Напомним, что катет ВС называют противолежащим углу А, а катет АС — прилежащим к этому углу.

Определение. Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.

Синус угла А обозначают так: sin А (читают: «синус А»). Для острых углов А и В прямоугольного треугольника АВС имеем:

Для прямоугольного треугольника, изображенного на рисунке 181, можно записать:

Рассмотрим прямоугольный равнобедренный треугольник АВС в котором АС = ВС = а (рис. 182).

Имеем:
По определению отсюда Видим, что синус острого угла прямоугольного равнобедренного треугольника не зависит от размеров треугольника, так как полученное значение синуса одинаково для всех значений а. Поскольку Эту запись не связывают с конкретным прямоугольным равнобедренным треугольником.

Вообще, если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны.

Действительно, эти прямоугольные треугольники подобны по первому признаку подобия треугольников. Поэтому отношение катета к гипотенузе одного треугольника равно отношению соответственного катета к гипотенузе другого треугольника.

Например, запись sin 17° можно отнести ко всем углам, градусные меры которых равны 17°. Значение этого синуса можно вычислить один раз, выбрав произвольный прямоугольный треугольник с острым углом 17°.
Следовательно, синус острого угла зависит только от величины этого угла.

Определение. Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.

Косинус угла А обозначают так: cos А (читают: «косинус А»).
Для острых углов А и В прямоугольного треугольника АВС (рис. 180) можно записать:

Отметим, что катет прямоугольного треугольника меньше его гипотенузы, а поэтому синус и косинус острого угла меньше 1.

Определение. Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.

Тангенс угла А обозначают так: tg А (читают: «тангенс А»).
Для острых углов А и В прямоугольного треугольника АВС (рис. 180) можно записать:

Определение. Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.

Котангенс угла А обозначают так: ctg А (читают: «котангенс А»). Для острых углов А и В прямоугольного треугольника АВС (рис. 180) можно записать:

Для прямоугольного треугольника, изображенного на рисунке 181, записывают:

Как было установлено, синус угла зависит только от величины угла. Рассуждая аналогично, можно прийти к следующему выводу: косинус, тангенс и котангенс острого угла зависят только от величины этого угла.

Вообще, каждому острому углу а соответствует единственное число — значение синуса (косинуса, тангенса, котангенса) этого угла. Поэтому зависимость значения синуса (косинуса, тангенса, котангенса) острого угла от величины этого угла является функциональной. Функцию, соответствующую этой зависимости, называют тригонометрической. Так, — тригонометрические функции, аргументами которых являются острые углы.

С древних времен люди составляли таблицы приближенных значений тригонометрических функции с некоторым шагом, один раз вычисляя значения тригонометрических функций для конкретного аргумента. Затем эти таблицы широко использовались во многих областях науки и техники.

В наше время значения тригонометрических функций острых углов удобно находить с помощью микрокалькулятора.

Тангенс и котангенс острого угла можно выразить через синус и косинус этого же угла. Рассмотрим прямоугольный треугольник (рис. 181).

Запишем: Следовательно, получаем такие формулы:

Заметим, что тангенс и котангенс одного и того же острого угла являются взаимно обратными числами, то есть имеет место равенство:

По теореме Пифагора Обе части этого равенства делим на Имеем: Учитывая, что получим:

Принято записывать:

Отсюда имеем:
Эту формулу называют основным тригонометрическим тождеством.

Отметим, что Поскольку то получаем такие формулы:

Мы уже знаем, что Найдем теперь cos 45°, tg 45° и ctg 45°.

Имеем:

Найдем синус, косинус, тангенс и котангенс углов 30° и 60°. Рассмотрим прямоугольный треугольник АВС, в котором (рис. 183).

Пусть ВС = а. Тогда по свойству катета, лежащего против угла 30°, получаем, что АВ = 2а. Из теоремы Пифагора следует, что

Имеем:
Отсюда находим:

Поскольку 60° = 90° – 30°, то получаем:

Значения синуса, косинуса, тангенса и котангенса для углов 30°, 45° и 60° полезно запомнить.

Решение прямоугольных треугольников

На рисунке 185 изображен прямоугольный треугольник с острыми углами катеты которого равны а и b, а гипотенуза равна с.
По определению синуса острого угла прямоугольного треугольника

Отсюда

Следовательно, катет прямоугольного треугольника равен произведению гипотенузы на синус угла, противолежащего этому катету.

По определению косинуса острого угла прямоугольного треугольника Отсюда

Следовательно, катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, прилежащего к этому катету.

По определению тангенса острого угла прямоугольного треугольника Отсюда

Следовательно, катет прямоугольного треугольника равен произведению второго катета на тангенс угла, противолежащего первому катету.

По определению котангенса острого угла прямоугольного треугольника Отсюда
Следовательно, катет прямоугольного треугольника равен произведению второго катета на котангенс угла, прилежащего к первому катету.
Из равенств получаем:
Следовательно, гипотенуза прямоугольного треугольника равна частному от деления катета на синус противолежащего ему угла;

• гипотенуза прямоугольного треугольника равна частному от деления катета на косинус прилежащего к нему угла.

Решить прямоугольный треугольник означает найти его стороны и углы по известным сторонам и углам.

Приведенные выше правила позволяют решать прямоугольный треугольник по одной стороне и одному острому углу.

В задачах на решение прямоугольных треугольников, если не обусловлено иначе, приняты такие обозначения (см. рис. 185): с — гипотенуза, а и b — катеты, — углы, противолежащие катетам а и b соответственно.

Пример №1

Решите прямоугольный треугольник по катету и острому углу: a = 14 см, = 38°. (Значения тригонометрических функций найдите с помощью микрокалькулятора и округлите их до сотых. Значения длин сторон округлите до десятых.)

Решение:

Ответ:

Отметим, что эту задачу можно было решить и другим способом: например, найти гипотенузу, используя теорему Пифагора.

Пример №2

Решите прямоугольный треугольник по катету и гипотенузе:

a = 26 см, с = 34 см.

Решение:

Имеем:

Вычисляем угол с помощью микрокалькулятора: Тогда

Ответ:

Пример №3

Высота AD треугольника АВС (рис. 186) делит его сторону ВС на отрезки BD и CD такие, что Найдите стороны АВ и АС, если

Решение:

Из треугольника получаем:

Из треугольника получаем:
Ответ:

Пример №4

Боковая сторона равнобедренного треугольника равна b, угол при основании равен Найдите радиус окружности, вписанной в треугольник.

Решение:

В треугольнике АВС (рис. 187)

Проведем высоту BD.

Из треугольника получаем:

Точка О — центр окружности, вписанной в треугольник АВС. Следовательно, точка О принадлежит высоте ВD и биссектрисе АО угла ВАС. Поскольку то вписанная окружность касается стороны АС в точке D. Таким образом, OD — радиус вписанной окружности. Отрезок АО — биссектриса угла BAD, поэтому

Из треугольника получаем:

Ответ:

Напомню:

Метрические соотношения в прямоугольном треугольнике

• Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу.
• Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

Теорема Пифагора

• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Синус острого угла прямоугольного треугольника

• Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.

Косинус острого угла прямоугольного треугольника

• Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.

Тангенс острого угла прямоугольного треугольника

• Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.

Котангенс острого угла прямоугольного треугольника

• Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.

Тригонометрические формулы

– основное тригонометрическое тождество

Соотношения между сторонами и значениями тригонометрических функций углов в прямоугольном треугольнике

• Катет прямоугольного треугольника равен произведению гипотенузы на синус угла, противолежащего этому катету.
• Катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, прилежащего к этому катету.
• Катет прямоугольного треугольника равен произведению второго катета на тангенс угла, противолежащего первому катет>г.
• Катет прямоугольного треугольника равен произведению второго катета на котангенс угла, прилежащего к первому’ катету.
• Гипотенуза прямоугольного треугольника равна частному от деления катета на синус противолежащего ему угла.
• Гипотенуза прямоугольного треугольника равна частному от деления катета на косинус прилежащего к нему угла.

Четырехугольник, его элементы. Сумма углов четырехугольника

Рассмотрим одну из важнейших теорем геометрии, которая показывает зависимость между катетами и гипотенузой прямоугольного треугольника.

Теорема 1 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На сегодняшний день известны более ста доказательств этой теоремы. Рассмотрим одно из них.

Доказательство:

Пусть -данный прямоугольный треугольник, у которого (рис. 172). Докажем, что

1) Проведем высоту
2) По теореме о средних пропорциональных отрезках в прямоугольном треугольнике имеем:

и

3) Сложим эти два равенства почленно. Учитывая, что получим:

4) Следовательно,

Если в треугольнике обозначить (рис. 173), то теорему Пифагора можно записать формулой:

Таким образом, зная две стороны прямоугольного треугольника, с помощью теоремы Пифагора можно найти третью. В этом нам поможет следующая схема:

Пример №5

Катеты прямоугольного треугольника равны 7 см и 24 см. Найдите гипотенузу.

Решение:

Пусть тогда

Пример №6

Гипотенуза прямоугольного треугольника равна 17 см, а один из катетов – 15 см. Найдите второй катет.

Решение:

Пусть тогда

Пример №7

Найдите диагональ квадрата, сторона которого равна

Решение:

Рассмотрим квадрат у которого (рис. 174). Тогда

Ответ.

Пример №8

Найдите медиану равностороннего треугольника со стороной

Решение:

Рассмотрим равносторонний треугольник со стороной – его медиана (рис. 175).

Так как – медиана равностороннего треугольника, то она является и его высотой.

Из Тогда

Ответ:

Пример №9

Основания равнобокой трапеции равны 12 см и 22 см, а боковая сторона – 13 см. Найдите высоту трапеции.

Решение:

Пусть – данная трапеция, (рис. 176).

1) Проведем высоты и

2) (по катету и гипотенузе), поэтому

3) Из по теореме Пифагора имеем:

Пример №10

Один из катетов прямоугольного треугольника равен 8 см, а второй на 2 см меньше гипотенузы. Найдите неизвестный катет треугольника.

Решение:

Пусть см и см- катеты треугольника, тогда см – его гипотенуза.

Так как по теореме Пифагора получим уравнение: откуда (см).

Следовательно, неизвестный катет равен 15 см.

Верно и утверждение, обратное теореме Пифагора.

Теорема 2 (обратная теореме Пифагора). Если для треугольника справедливо равенство то угол этого треугольника — прямой.

Доказательство:

Пусть в треугольнике Докажем, что (рис. 177).

Рассмотрим у которого Тогда по теореме Пифагора а следовательно,

Но по условию, поэтому то есть

Таким образом, (по трем сторонам), откуда

Так как то треугольник со сторонами 3, 4 и 5 является прямоугольным. Такой треугольник часто называют египетским, потому что о том, что он прямоугольный, было известно еще древним египтянам.

Тройку целых чисел, удовлетворяющую теореме Пифагора, называют пифагоровой тройкой чисел, а треугольник, стороны которого равны этим числам, – пифагоровым треугольником. Например, пифагоровой является не только тройка чисел 3, 4, 5, но и 7, 24, 25 или 9, 40, 41 и т. п.

Заметим, что из теоремы Пифагора и теоремы, ей обратной, следует, что

треугольник является прямоугольным тогда и только тогда, когда квадрат наибольшей стороны треугольника равен сумме квадратов двух других его сторон.

Пример №11

Является ли прямоугольным треугольник со сторонами: 1) 6; 8; 10; 2) 5; 7; 9?

Решение:

1) Так как то треугольник является прямоугольным.

2) Так как то треугольник не является прямоугольным.

Ответ. 1) Да; 2) нет.

Теорема, названная в честь древнегреческого философа и математика Пифагора, была известна задолго до него. В текстах давних вавилонян о ней вспоминалось еще за 1200 лет до Пифагора. Скорее всего, доказывать эту теорему вавилоняне не умели, а зависимость между катетами и гипотенузой прямоугольного треугольника установили опытным путем. Также эта теорема была известна в Древнем Египте и Китае.

Считается, что Пифагор – первый, кто предложил строгое доказательство теоремы. Он сформулировал теорему так: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах». Именно в такой формулировке она и была доказана Пифагором.

Рисунок к этому доказательству еще называют «пифагоровыми штанами».

Зная, что треугольник со сторонами 3, 4 и 5 является прямоугольным, землемеры Древнего Египта использовали его для построения прямого угла. Бечевку делили узлами на 12 равных частей и соединяли ее концы. Потом веревку растягивали и с помощью колышков фиксировали на земле в виде треугольника со сторонами 3; 4; 5. В результате угол, противолежащий стороне, длина которой 5, был прямым.

Перпендикуляр и наклонная, их свойства

Пусть – перпендикуляр, проведенный из точки к прямой (рис. 185). Точку называют основанием перпендикуляра Пусть – произвольная точка прямой отличающаяся от Отрезок называют наклонной, проведенной из точки к прямой а точку основанием наклонной. Отрезок называют проекцией наклонной на прямую

Рассмотрим свойства перпендикуляра и наклонной.

1. Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из этой точки к этой прямой.

Действительно, в прямоугольном треугольнике -катет, – гипотенуза (рис. 185). Поэтому

2. Если две наклонные, проведенные к прямой из одной точки, равны, то равны и их проекции.

Пусть из точки к прямой проведены наклонные и и перпендикуляр (рис. 186). Тогда (по катету и гипотенузе), поэтому

Верно и обратное утверждение.

3. Если проекции двух наклонных, проведенных из точки к прямой, равны, то равны и сами наклонные.

(по двум катетам), поэтому (рис. 186).

4. Из двух наклонных, проведенных из точки к прямой, большей является та, у которой больше проекция.

Пусть и – наклонные, (рис. 187). Тогда (из ), (из ). Но поэтому следовательно,

Свойство справедливо и в случае, когда точки и лежат на прямой по одну сторону от точки

Верно и обратное утверждение.

5. Из двух наклонных, проведенных из точки к прямой, большая наклонная имеет большую проекцию.

Пусть и – наклонные, (рис. 187).

Тогда (из ),

(из ). Но поэтому следовательно,

Пример №12

Из точки к прямой проведены две наклонные. Длина одной из них равна 10 см, а ее проекции – 6 см. Найдите длину второй наклонной, если она образует с прямой угол 30°.

Решение:

Пусть на рисунке 187

1) Из (см).

2) Из по свойству катета, противолежащего углу 30°,

будем иметь:

Поэтому

Ответ. 16 см.

Пример №13

Из точки прямой проведены две наклонные, проекции которых равны 30 см и 9 см. Найдите длины наклонных, если их разность равна 9 см.

Решение:

Пусть на рисунке 187 По свойству 4: Обозначим см. Тогда см.

Из поэтому

Из поэтому

Левые части полученных равенств равны, следовательно, равны и правые их части.

Имеем уравнение: откуда Следовательно, см, (см).

Ответ. 41 см, 50 см.

Синус, косинус и тангенс острого угла прямоугольного треугольника. Соотношения между сторонами и углами в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник с прямым углом (рис. 190). Для острого угла катет является противолежащим катетом, а катет – прилежащим катетом. Для острого угла катет является противолежащим, а катет – прилежащим.

Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.

Синус угла обозначают так: Следовательно,

Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.

Косинус угла обозначают так: Следовательно,

Так как катеты и меньше гипотенузы то синус и косинус острого угла прямоугольного треугольника меньше единицы.

Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.

Тангенс угла обозначают так: Следовательно,

Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

Рассмотрим прямоугольные треугольники и у которых (рис. 191). Тогда (по острому углу). Поэтому

Из этого следует, что и поэтому

Аналогично поэтому

поэтому

Таким образом, приходим к выводу: синус, косинус и тангенс острого угла прямоугольного треугольника зависят только от градусной меры угла.

Из определений синуса, косинуса и тангенса угла получаем следующие соотношения между сторонами и углами в прямоугольном треугольнике.

1. Катет равен гипотенузе, умноженной на синус противолежащего ему угла или на косинус прилежащего: и
2. Гипотенуза равна катету, деленному на синус противолежащего ему угла или на косинус прилежащего:

3. Катет, противолежащий углу равен произведению второго катета на тангенс этого угла:
4. Катет, прилежащий к углу равен частному от деления другого катета на тангенс этого угла:

Значения можно находить с помощью специальных таблиц, калькулятора или компьютера. Для вычислений используем клавиши калькулятора и (на некоторых калькуляторах Последовательность вычислений у разных калькуляторов может быть разной. Поэтому советуем внимательно познакомиться с инструкцией к калькулятору.

Пример №14

В треугольнике Найдите

Решение:

(рис. 190). (см).

Пример №15

В треугольнике Найдите (с точностью до десятых сантиметра).

Решение:

(рис. 190). С помощью таблиц или калькулятора находим Следовательно,

Ответ. 2,9 см.

С помощью таблиц, калькулятора или компьютера можно по данному значению или находить угол Для вычислений используем клавиши калькулятора и

Пример №16

В треугольнике

Найдите острые углы треугольника.

Решение:

(рис. 190). С помощью калькулятора находим значение угла в градусах: 51,34019. Представим его в градусах и минутах (в некоторых калькуляторах это возможно сделать с помощью специальной клавиши): Тогда

Ответ.

Найдем синус, косинус и тангенс углов 30° и 60°. Рассмотрим у которого (рис. 192).

Тогда по свойству катета, противолежащего углу 30°,

По теореме Пифагора:

то есть

то есть

то есть

то есть

то есть

то есть

Найдем синус, косинус и тангенс угла 45°.

Рассмотрим у которого

(рис. 193). Тогда По теореме Пифагора:

то есть

то есть

то есть

Систематизируем полученные данные в таблицу:

Пример №17

Найдите высоту равнобедренного треугольника, проведенную к основанию, если основание равно 12 см, а угол при вершине треугольника равен 120°.

Решение:

Пусть – данный треугольник, (рис. 194).

Проведем к основанию высоту являющуюся также медианой и биссектрисой. Тогда

Из

отсюда (см).

Ответ. см.

Вычисление прямоугольных треугольников

Решить треугольник – значит найти все неизвестные его стороны и углы по известным сторонам и углам.

Для того чтобы можно было решить прямоугольный треугольник, известными должны быть или две стороны треугольника или одна из сторон и один из острых углов треугольника.

Используя в прямоугольном треугольнике обозначение (рис. 198) и соотношение между его сторонами и углами:

(теорема Пифагора);

можно решить любой прямоугольный треугольник.

Рассмотрим четыре вида задач на решение прямоугольных треугольников.

Образцы записи их решения в общем виде и примеры задач представлены в виде таблиц.

Решение прямоугольных треугольников по гипотенузе и острому углу

Пример:

Дано гипотенузу и острый угол прямоугольного треугольника. Найдите второй острый угол треугольника и его катеты.

Решение прямоугольных треугольников по катету и острому углу

Пример:

Дано катет и острый угол прямоугольного треугольника. Найдите второй острый угол треугольника, второй катет и гипотенузу.

Решение прямоугольных треугольников по двум катетам

Пример:

Дано катеты и прямоугольного треугольника. Найдите гипотенузу и острые углы треугольника.

Решение прямоугольных треугольников по катету и гипотенузе

Пример:

Дано катет и гипотенуза прямоугольного треугольника. Найдите второй катет и острые углы треугольника.

Пример:

Найдите высоту дерева основание которого является недоступным (рис. 199).

Решение:

Обозначим на прямой, проходящей через точку – основание дерева, точки и и измеряем отрезок и и

1) В

2) В

3) Так как имеем:

откуда

Ответ.

Определение прямоугольных треугольников

Из этой главы вы узнаете, как решать прямоугольные треугольники, т. е. находить их неизвестные стороны и углы по известным. Необходимые для этого теоретические знания можно почерпнуть из раздела математики, родственного как с геометрией, так и с алгеброй, — из тригонометрии. Собственно, само слово «тригонометрия» в переводе с греческого означает «измерение треугольников». Поэтому отношения сторон прямоугольного треугольника, с которыми вы познакомитесь далее, получили название тригонометрических функций.

Соотношения, которые будут применяться в этой главе, в полной мере можно считать проявлением подобия треугольников. Вообще, подобие треугольников, теорема Пифагора и площадь — это те три кита, на которых держится геометрия многоугольника. Именно исследование взаимосвязей между этими теоретическими фактами и составляет основное содержание курса геометрии в восьмом классе.

Синус, косинус и тангенс

Как уже было доказано, все прямоугольные треугольники, имеющие по равному острому углу, подобны. Свойство подобия обусловливает не только равенство отношений пропорциональных сторон этих треугольников, но и равенство отношений между катетами и гипотенузой каждого из этих треугольников. Именно эти отношения и будут предметом дальнейшего рассмотрения.

Пусть дан прямоугольный треугольник с катетами гипотенузой и острым углом (рис. 168).

Определение

Синусом острого угла прямоугольного треугольника (обозначается называется отношение противолежащего катета к гипотенузе:

Косинусом острого угла прямоугольного треугольника (обозначается называется отношение прилежащего катета к гипотенузе:

Тангенсом острого угла прямоугольного треугольника (обозначается называется отношение противолежащего катета к прилежащему:

Кроме синуса, косинуса и тангенса, рассматривают также котангенс острого угла прямоугольного треугольника (обозначается который равен отношению прилегающего катета к противолежащему:

Поскольку катет прямоугольного треугольника меньше гипотенузы, то синус и косинус острого угла меньше единицы.

Покажем, что значения тригонометрических функций зависят только от величины угла. Пусть прямоугольные треугольники имеют равные острые углы (рис. 169).

Эти треугольники подобны, отсюда или по основному свойству пропорции,

Правая и левая части этого равенства по определению равны синусам острых углов соответственно. Имеем:

т.е. синус угла не зависит от выбора треугольника. Аналогичные рассуждения можно провести и для других тригонометрических функций (сделайте это самостоятельно). Таким образом, тригонометрические функции острого угла зависят только от величины угла.

Имеет место еще один важный факт: если значения некоторой тригонометрической функции для острых углов равны, то Иначе говоря, каждому значению тригонометрической функции соответствует единственный острый угол.

Пример №18

Найдите синус, косинус и тангенс наименьшего угла египетского треугольника.

Решение:

Пусть в треугольнике (рис. 170).

Поскольку в треугольнике наименьший угол лежит против наименьшей стороны, то угол — наименьший угол треугольника По определению

Ответ:

Тригонометрические тождества

Выведем соотношения (тождества), которые выражают зависимость между тригонометрическими функциями одного угла.

Теорема (основное тригонометрическое тождество)

Для любого острого угла

По определению синуса и косинуса острого угла прямоугольного треугольника (см. рис. 168) имеем:

По теореме Пифагора числитель этой дроби равен

Следствие

Для любого острого угла

Докажем еще несколько тригонометрических тождеств.

Непосредственно из определений синуса

sin a а b ас а и косинуса имеем: т.е.

Аналогично доказывается, что

Отсюда следует, что

Пример №19

Найдите косинус и тангенс острого угла прямоугольного треугольника, синус которого равен 0,8.

Решение:

Пусть для острого угла Тогда

Поскольку

Ответ:

Вычисление значений тригонометрических функций. Формулы дополнения

Тригонометрические тождества, которые мы рассмотрели, устанавливают взаимосвязь между разными тригонометрическими функциями одного угла. Попробуем установить связь между функциями двух острых углов прямоугольного треугольника.

Теорема (формулы дополнения)

Для любого острого угла

Рассмотрим прямоугольный треугольник с гипотенузой (рис. 172).

Если Выразив синусы и косинусы острых углов треугольника, получим:

Следствие

Для любого острого угла

Заметим, что название «формулы дополнения», как и название «косинус», в котором префикс «ко» означает «дополнительный», объясняется тем, что косинус является синусом угла, который дополняет данный угол до Аналогично объясняется и название «котангенс».

Значения тригонометрических функций углов 30 45 60

Вычислим значения тригонометрических функций угла Для этого в равностороннем треугольнике со стороной проведем высоту которая является также биссектрисой и медианой (рис. 173).

В треугольнике и по теореме Пифагора Имеем:

С помощью формул дополнения получаем значения тригонометрических функций угла

Для вычисления значений тригонометрических функций угла рассмотрим равнобедренный прямоугольный треугольник с катетами (рис. 174).

По теореме Пифагора Имеем:

Представим значения тригонометрических функций углов в виде таблицы.

Значения тригонометрических функций других углов можно вычислить с помощью калькулятора или специальных таблиц (см. Приложение 3).

Решение прямоугольных треугольников

Нахождение неизвестных сторон прямоугольного треугольника

Пусть дан прямоугольный треугольник с катетами гипотенузой и острыми углами (рис. 175).

Зная градусную меру угла и длину любой из сторон треугольника, мы имеем возможность найти две другие его стороны. Правила нахождения неизвестных сторон прямоугольного треугольника непосредственно следуют из определений тригонометрических функций и могут быть обобщены в виде справочной таблицы.

Заметим, что для нахождения неизвестных сторон прямоугольного треугольника можно использовать и (соответствующие правила и формулы получите самостоятельно).

Запоминать содержание справочной таблицы не обязательно. Для нахождения неизвестной стороны прямоугольного треугольника можно действовать по такому плану.

1. Выбрать формулу определения той тригонометрической функции данного угла, которая связывает искомую сторону с известной (этот этап можно выполнить устно).

2. Выразить из этой формулы искомую сторону.

3. Провести необходимые вычисления.

Пример №20

В прямоугольном треугольнике с гипотенузой 12 м найдите катет, прилежащий к углу

Решение:

Пусть в прямоугольном треугольнике (см. рисунок) Найдем катет

Поскольку

Ответ: 6 м.

Примеры решения прямоугольных треугольников

Решить треугольник означает найти его неизвестные стороны и углы по известным сторонам и углам. Прямоугольный треугольник можно решить по стороне и острому углу или по двум сторонам. Рассмотрим примеры конкретных задач на решение прямоугольных треугольников, пользуясь обозначениями рисунка 175. При этом договоримся округлять значения тригонометрических функций до тысячных, длины сторон — до сотых, а градусные меры углов — до единиц.

Пример №21

Решите прямоугольный треугольник по гипотенузе и острому углу (см. рисунок).

Решение:

Поскольку сумма острых углов прямоугольного треугольника равна

Поскольку

т.е.

Поскольку

т.е.

Пример №22

Решите прямоугольный треугольник по катету и острому углу (см. рисунок).

Решение:

Поскольку сумма острых углов прямоугольного треугольника равна

Поскольку

Поскольку

Пример №23

Решите прямоугольный треугольник по гипотенузе и катету (см. рисунок).

Решение:

По теореме Пифагора

Поскольку откуда

Поскольку сумма острых углов прямоугольного треугольника равна

Пример №24

Решите прямоугольный треугольник по катетам (см. рисунок).

Решение:

По теореме Пифагора

Поскольку откуда

Поскольку сумма острых углов прямоугольного треугольника равна

На отдельных этапах решения задач 1—4 можно использовать другие способы. Но следует заметить, что в том случае, когда одна из двух сторон треугольника найдена приближенно, для более точного нахождения третьей стороны целесообразно использовать определения тригонометрических функций.

Рассмотрим примеры применения решения треугольников в практических задачах.

Пример №25

Найдите высоту данного предмета (рис. 176).

Решение:

На определенном расстоянии от данного предмета выберем точку и измерим угол

Поскольку в прямоугольном треугольнике

Для определения высоты предмета необходимо прибавить к высоту прибора, с помощью которого измерялся угол. Следовательно,

Пример №26

Насыпь шоссейной дороги имеет ширину 60 м в верхней части и 68 м в нижней. Найдите высоту насыпи, если углы наклона откосов к горизонту равны

Решение:

Рассмотрим равнобедренную трапецию (рис. 177), в которой

Проведем высоты Поскольку (докажите это самостоятельно), то В треугольнике

Поскольку

т.е.

Ответ:

Синусом острого угла называется отношение противолежащего катета к гипотенузе:

Косинусом острого угла называется отношение прилежащего катета

Тангенсом острого угла называется отношение противолежащего катета к прилежащему:

Котангенсом острого угла называется отношение прилежащего катета к противолежащему:

Тригонометрические тождества

Значения тригонометрических функций некоторых углов

Историческая справка

Умение решать треугольники необходимо при рассмотрении многих практических задач, возникающих в связи с потребностями географии, астрономии, навигации. Поэтому элементы тригонометрии появились еще в Древнем Вавилоне в период интенсивного развития астрономии. В работе греческого ученого Птолемея «Альмагест» (II в. н. где изложена античная система мира, содержатся элементы сферической тригонометрии.

В Древней Греции вместо синуса угла рассматривали длину хорды, соответствующей центральному углу Действительно, если радиус окружности равен единице, то измеряется половиной такой хорды (проверьте это самостоятельно). Первые тригонометрические таблицы были составлены Гиппархом во II в. н.э.

Синус и косинус как вспомогательные величины использовались индийскими математиками в V в., а тангенс и котангенс впервые появились в работах арабского математика X в. Абу-аль-Вефы.

Как отдельный раздел математики тригонометрия выделилась в произведениях персидского ученого Насреддина Туси (1201-1274), а системное изложение тригонометрии первым из европейцев представил немецкий математик и механик Иоганн Мюллер (1436-1476), более известный под псевдонимом Региомонтан.

Современную форму изложения и современную символику тригонометрия приобрела благодаря Леонарду Эйлеру в XVIII в. Кроме известных вам четырех тригонометрических функций иногда рассматриваются еще две:

секанс

и косеканс

Приложения

Обобщенная теорема Фалеса и площадь прямоугольника

В ходе доказательства некоторых геометрических теорем используется процедура деления отрезка на некоторое количество равных частей. Это позволяет дать числовые оценки в виде неравенств и с их помощью получить противоречие.

В курсе геометрии 8 класса такой подход целесообразно применить для доказательства двух приведенных ниже теорем.

Теорема (обобщенная теорема Фалеса)

Параллельные прямые, пересекающие стороны угла, отсекают на сторонах этого угла пропорциональные отрезки.

По данным рисунка 180 докажем три формулы:

Докажем сначала формулу 1. Пусть отрезок можно разделить на равных отрезков так, что одна из точек деления совпадет с точкой причем на отрезке будут лежать точек деления. Тогда, проведя через точки деления прямые, параллельные по теореме Фалеса получим деление отрезков соответственно на равных отрезков. Следовательно, что и требовалось доказать.

Если описанное деление отрезка невозможно, то докажем формулу 1 от противного. Пусть

Рассмотрим случай, когда (другой случай рассмотрите самостоятельно).

Отложим на отрезке отрезок (рис. 181).

Разобьем отрезок на такое количество равных отрезков чтобы одна из точек деления попала на отрезок Проведем через точки деления прямые, параллельные Пусть прямая, проходящая через точку пересекает луч в точке Тогда по доказанному Учитывая, что в этой пропорции имеем:

Это неравенство противоречит выбору длины отрезка Следовательно, формула 1 доказана полностью.

Докажем формулы 2 и 3. Пользуясь обозначениями рисунка 180,
по формуле 1 имеем Разделив в каждом из этих равенств числитель на знаменатель, получим:

Откуда Таким образом, доказано, что т.е. формулы 2 и 3 выполняются.

Теорема доказана полностью.

Из курса математики 5 класса известно, что площадь прямоугольника равна произведению двух его соседних сторон. Так, на рисунке 182 дан прямоугольник который делится на 15 квадратов площадью 1. Следовательно, по аксиомам площади, его площадь равна 15 кв. ед., то есть Рис- 182. кв. ед.

Таким способом легко найти площадь прямоугольника, у которого длины сторон выражены любыми целыми числами. Но справедливость этой формулы при условии, что длины сторон прямоугольника не являются целыми числами,— совсем неочевидная теорема. Докажем ее.

Теорема (формула площади прямоугольника)

Площадь прямоугольника равна произведению его соседних сторон:

— стороны прямоугольника.

Докажем сначала, что площади прямоугольников с одним равным измерением относятся как длины других измерений.

Пусть прямоугольники имеют общую сторону (рис. 183,

Разобьем сторону равных частей. Пусть на отрезке лежит точек деления, причем точка деления имеет номер а точка —номер Тогда откуда —

Теперь проведем через точки деления прямые, параллельные Они разделят прямоугольник равных прямоугольников (т. е. таких, которые совмещаются при наложении). Очевидно, что прямоугольник содержится внутри прямоугольника а прямоугольник содержит прямоугольник

Следовательно,

Имеем:

Сравнивая выражения для убеждаемся, что оба эти отношения расположены между т.е. отличаются не больше чем на натуральное число). Докажем от противного, что эти отношения равны.

Действительно, если это не так, т.е. такое натуральное число что Полученное противоречие доказывает, что площади прямоугольников с одним равным измерением относятся как длины других измерений.

Рассмотрим теперь прямоугольники со сторонами со сторонами и 1 и квадрат со стороной 1 (рис. 183, б).

Тогда по доказанному

Поскольку кв. ед., то, перемножив полученные отношения, имеем

Золотое сечение

С давних времен люди старались познать мир путем поиска гармонии и совершенства. Одним из вопросов, которыми задавались еще древние греки, был поиск наилучшего соотношения неравных частей одного целого. Таким соотношением еще со времен Пифагора считали гармоническое деление, при котором меньшая часть относится к большей, как большая часть относится ко всему целому. Такое деление отрезка на части описано во II книге «Начал» Евклида и названо делением в среднем и крайнем отношении. Рассмотрим деление отрезка точкой при котором (рис. 184). Пусть длина отрезка равна а длина отрезка равна Тогда

Отсюда Поскольку то геометрический смысл имеет только значение Значит, если длина данного отрезка равна 1, то при делении в крайнем и среднем отношении его большая часть приблизительно равна 0,6. Полученное число обозначают греческой буквой Кроме того, часто рассматривают и отношение Заметим, что — первая буква имени древнегреческого скульптора Фидия, который часто использовал такое деление в своем творчестве (в частности, в знаменитой статуе Зевса Олимпийского, которую считают одним из семи чудес света).

В эпоху Возрождения (XV—XVII вв.) интерес к гармоническому делению чрезвычайно возрос. Выдающийся ученый и художник Леонардо да Винчи (1452—1519) назвал такое деление золотым сечением, а его современник и соотечественник, итальянский монах-математик Лука Па-чоли (1445—1514) — божественной пропорцией. Золотое сечение и близкие к нему пропорциональные отношения составляли основу композиционного построения многих произведений мирового искусства, в частности архитектуры Античности и Возрождения. Одно из величайших сооружений Древней Эллады — Парфенон в Афинах (V в. до н. э.) — содержит в себе золотые пропорции (в частности, отношение высоты к длине этого сооружения равно

Итак, дадим определение золотому сечению.

Определение:

Золотым сечением называется такое деление величины на две неравные части, при котором меньшая часть относится к большей, как большая часть относится ко всему целому.

Иначе говоря, золотое сечение — это деление величины в отношении (или

Построить золотое сечение отрезка заданной длины с помощью циркуля и линейки довольно просто: для этого достаточно построить прямоугольный треугольник с катетами и провести две дуги из вершин острых углов так, как показано на рисунке 185.

По теореме о пропорциональности отрезков секущей и касательной Поскольку по построению и по определению золотого сечения. Следовательно, Убедиться в правильности построения можно также с помощью теоремы Пифагора (сделайте это самостоятельно.)

С золотым сечением связывают геометрические фигуры, при построении которых используются отношения Рассмотрим некоторые из них.

Равнобедренный треугольник называется золотым, если две его стороны относятся в золотом сечении. Докажем, что треугольник с углами (рис. 186, а) является золотым. Действительно, пусть в треугольнике биссектриса. Тогда по двум углам. Следовательно, т. е. треугольник — золотой.

И наоборот: если в равнобедренном треугольнике то такой треугольник подобен треугольнику т. е. имеет углы

Предлагаем самостоятельно убедиться в том, что золотым является также треугольник с углами (рис. 186, б) и других золотых треугольников не существует.

Золотые треугольники связаны с правильным пятиугольником (т.е. выпуклым пятиугольником, у которого все стороны равны и все углы равны).

В правильном пятиугольнике:

1) диагональ относится к стороне в золотом сечении;

2) точка пересечения диагоналей делит каждую из них в золотом сечении;

3) диагональ делит другую диагональ на два отрезка, один из которых делится в золотом сечении еще одной диагональю.

Согласно обозначениям рисунка 187 это означает, что Для доказательства этих свойств достаточно заметить, что в правильном пятиугольнике все углы равны следовательно, треугольники являются золотыми. Подробные доказательства предлагаем провести самостоятельно.

Диагонали правильного пятиугольника образуют звезду, которая в древние времена олицетворяла совершенство и имела мистическое значение. Пифагорейцы называли ее пентаграммой и избрали символом своей научной школы. В наши дни пятиконечная звезда — самая распространенная геометрическая фигура на флагах и гербах многих стран (приведите соответствующие примеры из истории и географии).

Прямоугольник называется золотым, если его стороны относятся в золотом сечении. Для построения золотого прямоугольника произвольный квадрат перегибаем пополам (рис. 188, а), проводим диагональ одного из полученных прямоугольников (рис. 188, б) и радиусом, равным этой диагонали, проводим дугу окружности с центром (рис. 188, в). Полученный прямоугольник — золотой (убедитесь в этом самостоятельно).

Если от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то оставшийся прямоугольник также будет золотым. Действительно, на рисунке 189, а имеем тогда Неограниченно продолжая этот процесс (рис. 189, б), можно получить так называемые вращающиеся квадраты, и весь данный прямоугольник будет составлен из таких квадратов.

Через противолежащие вершины квадратов проходит так называемая золотая спираль, которая часто встречается в природе. Например, по принципу золотой спирали располагаются семена в подсолнечнике; по золотой спирали закручены раковины улиток, рога архаров, паутина отдельных видов пауков и даже наша Солнечная система, как и некоторые другие галактики.

Отметим также, что золотое сечение имеет немало алгебраических свойств. Отношение приближенно может быть выражено дробями так называемые числа Фибоначчи. Приведем без доказательства две алгебраические формулы, связанные с числами

Золотое сечение, золотые многоугольники и золотая спираль являются математическими воплощениями идеальных пропорций в природе. Недаром великий немецкий поэт Иоганн Вольфганг Гете считал их математическими символами жизни и духовного развития.
Приложение 3. Таблица значений тригонометрических функций

Значение тригонометрических функций острых углов можно приближенно определять с помощью специальных таблиц. Одна из таких таблиц представлена выше.

Таблица составлена с учетом формул дополнения. В двух крайних столбцах указаны градусные меры углов (в левом — от в правом — от Между этими столбцами содержатся четыре столбца значений тригонометрических функций:

1-й — синусы углов от (или косинусы углов от

2-й — тангенсы углов от (или котангенсы углов от

3-й — котангенсы углов от (или тангенсы углов от

4-й — косинусы углов от (или синусы углов от

Рассмотрим несколько примеров применения данной таблицы. 1) Определим Поскольку найдем в крайнем левом столбце значение 25 и рассмотрим соответствующую строку первого столбца значений. Углу в ней соответствует число 0,423. Следовательно,

2) Определим Поскольку 45° ے C = 90° (рис. 412).

Доказать:

Доказательство. Проведём из вершины прямого угла С высоту CD. Каждый катет прямоугольного треугольника является средним пропорциональным между гипотенузой и его проекцией на гипотенузу. Поэтому и . Сложив равенства почленно и зная, что AD+ DB= АВ, получим: . Следовательно,

Если а и b — катеты прямоугольного треугольника, с – его гипотенуза, то из формулы получим следующие формулы:

Используя эти формулы, по двум любым сторонам прямоугольного треугольника находим его третью сторону (табл. 28).

Справедлива и теорема, обратная теореме Пифагора: если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то этот треугольник – прямоугольный.

Согласно теореме, обратной теореме Пифагора, треугольник со сторонами 3 см, 4 см и 5 см – прямоугольный, поскольку . Такой треугольник иногда называют египетским.

Пример №27

Сторона ромба равна 10 см, а одна из его диагоналей — 16 см. Найдите другую диагональ ромба.

Решение:

Пусть ABCD— ромб (рис. 413), АС= 16см,AD = 10см. Найдём диагональ BD. Как известно, диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам. Поэтому ∆AOD — прямоугольный ( ے 0= 90°). АС 16

В нём: катет гипотенуза AD= 10 см.

Для того чтобы найти определённый элемент фигуры (сторону, высоту, диагональ), выделите на рисунке прямоугольный треугольник, воспользовавшись свойствами фигуры, и примените теорему Пифагора.

Пусть ВС – перпендикуляр, проведённый из точки В на прямую а (рис. 414). Возьмём произвольную точку А на прямой а, отличную от точки С, и соединим точки А и В. Отрезок АВ называется наклонной, проведённой из точки В на прямую а. Точка А называется основанием наклонной, а отрезок АС – проекцией наклонной.

Наклонные имеют следующие свойства. Если из данной точки к прямой провести перпендикуляр и наклонные, то:

1. любая наклонная больше перпендикуляра;
2. равные наклонные имеют равные проекции;
3. из двух наклонных больше та, проекция которой больше.

Покажем, что свойства наклонных следуют из теоремы Пифагора.

1. По теореме Пифагора, (рис. 415), тогда или АВ > ВС.
2. Из прямоугольных треугольников ABD и CBD (рис. 416) имеем:
3. Поскольку в этих равенствах АВ = ВС (по условию), то AD = DC.
4. Из прямоугольных треугольников ABD и CBD (рис. 417) имеем: . В этих равенствах AD > DC. Тогда АВ > ВС.

Пример №28

Из точки к прямой проведены две наклонные, проекции которых равны 5 см и 9 см. Найдите наклонные, если одна из них на 2 см больше другой.

Решение:

Пусть AD = 5 см, DC = 9 см (рис. 418). Поскольку AD ے A = a (рис. 441). Вы знаете, что катет а – противолежащий углу а, катет b – прилежащий к углу a . Отношение каждого катета к гипотенузе, а также катета к катету имеют специальные обозначения:

• – отношение обозначают sin а и читают «синус альфа»;
• – отношение обозначают cos а и читают «косинус альфа»;
• – отношение обозначают tg а и читают «тангенс альфа».

Сформулируем определения sin a, cos а и tg а.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Отношение сторон прямоугольного треугольника и их обозначения указаны в

Зависят ли синус, косинус и тангенс острого угла от размеров треугольника?

Нет, не зависят. Итак, пусть ABC и -два прямоугольных треугольника, в которых (рис. 442). Тогда по двум углам (). Соответствующие стороны этих треугольников пропорциональны:

Из этих равенств следует:

Следовательно, в прямоугольных треугольниках с одним и тем же острым углом синусы этого утла равны, косинусы и тангенсы – равны. Если градусную меру угла изменить, то изменится и соотношение сторон прямоугольного треугольника. Это означает, что синус, косинус и тангенс острого угла прямоугольного треугольника зависят только от градусной меры угла и не зависят от размеров треугольника.

По исходному значению sin A, cos А или tg А можно построить угол А.

Пример №29

Постройте угол, синус которого равен .

Решение:

Выбираем некоторый единичный отрезок (1 мм, 1 см, 1 дм). Строим прямоугольный треугольник, катет ВС которого равен двум единичным отрезкам, а гипотенуза АВ — трём (рис. 443). Угол А, лежащий против катета ВС, — искомый, поскольку sin А =

В прямоугольном треугольнике любой из двух катетов меньше гипотенузы. Поэтому sin а ے C = а (рис. 452). Проведём высоту BD. В прямоугольном треугольнике DBCкатет DC, прилежащий к углу а, равен произведению гипотенузы а на cos a: DC = a cos а. Поскольку высота равнобедренного треугольника, опущенная на основание, является медианой, то DC = AD. Тогда основание АС = 2 DC =2 a cos а.

В этой главе вы ознакомились с новыми приёмами вычисления длин сторон и градусных мер углов прямоугольного треугольника. Может возникнуть вопрос: Какова необходимость использования этих приёмов? Вы знаете, что в древности расстояния и углы сначала измеряли непосредственно инструментами. Например, транспортиром пользовались вавилоняне ещё за 2 ООО лет до н. э.

Но на практике непосредственно измерять расстояния и углы не всегда возможно. Как вычислить расстояние между двумя пунктами, которые разделяет препятствие (река, озеро, лес), расстояние до Солнца, Луны, как измерить высоту дерева, горы, как найти угол подъёма дороги либо угол при спуске с горы? Поэтому были открыты приёмы опосредствованного измерения расстояний и углов. При этом использовали равные либо подобные треугольники и геометрические построения. Строили на местности вспомогательный треугольник и измеряли необходимые его элементы.

Итак, вы знаете, как определить расстояние между пунктами А и В, разделёнными препятствием (рис. 453). Для этого строим ∆COD = ∆АОВ и вместо искомого расстояния Ив измеряем равное ему расстояние CD.

Но при использовании этих приёмов получали недостаточно точные результаты, особенно при измерении значительных расстояний на местности. Кроме того, без угломерных инструментов нельзя найти градусные меры углов по длинам тех или других отрезков. Поэтому возникла необходимость в таких приёмах, когда непосредственные измерения сводились к минимуму, а результаты получали преимущественно вычислением элементов прямоугольного треугольника. В основе таких приёмов лежит использование cos а, sin а и tg а. Накопление вычислительных приёмов решения задач обусловило создание нового раздела математики, который в XVI в. назвали тригонометрией. Слово «тригонометрия» происходит от греческих слов trigonon — треугольник и metreo — измеряю. Греческих математиков Гиппарха (II в. до н. э.) и Птолемея (II в.) считают первыми, кто использовал тригонометрические приёмы для решения разных задач. В дальнейшем их усовершенствовали индийский математик Брамагупта (VI в.), узбекские математики аль-Каши и Улугбек (XII в.). В работах академика Леонарда Эйлера (XVIII в.) тригонометрия приобретает тот вид, который в основном имеет и в наше время.

Вычисление значений sin a, cos а и tg а

ЕЭ| Пусть в прямоугольном треугольнике ABC ZA = а, тогда ZB – 90° – а (рис. 467). Из определения синуса и косинуса следует:

Сравнивая эти два столбца, находим: sin а = cos (90° – а), cos а = sin (90° – а).

Как видим, между синусом и косинусом углов а и 90° – а, которые дополняют друг друга до 90°, существует зависимость: синус одного из этих углов равен косинусу другого.

Например:

Найдём значения синуса, косинуса и тангенса для углов 45°, 30°, 60°. 1) Для угла 45°. Пусть ABC – прямоугольный треугольник с гипотенузой С и ے A = 45° (рис. 468). Тогда ے B = 45°. Следовательно, ∆ABC – равнобедренный. Пусть АС = ВС = а. Согласно теореме Пифагора,

2) Для углов 30° и 60°.

Пусть ABC – прямоугольный треугольник с гипотенузой с и ے A = 30″ (рис. 469). Найдём катеты АС и ВС.

ВС = как катет, лежащий против угла 30°.

Согласно теореме Пифагора,

Тогда

Если в прямоугольном треугольнике ABC ے A = 30° (рис. 469),

Составим таблицу 35 значений синуса, косинуса и тангенса для углов 30°, 45°, 60°

Таблица 35

Из таблицы видно, что при увеличении угла синус и тангенс острого угла возрастают, а косинус — уменьшается. При уменьшении угла синус и тангенс острого угла уменьшаются, а косинус – увеличивается.

Пример №31

Сторона ромба равна 6 см, а один из его углов Найдите высоту ромба.

Решение:

Пусть ABCD — ромб (рис. 470), в котором АВ = 6 см, ے А = 60°. Проведём высоту ВМ. Из прямоугольного треугольника АВМ: Как вычислить значения синусов, косинусов и тангенсов углов, отличных от 30°, 45°, 60°?

При помощи инженерных калькуляторов (или программы «калькулятор» компьютера) либо специальных таблиц можно решить две задачи:

1) для заданного угла а найти sin a, cos а, tg а;

2) по заданному значению sin a, cos а, tg а найти угол а.

Если вы используете калькулятор, а угол указан в градусах и минутах, то минуты переведите в десятые доли градуса (разделите их на 60). Например, для угла 55°42° получите 55,7°. Если, например, для cos 0,8796 нашли 28,40585° то доли градуса переведите в минуты (умножьте дробную часть на 60). Округлив, получите: 28°24°.

Значение sin a, cos а, tg а находим по таблицам.

Таблица синусов и косинусов (см. приложение 1) состоит из четырёх столбцов. В первом столбце слева указаны градусы от 0° до 45°, а в четвёртом – от 90° до 45°. Над вторым и третьим столбцами указаны названия «синусы» и «косинусы», а в нижней части этих столбцов – «косинусы» и «синусы».

Верхние названия «синусы» и «косинусы» отображают значения углов, которые меньше 45°, а нижние – больше 45°. Например, по таблице находим: sin34° 0,559, cos67° 0,391, sin85° 0,996 и т. д. По таблице можно найти угол а по заданному значению sin a, cos а. Например, нужно найти угол а, если sin 0,615. В столбцах синусов находим число, приближённое к 0,615. Таким числом является 0,616. Следовательно, 38″.

Таблица тангенсов (см. приложение 2) состоит из двух столбцов: в одном указаны углы от 0° до 89°, в другом – значения тангенсов этих углов.

Например, tg 19° 0,344. Если tg 0,869, то 41°.

1. Вы уже знаете, что каждой градусной мере угла а прямоугольного треугольника соответствует единственное значение sin a, cos а, tg а. Поэтому синус, косинус и тангенс угла а являются функциями данного угла. Эти функции называются тригонометрическими функциями, аргумент которых изменяется от О° до 90°.

2. Уточним происхождение слова «косинус». Именно равенство cos а = sin (90° — а) явилось основой образования латинского слова cosinus — дополнительный синус, то есть синус угла, дополняющий заданный до 90°.

3. Первые таблицы синусов углов от 0° до 90° составил греческий математик Гиппарх (II в. до н. э.). Эти таблицы не сохранились. Нам известны только тригонометрические таблицы, помещённые в работе «Альмагест» александрийского учёного Клавдия Птолемея (II в.). Птолемей Также сохранились таблицы синусов и косинусов индийского учёного Ариаб-хаты (V в.), таблицы тангенсов арабских учёных аль-Баттани и Абу-ль-Вефа (X в.).

Как решать прямоугольные треугольники

Решить прямоугольный треугольник – это означает по заданным двум сторонам либо стороне и острому углу найти другие его стороны и острые углы.

Возможны следующие виды задач, в которых требуется решить прямоугольный треугольник по: 1) катетам; 2) гипотенузе и катету; 3) гипотенузе и острому углу; 4) катету и острому углу. Алгоритмы решения этих четырёх видов задач изложены в таблице 36.

Пример №32

Решите прямоугольный треугольник по гипотенузе с= 16 и углу а = 76°21′ (рис. 482).

Решение. Это задача третьего вида. Алгоритм её решения указан в таблице 38.

Решение многих прикладных задач основано на решении прямоугольных треугольников. Рассмотрим некоторые виды прикладных задач.

1. Задачи на нахождение высоты предмета, основание которого доступно.

Пример №33

Найдите высоту дерева (рис. 483).

Решение:

На некотором расстоянии MN= а от дерева устанавливаем угломерный прибор AM (например, теодолит) и находим угол а между горизонтальным направлением АС и направлением на верхнюю точку В дерева. Из прямоугольного треугольника ABC получим: ВС= a • tg а. С учётом высоты угломерного прибора AM= h имеем формулу для вычисления высоты дерева: BN= о • tg а + h.

Пусть результаты измерения следующие: .

Тогда (м).

2. Задачи на нахождение высоты предмета, основание которого недоступно.

Пример №34

Найдите высоту башни, которая отделена от вас рекой (рис. 484).

Решение:

На горизонтальной прямой, проходящей через основание башни (рис. 484), обозначим две точки М и N, измерим отрезок MN= а и углы . Из прямоугольных треугольников ADC и BDC получим:

Почленно вычитаем полученные равенства:

Отсюда

Следовательно,

Прибавив к DC высоту прибора AM= Н, которым измеряли углы, получим

формулу для вычисления высоты башни:

Пусть результаты измерения следующие:

Тогда

3. Задачи на нахождение расстояния между двумя пунктами, которые разделяет препятствие.

Пример №35

Найдите расстояние между пунктами А и В, разделёнными рекой (рис. 485).

Решение:

Провешиваем прямую и отмечаем на ней точку С. Измеряем расстояние АС= а и угол а. Из прямоугольного треугольника ABC получим формулу АВ= a- tg а для определения расстояния между пунктами А и В. Пусть результаты измерения следующие:

Тогда АВ =

4. Задачи на нахождение углов (угла подъёма дороги; угла уклона; угла, под которым виден некоторый предмет, и т. д.).

Пример №36

Найдите угол подъёма шоссе, если на расстоянии 200 м высота подъёма составляет 8 м.

Решение:

На рисунке 486 угол a — это угол подъёма дороги, АС— горизонтальная прямая. Проведём , тогда ВС- высота подъёма дороги. По условию, АВ = 200 м, ВС = 8 м. Угол a найдём из прямоугольного треугольника Тогда

У вас может возникнуть вопрос: Почему в геометрии особое внимание уделяется прямоугольному треугольнику, хотя не часто встречаются предметы подобной формы?

Итак, поразмышляем. Как в химии изучают вначале элементы, а затем — их соединения, в биологии — одноклеточные, а потом — многоклеточные организмы, так и в геометрии изучают сначала простые геометрические фигуры — точки, отрезки и треугольники, из которых состоят другие геометрические фигуры. Среди этих фигур прямоугольный треугольник играет особую роль. Действительно, любой многоугольник можно разбить на треугольники (рис. 487).

Умея находить угловые и линейные элементы этих треугольников, можно найти все элементы многоугольника. В свою очередь, любой треугольник можно разбить одной из его высот на два прямоугольных треугольника, элементы которых связаны более простой зависимостью (рис. 488). Найти элементы треугольника можно, если свести задачу к решению этих двух прямоугольных треугольников. Проиллюстрируем это на примере.

Пример №37

(рис. 489). Найдите ے B, ے C и сторону а.

Решение:

Проведём высоту BD. Точка D будет лежать между точками А и С, поскольку ے A — острый и b> с.

Из прямоугольного треугольника ABD:

Из прямоугольного треугольника

Из прямоугольного треугольника BDC:

Рекомендую подробно изучить предметы:

Геометрия Аналитическая геометрия Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

• Параллелограмм
• Теорема синусов и теорема косинусов
• Параллельность прямых и плоскостей
• Перпендикулярность прямой и плоскости
• Площадь трапеции
• Центральные и вписанные углы
• Углы и расстояния в пространстве
• Подобие треугольников

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Свойства прямоугольного треугольника

• В прямоугольном треугольнике гипотенуза является наибольшей стороной.
• В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

• Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
• Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

1. по катетам;
2. по катету и прилежащему острому углу;
3. по гипотенузе и острому углу;
4. по гипотенузе и катету.

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.

[spoiler title=”источники:”]

http://www.evkova.org/reshenie-pryamougolnyih-treugolnikov

[/spoiler]