Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.

Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:

Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:

Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Площадь круга, вписанного в квадрат: формула, примеры решения задач

Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:

Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Площадь круга, описанного около квадрата: формула, примеры решения задач

Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:

Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач

Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:

Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:

Примеры решения заданий:
Задача №1

Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2

Решение:

Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:

Примеры решения задач:

Вот еще пример решения задачи с использованием формулы Герона.

Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
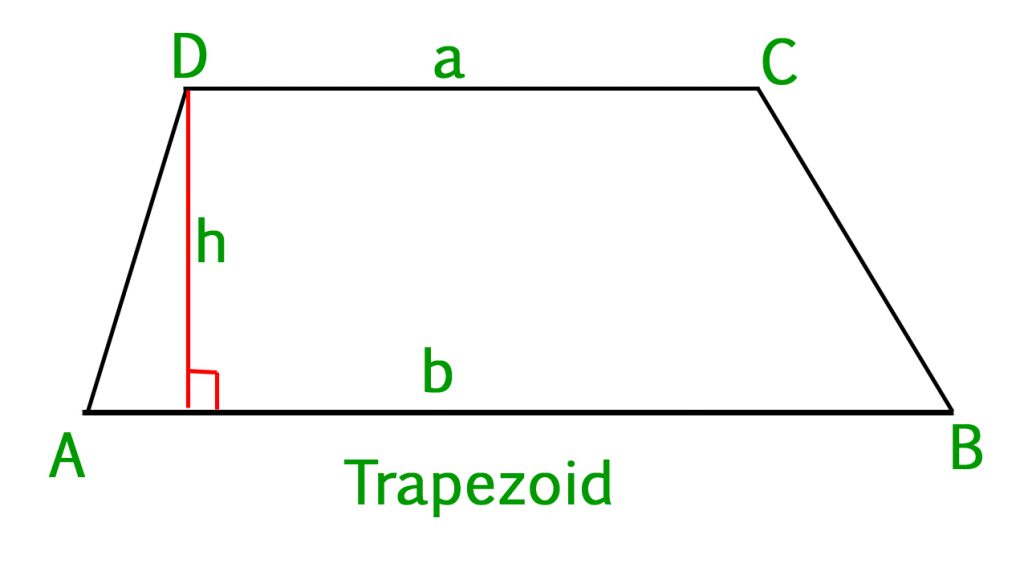
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:

Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:

Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:


Примеры решения задач:

Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
Окружность, вписанная в трапецию
Что такое окружность, вписанная в трапецию
Окружность можно вписать в любой треугольник. Однако это утверждение нельзя применить к любому из четырехугольников.
Прежде чем приступить к рассмотрению темы о вписанной в трапецию окружности, дадим определение вписанной окружности.
Вписанной в многоугольник окружностью называют окружность, которая касается каждой из сторон многоугольника в одной точке. Многоугольник в этом случае называют описанным около окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема 1
Теорема о вписанной окружности: в произвольный выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство: пусть имеется произвольный четырехугольник MNKL и вписанная в него окружность. Обозначим точки касания окружности со сторонами четырехугольника как O, P, R, S.
Если касательные проведены из одной точки, то отрезки, построенные от этой точки до точки касания с окружностью, равны. Тогда KS=KR, LS=LO, MO=MP, NR=NP. Вычислим суммы противоположных сторон: MN+KL=(MP+NP)+(KS+LS) и NK+ML=(NR+KR)+(MO+LO).
Из равенства отрезков получим, что MN+KL= NK+ML.
Примечание 1
Четырехугольник считают выпуклым, если он расположен в одной полуплоскости относительно линии, проходящей через любую из его сторон.
Трапеция является выпуклым четырехугольником. При этом две параллельные стороны трапеции называют основаниями, а две остальные — боковыми сторонами.
Тогда необходимым условием наличия вписанной окружности в трапецию будет равенство суммы ее оснований и боковых сторон.
Для обратного случая — окружность описана вокруг трапеции, трапеция должна быть равнобедренной, то есть ее боковые стороны должны быть равными.
Рассмотрим свойства вписанной в трапецию окружности.
Из свойства биссектрис при боковых сторонах трапеции следует, что радиусы вписанной окружности, проведенные к вершинам боковой стороны и лежащие на биссектрисах, образуют прямой угол.
Примечание 2
Биссектрисы трапеции пересекаются под углом 90°.
Радиус вписанной окружности, проведенный к точкам касания, перпендикулярен сторонам трапеции (по свойству перпендикулярности радиуса и касательной).
Из предыдущего свойства вытекает следующее: радиус вписанной окружности равен половине высоты трапеции, а диаметр — полной длине высоты.
Примечание 3
Высота трапеции — прямая, опущенная от одного основания к другому под прямым углом.
Где находится центр такой окружности
Для построения и решения задача необходимо определить, где расположен центр вписанной окружности.
Примечание 4
Центр окружности, вписанной в трапецию, лежит в точке пересечения биссектрис.
Биссектрисы трапеции пересекаются под прямым углом, отсюда можно сделать следующий вывод: треугольники MON и KOL — прямоугольные.
Формулы для расчета
Основными характеристиками любой окружности являются радиус и диаметр.
Точка касания окружности радиусом R и боковой стороны делит последнюю на два отрезка v и q. Тогда формула для вычисления радиуса будет иметь вид:
Формула 1
(R=sqrt{vcdot q})
Если трапеция равнобедренная и сумма длин оснований равна двум длинам боковой стороны, радиус вписанной окружности:
Формула 2
(R=frac{sqrt{vcdot q}}2)
Диаметр равен длине двух радиусов, значит:
Формула 3
(D=2sqrt{vcdot q})
Формула радиуса через высоту трапеции:
Диаметр через высоту:
Если значение высоты неизвестно, ее можно найти через длины диагоналей (d_1) и (d_2) и оснований a и b трапеции:
Формула 6
(h=frac{d_1cdot d_2}{a+b}singamma)
где γ — угол между диагоналями трапеции.
Площадь вписанной окружности через параметры трапеции (высоту, отрезки боковой стороны):
Формула 7
(S=pi R^2=frac14pi h^2)
или
Формула 8
(S=pi R^2=picdot vcdot q)
В случае равнобедренной трапеции:
Формула 9
(S=pi R^2=frac{picdot vcdot q}4)
Периметр вписанной окружности через параметры трапеции:
Формула 10
(P=2mathrm{πR}=mathrm{πh})
или
Формула 11
Если трапеция равнобедренная:
Формула 12
(P=2mathrm{πR}=mathrmpisqrt{mathrm{vq}})
Приведем формулы для вычисления произвольной и равнобедренной трапеции через радиус вписанной окружности R.
Площадь трапеции:
Формула 13
(S=frac{a+b}2h=(a+b)R)
Полусумма оснований a и b равна средней линии l, тогда:
Формула 14
(S=2cdot lcdot R)
Площадь равнобедренной трапеции:
Формула 15
( S=frac{4R^2}{sinalpha})
где α — угол между основанием и боковой стороной.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given two bases of the isosceles trapezoid ABCD as a and b, the task is to find the area of circle inscribed in this trapezoid
Examples:
Input: a = 10, b = 30 Output: Area = 235.57 Input: a = 20, b = 36 Output: Area = 565.38
Derivation: Given a circle inscribed in trapezium ABCD (sides AB = n and CD = m), we need to find out the height of the trapezium i.e., (AL), which is half of the radius of the circle to find the area of the circle.
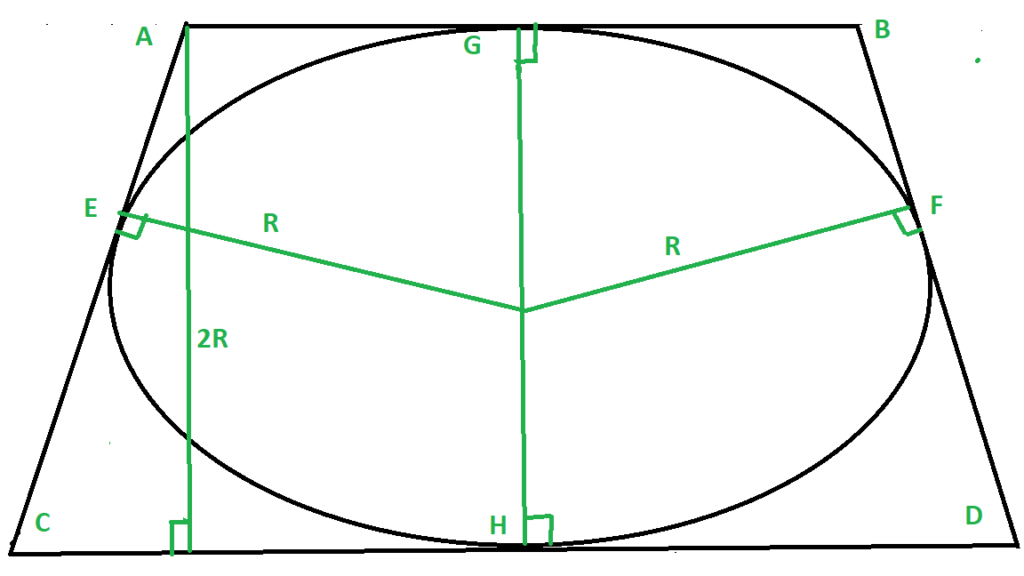
For finding the height of circle we do following operation.
- The circle will always touch the sides of trapezium at their midpoints, Say the midpoints of AB, BD, CD, AC are G, F, H, E, and join them with the center of the circle.
- Now from Symmetry, we can see that
AG = AE = n/2, EC = CG = m/2, HD = DF = n/2, GB = FB = m/2
- Now in Triangle ACL apply the Pythagoras theorem.
Hypotenuse AC = m/2 + n/2 Base CL = CH - AG = m/2 - n/2 we get Perpendicular AL = Square_root(m * n)
- Therefore the height of the Trapezium = AL = Square_Root(Product of given sides)
- Now the radius of the circle is simple half of the height and hence the area can be calculated easily.
Approach:
- Find the height of the trapezoid as (square_root( m * n )).
- Find the radius of the incircle
R = height / 2 = square_root(m * n) / 2
- Now find the area of the circle
= Pi * R2 = ( 3.141 * m * n ) / 4
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
double area_of_circle(int m, int n)
{
int square_of_radius = ( m * n ) / 4;
double area = ( 3.141 * square_of_radius );
return area;
}
int main(){
int n = 10;
int m = 30;
cout << (area_of_circle(m, n));
}
Java
class GFG
{
static double area_of_circle(int m, int n)
{
int square_of_radius = ( m * n ) / 4;
double area = ( 3.141 * square_of_radius );
return area;
}
public static void main (String[] args)
{
int n = 10;
int m = 30;
System.out.println(area_of_circle(m, n));
}
}
Python3
def area_of_circle(m, n):
square_of_radius = ( m * n ) / 4
area = ( 3.141 * square_of_radius )
return area
if __name__=='__main__':
n = 10
m = 30
print(area_of_circle(m, n))
C#
using System;
class GFG
{
static double area_of_circle(int m, int n)
{
int square_of_radius = ( m * n ) / 4;
double area = ( 3.141 * square_of_radius );
return area;
}
public static void Main ()
{
int n = 10;
int m = 30;
Console.WriteLine(area_of_circle(m, n));
}
}
Javascript
<script>
function area_of_circle(m, n)
{
var square_of_radius = ( m * n ) / 4;
var area = ( 3.141 * square_of_radius );
return area;
}
var n = 10;
var m = 30;
document.write(area_of_circle(m, n));
</script>
Time complexity: O(1)
space complexity: O(1)
Last Updated :
21 Jun, 2022
Like Article
Save Article
 Главная
Главная  Учёба
Учёба  Площадь круга
Площадь круга  Площадь круга вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании
Площадь круга вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании
Площадь круга вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании
Формула расчёта площади круга вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании Вам необходимо указать сторону равнобедренной трапеции (b) и угол при основании (α).
Расчёт происходит по формуле 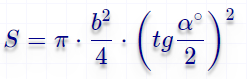 .
.
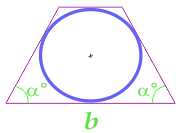 Другая Формула
Другая Формула
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Светило науки – 7292 ответа – 165986 раз оказано помощи
Ответ: S=π•[(ab/(a+b)]²
Объяснение: Обозначим трапецию АВСD, ВС||AD, СВА=ВАD=90°. ВС=а, AD=b.
Формула площади трапеции
Ѕ=0,5•(а+b)•h
Высота трапеции равна диаметру вписанной окружности=2r ⇒
S=(a+b)•2r/2 ⇒
r=S/(a+b)
Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. S=ab
ab=(a+b)•r ⇒ r=ab/(a+b)
S(круга)=πr²
S=π•[(ab/(a+b)]²
* * *
Несложно доказать, что в такой трапеции S=ab, если соединить вершины С и D с центром окружности и выразить r=высоту прямоугольного ∆ СОD из произведения отрезков касательных, но это уже другая задача.
* * *
Задачу можно решить и другим способом :
Если в четырехугольник вписана окружность. суммы длин его противоположных сторон равны.
Тогда АВ+CD=a+b. В прямоугольном треугольнике СНD по т.Пифагора СН²=СD²-DH²
CH=2r, HD=AD-BC=b-a, а CD=a+b-2r. Найденный радиус также будет ав/(а+в)

