Метод эквивалентного генератора:
Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощностн и др.) только одной ветви сложной электрической цепи.
Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление R, ток которого 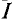
Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС 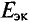
Ток в резисторе с сопротивлением R определяют по закону Ома
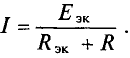
Таким образом, определение тока 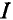 сводится к вычислению ЭДС эквивалентного генератора
сводится к вычислению ЭДС эквивалентного генератора 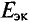 и его внутреннего сопротивления
и его внутреннего сопротивления 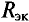 .
.
Величина ЭДС 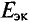 определяется любым методом расчета цепей постоянного тока относительно точек А а В при разомкну-клеммах, т. е. в режиме холостого хода. Практически эту ЭДС о измерить вольтметром, подключенным к клеммам А и В холостом ходе.
определяется любым методом расчета цепей постоянного тока относительно точек А а В при разомкну-клеммах, т. е. в режиме холостого хода. Практически эту ЭДС о измерить вольтметром, подключенным к клеммам А и В холостом ходе.
Внутреннее сопротивление эквивалентного генератора 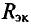 выявляется относительно точек А и В после предварительной смены всех источников сложной схемы эквивалентного генера-а их внутренними сопротивлениями.
выявляется относительно точек А и В после предварительной смены всех источников сложной схемы эквивалентного генера-а их внутренними сопротивлениями.
Практически для определения внутреннего сопротивления эквивалентного генератора измеряют амперметром ток между точки А и В работающего двухполюсника при коротком замыкании так как сопротивление амперметра настолько мало, что им можно пренебречь. Тогда

где 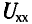 — напряжение холостого хода,
— напряжение холостого хода, 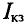 — ток короткого замыкания.
— ток короткого замыкания.
Такой метод практического определения внутреннего сопротивления эквивалентного генератора 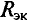 называется методом хо-ого хода и короткого замыкания. Расчет параметров эквивалентного генератора, его ЭДС
называется методом хо-ого хода и короткого замыкания. Расчет параметров эквивалентного генератора, его ЭДС 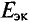 и внутреннего сопротивления
и внутреннего сопротивления 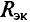 , рассматриваются в примерах 4.12 4.13.
, рассматриваются в примерах 4.12 4.13.
Пример 4.12
Определить ток в сопротивлении 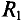 , подключенном к точкам А В электрической цепи (рис. 4.8а) примера 4.6 методом эквивалентного генератора.
, подключенном к точкам А В электрической цепи (рис. 4.8а) примера 4.6 методом эквивалентного генератора.
Решение
Для определения тока 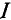 в сопротивлении
в сопротивлении 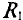 определим ЭДС эквивалентного генератора
определим ЭДС эквивалентного генератора 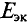 (рис. 4.16а) и его внутреннее сопротивление
(рис. 4.16а) и его внутреннее сопротивление 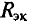 (рис. 4.166) при холостом ходе, т. е. разомкнутой цепи (между точками А и В).
(рис. 4.166) при холостом ходе, т. е. разомкнутой цепи (между точками А и В).
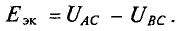
Знак «минус» обусловлен тем, что источники в схеме включены встречно и потенциал в точке А больше потенциала в точке В, так как 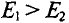 (см. пример 4.6).
(см. пример 4.6).
Напряжение
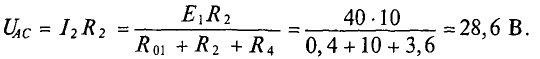
Напряжение
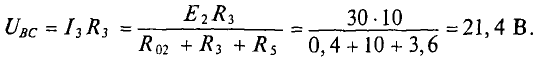
Следовательно, 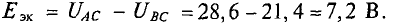 Внутреннее сопротивление эквивалентного генератора
Внутреннее сопротивление эквивалентного генератора
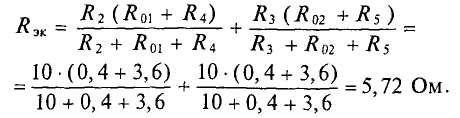
Искомый ток 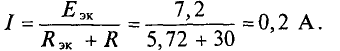
Такой же ток получен в примере 4.6 на сопротивлении 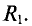
Пример 4.13
В схеме рис. 4.17а сопротивления плеч моста равны 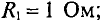
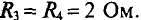
Сопротивление гальванометра Rr = 98,33 Ом, ЭДС источника 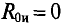 . Методом эквивалентного генератора определить в ветви гальванометра (между точками А и В).
. Методом эквивалентного генератора определить в ветви гальванометра (между точками А и В).
Решение
Для определения тока в цепи гальванометра 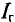 методом эквивалентного генератора необходимо вычислить ЭДС эквивалентного генератора
методом эквивалентного генератора необходимо вычислить ЭДС эквивалентного генератора 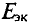 между точками А и В (рис. 4.176) и внутреннее сопротивление эквивалентного генератора
между точками А и В (рис. 4.176) и внутреннее сопротивление эквивалентного генератора 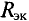 относительно точек А и В при присутствии гальванометра, заменив в схеме (рис. 4.17в) источник ЭДС
относительно точек А и В при присутствии гальванометра, заменив в схеме (рис. 4.17в) источник ЭДС 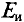 его внутренним сопротивлением (
его внутренним сопротивлением (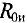 = 0) равным нулю.
= 0) равным нулю.
Для определения ЭДС эквивалентного генератора 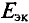 принимают потенциал точки С схемы (рис. 4.176) равным нулю, т. е. фс=о.
принимают потенциал точки С схемы (рис. 4.176) равным нулю, т. е. фс=о.
Тогда
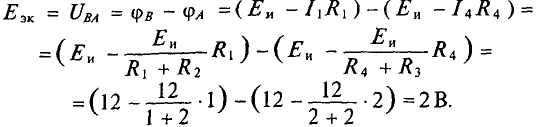
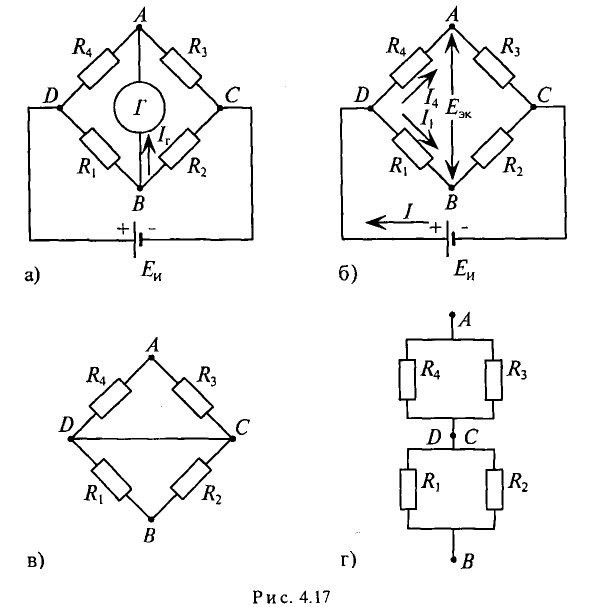
При замене источника ЭДС 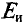 его внутренним сопротивлением, равным нулю, замыкаются накоротко точки С и D схемы (рис. 4.17в). При этом (рис. 4.17г) сопротивления
его внутренним сопротивлением, равным нулю, замыкаются накоротко точки С и D схемы (рис. 4.17в). При этом (рис. 4.17г) сопротивления 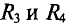 соединены между собой параллельно. Также параллельно соединены между собой сопротивления
соединены между собой параллельно. Также параллельно соединены между собой сопротивления 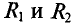 . Между точками А и В сопротивления
. Между точками А и В сопротивления 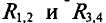 соединены последовательно. Следовательно, сопротивление эквивалентного генератора относительно точек А и В будет равно
соединены последовательно. Следовательно, сопротивление эквивалентного генератора относительно точек А и В будет равно
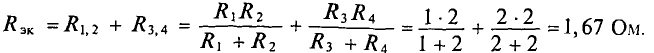
Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с наименьшим потенциалом (рис. 4.17а), будет равен
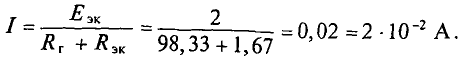
Метод эквивалентного генератора (активного двухполюсника)
Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.
Пусть дана некоторая электрическая цепь, которую заменим активным двухполюсником (рис. 3.10), оставив только ветвь 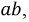 в которой необходимо рассчитать ток.
в которой необходимо рассчитать ток.
Сначала, введем в ветвь 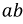 два источника ЭДС
два источника ЭДС 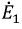 и
и 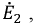 одинаковые по величине и противоположно направленные:
одинаковые по величине и противоположно направленные:
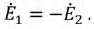
Затем, используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС 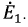 Вторая цепь представляет собой пассивный двухполюсник, имеющий входное сопротивление
Вторая цепь представляет собой пассивный двухполюсник, имеющий входное сопротивление 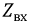 и источник ЭДС
и источник ЭДС 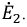
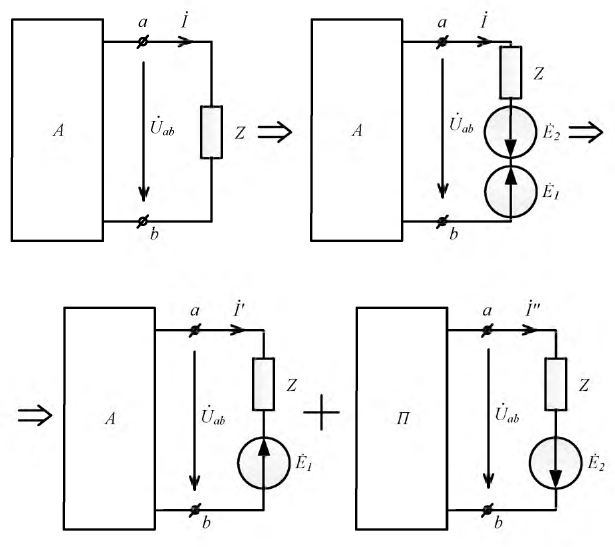
Рис. 3.10. Преобразование исходного двухполюсника в сумму двух цепей
На основании принципа наложения ток ветви 
Поскольку  и они могут быть любые по величине, то подберем их значения такими, чтобы ток
и они могут быть любые по величине, то подберем их значения такими, чтобы ток 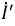 был равен нулю. Для этого выберем
был равен нулю. Для этого выберем 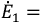
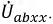
Напряжение на зажимах источника в режиме холостого хода численно равно его ЭДС. Тогда активный двухполюсник с источником 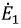 может быть представлен в виде, представленном на рис. 3.11:
может быть представлен в виде, представленном на рис. 3.11:
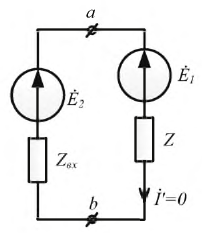
Рис. 3.11. Схема замещения активного двухполюсника
В этой схеме ЭДС 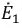 численно равна
численно равна 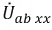 активного двухполюсника, и, следовательно, ток:
активного двухполюсника, и, следовательно, ток:
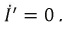
Таким образом, ток в ветви 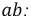

Пусть дана цепь (рис. 3.12), в которой необходимо рассчитать ток 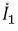 методом эквивалентного генератора.
методом эквивалентного генератора.
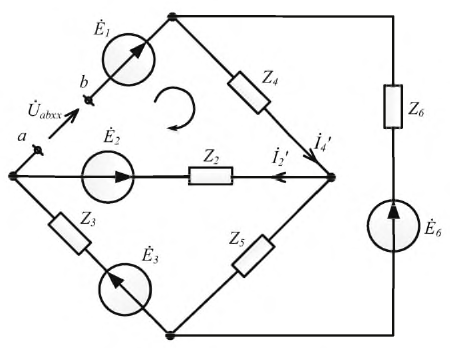
Рис. 3.12. Исходная цепь
Последовательность расчета:
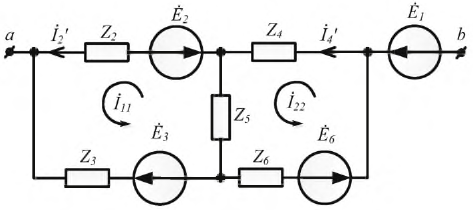
1. Разомкнем ветвь с сопротивлением 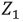 или примем
или примем 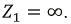
2. Зададим положительное направление 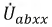 и для произвольно выбранных положительных направлений токов. Например, для первого контура запишем уравнение по второму закону Кирхгофа:
и для произвольно выбранных положительных направлений токов. Например, для первого контура запишем уравнение по второму закону Кирхгофа:
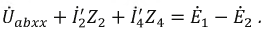
3. Токи 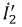 и
и 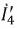 в преобразованной схеме по рис. 3.13 рассчитываем любым известным методом, например, методом контурных токов
в преобразованной схеме по рис. 3.13 рассчитываем любым известным методом, например, методом контурных токов
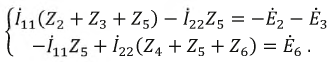
Тогда 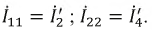
4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя в схеме для реальных источников их внутренние сопротивления.
В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов 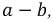 так как нет последовательно-параллельного соединения приемников, поэтому необходимо выполнить преобразование какого-либо участка цепи из «треугольника» в «звезду» или выполнить обратное преобразование.
так как нет последовательно-параллельного соединения приемников, поэтому необходимо выполнить преобразование какого-либо участка цепи из «треугольника» в «звезду» или выполнить обратное преобразование.
Преобразуем, например, «треугольник» сопротивлений 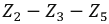 в «звезду»
в «звезду» 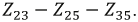 При этом получится схема с последовательно-параллельным соединением приемников (рис. 3.14).
При этом получится схема с последовательно-параллельным соединением приемников (рис. 3.14).
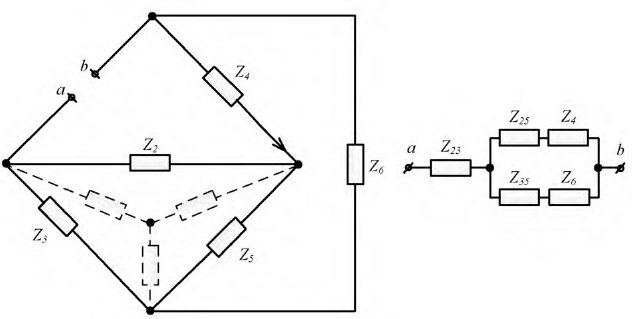
Рис. 3.14. Схема пассивного двухполюсника
Сопротивления этой схемы будут:
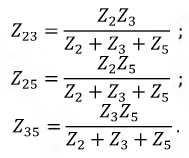
Входное сопротивление цепи 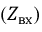 относительно зажимов
относительно зажимов  и
и  запишем в виде:
запишем в виде:
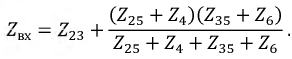
Окончательно имеем:
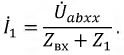
- Теоремы теории цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений

Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.
Алгоритм состоит из следующих шагов:
- Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
- Рассчитывается эквивалентная эдс генератора.
- Определяется эквивалентное сопротивление генератора.
- По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.
Метод эквивалентного генератора: примеры решения
Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).

Допустим, что необходимо рассчитать ток Iab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.

После преобразования ток через резистор Rab (R4) определяется по формуле
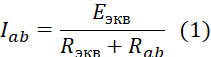
Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).

Для представленной схемы напряжение Еэкв будет равно

Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).

Эквивалентное сопротивление полученной схемы определяется по формуле

Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).

Поставленная задача решена.
Продолжаем решать задачи по основам электротехники(ТОЭ). В сегодняшней статье будет метод, по которому задают больше всего вопросов. Это понятно, поскольку этот метод является, на мой взгляд, самым сложным методом расчета сложных электрических цепей постоянного тока.
В свое время и я его понял далеко не сразу. Поэтому рассмотрим каждый пункт подробно. Начнём с того, что необходимо знать и понимать для успешного решения этим методом.
1) Закон Ома. Без него не только этот метод, но и многие другие задачи не решаются.
2) Правила последовательного и параллельного соединения резисторов.
3) Хотя бы один любой метод расчета сложных цепей, то есть по Кирхгофу, контурными токами, узловыми потенциалами и так далее.
4) И, самое важное, для этого метода – это умение строить потенциальную диаграмму. Именно потенциальную, а не векторную. Потому что векторная диаграмма строится для цепей переменного тока, а мы рассматриваем цепь постоянного тока. Строить мы конечно потенциальную диаграмму тут не будем. Но чтобы её построить, необходимо знать два основных правила, которые нужны и в методе эквивалентного генератора.
Первое правило: ток течет через резистор всегда от большего потенциала к меньшему.
Второе правило: у ЭДС “+” всегда больше “-“.
Давайте перейдем к решению задачи. На конкретном примере всегда понятнее.
Имеется данная схема цепи. Даны ЭДС и сопротивления резисторов. Требуется найти ток I3 методом эквивалентного генератора.
Поскольку нужно найти ток I3, который протекает по третьей ветви, нам нужно обеспечить холостой ход, сделав обрыв той части цепи, по которой протекает интересующий нас ток. То есть делаем обрыв третьей ветви. Это ветвь подключена между точками “c” и “d”. Сами точки мы не трогаем, а лишь убираем только ветвь.
В точках “c” и “d” узлов нет, поскольку там сходятся только по две ветви. А узел – это место соединения трех и более ветвей.
Наша цель – определить две величины:
1) Напряжение Ucd между точками “c” и “d”, оно же ЭДС эквивалентного генератора(Еэг). И, поскольку, мы обеспечили холостой ход, оборвав третью ветвь, все токи и напряжения будем указываем на схеме с индексом “х”, при коротком замыкании указывают кз.
2) Сопротивление эквивалентного генератора rэг, оно же сопротивление между точками “c” и “d”. А определить это сопротивление нам поможет правило последовательного и параллельного соединения резисторов.
В первом случае, когда мы ищем напряжение Ucd(оно же Еэг), применим один любой метод расчета сложных электрических цепей.
Сложной считается цепь, если в ней два и более источников энергии.
В данном случае два источника. Давайте для начала найдём, каким будет напряжение между точками “c” и “d”. Воспользуемся методом контурных токов.
Получили два неизвестных контурных тока. В цепи, в общем случае, три ветви и два узла. Поскольку две неизвестные, значит составим два уравнения и из этих уравнений найдём контурные токи I11 и I22.
Напряжение Ucd снимается с точек “c” и “d”, а между ними включены резисторы r2 и r4. Нам остается найти напряжение на этих элементах. Их сопротивления известны. Найдем токи I4 и I2, умножим эти токи на сопротивления, получим напряжения.
Контурные токи мы уже нашли. Тогда токи ветвей:
I2x=-I22=0.3333 A; I4x=-I11=0.2222 A;
Напряжения на резисторах r4 и r2:
U4x=I4x*r4=0.2222*4=0.8888 B; U2x=I2x*r2=0.3333*2=0.6666 B;
Так как оба тока направлены в одну и ту же сторону, тогда
Ucdx=U2x+U4x=0.6666+0.8888=1.5554 B;
А теперь самое главное в этом методе. Почему именно взяли U2 + U4? Почему не -U2-U4? А здесь нужно воспользоваться правилом, что ток течет от большего потенциала к меньшему и стрелкой под напряжением Ucdx мы указали, что φс больше чем φd. А так как нам нужно найти ЭДС эквивалентного генератора, давайте представим именно эту часть схемы отдельно.
Предположим, что φc больше чем φd и стрелкой под напряжением укажем направление от большего потенциала к меньшему.
Заменим напряжение Ucd на Eэг. Еэг будет направлен от “d” к “c”(минусом на “d”, а плюсом на “c”, потому что “плюс” у ЭДС всегда больше чем “минус”).
Запишем второй закон Кирхгофа:
I4x*r4+I2x*r2=-Еэг
В данном случае ЭДС эквивалентного генератора Еэг получится отрицательным. Можно в принципе оставить как есть, это ошибкой не будет. Но если мы на данном этапе поменяем направление ЭДС эквивалентного генератора на этой схеме, тогда мы получим положительное значение ЭДС эквивалентного генератора. Или оставляем как есть. Как поступить – без разницы. Давай поменяем направление.
Тогда I4x*r4+I2x*r2=Еэг; Еэг=U4x+U2x=0.8888+0.6666=1.5554 B;
Это говорит о том, что потенциал в точке “d” большие чем в точке “с”. Это и так изначально было понятно cудя по тому, как мы направили токи. А ток течет от большего потенциала к меньшему, т. е. мы изначально указали точки от “d” к “e” и от “e” к “c” и эти токи получились положительными. Значит мы их верно расставили.
С ЭДС эквивалентного генератора мы разобрались, осталось посчитать сопротивление эквивалентного генератора (сопротивление между точками “c” и “d”). Для этого мы должны исключить все источники энергии и оставить только резисторы.
Когда исключаем ЭДС, на его месте остается короткое замыкание (это в случае если источник напряжения идеальный и его внутреннее сопротивление равно нулю). Если имеется какое-то внутреннее сопротивление, то оно остается в ветви, это нужно учитывать. Если в схеме цепи есть источник тока, то после его исключения на его месте остается обрыв, поскольку его внутреннее сопротивление бесконечно большое. А после исключения источника тока, его внутреннее сопротивление остается в схеме, и так как оно бесконечно большое, это равносильно обрыву.
В схеме, изображенной на рисунке 9, применяя правила последовательного и параллельного соединения резисторов:
r4 и r5 включены параллельно;
r1 и r2 включены параллельно;
r45 и r12 включены последовательно;
Численные значения r45, r12 и rэг рассчитаны на рисунке 9.
Осталось изобразить последнюю схему, в которой будет протекать ток I3.
Ток получился отрицательным, значит на самом деле он течет не вправо, а влево от “d” к “c”. Это и понятно, поскольку, как мы ранее выяснили, φd больше чем φc, и, повторюсь, ток течет от большего потенциала к меньшему.
Таким образом решаются задачи методом эквивалентного генератора.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
Этот
метод обычно применяется в тех случаях,
когда требуется найти ток в какой-то
одной ветви при различных значениях
сопротивления этой ветви и неизменных
остальных параметрах цепи.
Пусть
в схеме на рис. 6.1, а нам
необходимо найти ток I1.
Тогда всю цепь относительно зажимов
первой ветви (узлов b и c)
мы представляем как активный двухполюсник
(рис. 6.1, б),
который, в свою очередь, заменяем
эквивалентным генератором (рис. 6.1, в).
ЭДС
эквивалентного генератора Eэ равна
напряжению холостого хода Uх на
разомкнутых зажимах двухполюсника
(рис. 6.2, а): ![]()
![]() ,
,
а его внутреннее сопротивление в
соответствии со схемой рис.
6.3,а определяется
по формуле
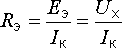 , (6.1)
, (6.1)
где ![]() –
–
ток короткого замыкания двухполюсника.

Рис.
6.1. Замена части электрической цепи
эквивалентным генератором

Рис.
6.2. Холостой ход активного двухполюсника
После
определения ![]() и
и![]() интересующий
интересующий
нас ток находится из схемы рис. 6.1,в по
формуле
 . (6.2)
. (6.2)
Заменяя
активный двухполюсник эквивалентным
генератором, ЭДС последнего мы можем
направлять произвольно – например, на
рис. 6.1, в ее
можно направить и вниз (при этом следует
поменять и знак перед ![]() вформуле
вформуле
(6.2)). Но в схемах на рис. 6.2, в и
6.3, в этот
произвол исключен.

Рис.
6.3. Короткое замыкание двухполюсника
Если
на рис. 6.1, в мы
направили ![]() вверх,
вверх,
от c к b,
то в режиме холостого хода точка b имеет
положительный потенциал, а c –
отрицательный (рис. 6.2, а).
Поэтому стрелка![]() в
в
схемах рис. 6.2 направляется от b к c (от
плюса к минусу). Точно так же, от b к c,
т. е. в сторону действия ЭДС ![]() ,
,
должен быть направлен и ток ![]() (рис.
(рис.
6.3).
Итак,
для того чтобы найти параметры
эквивалентного генератора, необходимо
рассмотреть два режима – холостого
хода и короткого замыкания.
Рассчитать
эти режимы можно любым методом. По
заданию требуется применить здесь метод
наложения.
6.1. Расчет режима холостого хода
В
соответствии с принципом наложения
(суперпозиции) напряжение холостого
хода может быть найдено как сумма
напряжений от действия каждой ЭДС в
отдельности:
![]() ,
,
где ![]() –
–
напряжение холостого хода, создаваемое
ЭДС ![]() (рис.
(рис.
6.4, а); ![]() –
–
напряжение
холостого
хода от действия ЭДС ![]() (рис.
(рис.
6.4, б).
Знаки
в правой части последнего уравнения
определяются взаимными направлениями
стрелок ![]() ,
,![]() и
и![]() (рис.
(рис.
6.2. и 6.4).
Как следует направлять ![]() ,
,
мы только что выяснили.
Напряжения![]() и
и![]() рекомендуется
рекомендуется
направлять в ту же сторону, хотя это
необязательно. Если мы решили
направить![]() и
и![]() в
в
разные стороны, то![]() будет
будет
равно их разности.
Токи
от действия каждой ЭДС в отдельности,
называемые частичными токами, на схемах
рис. 6.4, а и
6.4, б направляются
уже не произвольно, а в соответствии с
действующей в цепи единственной ЭДС –
по её стрелке.
Для
облегчения понимания структуры цепи
рекомендуется представить ее в более
удобном виде. Схему рис. 6.4, а,
например, можно изобразить так, как
показано на рис. 6.5.

Рис.
6.4. Схемы для расчета напряжения холостого
хода

Рис.
6.5. Упрощенная схема
Порядок
расчета схемы рис. 6.5 следующий.
Определяем
общее сопротивление цепи относительно
зажимов источника:
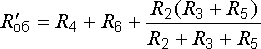 .
.
Находим
ток, протекающий по ветви с ЭДС:
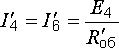 .
.
Рассчитываем
напряжение ![]() на
на
зажимах параллельно соединенных ветвей:
![]() .
.
И
наконец, находим токи в параллельных
ветвях:
 ;
;  .
.
Последние
два тока можно рассчитать, и не находя
напряжения ![]() .
.
Рассмотрим
часть электрической цепи, состоящей из
двух параллельно соединенных сопротивлений
(рис.6.6).
Требуется
по известному току ![]() найти
найти
токи ![]() и
и ![]() .
.
Сначала определяем напряжение на
участке ab:
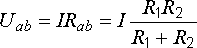 .
.
Затем
по закону Ома находим токи:
 ;
; 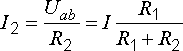 .
.
Полученные
формулы дают следующее простое правило.
Ток
в одной из параллельных ветвей равен
произведению общего тока и сопротивления
соседней ветви, деленному на сумму
сопротивлений параллельных ветвей.

Рис.6.6.
Определение токов в параллельных ветвях
В
соответствии с этим правилом для схемы
рис. 6.5 имеем:
 ;
;  .
.
Напряжение ![]() находим
находим
по схеме рис. 6.4,а из
уравнения, составленного по второму
закону Кирхгофа для контура, включающего
в себя это напряжение. Например, контур,
отмеченный дугообразной пунктирной
стрелкой 1, состоит из двух ветвей (шестой
и пятой) и стрелки ![]() .
.
ЭДС в этом контуре нет, поэтому в
соответствии со вторым законом Кирхгофа
![]() .
.
Отсюда
![]() .
.
Можно
воспользоваться и контуром 2. Для него
![]() ,
,
откуда
![]() .
.
Схема
рис. 6.4, б рассчитывается
аналогично:
 ;
;  ;
;
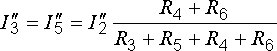 ;
;
![]() или
или ![]() .
.
Если
в результате расчета ЭДС ![]() окажется
окажется
отрицательной, то во все формулы ее
значение следует подставлять со знаком
минус, не меняя, конечно, самих формул
и схем.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
Метод эквивалентного генератора основан на теореме об эквивалентном источнике (теорема Тевенена) — активном двухполюснике.
Теорема Тевенена для линейных электрических цепей утверждает, что любая электрическая цепь, имеющая два вывода и состоящая из комбинации источников напряжения, источников тока и резисторов (сопротивлений), с электрической точки зрения эквивалентна цепи с одним источником напряжения E и одним резистором R, соединенными последовательно.
В методе эквивалентного генератора (метод эквивалентного источника ЭДС) сложную разветвленную схему рассматривают как активный двухполюсник по отношению к ветви R с искомым током I, который определяют по выражению
I = EЭГ/ (RЭГ + R),
где
EЭГ = Uхх — ЭДС эквивалентного генератора равная напряжению холостого хода между зажимами подключенного пассивного элемента R в ветви с искомым током;
RЭГ = Rвх — сопротивление эквивалентного генератора равное входному сопротивлению пассивного двухполюсника относительно разомкнутых зажимов.
Алгоритм метода эквивалентного генератора (метод эквивалентного источника ЭДС)
1. Определяют напряжение холостого хода Uхх. Для этого ветвь с искомым током разрывают, удаляя сопротивление, и оставляют ЭДС в этой ветви, если она имеется.
2. Задаются направлением токов в ветвях оставшейся схемы после размыкания ветви. Записывают выражение для напряжения Uхх между разомкнутыми зажимами по второму закону Кирхгофа. В это уравнение войдет ЭДС разомкнутой ветви.
3. Рациональным методом рассчитываются токи в схеме, вошедшие в выражение напряжения Uхх.
4. Определяют входное сопротивление двухполюсника относительно разомкнутых зажимов.
Индивидуалка Вика (24 лет) т.8 985 260-71-05 Москва, метро Ясенево. платно терапевт самара.
5. В соответствии с методом эквивалентного генератора (метод эквивалентного источника ЭДС), определяют искомый ток ветви.
Решение задач методом эквивалентного генератора (методом эквивалентного источника ЭДС)
Задача 1.5.1 В схеме рис. 1.5.1 амперметр показывает 0,5 А. Определить его показания в схеме рис. 1.5.2.
Решение. Можно считать, что в схеме рис. 1.5.2 резистор R5 подключен к зажимам эквивалентного генератора, который в схеме рис. 1.5.1 работает в режиме короткого замыкания.
Рис. 1.5.3
Определим внутреннее сопротивление эквивалентного генератора по схеме рис. 1.5.3, где заменим треугольник сопротивлений R1R3R0 эквивалентным соединением звездой
R 13 = R 1 ⋅ R 3 R 1 + R 3 + R 0 = 2⋅4 2+4+4 =0,8 Ом; R 01 = R 1 ⋅ R 0 R 1 + R 3 + R 0 = 4⋅2 2+4+4 =0,8 Ом; R 03 = R 0 ⋅ R 3 R 1 + R 3 + R 0 = 4⋅4 2+4+4 =1,6 Ом; R Э = R 13 + ( R 01 + R 2 )⋅ ( R 03 + R 4 ) ( R 01 + R 2 )+ ( R 03 + R 4 ) = =0,8+ ( 0,8+4 )⋅ ( 1,6+2 ) ( 0,8+4 )+ ( 1,6+2 ) =2,86 Ом.
ЭДС эквивалентного генератора определим из формулы I = EЭГ/ (RЭГ + R) метода эквивалентного генератора. При коротком замыкании I = EЭГ/RЭГ. Откуда ЭДС эквивалентного генератора
E Э =I⋅ R Э =0,5⋅2,86=1,43 В.
Ток I5 в схеме рис. 1.5.2 по методу эквивалентного генератора (методу эквивалентного источника ЭДС)
I 5 = E Э R Э + R 5 = 1,43 2,86+1 =0,371 А.
Метод эквивалентного источника напряжения, метод эквивалентного источника тока, метод активного двухполюсника в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи
 теорема Тевенена,
теорема Тевенена,
теорема об эквивалентном источнике,
метод эквивалентного источника ЭДС,
метод эквивалентного генератора
