Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)
Формула работа выхода электронов
В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении. Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.
Потенциальная энергия электрона внутри металла постоянна и равна:
Wp = -eφ , где j – потенциал электрического поля внутри металла.
При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.
В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.
Aвых = eφ
Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.
Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми EF . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.
Aвых = eφ’ – EF
где φ’ – среднее значение потенциала электрического поля внутри металла.
Таблица работа выхода электронов из простых веществ
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
|
Вещество |
Формула вещества |
Работа выхода электронов (W, эВ) |
|
серебро |
Ag |
4,7 |
|
алюминий |
Al |
4,2 |
|
мышьяк |
As |
4,79 – 5,11 |
|
золото |
Au |
4,8 |
|
бор |
B |
(4,60) |
|
барий |
Ba |
2,52 |
|
бериллий |
Be |
3,92 |
|
висмут |
Bi |
4,34 |
|
углерод (графит) |
C |
4,45 – 4,81 |
|
кальций |
Ca |
2,76 – 3,20 |
|
кадмий |
Cd |
4,04 |
|
церий |
Ce |
2,6 – 2,88 |
|
кобальт |
Co |
4,40 |
|
хром |
Cr |
4,60 |
|
цезий |
Cs |
1,94 |
|
медь |
Cu |
4,36 |
|
железо |
Fe |
4,40 – 4,71 |
|
галлий |
Ga |
3,96 – 4,16 |
|
германий |
Ge |
4,66 |
|
гафний |
Hf |
(3,53) |
|
ртуть |
Hg |
4,52 |
|
индий |
In |
(3,60 – 4,09) |
|
иридий |
Ir |
(4,57) |
|
калий |
K |
2,25 |
|
лантан |
La |
(3,3) |
|
литий |
Li |
2,49 |
|
магний |
Mg |
3,67 |
|
марганец |
Mn |
3,76 – 3,95 |
|
молибден |
Mo |
4,20 |
|
натрий |
Na |
2,28 |
|
ниобий |
Nb |
3,99 |
|
неодим |
Nd |
(3,3) |
|
никель |
Ni |
4,91 – 5,01 |
|
осмий |
Os |
(4,55) |
|
свинец |
Pb |
4,05 |
|
палладий |
Pd |
(4,98) |
|
празеодим |
Pr |
(2,7) |
|
платина |
Pt |
5,30 – 5,55 |
|
рубидий |
Rb |
2,13 |
|
рений |
Re |
4,98 |
|
родий |
Rh |
4,75 |
|
рутений |
Ru |
(4,52) |
|
сурьма |
Sb |
4,08 – 4,56 |
|
скандий |
Sc |
(3,2 – 3,33) |
|
селен |
Se |
4,86 |
|
кремний |
Si |
3,59 – 4,67 |
|
самарий |
Sm |
(3,2) |
|
олово (γ-форма) |
Sn |
4,38 |
|
олово (β-форма) |
Sn |
4,50 |
|
стронций |
Sr |
2,74 |
|
тантал |
Ta |
4,13 |
|
теллур |
Te |
4,73 |
|
торий |
Th |
3,35 – 3,47 |
|
титан |
Ti |
4,14 – 4,50 |
|
таллий |
Tl |
3,68 – 4,05 |
|
уран |
U |
3,27 – 4,32 |
|
ванадий |
V |
3,77 – 4,44 |
|
вольфрам |
W |
4,54 |
|
цинк |
Zn |
4,22 – 4,27 |
|
цирконий |
Zr |
3,96 – 4,16 |
Таблица работа выхода электронов из неорганических соединений
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
|
Вещество |
Формула вещества |
Работа выхода электронов (W, эВ) |
|
бромистое серебро |
AgBr |
~3,9 |
|
хлористое серебро |
AgCl |
~4,6 |
|
иодистое серебро |
AgI |
~4,0 |
|
сульфид серебра |
Ag2S |
~3,8 |
|
триоксид бора |
B2O3 |
4,7 |
|
оксид бария |
BaO |
1,0 – 1,6 |
|
барий вольфрамовокислый |
BaWO4 |
2,27 |
|
окись бериллия |
BeO |
3,8 – 4,7 |
|
окись кальция |
CaO |
1,8 – 2,4 |
|
ортовольфрамат кальция |
Ca3WO6 |
2,13 |
|
борид хрома |
CrB2 |
3,36 |
|
окись цезия |
Cs2O |
1,0 – 1,17 |
|
окись меди |
CuO |
4,35 – 5,34 |
|
закись меди |
Cu2O |
5,15 |
|
окись железа |
FeO |
3,85 |
|
вода |
H2O |
6,1 |
|
карбид гафния |
HfC |
2,04 |
|
оксид магния |
MgO |
3,1 – 4,4 |
|
диборид марганца |
MnB2 |
4,14 |
|
диборид молибдена |
MoB2 |
3,38 |
|
триоксид молибдена |
MoO3 |
4,25 |
|
силицид молибдена |
MoSi2 |
5,0 – 6,0 |
|
хлористый натрий |
NaCl |
4,2 |
|
борид ниобия |
NbB2 |
3,65 |
|
карбид ниобия |
NbC |
2,24 |
|
окись никеля |
NiO |
5,55 |
|
борид скандия |
ScB2 |
2,3 – 2,9 |
|
кремнезём |
SiO2 |
5,0 |
|
окись стронция |
SrO |
2,0 – 2,6 |
|
карбид тантала |
TaC |
3,05 – 3,14 |
|
пентаоксид тантала |
Ta2O5 |
4,65 |
|
дикарбид тория |
ThC2 |
3,5 |
|
оксид тория |
ThO2 |
2,54 – 2,67 |
|
сульфид титана |
TiS |
3,4 |
|
диборид титана |
TiB2 |
3,88 – 3,95 |
|
карбид титана |
TiC |
2,35 – 3,35 |
|
нитрид титана |
TiN |
2,92 |
|
окись титана |
TiO |
2,96 – 3,1 |
|
двуокись титана |
TiO2 |
4,7 |
|
карбид урана |
UC |
2,9 – 4,6 |
|
диборид ванадия |
VB2 |
3,88 – 3,95 |
|
диборид вольфрама |
WB2 |
2,62 |
|
диоксид вольфрама |
WO2 |
4,96 |
|
дисилицид вольфрама |
WSi2 |
5,0 – 6,0 |
|
борид циркония |
ZrB |
4,48 |
|
диборид циркония |
ZrB2 |
3,70 |
|
карбид циркония |
ZrC |
2,2 – 3,8 |
|
нитрид циркония |
ZrN |
2,92 |
_______________
Источник информации:
1. Landolt-Borstein’s Zahlenwerte und Funktionen aus Phsik, Chemie, Astrunumie, Geophysik, Thechnik, 6-е издание., Берлин, т. I, ч.4, 1955; т. II, ч.6, разд. 1, 1959.
2. В.С. Фоменко. Эмиссионные свойства элементов и химических соединений. Изд. АН УСССР, Киев, 1961.
Работа выхода в металлах
В металлах, согласно электронной теории проводимости, свободные электроны находятся в состоянии постоянного хаотичного теплового движения. Однако при нормальных температурах они не покидают металл. У поверхности металла существует задерживающее электрическое поле. Чтобы вылететь из металла электрон должен совершить работу по преодолению задерживающих сил. Эта работа называется работой выхода.
Работа выхода – работа, которую должен совершить электрон, чтобы выйти из металла.
Формула для работы выхода:
A=eU,
где e – заряд электрона, U – разность потенциалов между точками в металле и за пределами задерживающего слоя.
Работа выхода измеряется в электронвольтах.
Электронвольт – внесистемная единица измерения, равная энергии, которую приобретает электрон при движении между двумя точками с разностью потенциалов в 1 Вольт.
Как у поверхности металла образуется задерживающее поле?
- Вследствие теплового движения электроны с поверхности металла могут отрываться и образуют над поверхностью электронное облако.
- На местах покинувших металл электронов образуются положительные ионы. По закону Кулона, они стремяться вернуть покинувшие металл электроны обратно.
В результате у поверхности металла образуется двойной электрический слой.

В вакууме за пределами задерживающего слоя поле отсутствует, поэтому формула для работы выхода запишется в виде:
A=eφ,
где φ – потенциал выхода, равный потенциалу поля внутри металла.
Контактная разность потенциалов
Явление контактной разности потенциалов в 1797 году открыл Алессандро Вольта (1745 -1827).
Контактная разность потенциалов – разность потенциалов, которая возникает при контакте поверхностей двух разных металлов.
- Разность потенциалов, возникающая при контакте двух разных металлов, зависит от их химического состава и температуры.
- Если цепь составлена из нескольких разных проводников при одинаковой температуре, контактная разность потенциалов определяется только контактной разностью между крайними проводниками.
Причины возникновения контактной разности потенциалов:
- Разная работа выхода для разных металлов.
- Разная концентрация свободных электронов в разных металлах.
Схематически рассмотрим контакт двух металлов. Пусть у металла 1 работа выхода больше, чем у металла 2, и в металле 1 концентрация свободных электронов больше.
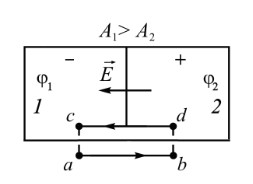
Между точками a и b, лежащими рядом с поверхностью, но не принадлежащими проводнику, возникает внешняя контактная разность потенциалов.
Электроны диффундируют из одного металла в другой, при этом из металла 1 в металл 2 уходит больше электронов, так как n1>n2. В результате металл 1 приобретает положительный, а металл 2 – отрицательный заряд. Возникшая разность потенциалов называется внутренней контактной разностью потенциалов.
88
Цель
работы:
изучение явления внешнего фотоэффекта,
нахождение его красной границы и работы
выхода электрона из металла.
1. Введение
Внешним
фотоэффектом
называется испускание электронов
веществом под действием света.
Энергетический баланс при фотоэффекте
выражается уравнением Эйнштейна
![]() , (1)
, (1)
где
hν
– энергия светового кванта, переданная
электрону; A
–
работа выхода электрона за пределы
вещества;
![]() – максимальная кинетическая энергия
– максимальная кинетическая энергия
освободившегося электрона. Уравнение
(1) получено в предположении, что
электромагнитное излучение представляет
собой поток частиц, называемых фотонами.
Фотон несет энергию![]() ,
,
при этом он неделим и при взаимодействии
отдает свою энергию полностью. Фотон
обладает также импульсом![]() .
.
Фотоэффект можно рассматривать как
процесс соударения фотона с электроном.
Уравнение
(1) дает теоретическое обоснование
законов фотоэффекта, экспериментально
установленных Столетовым:
1)
фототок насыщения пропорционален
световому потоку;
2)
максимальная скорость фотоэлектронов
определяется частотой света
и не зависит от его интенсивности;
3)
для каждой поверхности существует
минимальная частота ν0
(красная граница фотоэффекта), ниже
которой фотоэффект не возможен:
![]() . (2)
. (2)
Определив
ν0
экспериментально,
из формулы (2) можно найти работу выхода
электронов A
для данного вещества.
Простейшим
прибором для наблюдения фотоэффекта
является вакуумный фотоэлемент (рис.1).
Это откачанный стеклянный баллон, одна
половина которого покрыта изнутри
металлом, играющим роль фотокатода К.
Анод А
обычно выполняется в форме кольца или
шарика. Между катодом и анодом с помощью
батареи Б
создается ускоряющая разность потенциалов.
При освещении катода он испускает
электроны, которые подхватываются полем
и попадают на анод. Цепь замыкается, и
в ней течет ток. В данной установке
использован фотоэлемент с катодом,
красная граница которого лежит в видимой
области спектра. Это позволяет использовать
в качестве источника света лампу
накаливания.
|
Один |
Рис. |
разности
потенциалов Uзадер.
ни одному из электронов, даже обладающему
при вылете из катода К
наибольшим значением скорости
![]() ,
,
не удастся достигнуть анодаА.
Фототок прекращается. Это условие можно
записать:
![]() , (3)
, (3)
Измерив
задерживающее напряжение Uзадер
и, зная частоту излучения ,
из формулы (1) можно найти работу выхода
А,
затем по формуле (2) определить красную
границу фотоэффекта 0.
В
данной работе для определения красной
границы при неизменной ускоряющей
разности потенциалов будем изменять
частоту падающего излучения .
При некоторой частоте 0
фототок должен прекратится. Однако этот
метод требует более тщательного, хотя
бы качественного анализа причин,
определяющих величину фототока. Очевидно,
что фототок при данной частоте излучения
определяется числом фотонов Nфот(),
падающих на фотокатод в единицу времени,
и вероятностью взаимодействия фотона
с электроном P(),
приводящего к выходу электрона из
вещества:
![]() . (4)
. (4)
Число
фотонов в световом потоке Nфот()
определяется излучательной способностью
источника света R,T.
Если предположить, что лампа накаливания
излучает как чёрное тело (см. введение
к работе 14), то её излучательная способность
может быть представлена графиком,
приведенным на рис. 2.
|
Рис. |
Рис. |
Количество
энергии, излучаемой лампой в области
частот от
до +,
определяется площадью, заштрихованной
на графике рис. 2: W=
R,T·.
Тогда число фотонов, излучаемых в
интервале частот
будет равно:
![]() .
.
В
области низких частот справедлив закон
Релея-Джинса, согласно которому R,T
~ 2.
Следовательно, в этой области отношение
![]() ,
,
равное![]() ,
,
будет пропорционально
(рис. 3). В области ожидаемого значения
красной границы, R,T
растет линейно (в районе точки перегиба
R,T
~ )
и, следовательно, отношение
![]() остается величиной постоянной для
остается величиной постоянной для
разных частот. При больших частотах (
> экстр)
излучательная способность тела
уменьшается и одновременно растет
“удельный вес” фотонов h.
В результате отношение
![]() резко падает. Следовательно, в области
резко падает. Следовательно, в области
значения частоты0,
число фотонов, испускаемых лампой
накаливания на разных частотах, остается
величиной постоянной.
Величина
второго сомножителя
![]() в формуле (4) определяется многими
в формуле (4) определяется многими
причинами. Одним из решающих факторов
является число электронов, взаимодействие
с которыми может привести к появлению
фототока. Электроны проводимости в
металле не могут самопроизвольно
покинуть вещество, так как металл
представляет для них потенциальную
яму. При температуреT
= 0 К все нижние энергетические уровни
ямы заняты электронами. Последний
занятый уровень носит название уровня
Ферми. Разность между глубиной
потенциальной ямы Ep0
и энергией Ферми EF
определяет работу выхода электрона из
металла:
![]() (рис. 4). Если энергия фотона
(рис. 4). Если энергия фотона
![]() ,
,
то такой фотон не может “вытащить”
электрон из потенциальной ямы. При
взаимодействии с фо-
|
тоном, |
Рис. |
ности
![]() ,
,
которая равна![]() .
.
Следовательно, вероятность выбивания
электрона из металла![]() .
.
В
итоге, в формуле (4) число фотонов,
испускаемых лампой накаливания в единицу
времени в области частот, лежащих вблизи
красной границы, остается величиной
постоянной на разных частотах, а
вероятность взаимодействия фотона с
электроном пропорциональна разности
частот
![]() .
.
Следовательно, в области красной границы
фототок пропорционален разности![]() .
.
При больших частотах фототок должен
уменьшаться с ростом
за счет
уменьшения числа фотонов, излучаемых
источником света в этой спек
тральной области. Таким образом,
ожидаемая зависимость фототока от
частоты должна
|
иметь |
Рис. |
Итак,
для экспериментального определения
красной границы фотоэффекта и работы
выхода необходимо снять зависимость
фототока от частоты излучения и,
аппроксимируя линейный участок графика
в области низких частот до пересечения
с осью частот, определить 0.
По формуле (2) можно определить работу
выхода электронов из металла.
Содержание
- Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)
- Формула работа выхода электронов
- Таблица работа выхода электронов из простых веществ
- Как найти работу выхода электрона с поверхности некоторого металла
- Примеры решенных задач по физике на тему «Фотоэффект»
Формула работа выхода электронов
В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении. Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.
Потенциальная энергия электрона внутри металла постоянна и равна:
Wp = -eφ , где j – потенциал электрического поля внутри металла.
При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.
В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.
Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.
Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми EF . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.
где φ’ – среднее значение потенциала электрического поля внутри металла.
Таблица работа выхода электронов из простых веществ
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
Источник
Как найти работу выхода электрона с поверхности некоторого металла
КВАНТОВАЯ ОПТИКА И ЯДЕРНАЯ ФИЗИКА
Красная граница фотоэффекту для некоторого металла равняется 275 нм. Найти:
а) работу выхода электрона из металла;
б) максимальную скорость электронов, которые вырываются из металла
светом с длиной волны 180 нм ;
в) максимальную кинетическую энергию электронов.
Дано:
λкр = 275 нм =275·10 -9 м
λкр = 180 нм =180 · 10 -9 м
Решение:
Зная красную границу фотоэффекта, найдем работу выхода


Уравнение Эйнштейна для внешнего фотоэффекта

Откуда максимальная кинетическая энергия

Максимальная скорость фотоэлектронов


Ответ:  ;
;  ;
;  .
.
Источник
Примеры решенных задач по физике на тему «Фотоэффект»
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Явление фотоэффекта заключается в испускании веществом электронов под действием падающего света. Теория фотоэффекта разработана Эйнштейном и заключается в том, что поток света представляет собой поток отдельных квантов(фотонов) с энергией каждого фотона h n . При попадании фотонов на поверхность вещества часть из них передает свою энергию электронов. Если этой энергия больше работы выхода из вещества, электрон покидает металл. Уравнение эйнштейна для фотоэффекта:  где
где  — максимальная кинетическая энергия фотоэлектрона.
— максимальная кинетическая энергия фотоэлектрона.
Длина волны красной границы фотоэффекта для некоторого металла составляет 307 нм. Максимальная кинетическая энергия фотоэлектронов – 1 эВ. Найти отношение работы выхода электрона к энергии падающего фотона.

Частота света красной границы фотоэффекта для некоторого металла составляет 6*10 14 Гц, задерживающая разность потенциалов для фотоэлектронов – 2В. Определить частоту падающего света и работу выхода электронов.

Работа выхода электрона из металла составляет 4,28эВ. Найти граничную длину волны фотоэффекта.

На медный шарик радает монохроматический свет с длиной волны 0,165 мкм. До какого потенциала зарядится шарик, если работа выхода электрона для меди 4,5 эВ?

Работа выхода электрона из калия составляет 2,2эВ, для серебра 4,7эВ. Найти граничные длину волны фотоэффекта.

Длина волны радающего света 0,165 мкм, задерживающая разность потенциалов для фотоэлектронов 3В. Какова работа выхода электронов?
Красная граница фотоэффекта для цинка 310 нм. Определить максимальную кинетическую энергию фотоэлектронов, если на цинк падает свет с длиной волны 200нм.

На металл с работой выхода 2,4эВ падает свет с длиной волны 200нм. Определить задерживающую разность потенциалов.

На металл падает свет с длиной волны 0,25 мкм, задерживающая разность потенциалов при этом 0,96В. Определить работу выхода электронов из металла.

При изменении длины волны падающего света максимальные скорости фотоэлектронов изменились в 3/4 раза. Первоначальная длина волны 600нм, красная граница фотоэффекта 700нм. Определить длину волны после изменения.


Работы выхода электронов для двух металлов отличаются в 2 раза, задерживающие разности потенциалов — на 3В. Определить работы выхода.

Максимальная скорость фотоэлектронов равно 2,8*10 8 м/с. Определить энергию фотона.
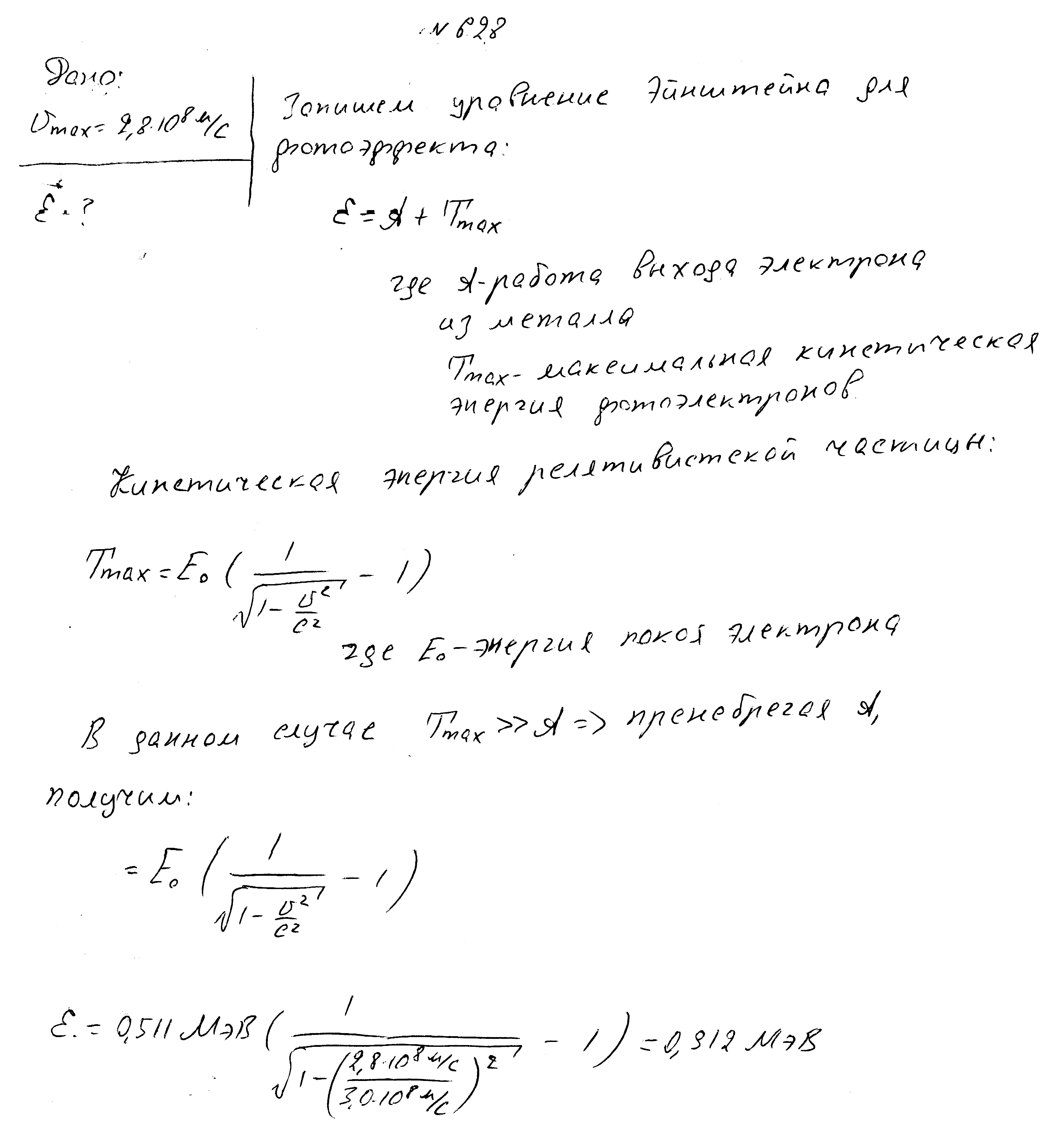
Энергии падающих на металл фотонов равны 1,27 МэВ. Найти максимальную скорость фотоэлектронов.

Максимальная скорость фотоэлектронов равно 0,98с, где с — скорость света в вакууме. Найти длину волны падающего света.
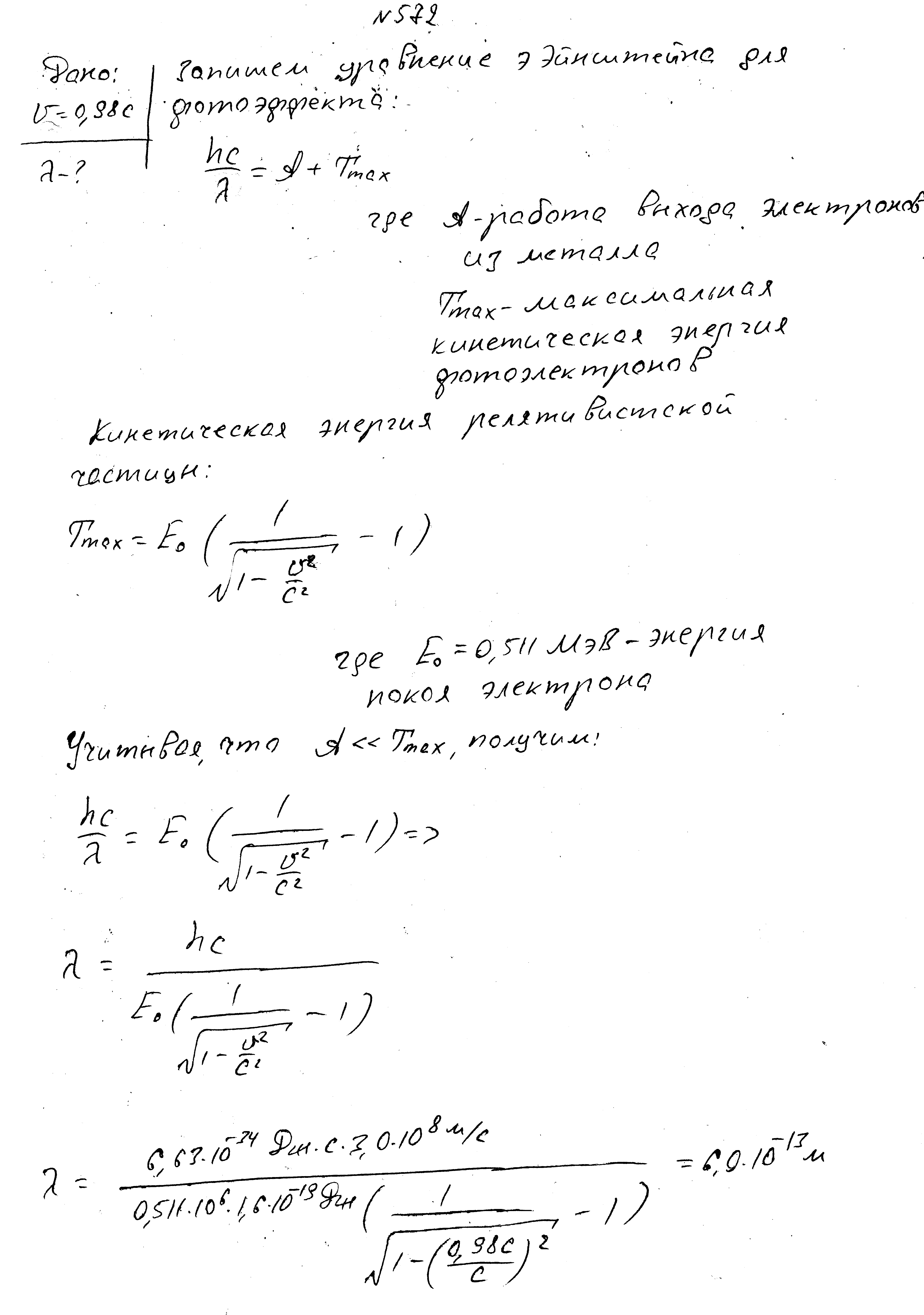
Энергия фотона в пучке света, падающего на поверхность металла, равно 1,53 МэВ. Определить максимальную скорость фотоэлектронов.
На шарик из металла падает свет с длиной волны 0,4 мкм, при этом шапик заряжается до потенциала 2В. До какого потенциала зарядится шарик, если длина волны станет равной 0,3 мкм?

После изменения длины волны падающего света в 1,5 раза задерживающая разность потенциалов изменилась с 1,6В до 3В. Какова работа выхода?
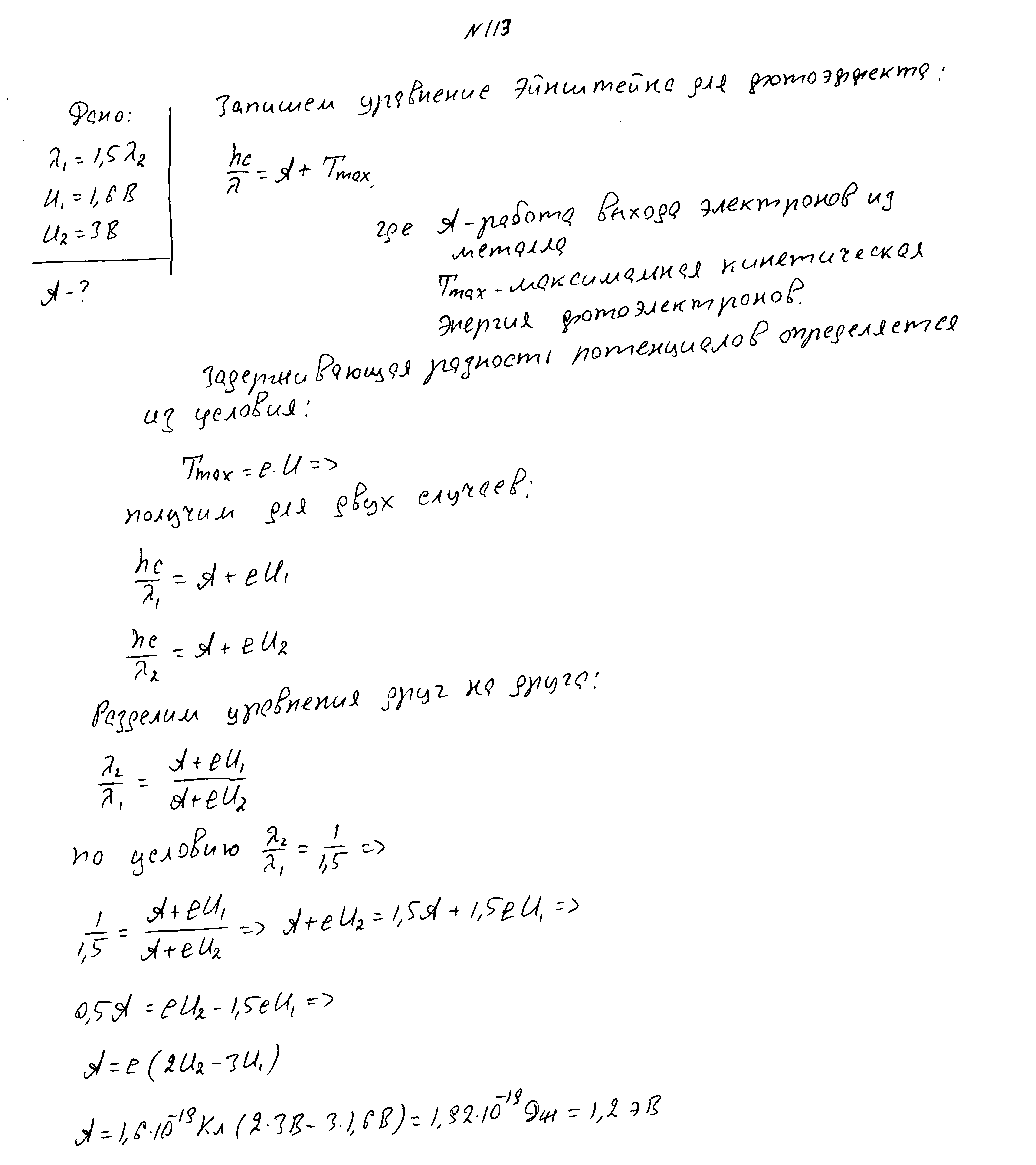
Красная граница фотоэффекта 560нм, частота падающего света 7,3*10 14 Гц. Найти максимальную скорость фотоэлектронов.
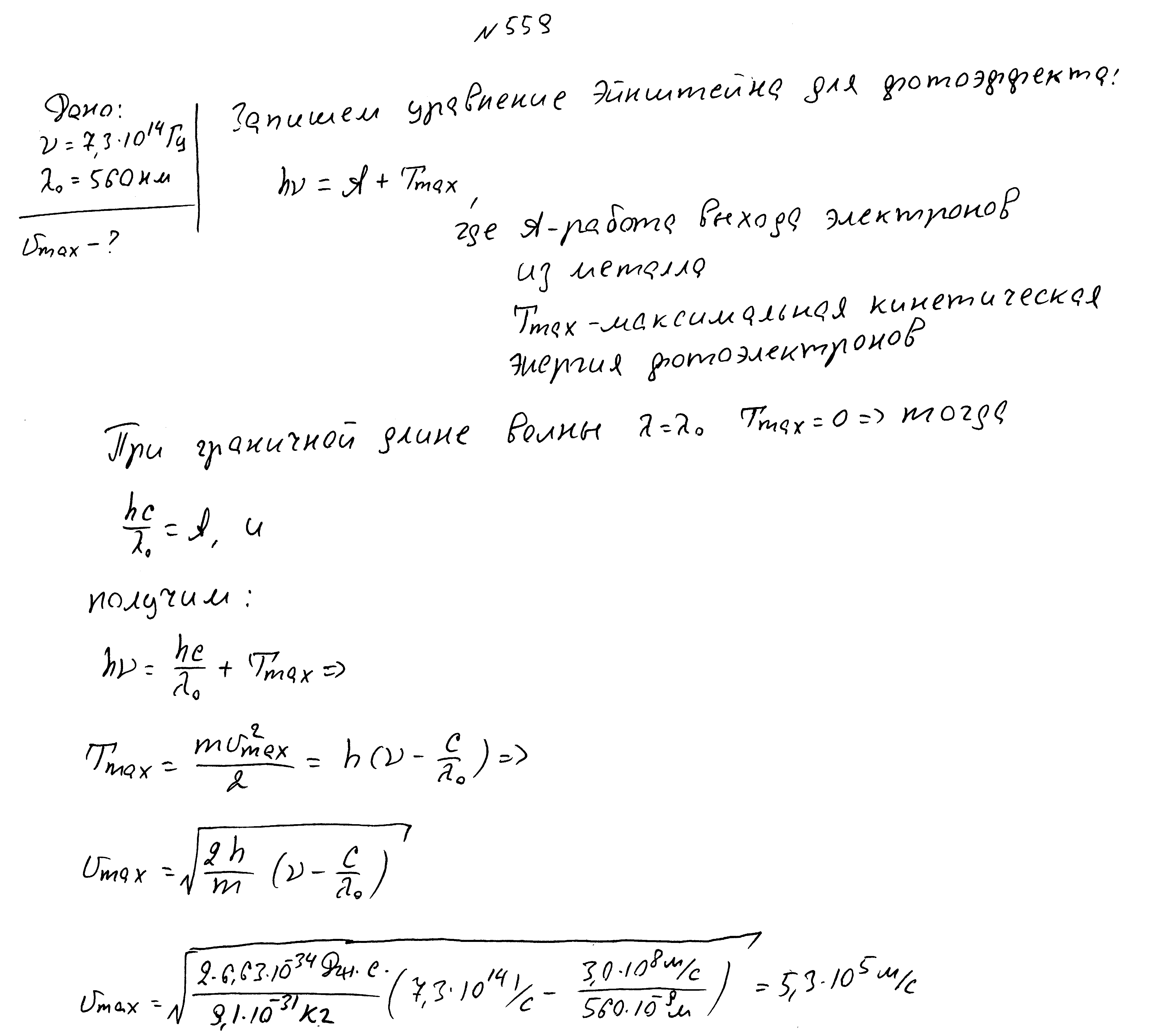
Красная граница фотоэффекта 2800 ангстрем, длина волны падающего света 1600 ангстрем. Найти работу выхода и максимальную кинетическую энергию фотоэлектрона.

Задерживащая разность потенциалов 1,5В, работа выхода электронов 6,4*10 -19 Дж. Найти длину волны падающего света и красную границу фотоэффекта.

Работа выхода электронов из металла равна 3,3 эВ. Во сколько раз изменилась кинетическая энергия фотоэлектронов. если длина волны падающего света изменилась с 2,5*10 -7 м до 1,25*10 -7 м?
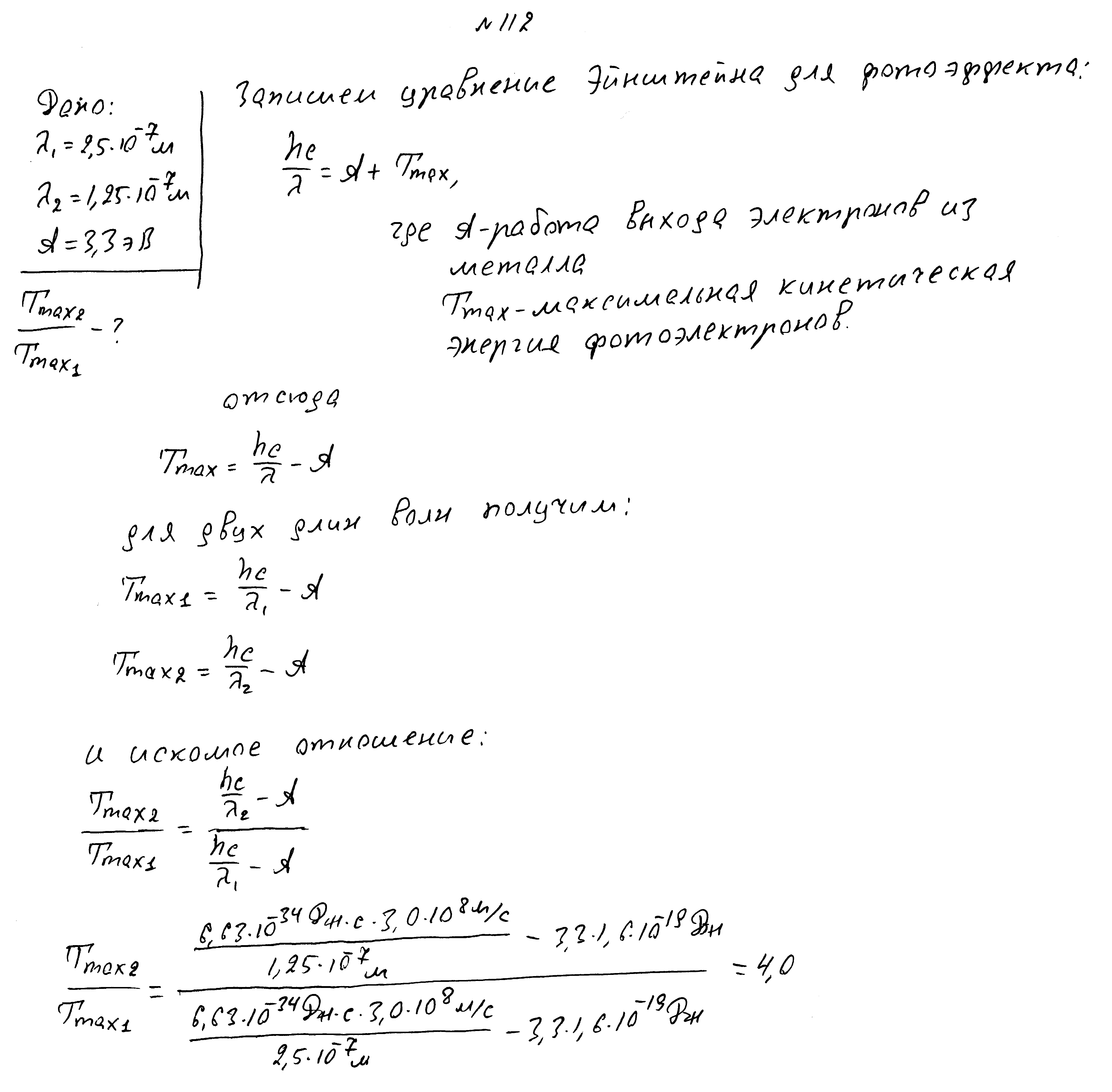
Найти максимальную скорость фотоэлектронов для видимого света с энергией фотона 8 эВ и гамма излучения с энергией 0,51 МэВ. Работа выхода электронов из металла 4,7 эВ.
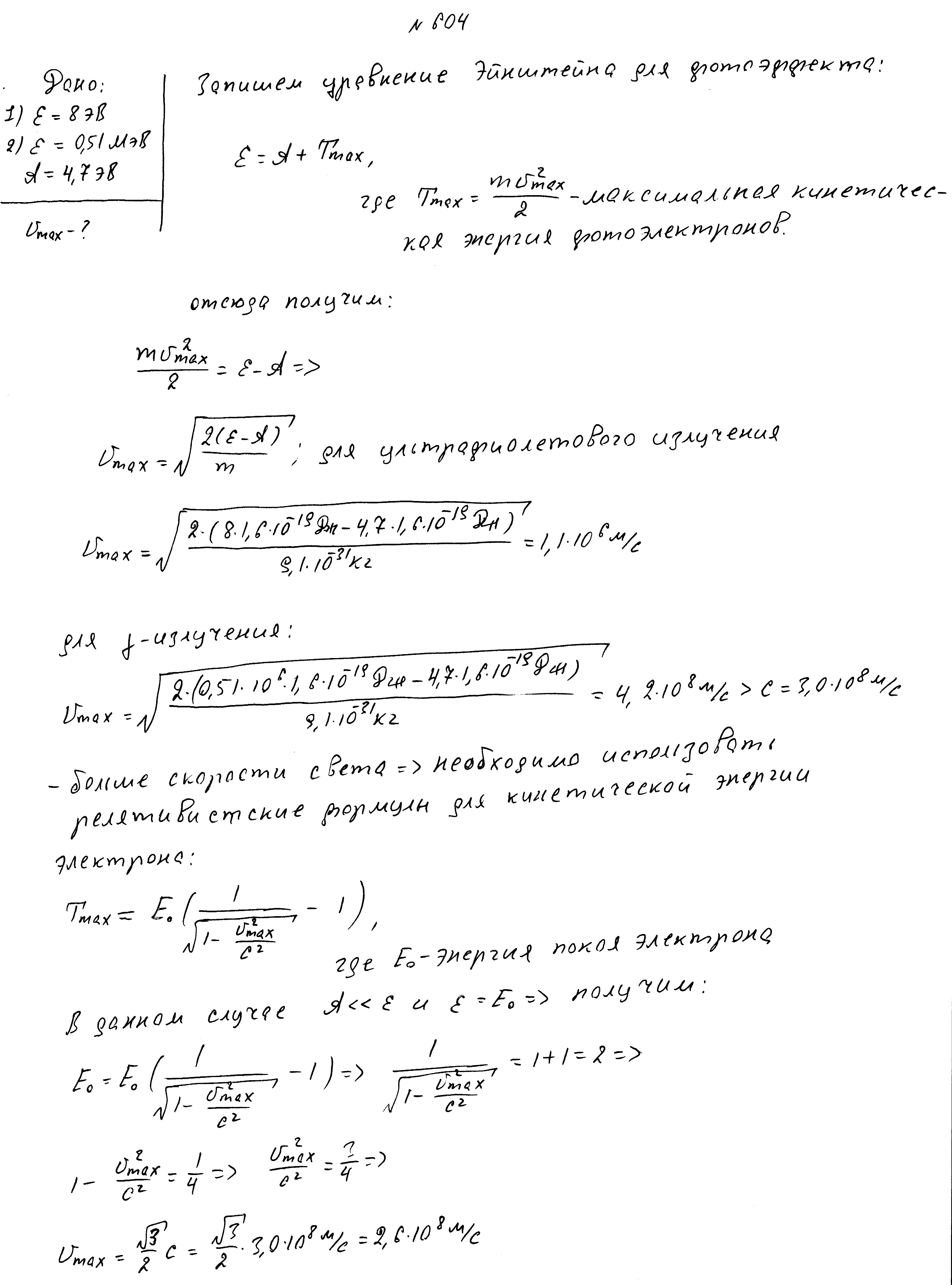
Фототок прекращается при задерживающей разности потенциалов 3,7 В. Работа выхода электронов равна 6,3 эВ. Какая работа выхода электронов у другого металла, если там фототок прекращается при разности потенциалов, большей на 2,3В.
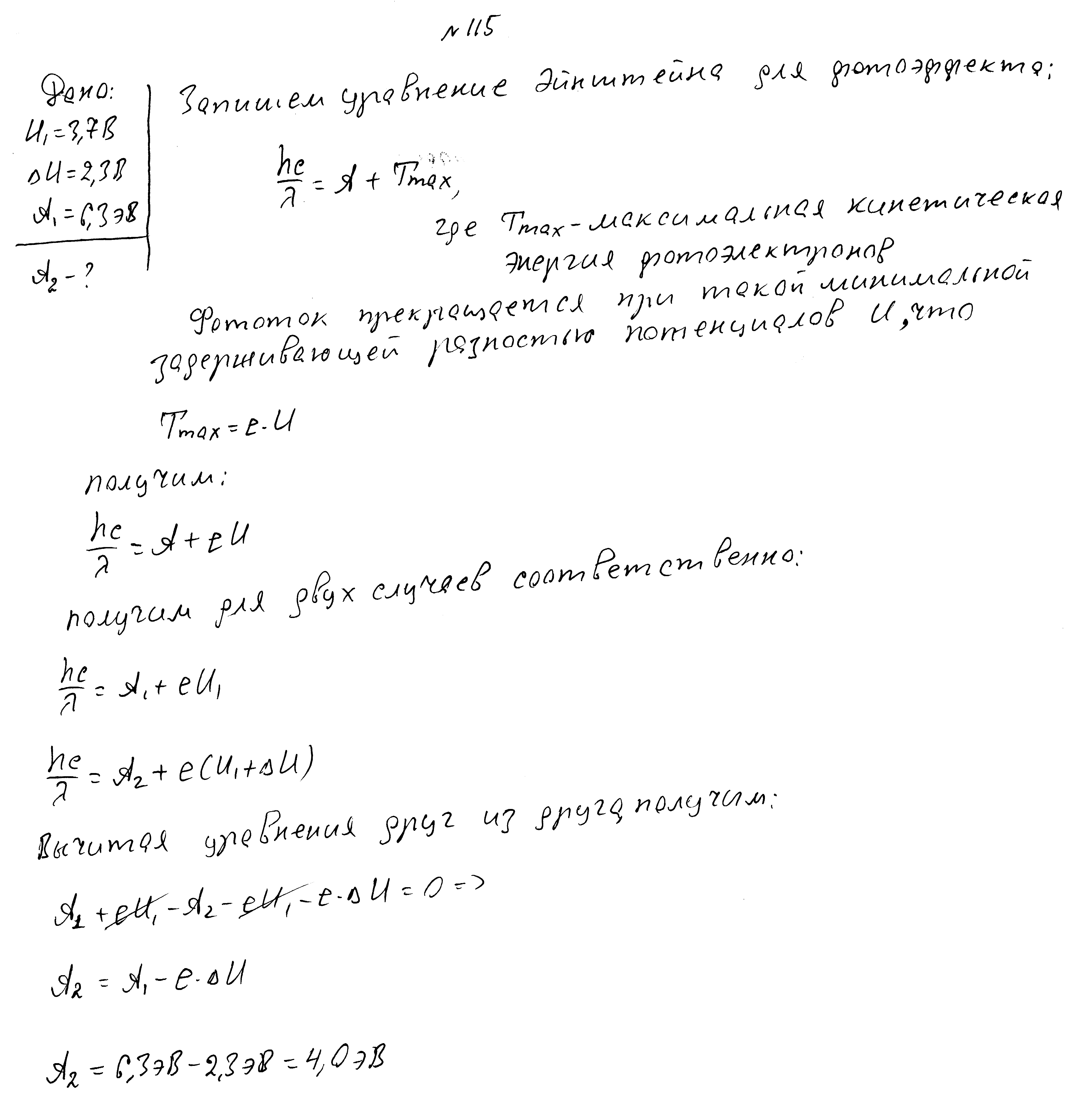
Работа выхода электронов из металла 4,5 эВ, энергия падающих фотонов 4,9 эВ. Чему равен максимальный импульс фотоэлектронов?
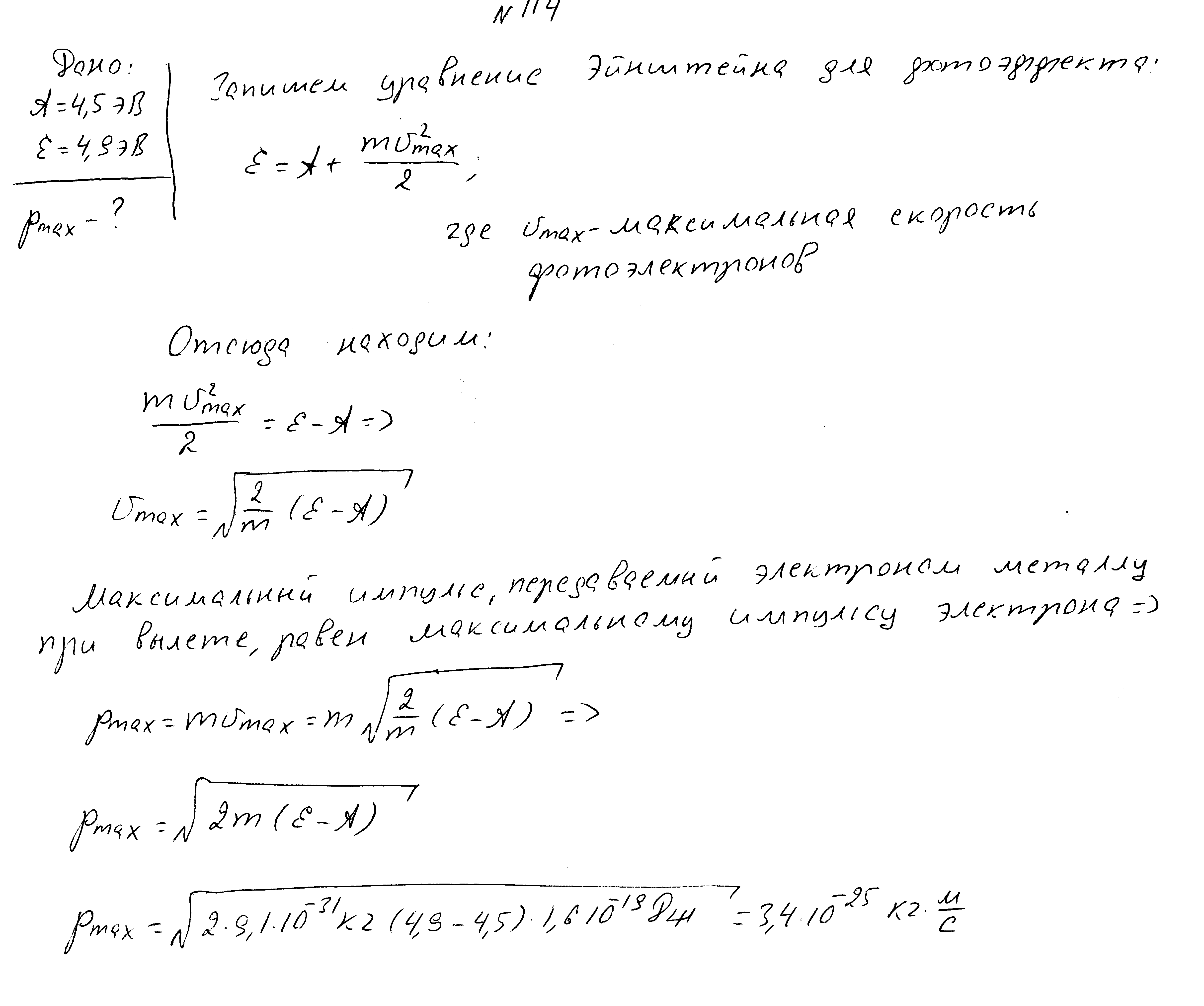
Красная граница фотоэффекта 2900 ангстрем, максимальная скорость фотоэлектронов 10 8 м/с. Найти отношение работы выхода электронов к энергии палающих фотонов.
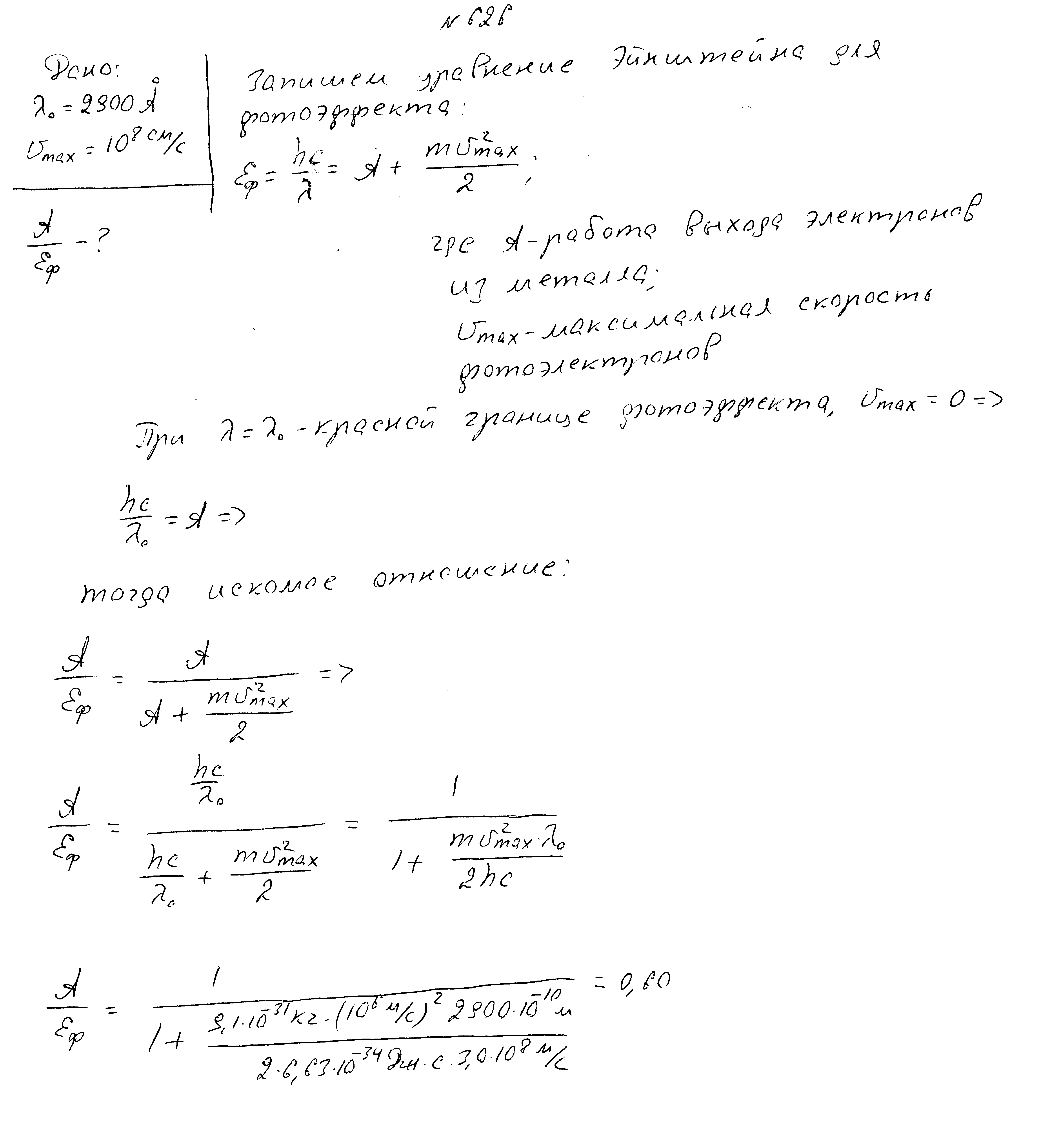
Длина волны падающего света 400нм, красная граница фотоэффекта равна 400нм. Чему равна максимальная скорость фотоэлектронов?
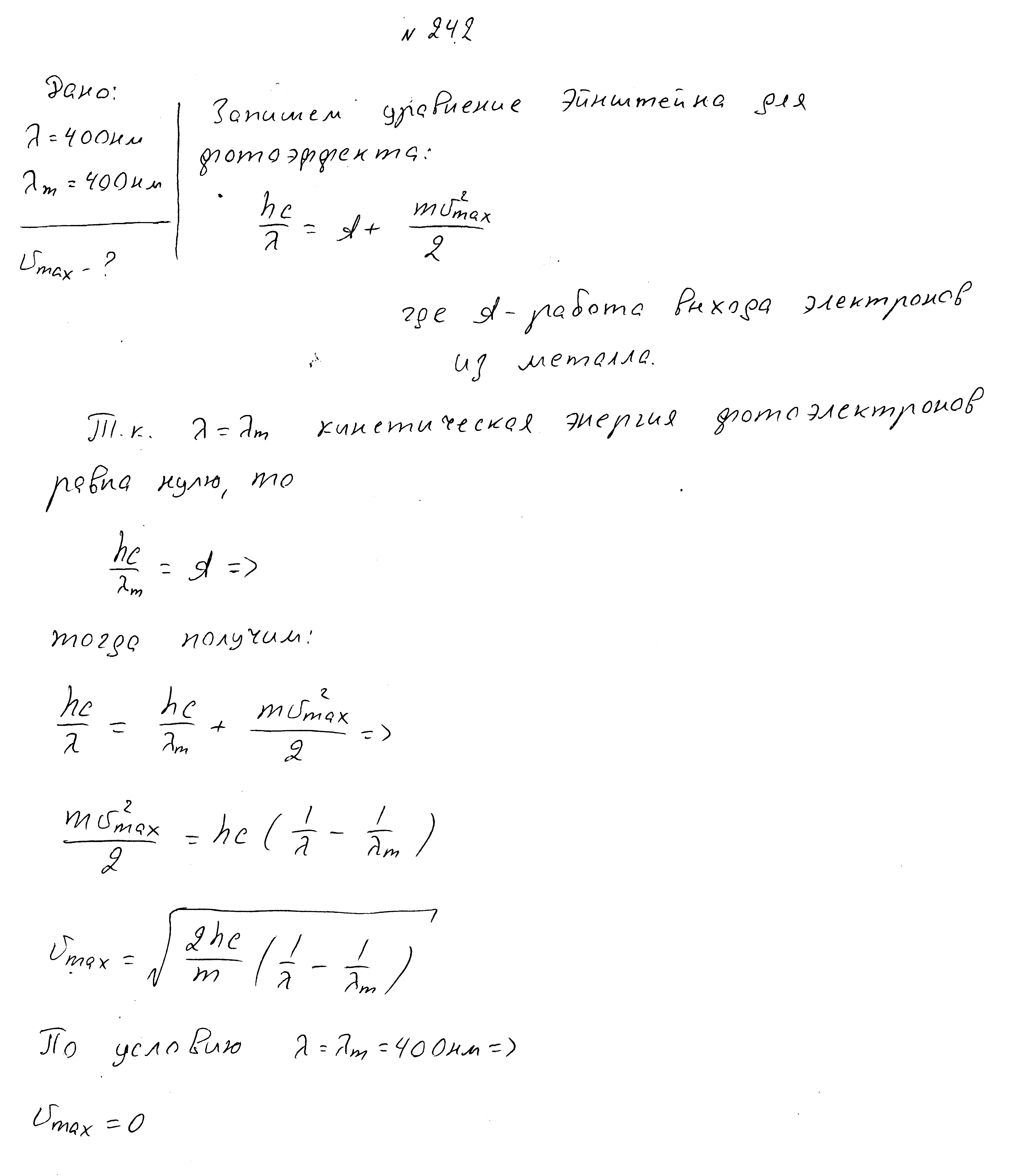
Длина волны падающего света 300нм, работа выхода электронов 3,74 эВ. Напряженность задерживающего электростатического поля 10 В/см.Какой максимальный путь фотоэлектронов при движении в направлении задерживающего поля?
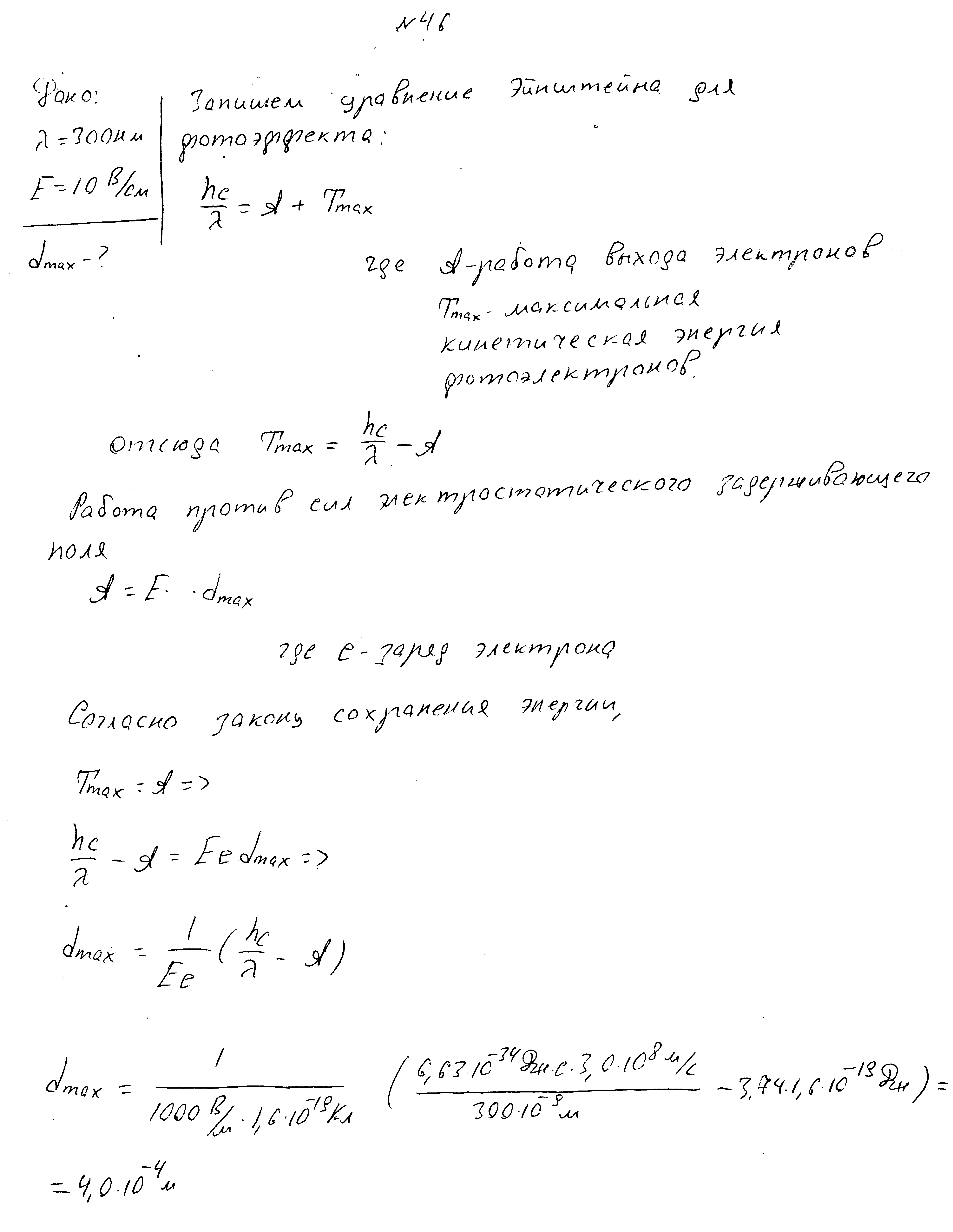
Длина волны падающего света 100 нм, работа выхода электронов 5,30эВ. Найти максимальную скорость фотоэлектронов.
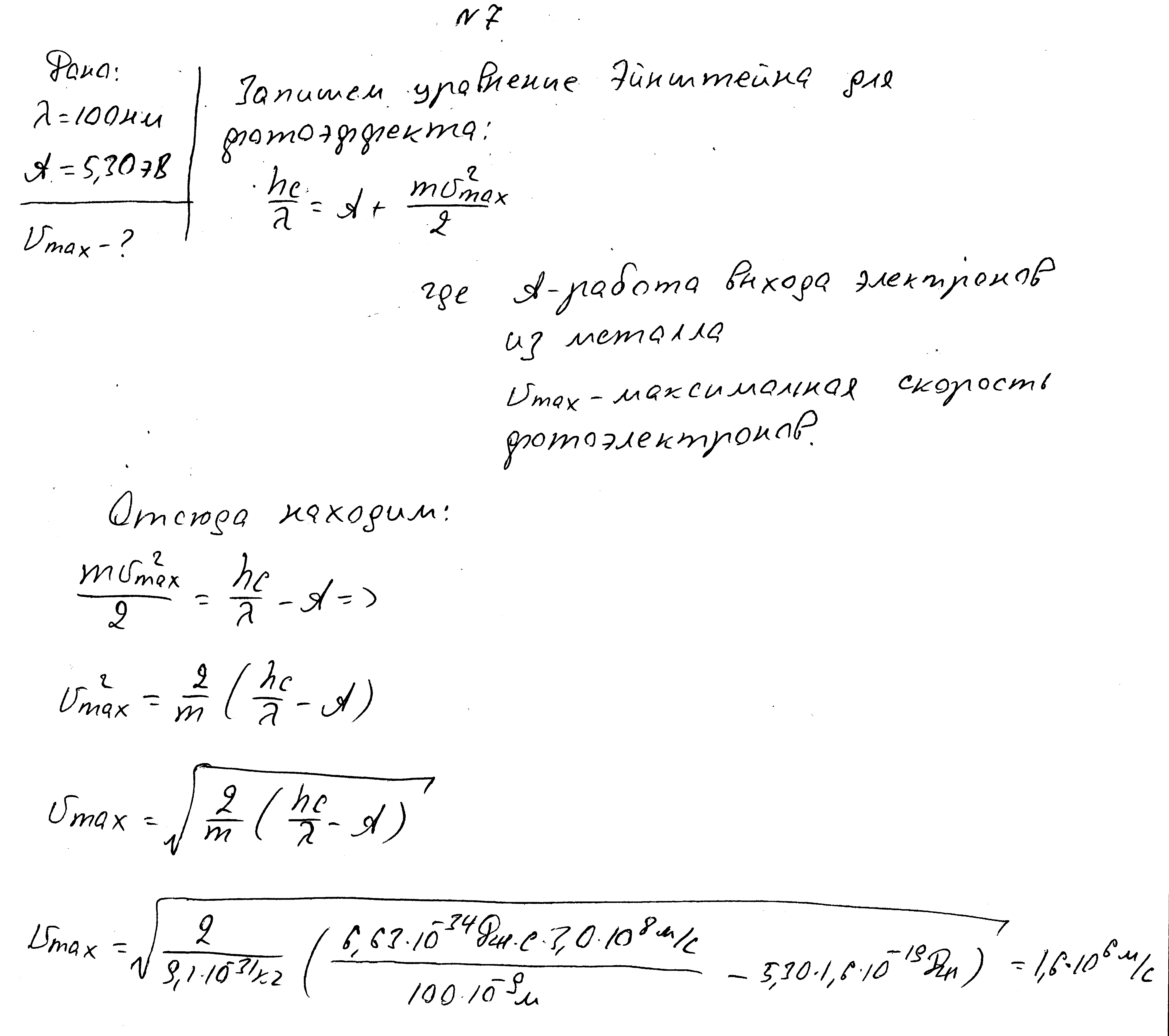
При длине волны радающего света 491нм задерживающая разность потенциалов 0,71В. Какова работа выхода электронов? Какой стала длина волны света, если задерживающая разность потенциалов стала равной 1,43В?
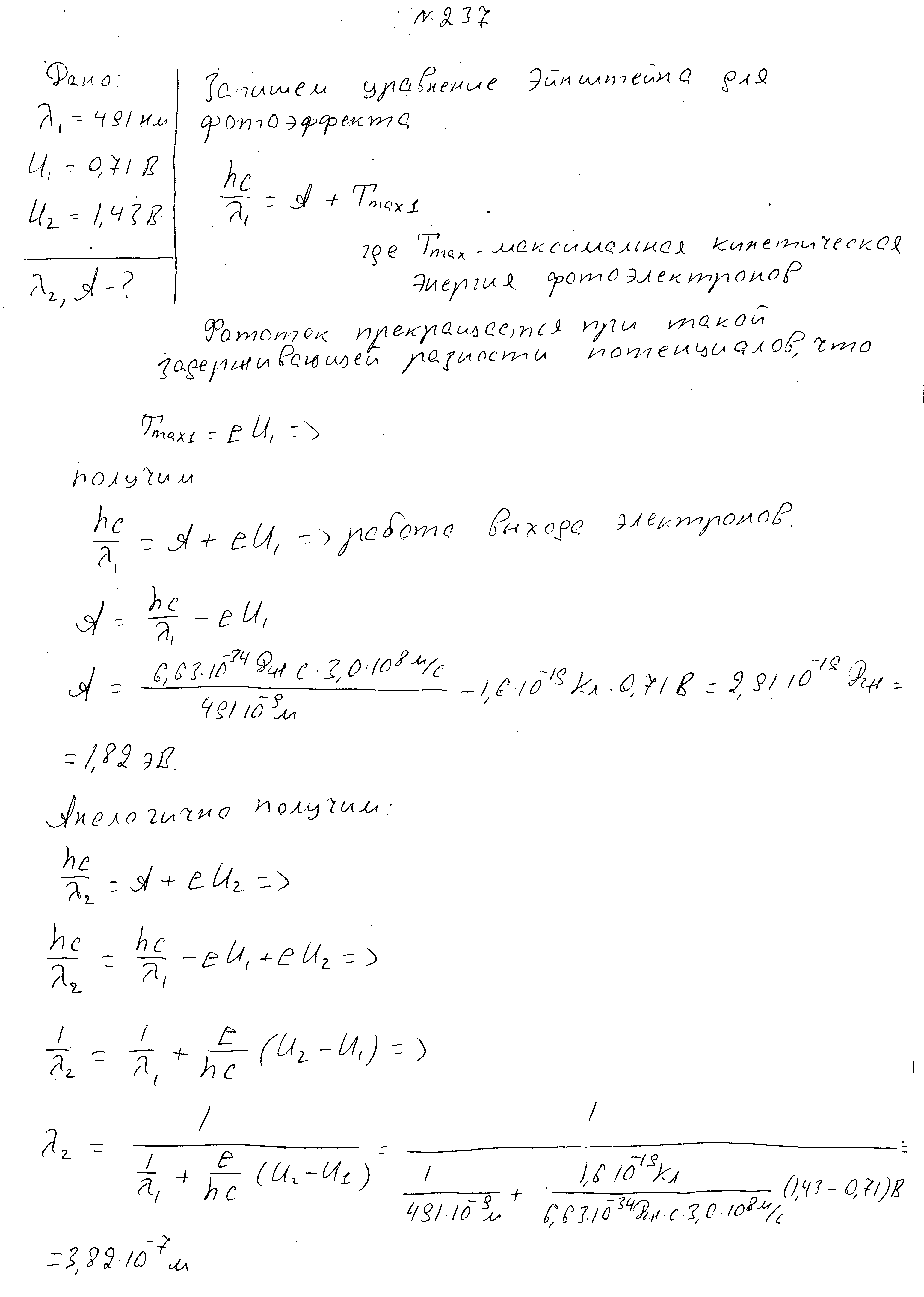
Кинетическая энергия фотоэлектронов 2,0 эВ, красная граница фотоэффекта 3,0*10 14 Гц. Определить энергию фотонов.

Красная граница фотоэффекта 0,257 мкм, задерживающая разность потенциалов 1,5В. Найти длину волны падающего света.
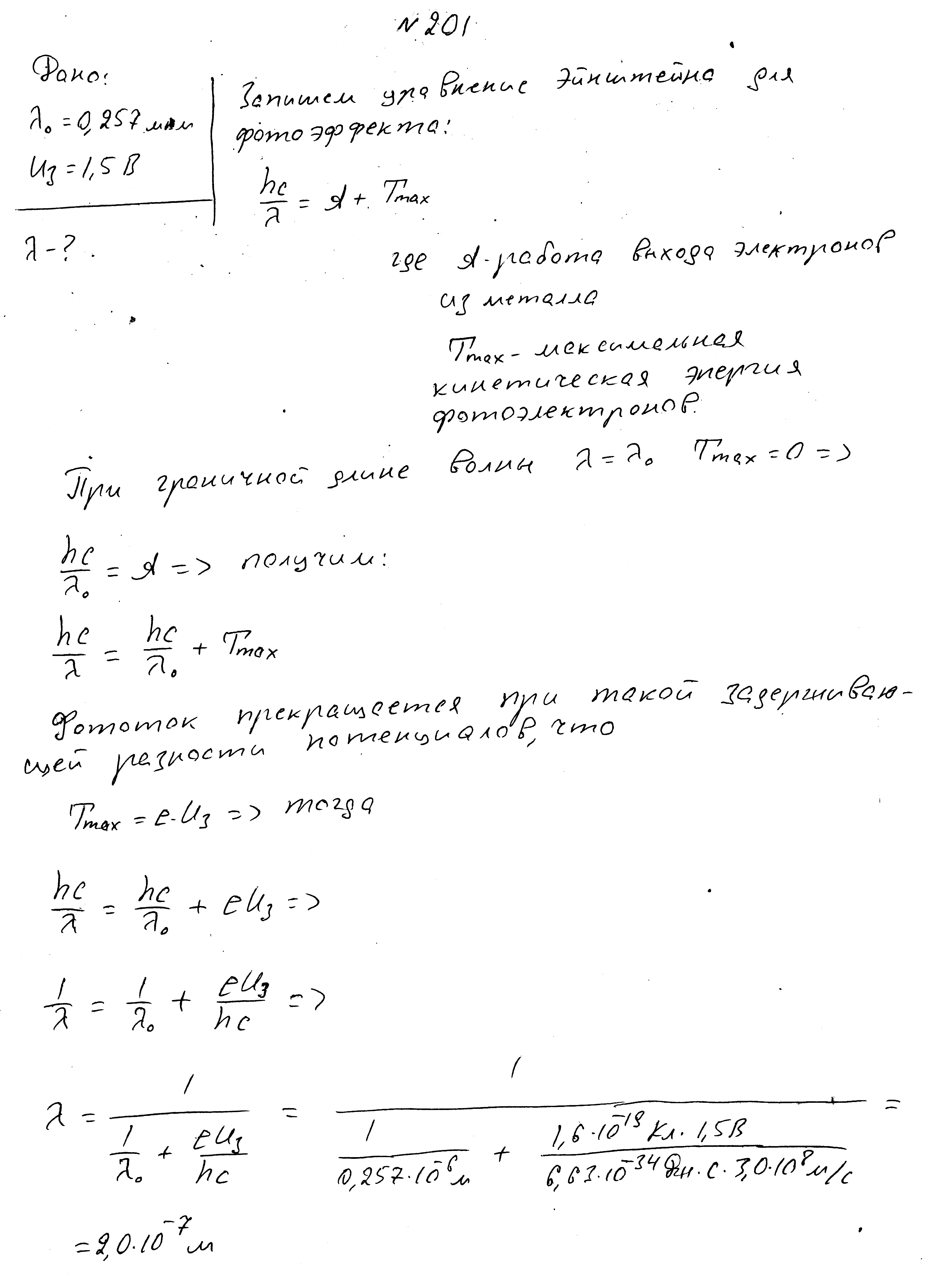
Красная граница фотоэффекта 2850 ангстрем. Минимальное значение энергии фотона, при котором возможен фотоэффект?
Источник
Одним из интереснейших квантовых эффектов, рассматриваемых в курсе школьной физики, является фотоэлектрический эффект или фотоэффект. Фотоэффект — явление взаимодействия света с веществом, в результате которого энергия фотонов передаётся электронам вещества.

Рис. 1. Фотоэффект
Облучаем поверхность вещества. Энергия каждого фотона равна . Фотон, попадающий внутрь вещества, поглощается электроном, который, в свою очередь, приобретает дополнительную энергию. Вырываясь из поверхности вещества, электрон теряет часть энергии (взаимодействуя с ионами вещества) и, становясь свободным (когда электрон перестаёт взаимодействовать с веществом), улетает в пространство.
С точки зрения зрения закона сохранения энергии, можно получить уравнение Эйнштейна:
(1)
- где
Работа выхода электрона () — минимальная энергия, которую необходимо передать электрону, чтобы он «выбрался» на поверхность. Если энергия фотона равна точно энергии выхода, то электрон, «выйдя» на поверхность, там и останавливается, т.е. после выхода электрона, его кинетическая энергия численно равна нулю. Тогда уравнение Эйнштейна примет вид:
(2)
- где
Красная граница фотоэффекта () — частота излучения (фотона), ниже которой фотоэффект не происходит.
Аналогично можно ввести:
(3)
Вывод: задачи на фотоэффект вводятся именно этим словом. Единственное, что мы можем использовать при этом, — уравнение Эйнштейна (1).





