Видео занятия
Строим корреляционную матрицу. Для этого используем надстройку «Анализ данных»
Выбираем в диалоговом окне «Анализа данных» – корреляция.
Далее заполняем диалоговое окно:
Получим корреляционную матрицу:
Наблюдается тесная связь между переменной Y и Х1, Y и X2, так как попарные коэффициенты корреляции составляют 0,8602 и 0,7479 соответственно. Это выше 0,7 – связь достаточно тесная.
Межу объясняющими переменными Х1 и Х2 коэффициент составляет 0,6311. Он ниже других, но имеет значение больше 0,6. Значит между объясняющими переменными, может быть корреляционная связь (явление мультиколлинеарности). Для обнаружения мультиколлинеарности есть ряд критериев, например VIF-критерий.
Парные коэффициенты корреляции можно ещё найти с помощью статистической функции КОРРЕЛ.
Заполняем диалоговое окно статистической функции КОРРЕЛ.
Получаем тоже значение, что и корреляционной матрице для Y и X1: 0,860227
Аналогично по отдельности можем найти и другие парные коэффициенты корреляции.
Строим множественную регрессию. Для этого в надстройке «Анализ данных» выбираем регрессия. Заполняем диалоговое окно.
Выбираем уровень надёжности 98%. Для коэффициентов регрессии будет найден доверительный интервал с уровнем с доверительной вероятностью 98%. Так же выбираем остатки, график остатков. Эти данные необходимы нам для дальнейшего анализа во второй части.
Получим.
Проведём анализ полученных данных.
Здесь выводятся: множественный коэффициент корреляции, коэффициент детерминации (R-квадрат), скорректированный коэффициент детерминации (нормированный R-квадрат), стандартная ошибка регрессии (S).
R-квадрат = RSS/TSS
Стандартная ошибка = (ESS/(n-m-1))^0.5
ESS (error sum of squares) – остаточная сумма квадратов.
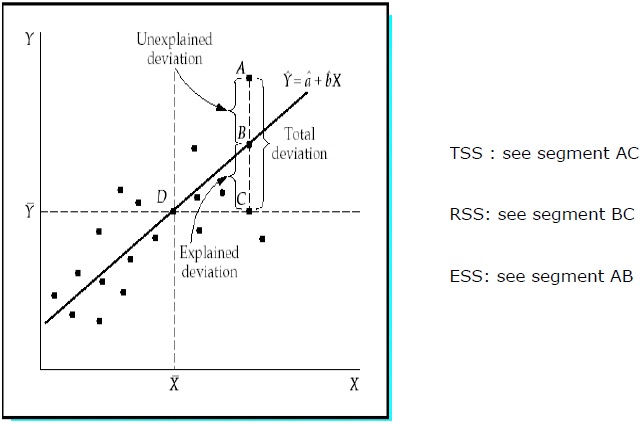
Построенное уравнение регрессии объясняет изменение результативного показателя Y на 80,99%. Остальные 10,01% приходятся на случайные факторы и факторы не включённые в модель.
Здесь даны столбцы: со степенями свободы (df); суммой квадратов (SS), суммой квадратов, делённых на степень свободы (MS=SS/df). Так же дано значение F-критерия Фишера и вероятность принятия нулевой гипотезы о равенстве коэффициента детерминации нулю (Значимость F).
TSS (total sum of squares) – общая сумма квадратов отклонений зависимой переменной от средней или вся дисперсия зависимой переменной;
RSS (regression sum of squares) – сумма квадратов, обусловленная регрессией или объясненная часть всей дисперсии;
ESS (error sum of squares) – остаточная сумма квадратов, характеризующая влияние неучтенных факторов или необъясненная дисперсия.
F= (ESS/m)/(RSS/(n-m-1)), n=32 m=2
Значимость F= 3,51562998617576E-11 <<<<0.01. Не можем принять нулевую гипотезу, принимаем альтернативную. Коэффициент детерминации отличен от нуля. Уравнение значимо в целом.
Так же можно сравнить наблюдаемое значение F-критерия с критическим. Берём уровень значимости 0,01, число степеней свободы 2 и 29. И с помощью статистической функции F.ОБР.ПХ находим критическое значение распределения Фишера
F.ОБР.ПХ(0,01;2;29) = 5,420445
Наблюдаемое значение оказалось выше критического (61,766> 5,420445), отвергаем нулевую гипотезу – уравнение значимо в целом.
В данной таблице выводятся столбцы: коэффициентов регрессии; стандартных ошибок коэффициентов регрессии; t-статистик; вероятности принятия нулевой гипотезы для коэффициентов (Р-значение); доверительные интервалы для коэффициентов регрессии (95% интервал считается по умолчанию, 98% – мы задали сами в диалоговом окне регрессия).
Запишем полученное уравнение множественной регрессии.
Если P-значение < 0.05, то коэффициент регрессии можем принять значимым при 5% уровне.
Т. е. отвергаем нулевую гипотезу при 5% уровне значимости. Т. е. все коэффициенты полученного уравнения статистически значимы при 5% уровне, т. к. для них всех р-значение меньше 0,05.
Так же можем определить значимость коэффициентов, сравнивая наблюдаемые значения t-статистик с критическими. Находим критическое значения с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х.
СТЬЮДЕНТ.ОБР.2Х(0,05;29)= 2,04523
Наблюдаемые значения t-статистик из таблицы, выше критического значения при 5% уровне значимости, отвергаем нулевую гипотезу. Коэффициенты регрессии являются статистически значимыми.
Так же можем получить расчёт для множественной регрессии, используя статистическую функцию Excel – ЛИНЕЙН.
Для неё берётся число столбцов, равное количеству объясняющих переменных плюс один (в нашем случае три), а количество строк всегда пять.
Выделяем диапазон: E37:G41. Ставим знак равно и находим функцию ЛИНЕЙН в статистических функциях.
Заполняем диалоговое окно:
Нажимаем клавиши
Получаем результат:
t-статистики определим делением коэффициента регрессии на стандартную ошибку.
Получим следующую таблицу.
Кроме t-статистики в этой таблице считает функция ЛИНЕЙН. t-статистики мы подсчитали сами дополнительно.
Принципиальное отличие функции ЛИНЕЙН от регрессии в пакете «Анализ данных» заключается в том, что при изменении самих данных, все значения в таблице ЛИНЕЙН пересчитываются автоматически сразу. А при работе с пакетом «анализа данных» надо запускать процесс ещё раз, т. е. вызывать диалоговое окно, заполнять его и нажимать «ок».
В следующей части мы рассмотрим тестирование полученной модели на наличие автокорреляции остатков и на наличие гетероскедастичности.
Материал подготовлен сайтом: https://pro-smysl.ru/
Онлайн помощь в решении задач, консультации, создание обучающих роликов.
Подписывайтесь на наши каналы:
https://vk.com/sm_smysl
https://www.youtube.com/@SMYS_L
From Wikipedia, the free encyclopedia
In statistics, the explained sum of squares (ESS), alternatively known as the model sum of squares or sum of squares due to regression (SSR – not to be confused with the residual sum of squares (RSS) or sum of squares of errors), is a quantity used in describing how well a model, often a regression model, represents the data being modelled. In particular, the explained sum of squares measures how much variation there is in the modelled values and this is compared to the total sum of squares (TSS), which measures how much variation there is in the observed data, and to the residual sum of squares, which measures the variation in the error between the observed data and modelled values.
Definition[edit]
The explained sum of squares (ESS) is the sum of the squares of the deviations of the predicted values from the mean value of a response variable, in a standard regression model — for example, yi = a + b1x1i + b2x2i + … + εi, where yi is the i th observation of the response variable, xji is the i th observation of the j th explanatory variable, a and bj are coefficients, i indexes the observations from 1 to n, and εi is the i th value of the error term. In general, the greater the ESS, the better the estimated model performs.
If 

is the i th predicted value of the response variable. The ESS is then:
- where
the value estimated by the regression line .[1]
In some cases (see below): total sum of squares (TSS) = explained sum of squares (ESS) + residual sum of squares (RSS).
Partitioning in simple linear regression[edit]
The following equality, stating that the total sum of squares (TSS) equals the residual sum of squares (=SSE : the sum of squared errors of prediction) plus the explained sum of squares (SSR :the sum of squares due to regression or explained sum of squares), is generally true in simple linear regression:
Simple derivation[edit]
Square both sides and sum over all i:
Here is how the last term above is zero from simple linear regression[2]
So,
Therefore,
Partitioning in the general ordinary least squares model[edit]
The general regression model with n observations and k explanators, the first of which is a constant unit vector whose coefficient is the regression intercept, is
where y is an n × 1 vector of dependent variable observations, each column of the n × k matrix X is a vector of observations on one of the k explanators, 

The residual vector 


Denote as 

The explained sum of squares, defined as the sum of squared deviations of the predicted values from the observed mean of y, is
Using 







![X^{T}{hat e}=X^{T}[I-X(X^{T}X)^{{-1}}X^{T}]y=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/48b919724d6469ec94125e22146b93be8608cd05)

In linear algebra terms, we have 


The proof can be simplified by noting that 
Thus,
which again gives the result that TSS = ESS + RSS, since 
See also[edit]
- Sum of squares (statistics)
- Lack-of-fit sum of squares
- Fraction of variance unexplained
Notes[edit]
- ^ “Sum of Squares – Definition, Formulas, Regression Analysis”. Corporate Finance Institute. Retrieved 2020-06-11.
- ^ Mendenhall, William (2009). Introduction to Probability and Statistics (13th ed.). Belmont, CA: Brooks/Cole. p. 507. ISBN 9780495389538.
References[edit]
- S. E. Maxwell and H. D. Delaney (1990), “Designing experiments and analyzing data: A model comparison perspective”. Wadsworth. pp. 289–290.
- G. A. Milliken and D. E. Johnson (1984), “Analysis of messy data”, Vol. I: Designed experiments. Van Nostrand Reinhold. pp. 146–151.
- B. G. Tabachnick and L. S. Fidell (2007), “Experimental design using ANOVA”. Duxbury. p. 220.
- B. G. Tabachnick and L. S. Fidell (2007), “Using multivariate statistics”, 5th ed. Pearson Education. pp. 217–218.
++++++++++++++++++++++
Обратитесь к многим статьям
++++++++++++++++++++++
Во-первых: гипотеза
Бросать монету
- Гипотеза H0 [Гипотеза]: Монеты являются справедливыми [появляется в положительных и скоростях реакции]
- HA Гипотеза [Осмотр]: Монеты проблематичны
Весь процесс тестирования гипотезы заключается в том, чтобы проверить по гипотезам H0, и если вывод противоречивой получен, то предположения H0 будут отклонены.
Так называемое противоречие, результаты теста, вероятность, которая появляется в условиях гипотезы H0. 】
Р значение: в гипотезе первоначальной гипотезы (H0) правильно,Вероятность появления статуса или хуже.
1.1 H0 Предположения, мы знаем, что монеты бросают, а количество положительных, в соответствии с бинарным распределением.
А, мы бросаем 10 монет.
Результат появился 8 фронт.
B, запрашивать два таблица распределения,Одностороннее значение p【8,9,10】
p(8/9/10)=0.05
Как этот результат этого?
В H0 гипотезе [ярмарка монет], бросить 8 передних и более экстремальных случаевОдностороннее значение p0,05, если существует значительный уровень 0,05, то мы отказываемся изменить предположения H0 и думать, что монета проблематичная.
1.2 Так как фронт брошен 8 раз, почему также добавляют 9 спереди, 10 фронт, эти еще две экстремальные вероятности?
- Во-первых, определение значения p есть.
- Во-вторых, вообще распределенные, нездоровые к единственной вероятности, вероятность поиска области очень проста, то есть область.

1.3 Значительный уровень 0,05
Фактически, значительный уровень – это субъективное определенное значение.
Например, мы определяем значительный уровень 0,01.
Затем вышеупомянутое тестовое значение p = 0,05, меньше, чем значительный уровень 0,01, то это означает, что мы не можем отклонить гипотезу H0, нужно больше тестов, а то как менее, чем этот уровень 0,01, мы можем отказаться от предположений H0.
Второй: T тест
2.1, две поля пшеницы, A и B, MirafaDian традиционный процесс, процесс улучшения полей Эмиана.
Известно, что выход выхода μ0 = 100, стандартное отклонение от пробы σ [стандартное отклонение неизвестно];
B Образец n, выхода выходов деформации образца X = 120, стандарт образца плохой S,Формула Xi – это единый выход растений [может рассматривать каждый отдельных штамма B], среднее значение X – это среднее значение A, поскольку в целом a, но потому, что мы предполагаем, что он является частью одного из одного общего Все отдельные растения единого растительного производства с одним заводом B.

2.2, гипотеза
- H0 Гипотеза [Гипотеза]: B не улучшается, Jiajia находится под распределением
- HA Гипотеза: в гипотезе H0, небесное значение x = 120, может ли образец стандартной дифы не может произойти?
Известно, что нормальное распределение, N (μ0, σ ^ 2) от μ0 = 100, стандартное отклонение σ.

2.3, происхождение значения T
T статистика формулы:

А, молекула = x – μ0, согласно главной карте Taizu, промежуток является стандартным отклонением σ, чтобы исключить влияние пролета, мы разделяем молекулы в стандартном отклонении, (x – μ0) / σ, Но потому что σ неизвестный, заменен B, Final (x – μ0) / s
【Из-за стандартной разницы σ a a, мы предполагаем, что часть из того же распределения, поэтому стандартная разница между B составляет приблизительно。】
****************************************************************************************************************************
Мы всеСредство двух образцов, стандартного отклонения и стандартного отклонения их соответствующих матерей.
****************************************************************************************************************************
b、Сплит S / √n означает: стандартная ошибка выводится образец.
Объяснение: Я с различными этимиками, если мы очень, тогда мы будем подчиняться, B. x = 120, подробное объяснение B улучшить производство.
Чтобы отразить влияние N количества образцов в формулу, мы позволяем Splitter S, которое делится на корневом номере N, тем самым уменьшая родительское значение, в конечном итоге увеличивая значение T, чтобы отразить эффект образца N.
2.4, T распределение
Мы находим значение T, так как вы знаете значение P, соответствующую значение T?
A, Функция плотности вероятности

B, карта распределения

Согласно Freedom V = N-1, таблица проверяется, чтобы найти соответствующее значение P, и если он может отказаться от первоначальной гипотезы H0 под соответствующим значительным уровнем.
В-третьих: наименьший квадрат
****************************************************************************************************************************
1, стандартное отклонение »[отражает флуктуацию точек данных]: указывает на индикатор варианта личности, отражающий степень дискретной к среднему образцу образца, является индикатором измерения точности данных.
2, Стандартная ошибка) [Светоотражающая волновая волна ситуации]: относится к испытанию отбора проб (или повторных и других прецизионных измерений)Стандартная разница в среднем образцаОтражает степень изменчивости образца среднего размера в среднем средне, отражая размер ошибки выборки, является индикатором измерения метрики.
Объяснение: в качестве количества образцов (или количество измерений) n увеличивается, стандартное отклонение имеет тенденцию к устойчивому значению, тем ближе стандарт образца, тем ближе к общему стандартному отклонению, а стандартная ошибка последовала за количеством образцов ( Или количество измерений) n увеличение постепенно уменьшается, тем больше средних средств образцов ближе к общей среднему среднему μ;
3, интервал доверия: даВерныйНекоторые из образцовИнтервальная оценка общих параметров,Настоящее значение этого параметра имеет определенную вероятность падения по результатам измерения.
4, Формула
А, стандартная формула отклонения:

B, стандартная ошибка формулы:
Ошибка настройки n измеренийE1、E2……EnЗатем стандартная ошибка σ этого набора измерений равна:

среди них,E = Xi − TГде: e- ошибка;Xi– Определите значение; T-Tright Value.
Из-за измеренногоПравда неизвестнаОшибки каждой оценки измерения не знают, поэтому его нельзя получить в формуле.
Арифметический средний может быть получен при измерении, он ближе всего к истинному значению (N), и это легко рассчитатьРазница между измерением и арифметическим средним, называется остаточным(Помните в V). Теоретический анализ показывает, что остаточный V используется для представления ограниченного времени (N раз) наблюденияРезультаты измеренийСтандартная ошибка σ, его формула расчета:

Для набора одинаковых точности измерений (N раз) измерения данных средних арифметических, его ошибка должна быть меньше. Теоретический анализ показывает, что его арифметическая средняя стандартная ошибка. В некоторых книгах или в калькуляторе используйте символы S):

c、Стандартная ошибка 1 /
D, доверительный интервал
95% доверительный интервал β1 = [β1-2SE(β1),β1+2SE(β1)】
****************************************************************************************************************************
Минимальный множитель: самая маленькая, подтвердила значение элементов коэффициентов и перехвата через RSS.
На практике мы можем получить порцию данных наблюдений, рассчитать параметры наименьших квадратов линии, но общая регрессия не наблюдается.
У нас есть группа наблюдения [y, x], есть n значений
Среди них, Y-переменные: Y1, Y2, Y3, ,,,,,,,,,,,, Ю.Н.
X-переменная соответствует x1, x2, x3 ,,,,,,,,,,,,,,,,
а, образец средней оценки общего среднего
Итак, как наш единственный набор Y переменной средней х0, насколько точна оценка генерал- Y истинного среднего ц? Насколько это далеко?
Общее уравнение регрессии: стандартное отклонение SE (μ0) = σ / √n
Вариация: var (μ0) = σ ^ 2 / n
Среди них: молекулярное σ,Общее наблюдениеYi значитСтандартное отклонение,Оценка ошибки остаточных стандартов RSEЗнаменатель – корневое значение номера образца N.
Стандартное отклонение SE (μ0) говорит нам о том, что выборочное среднее μ0 оценивается отклонение от общего среднего реального среднего мкм.
Стандартная формула отклонения, сообщите мне, что количество образцов n, тем меньше отклонение.
B. Исследуйте наименьшие квадраты β0, β1, с общем истинным β0, β1 подход
SE(β0)
SE(β1)
С. Оценка стандартного отклонения SE (х0) является остаточным стандартной ошибкой РГП / √N [имеется в виде модели является правильным, и β0, β1 реальным значением, но все же отклонение].
Общее наблюдение за стандартным отклонением Yi означаетДисперсия σ ^ 2,отRSSПо оценкам.
В-четвертых: линейная регрессия существительное
1, остаточная площадь и RSS (остаточная сумма квадратов) [Не называйте SSE (сумма квадратов для ошибки)
RSS = Σi=1n (yi – yi^)2

2, остаточная стандартная ошибка RSE (остаточная стандартная ошибка)
RSE = √(RSS/(n-2))
3, вернитесь на квадрат иSSR(Сумма квадратов для регрессии)SSM(Sum of Squares for Model)】
【ПрозвищеESS(explained sum of squares) 】
SSR = Σi=1n (yi^ – y)2
4, общая площадь и SST (сумма квадратов общего)
SST = Σi=1n (yi – y)2
5, в целом: общая площадь и = квадрат возврата и + остаточные квадраты
SST=SSR + RSS
доказывать:Доказательство Вики
Объяснение: Общая площадь и представление SST, общая разность данных, мы знаем, что общая разница, две части, можно интерпретировать + unplanable.
ССР регрессионный площадь и представление, данные могут быть интерпретированы [то есть, разница в уравнении регрессии может объяснить]
Остаточная фракция RSS и указывает на то, что разница не объяснена. [Уравнение регрессии не может объяснить]
6, Свобода [Количество р регрессионного фактора]
RSS остаточный квадрат и свобода DFR = N -P -1
SSR регрессионный квадрат и свобода DFM = P
Общая площадь и свобода DFT = N -1
dft = dfr + drm
============================================================================
В статистике, степень свободы относится к числу переменных, которые не ограничены при расчете определенной статистики. Обычно DF = N-K. Там, где п является содержанием образца, к этому число ограниченных условий или переменным, или числа других независимых статистических данных при вычислении статистики. По оценкам, общая дисперсия оценивается, разведенный квадрат и. До тех пор пока N-1 число расщепленных квадратов определяется, дисперсия определяется, так как значение числа N-1 известен после того, как среднее значение определяется, величина п-1 определяется. Здесь, средний эквивалентен условие рестрикции, и так как это условие ограничения добавляется, степень свободы от общей дисперсии является N-1.
============================================================================
7、Остаточная сумма квадратов [незапланированная дисперсия]
MSR(Mean of Squares for residual) = RSS / DFR
Возвращение с площади и означающее [Развращение объяснения]
MSM( Mean of Squares for Model) = SSR /DFM
Пятый: линейная регрессия и анализ отклонений
1. Анализ переменных в дисперсионном анализе фактически являются переменными в линейной регрессии, а переменный пакет в дисперсионном анализе являются независимым переменными в линейной регрессии.
Анализ линейной регрессии и дисперсии одинаковы из-за переменных, являются непрерывной информацией,
Аргумент отличается, и дисперсия представляет собой классифицированную переменную, а линейная регрессия представляет собой непрерывные данные.
2, разностное сравнение[Исследование три препарата в ABC, влияя на объем легочной емкости, разделенный на три группы, каждую группу из 5 тестов лиц, целью которых является естественным, чтобы увидеть, если есть разница между этими тремя препаратами, то есть ли разница между Переменные значительны]
А, анализ дисперсии

б, изменение в линейную регрессию

3, объяснение
Как, эта форма почти форма линейной регрессии?
Y связано с переменными, X является собственной переменной. Единственное место с линейной регрессией:X и Y в линейной регрессии соответствуют одному。
————————————————————————————————————————————————————————-
[Раннее обнаружение дифференциального [различные образцы, по существу равны], линейная регрессия, потому что мы не можем сделать данные [X1, Y1], потому что X1 может только соответствовать одному Y1, но реальный общий, один X1 Значение может соответствовать Значение бесчисленного y1, но в целом никто не знает. На практике мы должны увидеть карту остаточной распределения, если она случайно распределяется, то мы считаем, что детектирование частичного разности удовлетворено. 】
————————————————————————————————————————————————————————-
X и Y дисперсионного анализа – один ко многим, а именно один х, соответствующий нескольким значениям Y, но это не влияет на анализ.
Фактически, даже в линейной регрессии, иногда будет пару явлений. Например, эффект веса на грузоподъемность легких, если есть несколько человек с той же весом тела, есть пара явлений. Это больше похоже на анализ дисперсии.
Наконец, добавьте некоторые резюме, теоретические вещи, общие линейные модели могут быть примерно так:
y=α+βx+ε,
На самом деле, каждый должен быть очень знакомым, что, как правило, имеет эту формулу в главе линейной регрессии в учебнике статистики. Y – это потому, что переменная – это переменная, но необходимо обратить внимание на классификационную переменную. Когда X – это форма переменных, когда X представляет собой непрерывную переменную, она становится линейной. Форма регрессии в форме.
Шестое: T Осмотр линейной регрессии
Тестовый объект: является ли параметр коэффициента одного регрессии значительно 0.
Принцип строительства: это фактор обнаружения достаточно близко? Послушное распределение – это T распределение.
Предварительные условия: простота обнаружения различий [разные образцы по существу равномерно], линейная регрессия, поскольку мы не можем сделать данные [x1, y1], потому что x1 – это только один y1, но это правда, значение x1 может соответствовать бесчисленным Y1, но в целом никто не знает. На практике мы должны увидеть карту остаточной распределения, если она случайно распределяется, то мы считаем, что детектирование частичного разности удовлетворено.
Если распределение остатков регулярно, то мы должны делать трансформацию, такие как трансформация журнала, соответствующие ядерные функции и т. Д.
Линейная регрессия: y = β1 * x + β0 + e
y = 8*x + 6 + e
- H0 Гипотеза [Гипотеза]: β1 = 0
- HA Гипотеза [Осмотр]: Если вы найдете значение β1, очень мало под Beta1 = 0?
T Испытание оригинальной формулы:

Линейная регрессионная тестовая формула:
t=(β1 – 0)/ SE(β1 )
Где: Se (β1) относится к стандартному отклонению β1 коэффициента регрессии.
Седьмое: линейная регрессия F осмотр
============================================================================
Определение: F Test также называют дисперсией дисперсии, в основном путем сравнения дисперсии S ^ 2 из двух наборов данных, чтобы определить, имеет ли их распределение значительную разницу. Что касается того, существует ли системная ошибка между двумя наборами данных, тест T выполняется после выполнения FET F и определяется, что их распределение не имеет существенных различий.
Другие объяснения: Одним из них является то, что остаточная дисперсия недостаточно снижается по сравнению с дисперсией образца, указывающая на то, что большинство примеров информации уже включена в основную модель.
============================================================================
Структурный принцип: от формулы фракционного квадрата и разложения, интерпретация линейной зависимости переменной интерпретации значительна к интерпретации переменных из квадрата мокроты и формулы разложения.
Тестовый объект: все коэффициенты регрессии всего уравнения все обнаружены до 0.
Линейная регрессия: y = β0 + β1 * x + β2 * x ,, βp * x + e
- H0 Гипотеза [Гипотеза]: β1 = β2 = βp = 0
- HA Гипотеза [Осмотр]: по крайней мере один β не 0,H0 Гипотеза [Гипотеза] Условия, F Тестовые презентационные карты Распределение карты。
F Test Formula = MSM / MSR
=(SSR/p) / (RSS/n-p-1)
= Я могу объяснить / неизвестно вызывает [остаточный ущерб]
F Результаты обнаружения, проверьте значение таблицы P, см. Если он может отказаться от первоначальной гипотезы.
При отклонении, то есть как минимум один β не 0.
Также: линейная регрессия, f = t ^ 2.Ссылка ссылки: документ Baidu
Регрессия – это статистический метод, который помогает квалифицировать отношения между взаимосвязанными экономическими переменными. Первый шаг включает в себя оценку коэффициента независимой переменной, а затем измерение достоверности оцененного коэффициента. Это требует формулирования гипотезы, и на основе гипотезы мы можем создать функцию.
Если менеджер хочет определить взаимосвязь между рекламными расходами фирмы и доходами от продаж, он подвергнется проверке гипотезы. Предполагая, что более высокие расходы на рекламу приводят к увеличению продаж для фирмы. Менеджер собирает данные о расходах на рекламу и о выручке от продаж за определенный период времени. Эта гипотеза может быть переведена в математическую функцию, где она приводит к –
Y = A + Bx
Где Y – продажи, x – расходы на рекламу, A и B – постоянные.
После перевода гипотезы в функцию основание для этого должно найти связь между зависимой и независимой переменными. Значение зависимой переменной имеет наибольшее значение для исследователей и зависит от значения других переменных. Независимая переменная используется для объяснения изменения зависимой переменной. Это может быть классифицировано в два типа –
-
Простая регрессия – одна независимая переменная
-
Множественная регрессия – несколько независимых переменных
Простая регрессия – одна независимая переменная
Множественная регрессия – несколько независимых переменных
Простая регрессия
Ниже приведены шаги для построения регрессионного анализа –
- Укажите модель регрессии
- Получить данные о переменных
- Оценить количественные отношения
- Проверьте статистическую значимость результатов
- Использование результатов в принятии решений
Формула для простой регрессии –
Y = a + bX + u
Y = зависимая переменная
X = независимая переменная
а = перехват
б = уклон
и = случайный фактор
Данные поперечного сечения предоставляют информацию о группе объектов в данный момент времени, тогда как данные временных рядов предоставляют информацию об одном объекте с течением времени. Когда мы оцениваем уравнение регрессии, оно включает в себя процесс определения наилучшей линейной зависимости между зависимой и независимой переменными.
Метод обыкновенных наименьших квадратов (OLS)
Обычный метод наименьших квадратов предназначен для подгонки линии через разброс точек таким образом, чтобы сумма квадратов отклонений точек от линии сводилась к минимуму. Это статистический метод. Обычно программные пакеты выполняют оценку OLS.
Y = a + bX
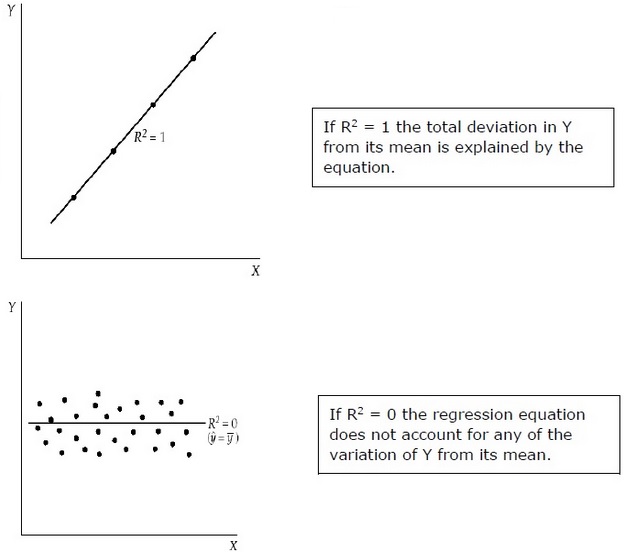
Коэффициент определения (R 2 )
Коэффициент детерминации – это мера, которая показывает процент изменения зависимой переменной из-за изменений в независимых переменных. R 2 является показателем качества модели соответствия. Ниже приведены методы –
Общая сумма квадратов (TSS)
Сумма квадратов отклонений значений выборки Y от среднего значения Y.
TSS = SUM (Y i – Y) 2
Y i = зависимые переменные
Y = среднее значение зависимых переменных
я = количество наблюдений
Регрессия Сумма квадратов (RSS)
Сумма квадратов отклонений расчетных значений Y от среднего значения Y.
RSS = СУММА (Ỷ i – uY) 2
Ỷ i = оценочное значение Y
Y = среднее значение зависимых переменных
я = количество вариантов
Ошибка суммы квадратов (ESS)
Сумма квадратов отклонений выборочных значений Y от расчетных значений Y.
ESS = СУММА (Y i – Ỷ i ) 2
Ỷ i = оценочное значение Y
Y i = зависимые переменные
я = количество наблюдений
R2 =
RSS / TSS
= 1 –
ESS / TSS
R 2 измеряет долю общего отклонения Y от его среднего значения, что объясняется регрессионной моделью. Чем ближе R 2 к единице, тем больше объясняющая сила уравнения регрессии. Значение R 2, близкое к 0, указывает на то, что уравнение регрессии будет иметь очень мало объяснительной силы.
Для оценки коэффициентов регрессии используется выборка из совокупности, а не всей совокупности. Важно делать предположения о населении на основе выборки и делать выводы о том, насколько хороши эти предположения.
Оценка коэффициентов регрессии
Каждая выборка из населения генерирует свой собственный перехват. Для расчета статистической разницы можно использовать следующие методы:
Двуххвостый тест –
Нулевая гипотеза: H 0 : b = 0
Альтернативная гипотеза: H a : b ≠ 0
Один хвостатый тест –
Нулевая гипотеза: H 0 : b> 0 (или b <0)
Альтернативная гипотеза: H a : b <0 (или b> 0)
Статистический тест –
б = расчетный коэффициент
E (b) = b = 0 (нулевая гипотеза)
SE b = стандартная ошибка коэффициента
,
Значение t зависит от степени свободы, одного или двух неудачных испытаний и уровня значимости. Для определения критического значения t можно использовать t-таблицу. Затем идет сравнение t-значения с критическим значением. Нужно отклонить нулевую гипотезу, если абсолютное значение статистического теста больше или равно критическому t-значению. Не отвергайте нулевую гипотезу, если абсолютное значение статистического теста меньше критического t-значения.
Множественный регрессионный анализ
В отличие от простой регрессии в множественном регрессионном анализе, коэффициенты указывают на изменение зависимых переменных, предполагая, что значения других переменных постоянны.
Тест статистической значимости называется F-тестом . F-тест полезен, поскольку он измеряет статистическую значимость всего уравнения регрессии, а не только для отдельного человека. Здесь В нулевой гипотезе нет никакой связи между зависимой переменной и независимыми переменными совокупности.
Формула – H 0 : b1 = b2 = b3 =…. = bk = 0
Не существует никакой связи между зависимой переменной и k независимыми переменными для совокупности.
F-тест статический –
F= frac left( fracR2K right) frac(1−R2)(nk−1)
Критическое значение F зависит от числителя и знаменателя, степени свободы и уровня значимости. F-таблица может быть использована для определения критического значения F. По сравнению с F – значением с критическим значением (F *) –
Если F> F *, нам нужно отвергнуть нулевую гипотезу.
Если F <F *, не отклоняйте нулевую гипотезу, так как нет существенной связи между зависимой переменной и всеми независимыми переменными.

|
Основные показатели качества: |
|||
|
1. |
Коэффициент детерминации R2 |
||
|
2. |
Скорректированный коэффициент детерминации |
||
|
R |
2 |
||
|
3. |
Значение F-статистики |
||
4.Сумма квадратов остатков (RSS)
5.Стандартная ошибка регрессии Se
6.Прочие показатели: средняя ошибка аппроксимации, индекс множественной корреляции и т.д.
21

Коэффициент
детерминации R2
 Коэффициент R2 показывает долю объясненной вариации зависимой переменной:
Коэффициент R2 показывает долю объясненной вариации зависимой переменной:
|
2 |
1 |
ei2 |
||||
|
R |
||||||
|
( yi |
||||||
|
y)2 |
||||||
R2 всегда увеличивается с включением новой переменной
22

|
3. |
F-статистика |
для |
|
проверки |
качества |
уравнения регрессии
F-статистика представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую
переменную)
к остаточной сумме квадратов (в расчете на одну степень свободы)
ESS
F m
RSS
n m 1
n – число выборочных наблюдений, m – число объясняющих переменных
23

F-статистика для проверки
значимости коэффициента
R2
F-статистика рассчитывается на основе коэффициента детерминации
|
F |
ESS / m |
(ESS / TSS) / m |
R2 / m |
||
|
RSS /(n m 1) |
(RSS / TSS) /(n m 1) |
(1 R2 ) /(n m 1) |
Для проверки значимости F-статистики используются таблицы F-распределения с m и (n–m–1) степеней свободы
24

Сумма квадратов остатков RSS
 Является оценкой необъясненной части вариации зависимой переменной
Является оценкой необъясненной части вариации зависимой переменной
n
RSS ei2
i 1
Используется как основная минимизируемая величина в МНК, а также для расчета других показателей
25

Стандартная ошибка регрессии Se
Является оценкой величины квадрата ошибки, приходящейся на одну степень свободы модели
n
ei2
Используется как основная величина для измерения качества модели (чем она меньше, тем лучше)
26

Индекс множественной корреляции
Тесноту совместного влияния факторов на результат характеризует индекс (показатель)
множественной корреляции:
|
S2 |
|||||
|
R Ryx x |
1 |
R2 |
|||
|
e |
|||||
|
Sy2 |
|||||
|
1 |
m |
Диапазон значений лежит от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака Y со всем набором объясняющих факторов Xi
27

4. Расчет прогноза. Средняя ошибка прогноза, доверительные интервалы прогноза.
Под прогнозом по множественной регрессионной модели понимается оценка значения зависимой переменной для значений объясняющих переменных, которых нет в исходных наблюдениях. Как и в случае парной модели, различают точечный и интервальный прогнозы.
Точечный прогноз по уравнению регрессии осуществляется путем подстановки значений регрессоров в уравнение регрессии. В дополнение к точечному прогнозу можно определить (по аналогии с парным случаем) границы возможного изменения прогнозируемого показателя, т.е. с заданным уровнем значимости вычислить доверительный интервал для прогнозируемого значения зависимой переменной .

4. Расчет прогноза. Средняя ошибка прогноза, доверительные интервалы прогноза.
|
Y p t |
; k |
S |
(X p ) |
Yp Y p t |
S |
|||
|
2 |
y |
2 |
; k y(X p ) |
|||||
|
k n m 1, |
Y p y(Xp ) b0 bj xpj |
|||||||
|
S |
S 1 XTp (XT X) 1 Xp |
|||||||
|
y |
(X p ) |
29
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #










![{displaystyle {begin{aligned}&sum _{i=1}^{n}2({hat {y}}_{i}-{bar {y}})(y_{i}-{hat {y}}_{i})=2{hat {b}}sum _{i=1}^{n}(x_{i}-{bar {x}})(y_{i}-{hat {y}}_{i})\[4pt]={}&2{hat {b}}sum _{i=1}^{n}(x_{i}-{bar {x}})((y_{i}-{bar {y}})-{hat {b}}(x_{i}-{bar {x}}))\[4pt]={}&2{hat {b}}left(sum _{i=1}^{n}(x_{i}-{bar {x}})(y_{i}-{bar {y}})-sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}{frac {sum _{j=1}^{n}(x_{j}-{bar {x}})(y_{j}-{bar {y}})}{sum _{j=1}^{n}(x_{j}-{bar {x}})^{2}}}right)\[4pt]={}&2{hat {b}}(0)=0end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0df16697d14368c46e7270b6e4e5ee0d1b819d29)







