Как определить силу натяжения нити между двумя телами
Содержание:
- Сила натяжения нити — основные понятия, обозначение, единица измерения
-
Как определить для разных условий, формулы для расчета
- Определение силы натяжения на одной нити
- Нахождение силы натяжения на нескольких нитях
- Примеры решения задач
Сила натяжения нити — основные понятия, обозначение, единица измерения
Сила натяжения — сила, которую прикладывают к концам объекта, она создает внутри объекта упругую деформацию.
Длина тела, к которому прилагают силу, обычно во много раз больше, чем толщина этого тела. Такими телами могут быть обыденные вещи — канат, веревка, трос, проволока, леска и т. д.
Приведем примеры силы натяжения нити в быту:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- применение отвеса для строительства;
- установка растяжек для того, чтобы зафиксировать радиоантенны;
- характер арматуры внутри напряженного бетона;
- устройство такелажа корабля.
Фото такелажа:

Сила натяжения нити является суммой сил, которые действуют на нить, а также противоположна по своему направлению.
F=-F
Здесь F — сила натяжения. Также встречаются обозначения силы натяжения нити с помощью букв «T» и «N». За единицу измерения у силы натяжения нити принимают Ньютон (сокращенно — H).
Как определить для разных условий, формулы для расчета
Существует множество разных вариантов определения силы напряжения нити. Рассмотрим некоторые из них.
Определение силы натяжения на одной нити
Определение силы натяжения на одной нити происходит в несколько этапов.
Первый этап — нужно определить силы на обоих концах нити. Сила натяжения этой нити или веревки считается результатом сил, которые натягивают веревку с каждого из концов.
Напомним, что сила будет равна произведению массы m на ускорение a.
Предположим, что веревка туго натянута. Каждое изменение массы или ускорения объекта, который подвешен на веревке, приведет к тому, что силы на самой веревке изменятся. Не стоит забывать также о постоянном ускорении силы тяжести. Учитывать его нужно даже тогда, когда система остается в покое, а составляющие системы являются объектами воздействия силы тяжести.
Формула 1
Можно сделать предположение, что сила натяжение этой веревки будет рассчитываться по следующей формуле: (T=(mtimes{g})+(mtimes{a})). В данной формуле (g) будет ускорением силы тяжести тела, которое поддерживается веревкой, а показатель «a» будет любым иным ускорением, которое действует на тело.
Примечание 1
Для решения большей части физических задач предполагается, что веревка идеальна. То есть, она идеально тонкая, у нее нет массы, она не способна рваться и растягиваться.
Пример 1
Рассмотрим пример, в котором груз подвешивается к деревянной балке при помощи одной веревки. Ни веревка, и груз не передвигаются — система в абсолютном покое. Чтобы груз находился в полном равновесии, сила натяжения обязана равняться силе тяжести: (F_{т}=F_{g}=mtimes{g}). Если у груза масса 10 кг, то сила натяжения будет равна (98 Н (10times9,8)).
Второй этап — нужно учитывать ускорение. Сила тяжести является не единственной силой, которая может повлиять на силу натяжения нити. Ровно такое же действие совершает каждая сила, которую прикладывают к объекту на нити с ускорением.
Пример 2
Если объект, который подвешен на кабеле или веревке, ускоряется под воздействием силы, то к силе натяжения будет добавляться сила ускорения. Представим, что на веревку подвешивают груз с массой в 10 кг, потом тянут вверх с ускорением, которое равно 1 м/с². В данном случае нужно учитывать ускорение груза вместе с ускорением силы тяжести:
(F=F+(mtimes{a}))
(F=98+(10times{1}))
(F=108 Н.)
Третий этап — нужно учитывать угловое ускорение. Тело находится на веревке, которая вращается вокруг определенной точки, ее считают условным центром (по типу маятника). Оно оказывает натяжение на нить при помощи центробежной силы.
Центробежная сила — побочная сила натяжения, вызванная веревкой. Возникает при толчке внутрь веревки таким образом, чтобы груз сохранял свое движение по дуге, а не по прямой. Центробежная сила тем больше, чем быстрее движется объект: (F=mfrac{v^{2}}{r}.)
В этой формуле m является массой, v — скоростью, r — радиусом окружности, по которой происходит движение груза.
Так как значение и направление центробежной силы изменяются в зависимости от того, как тело передвигается и изменяет собственную скорость, полное натяжение нити становится параллельным нити в центральной точке.
Важно запомнить, что сила притяжения всегда воздействует на тело, тянет его вниз. Если объект совершает амплитудное действие вертикально, полное натяжение сильнее всего будет в нижней точке дуги (точка равновесия для маятника) — когда тело достигает самой большой скорости, а слабее всего — в верхней точке дуги, когда тело начинает замедляться.
Пример 3
Приведем пример: объект не ускоряется вверх, а раскачивается как маятник. Допустим, что нить будет иметь длину 1,5 м, а груз передвигается со скоростью 2 м/с (в случае прохождения через нижнюю точку размаха). Если необходимо рассчитать силу натяжения в нижней точке дуги (в момент, когда она самая большая), то нужно найти сначала, какое давление силы тяжести ощущает на себе груз в данной точке (в состоянии покоя — 98 Н). Для нахождения центробежной силы нужно применить следующие формулы:
(F=mfrac{v^{2}}{r})
(F=10frac{2^{2}}{1,5})
(F=10times2,67=26,7 Н.)
Так полное натяжение нити будет (98+26,7=124,7 Н.)
Еще одна формула — сила натяжения способна изменяться по мере того, как проходит груз по дуге. Величина и направление центробежной силы изменяются по мере того, как тело качается. Даже если сила тяжести постоянная, результирующая сила натяжения изменяется. В тот момент, когда качающееся тело располагается не в нижней точке дуги, сила тяжести тащит тело вниз, однако сила натяжения тянет тело вверх под углом. По данной причине сила натяжения обязана находиться в противодействии лишь части силы тяжести, а не всей.
Деление силы гравитации на два вектора может помочь визуально показать данное состояние. В каждой точке дуги объекта, который раскачивается вертикально, нить создает угол (ominus) с линией, проходящей через точку равновесия, центр вращения. После того как маятник раскачивается, сила гравитации разделяется на два вектора:
- (mgsinominus), воздействует по касательной к дуге по направлению к точке равновесия;
- (mgcosominus), воздействует параллельно силе натяжения, однако в ином направлении.
Натяжение имеет возможность противостоять (mgcosominus)— только такой силе, которая направлена против нее, а не полноценной силе тяготения (кроме точки равновесия).
Пример 4
Представим пример: маятник имеет отклонение в 15° от вертикали, движение происходит со скоростью 1,5 м/с. Можно найти силу натяжения следующим образом:
- Найдем отношение силы натяжения к силе тяготения: (Т=98cos15=98(0,96)=94,08 Н).
- Найдем центробежную силу: (F=10timesfrac{1,5^{2}}{1,5}=10times1,5=15).
- Полное натяжение будет следующим: (T + F = 94,08 + 15 = 109,08 Н).
Еще одна формула — с учетом расчета трения. Каждый объект, который тянут нитью по поверхности, чувствует на себе силу замедления из-за трения, и передает данное воздействие натяжению в нити.
Сила трения между двумя телами рассчитывается, как и в другой любой ситуации, в соответствии со следующим уравнением: (F=(mu)N). В данной формуле (mu) является коэффициентом силы трения между телами, N является силой взаимодействия двух объектовсила, с которой они воздействуют друг на друга.
Примечание 2
Трение покоя — трение, возникающее в итоге попыток привести тело, находящееся в состоянии покоя, в движение.
Трение движения — трение, которое возникает в итоге попыток заставить движущееся тело продолжать это движение.
Приведем пример: представим, что груз в 10 кг не раскачивается, его тянут по горизонтальной плоскости при помощи нитиверевки. Коэффициент трения по земле будет равен 0,5. Груз передвигается со скоростью, которая постоянна, однако нужно придать телу ускорение в 1 м/с².
Нужно сделать следующие расчеты: (F=10times9,8 =98 Н.)
Сила трения будет рассчитана по формуле: (F=0,5times98=49 Н.)
Сила ускорения будет рассчитана по формуле: (F=10times1=10 Н).
Общее натяжение: (F+F=49+10=59 Н.)
Нахождение силы натяжения на нескольких нитях
Один из способов нахождения силы натяжения нити — использовать вертикальные параллельные грузы при помощи блока.
Блок — простой механизм, который состоит из подвесного диска. Это помогает ему изменять направление силы натяжения веревки.
В обычном расположении блока кабельнитьверевка начинаются от подвешенного объекта вверх к блоку, потом вниз к иному объекту. Так создаются два разных участка веревки. В таком случае натяжение на всех участках становятся одинаковыми, если оба конца натягиваются силами различных величин.
Для системы масс, подвешенных вертикально в блоке, сила натяжения будет равна (T=frac{2g(m1)(m2)}{m2+m1)}). В данной формуле g будет ускорением силы тяжести, m1 — массой первого тела, m2 — массой второго тела.
Примечание 3
Во многих физических задачах блоки являются идеальными — не обладают массой, трением, не ломаются, не отделяются от нити, не деформируются.
Приведем пример: есть два груза, которые подвешены через блок на параллельных концах нити. Один груз обладает массой в 10 кг, а второй груз обладает массой в 5 кг. В данном случае нужно произвести расчет по следующим формулам:
(T=frac{2g(m1)(m2)}{m2+m1)})
(T=frac{2(9,8)(10)(5)}{5+10)}=frac{980}{15}=65,33 Н.)
Важно понимать, что из-за того, что один груз является более тяжелым, другие элементы будут равны, данная система будет ускоряться, значит, груз в 10 кг будет передвигаться вниз, заставляя второй объект идти вверх.
Другая формула — подвешиваем грузы, берем блоки с нитями, которые не параллельны. Блоки часто используют для того, чтобы направить силу натяжения в другую сторону. Если груз подвешивается вертикально к одному концу нити, а другой конец поддерживает груз в диагональной плоскости, то система блоков — непараллельная — формирует треугольную форму с углами в точках с первым грузом, вторым, а также самим блоком. В данном случае натяжение в веревке будет зависеть от силы тяжести, силы натяжения, которая будет параллельная диагональной части нити.
Пример 5
Приведем пример: есть система с объектом в 10 кг, подвешенным вертикально, соединяющимся с грузом в 5 кг, который находится на наклонной плоскости в 60° (нет трения). Для нахождения натяжения в нити нужно составить следующие уравнения:
- Груз, который подвешивают, намного тяжелее, трение не создается, потому что мы знаем, что груз ускоряется вниз. Натяжение в веревке тащит вверх, поэтому объект ускоряется по отношению к силе (равнодействующей) (F=m1times{g}-T=98-Т.)
- Груз на плоскости, которая находится под наклоном, ускоряется вверх. Так как трения нет у данной плоскости, натяжение тянет груз вверх по плоскости, вниз объект тянет собственный вес. Часть силы, которая тянет вниз по наклонной, будет вычисляться как (mgsinominus). Можно предположить, что тело ускоряется по отношению к равнодействующей силе: (F=T-m^{2}(g)sin60=T-5(9,8)(0,87)=T-42,14).
- Если сравнять оба уравнения, то получится следующее: (98-T=T-42,12). Вычисляем T, получается, что (2T=140,14. Так T=70,07 )Н.
Последняя формула — использование нескольких нитей для того, чтобы подвесить тело. Представим, что объект подвешивается на «Y-образной» системе нитей — две нити закрепляются на потолке, встречаются в центральной точке, из которой третья нить идет с объектом. Сила натяжения третьей нити проста — обычное натяжение в итоге действия силы тяжести или же m(g).
Натяжение на других нитях отличается, они обязаны составлять в совокупности силу, которая равна силе тяжести вверх в вертикальном положении, а также равны нулю в обоих горизонтальных направлениях. Однако нужно взять во внимание, что система покоится. Натяжение в нити зависит напрямую от массы подвешенных грузов, а также от угла, на который происходит наклон каждой нити от потолка.
Пример 6
Приведем пример: в системе Y-образной нижний груз обладает массой в 10 кг, подвешивается на двух нитях, угол одной из нитей составляет 30° с потолком. Угол второй нити составляет 60°. Если необходимо найти натяжение каждой нити, необходимо рассчитать вертикальную и горизонтальную части натяжения. Для того чтобы найти T1 (натяжение с наклоном в 30°), T2 (натяжение с наклоном в 60°), нужно рассчитать:
- По законам тригонометрии, соотношение между T=m(g) и Т1, Т2 будет равно косинусу угла между нитями и потолком. Для натяжения T1 будет (cos30=0,87). Для натяжения T2 будет (cos60=0,5).
- Нужно умножить натяжение в нижней нити на косинус всех углов, чтобы найти общее натяжение. (T1=0,87times{mg}=0,87times10(9,8)=85,26) Ньютонов. (T2=0,5times{mg}=0,5times10(9,8)=49) Ньютонов.
Примеры решения задач
Задача
Нерастяжимая, с малым весом нить может выдержать силу натяжения в T=4400 Н. Какое максимальное ускорение может быть, чтобы поднять груз с массой в 400 кг? Груз подвешивают на данную нить. Нужно, чтобы нить при этом не разорвалась, и не произошло падение груза.
На рисунке ниже изображены все силы, которые воздействуют на груз.
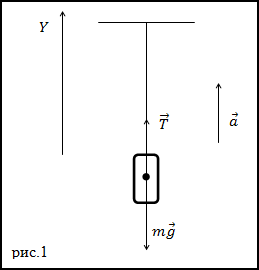
Запишем второй закон Ньютона. Объект считается материальной точкой, все силы прикладываются к центру масс объекта: (T+mg=ma).
Далее записываем проекции уравнения на ось Y: (T-mg=ma).
Получаем уравнение: (a=frac{T-mg}{m}).
Произведем расчеты: (a=frac{4400-400times9,8}{400}=1,2 м/с²).
Ответ: 1,2 м/с².
Загрузить PDF
Загрузить PDF
В физике, сила натяжения — это сила, действующая на веревку, шнур, кабель или похожий объект или группу объектов. Все, что натянуто, подвешено, поддерживается или качается на веревке, шнуре, кабеле и так далее, является объектом силы натяжения. Подобно всем силам, натяжение может ускорять объекты или становиться причиной их деформации. Умение рассчитывать силу натяжения является важным навыком не только для студентов физического факультета, но и для инженеров, архитекторов; те, кто строит устойчивые дома, должны знать, выдержит ли определенная веревка или кабель силу натяжения от веса объекта так, чтобы они не проседали и не разрушались. Приступайте к чтению статьи, чтобы научиться рассчитывать силу натяжения в некоторых физических системах.
-

1
Определите силы на каждом из концов нити. Сила натяжения данной нити, веревки является результатом сил, натягивающих веревку с каждого конца. Напоминаем, сила = масса × ускорение. Предполагая, что веревка натянута туго, любое изменение ускорения или массы объекта, подвешенного на веревке, приведет к изменению силы натяжения в самой веревке. Не забывайте о постоянном ускорении силы тяжести — даже если система находится в покое, ее составляющие являются объектами действия силы тяжести. Мы можем предположить, что сила натяжения данной веревки это T = (m × g) + (m × a), где «g» — это ускорение силы тяжести любого из объектов, поддерживаемых веревкой, и «а» — это любое другое ускорение, действующее на объекты.
- Для решения множества физических задач, мы предполагаем идеальную веревку — другими словами, наша веревка тонкая, не обладает массой и не может растягиваться или рваться.
- Для примера, давайте рассмотрим систему, в которой груз подвешен к деревянной балке с помощью одной веревки (смотрите на изображение). Ни сам груз, ни веревка не двигаются — система находится в покое. Вследствие этого, нам известно, чтобы груз находился в равновесии, сила натяжения должна быть равна силе тяжести. Другими словами, Сила натяжения (Ft) = Сила тяжести (Fg) = m × g.
- Предположим, что груз имеет массу 10 кг, следовательно, сила натяжения равна 10 кг × 9,8 м/с2 = 98 Ньютонов.
-

2
Учитывайте ускорение. Сила тяжести — не единственная сила, что может влиять на силу натяжения веревки — такое же действие производит любая сила, приложенная к объекту на веревке с ускорением. Если, к примеру, подвешенный на веревке или кабеле объект ускоряется под действием силы, то сила ускорения (масса × ускорение) добавляется к силе натяжения, образованной весом этого объекта.
- Предположим, что в нашем примере на веревку подвешен груз 10 кг, и вместо того, чтобы быть прикрепленным к деревянной балке, его тянут вверх с ускорением 1 м/с2. В этом случае, нам необходимо учесть ускорение груза, также как и ускорение силы тяжести, следующим образом:
- Ft = Fg + m × a
- Ft = 98 + 10 кг × 1 м/с2
- Ft = 108 Ньютонов.
- Предположим, что в нашем примере на веревку подвешен груз 10 кг, и вместо того, чтобы быть прикрепленным к деревянной балке, его тянут вверх с ускорением 1 м/с2. В этом случае, нам необходимо учесть ускорение груза, также как и ускорение силы тяжести, следующим образом:
-

3
Учитывайте угловое ускорение. Объект на веревке, вращающийся вокруг точки, которая считается центром (как маятник), оказывает натяжение на веревку посредством центробежной силы. Центробежная сила — дополнительная сила натяжения, которую вызывает веревка, «толкая» ее внутрь так, чтобы груз продолжал двигаться по дуге, а не по прямой. Чем быстрее движется объект, тем больше центробежная сила. Центробежная сила (Fc) равна m × v2/r где «m»– это масса, «v» — это скорость, и «r» — радиус окружности, по которой движется груз.
- Так как направление и значение центробежной силы меняются в зависимости от того, как объект движется и меняет свою скорость, то полное натяжение веревки всегда параллельно веревке в центральной точке. Запомните, что сила притяжения постоянно действует на объект и тянет его вниз. Так что, если объект раскачивается вертикально, полное натяжение сильнее всего в нижней точке дуги (для маятника это называется точкой равновесия), когда объект достигает максимальной скорости, и слабее всего в верхней точке дуги, когда объект замедляется.
- Давайте предположим, что в нашем примере объект больше не ускоряется вверх, а раскачивается как маятник. Пусть наша веревка будет длиной 1,5 м, а наш груз движется со скоростью 2 м/с, при прохождении через нижнюю точку размаха. Если нам нужно рассчитать силу натяжения в нижней точке дуги, когда она наибольшая, то сначала надо выяснить равное ли давление силы тяжести испытывает груз в этой точке, как и при состоянии покоя — 98 Ньютонов. Чтобы найти дополнительную центробежную силу, нам необходимо решить следующее:
- Fc = m × v2/r
- Fc = 10 × 22/1.5
- Fc =10 × 2,67 = 26,7 Ньютонов.
- Таким образом, полное натяжение будет 98 + 26,7 = 124,7 Ньютона.
-

4
Учтите, что сила натяжения благодаря силе тяжести меняется по мере прохождения груза по дуге. Как было отмечено выше, направление и величина центробежной силы меняются по мере того, как качается объект. В любом случае, хотя сила тяжести и остается постоянной, результирующая сила натяжения в результате тяжести тоже меняется. Когда качающийся объект находится не в нижней точке дуги (точке равновесия), сила тяжести тянет его вниз, но сила натяжения тянет его вверх под углом. По этой причине сила натяжения должна противодействовать части силы тяжести, а не всей ее полноте.
- Разделение силы гравитации на два вектора сможет помочь вам визуально изобразить это состояние. В любой точке дуги вертикально раскачивающегося объекта, веревка составляет угол «θ» с линией, проходящей через точку равновесия и центр вращения. Как только маятник начинает раскачиваться, сила гравитации (m × g) разбивается на 2 вектора — mgsin(θ), действуя по касательной к дуге в направлении точки равновесия и mgcos(θ), действуя параллельно силе натяжения, но в противоположном направлении. Натяжение может только противостоять mgcos(θ) — силе, направленной против нее — не всей силе тяготения (исключая точку равновесия, где все силы одинаковы).
- Давайте предположим, что, когда маятник отклоняется на угол 15 градусов от вертикали, он движется со скоростью 1,5 м/с. Мы найдем силу натяжения следующими действиями:
- Отношение силы натяжения к силе тяготения (Tg) = 98cos(15) = 98(0,96) = 94,08 Ньютона
- Центробежная сила (Fc) = 10 × 1,52/1,5 = 10 × 1,5 = 15 Ньютонов
- Полное натяжение = Tg + Fc = 94,08 + 15 = 109,08 Ньютонов.
-

5
Рассчитайте трение. Любой объект, который тянется веревкой и испытывает силу «торможения» от трения другого объекта (или жидкости), передает это воздействие натяжению в веревке. Сила трения между двумя объектами рассчитывается также, как и в любой другой ситуации — по следующему уравнению: Сила трения (обычно пишется как Fr) = (mu)N, где mu — это коэффициент силы трения между объектами и N — обычная сила взаимодействия между объектами, или та сила, с которой они давят друг на друга. Отметим, что трение покоя — это трение, которое возникает в результате попытки привести объект, находящийся в покое, в движение — отличается от трения движения — трения, возникающего в результате попытки заставить движущийся объект продолжать движение.
- Давайте предположим, что наш груз в 10 кг больше не раскачивается, теперь его буксируют по горизонтальной плоскости с помощью веревки. Предположим, что коэффициент трения движения земли равен 0,5 и наш груз движется с постоянной скоростью, но нам нужно придать ему ускорение 1м/с2. Эта проблема представляет два важных изменения — первое, нам больше не нужно рассчитывать силу натяжения по отношению к силе тяжести, так как наша веревка не удерживает груз на весу. Второе, нам придется рассчитать натяжение, обусловленное трением, также как и вызванное ускорением массы груза. Нам нужно решить следующее:
- Обычная сила (N) = 10 кг & × 9,8 (ускорение силы тяжести) = 98 N
- Сила трения движения (Fr) = 0,5 × 98 N = 49 Ньютонов
- Сила ускорения (Fa) = 10 kg × 1 м/с2 = 10 Ньютонов
- Общее натяжение = Fr + Fa = 49 + 10 = 59 Ньютонов.
Реклама
- Давайте предположим, что наш груз в 10 кг больше не раскачивается, теперь его буксируют по горизонтальной плоскости с помощью веревки. Предположим, что коэффициент трения движения земли равен 0,5 и наш груз движется с постоянной скоростью, но нам нужно придать ему ускорение 1м/с2. Эта проблема представляет два важных изменения — первое, нам больше не нужно рассчитывать силу натяжения по отношению к силе тяжести, так как наша веревка не удерживает груз на весу. Второе, нам придется рассчитать натяжение, обусловленное трением, также как и вызванное ускорением массы груза. Нам нужно решить следующее:
-

1
Поднимите вертикальные параллельные грузы с помощью блока. Блоки — это простые механизмы, состоящие из подвесного диска, что позволяет менять направление силы натяжения веревки. В простой конфигурации блока, веревка или кабель идет от подвешенного груза вверх к блоку, затем вниз к другому грузу, создавая тем самым два участка веревки или кабеля. В любом случае натяжение в каждом из участков будет одинаковым, даже если оба конца будут натягиваться силами разных величин. Для системы двух масс, подвешенных вертикально в блоке, сила натяжения равна 2g(m1)(m2)/(m2+m1), где «g» — ускорение силы тяжести, «m1» — масса первого объекта, «m2»– масса второго объекта.
- Отметим следующее, физические задачи предполагают, что блоки идеальны — не имеют массы, трения, они не ломаются, не деформируются и не отделяются от веревки, которая их поддерживает.
- Давайте предположим, что у нас есть два вертикально подвешенных на параллельных концах веревки груза. У одного груза масса 10 кг, а у второго — 5 кг. В этом случае, нам необходимо рассчитать следующее:
- T = 2g(m1)(m2)/(m2+m1)
- T = 2(9,8)(10)(5)/(5 + 10)
- T = 19,6(50)/(15)
- T = 980/15
- T = 65,33 Ньютонов.
- Отметим, что, так как один груз тяжелее, все остальные элементы равны, эта система начнет ускоряться, следовательно, груз 10 кг будет двигаться вниз, заставляя второй груз идти вверх.
-
2
Подвесьте грузы, используя блоки с не параллельными вертикальными нитями. Блоки зачастую используются для того, чтобы направлять силу натяжения в направлении, отличном от направления вниз или вверх. Если, к примеру, груз подвешен вертикально к одному концу веревки, а другой конец держит груз в диагональной плоскости, то непараллельная система блоков принимает форму треугольника с углами в точках с первых грузом, вторым и самим блоком. В этом случае натяжение в веревке зависит как от силы тяжести, так и от составляющей силы натяжения, которая параллельна к диагональной части веревки.
- Давайте предположим, что у нас есть система с грузом в 10 кг (m1), подвешенным вертикально, соединенный с грузом в 5 кг(m2), расположенным на наклонной плоскости в 60 градусов (считается, что этот уклон не дает трения). Чтобы найти натяжение в веревке, самым легким путем будет сначала составить уравнения для сил, ускоряющих грузы. Далее действуем так:
- Подвешенный груз тяжелее, здесь нет трения, так что мы знаем, что он ускоряется вниз. Натяжение в веревке тянет вверх, так что он ускоряется по отношению к равнодействующей силе F = m1(g) – T, или 10(9,8) – T = 98 – T.
- Мы знаем, что груз на наклонной плоскости ускоряется вверх. Так как она не имеет трения, мы знаем, что натяжение тянет груз вверх по плоскости, а вниз его тянет только свой собственный вес. Составляющая силы, тянущей вниз по наклонной, вычисляется как mgsin(θ), так что в нашем случае мы можем заключить, что он ускоряется по отношению к равнодействующей силе F = T – m2(g)sin(60) = T – 5(9,8)(0,87) = T — 42,14.
- Если мы приравняем эти два уравнения, то получится 98 – T = T – 42,14. Находим Т и получаем 2T = 140,14, или T = 70,07 Ньютонов.
- Давайте предположим, что у нас есть система с грузом в 10 кг (m1), подвешенным вертикально, соединенный с грузом в 5 кг(m2), расположенным на наклонной плоскости в 60 градусов (считается, что этот уклон не дает трения). Чтобы найти натяжение в веревке, самым легким путем будет сначала составить уравнения для сил, ускоряющих грузы. Далее действуем так:
-

3
Используйте несколько нитей, чтобы подвесить объект. В заключение, давайте представим, что объект подвешен на «Y-образной» системе веревок — две веревки закреплены на потолке и встречаются в центральной точке, из которой идет третья веревка с грузом. Сила натяжения третьей веревки очевидна — простое натяжение в результате действия силы тяжести или m(g). Натяжения на двух остальных веревках различаются и должны составлять в сумме силу, равную силе тяжести вверх в вертикальном положении и равны нулю в обоих горизонтальных направлениях, если предположить, что система находится в состоянии покоя. Натяжение в веревке зависит от массы подвешенных грузов и от угла, на который отклоняется от потолка каждая из веревок.
- Давайте предположим, что в нашей Y-образной системе нижний груз имеет массу 10 кг и подвешен на двух веревках, угол одной из которых составляет с потолком 30 градусов, а угол второй — 60 градусов. Если нам нужно найти натяжение в каждой из веревок, нам понадобится рассчитать горизонтальную и вертикальную составляющие натяжения. Чтобы найти T1 (натяжение в той веревке, наклон которой 30 градусов) и T2 (натяжение в той веревке, наклон которой 60 градусов), нужно решить:
- Согласно законам тригонометрии, отношение между T = m(g) и T1 и T2 равно косинусу угла между каждой из веревок и потолком. Для T1, cos(30) = 0,87, как для T2, cos(60) = 0,5
- Умножьте натяжение в нижней веревке (T=mg) на косинус каждого угла, чтобы найти T1 и T2.
- T1 = 0,87 × m(g) = 0,87 × 10(9,8) = 85,26 Ньютонов.
- T2 =0,5 × m(g) = 0,5 × 10(9,8) = 49 Ньютонов.
Реклама
- Давайте предположим, что в нашей Y-образной системе нижний груз имеет массу 10 кг и подвешен на двух веревках, угол одной из которых составляет с потолком 30 градусов, а угол второй — 60 градусов. Если нам нужно найти натяжение в каждой из веревок, нам понадобится рассчитать горизонтальную и вертикальную составляющие натяжения. Чтобы найти T1 (натяжение в той веревке, наклон которой 30 градусов) и T2 (натяжение в той веревке, наклон которой 60 градусов), нужно решить:
Об этой статье
Эту страницу просматривали 287 132 раза.
Была ли эта статья полезной?
Сила натяжения нити, теория и онлайн калькуляторы
Сила натяжения нити
Понятие силы натяжения нити
Пусть тело прикреплено к нити, тогда силой натяжения нити называют силу, действующую на рассматриваемое тело, равную по величине и противоположную по направлению равнодействующей, приложенной к нити. Силу натяжения нити обозначают по-разному, чаще всего: $overline{N}$, $overline{T}, overline{F}$. Если равнодействующую, приложенную к нити обозначить как $overline{R}$, то в соответствии с третьим законом Ньютона имеем:
[overline{N}=-overline{R}left(1right).]
Сила натяжения нити является реакцией подвеса (нити), на действие со стороны тела на подвес. Сила натяжения нити всегда имеет направление вдоль нити.
Очень часто при решении задач указывают, что нить является невесомой (массой нити в сравнении с массой груза можно пренебречь). Если нить невесома и нерастяжима, то такую нить рассматривают как проводник силы.
Если следует учитывать растяжение нити, при этом нагрузки малы, а нить упругая, то при вычислении силы натяжения используют закон Гука:
[overline{N}={overline{F}}_u=kDelta overline{l}left(2right),]
где ${overline{F}}_u$ – сила упругости нити;$ k$ – коэффициент упругости нити; $Delta l$ – удлинение нити.
Единицей измерения силы натяжения нити в Международной системе единиц (СИ) (как и для любой другой силы) является ньютон:
[left[Nright]=H=frac{кгcdot м}{с^2}.]
Примеры задач на силу натяжения нити
Пример 1
Задание. Какой будет сила натяжения нерастяжимой нити, связывающей два груза находящихся на горизонтальной гладкой поверхности (рис.1), если массы грузов равны $m_1$ и $m_2. $К одному из грузов приложена горизонтальная сила $F.$ Трение брусков о поверхность не учитывать. Нить считать невесомой.
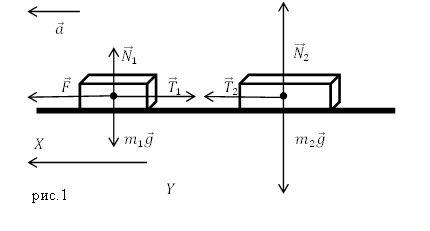
Решение. Рассмотрим силы, которые приложены к первому грузу, запишем второй закон Ньютона для этого тела:
[overline{F}+m_1overline{g}+{overline{N}}_1+{overline{T}}_1=m_1overline{a}left(1.1right),]
$m_1overline{g}$ – сила тяжести, действующая на первый груз; ${overline{N}}_1$ – сила реакции горизонтальной опоры; ${overline{T}}_1$ – сила натяжения нити.
Проектируя на оси X и Y уравнение (1.1) получаем:
[left{ begin{array}{c}
X:F-T_1=m_1aleft(1.2right). \
m_1g=N_1left(1.3right). end{array}
right.]
Рассмотрим силы, действующие на второй груз, запишем второй закон Ньютона для этих сил:
[overline{F}+m_2overline{g}+{overline{N}}_2+{overline{T}}_2=m_2overline{a}left(1.4right).]
В проекциях на оси X и Y получаем систему уравнений:
[left{ begin{array}{c}
X:T_2=m_2aleft(1.5right). \
m_2g=N_2left(1.6right). end{array}
right.]
Так как нить считаем невесомой, то имеем:
[T_1=T_2=Tleft(1.7right).]
Из уравнения (1.5) выразим ускорение и подставим его в (1.2)получим величину силы натяжения нити:
[F-T=m_1frac{T}{m_2}to T=frac{Fm_2}{m_1+m_2}.]
Ответ. $T=frac{Fm_2}{m_1+m_2}$
Пример 2
Задание. К нерастяжимой нити подвешен массивный шарик. Шарик подняли так, что нить приняла горизонтальное положение, затем шарик отпустили. Какова сила натяжения нити в момент, когда шарик проходит положение равновесия? Какой угол составляет нить с вертикалью, если сила натяжения равна силе тяжести, действующая на шарик?
Решение. Сделаем рисунок.
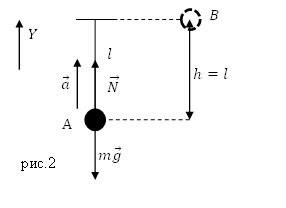
1) Силы, действующие на шарик в момент прохождения положения равновесия (положение А на рис.2): сила тяжести и сила натяжения нити. Для них запишем второй закон Ньютона:
[moverline{g}+overline{N}=moverline{a}left(2.1right).]
Запишем проекцию выражения (2.1) на ось Y:
[N-mg=ma_nleft(2.2right),]
где шарик движется с центростремительным ускорением, равным:
[a_n=frac{v^2}{l}left(2.3right),]
$l$ – длина нити; $v$ – величина скорости движения шарика в точке А.
Скорость $v$ найдем из закона сохранения энергии (см. рис.2 $h=l$), который запишем для положений B (максимальная потенциальная энергия шара) и A (максимальная кинетическая энергия шара):
[mgl=mfrac{v^2}{2}to v^2=2gl left(2.4right).]
Выразим силу натяжения нити из (2.2), подставим найденное ускорение, учитывая (2.4):
[N=mg-mfrac{v^2}{l}=mg+mfrac{2gl}{l}=3mg.]
2)
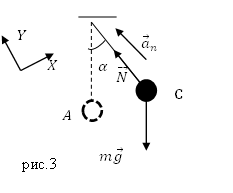
Ось Y направим по нити, ось X перпендикулярно оси Y (рис.3).
Запишем проекцию уравнения (2.1) на новую ось Y:
[N-mg{cos alpha }=ma_{n }left(2.5right).]
Выразим силу натяжения нити:
[N=ma_{n }+mg{cos alpha }left(2.6right).]
Учитывая (2.3), получим:
[N=mfrac{v^2}{l}+mg{cos alpha }left(2.7right).]
Потенциальная энергия шарика в положении C равна $E_p=mgl{cos alpha }$, она переходит полностью в кинетическую энергию положения А ($E_k=mfrac{v^2}{2}$):
[mfrac{v^2}{2}=mgl{cos alpha }left(2.8right).]
Из (2.6) выразим $v^2$, имеем:
[v^2=2gl{cos alpha }left(2.9right).]
Подставим результат (2.9) в формулу (2.7), получили:
[N=mfrac{2gl{cos alpha }}{l}+mg{cos alpha } left(2.10right).]
Приравниваем по условию силу натяжения нити к силе тяжести, выражаем величину угла:
[mg=mfrac{2gl{cos alpha }}{l}+mg{cos alpha }to 1=3{cos alpha to alpha =arc{cos frac{1}{3} } }.]
Ответ. 1) $N=3mg$. 2) $alpha =arc{cos frac{1}{3} }$
Читать дальше: сообщающиеся сосуды.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Шмидт М.П., Шмидт А.М. Равновесие гибкой нерастяжимой подвешенной нити // Фiзiка: праблемы выкладання. – 2005. – № 1. – С. 23-25.
Задача об определении силы натяжения в подвешенной тяжелой нити связана с проблемой прочности тросов, цепей или проводов линий электропередачи. Будем считать, что нить идеально гибкая и нерастяжимая и что ее провисание происходит только из-за различия между длиной нити L и расстоянием между опорами l. Расстояние f по вертикали между нижней точкой нити и опорами называется стрелой провеса (рис. 1, а).
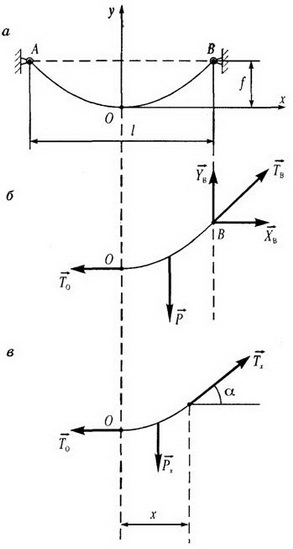
Рис. 1.
Обозначим через q силу тяжести единицы длины нити. Для пологой кривой можно принять, что сила тяжести равномерно распределена не по кривой АОВ, а по ее проекции АВ. Таким образом, силу тяжести нити будем считать равной 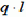 .
.
Рассмотрим условия равновесия правой половины нити. Действующие на нее силы изображены на рис. 1, б. Следует отметить, что сила натяжения в любом сечении нити направлена по касательной к кривой в соответствующем месте (это следует из предположения, что нить идеально гибкая). Поэтому в нижней точке нити О, принятой за начало координатной системы хОу, сила натяжения 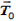 (сила, с которой левая часть нити действует на правую) горизонтальна.
(сила, с которой левая часть нити действует на правую) горизонтальна.
Запишем уравнение моментов относительно точки В
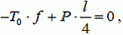 (1)
(1)
где 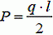 – сила тяжести половины нити. Из этого уравнения находим, что
– сила тяжести половины нити. Из этого уравнения находим, что
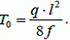 (2)
(2)
Из выражения (2) следует, что чем меньше стрела провеса нити f, тем больше сила натяжения Т0.
Из двух уравнений для проекций сил на оси x и у можно найти составляющие ХВ и ΥB в силы натяжения нити в точке В.
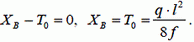 (3)
(3)
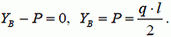 (4)
(4)
Сила натяжения в точке B
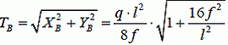 (5)
(5)
или
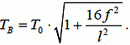 (6)
(6)
Второе слагаемое в сумме под знаком корня значительно меньше единицы, и можно воспользоваться приближенной формулой 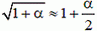 , достаточно точной для малых по модулю значений α. Тогда выражение (6) запишется
, достаточно точной для малых по модулю значений α. Тогда выражение (6) запишется
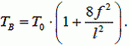 (7)
(7)
Формула (7) определяет наибольшее натяжение нити в точке подвеса, которое мало отличается от наименьшего натяжения Т0 в средней точке.
Для нахождения Τ0 и ТB по формулам (2) и (7) необходимо знать стрелу провеса f, а для нахождения стрелы провеса f нужно знать уравнение кривой, по которой провисает нить. Для получения требуемого уравнения рассмотрим часть нити, расположенную между началом координат и произвольным сечением с абсциссой x (рис. 1, в).
Для этой части нити запишем два уравнения равновесия (для проекций сил на оси x и y):
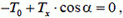 (8)
(8)
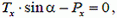 (9)
(9)
где 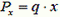 – сила тяжести рассматриваемой части нити, Тх – сила натяжения на правом конце этой части.
– сила тяжести рассматриваемой части нити, Тх – сила натяжения на правом конце этой части.
Из уравнения (8) следует, что с удалением от нижней точки О, т.е. с увеличением угла α, сила натяжения нити возрастает и достигает максимума в точках подвеса.
Исключив из уравнений (8) и (9) Тх, с учетом уравнения (2) получим
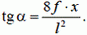 (10)
(10)
Так как 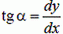 , равенство (10) запишется
, равенство (10) запишется
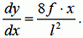 (11)
(11)
Соотношение (10) представляет собой дифференциальное уравнение, определяющее форму нити в положении равновесия.
Интегрируя (11), получим
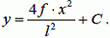 (12)
(12)
Постоянную интегрирования С найдем из граничного условия. При
х = 0, y = 0. Откуда следует, что С = 0. Тогда выражение (12) запишется
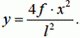 (13)
(13)
Таким образом, при сделанных нами предположениях (стрела прогиба f мала по сравнению с длиной пролета l), тяжелая нить в положении равновесия принимает форму параболы. В более точных предположениях (стрела прогиба f не мала по сравнению с длиной пролета l) уравнение кривой равновесия тяжелой нити определяет цепную линию.
Располагая уравнением (13), можно выразить стрелу провеса f через L и l. Бесконечно малый элемент длины нити равен  . Откуда
. Откуда
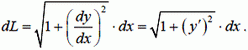
Для пологой нити квадрат производной 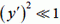 . Поэтому
. Поэтому
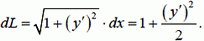
Тогда длина нити
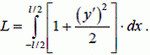 (14)
(14)
Так как 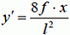 , то выражение (14) запишется
, то выражение (14) запишется
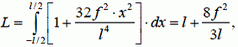
откуда находим стрелу прогиба
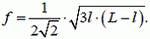 (15)
(15)
Задача. Определите наименьшую и наибольшую силу натяжения троса, если сила тяжести единицы длины q = 10 Н/м, длина пролета l = 20 м, а длина троса L = 21 м.
Решение. По формуле (15) находим стрелу прогиба
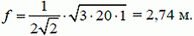
Наименьшую силу натяжения определим по формуле (2)
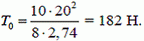
Наибольшую силу натяжения определим по формуле (7)
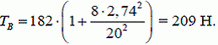
Ответ: f= 2,74 м, Т0 = 182 Н, ТВ = 209 Н.
Замечание. При более точных предположениях уравнение кривой равновесия тяжелой нити представляет собой не параболу, а цепную линию. Не приводящиеся здесь вычисления дают в этом случае следующие значения искомых величин:
f= 2,76 м, T0 = 185 Н, ТВ = 213 Н.
Сравнение более точных и приближенных значений подтверждает справедливость сделанных нами предположений для практических расчетов.
1. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. – Т.З. – М.: Наука, 1973.
Сила натяжения нити — формулировка
Определение
Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.
Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:
- создание строительного отвеса;
- установка растяжек для фиксации радиоантенн;
- поведение арматуры внутри напряженного бетона;
- устройство корабельного такелажа.
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
(F=F_{тяж}=m*g)
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
(F_n=m*g*cos(a))
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
(F=F_{тяж}+m*a)
Сила натяжения во вращающейся системе
Описание
Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:
- приближение к земле приводит к увеличению силы;
- во время удаления от земли сила слабеет.
Формула расчета
Рассчитать силу натяжения в условиях вращающейся системы можно так:
(F=frac{mtimes nu ^{2}}{r})
Обозначение, единица измерения
Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)
(H=frac{kgtimes m}{c^{2}})
Примеры решения задач
Задание 1
На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.
Решение
Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.
(bar{T}+mbar{g}=mbar{a})
(bar{T}) является силой натяжения нити.
Проекция уравнения будет иметь следующий вид:
(T – mg = ma)
Данное выражение позволяет рассчитать ускорение:
(a=frac{T-mg}{m})
Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления
(a=frac{4400-4*9,8}{400})
Ответ: a = 1.2 (м/с^2)
Задание 2
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.
Решение
Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:
(bar{T}+mbar{g}=mbar{a})
Проекции данной формулы по осям определяются следующим образом:
X: (T sin α = ma = mω2R)
Y: (-mg + T cos α = 0)
Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:
(T=frac{mg}{cos alpha })
Анализ рисунка позволяет вывести следующее уравнение:
(sin alpha = frac{R}{l}rightarrow cos alpha = sqrt{1-left(frac{R}{l} right)^{2}})
Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:
(T=frac{mg}{sqrt{1-left(frac{R}{l} right)^{2}}}= frac{mgl}{sqrt{l^{2}-R^{2}}})
Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:
(T=frac{0,1*9,8*5}{sqrt{5^{2}-3^{2}}}=1,225left(H right))
Ответ: Т=1,225 H
