The value of cos 630 degrees is 0. Cos 630 degrees in radians is written as cos (630° × π/180°), i.e., cos (7π/2) or cos (10.995574. . .). In this article, we will discuss the methods to find the value of cos 630 degrees with examples.
- Cos 630°: 0
- Cos (-630 degrees): 0
- Cos 630° in radians: cos (7π/2) or cos (10.9955742 . . .)
What is the Value of Cos 630 Degrees?
The value of cos 630 degrees is 0. Cos 630 degrees can also be expressed using the equivalent of the given angle (630 degrees) in radians (10.99557 . . .)
We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 630 degrees = 630° × (π/180°) rad = 7π/2 or 10.9955 . . .
∴ cos 630° = cos(10.9955) = 0

Explanation:
For cos 630°, the angle 630° > 360°. Given the periodic property of the cosine function, we can represent it as cos(630° mod 360°) = cos(270°). The angle 630°, coterminal to angle 270°, lies on the negative y-axis.
Thus, cos 630 degrees value = 0
Similarly, cos 630° can also be written as, cos 630 degrees = (630° + n × 360°), n ∈ Z.
⇒ cos 630° = cos 990° = cos 1350°, and so on.
Note: Since, cosine is an even function, the value of cos(-630°) = cos(630°) = 0.
Methods to Find Value of Cos 630 Degrees
The value of cos 630° is given as 0. We can find the value of cos 630 degrees by:
- Using Unit Circle
- Using Trigonometric Functions
Cos 630 Degrees Using Unit Circle
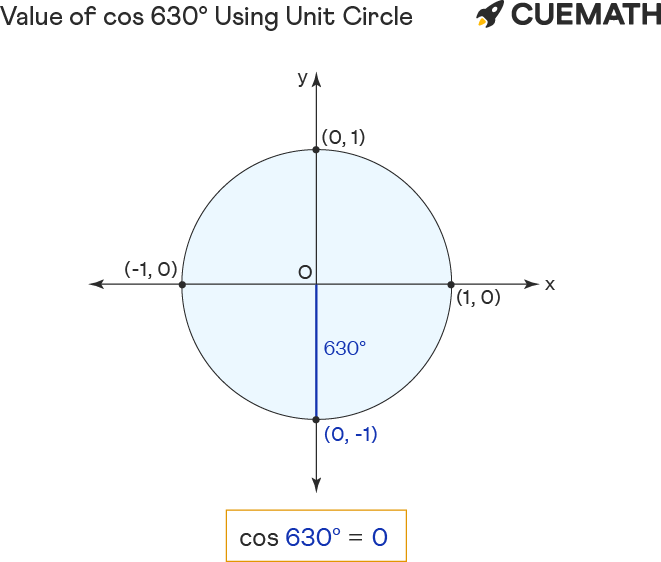
To find the value of cos 630 degrees using the unit circle, represent 630° in the form (1 × 360°) + 270° [∵ 630°>360°] ∵ cosine is a periodic function, cos 630° = cos 270°.
- Rotate ‘r’ anticlockwise to form 270° or 630° angle with the positive x-axis.
- The cos of 630 degrees equals the x-coordinate(0) of the point of intersection (0, -1) of unit circle and r.
Hence the value of cos 630° = x = 0
Cos 630° in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the cos 630 degrees as:
- ± √(1-sin²(630°))
- ± 1/√(1 + tan²(630°))
- ± cot 630°/√(1 + cot²(630°))
- ±√(cosec²(630°) – 1)/cosec 630°
- 1/sec 630°
Note: Since 630° lies on the negative y-axis, the final value of cos 630° is 0.
We can use trigonometric identities to represent cos 630° as,
- -cos(180° – 630°) = -cos(-450°)
- -cos(180° + 630°) = -cos 810°
- sin(90° + 630°) = sin 720°
- sin(90° – 630°) = sin(-540°)
☛ Also Check:
- cos 135 degrees
- cos 1 degrees
- cos 120 degrees
- cos 43 degrees
- cos 585 degrees
- cos 244 degrees
FAQs on Cos 630 Degrees
What is Cos 630 Degrees?
Cos 630 degrees is the value of cosine trigonometric function for an angle equal to 630 degrees. The value of cos 630° is 0.
How to Find the Value of Cos 630 Degrees?
The value of cos 630 degrees can be calculated by constructing an angle of 630° with the x-axis, and then finding the coordinates of the corresponding point (0, -1) on the unit circle. The value of cos 630° is equal to the x-coordinate (0). ∴ cos 630° = 0.
How to Find Cos 630° in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of cos 630° can be given in terms of other trigonometric functions as:
- ± √(1-sin²(630°))
- ± 1/√(1 + tan²(630°))
- ± cot 630°/√(1 + cot²(630°))
- ± √(cosec²(630°) – 1)/cosec 630°
- 1/sec 630°
☛ Also check: trigonometry table
What is the Value of Cos 630° in Terms of Cosec 630°?
Since the cosine function can be represented using the cosecant function, we can write cos 630° as -[√(cosec²(630°) – 1)/cosec 630°]. The value of cosec 630° is equal to -1.
What is the Value of Cos 630 Degrees in Terms of Cot 630°?
We can represent the cosine function in terms of the cotangent function using trig identities, cos 630° can be written as cot 630°/√(1 + cot²(630°)). Here, the value of cot 630° is equal to 0.
Вычислить с помощью формул приведения cos630 – sin1470 – ctg 1125.
Вы зашли на страницу вопроса Вычислить с помощью формул приведения cos630 – sin1470 – ctg 1125?, который относится к
категории Математика. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
люди помогите пожалуйста с тригонометрией
Профи
(917),
закрыт
12 лет назад
Татьяна Мещерякова
Мастер
(2157)
12 лет назад
Во-первых, значения углов, стоящих под знаком синуса или косинуса, можно уменьшать на число, кратное 360, т. к. sin(360n+t)=sint, cos(360n+t)=cost. Таким образом, можно отбрасывать 360, 720, 1080, 1440 градусов и т. д.
а) =cos270-sin30-ctg45. Дальше по таблице.
Если угол дан в радианах, то отбрасывать можно 2П (360 градусов) .
Тигрокроль
Мыслитель
(5416)
12 лет назад
Инженерный калькулятор открой, а так П= 180градусов, остальные вычти 360 град, если 180 град, то знак “минус” будет у синуса, если 270, то знак минуса будет у косинуса
чтоб проще считать было, нарисуй круг – синусы на горизонтальной, косинусы на вертикальной оси, котангенс это частное от косинуса на синус
630 градусов на окружности
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.
Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.
Раздел: Таблицы численных значений + Таблицы Брадиса:
Перевести градусы в радианы
Онлайн калькулятор для перевода градусов в радианы, помимо этого конвертер выполнит перевод и в другие единицы измерения угловой меры.
Формула перевода градусов в радианы: xрад=х°⋅π/180
1 градус = 0.01745329252 радиана;
30 градусов = 0.5235987756 радиана;
45 градусов = 0.7853981634 радиана;
180 градусов = 3.14159265359 радиана;
Градус (обозначаение °). Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.
Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.
Раздел: Таблицы численных значений + Таблицы Брадиса:
Как посчитать длину окружности
Онлайн калькулятор
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.
[spoiler title=”источники:”]
http://tehtab.ru/guide/guidemathematics/guidemathematicsfigurestables/prymygoltrygon/
http://poschitat.online/dlina-okruzhnosti
[/spoiler]
Таблица косинусов
Таблица косинусов – это записанные в таблицу посчитанные значения косинусов углов от 0° до 360°. Используя таблицу косинусов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение косинуса от нужного Вам угла, достаточно найти его в таблице или вычислить с помощью калькулятора.
Калькулятор – косинус угла
cos(°) = 1
Калькулятор – арккосинус угла
arccos() = 0°
Таблица косинусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| cos α | 1 | √32 | √22 | 12 | 0 | -1 | 0 | 1 |
Таблица косинусов углов от 0° до 180°
| cos(0°) = 1 cos(1°) = 0.999848 cos(2°) = 0.999391 cos(3°) = 0.99863 cos(4°) = 0.997564 cos(5°) = 0.996195 cos(6°) = 0.994522 cos(7°) = 0.992546 cos(8°) = 0.990268 cos(9°) = 0.987688 cos(10°) = 0.984808 cos(11°) = 0.981627 cos(12°) = 0.978148 cos(13°) = 0.97437 cos(14°) = 0.970296 cos(15°) = 0.965926 cos(16°) = 0.961262 cos(17°) = 0.956305 cos(18°) = 0.951057 cos(19°) = 0.945519 cos(20°) = 0.939693 cos(21°) = 0.93358 cos(22°) = 0.927184 cos(23°) = 0.920505 cos(24°) = 0.913545 cos(25°) = 0.906308 cos(26°) = 0.898794 cos(27°) = 0.891007 cos(28°) = 0.882948 cos(29°) = 0.87462 cos(30°) = 0.866025 cos(31°) = 0.857167 cos(32°) = 0.848048 cos(33°) = 0.838671 cos(34°) = 0.829038 cos(35°) = 0.819152 cos(36°) = 0.809017 cos(37°) = 0.798636 cos(38°) = 0.788011 cos(39°) = 0.777146 cos(40°) = 0.766044 cos(41°) = 0.75471 cos(42°) = 0.743145 cos(43°) = 0.731354 cos(44°) = 0.71934 cos(45°) = 0.707107 |
cos(46°) = 0.694658 cos(47°) = 0.681998 cos(48°) = 0.669131 cos(49°) = 0.656059 cos(50°) = 0.642788 cos(51°) = 0.62932 cos(52°) = 0.615661 cos(53°) = 0.601815 cos(54°) = 0.587785 cos(55°) = 0.573576 cos(56°) = 0.559193 cos(57°) = 0.544639 cos(58°) = 0.529919 cos(59°) = 0.515038 cos(60°) = 0.5 cos(61°) = 0.48481 cos(62°) = 0.469472 cos(63°) = 0.45399 cos(64°) = 0.438371 cos(65°) = 0.422618 cos(66°) = 0.406737 cos(67°) = 0.390731 cos(68°) = 0.374607 cos(69°) = 0.358368 cos(70°) = 0.34202 cos(71°) = 0.325568 cos(72°) = 0.309017 cos(73°) = 0.292372 cos(74°) = 0.275637 cos(75°) = 0.258819 cos(76°) = 0.241922 cos(77°) = 0.224951 cos(78°) = 0.207912 cos(79°) = 0.190809 cos(80°) = 0.173648 cos(81°) = 0.156434 cos(82°) = 0.139173 cos(83°) = 0.121869 cos(84°) = 0.104528 cos(85°) = 0.087156 cos(86°) = 0.069756 cos(87°) = 0.052336 cos(88°) = 0.034899 cos(89°) = 0.017452 cos(90°) = 0 |
cos(91°) = -0.017452 cos(92°) = -0.034899 cos(93°) = -0.052336 cos(94°) = -0.069756 cos(95°) = -0.087156 cos(96°) = -0.104528 cos(97°) = -0.121869 cos(98°) = -0.139173 cos(99°) = -0.156434 cos(100°) = -0.173648 cos(101°) = -0.190809 cos(102°) = -0.207912 cos(103°) = -0.224951 cos(104°) = -0.241922 cos(105°) = -0.258819 cos(106°) = -0.275637 cos(107°) = -0.292372 cos(108°) = -0.309017 cos(109°) = -0.325568 cos(110°) = -0.34202 cos(111°) = -0.358368 cos(112°) = -0.374607 cos(113°) = -0.390731 cos(114°) = -0.406737 cos(115°) = -0.422618 cos(116°) = -0.438371 cos(117°) = -0.45399 cos(118°) = -0.469472 cos(119°) = -0.48481 cos(120°) = -0.5 cos(121°) = -0.515038 cos(122°) = -0.529919 cos(123°) = -0.544639 cos(124°) = -0.559193 cos(125°) = -0.573576 cos(126°) = -0.587785 cos(127°) = -0.601815 cos(128°) = -0.615661 cos(129°) = -0.62932 cos(130°) = -0.642788 cos(131°) = -0.656059 cos(132°) = -0.669131 cos(133°) = -0.681998 cos(134°) = -0.694658 cos(135°) = -0.707107 |
cos(136°) = -0.71934 cos(137°) = -0.731354 cos(138°) = -0.743145 cos(139°) = -0.75471 cos(140°) = -0.766044 cos(141°) = -0.777146 cos(142°) = -0.788011 cos(143°) = -0.798636 cos(144°) = -0.809017 cos(145°) = -0.819152 cos(146°) = -0.829038 cos(147°) = -0.838671 cos(148°) = -0.848048 cos(149°) = -0.857167 cos(150°) = -0.866025 cos(151°) = -0.87462 cos(152°) = -0.882948 cos(153°) = -0.891007 cos(154°) = -0.898794 cos(155°) = -0.906308 cos(156°) = -0.913545 cos(157°) = -0.920505 cos(158°) = -0.927184 cos(159°) = -0.93358 cos(160°) = -0.939693 cos(161°) = -0.945519 cos(162°) = -0.951057 cos(163°) = -0.956305 cos(164°) = -0.961262 cos(165°) = -0.965926 cos(166°) = -0.970296 cos(167°) = -0.97437 cos(168°) = -0.978148 cos(169°) = -0.981627 cos(170°) = -0.984808 cos(171°) = -0.987688 cos(172°) = -0.990268 cos(173°) = -0.992546 cos(174°) = -0.994522 cos(175°) = -0.996195 cos(176°) = -0.997564 cos(177°) = -0.99863 cos(178°) = -0.999391 cos(179°) = -0.999848 cos(180°) = -1 |
Таблица косинусов углов от 181° до 360°
| cos(181°) = -0.999848 cos(182°) = -0.999391 cos(183°) = -0.99863 cos(184°) = -0.997564 cos(185°) = -0.996195 cos(186°) = -0.994522 cos(187°) = -0.992546 cos(188°) = -0.990268 cos(189°) = -0.987688 cos(190°) = -0.984808 cos(191°) = -0.981627 cos(192°) = -0.978148 cos(193°) = -0.97437 cos(194°) = -0.970296 cos(195°) = -0.965926 cos(196°) = -0.961262 cos(197°) = -0.956305 cos(198°) = -0.951057 cos(199°) = -0.945519 cos(200°) = -0.939693 cos(201°) = -0.93358 cos(202°) = -0.927184 cos(203°) = -0.920505 cos(204°) = -0.913545 cos(205°) = -0.906308 cos(206°) = -0.898794 cos(207°) = -0.891007 cos(208°) = -0.882948 cos(209°) = -0.87462 cos(210°) = -0.866025 cos(211°) = -0.857167 cos(212°) = -0.848048 cos(213°) = -0.838671 cos(214°) = -0.829038 cos(215°) = -0.819152 cos(216°) = -0.809017 cos(217°) = -0.798636 cos(218°) = -0.788011 cos(219°) = -0.777146 cos(220°) = -0.766044 cos(221°) = -0.75471 cos(222°) = -0.743145 cos(223°) = -0.731354 cos(224°) = -0.71934 cos(225°) = -0.707107 |
cos(226°) = -0.694658 cos(227°) = -0.681998 cos(228°) = -0.669131 cos(229°) = -0.656059 cos(230°) = -0.642788 cos(231°) = -0.62932 cos(232°) = -0.615661 cos(233°) = -0.601815 cos(234°) = -0.587785 cos(235°) = -0.573576 cos(236°) = -0.559193 cos(237°) = -0.544639 cos(238°) = -0.529919 cos(239°) = -0.515038 cos(240°) = -0.5 cos(241°) = -0.48481 cos(242°) = -0.469472 cos(243°) = -0.45399 cos(244°) = -0.438371 cos(245°) = -0.422618 cos(246°) = -0.406737 cos(247°) = -0.390731 cos(248°) = -0.374607 cos(249°) = -0.358368 cos(250°) = -0.34202 cos(251°) = -0.325568 cos(252°) = -0.309017 cos(253°) = -0.292372 cos(254°) = -0.275637 cos(255°) = -0.258819 cos(256°) = -0.241922 cos(257°) = -0.224951 cos(258°) = -0.207912 cos(259°) = -0.190809 cos(260°) = -0.173648 cos(261°) = -0.156434 cos(262°) = -0.139173 cos(263°) = -0.121869 cos(264°) = -0.104528 cos(265°) = -0.087156 cos(266°) = -0.069756 cos(267°) = -0.052336 cos(268°) = -0.034899 cos(269°) = -0.017452 cos(270°) = -0 |
cos(271°) = 0.017452 cos(272°) = 0.034899 cos(273°) = 0.052336 cos(274°) = 0.069756 cos(275°) = 0.087156 cos(276°) = 0.104528 cos(277°) = 0.121869 cos(278°) = 0.139173 cos(279°) = 0.156434 cos(280°) = 0.173648 cos(281°) = 0.190809 cos(282°) = 0.207912 cos(283°) = 0.224951 cos(284°) = 0.241922 cos(285°) = 0.258819 cos(286°) = 0.275637 cos(287°) = 0.292372 cos(288°) = 0.309017 cos(289°) = 0.325568 cos(290°) = 0.34202 cos(291°) = 0.358368 cos(292°) = 0.374607 cos(293°) = 0.390731 cos(294°) = 0.406737 cos(295°) = 0.422618 cos(296°) = 0.438371 cos(297°) = 0.45399 cos(298°) = 0.469472 cos(299°) = 0.48481 cos(300°) = 0.5 cos(301°) = 0.515038 cos(302°) = 0.529919 cos(303°) = 0.544639 cos(304°) = 0.559193 cos(305°) = 0.573576 cos(306°) = 0.587785 cos(307°) = 0.601815 cos(308°) = 0.615661 cos(309°) = 0.62932 cos(310°) = 0.642788 cos(311°) = 0.656059 cos(312°) = 0.669131 cos(313°) = 0.681998 cos(314°) = 0.694658 cos(315°) = 0.707107 |
cos(316°) = 0.71934 cos(317°) = 0.731354 cos(318°) = 0.743145 cos(319°) = 0.75471 cos(320°) = 0.766044 cos(321°) = 0.777146 cos(322°) = 0.788011 cos(323°) = 0.798636 cos(324°) = 0.809017 cos(325°) = 0.819152 cos(326°) = 0.829038 cos(327°) = 0.838671 cos(328°) = 0.848048 cos(329°) = 0.857167 cos(330°) = 0.866025 cos(331°) = 0.87462 cos(332°) = 0.882948 cos(333°) = 0.891007 cos(334°) = 0.898794 cos(335°) = 0.906308 cos(336°) = 0.913545 cos(337°) = 0.920505 cos(338°) = 0.927184 cos(339°) = 0.93358 cos(340°) = 0.939693 cos(341°) = 0.945519 cos(342°) = 0.951057 cos(343°) = 0.956305 cos(344°) = 0.961262 cos(345°) = 0.965926 cos(346°) = 0.970296 cos(347°) = 0.97437 cos(348°) = 0.978148 cos(349°) = 0.981627 cos(350°) = 0.984808 cos(351°) = 0.987688 cos(352°) = 0.990268 cos(353°) = 0.992546 cos(354°) = 0.994522 cos(355°) = 0.996195 cos(356°) = 0.997564 cos(357°) = 0.99863 cos(358°) = 0.999391 cos(359°) = 0.999848 cos(360°) = 1 |

