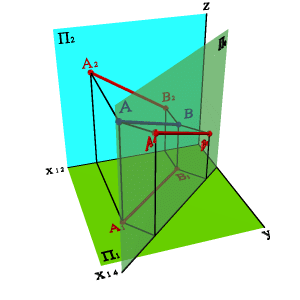
§11. Построение линии пересечения двух плоскостей. (Вторая позиционная задача).
Результатом пересечения двух плоскостей является прямая . Для построения этой прямой достаточно найти две точки, принадлежащие обеим плоскостям и провести через них прямую линию.
Если мы возьмем прямую, принадлежащую одной плоскости и найдем точку ее пересечения с другой плоскостью, то эта точка будет общей для обеих плоскостей. Таким образом, построение линии пересечения двух плоскостей сводится к решению первой позиционной задачи, повторенному дважды.
Задача 11.1. Построить линию пересечения плоскости α, заданной треугольником АВС, и плоскости β, заданной двумя пересекающимися прямыми МЕ и МК (рисунок 11.1). Определить видимость плоскостей.
Решение.
1. Возьмем прямую АВ, принадлежащую плоскости α, и найдем точку ее пересечения с плоскостью β. Для этого заключим ее в проецирующую плоскость и найдем точку пересечения, используя алгоритм для решения первой позиционной задачи (см. §7).
На рисунке 11.2 продемонстрирован этот этап решения – точка N является точкой пересечения прямой АВ и плоскости β(МК, МЕ). В данном случае мы заключили прямую в фронтально-проецирующую плоскость ФП, прямая 1-2 является результатом пересечения плоскости ФП и плоскостиβ.
Не нужно забывать о том, что все точки на чертеже отображены в проекциях. Так, например, на рисунке 11.2. точка N представлена проекциями N1 и N2.
2. Возьмем прямую МК, принадлежащую плоскости β, и найдем точку ее пересечения с плоскостью α. Заключив ее в горизонтально-проецирующую плоскость, и проведя аналогичные построения, найдем точку L (рисунок 11.3).
3. Проведем прямую NL, являющуюся линией пересечения плоскостей α и β (рисунок 11.4).
4. Определяем видимость плоскостей (рисунок 11.5).
Применяем метод конкурирующих точек – для определения видимости на фронтальной проекции берем конкурирующие точки, проекции которых совпадают с точкой 22, для определения видимости на горизонтальной проекции берем точки с проекцией в 41. Конкурирующие точки 22 принадлежат фронтальной проекции АВ и МК. Пройдя по стрелке взгляда вниз, видим, что точка, лежащая на прямой АВ находится ближе к наблюдателю, так как у нее координата у больше, поэтому в районе проекции прямая АВ видимая, а МК – невидимая. Следовательно, проекция М2К2 в точке 22 меняет свой вид с видимой на невидимую.
Точка 41 лежит на горизонтальной проекции ВС и МК. Видимой будет та прямая, которая по стрелке взгляда находится выше на фронтальной проекции, в данном случае это прямая ВС.
Нужно обратить внимание на то, что прямые АВ и ВС меняют видимость в точках пересечения с прямой NL. Линия пересечения плоскостей всегда видимая.
На рисунке 11.6 показано окончательное решение задачи, для наглядности плоскости затонированы.
Задача 11.2. Построить линию пересечения плоскостей α и β, заданных следами (рисунок 11.7). Определить видимость плоскостей.
Решение.
Поскольку следы плоскости – это прямые, принадлежащие этой плоскости, а точки пересечения 1 и 2 одноименных проекций следов являются общими для обеих плоскостей, то очевидно, что результат пересечения плоскостей – это прямая, проходящая через эти точки. На эпюре Монжа определяем фронтальные и горизонтальные проекции точек 1 и 2 (рисунок 11.8).
Как видно на рисунке 11.8, горизонтальная проекция точки 1, являющейся точкой пересечения фронтальных следов α и β, а также фронтальная проекция точки 2 – лежат она оси х, поскольку сами прямые принадлежат плоскостям проекций. Соединив одноименные проекции точек 1 и 2, получим линию пересечения плоскостей (рисунок 11.9).
Определив видимость плоскостей в проекциях, получим окончательное решение задачи (рисунок 11.10)
Построение линии пересечения плоскостей, заданных различными способами
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.
Задача
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.

Решение
- Вводим вспомогательную горизонтальную плоскость γ1. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1”C” и 2”3”, совпадают с фронтальным следом пл. γ1. Он обозначен на рисунке как f0γ1 и расположен параллельно оси x.
- Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
- Находим горизонтальную проекцию точки L1 на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L1 лежит на фронтальном следе плоскости γ.
- Вводим вспомогательную горизонтальную плоскость γ2. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L2.
- Через L1 и L2 проводим искомую прямую l.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
Пересечение плоскостей, заданных следами
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.

Алгоритм построения
- Находим точку L’1, расположенную на пересечении горизонтальных следов h0α и h0β. Точка L”1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’1.
- Находим точку L”2 на пересечении фронтальных следов пл. α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L”2.
- Проводим прямые l’ и l” через соответствующие проекции точек L1 и L2, как это показано на рисунке.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
Пересечение плоскостей треугольников
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

Алгоритм построения
- Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3”=A”B”∩f0σ и 5”=A”С”∩f0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
- Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N” расположена на фронтальном следе f0σ на одной линии связи с N’.
-
Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
- Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.
Определение видимости
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N”K” видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6” находится выше, чем (∙)7”, то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Дополнительные материалы:
- Способы задания плоскости на чертеже
- Точка пересечения прямой и плоскости
Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям. Так, прямая K1К2 (рис. 163), по которой пересекаются между собой плоскость, заданная треугольником АВС, и пл. β, заданная прямыми DE и DF, проходит через точки K1 и K2; но в этих точках прямые АВ и АС первой плоскости пересекают пл. β т. е. точки К1 и К2 принадлежат обеим плоскостям.
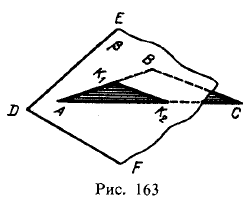
Следовательно, в общем случае для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям; эти точки определяют линию пересечения плоскостей.
Для нахождения каждой из таких двух точек обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна к плоскости проекций, то построение проекций линии пересечения упрощается. Начнем с такого случая.
На рис. 164 показано пересечение двух плоскостей, из которых одна (заданная треугольником DEF) расположена перпендикулярно к пл. π2. Так как треугольник DEF проецируется на пл.π2 в виде прямой линии (D”F”), то фронтальная проекция отрезка прямой, по которому пересекаются оба треугольника, представляет собой отрезок К”1К”2 на проекции D”F”. Дальнейшее построение ясно из чертежа.
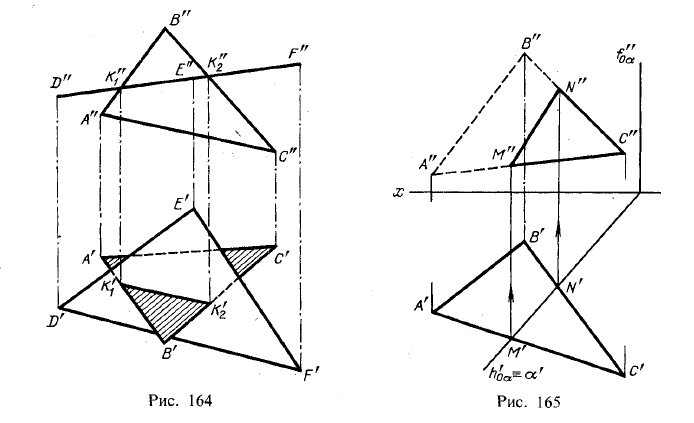
Другой пример дан на рис. 165. Горизонтально-проецирующая плоскость α пересекает плоскость треугольника АВС. Горизонтальная проекция линии пересечения этих плоскостей — отрезок M’N’ — определяется на следе α’.
Теперь рассмотрим общий случай построения линии пересечения двух плоскостей. Пусть одна из плоскостей, β, задана двумя пересекающимися прямыми, а другая, γ,— двумя параллельными прямыми. Построение показано на рис. 166. В результате взаимного пересечения плоскостей β и γ получена прямая K1K2. Выразим это записью: β × γ = К1K2.
Для определения положения точек K1 и К2 возьмем две вспомогательные фронтально-проецирующие плоскости (α1, и α2), пересекающие каждую из плоскостей β и γ. При пересечении плоскостей β и γ плоскостью α1. получаем прямые с проекциями 1″2″, 1’2′ и 3″4″, 3’4′. Эти прямые, расположенные в пл. α1, в своем пересечении определяют первую точку, К1, линии пересечения плоскостей β и γ.
Введя, далее, ил. α2, получаем в ее пересечении с β и γ прямые с проекциями 5″6″, 5’6′ и 7″8″, 7’8′. Эти прямые, расположенные в пл. α2, в своем пересечении определяют вторую точку, К2, общую для β и γ.
Получив проекции К’1 и К’2 находим на следах и α”1 и α”2 проекции К”1 и К”2. Этим определяются проекции К’1К’2 и К”1К”2 искомой прямой пересечения плоскостей β и γ(проекции проведены штрихпунктирной линией).
При построении можно иметь в виду следующее: так как вспомогательные секущие плоскости α1 и α2 взаимно параллельны, то, построив проекции 1’2′ и 3’4′ следует для проекций 5’6′ и 7’8′ взять по одной точке, хотя бы 5 и 8, так как 5’6’||1’2′ и 7’8’||3’4′.
В рассмотренном построении были взяты в качестве вспомогательных две фронгально- проецирующие плоскости. Конечно, можно было взять и иные плоскости, например две горизонтальные или одну горизонтальную, другую фронтальную и т. д. Сущность построений от этого не меняется. Однако может встретиться такой случай. Положим, что были взяты в качестве вспомогательных две горизонтальные плоскости и полученные при пересечении ими
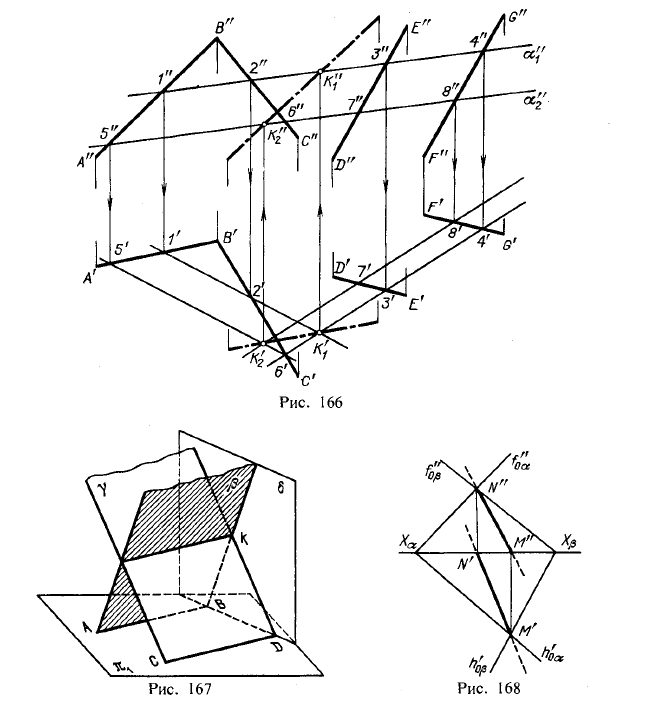
плоскостей β и γ горизонтали оказались взаимно параллельными. Но рис. 167 показывает, что β и γ пересекаются между собой, хотя их горизонтали параллельны. Следовательно, получив взаимно параллельные горизонтальные проекции горизонталей АВ и CD и зная, что плоскости при этом не обязательно параллельны, а могут пересекаться (по общей для них горизонтали), надо испытать плоскости β и γ при помощи хотя бы, горизонгально-проецирующей плоскости (см. рис. 167); если прямые, по которым эта вспомогательная плоскость σ, пересечет β и γ, также оказались бы параллельны одна другой, то плоскости β и γ не пересекаются, а параллельны одна другой. На рис. 167 эти прямые пересекаются в точке К, через которую и проходит линия пересечения плоскостей β и γ параллельно прямым ВА и CD.
Если плоскости заданы их следами на плоскостях проекций, то естественно искать точки, определяющие прямую пересечения плоскостей, в точках пересечения одноименных следов плоскостей (рис. 168): прямая, проходящая через эти точки, является общей для обеих плоскостей, т. е. их линией пересечения.
Схему построения линии пересечения двух плоскостей (см. рис. 166) можно, конечно, распространить и на случай задания плоскостей их следами. Здесь роль вспомогательных секущих плоскостей исполняют сами плоскости проекций:
α × π1=h’0α; β× π1=h’0β; h’0α × h’0β=M;
α × π2=f”0α; β× π2=f”0β; f”0α × f”0β=N.
Точки пересечения одноименных следов плоскостей являются следами линии пересечения этих плоскостей. Поэтому для построения проекций линии пересечения плоскостей α и β (рис. 168) надо: 1) найти точку М’ в пересечении следов h’0α и h’0β
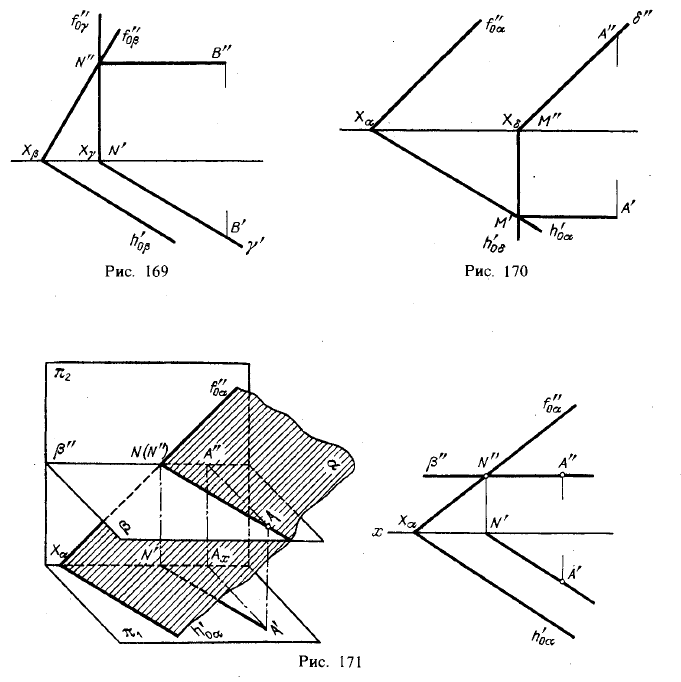
и точку N” в пересечении f”0α и f”0β, а по ним — проекции М” и N’; 2) провести прямые линии M”N” и M’N’,
На рис. 169—171 показаны случаи, когда известно направление линии пересечения. Поэтому достаточно иметь лйшь одну точку от пересечения следов и далее провести через эту точку прямую, исходя из положения плоскостей и их следов.
Вопросы к §§ 22-24
- Какое взаимное положение могут занимать две плоскости?
- Каков признак параллельности двух плоскостей?
- Как взаимно располагаются фронтальные следы двух параллельных между собой фронтально-проецирующих плоскостей?
- Как взаимно располагаются горизонтальные следы двух параллельных между собой горизонтально-проецирующих плоскостей?
- Как взаимно располагаются одноименные следы двух параллельных между собой плоскостей?
- Служит ли признаком взаимного пересечения двух плоскостей пересечение хотя бы одной пары их одноименных следов?
- Как установить взаимное положение прямой и Плоскости?
- Как строится точка пересечения прямой линии с плоскостью, перпендикулярной к одной или к двум плоскостям проекций?
- Какая точка из числа расположенных на общем перпендикуляре к а) пл. π1 б) пл. π2 считается видимой соответственно на π1, на π2?
- Как строится линия пересечения двух плоскостей, из которых хотя бы одна перпендикулярна к пл. π1 или к пл. π2?
- В чем заключается общий способ построения линии пересечения двух плоскостей?
В задаче необходимо найти линию пересечения двух плоскостей и определить натуральную величину одной из них методом плоскопараллельного перемещения.
Для решения такой классической задачи по начертательной геометрии необходимо знать следующий теоретический материал:
— нанесение проекций точек пространства на комплексный чертеж по заданным координатам;
— способы задания плоскости на комплексном чертеже, плоскости общего и частного положения;
— главные линии плоскости;
— определение точки пересечения прямой линии с плоскостью (нахождение «точки встречи»);
— метод плоскопараллельного перемещения для определения натуральной величины плоской фигуры;
— определение видимости на чертеже прямых линий и плоскостей с помощью конкурирующих точек.
Порядок решения Задачи
1. Согласно варианту Задания по координатам точек наносим на комплексный чертеж две плоскости, заданные в виде треугольников ABC (A’, B’, C’; A, B, C) и DKE (D’, K’, E’; D, K, Е) (рис.1.1).
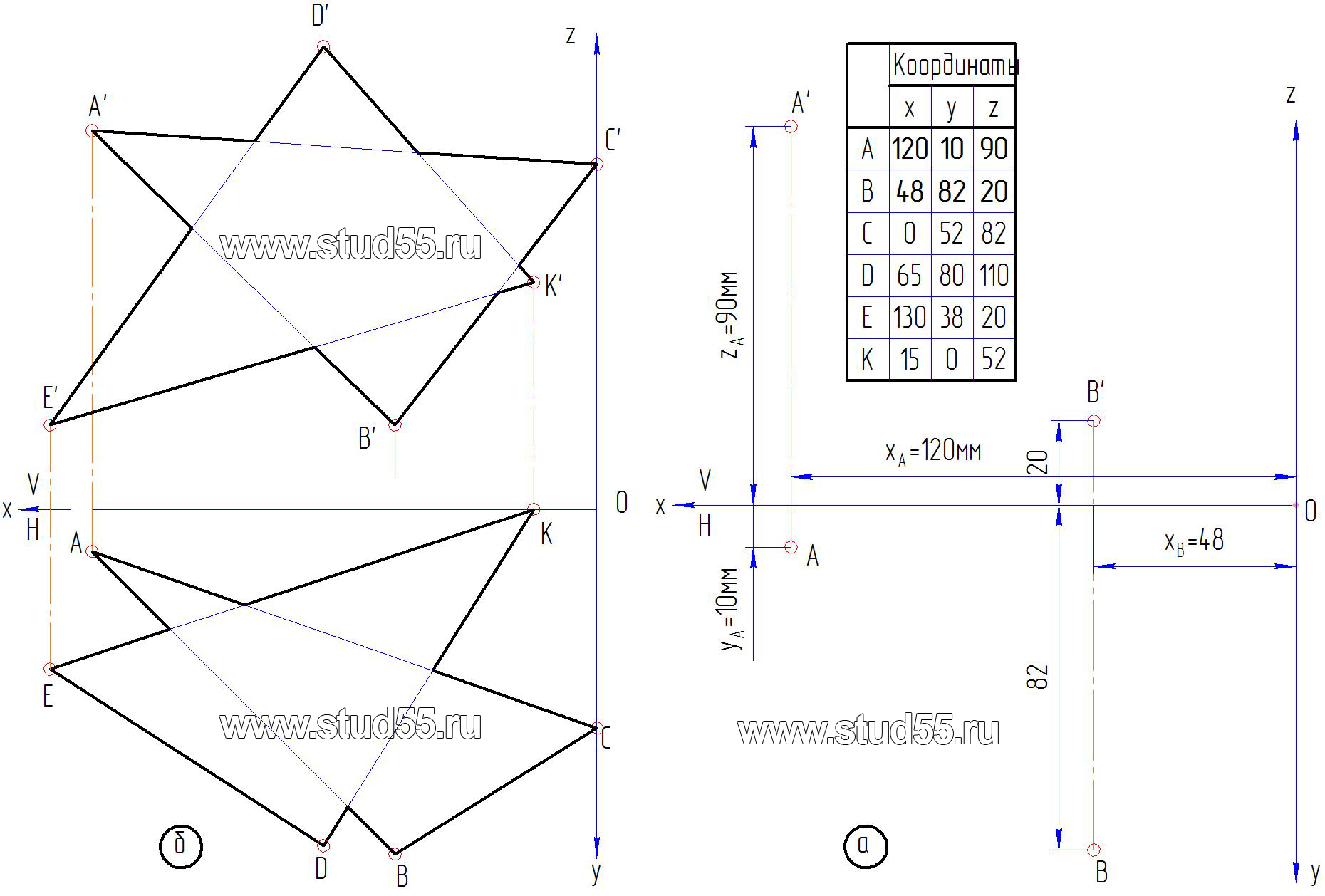
Рис.1.1
2. Для нахождения линии пересечения воспользуемся методом проецирующей плоскости. Суть его в том, что берется одна сторона (линия) первой плоскости (треугольника) и заключается в проецирующую плоскость. Определяется точка пересечения этой линии с плоскостью второго треугольника. Повторив эту задачу еще раз, но для прямой второго треугольника и плоскости первого треугольника, определим вторую точку пересечения. Так как полученные точки одновременно принадлежат обеим плоскостям, они должны находиться на линии пересечения этих плоскостей. Соединив эти точки прямой, будем иметь искомую линию пересечения плоскостей.
3. Задача решается следующим образом:
а) заключаем в проецирующую плоскость Ф(Ф’) сторону AB(A’B’) первого треугольника во фронтальной плоскости проекций V. Отмечаем точки пересечения проецирующей плоскости со сторонами DK и DE второго треугольника, получая точки 1(1’) и 2 (2’). Переносим их по линиям связи на горизонтальную плоскость проекций H на соответствующие стороны треугольника, точка 1(1) на стороне DE и точка 2(2) на стороне DK.
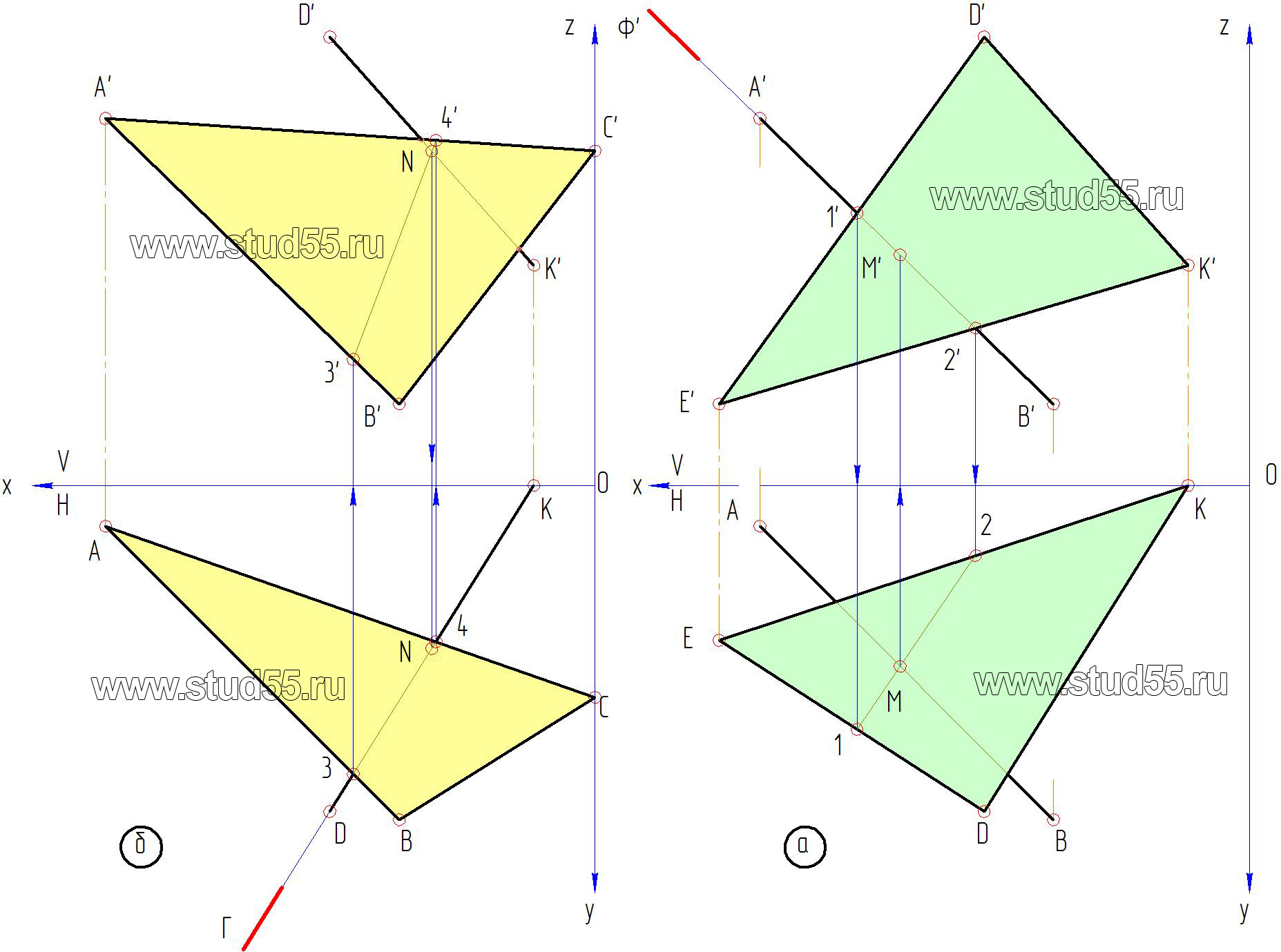
Рис.1.2
б) соединив проекции точек 1 и 2, будем иметь проекцию проецирующей плоскости Ф. Тогда точка пересечения прямой АВ с плоскостью треугольника DKE определится (согласно правилу) вместе пересечения проекции проецирующей плоскости 1-2 и одноименной проекции прямой AB. Таким образом, получили горизонтальную проекцию первой точки пересечения плоскостей – M, по которой определяем (проецируем по линиям связи) её фронтальную проекцию – M’ на прямой A’B’(рис.1.2.а);
в) аналогичным путем находим вторую точку. Заключаем в проецирующую плоскость Г(Г) сторону второго треугольника DK(DK). Отмечаем точки пересечения проецирующей плоскости со сторонами первого треугольника AC и BC во горизонтальной проекции, получая проекции точек 3 и 4. Проецируем их на соответствующие стороны в фронтальной плоскости, получаем 3’ и 4’. Соединив их прямой, имеем проекцию проецирующей плоскости. Тогда вторая точка пересечения плоскостей будет в месте пересечения линии 3’-4’ со стороной треугольника D’K’, которую заключали в проецирующую плоскость. Таким образом, получили фронтальную проекцию второй точки пересечения – N’, по линии связи находим горизонтальную проекцию – N (рис.1.2.б).
г) соединив полученные точки MN(MN) и (M’N’) на горизонтальной и фронтальной плоскостях, имеем искомую линию пересечения заданных плоскостей.
4. С помощью конкурирующих точек определяем видимость плоскостей. Возьмем пару конкурирующих точек, например, 1’=5’ во фронтальной проекции. Спроецируем их на соответствующие стороны в горизонтальную плоскость, получим 1 и 5. Видим, что точка 1, лежащая на стороне DЕ имеет большую координату до оси x, чем точка 5, лежащая на стороне AВ. Следовательно, согласно правилу, большей координаты, точка 1 и сторона треугольника D’Е’ во фронтальной плоскости будут видимые. Таким образом, определяется видимость каждой стороны треугольника в горизонтальной и фронтальной плоскостях. Видимые линии на чертежах проводятся сплошной контурной линией, а не видимые — штриховой линией. Напомним, что в точках пересечения плоскостей (M—N и M’-N’) будет происходить смена видимости.

Рис.1.3
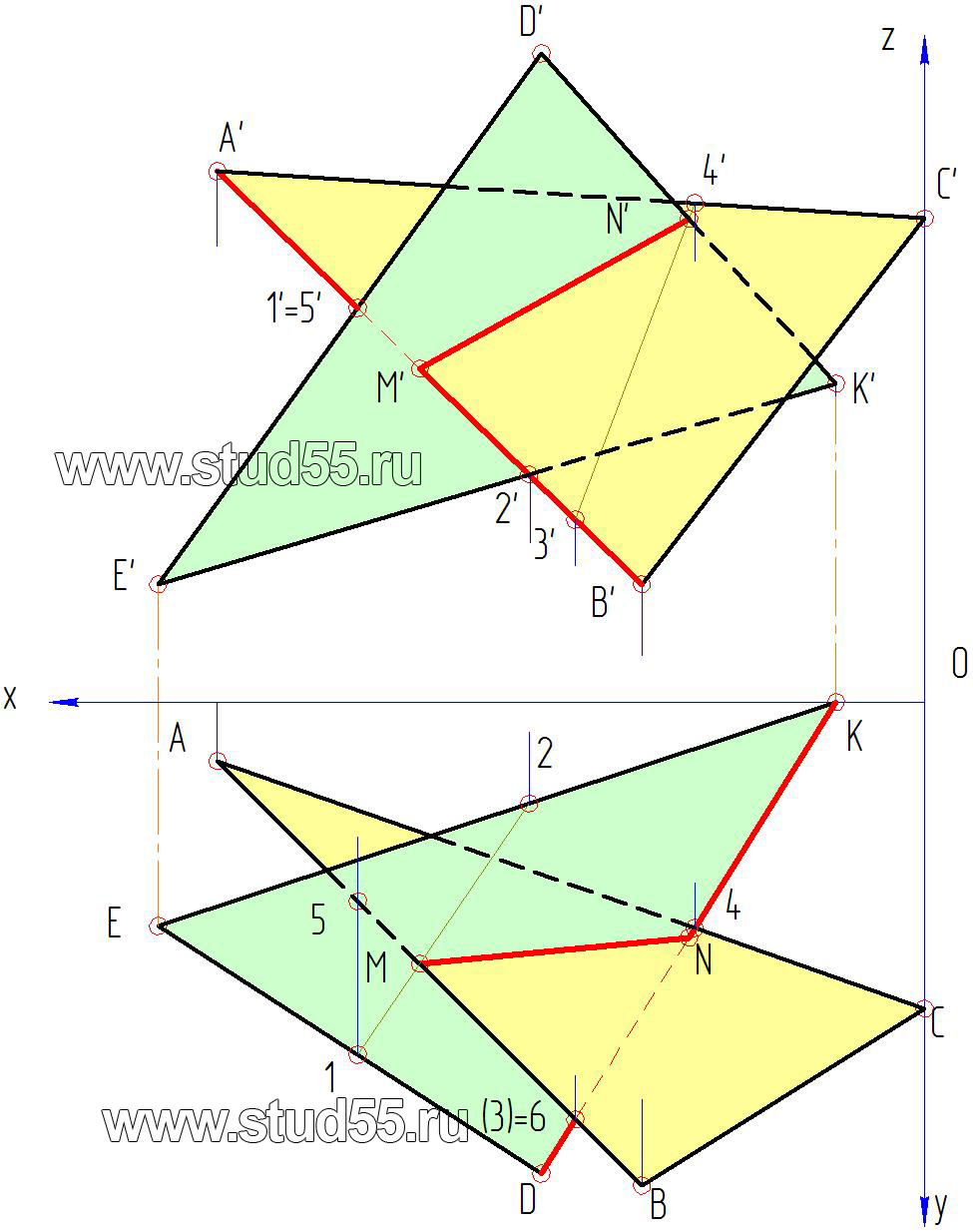
Рис.1.4.
На эпюре дополнительно показано определение видимости в горизонтальной плоскости с использованием конкурирующих точек 3 и 6 на прямых DK и АВ.
5. Методом плоскопараллельного перемещения определяем натуральную величину плоскости треугольника ABC, для чего:
а) в указанной плоскости через точку С(С) проводим фронталь C—F (С-F и C’-F’);
б) на свободном поле чертежа во горизонтальной проекции берем (отмечаем) произвольную точку С1, считая, что это одна из вершин треугольника (конкретно вершина C). Из нее восстанавливаем перпендикуляр к фронтальной плоскости (через ось х);
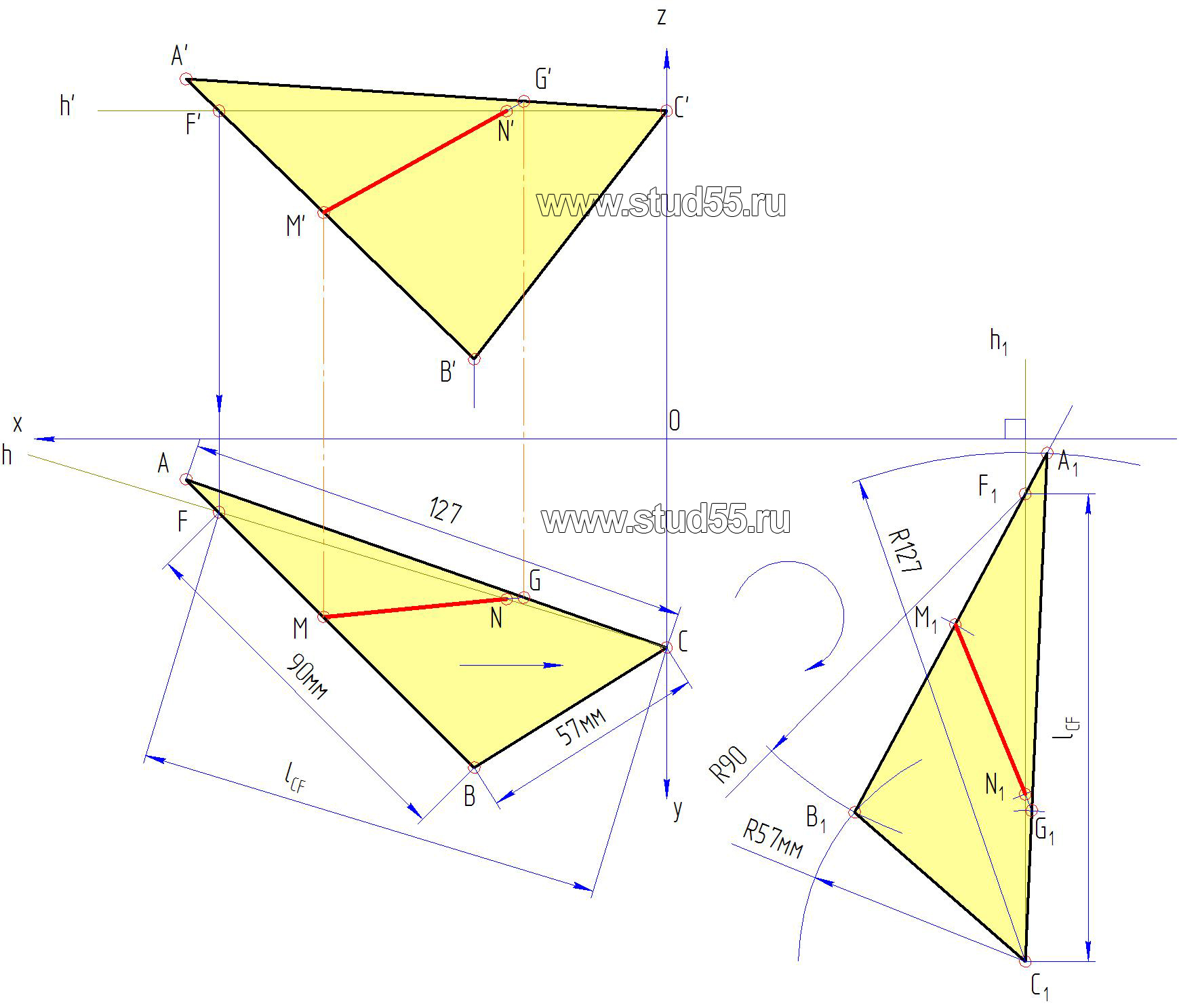
Рис.1.5
в) плоскопараллельным перемещением переводим горизонтальную проекцию треугольника ABC, в новое положение A1B1C1 таким образом, чтобы в фронтальной проекции он занял проецирующее положение (преобразовался в прямую линию). Для этого: на перпендикуляре от точки С1, откладываем фронтальную проекцию горизонтали C1—F1 (длина lCF) получаем точку F1. Раствором циркуля из точки F1 величиною F-A делаем дуговую засечку, а из точки C1 — засечку величиной CA, тогда в пересечении дуговых линий получаем точку A1 (вторая вершина треугольника);
— аналогично получаем точку B1 (из точки C1 делаем засечку величиной C—B (57мм), а из точки F1 величиной F—B (90мм).Заметим, что при правильном решении три точки A1 F’1 и B’1 должны лежать на одной прямой (сторона треугольника A1—B1)две другие стороны С1—A1 и C1—B1 получаются путем соединения их вершин;
г) из метода вращения следует, что при перемещении или вращении точки в какой-то плоскости проекций — на сопряженной плоскости проекция этой точки должна двигаться по прямой линии, в нашем конкретном случае по прямой параллельной оси х. Тогда проводим из точек A’B’C’ фронтальной проекции эти прямые (их называют плоскостями вращения точек), а из фронтальных проекций перемещенных точек A1 В1 C1 восстановим перпендикуляры (линии связи) (рис.1.6).
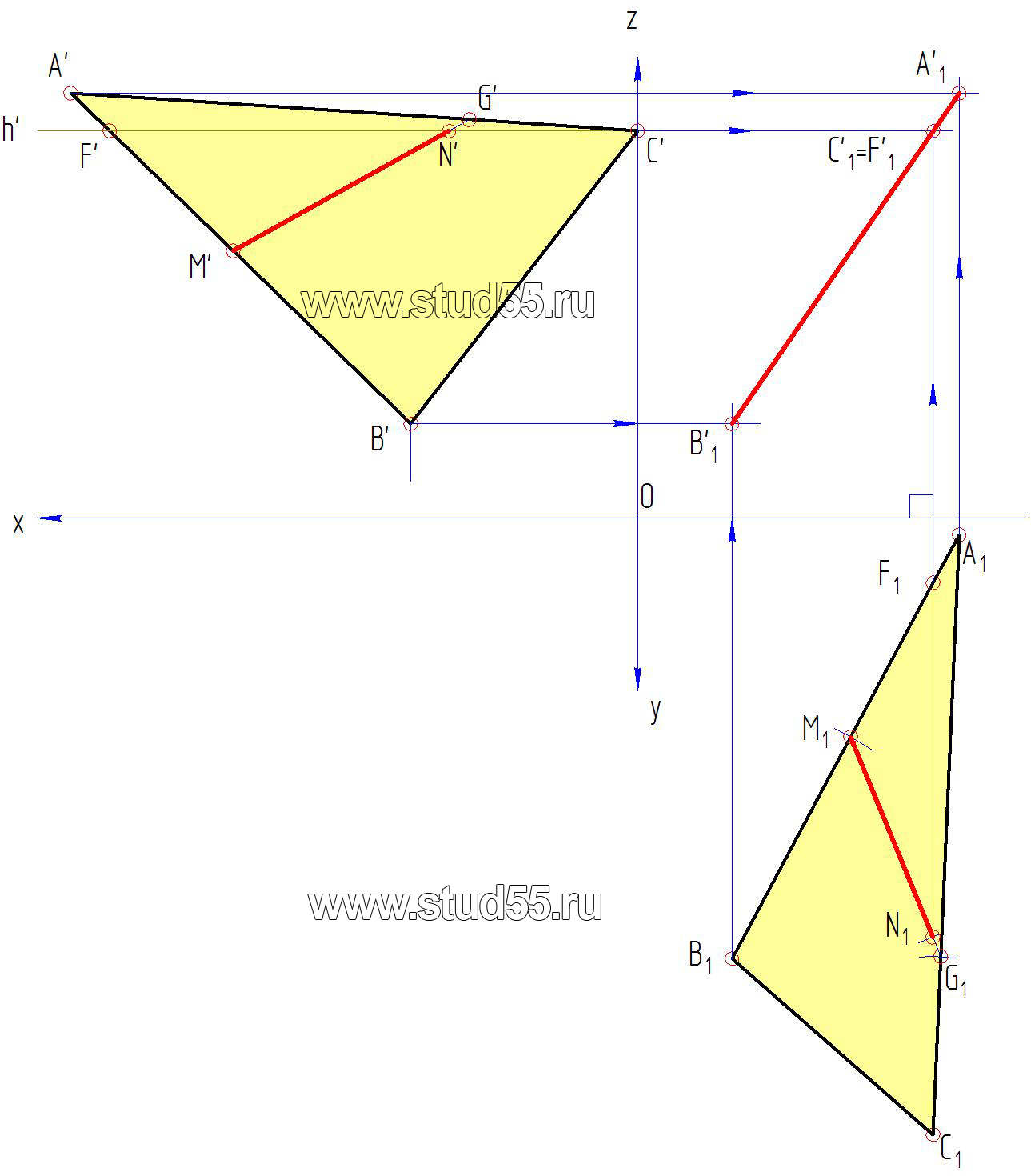
Рис.1.6
Пересечения указанных линий с соответствующими перпендикулярами дает новые положения фронтальной проекции треугольника ABC, конкретно A’1В’1C’1 который должен стать проецирующим (прямой линией), поскольку горизонталь h1 мы провели перпендикулярно фронтальной плоскости проекций (рис.1.6);
5) тогда для получения натуральной величины треугольника достаточно его фронтальную проекцию развернуть до параллельности с горизонтальной плоскостью. Разворот осуществляем с помощью циркуля через точку А’1, считая ее как центр вращения, ставим треугольник A’1В’1C’1 параллельно оси х, получаем A’2В’2C’2. Как было сказано выше, при вращении точки, на сопряженной (теперь на горизонтальной) проекции они двигаются по прямым параллельным оси х. Опуская перпендикуляры (линии связи) из фронтальных проекций точек A’2 В’2 C’2 пересечения их с соответствующими линиями находим горизонтальную проекцию треугольника ABC (A2В2C2) в натуральную величину (рис.1.7).
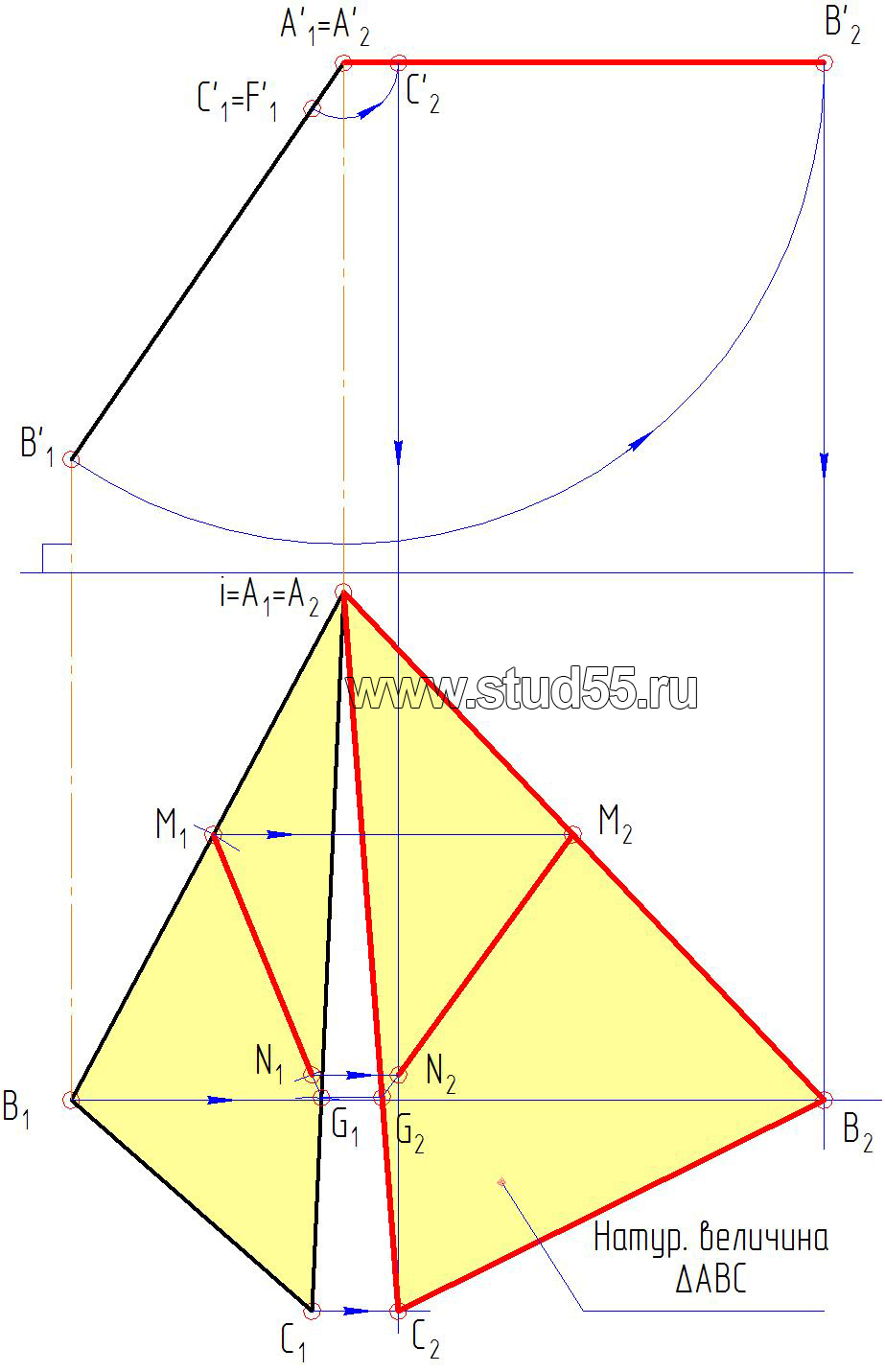
Рис. 1.7
У меня есть все готовые решения задач с такими координатами, купить можно >>здесь<<

Цена 55 руб, чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;
Раздел: Начертательная геометрия /
- Рекомендуем
- Комментарии
- Наши товары
Одной
из основополагающих задач начертательной
геометрии является задача на на построение
линии пересечения двух плоскостей
общего положения. Случаи задания
плоскостей бывают разные, но в любом
случае вам встретится задача, в которой
будет необходимо построить линию
пересечения двух плоскостей заданных
треугольниками (или другими плоскими
геометрическими фигурами). Алгоритм
решения такой задачи я и предлагаю
рассмотреть сейчас.
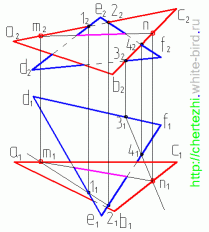
Итак,
даны две плоскости, заданные треугольниками
АВС и DEF. Метод сводится к тому, что бы
поочередно найти две точки пересечения
двух ребер одного треугольника с
плоскостью другого. Соединив эти точки
мы получим линию пересечения двух
плоскостей. Построение точки пересечения
прямой с плоскостью более подробно было
рассмотрено в предыдущем уроке, напомню
только механические действия:
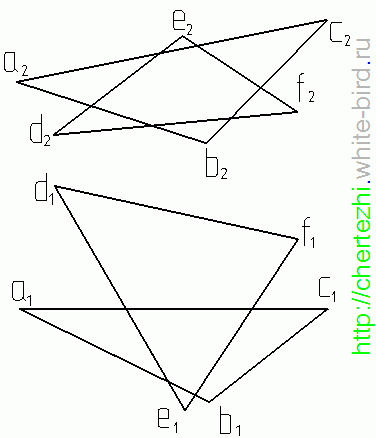
–
Заключим прямую АС во фронтально-проецирующую
плоскость и перенесем по линиям связи
на горизонтальную проекцию точки
пересечения этой плоскости с прямыми
DE и DF – точки 1 и 2
–
На горизонтальной проекции соединим
проекции точек 1 и 2 и найдем точку
пересечения получившейся линии с
горизонтальной проекцией той прямой,
которую мы заключали во фронтально-проецирующую
плоскость, в этом случае – с прямой AC. Мы
получили точку M.
–
Заключим прямую BС во фронтально-проецирующую
плоскость и перенесем по линиям связи
на горизонтальную проекцию точки
пересечения этой плоскости с прямыми
EF и DF – точки 3 и 4
Соединим
их горизонтальные проекции и получим
точку пересечения этой прямой с прямой
ВС – точку N.
–
Соединив точки M и N мы получим линию
пересечения плоскостей заданных
треугольниками. По сути линия пересечения
уже найдена. – Осталось лишь определить
видимость ребер треугольников. Это
делается методом конкурирующих точек.
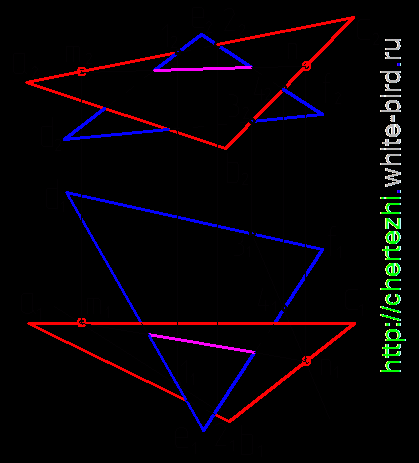
При
помощи наиболее внимательных посетителей
сайта удалось найти неточность при
определении видимости плоскостей. Ниже
приведен чертеж, на котором исправлена
видимость линий, ограничивающих плоскости
на горизонтальной плоскости
17. Метод замены плоскостей проекций.
|
МЕТОД |
Изменение
взаимного положения изучаемого объекта
и плоскостей проекций достигается путем
замены одной из плоскостей П1 или П2 новой
плоскостями П4 (рис. 148). Новая
плоскость всегда выбирается перпендикулярно
оставшейся плоскости проекций.
Для
решения некоторых задач может потребоваться
двойная замены плоскостей проекций
(рис. 149).
Последовательный переход от одной
системы плоскостей проекций к другой
необходимо осуществлять, выполняя
следующее правило: расстояние
от новой проекции точки до новой
оси должно равняться расстоянию от
заменяемой проекции точки до заменяемой оси.
Задача
1:
Определить натуральную величину
отрезка АВ прямой
общего положений (рис. 148).
Из свойства параллельного проецирования
известно, что отрезок проецируется на
плоскость в натуральную величину, если
он параллелен этой плоскости.
Выберем
новую плоскость проекций П4,
параллельно отрезку АВ и
перпендикулярно плоскости П1.
Введением новой плоскости, переходим
из системы плоскостей П1П2 в
систему П1П4 ,
причем в новой системе плоскостей
проекция отрезка А4 В4 будет
натуральной величиной отрезка АВ.
|
|
|
||
|
а) |
б) |
||
|
Рисунок |
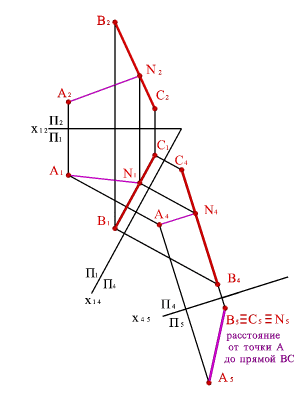
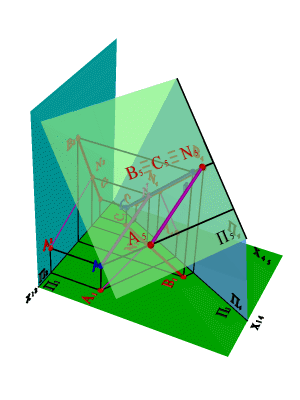
Задача
2:
Определить расстояние от точки А до
прямой общего положения, заданной
отрезком ВС (рис._149).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #