Комплексное сопротивление элемента (участка цепи)
Под комплексным сопротивлением понимают
отношения комплексной амплитуды входного
напряжения к комплексной амплитуде
входного тока:
 .
.
(1.6)
где Z
–модуль
комплексного сопротивления, φ=ψu
– ψi
– начальная фаза или аргумент комплексного
сопротивления; R
– активного
сопротивления, X–
реактивному сопротивлению, причем
Z=(R2+X2)1/2,
а φz(ω)=ψu–ψi
=arctg(X/R).
По виду записи
комплексного сопротивления можно судить
о характере участка цепи: Z=R
– активное (резистивное) сопротивление;
Z=R+jX —
активно-индуктивное сопротивление; Z=R
– j X —
активно-емкостное
![]() –
–
комплексная проводимость, величина,
обратная комплексному сопротивлению:
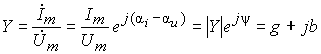
Метод комплексных амплитуд состоит
в следующем:
1) исходная
схема электрической цепи заменяется
комплексной схемой замещения, в которой:
а) все пассивные элементы заменяются
их комплексными сопротивлениями, как
показано на рис. 4.27.
б )
)
все токи и напряжения в схеме заменяются
их комплексными амплитудами, т.е.х(t) =Xm
cos(0t
– x) Xm
=Xm
e–jx.

R
ZR=R
C
ZC=1/(jC)
L
ZL=jL
Рис. 4.27
2 )
)
Расчет электрической цепи сводится к
составлению уравнений состояния цепи
на основе законов Ома и Кирхгофа в
комплексной форме и нахождениюкомплексных
амплитуд токов или напряжений на
интересующих нас участках цепи, т.е.Ym
= Ym
e–jy.
3) Запись окончательного решения состоит
в замене рассчитанных комплексных
амплитуд на гармонические функции
времени, т.е.
Y m=Ym
m=Ym
e –jy
y(t) =Ym
cos(0t – y).
Пример 5. Алгоритм
метода рассмотрим на примере анализа
цепи, структура которой приведена на
рис. 4.29.
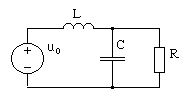
Рис. 4.29. RLC-цепь
второго порядка
На вход цепи
подается синусоидальное воздействие
![]() .
.
Параметры воздействия и элементов цепи
известны:Um=1
В, ω =1 с-1
, φ u=900
, R=1
Ом, L=1
Гн, C=1
Ф. Требуется определить токи и напряжения
ветвей, построить векторную диаграмму.
Решение.
-
Представим
воздействие в комплексной форме:
![]() .
.
-
Построим схему
замещения цепи в частотной области,
заменив элементы цепи комплексными
двухполюсниками, как это показано на
рис. 4.30.
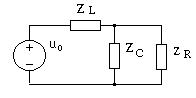
Рис. 4.30. Схема
замещения цепи в частотной области
3. Произведем расчет
реакций (токов и напряжений) в комплексной
области. При этом можно воспользоваться
законами Кирхгофа и Ома в комплексной
форме, а также известными методами
расчета резистивных цепей:
![]() ,
,
![]() ,
, ,
,
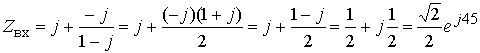 ,
,
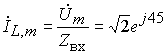 ,
,
![]() ,
,
![]() ,
,
 ,
,
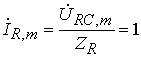 .
.
-
Построим векторную
диаграмму для токов и напряжений в
цепи. Для этого на комплексной плоскости
откладываются в соответствующем
масштабе найденные токи и напряжения,
как показано на рис. 4.31.

Рис. 4.31. Векторная
диаграмма
Построение
векторной диаграммы, как правило,
является конечным результатом решения
подобных задач. Векторная диаграмма
показывает амплитуду и начальную фазу
любого тока или напряжения. При
необходимости записать временную
функцию тока или напряжения, это всегда
можно сделать, имея векторную диаграмму.
Например, напряжение на L-элементе
имеет амплитуду
![]() ,
,
а начальную фазу 1350,
значит, во временной области это
напряжение можно записать так:
![]() .
.
Пример 2.
Активное сопротивление
катушки Rк=6
Ом, индуктивное Xl=10
Ом. Последовательно с катушкой включено
ативное сопротивление R=2Ом
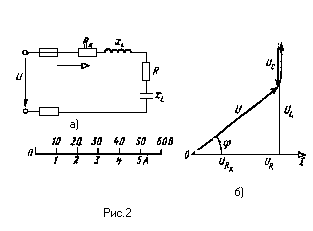
и конденсатор сопротивлением хс=4
Ом (рис.2,а). К цепи приложено напряжение
U=50В
( действующее значение). Определить :1)
полное сопротивление цепи;2)ток;3)коэффициент
мощности;4)активную, реактивную и полную
мощности;5) напряжения на каждом
сопротивлении. Начертите в масштабе
векторную диаграмму цепи.
Решение:
1.Определяем полное
сопротивление цепи
![]()
2.Определяем ток
![]()
3.Определяем
коэффициент мощности цепи
![]()
по таблицам Брадиса
находим =36050’
. Угол сдвига фаз
находим по синусу во избежание потери
знака угла ( косинус является четной
функцией)
4.Определяем
активную мощность цепи
![]()
или
![]()
Здесь
![]()
5.Определяем
реактивную мощность цепи
![]()
6.Определяем
активную мощность цепи
![]()
или
![]()
7.Определяем падение
напряжения на сопротивлениях цепи
![]() ;
;
![]() ;
;![]() ;
;
![]()
Построение векторной
диаграммы начинаем с выбора масштаба
для тока и напряжения. Задаемся масштабом
по току : в 1см – 1,0А и масштабом по
напряжению : 1см- 10В. Построение векторной
диаграмм ( рис.2,.б) начинаем с вектора
тока, который откладываем по горизонтали
в масштабе
Вдоль вектора тока
откладываем векторы падения напряжения
на активных сопротивления URк
и UR:
Из конца вектора
UR
откладываем
в сторону опережения вектора тока на
900
вектор падения напряжения UL
на индуктивном сопротивлении длиной
![]() .Из
.Из
конца вектораUI
откладываем в сторону отставания от
вектора тока на 900
вектор падения напряжения на конденсаторе
UC
длиной
![]()
![]() .
.
Геометрическая сумма векторовURк,
UR,
UL
и UC
равна полному напряжению U,
приложенному к цепи .
Пример 3.
На рис. 3,а задана
векторная диаграмма для неразветвленной
цепи, ток I
и падения напряжений на каждом
сопротивлении ( U1,
U2
и т.д.) Определить характер и величину
каждого сопротивления, начертить
эквивалентную схему цепи, вычислить
приложенное напряжение и угол сдвига
фаз .

Решение:
1.Из векторной
диаграммы следует, что напряжение U1
отстает от тока на угол 900.
Следовательно, на первом участке
включен конденсатор, сопротивление
которого
![]()
Вектор напряжение
на втором участке U2
направлен параллельно вектору тока,
т.е. совпадает с ним по фазе. Значит, на
втором участке включено активное
сопротивление
![]()
Вектор напряжения
на третьем участке U3
опережает вектор тока на угол 900,
что характерно для индуктивности,
сопротивление которой
![]()
На четвертом
участке включено активное сопротивление
![]()
Эквивалентная
схема цепи приведена на рис. 3, б.
2.Из векторной
диаграммы определяем значение приложенного
напряжения и угол сдвига фаз:
![]() .
.
Пример:
К электрической
цепи, рис. 3.12, а, подведено синусоидальное
напряжение частотой f
= 50 Гц с действующим значением U
= 100 В. Параметры элементов схемы: R1
= 30 Ом, L
= 0,1 Гн, C
= 50 мкФ, R2
= 20 Ом. Определить токи в ветвях схемы и
показания приборов. Составить баланс
мощности. Построить в масштабе векторную
диаграмму токов и напряжения.
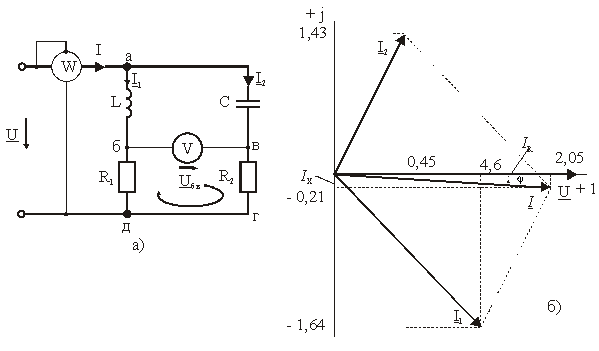
Рис.
3.12 – Параллельная цепь:
а) схема
замещения; б) векторная диаграмма
Решение
Определяем
комплексные сопротивления параллельных
ветвей. Сопротивление первой ветви
Z1
= R1
+ jXL,
где
XL
= jωL
= 2πfL
= 6,28∙50∙0,1 = 31,4 Ом;
Z1
= 30 + j31,4
Ом.
Комплексное
сопротивление второй ветви
Z2
= R2
– jXС;
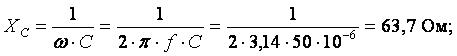
Z2
= 20 – j63,7
Ом.
Находим комплексные
значения токов в ветвях
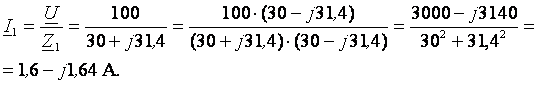

I
= I1
+ I2
= 1,6 – j1,64
+ 0,45 + j1,43
= 2,05 – j0,21
A.
Действующие
значения
![]()
![]()
![]()
Для определения
показания вольтметра составляем
уравнение согласно второго закона
Кирхгофа для контура б, в, г, д, б.
Произвольно выбираем направление обходе
контура, показанное на рис. 3.12, а стрелкой
0 = Uбв
+ R2I2
– R1I1;
1. . Uбв
= R2I2
– R1I1
= 20·(0,45 + j1,43)
– 30(1,6 – j1,64)
=
= 9 + j28,6
– 48 + j49,2
= – 39 + j77,8;
Uбв
= 39 – j77,8
В.
Вольтметр покажет
действующее значение напряжения Uбв
![]()
Ваттметр измеряет
мощность, потребляемую активной нагрузкой
(R1
и R2).
Известно, что
Р
= U·I·cosφ.
В этом выражении
неизвестным является cosφ,
где φ
угол сдвига между напряжением U
и током I.
Определить угол φ
(или cosφ)
можно разными путями. Например, cosφ
можно найти из выражения для общего
тока, учитывая, что начальная фаза
напряжения равна нулю. Для этого обратимся
к комплексному значению общего тока
I
= 2,05 – j0,21
A,
где IR
= 2,05 – активная составляющая тока
(проекция комплексного вектора полного
тока на ось действительных чисел);
IX
= – j0,21
– реактивная составляющая тока (проекция
комплексного вектора полного тока на
ось мнимых чисел).
Тогда

где I
= 2,06 А – действующее значение общего
тока.
Показание ваттметра
Р
= 100∙2,06∙0,995 = 205 Вт.
Составим баланс
мощностей.
Полная мощность,
поступающая от источника
![]()
где PИ
= 205 Вт; QИ
= 21 Вар.
Мощности приёмников
![]()
![]()
SП
= РП
+ jQП
= 205 + j21,34
ВА.
Результаты расчётов
показывают, что баланс мощности сходится,
т. е. токи найдены правильно.
Векторную диаграмму
строим на комплексной плоскости, рис.
3.12, б. Выбираем масштабы тока и напряжения:
![]() (Масштаб
(Масштаб
выбирается с таким расчётом, чтобы
векторная диаграмма занимала примерно
половину страницы). Откладываем вектор
напряжения совпадающий с осью+1.
Затем откладываем вычисленные значения
токов I1,
I2,
I.
Действительные значения – на оси +1,
мнимые значения – на оси +j.
Контрольные
вопросы к экзамену (зачету)
Контрольные вопросы к зачету
(экзамену ) по разделу “Основы
электротехники”.
1. Электробезопасность.
Характеристики поражения человека
электрическим током.
2. Основные определения: электротехника,
электричество, электрическое поле,
потенциал, напряжение, электрический
ток, источники тока , электродвижущая
сила (ЭДС), закон Ома , законы Кирхгофа.
3. Электрическая цепь. Пассивные и
активные элементы цепи. Параметры
электрической цепи.
4. Расчет электрических
цепей постоянного тока методом законов
Кирхгофа, методом контурных токов.
5. Энергия и мощность
постоянного тока. Баланс мощностей.
6. Переменный ток. Однофазный синусоидальный
ток. Основные параметры: мгновенные,
действующие и средние значения тока,
напряжения и ЭДС. Генерирование
переменного тока.
7. Представление переменного тока
комплексными величинами. Метод комплексных
диаграмм.
8. Метод комплексных амплитуд.
Закон Ома и законы Кирхгофа в комплексной
форме.
9. Активное сопротивление,
индуктивность и емкость в цепи переменного
тока.
10. Последовательная и разветвленные
цепи переменного тока с активным
сопротивлением, емкостью и индуктивностью.
Резонанс тока. Резонанс напряжения.
11.Мощность и энергия в цепи переменного
тока. Активная, реактивная и полная
мощность. Единицы измерения. Баланс
мощностей.
12.Трехфазные электрические цепи. Основные
определения. Линейные и фазные токи и
напряжения. Маркировка фазы. Способы
соединения генераторов и приемников
типа звезда и треугольник. Трехпроводные
и четырехпроводные цепи. Нейтральный
провод.
13. Короткое замыкание фазы. Разрыв
линейного провода. Мощность в цепи
трехфазного тока.
14. Нелинейные электрические цепи.
Аппроксимация нелинейных характеристик.
15. Расчет цепей постоянного тока с одним
или несколькими нелинейными элементами.
16. Основные магнитные величины. Магнитные
цепи постоянного тока.
17. Магнитные цепи переменного тока.
Ферромагнитные материалы.
18. Расчет катушки с магнитопроводом и
воздушным зазором.
19. Энергия и основные потери в
магнитопроводе.
20 Трансформатор. Основные режимы работы.
21. Устройство и принцип действия машин
постоянного тока.
22. Генератор постоянного тока. Основные
характеристики.
23.Двигатель постоянного тока. Основные
характеристики.
24.Устройство и принцип действия машины
переменного тока.
25. Асинхронный двигатель. Основные
характеристики.
26. Синхронный генератор. Основные
характеристики.
Темы
рефератов.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Самостоятельная работа студентов
состоит в изучении ряда теоретических
вопросов по темам дисциплины, перечень
которых приведен в таблице 5 и составления
рефератов..
Таблица 5
|
№ п/п |
Тема |
|
1 |
2 |
|
1 |
Тема 1. Основные |
|
2 |
Тема 2. Методы расчета линейных |
|
3 |
Тема З. Однофазный переменный ток |
|
4 |
Тема |
|
5 |
Тема 5. Магнитные цепи и электромагнитные |
|
6 |
Тема 6. Трансформаторы |
|
7 |
Тема 7. Асинхронные машины |
|
8 |
Тема 8. Машины постоянного тока (МПТ) |
|
9 |
Тема 9. Синхронные машины |
|
10 |
Тема 10. Электрические измерения и |
|
11 |
Тема 11. Основы электроники и элементной |
|
12 |
Тема 12. Источники вторичного |
|
13 |
Тема 13. Усилители электрических |
|
14 |
Тема 14. Импульсные и автогенераторные |
|
15 |
Тема 15. Основы цифровой электроники |
|
16 |
Тема 16. Микропроцессорные средства |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое комплексное сопротивление или импеданс
Содержание
- 1 Что такое импеданс и его составляющие
- 2 Последовательность расчета компонентов импеданса
- 3 Определение импеданса
- 4 Видео по теме
Электрический импеданс — это термин, относящийся к цепям переменного тока. Слово происходит от латинского impedіо (сопротивляться). Расчёт комплексного сопротивления или импеданса представляет собой важный этап разработки различных электрических и электронных устройств.

Электронные устройства, требующие определения импеданса
Что такое импеданс и его составляющие
Импеданс электрических цепей — это векторная (двумерная) величина, состоящая из двух независимых скалярных (одномерных) компонентов: активного и реактивного сопротивления. Он обозначается буквой Z и выражает противодействие, которое электронный элемент, схема или система оказывает переменному электротоку. Измеряется в омах.

Виды сопротивлений в электроцепи
Активное сопротивление (R) является мерой интенсивности противодействия движению электронов между атомами. Чем легче атомы отдают/принимают электроны, тем ниже этот параметр, выражающийся в положительных действительных числах. Реактивное сопротивление, обозначаемое буквой Х, представляет собой выражение степени, с которой электронный компонент, схема или система накапливает или высвобождает энергию при колебаниях тока и напряжения за каждый единичный цикл переменного тока. Импедансом часто называют модуль комплексного сопротивления, поэтому реактивное сопротивление выражается в так называемых «мнимых» омах. Оно характерно только для линий переменного тока.
Когда переменный электроток проходит через катушку индуктивности, накапливаемая энергия высвобождается в виде магнитного поля. В этом случае реактивная составляющая импеданса является индуктивной (обозначается +jXL). Чем быстрее меняется направление тока, тем ХL больше.
Однако энергия может запасаться и высвобождаться в виде электрического поля, тогда данный параметр будет емкостным (обозначается –jXC ). Когда ток меняет направление, конденсатор многократно заряжается и разряжается. Чем больше времени конденсатор заряжается, тем сильнее он противодействует электротоку. Поэтому чем быстрее меняется направление электротока, тем ниже емкостное сопротивление.
Реактивное сопротивление обычно умножается на положительный квадратный корень из –1, который представляет собой единичное мнимое число j. Тогда комплексное сопротивление Z выражается как R + jXL или R – jXC. Следовательно, активное сопротивление R — это действительная часть комплексного импеданса, а реактивное Х — мнимая.

Графическая интерпретация составляющих импеданса
Левая половина координатной плоскости, представленной на рисунке выше, обычно не используется, поскольку на практике отрицательные сопротивления не встречаются. Индуктивное сопротивление указывается на положительной части линии мнимой оси, а ёмкостное — на отрицательной части линии.
Комплексное электрическое сопротивление фаз может быть определено как отношение электронапряжения к амплитуде электротока, что идентично закону Ома. Фаза импеданса является фазовым сдвигом, соответствующим отставанию электротока от электронапряжения.
Последовательность расчета компонентов импеданса
Найти импеданс или полное сопротивление последовательной цепи довольно просто, если в ней присутствует только какой-то один вид элементов. Импеданс идеального резистора соответствует его активному сопротивлению R, которое называется еще резистивным. Импеданс для катушки индуктивности — это мнимое реактивное сопротивление XL, а для конденсатора —ХС.
Если имеется активное сопротивление и один тип реактивного, тогда вычисления выполняются по формуле:

Формула импеданса при наличии активного и одного вида реактивного сопротивления
При наличии всех составляющих полное сопротивление или импеданс находим с помощью такого выражения:

Формула импеданса при наличии всех видов сопротивления в электроцепи
Таким образом, комплексное входное сопротивление цепи выражается как R + jX, где j — мнимое число √(–1).

Векторная диаграмма импеданса
Для расчетов всех составляющих импеданса используются формулы:

Формулы для расчета составляющих импеданса
Комплексное сопротивление и проводимости участков характеризуют замедление тока, которое связано с влиянием материала и формой резистора. Реактивное сопротивление X — это замедление тока из-за электрических и магнитных полей, противодействующих изменениям тока или напряжения. Этот параметр важен для конденсаторов и катушек индуктивности.

Импеданс в цепи переменного электротока
Определение импеданса
Рассчитать импеданс проще всего, если в цепи есть n резисторов, но нет катушек индуктивности или конденсаторов. Сначала измеряется сопротивление на каждом резисторе (или любом аналогичном компоненте). Найденные значения суммируются, если элементы соединены последовательно: R = R1 + R2 + … + Rn.
Результирующая величина для n резисторов, включённых параллельно, определяется следующим образом: 1/R = 1/R1 + 1/R2 + … + 1/Rn.
Если в цепи есть только индуктивная нагрузка или емкостная, импеданс будет соответствовать реактивному сопротивлению:
- Для последовательно соединенных катушек индуктивности X = XL1+ XL2 + …
- Для последовательно соединенных конденсаторов C =XC1 + XC2 + …
- Для катушек индуктивности, соединенных параллельно X = 1/(1/XL1+ 1/XL2 …)
- Для конденсаторов, соединенных параллельно: C = 1/(1/XC1+ 1/XC2 …)
С ростом частоты электротока сопротивление индуктивностей увеличивается, а конденсаторов уменьшается. Поэтому при их совместном использовании в электрической линии они уравновешивают друг друга. Чтобы найти общее реактивное сопротивление, надо вычесть одно значение из другого: X = |XC – XL|.
Величину импеданса можно вычислить для любой электроцепи переменного тока, состоящей из таких линейных пассивных элементов, как резисторы, индуктивности и конденсаторы. Для электроцепи с постоянным током не существует различия между импедансом и сопротивлением. Последний параметр можно рассматривать как импеданс, фазовый угол которого равняется нулю.
Видео по теме
Содержание:
Частотные характеристики линейных электрических цепей:
Задача анализа электрической цепи была сформулирована ранее как задача определения реакции цепи на заданное внешнее воздействие. Пусть для некоторой линейной электрической цепи это воздействие задано в виде токов и напряжений нескольких независимых источников тока и напряжения, а искомая реакция (отклик) цепи представляет собой совокупность токов или напряжений отдельных элементов (нагрузок). Вынесем из рассматриваемой цепи все ветви, содержащие независимые источники тока и напряжения, а также ветви, токи или напряжения которых подлежат определению. Оставшуюся часть цепи, содержащую идеализированные пассивные элементы и, возможно, управляемые источники, представим в виде многополюсника (рис. 3.1,а).
Уточним понятия входов и выходов цепи. Входными будем называть пару зажимов (полюсов), к которым подключается каждый из независимых источников, задающих внешнее воздействие на цепь. Зажимы, служащие для подключения нагрузки, т. е. ветви, ток или напряжение которой необходимо определить, назовем выходными. Пары входных и выходных зажимов образуют соответственно входы и выходы цепи, точнее, входы и выходы многополюсника, который получается из цепи при вынесении из нее источников внешнего воздействия и нагрузок. Деление зажимов на входные и выходные является в некоторой степени условным, так как одна и та же пара зажимов может одновременно быть и входной, и выходной (например, когда внешнее воздействие на цепь задается некоторым независимым источником напряжения и требуется определить ток ветви, содержащей этот источник). В связи с этим наряду с понятиями входа и выхода в теории цепей широко используется понятие стороны многополюсника.
Стороной многополюсника, или портом, называется пара зажимов, которые служат либо входом, либо выходом, либо и входом и выходом одновременно.
Из определений входных и выходных зажимов следуют важные особенности зажимов, образующих порт многополюсника:
- ток, втекающий через один зажим порта, равен току, вытекающему через другой зажим этого же порта
- между парами полюсов, принадлежащих к разным портам, не должно быть никаких внешних по отношению к многополюснику соединений (внутри многополюсника соединения, естественно могут быть).
Зажимы, образующие одну сторону многополюсника, будем обозначать одинаковыми цифрами (со штрихом и без штриха) 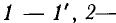
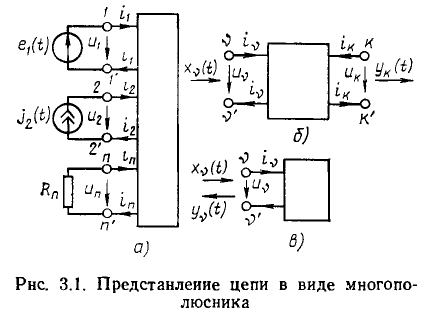
Пусть внешнее воздействие на цепь задано только на одной паре полюсов 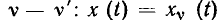 и необходимо найти реакцию цепи также только на одной паре полюсов k — k’ (рис. 3.1, б):
и необходимо найти реакцию цепи также только на одной паре полюсов k — k’ (рис. 3.1, б): 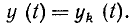 Поскольку процессы на остальных полюсах в данном случае интереса не представляют, их можно не выделять из цепи. Исследуемую цепь удобно рассматривать как двусторонний четырехполюсник. Если v = k, то исследуемая цепь становится односторонней, т. е. превращается в двухполюсник (рис. 3.1, в).
Поскольку процессы на остальных полюсах в данном случае интереса не представляют, их можно не выделять из цепи. Исследуемую цепь удобно рассматривать как двусторонний четырехполюсник. Если v = k, то исследуемая цепь становится односторонней, т. е. превращается в двухполюсник (рис. 3.1, в).
Ограничимся рассмотрением случая гармонического внешнего воздействия; при этом от исследования соотношений между мгновенными значениями реакции цепи 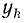 (t) и внешнего воздействия
(t) и внешнего воздействия 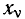 (f) можно перейти к исследованию соотношений между их комплексными изображениями.
(f) можно перейти к исследованию соотношений между их комплексными изображениями.
По определению, комплексной частотной характеристикой цепи называется отношение комплексных изображений отклика и воздействия:
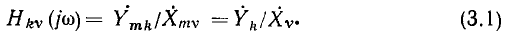
Здесь 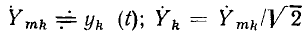 — комплексные амплитуда и действующее значение реакции цепи;
— комплексные амплитуда и действующее значение реакции цепи; 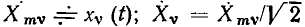 — комплексные амплитуда и действующее значение внешнего воздействия; k — номер выходных зажимов; v — номер входных зажимов.
— комплексные амплитуда и действующее значение внешнего воздействия; k — номер выходных зажимов; v — номер входных зажимов.
Размерность комплексной частотной характеристики (КЧХ) равна отношению размерностей отклика цепи и внешнего воздействия. В зависимости от того, какие величины (токи или напряжения) рассматриваются в качестве откликов и внешних воздействий, КЧХ может иметь размерность сопротивления (внешнее воздействие — 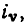 реакция цепи —
реакция цепи — 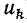 ), проводимости (внешнее воздействие —
), проводимости (внешнее воздействие — 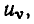 реакция цепи –
реакция цепи – 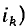 или быть безразмерной (внешнее воздействие —
или быть безразмерной (внешнее воздействие — 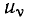 и реакция цепи —
и реакция цепи — 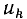 либо внешнее воздействие —
либо внешнее воздействие — 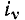 и реакция цепи —
и реакция цепи — 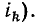
Как и всякое комплексное число, КЧХ цепи может быть записана в показательной
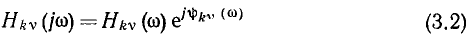
или в алгебраической
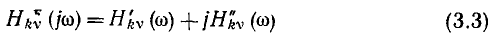
форма. Представляя комплексные изображения отклика и воздействия в показательной форме
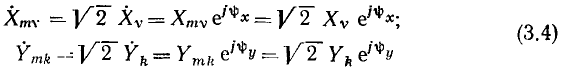
и подставляя (3.4) в выражение (3.1), определяем модуль и аргумент КЧХ:
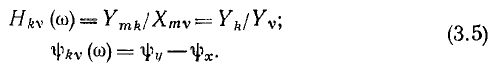
Таким образом, модуль КЧХ равен отношению амплитуд или действующих значений отклика цепи и внешнего воздействия, а ее аргумент представляет собой разность начальных фаз отклика и внешнего воздействия.
Если 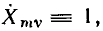 КЧХ определяется выражением
КЧХ определяется выражением
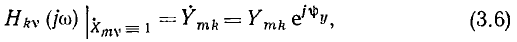
следовательно, КЧХ цепи численно равна комплексной амплитуде реакции цепи на внешнее воздействие с единичной амплитудой и нулевой начальной фазой.
Зависимости модуля 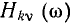 и аргумента
и аргумента 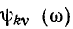 комплексной частотной характеристики от частоты
комплексной частотной характеристики от частоты 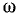 называются амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками цепи. Из сравнения выражений (3.2) и (3.6) видно, что АЧХ и ФЧХ цепи характеризуют зависимости от частоты соответственно амплитуды и начальной фазы отклика цепи на внешнее воздействие с
называются амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками цепи. Из сравнения выражений (3.2) и (3.6) видно, что АЧХ и ФЧХ цепи характеризуют зависимости от частоты соответственно амплитуды и начальной фазы отклика цепи на внешнее воздействие с 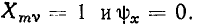 Таким образом, КЧХ сочетает в себе амплитудно-частотную и фазо-частотную характеристики цепи.
Таким образом, КЧХ сочетает в себе амплитудно-частотную и фазо-частотную характеристики цепи.
При графическом представлении комплексных частотных характеристик цепи обычно строят либо отдельно АЧХ и ФЧХ, либо изображают зависимости от частоты вещественной 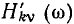 и мнимой
и мнимой 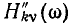 составляющих КЧХ, которые однозначно выражаются через
составляющих КЧХ, которые однозначно выражаются через 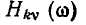 и
и 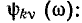
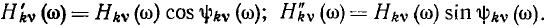
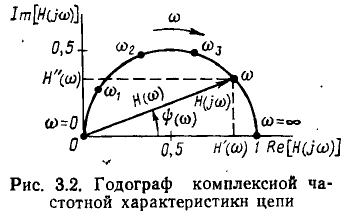
Комплексную частотную характеристику можно изобразить и в виде одной зависимости — годографа КЧХ, построенного на комплексной плоскости. Годограф КЧХ представляет собой геометрическое место концов вектора 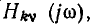 соответствующих изменению часто
соответствующих изменению часто
ты от 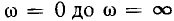 (рис. 3.2). На годографе указывают точки, соответствующие некоторым значениям частоты
(рис. 3.2). На годографе указывают точки, соответствующие некоторым значениям частоты 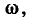 и стрелкой показывают направление перемещения конца вектора
и стрелкой показывают направление перемещения конца вектора 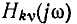 при увеличении частоты. Как видно из рисунка, годограф КЧХ позволяет одновременно судить как об АЧХ и ФЧХ, так и о зависимости вещественной
при увеличении частоты. Как видно из рисунка, годограф КЧХ позволяет одновременно судить как об АЧХ и ФЧХ, так и о зависимости вещественной 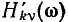 и мнимой
и мнимой 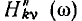 составляющих КЧХ от частоты. Годограф КЧХ иногда называют амплитудно-фазовой характеристикой цепи.
составляющих КЧХ от частоты. Годограф КЧХ иногда называют амплитудно-фазовой характеристикой цепи.
Комплексные частотные характеристики цепи делятся на входные и передаточные. Когда отклик и внешнее воздействие рассматриваются (см. рис. 3.1, в), КЧХ называется входной. Если отклик и внешнее воздействие задаются на разных зажимах цепи (см. рис. 3.1, б), КЧХ называется передаточной. Различают два вида входных и четыре вида передаточных характеристик.
Если внешнее воздействие на цепь является током 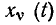
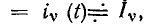 а реакция — напряжением
а реакция — напряжением 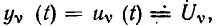 to КЧХ цепи представляет собой комплексное входное сопротивление цепи относительно зажимов
to КЧХ цепи представляет собой комплексное входное сопротивление цепи относительно зажимов 
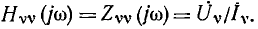
К входным характеристикам цепи относится также комплексная входная проводимость
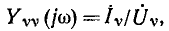
при этом внешнее воздействие — напряжение 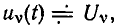 а реакция — ток
а реакция — ток 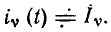
К передаточным характеристикам цепи относятся: комплексный коэффициент передачи по напряжению
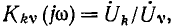
комплексный коэффициент передачи по току
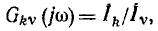
комплексное передаточное сопротивление
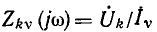
и комплексная передаточная проводимость
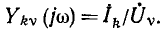
Очевидно, что комплексное входное сопротивление 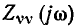 и комплексное передаточное сопротивление
и комплексное передаточное сопротивление 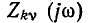 имеют размерность сопротивления, комплексная входная проводимость
имеют размерность сопротивления, комплексная входная проводимость 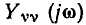 и комплексная передаточная проводимость
и комплексная передаточная проводимость 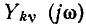 — размерность проводимости. Комплексные коэффициенты передачи по току
— размерность проводимости. Комплексные коэффициенты передачи по току 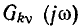 и напряжению
и напряжению 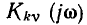 являются безразмерными величинами.
являются безразмерными величинами.
В дальнейшем будет показано, что КЧХ линейных цепей не зависят от амплитуды и начальной фазы внешнего воздействия, а определяются структурой цепи и параметрами входящих в нее элементов. Знание КЧХ позволяет определить реакцию цепи 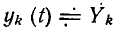 на заданное гармоническое воздействие
на заданное гармоническое воздействие 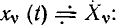
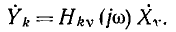
В общем случае каждая линейная цепь характеризуется большим числом комплексных частотных характеристик, так как любая из рассмотренных разновидностей КЧХ может быть определена для различных сочетаний пар входных и выходных зажимов и при различных значениях сопротивлений нагрузки.
Комплексные частотные характеристики идеализированных двухполюсных пассивных элементов
Идеализированные двухполюсные пассивные элементы обладают только входными КЧХ. В связи с этим у них имеется только одна пара внешних выводов, нумеровать выводы в обозначениях КЧХ не будем.
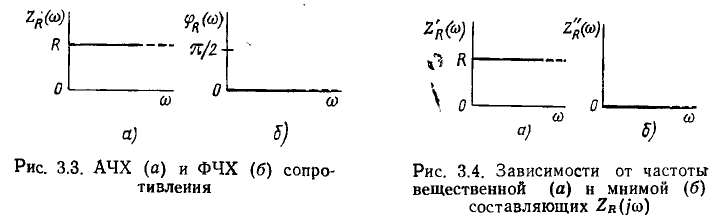
Сопротивление. Комплексное входное сопротивление этого элемента определяется выражением 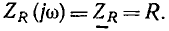
Модуль комплексного входного сопротивления 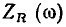 и его аргумент
и его аргумент 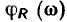 не зависят от частоты:
не зависят от частоты:
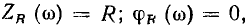
в связи с чем АЧХ и ФЧХ комплексного входного сопротивления имеют вид прямых линий с постоянной ординатой (рис. 3.3, а, б). Зависимости от частоты вещественной и мнимой составляющих комплексного входного сопротивления
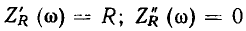
представлены на рис. 3.4. Поскольку 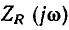 не зависит от частоты, годограф входного сопротивления вырождается в точку на комплексной плоскости (рис. 3.5).
не зависит от частоты, годограф входного сопротивления вырождается в точку на комплексной плоскости (рис. 3.5).
Индуктивность. Из выражения для комплексного входного сопротивления индуктивности 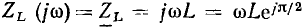 можно найти модуль комплексного входного сопротивления
можно найти модуль комплексного входного сопротивления 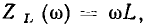 его аргумент
его аргумент 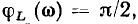 а также вещественную
а также вещественную 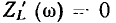 и мнимую
и мнимую 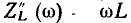 составляющие (рис. 3.6).
составляющие (рис. 3.6).

Из амплитудно-частотной и фазо-частотной характеристик входного сопротивления индуктивности (рис. 3.7) видно, что модуль входного сопротивления индуктивности линейно возрастает с ростом частоты, а аргумент равен 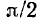 и не зависит от частоты. Так как комплексное
и не зависит от частоты. Так как комплексное
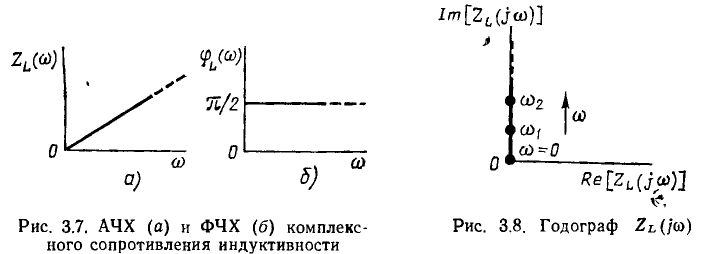
входное сопротивление индуктивности является чисто мнимой величиной, то при изменении частоты конец вектора 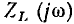 перемещается вдоль мнимой оси (рис. 3.8).
перемещается вдоль мнимой оси (рис. 3.8).
Емкость. Комплексное входное сопротивление емкости, как известно, определяется выражением
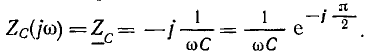
Отсюда можно определить модуль 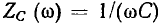 и аргумент
и аргумент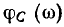
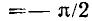 комплексного входного сопротивления емкости, а также его вещественную
комплексного входного сопротивления емкости, а также его вещественную 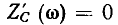 и мнимую
и мнимую 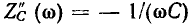 составляющие.
составляющие.
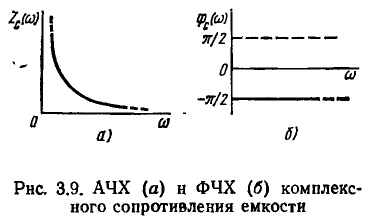
Как видно из рис. 3.9, с увеличением частоты модуль входного сопротивления уменьшается и равен нулю при  Аргумент комплексного входного сопротивления емкости равен –
Аргумент комплексного входного сопротивления емкости равен – 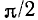 и от частоты не зависит. Зависимости
и от частоты не зависит. Зависимости 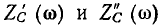 от частоты приведены на рис. 3.10, годограф
от частоты приведены на рис. 3.10, годограф 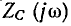 изображен на рис. 3.11.
изображен на рис. 3.11.
Аналогичным образом можно построить и частотные характеристики комплексной входной проводимости идеализированных пассивных элементов, причем в связи с тем, что емкость и индуктивность являются дуальными элементами, КЧХ входной проводимости индуктивности
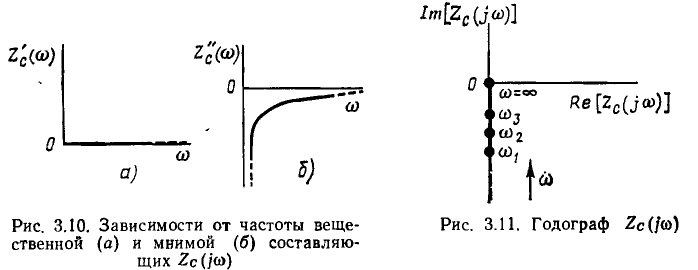
имеют такой же вид, что и КЧХ входного сопротивления емкости (см. рис. 3.9 — 3.11), а КЧХ входной проводимости емкости — такой же вид, как и КЧХ входного сопротивления индуктивности Гем. рис. 3.6— 3.8).
Комплексные частотные характеристики цепей с одним энергоемким элементом
Рассмотрим комплексные частотные характеристики простейших цепей (рис. 3.12, а, б), являющихся двусторонними и поэтому обладающими как входными, так и передаточными характеристиками. Обобщенная комплексная схема замещения этих цепей приведена на рис. 3.12, в.
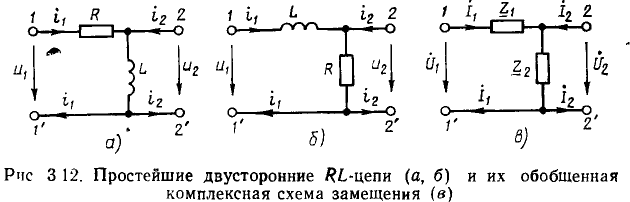
Комплексное входное сопротивление цепей со стороны зажимов 1— 1′ (2 — 2′) зависит от сопротивления нагрузки, подключенного к зажимам 2— 2′ (1 — 1′). Наиболее интересны случаи, когда сопротивление нагрузки равно нулю (режим короткого замыкания) или когда сопротивление нагрузки бесконечно велико (режим холостого хода). При холостом ходе на зажимах 2 — 2′ 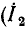 = 0) входное сопротивление цепей со стороны зажимов 1— 1′
= 0) входное сопротивление цепей со стороны зажимов 1— 1′
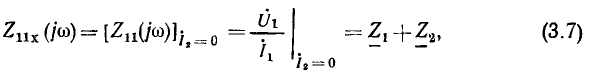
при коротком замыкании 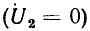
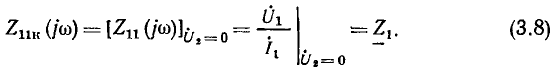
При холостом ходе со стороны зажимов 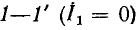 входное сопротивление со стороны зажимов
входное сопротивление со стороны зажимов 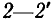
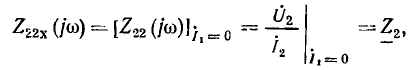
при коротком замыкании 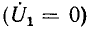
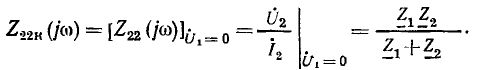
Комплексный коэффициент передачи цепи по напряжению от зажимов 1 — 1′ к зажимам 2— 2′ зависит от сопротивления нагрузки со стороны зажимов 2 — 2′. В режиме холостого хода на зажимах 2 — 2′ через сопротивления протекает один и тот же ток
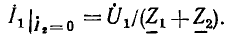
Напряжение, приложенное к зажимам 1 — 1′, распределяется между сопротивлениями 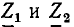 пропорционально значениям
пропорционально значениям 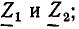 напряжение на зажимах 2 — 2′ при этом
напряжение на зажимах 2 — 2′ при этом
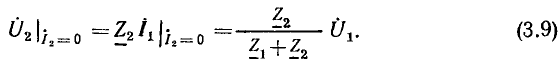
Цепи такого типа получили название делителей напряжения. Используя выражение (3.9), найдем коэффициент передачи цепей по напряжению от зажимов 1 — 1′ к зажимам 2—2′ в режиме холостого хода 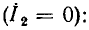
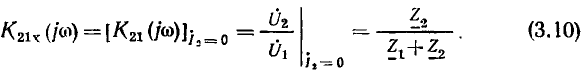
В режиме холостого хода на зажимах 1 — 1′ коэффициент передачи рассматриваемых цепей по напряжению от зажим ов 2—2′ к зажимам 1 — 1′
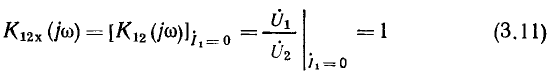
и не зависит от частоты внешнего воздействия. Подставляя в полученные выражения значения сопротивлений плеч делителя 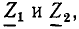 можно построить АЧХ и ФЧХ рассматриваемых цепей.
можно построить АЧХ и ФЧХ рассматриваемых цепей.
Определим в качестве примера комплексное входное сопротивление со стороны зажимов 1 — 1′ и комплексный коэффициент передачи от зажимов 1 — 1′ к зажимам 2—2′ в режиме холостого хода на выходе цепи, схема которой приведена на рис. 3.12, а. Подставляя в выражение (3.7) 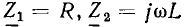 и выполняя преобразования
и выполняя преобразования
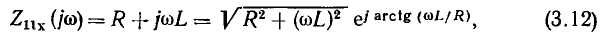
найдем аналитические выражения для АЧХ и ФЧХ входного сопротивления:
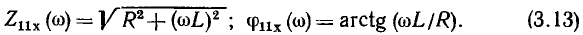
Непосредственное использование выражений (3.13) для построения АЧХ и ФЧХ весьма неудобно, так как для каждой пары значений параметров R и L необходимо строить отдельную кривую. Построение существенно упрощается при замене абсолютных значений частоты 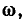 комплексного сопротивления
комплексного сопротивления 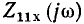 и полного сопротивления
и полного сопротивления 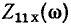 относительными (нормированными) значениями
относительными (нормированными) значениями
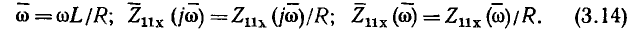
Из выражений (3.14) видно, что нормированная частота 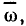 нормированное комплексное сопротивление
нормированное комплексное сопротивление 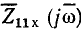 и нормированное полное сопротивление
и нормированное полное сопротивление 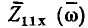 являются безразмерными величинами. С учетом (3.14) найдем выражения для нормированных АЧХ и ФЧХ входного сопротивления рассматриваемой цепи (рис. 3.13):
являются безразмерными величинами. С учетом (3.14) найдем выражения для нормированных АЧХ и ФЧХ входного сопротивления рассматриваемой цепи (рис. 3.13):
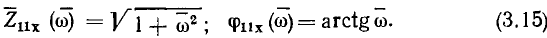
Годограф нормированного комплексного сопротивления этой цепи изображен на рис. 3.14.
Аналогичный вид имеют нормированные частотные характеристики входного сопротивления цепи, схема которой изображена на рис. 3.12, б.
Анализ полученных результатов показывает, что в области сравнительно низких частот, когда полное сопротивление индуктивности мало по сравнению с R 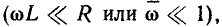 входные сопротивления цепей (см. рис. 3.12, а, б) определяются только значением R. Сопротивление индуктивности постоянному току равно нулю, поэтому на нулевой частоте входное сопротивление цепей имеет чисто резистивный характер
входные сопротивления цепей (см. рис. 3.12, а, б) определяются только значением R. Сопротивление индуктивности постоянному току равно нулю, поэтому на нулевой частоте входное сопротивление цепей имеет чисто резистивный характер
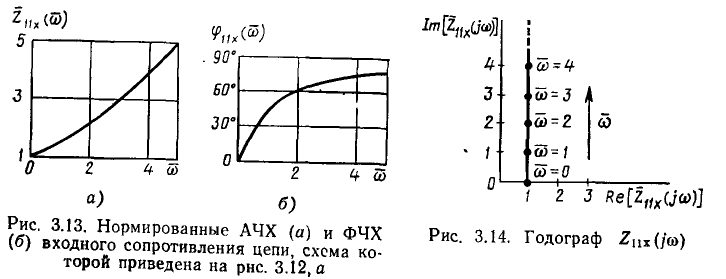
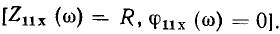 С ростом частоты модуль и аргумент входного сопротивления плавно увеличиваются, причем на достаточно высоких частотах
С ростом частоты модуль и аргумент входного сопротивления плавно увеличиваются, причем на достаточно высоких частотах 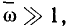 входное сопротивление цепи определяется только сопротивлением индуктивности
входное сопротивление цепи определяется только сопротивлением индуктивности 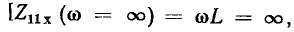
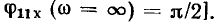
Рассмотрим частотные характеристики коэффициента передачи по напряжению 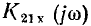 цепи, схема схема которой изображена на рис. 3.12, а. Подставляя в (3.10)
цепи, схема схема которой изображена на рис. 3.12, а. Подставляя в (3.10) 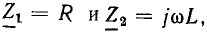 получаем
получаем
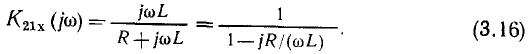
Переходя в (3.16) к показательной форме записи, находим аналитические выражения для АЧХ и ФЧХ коэффициента передачи цепи по напряжению (рис. 3.15):
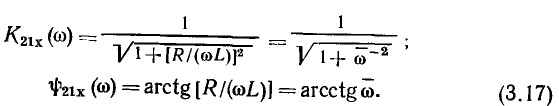
Годограф комплексного коэффициента передачи цепи по напряжению изображен на рис. 3.16.
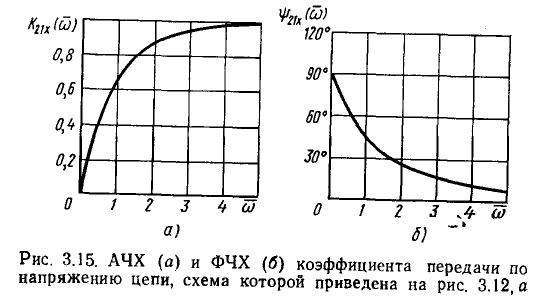
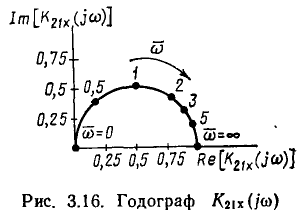
На сравнительно низких частотах 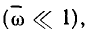 когда полное сопротивление индуктивности существенно меньше R, входное сопротивление цепи имеет характер, близкий к чисто резистивному, а входной ток цепи
когда полное сопротивление индуктивности существенно меньше R, входное сопротивление цепи имеет характер, близкий к чисто резистивному, а входной ток цепи 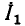 совпадает по фазе с напряжением
совпадает по фазе с напряжением 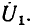 Распределение напряжения между плечами делителя напряжения пропорционально сопротивлению этих плеч, поэтому падение напряжения на индуктивности
Распределение напряжения между плечами делителя напряжения пропорционально сопротивлению этих плеч, поэтому падение напряжения на индуктивности 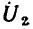 весьма мало, т. е. модуль коэффициента передачи по напряжению близок к нулю. Напряжение на индуктивности
весьма мало, т. е. модуль коэффициента передачи по напряжению близок к нулю. Напряжение на индуктивности 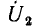 опережает по фазе ток индуктивности
опережает по фазе ток индуктивности 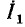 , а следовательно, и входное напряжение
, а следовательно, и входное напряжение 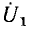 на угол, близкий к
на угол, близкий к 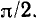 С ростом частоты сопротивление индуктивности увеличивается и вследствие этого распределение напряжений между плечами делителя изменяется. На достаточно высоких частотах
С ростом частоты сопротивление индуктивности увеличивается и вследствие этого распределение напряжений между плечами делителя изменяется. На достаточно высоких частотах 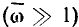 практически все входное напряжение оказывается приложенным к индуктивности, поэтому модуль коэффициента передачи по напряжению
практически все входное напряжение оказывается приложенным к индуктивности, поэтому модуль коэффициента передачи по напряжению 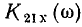 в этом случае близок к единице, а аргумент
в этом случае близок к единице, а аргумент 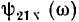 — к нулю.
— к нулю.
Понятие о резонансе в электрических цепях
Амплитудно-частотные характеристики пассивных линейных цепей с одним реактивным элементом имеют вид монотонно изменяющихся кривых, поэтому амплитуда отклика таких цепей также монотонно изменяется при увеличении или уменьшении частоты внешнего воздействия. Более сложный характер имеют процессы в электрических цепях, содержащих реактивные элементы различных типов. Амплитуда отклика таких цепей может резко изменяться, когда частота внешнего воздействия достигает некоторых определенных значений. Явление резкого возрастания амплитуды отклика цепи при приближении частоты внешнего воздействия к определенному значению называется резонансом. Такое определение резонанса заимствовано из механики и справедливо только для цепей с малыми потерями. Резонанс, отвечающий этому определению, условно называется амплитудным.
В теории цепей обычно используют другое определение резонанса, которое применяется как для цепей с малыми, так и для цепей с большими потерями. Под резонансом понимают такой режим работы электрической цепи, содержащей емкости и индуктивности, при котором реактивные составляющие входных сопротивления и проводимости Цепи равны нулю. Резонанс, отвечающий данному определению, условно называется фазовым. Можно показать, что резонансные частоты, соответствующие амплитудному и фазовому резонансам, совпадают только в идеализированном случае, когда потери в цепи равны нулю. В дальнейшем под термином резонанс будем понимать только фазовый резонанс, а под резонансной частотой—только частоту внешнего воздействия, соответствующую фазовому резонансу. Как следует из определения резонанса, на резонансной частоте входные сопротивление и проводимость электрической цепи имеют чисто резистивный характер, а входной ток цепи совпадает по фазе с приложенным напряжением.
Простейшей электрической цепью, в которой наблюдается явление резонанса, является одиночный колебательный контур, представляющий собой замкнутую цепь, состоящую из конденсатора и индуктивной катушки. В зависимости от способа подключения источника энергии, различают «последовательный» колебательный контур (источник энергии включен последовательно с конденсатором и индуктивной катушкой) и «параллельный» колебательный контур (источник энергии подключен параллельно реактивным элементам). Ранее, при изучении последовательной RLС-цепи, было установлено, что ее входное сопротивление может иметь чисто резистивный характер, когда мнимая составляющая входного сопротивления емкости по абсолютному значению равна мнимой составляющей входного сопротивления индуктивности 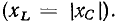 В этом случае напряжение на емкости равно по амплитуде и противоположно по фазе напряжению на индуктивности
В этом случае напряжение на емкости равно по амплитуде и противоположно по фазе напряжению на индуктивности 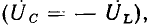 а напряжение на входе цепи
а напряжение на входе цепи 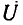 равно напряжению на сопротивлении
равно напряжению на сопротивлении 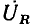 и совпадает по фазе с входным током
и совпадает по фазе с входным током 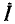 (см. рис. 2.21, в). Такая разновидность резонанса получила название резонанса напряжений.
(см. рис. 2.21, в). Такая разновидность резонанса получила название резонанса напряжений.
В параллельной RLС-цепи входная проводимость может иметь чисто резистивный характер, когда мнимые составляющие входных проводимостей емкости и индуктивности равны по абсолютному значению 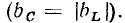 В этом случае ток индуктивности равен по амплитуде и противоположен по фазе току емкости
В этом случае ток индуктивности равен по амплитуде и противоположен по фазе току емкости  а входной ток цепи
а входной ток цепи 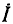 равен току через сопротивление
равен току через сопротивление 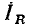 и совпадает по фазе с входным напряжением
и совпадает по фазе с входным напряжением 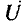 (см. рис. 2.23, в). Такая разновидность резонанса называется резонансом токов.
(см. рис. 2.23, в). Такая разновидность резонанса называется резонансом токов.
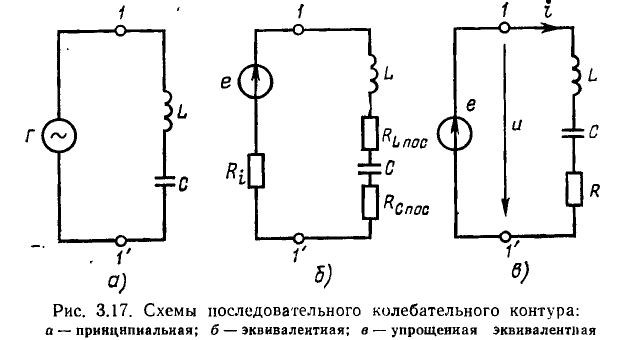
Последовательный колебательный контур
Последовательный колебательный контур представляет собой электрическую цепь, содержащую индуктивную катушку и конденсатор, включенные последовательно с источником энергии (рис. 3.17, а). Для анализа процессов, протекающих в контуре, необходимо перейти от его принципиальной схемы к эквивалентной путем замены каждого реального элемента его эквивалентной схемой.
Воспользуемся простейшими последовательной и параллельной схемами замещения индуктивной катушки (см. рис. 2.38, в и 2.39, в) и
конденсатора (см. рис. 2.38, б и 2.39, б), содержащими наряду с индуктивностью 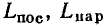 или емкостью
или емкостью 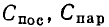 только сопротивления
только сопротивления 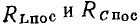 или
или 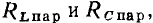 учитывающие все виды потерь в индуктивной катушке и конденсаторе соответственно. Соотношения между параметрами элементов таких схем приведены в табл. 2.1.
учитывающие все виды потерь в индуктивной катушке и конденсаторе соответственно. Соотношения между параметрами элементов таких схем приведены в табл. 2.1.
Рассмотрим векторные диаграммы, иллюстрирующие фазовые соотношения между токами и напряжениями последовательных RL- и RC-цепей, моделирующих индуктивную катушку и конденсатор (см. рис. 2.18, г, д; 2.19, г, д). Из диаграмм видно, что вследствие потерь
сдвиг фаз между током и напряжением на зажимах индуктивной катушки и конденсатора меньше 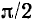 . Очевидно, что чем ближе к
. Очевидно, что чем ближе к 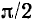 будет сдвиг фаз
будет сдвиг фаз 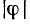 между током и напряжением, тем ближе будут свойства этих реальных элементов к свойствам индуктивности и емкости. Количественно степень приближения свойств реальных элементов к свойствам идеализированных элементов оценивается их добротностью, которая определяется как модуль тангенса сдвига фаз между током и напряжением на зажимах соответствующего элемента:
между током и напряжением, тем ближе будут свойства этих реальных элементов к свойствам индуктивности и емкости. Количественно степень приближения свойств реальных элементов к свойствам идеализированных элементов оценивается их добротностью, которая определяется как модуль тангенса сдвига фаз между током и напряжением на зажимах соответствующего элемента:
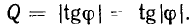
Из рис. 2.18, г и 2.19, г видно, что добротность индуктивной катушки
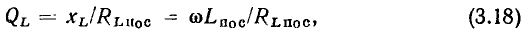
а добротность конденсатора
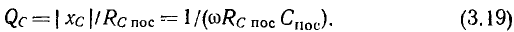
Обычно в колебательных контурах радиотехнических устройств стремятся использовать элементы с высокой добротностью, причем добротность индуктивных катушек лежит в пределах от нескольких десятков до нескольких сотен, а добротность конденсаторов — от нескольких сотен до нескольких тысяч. Таким образом, между параметрами рассматриваемых элементов последовательных схем замещения выполняются соотношения
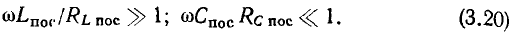
Экспериментально установлено, что 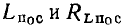 достаточно широком диапазоне частот можно приближенно считать независящими от частоты.
достаточно широком диапазоне частот можно приближенно считать независящими от частоты.
В соответствии с формулами, приведенными в табл. 2.1, параметры параллельной схемы замещения индуктивной катушки могут быть выражены через параметры элементов последовательной схемы замещения:
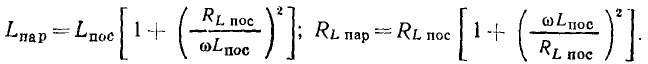
С учетом соотношений (3.20) эти выражения можно упростить:
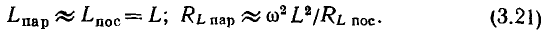
Таким образом, у индуктивных катушек с высокой добротностью значения индуктивностей параллельной и последовательной схем замещения приблизительно одинаковы и могут считаться не зависящими от частоты; значение сопротивления в параллельной схеме замещения обратно пропорционально значению сопротивления последовательной схемы замещения и сильно зависит от частоты.
Аналогичным образом найдем соотношения между параметрами элементов параллельной и последовательной схем замещения конденсатора:
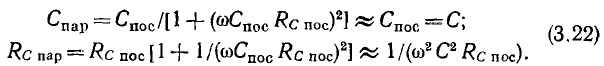
Экспериментально установлено, что параметры 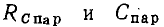 можно приближенно считать не зависящими от частоты. Из соотношений (3.22) следует, что у конденсаторов с высокой добротностью значения емкостей в последовательной и параллельной схемах замещения приблизительно одинаковы и могут считаться не зависящими от частоты; сопротивление
можно приближенно считать не зависящими от частоты. Из соотношений (3.22) следует, что у конденсаторов с высокой добротностью значения емкостей в последовательной и параллельной схемах замещения приблизительно одинаковы и могут считаться не зависящими от частоты; сопротивление 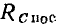 обратно пропорционально сопротивлению
обратно пропорционально сопротивлению 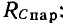
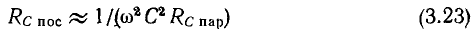
и зависит от частоты. Между параметрами сопротивлений потерь индуктивной катушки 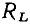 и конденсатора
и конденсатора 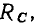 как правило, выполняются соотношения
как правило, выполняются соотношения
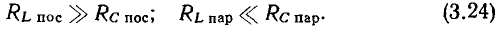
Для анализа процессов в последовательном колебательном контуре удобно воспользоваться последовательными схемами замещения индуктивной катушки, конденсатора и источника энергии. Представляя каждый из этих элементов его последовательной схемой замещения, получим эквивалентную схему последовательного колебательного контура (рис. 3.17, б). Эта схема может быть несколько упрощена, если пренебречь внутренним сопротивлением источника (далее будет рассмотрено влияние внутреннего сопротивления источника на характеристики контура) и заменить сопротивления потерь конденсатора 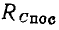 и индуктивной катушки
и индуктивной катушки 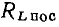 сопротивлением
сопротивлением
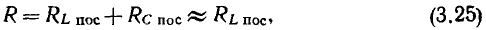
которое считается практически не зависящим от частоты (рис. 3.17,в).
Итак, с учетом принятых допущений исследование процессов в последовательном колебательном контуре сводится к исследованию последовательной RLC-цепи, к зажимам которой подключен идеальный источник напряжения. Ток, отдаваемый этим источником, назовем током контура; напряжение, создаваемое источником на зажимах 1 — 1′, — напряжением контура. Под входным сопротивлением контура будем понимать входное сопротивление последовательной RLC-цепи относительно зажимов 1 — 1′ определяемое выражением (2.96).
Резонансная частота, характеристическое сопротивление и добротность контура
По определению, мнимая составляющая входного сопротивления последовательного колебательного контура

должна быть равна нулю, когда угловая частота внешнего воздействия 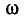 равна резонансной частоте контура
равна резонансной частоте контура 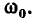 Полагая в выражении (3.26)
Полагая в выражении (3.26) 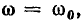 получаем уравнение для определения резонансной частоты последовательного колебательного контура:
получаем уравнение для определения резонансной частоты последовательного колебательного контура:
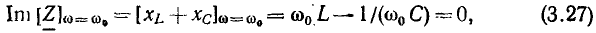
откуда
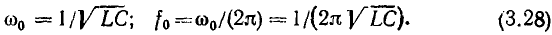
На резонансной частоте полное сопротивление емкости
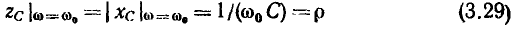
равно полному сопротивлению индуктивности
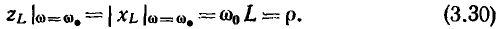
Величина 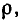 равная полному сопротивлению емкости или индуктивности контура на резонансной частоте, получила название характеристического сопротивления контура. Подставляя в (3.29) и (3.30) выражение для резонансной частоты контура, убеждаемся, что значение
равная полному сопротивлению емкости или индуктивности контура на резонансной частоте, получила название характеристического сопротивления контура. Подставляя в (3.29) и (3.30) выражение для резонансной частоты контура, убеждаемся, что значение 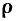 не зависит от частоты и определяется только параметрами реактивных элементов контура:
не зависит от частоты и определяется только параметрами реактивных элементов контура:
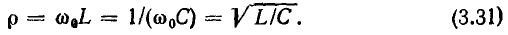
На резонансной частоте входное сопротивление контура имеет чисто резистивный характер и равно сопротивлению потерь контура 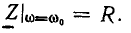 Действующее значение тока контура на резонансной частоте
Действующее значение тока контура на резонансной частоте

где U — действующее значение напряжения на контуре. Действующие значения напряжений на реактивных элементах контура на резонансной частоте определяются произведением характеристического сопротивления на действующее значение тока:
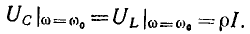
Отношение действующего значения напряжения на реактивном элементе контура к действующему значению напряжения на контуре на резонансной частоте называется добротностью контура
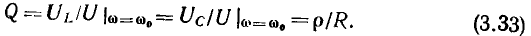
Используя выражение (3.31), добротность колебательною контура Q можно выразить через параметры его элементов

Как правило, добротность колебательных контуров современной радиотехнической аппаратуры лежит в пределах от нескольких десятков до нескольких сотен, поэтому в режиме резонанса напряжение на реактивных элементах контура может во много раз превышать приложенное к контуру напряжение. Как следует из выражения (3.34) при неизменной резонансной частоте 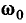 добротность контура растет с увеличением характеристического сопротивления контура и с уменьшением сопротивления потерь.
добротность контура растет с увеличением характеристического сопротивления контура и с уменьшением сопротивления потерь.
Добротность колебательного контура может быть выражена через добротности его элементов Действительно, рассматривая величину
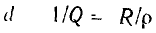
и учитывая, что сопротивление потерь контура равно сумме сопротивлений потерь индуктивной катушки и конденсатора в последовательных схемах замещения, находим
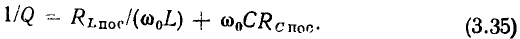
Сравнивая полученное выражение с соотношениями (3.18), (3.19), устанавливаем, что величины 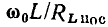 и
и 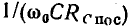 равны добротностям индуктивной катушки и конденсатора на резонансной частоте:
равны добротностям индуктивной катушки и конденсатора на резонансной частоте:
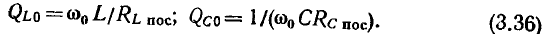
Подставляя (3.36) в (3.35), получаем простое выражение, связывающее добротность контура с добротностями элементов контура на резонансной частоте:
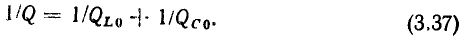
Анализ выражения (3.37) показывает, что добротность контура не может превышать добротности его элементов на резонансной частоте. Как правило, 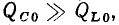 поэтому добротность контура в основном определяется добротностью индуктивной катушки на резонансной частоте. Величина d, обратная добротности контура, называется его затуханием.
поэтому добротность контура в основном определяется добротностью индуктивной катушки на резонансной частоте. Величина d, обратная добротности контура, называется его затуханием.
Энергетические процессы в последовательном колебательном контуре
Пусть последовательный колебательный контур настроен на частоту источника энергии, т. е. параметры реактивных элементов контура выбраны таким образом, что резонансная частота 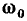 совпадает с частотой внешнего воздействия
совпадает с частотой внешнего воздействия 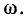 Определим мгновенные значения энергии, запасаемой реактивными элементами контура, и энергию, потребляемую им от источника.
Определим мгновенные значения энергии, запасаемой реактивными элементами контура, и энергию, потребляемую им от источника.
Как было установлено ранее, на резонансной частоте напряжение и ток контура совпадают по фазе (рис. 3.18, а): 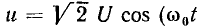
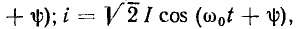 а их действующие значения связаны между собой соотношением (3.32). Мгновенное значение энергии, запасаемой в индуктивности, определяется током индуктивности
а их действующие значения связаны между собой соотношением (3.32). Мгновенное значение энергии, запасаемой в индуктивности, определяется током индуктивности
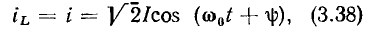
а мгновенное значение энергии, запасаемой в емкости, — напряжением на емкости (рис. 3.18, б)
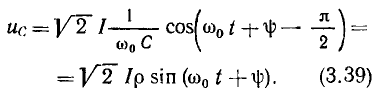
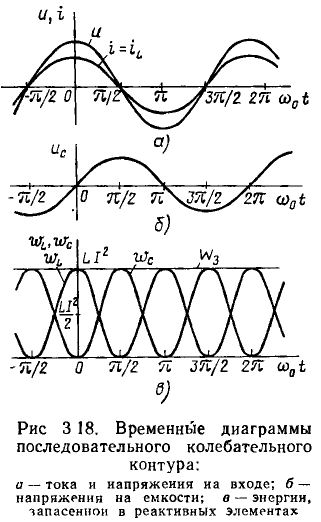
Подставляя (3.38), (3.39) в выражения (1.25) и (1.18), получаем
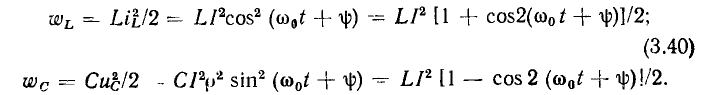
Зависимости мгновенных значений энергии, запасаемой в реактивных элементах контура, от времени приведены на рис. 3.18, в. Как видно из временных диаграмм и выражений (3.40), энергия, запасаемая в емкости и индуктивности, имеет две составляющие: постоянную 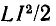 и переменную, изменяющуюся во времени по гармоническому закону с частотой
и переменную, изменяющуюся во времени по гармоническому закону с частотой 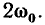 Переменные составляющие энергий емкости и индуктивности находятся в противофазе так, что максимальным значениям энергии, запасаемой в емкости, соответствуют нулевые значения энергии, запасенной в индуктивности, и наоборот. Несмотря на то что
Переменные составляющие энергий емкости и индуктивности находятся в противофазе так, что максимальным значениям энергии, запасаемой в емкости, соответствуют нулевые значения энергии, запасенной в индуктивности, и наоборот. Несмотря на то что 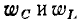 являются функциями времени, суммарная энергия, запасенная в реактивных элементах цепи, постоянна:
являются функциями времени, суммарная энергия, запасенная в реактивных элементах цепи, постоянна:

Емкость и индуктивность контура при резонансе непрерывно обмениваются энергией. Обмен энергией происходит без участия источника энергии: сдвиг фаз между током и напряжением в этом режиме равен нулю, поэтому реактивная мощность,отдаваемая источником, также равна нулю, и обмена энергией между контуром и источником не происходит.
Найдем энергию, потребляемую контуром от источника за промежуток времени, равный периоду внешнего гармонического воздействия Т:
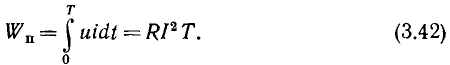
Из выражения (3.42) видно, что энергия, потребляемая контуром от источника, равна энергии, необратимо теряемой в сопротивлении потерь контура R. В идеальном случае, при отсутствии потерь в контуре (R=0), энергия, потребляемая контуром от источника, равна нулю. Колебательный процесс в таком контуре будет продолжаться неограниченно долго и при отключении контура от источника (при закорачивании зажимов 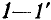 ). Таким образом, колебательный процесс в контуре без потерь должен иметь незатухающий характер. На практике при отключении контура от источника колебательный процесс в нем затухает, так как при каждом цикле колебаний часть электрической энергии, запасенной в контуре, необратимо преобразуется в другие виды энергии. Если контур с потерями подключить к источнику энергии, то амплитуда колебаний в установившемся режиме будет неизменной, так как потери энергии в контуре будут компенсироваться поступлением энергии от источника, и суммарная энергия, связанная с контуром, будет сохранять неизменное значение.
). Таким образом, колебательный процесс в контуре без потерь должен иметь незатухающий характер. На практике при отключении контура от источника колебательный процесс в нем затухает, так как при каждом цикле колебаний часть электрической энергии, запасенной в контуре, необратимо преобразуется в другие виды энергии. Если контур с потерями подключить к источнику энергии, то амплитуда колебаний в установившемся режиме будет неизменной, так как потери энергии в контуре будут компенсироваться поступлением энергии от источника, и суммарная энергия, связанная с контуром, будет сохранять неизменное значение.
Найдем отношение энергии, запасаемой в реактивных элементах контура, к энергии, потребляемой контуром от источника за период Т:
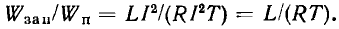
Принимая во внимание, что при резонансе период внешнего гармонического воздействия
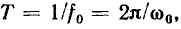
получаем
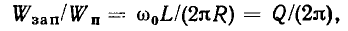
откуда

Таким образом, добротность последовательного контура равна отношению энергии, запасаемой в контуре, к энергии, потребляемой им за период колебаний, умноженному на 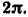 Выражение (3.43) носит общий характер и может применяться для оценки добротности колебательных систем самых различных типов (в том числе и неэлектрических).
Выражение (3.43) носит общий характер и может применяться для оценки добротности колебательных систем самых различных типов (в том числе и неэлектрических).
Входные характеристики последовательного колебательного контура
При рассмотрении комплексных частотных характеристик последовательный колебательный контур удобно представлять в виде многополюсника с тремя парами выводов (рис. 3.19, а, б). Внешнее воздействие на контур обычно задают в виде напряжения 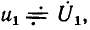 приложенного к зажимам 1 — 1′, в качестве отклика цепи рассматривают входной ток цепи
приложенного к зажимам 1 — 1′, в качестве отклика цепи рассматривают входной ток цепи 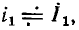 напряжение на емкости
напряжение на емкости 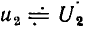 или напряжение на индуктивности
или напряжение на индуктивности 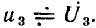 Таким образом, последовательный колебательный контур обладает как входными, так и передаточными характеристиками.
Таким образом, последовательный колебательный контур обладает как входными, так и передаточными характеристиками.
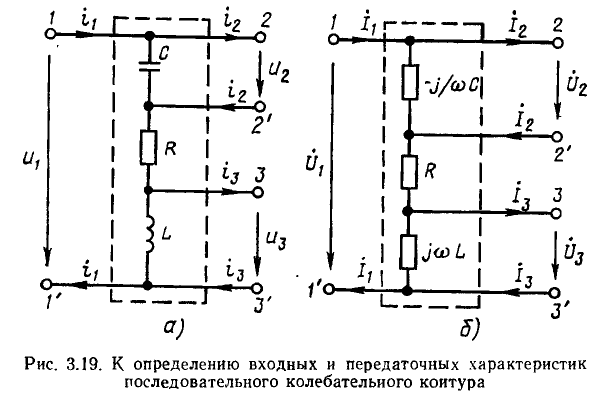
В качестве входной характеристики контура будем рассматривать его комплексную входную проводимость в режиме холостого хода на зажимах 2—2’ и 3—3′:
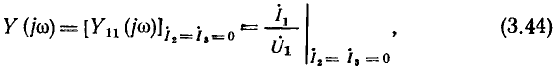
в качестве передаточных — комплексный коэффициент передачи по напряжению для случаев, когда напряжение снимается с емкости:
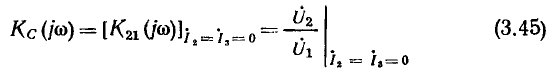
или с индуктивности
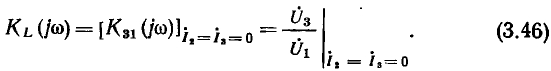
Рассмотрим амплитудно-частотные и фазо-частотные характеристики входной проводимости 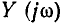 последовательного колебательного контура:
последовательного колебательного контура:
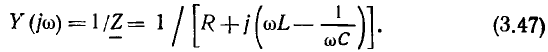
Представляя 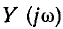 в показательной форме
в показательной форме
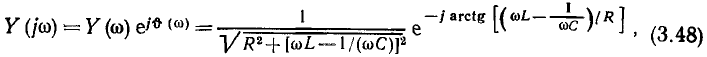
найдем аналитические выражения для АЧХ (рис. 3.20, а) и ФЧХ (рис. 3.20, б) входной проводимости:
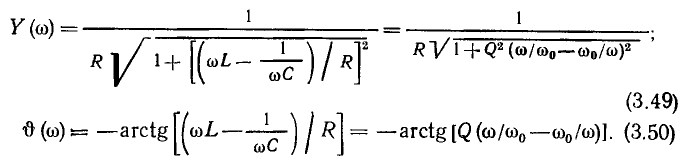
Для удобства приведем также амплитудно-частотные и фазо-частотные характеристики входного сопротивления контура (рис. 3.21), построенные в соответствии с выражениями:
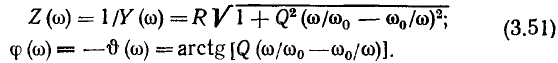
Если контур настроен на частоту источника, то мнимые составляющие входного сопротивления емкости 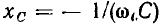 и индуктивности
и индуктивности 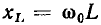 взаимно компенсируются, входное сопротивление контура имеет чисто резистивный характер и минимально по модулю, а полная входная проводимость
взаимно компенсируются, входное сопротивление контура имеет чисто резистивный характер и минимально по модулю, а полная входная проводимость 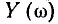 достигает максимального значения и равна 1/R. Векторные диаграммы, соответствующие этому случаю, изображены на рис. 2.20, е. Всякое отклонение частоты внешнего воздействия от резонансной приводит к нарушению баланса между мнимыми составляющими входного сопротивления емкости и индуктивности, что в свою очередь вызывает увеличение модуля входного сопротивления
достигает максимального значения и равна 1/R. Векторные диаграммы, соответствующие этому случаю, изображены на рис. 2.20, е. Всякое отклонение частоты внешнего воздействия от резонансной приводит к нарушению баланса между мнимыми составляющими входного сопротивления емкости и индуктивности, что в свою очередь вызывает увеличение модуля входного сопротивления 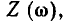 уменьшение модуля входной проводимости
уменьшение модуля входной проводимости 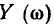 и отклонение аргумента входной проводимости
и отклонение аргумента входной проводимости 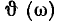 от нулевого значения. Из рис. 3.20 видно, что чем выше добротность контура Q, тем более заметно выражен максимум
от нулевого значения. Из рис. 3.20 видно, что чем выше добротность контура Q, тем более заметно выражен максимум 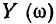 на резонансной частоте и более резко изменяется
на резонансной частоте и более резко изменяется 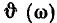 вблизи
вблизи 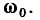
При частоте внешнего воздействия 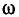 ниже резонансной мнимая составляющая входного сопротивления емкости по абсолютному значению превышает мнимую составляющую входного сопротивления индуктивности
ниже резонансной мнимая составляющая входного сопротивления емкости по абсолютному значению превышает мнимую составляющую входного сопротивления индуктивности 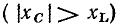 и входное сопротивление контура имеет резистивно-емкостный характер
и входное сопротивление контура имеет резистивно-емкостный характер  В пределе, при
В пределе, при 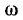 = 0, входное сопротивление контура будет иметь чисто емкостной характер
= 0, входное сопротивление контура будет иметь чисто емкостной характер  полное сопротивление контура
полное сопротивление контура 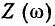 бесконечно велико, а модуль входной проводимости
бесконечно велико, а модуль входной проводимости 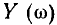 равен нулю. Векторные диаграммы для
равен нулю. Векторные диаграммы для 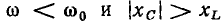 приведены на рис. 2.20, г.
приведены на рис. 2.20, г.
На частоте выше резонансной  мнимая составляющая входного сопротивления емкости по абсолютному значению меньше, чем мнимая составляющая входного сопротивления индуктивности
мнимая составляющая входного сопротивления емкости по абсолютному значению меньше, чем мнимая составляющая входного сопротивления индуктивности 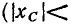
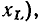 входное сопротивление контура имеет резистивно-индуктивный характер
входное сопротивление контура имеет резистивно-индуктивный характер 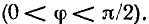 С увеличением частоты аргумент входного сопротивления контура
С увеличением частоты аргумент входного сопротивления контура 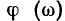 будет стремиться к
будет стремиться к 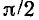 (аргумент входной проводимости
(аргумент входной проводимости 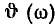 будет стремиться к —
будет стремиться к — 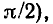 модуль входного сопротивления контура
модуль входного сопротивления контура 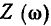 неограниченно возрастать, а модуль входной проводимости
неограниченно возрастать, а модуль входной проводимости 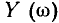 — стремиться к нулю.
— стремиться к нулю.
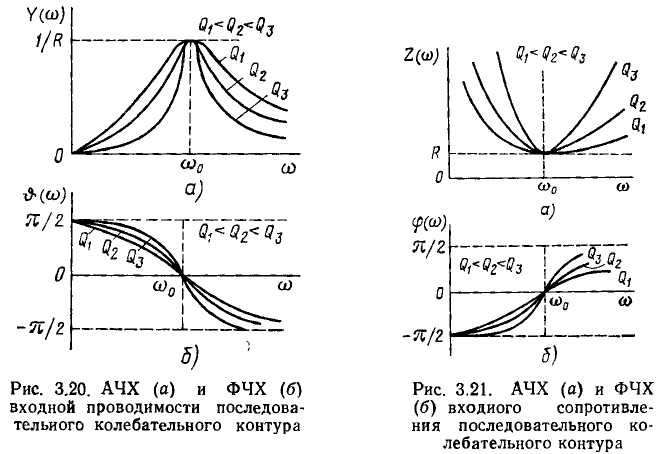
Комплексные частотные характеристики входной проводимости 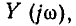 приведенные на рис. 3.20, имеют чисто качественный характер и неудобны для практического использования, так как содержат большое число параметров, причем для каждого сочетания R, Q и
приведенные на рис. 3.20, имеют чисто качественный характер и неудобны для практического использования, так как содержат большое число параметров, причем для каждого сочетания R, Q и 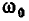 необходимо строить отдельные кривые. Поэтому на практике обычно применяют нормированные входные характеристики, которые позволяют в обобщенной форме построить кривые для всех возможных сочетаний значений параметров. В качестве аргумента нормированных характеристик удобно использовать так называемую обобщенную расстройку
необходимо строить отдельные кривые. Поэтому на практике обычно применяют нормированные входные характеристики, которые позволяют в обобщенной форме построить кривые для всех возможных сочетаний значений параметров. В качестве аргумента нормированных характеристик удобно использовать так называемую обобщенную расстройку 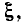 которая определяется выражением
которая определяется выражением
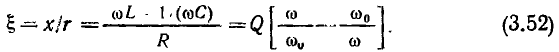
На резонансной частоте 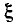 = 0, на частотах ниже резонансной
= 0, на частотах ниже резонансной 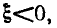 причем нулевому значению
причем нулевому значению 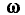 соответствует
соответствует 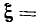
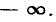 На частотах выше резонансной
На частотах выше резонансной  а при
а при 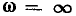 значение обобщенной расстройки также равно бесконечности. В ряде случаев в качестве аргумента нормированных частотных характеристик удобно использовать абсолютную расстройку
значение обобщенной расстройки также равно бесконечности. В ряде случаев в качестве аргумента нормированных частотных характеристик удобно использовать абсолютную расстройку 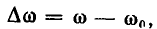 относительную расстройку
относительную расстройку 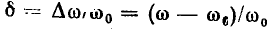 или нормированную частоту
или нормированную частоту 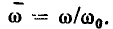
Комплексная входная проводимость 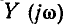 и ее модуль
и ее модуль 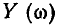 обычно нормируется по значению, которое они принимают на резонансной частоте
обычно нормируется по значению, которое они принимают на резонансной частоте 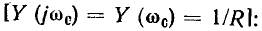
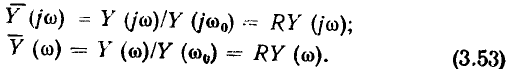
С использованием (3.52), (3.53) выражения (3.47), (3.49) (3.50) преобразуются к виду
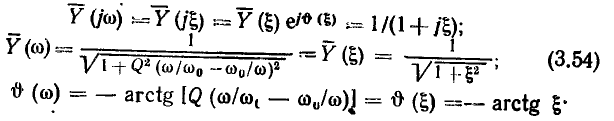
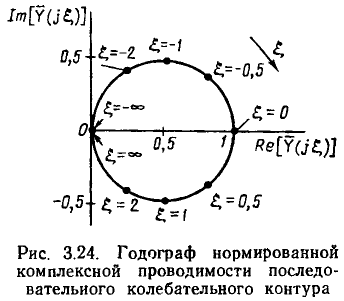
Нормированные амплитудно-частотные и фазо-частотные характеристики входной проводимости последовательного колебательного контура приведены на рис. 3.22 и 3.23 (в последнем случае комплексные частотные характеристики цепи называют обобщенными). Годограф нормированной комплексной входной проводимости последовательного колебательного контура 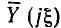 имеет вид окружности (рис. 3.24).
имеет вид окружности (рис. 3.24).
Используя входные характеристики, найдем зависимость входного контура от частоты. Пусть к зажимам 1—1′ контура (см. рис. 3.17, в) подключен идеальный источник напряжения 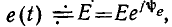 частота которого может изменяться в широких пределах, а действующее значение Е и начальная фаза
частота которого может изменяться в широких пределах, а действующее значение Е и начальная фаза 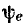 — постоянны. Комплексный ток контура
— постоянны. Комплексный ток контура 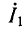 определяется произведением комплексной входной проводимости контура на комплексное действующее значение э. д. с.:
определяется произведением комплексной входной проводимости контура на комплексное действующее значение э. д. с.:
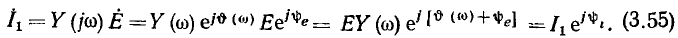
Из выражения (3.55) находим действующее значение входного тока контура и его начальную фазу как функции круговой частоты 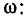
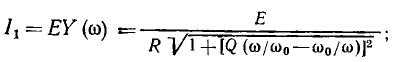
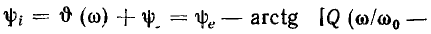
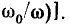
Нормируя ток 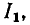 ( по его максимальному значению
( по его максимальному значению 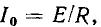 которое достигается, когда
которое достигается, когда 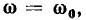 и переходя от круговой частоты
и переходя от круговой частоты 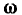 к обобщенной расстройке
к обобщенной расстройке 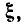 окончательно получаем
окончательно получаем
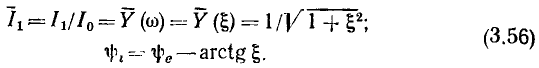
Таким образом, зависимость нормированного входного тока контура 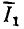 от частоты совпадает с нормированной амплитудно-частотной характеристикой входной проводимости контура, а зависимость начальной фазы
от частоты совпадает с нормированной амплитудно-частотной характеристикой входной проводимости контура, а зависимость начальной фазы 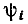 от частоты совпадает с нормированной фазо-частотной характеристикой контура, смещенной на
от частоты совпадает с нормированной фазо-частотной характеристикой контура, смещенной на 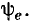
Передаточные характеристики последовательного колебательного контура
Найдем коэффициент передачи контура по напряжению 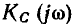 для случая, когда напряжение снимают с емкости (см. рис. 3.19). При холостом ходе на зажимах 2—2′ и 3 — 3′ через все элементы контура протекает один и тот же ток
для случая, когда напряжение снимают с емкости (см. рис. 3.19). При холостом ходе на зажимах 2—2′ и 3 — 3′ через все элементы контура протекает один и тот же ток 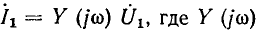 — комплексная входная проводимость контура, определяемая выражениями (3.47) и (3.48). Выходное напряжение контура
— комплексная входная проводимость контура, определяемая выражениями (3.47) и (3.48). Выходное напряжение контура
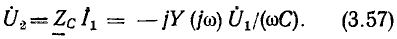
Поставляя (3.57) в (3.45), находим выражение для коэффициента передачи контура по напряжению
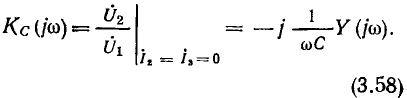
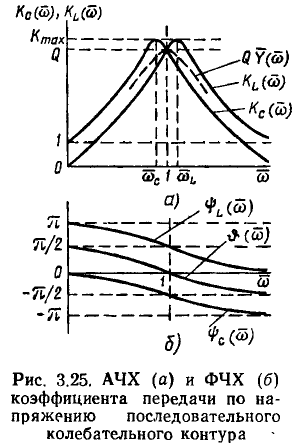
Умножая числитель и знаменатель (3.58) на 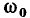 и используя соотношения (3.34), (3.53), преобразуем (3.58) к виду
и используя соотношения (3.34), (3.53), преобразуем (3.58) к виду
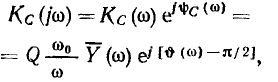
откуда можно определить модуль (рис. 3.25, а) и аргумент (рис. 3.25, б) комплексного коэффициента передачи цепи по напряжению:
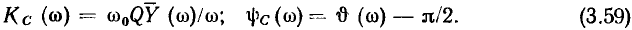
Здесь 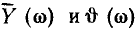 — нормированные АЧХ и ФЧХ входной проводимости последовательного колебательного контура, определяемые выражениями (3.54).
— нормированные АЧХ и ФЧХ входной проводимости последовательного колебательного контура, определяемые выражениями (3.54).
Используя аналогичный подход, находим модуль (рис. 3.25, а) и аргумент (рис. 3.25, б) комплексного коэффициента передачи цепи по напряжению
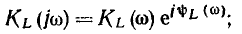
для случая, когда напряжение снимают с индуктивности,
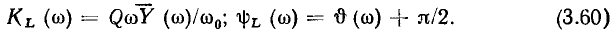
Как следует из определения добротности, на резонансной частоте 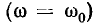 действующее значение напряжения на емкости равно действующему значению напряжения на индуктивности и в Q раз превышает напряжение на входе контура, поэтому
действующее значение напряжения на емкости равно действующему значению напряжения на индуктивности и в Q раз превышает напряжение на входе контура, поэтому 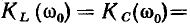
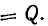 При
При 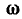 = 0 сопротивление емкости бесконечно велико, напряжение на емкости
= 0 сопротивление емкости бесконечно велико, напряжение на емкости 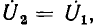 напряжение на индуктивности равно нулю. Поэтому
напряжение на индуктивности равно нулю. Поэтому 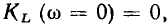
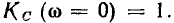 На высоких частотах
На высоких частотах 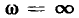 сопротивление индуктивности бесконечно велико, поэтому напряжение
сопротивление индуктивности бесконечно велико, поэтому напряжение 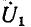 оказывается практически полностью приложенным к индуктивности, а напряжение на емкости равно нулю. Таким образом,
оказывается практически полностью приложенным к индуктивности, а напряжение на емкости равно нулю. Таким образом, 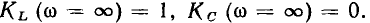
Максимум зависимости 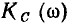 соответствует частоте, несколько более низкой, а максимум
соответствует частоте, несколько более низкой, а максимум 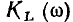 — частоте, несколько более высокой, чем резонансная. Однако эти смещения максимумов
— частоте, несколько более высокой, чем резонансная. Однако эти смещения максимумов 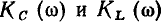 относительно резонансной частоты очень малы и на практике ими всегда можно пренебречь. Действительно, исследуя кривые
относительно резонансной частоты очень малы и на практике ими всегда можно пренебречь. Действительно, исследуя кривые 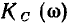 и
и 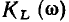 на экстремум, легко установить, что функция
на экстремум, легко установить, что функция 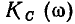 имеет максимум на частоте
имеет максимум на частоте
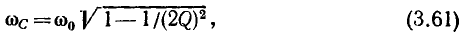
а функция 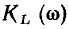 — на частоте
— на частоте
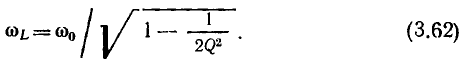
Подставляя (3.61) и (3.62) соответственно в выражения (3.59) и (3.60), находим, что максимальные значения обеих функций одинаковы:
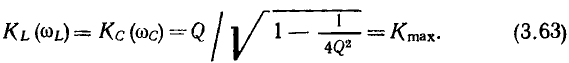
Рассматривая выражения (3.61)—(3.63), нетрудно прийти к заключению, что при  отличие
отличие 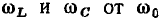 не превышает
не превышает 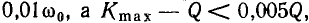 поэтому во всех практически важных случаях можно считать, что
поэтому во всех практически важных случаях можно считать, что 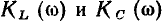 имеют максимум на резонансной частоте, причем
имеют максимум на резонансной частоте, причем 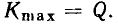
На рис. 3.25, а, который носит чисто качественный характер, смещение кривых 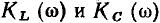 относительно друг друга преувеличено с тем, чтобы показать, что максимумы кривых
относительно друг друга преувеличено с тем, чтобы показать, что максимумы кривых 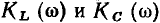 находятся на разных частотах. В действительности в узком диапазоне частот, близких к резонансной, когда можно положить
находятся на разных частотах. В действительности в узком диапазоне частот, близких к резонансной, когда можно положить 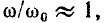 эти_зависимости почти совпадают друг с другом и с зависимостью
эти_зависимости почти совпадают друг с другом и с зависимостью 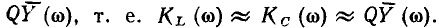
Если к входу последовательного колебательного контура подключить источник напряжения 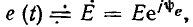 частота
частота 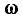 которого изменяется в широких пределах, а действующее значение э. д. с.
которого изменяется в широких пределах, а действующее значение э. д. с. 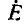 и начальная фаза
и начальная фаза 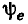 сохраняют неизменное значение, то зависимость нормированного выходного напряжения
сохраняют неизменное значение, то зависимость нормированного выходного напряжения 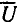 от частоты будет совпадать с нормированной АЧХ входной проводимости контура:
от частоты будет совпадать с нормированной АЧХ входной проводимости контура:
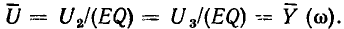
Напомним, что такой же вид имеет зависимость нормированного входного тока контура 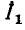 от частоты (3.56).
от частоты (3.56).
Таким образом, нормированную входную проводимость контура 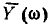 можно рассматривать как нормированную реакцию последовательного колебательного контура на воздействие в виде источника э. д. с. с изменяющейся частотой и неизменной амплитудой в режиме холостого хода на зажимах 2—2′ и 3—3′.
можно рассматривать как нормированную реакцию последовательного колебательного контура на воздействие в виде источника э. д. с. с изменяющейся частотой и неизменной амплитудой в режиме холостого хода на зажимах 2—2′ и 3—3′.
Избирательные свойства последовательного колебательного контура
Важнейшая особенность последовательного колебательного контура заключается в том, что амплитуда реакции контура на гармоническое воздействие существенно зависит от частоты. На резонансной частоте и в узком диапазоне частот около нее амплитуда отклика достигает наибольшего значения; на частотах, значительно отличающихся от резонансной, амплитуда отклика во много раз меньше максимального значения. Если на вход такого контура подать сумму гармонических колебаний различных частот, имеющих одинаковую амплитуду, то на выходе можно обнаружить, что амплитуда колебаний, частота которых близка к резонансной, значительно превышает амплитуду колебаний, частота которых отличается от резонансной. Контур как бы «пропускает» колебания одних частот и «не пропускает» колебания других частот. Способность электрической цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.
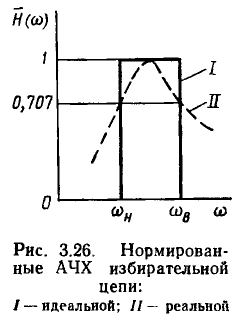
В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой пропускания цепи, и быть равным нулю за пределами этого диапазона. Нормированная АЧХ идеальной избирательной цепи должна иметь прямоугольную ферму (рис. 3.26, кривая I). АЧХ реальных избирательных цепей, в том числе и АЧХ последовательного колебательного контура, отличаются от характеристик идеальной избирательной цепи (рис. 3.26, кривая II) отсутствием резкой границы между диапазонами пропускаемых и задерживаемых (подавляемых) частот. Очевидно, избирательные свойства реальных цепей будут тем выше, чем ближе к прямоугольной будет форма их нормированной АЧХ.
Полоса пропускания реальных избирательных устройств условно определяется как диапазон частот, в пределах которого амплитуда отклика цепи не падает ниже уровня 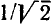 = 0,707 от максимального значения. На частотах, соответствующих границам полосы пропускания, амплитуда отклика составляет
= 0,707 от максимального значения. На частотах, соответствующих границам полосы пропускания, амплитуда отклика составляет 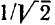 от максимального значения, а потребляемая цепью активная мощности
от максимального значения, а потребляемая цепью активная мощности 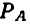
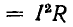 в 2 раза меньше максимальной.
в 2 раза меньше максимальной.
Избирательные свойства последовательного колебательного контура определяются формой нормированной АЧХ входной проводимости контура 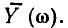 На резонансной частоте нормированная входная проводимость контура равна единице. Определим значения обобщенной расстройки
На резонансной частоте нормированная входная проводимость контура равна единице. Определим значения обобщенной расстройки 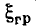 и угловой частоты
и угловой частоты 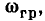 соответствующие границам полосы пропускания контура. Полагая в выражении (3.54)
соответствующие границам полосы пропускания контура. Полагая в выражении (3.54) 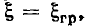
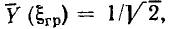 получим
получим 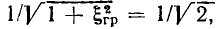 откуда
откуда 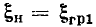
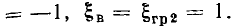
Меньшее значение обобщенной расстройки 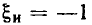 соответствует нижней границе полосы пропускания, большее
соответствует нижней границе полосы пропускания, большее 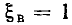 — верхней. Из выражений (3.54) следует, что на границах полосы пропускания аргумент входной проводимости контура равен
— верхней. Из выражений (3.54) следует, что на границах полосы пропускания аргумент входной проводимости контура равен 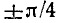 (см. рис. 3.23, б), а реактивная составляющая входного сопротивления
(см. рис. 3.23, б), а реактивная составляющая входного сопротивления 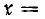
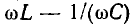 равна по абсолютному значению сопротивлению потерь контура R.
равна по абсолютному значению сопротивлению потерь контура R.
Полагая в выражении (3.52) 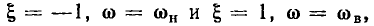 запишем систему уравнений для определения нижней
запишем систему уравнений для определения нижней 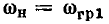 и верхней
и верхней 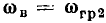 граничных частот:
граничных частот:
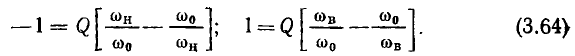
Решая (3.64), найдем
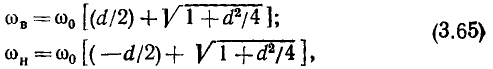
где 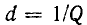 — затухание контура.
— затухание контура.
Ширина полосы пропускания пропорциональна резонансной частоте контура

а относительная ширина полосы пропускания

равна его затуханию.
Таким образом, избирательные свойства последовательного колебательного контура зависят от его добротности: чем выше добротность контура, тем меньше ширина полосы пропускания (см. рис. 3.22, а).
В связи с тем что 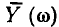 — это нормированный отклик цепи в режиме холостого хода на зажимах 2—2′ и 3—3′ на внешнее гармоническое воздействие, задаваемое источником напряжения, подключенным к зажимам 1—1′, из выражений (3.65)—(3.67) можно определить избирательность колебательного контура только в случае, когда внутреннее сопротивление источника энергии равно нулю, а входное сопротивление нагрузки, подключенной к зажимам 2—2′ или 3—3′, бесконечно велико. Рассмотрим влияние внутреннего сопротивления источника энергии и сопротивления нагрузки на избирательные свойства последовательного колебательного контура.
— это нормированный отклик цепи в режиме холостого хода на зажимах 2—2′ и 3—3′ на внешнее гармоническое воздействие, задаваемое источником напряжения, подключенным к зажимам 1—1′, из выражений (3.65)—(3.67) можно определить избирательность колебательного контура только в случае, когда внутреннее сопротивление источника энергии равно нулю, а входное сопротивление нагрузки, подключенной к зажимам 2—2′ или 3—3′, бесконечно велико. Рассмотрим влияние внутреннего сопротивления источника энергии и сопротивления нагрузки на избирательные свойства последовательного колебательного контура.
Пусть контур питается от источника энергии с конечным внутренним сопротивлением 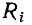 (рис. 3.27, а). Очевидно, что включенные последовательно сопротивления
(рис. 3.27, а). Очевидно, что включенные последовательно сопротивления 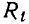 и R можно заменить сопротивлением
и R можно заменить сопротивлением 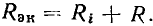 При этом рассматриваемая схема преобразуется в схему, приведенную на рис. 3.17, в, и может быть описана соотношениями, полученными на основании анализа этой схемы при замене R на
При этом рассматриваемая схема преобразуется в схему, приведенную на рис. 3.17, в, и может быть описана соотношениями, полученными на основании анализа этой схемы при замене R на 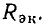
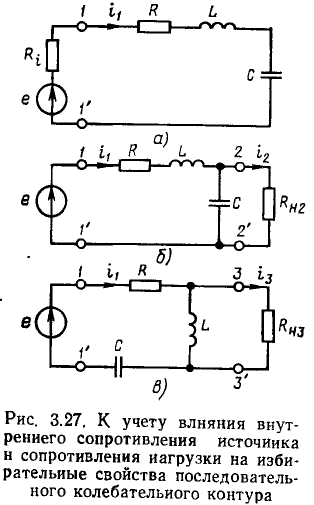
В частности, добротность такого контура определяется выражением
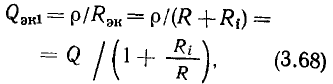
где 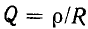 — добротность контура без учета сопротивления источника.
— добротность контура без учета сопротивления источника.
Ширина полосы пропускания контура с учетом внутреннего сопротивления источника энергии может быть найдена из выражения (3.66) при замене 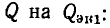
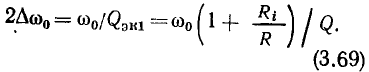
Как видно из выражений (3.68), (3.69), наличие внутреннего сопротивления источника энергии уменьшает эквивалентную добротность контура и снижает его избирательность. Поэтому с целью повышения избирательных свойств контура желательно, чтобы источник энергии, к которому, подключен контур, имел как можно меньшее внутреннее сопротивление, т. е. по свойствам приближался к идеальному источнику напряжения.
Пусть к зажимам 2-2′ или 3-3′ последовательного колебательного контура подключено сопротивление нагрузки (рис. 3.17, б, в) так, что ток 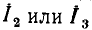 не равен нулю. Очевидно, что сопротивление нагрузки, подключенное параллельно емкости или индуктивности влияет на работу контура таким же образом, как сопротивления
не равен нулю. Очевидно, что сопротивление нагрузки, подключенное параллельно емкости или индуктивности влияет на работу контура таким же образом, как сопротивления 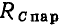 и
и 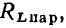 входящие в параллельные схемы замещения конденсатора и индуктивной катушки. Ранее отмечалось, что параллельные схемы замещения элементов могут быть заменены последовательными причем при высокой добротности элементов
входящие в параллельные схемы замещения конденсатора и индуктивной катушки. Ранее отмечалось, что параллельные схемы замещения элементов могут быть заменены последовательными причем при высокой добротности элементов 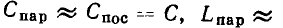
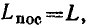 а сопротивления
а сопротивления 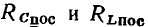 обратно пропорциональны сопротивлениям
обратно пропорциональны сопротивлениям 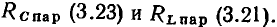 Таким образом, сопротивление нагрузки
Таким образом, сопротивление нагрузки 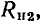 подключенное параллельно емкости, и
подключенное параллельно емкости, и 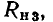 подключенное параллельно индуктивности, могут быть заменены последовательно включенными сопротивлениями
подключенное параллельно индуктивности, могут быть заменены последовательно включенными сопротивлениями
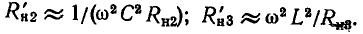
Сопротивления 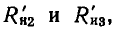 учитывающие влияние нагрузки на работу контура, назовем внесенными в контур сопротивлениями нагрузки. Если
учитывающие влияние нагрузки на работу контура, назовем внесенными в контур сопротивлениями нагрузки. Если 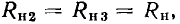 то на частотах, близких к резонансной
то на частотах, близких к резонансной 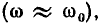 внесенные в контур сопротивления нагрузок
внесенные в контур сопротивления нагрузок
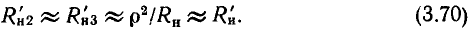
Влияние 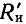 на параметры контура аналогично влиянию внутреннего сопротивления источника
на параметры контура аналогично влиянию внутреннего сопротивления источника 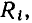 т. е. с увеличением
т. е. с увеличением 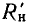 снижается эквивалентная добротность контура и ухудшается его избирательность. Используя (3.70), найдем выражения для эквивалентной добротности контура и ширины полосы пропускания:
снижается эквивалентная добротность контура и ухудшается его избирательность. Используя (3.70), найдем выражения для эквивалентной добротности контура и ширины полосы пропускания:
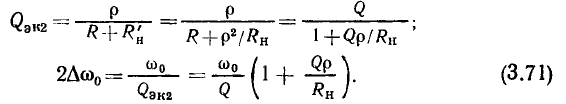
Из выражений (3.71) следует, что для увеличения эквивалентной добротности контура и улучшения его избирательности необходимо, чтобы сопротивление нагрузки контура 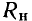 было бы как можно большим, т. е. чтобы на зажимах 2—2′ и 3—3′ был обеспечен режим работы, близкий к режиму холостого хода.
было бы как можно большим, т. е. чтобы на зажимах 2—2′ и 3—3′ был обеспечен режим работы, близкий к режиму холостого хода.
Параллельный колебательный контур
Виды параллельных колебательных контуров:
Параллельным колебательным контуром называется электрическая цепь, в которой индуктивные катушки и конденсаторы размещены в двух ветвях, подключенных параллельно источнику энергии. Принципиальные электрические схемы параллельных колебательных контуров различных видов приведены на рис. 3.28.
В простейшем случае параллельный колебательный контур содержит индуктивную катушку в одной из параллельных ветвей, а конденсатор — в другой (рис. 3.28, а). Такой контур называется параллельным колебательным контуром 1-го (основного) вида. Параллельный колебательный контур 2-го (с неполным включением индуктивности) вида содержит в одной ветви индуктивную катушку 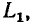 а в другой ветви конденсатор С и индуктивную катушку
а в другой ветви конденсатор С и индуктивную катушку 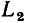 (рис. 3.28, в).
(рис. 3.28, в).
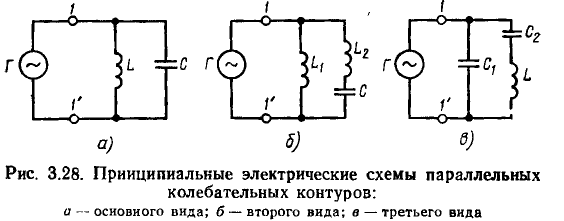
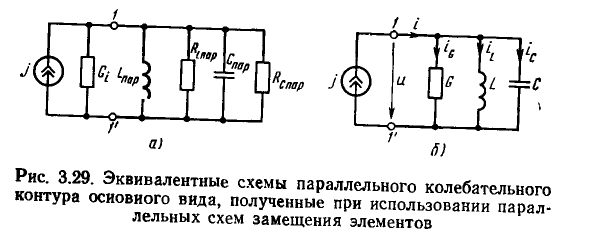
Рассмотрим контур 1-го вида. В соответствии с основным метолом теории цепей реальные элементы заменим упрощенными моделирующими цепями а принципиальную электрическую схему контура его эквивалентной схемой. Используя параллельные схемы замещения
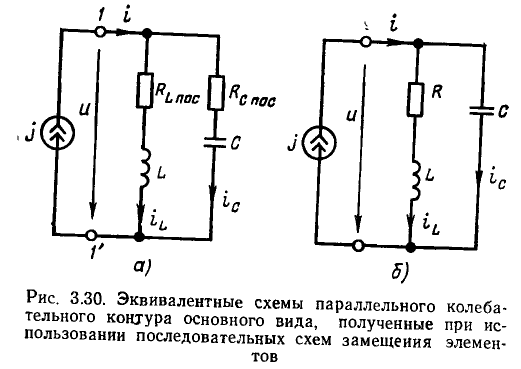
источника энергии, индуктивной катушки и конденсатора получим один из вариантов эквивалентной схемы контура (рис 3 29 а) Ограничим рассмотрение случаем, когда элементы контура имеют высокую добротность, при этом зависимостью 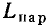 от частоты можно пренебречь и в соответствии с (3.21), (3.22) считать, что параметры реактивных элементов параллельной и последовательной схем замещения индуктивной катушки и конденсатора одинаковы:
от частоты можно пренебречь и в соответствии с (3.21), (3.22) считать, что параметры реактивных элементов параллельной и последовательной схем замещения индуктивной катушки и конденсатора одинаковы:
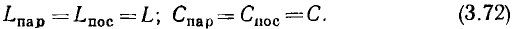
Заменяя сопротивления потерь одним элементом
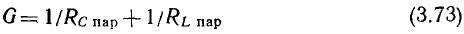
и пренебрегая внутренней проводимостью источника энергии, преобразуем рассмотренную схему в простейшую схему замещения (рис. 3.29, б).
Если каждый из пассивных элементов контура заменить последовательной схемой замещения, то при тех же допущениях получим несколько более сложную эквивалентную схему контура 1-го вида (рис. 3.30, а). В теории цепей в зависимости от характера решаемой задачи нашли применение оба варианта схем замещения.
Параллельный колебательный контур основного вида
Ранее было установлено, что идеализированные цепи, схемы которых приведены на рис. 3.29, б и 3.17, в, являются дуальными, поэтому при рассмотрении процессов в параллельном колебательном контуре основного типа с помощью простейшей схемы замещения, изображенной на рис. 3.29, б, можно воспользоваться всеми выражениями полученными для последовательного колебательного контура, произведя в них взаимные замены токов и напряжений, сопротивлений и проводимостей, емкостей и индуктивностей. Действительно, выражения для комплексной входной проводимости параллельной RLС-цепи (2.100) и комплексного входного сопротивления последовательной RLС-цепи (2.96) имеют одинаковую структуру и могут быть получены одно из другого путем упомянутых ранее замен. На резонансной частоте мнимая составляющая входной проводимости параллельной RLC-цепи должна быть равна нулю:
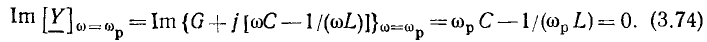
Решая уравнение (3.74), находим, что резонансная частота параллельного колебательного контура 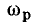 совпадает с резонансной частотой последовательного контура
совпадает с резонансной частотой последовательного контура 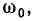 составленного из тех же элементов:
составленного из тех же элементов:
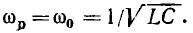
На резонансной частоте полные проводимости емкости
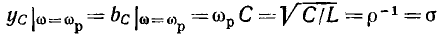
и индуктивности
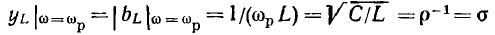
равны характеристической проводимости параллельного колебательного контура 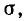 которая является величиной, обратной характеристическому сопротивлению контура
которая является величиной, обратной характеристическому сопротивлению контура 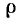 (выражения для характеристических сопротивлений параллельного и последовательного колебательных контуров совпадают). Как видно из векторных диаграмм параллельной RLС-цепи (см. рис. 2.23, в) при
(выражения для характеристических сопротивлений параллельного и последовательного колебательных контуров совпадают). Как видно из векторных диаграмм параллельной RLС-цепи (см. рис. 2.23, в) при 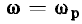 действующее значение тока емкости равно действующему значению тока индуктивности:
действующее значение тока емкости равно действующему значению тока индуктивности: 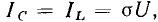 а входной ток контура (ток неразветвленной части параллельной RLС-цепи) равен току проводимости G:
а входной ток контура (ток неразветвленной части параллельной RLС-цепи) равен току проводимости G: 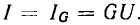
Отношение действующего значения тока реактивного элемента к входному току параллельного колебательного контура на резонансной частоте называется добротностью параллельного колебательного контура:
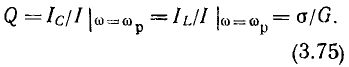
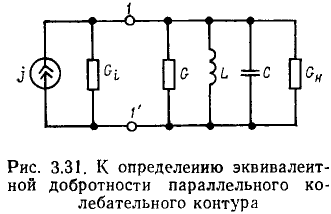
Выражение (3.75) имеет такую же структуру, как и выражение (3.33), и может быть получено из него заменой сопротивления потерь R и характеристического сопротивления 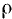 последовательного контура на проводимость потерь G и характеристическую проводимость о параллельного контура.
последовательного контура на проводимость потерь G и характеристическую проводимость о параллельного контура.
Из выражения (3.75) видно, что с увеличением проводимости потерь добротность параллельного колебательного контура падает. Таким же образом на добротность контура влияют внутренняя проводимость источника энергии 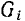 и проводимость нагрузки
и проводимость нагрузки 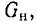 подключенная к зажимам контура
подключенная к зажимам контура 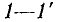 (рис. 3.31). Добротность параллельного колебательного контура с учетом внутренней проводимости источника
(рис. 3.31). Добротность параллельного колебательного контура с учетом внутренней проводимости источника 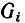 и проводимости нагрузки
и проводимости нагрузки 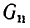 определяется выражением
определяется выражением
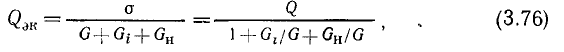
где Q — добротность параллельного контура без учета 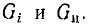 Таким образом, для повышения эквивалентной добротности параллельного колебательного контура желательно, чтобы проводимости источника энергии и нагрузки были бы близки к нулю, т. е. чтобы свойства источника энергии, к которому подключен контур, приближались к свойствам идеального источника тока, а сопротивление нагрузки контура было бы бесконечно большим.
Таким образом, для повышения эквивалентной добротности параллельного колебательного контура желательно, чтобы проводимости источника энергии и нагрузки были бы близки к нулю, т. е. чтобы свойства источника энергии, к которому подключен контур, приближались к свойствам идеального источника тока, а сопротивление нагрузки контура было бы бесконечно большим.
При исследовании комплексных частотных характеристик параллельного контура внешнее воздействие на контур обычно задают в виде тока идеального источника тока, подключенного к зажимам 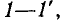 а в качестве реакции контура рассматривают напряжение
а в качестве реакции контура рассматривают напряжение 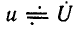 на этих же зажимах (см. рис. 3.29, б). В ряде случаев в качестве реакции контура рассматривают ток емкости
на этих же зажимах (см. рис. 3.29, б). В ряде случаев в качестве реакции контура рассматривают ток емкости 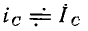 или ток индуктивности
или ток индуктивности 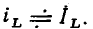 Следовательно, параллельному колебательному контуру, подобно последовательному, можно привести в соответствие как входные, так и передаточные характеристики.
Следовательно, параллельному колебательному контуру, подобно последовательному, можно привести в соответствие как входные, так и передаточные характеристики.
К входным характеристикам параллельного колебательного контура относится его комплексное входное сопротивление в режиме холостого хода 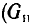 = 0)
= 0)
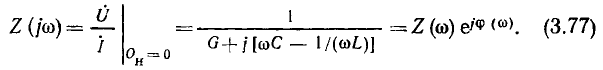
Выражения для нормированного модуля и аргумента комплексного входного сопротивления параллельного колебательного контура
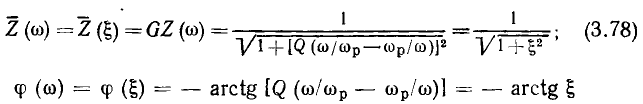
полностью совпадают с выражениями (3.54) для нормированного модуля и аргумента комплексной входной проводимости последовательного колебательного контура. Следовательно, нормированные АЧХ и ФЧХ входного сопротивления параллельного колебательного контура совпадают с соответствующими характеристиками входной проводимости последовательного колебательного контура (см. рис. 3.22, 3.23).
На частоте резонанса токов 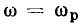 входное сопротивление параллельного колебательного контура имеет чисто резистивный характер
входное сопротивление параллельного колебательного контура имеет чисто резистивный характер 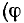 = 0), а модуль входного сопротивления достигает максимального значения:
= 0), а модуль входного сопротивления достигает максимального значения:

На частотах ниже резонансной входное сопротивление контура имеет резистивно-индуктивный характер 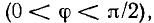 а на частотах выше резонансной — резистивно-емкостной
а на частотах выше резонансной — резистивно-емкостной 
Можно показать, что выражения для коэффициентов передачи параллельного колебательного контура по току 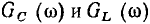 совпадают с выражениями для коэффициентов передачи последовательного контура по напряжению
совпадают с выражениями для коэффициентов передачи последовательного контура по напряжению 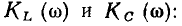
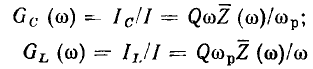
и иллюстрируются теми же кривыми (см. рис. 3.25, а).
О передаточных характеристиках параллельного колебательного контура можно сказать все то, что ранее говорилось о передаточных характеристиках последовательного колебательного контура. В частности, при высокой добротности контура на частотах, близких к резонансной, 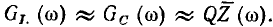
В связи с тем что нормированные входные и передаточные характеристики последовательного и параллельного колебательных контуров совпадают, избирательные свойства этих контуров одинаковы. Ширина полосы пропускания параллельного колебательного контура, если пренебречь внутренней проводимостью источника и проводимостью нагрузки, определяется выражением (3.66). Если необходимо учесть влияние проводимости нагрузки и внутренней проводимости источника энергии на избирательные свойства контура, то вместо Q в выражение (3.66) подставляют эквивалентную добротность 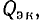 рассчитываемую с помощью выражения (3.76).
рассчитываемую с помощью выражения (3.76).
Таким образом, применение простейшей схемы замещения параллельного колебательного контура позволяет существенно упростить процесс рассмотрения свойств параллельного колебательного контура путем использования соответствующих выражений, полученных при исследовании последовательного колебательного контура. Однако непосредственное использование этих выражений на практике, в частности выражений (3.75), (3.76) и (3.79), в значительной степени затруднено в связи с тем, что в них входит проводимость потерь контура G, которая зависит от частоты.
При практическом использовании более удобными являются выражения для сопротивления на резонансной частоте и для добротности параллельного колебательного контура, полученные с помощью эквивалентной схемы контура, в которой катушка индуктивности и конденсатор представлены их последовательными схемами замещения.
Найдем комплексное входное сопротивление параллельного колебательного контура, используя эквивалентную схему, приведенную на рис. 3.30, а:
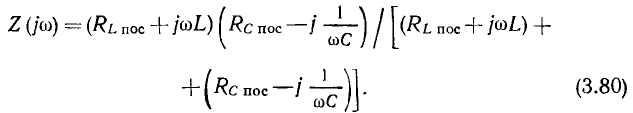
Ограничимся, как и ранее, случаем, когда элементы контура имеют высокую добротность 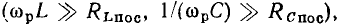 а частота внешнего воздействия ненамного отличается от резонансной. Тогда выражение (3.80) можно преобразовать:
а частота внешнего воздействия ненамного отличается от резонансной. Тогда выражение (3.80) можно преобразовать:
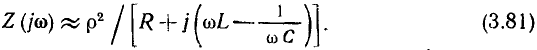
Здесь 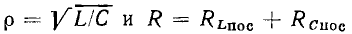 соответственно характеристическое сопротивление и сопротивление потерь последовательного колебательного контура, составленного из тех же элементов, что и рассматриваемый параллельный колебательный контур. С учетом соотношений (3.24) можно считать, что R практически равно
соответственно характеристическое сопротивление и сопротивление потерь последовательного колебательного контура, составленного из тех же элементов, что и рассматриваемый параллельный колебательный контур. С учетом соотношений (3.24) можно считать, что R практически равно 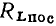 и не зависит от частоты. Таким образом, эквивалентная схема, приведенная на рис. 3.30, а, в большинстве важных для практического использования случаев может быть заменена более простой схемой (см. рис. 3.30, б), в которую входят те же элементы, что и в эквивалентную схему последовательного колебательного контура, параметры которых можно считать не зависящими от частоты.
и не зависит от частоты. Таким образом, эквивалентная схема, приведенная на рис. 3.30, а, в большинстве важных для практического использования случаев может быть заменена более простой схемой (см. рис. 3.30, б), в которую входят те же элементы, что и в эквивалентную схему последовательного колебательного контура, параметры которых можно считать не зависящими от частоты.
На резонансной частоте мнимая составляющая комплексного входного сопротивления контура должна быть равна нулю, что возможно только тогда, когда мнимая составляющая знаменателя выражения (3.81) равна нулю:
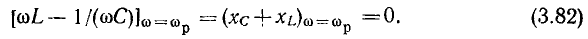
Из выражения (3.82) следует, что условие резонанса токов в параллельном колебательном контуре, при высокой добротности элементов, имеет такой же вид, как условие резонанса напряжений в последовательном колебательном контуре (3.27), и, следовательно, частота резонанса токов совпадает с резонансной частотой последовательного колебательного контура, составленного из тех же элементов:

Если элементы контура имеют невысокую добротность, для определения частоты резонанса токов необходимо приравнять нулю мнимую составляющую входного сопротивления контура, определяемую из выражения (3.80). При этом частота резонанса токов будет несколько отличаться от резонансной частоты последовательного контура:
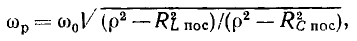
однако при 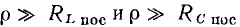 этим различием можно пренебречь.
этим различием можно пренебречь.
Как отмечалось ранее, характеристическое сопротивление параллельного колебательного контура, равное абсолютному значению мнимых составляющих сопротивлений ветвей контура на резонансной частоте, определяется тем же выражением, что и характеристическое сопротивление последовательного контура:
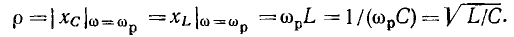
Входное сопротивление параллельного колебательного контура на резонансной частоте (резонансное сопротивление контура) имеет чисто резистивный характер и, как следует из (3.81), определяется выражением
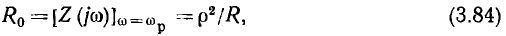
следовательно, ток i и напряжение и на зажимах  (см. рис. 3.30, б) на резонансной частоте совпадают по фазе, а их действующие значения
(см. рис. 3.30, б) на резонансной частоте совпадают по фазе, а их действующие значения 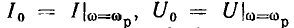 связаны между собой соотношением
связаны между собой соотношением 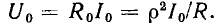
Действующие значения токов ветвей контура на резонансной частоте одинаковы
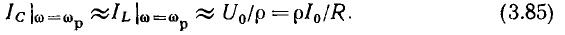
Используя выражение (3.85), найдем добротность параллельного колебательного контура:
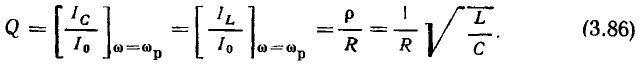
Таким образом, добротность параллельного колебательного контура основного вида совпадает с добротностью последовательного колебательного контура, составленного из тех же элементов.
Аналогичный результат может быть получен и из соотношения (3.43), пригодного для определения добротности любых колебательных систем.
Используя выражения (3.84), (3.86), представим комплексное сопротивление параллельного колебательного контура в следующей форме:
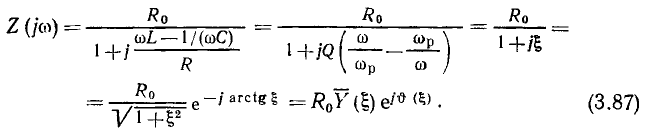
Из сравнения выражений (3.54), (3.77), (3.78), (3.87) следует, что как при использовании параллельных схем замещения элементов (см. рис. 3.29), так и при использовании последовательных схем замещения (см. рис. 3.30) зависимость комплексного входного сопротивления параллельного колебательного контура от частоты определяется обобщенными АЧХ и ФЧХ входной проводимости последовательного колебательного контура 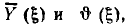 составленного из тех же элементов, что и рассматриваемый параллельный контур.
составленного из тех же элементов, что и рассматриваемый параллельный контур.
Применение последовательных схем замещения элементов позволяет получать более удобные выражения для добротности и резонансного сопротивления параллельного колебательного контура, не содержащие частотно-зависимых членов.
Параллельный колебательный контур второго вида
Конструктивной особенностью колебательного контура этого вида является наличие в нем индуктивной катушки с отводом или со скользящим контактом, разделяющим катушку на две секции (рис. 3.32); секция с индуктивностью 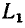 образует одну ветвь колебательного контура (см. рис. 3.28, б), а секция с индуктивностью
образует одну ветвь колебательного контура (см. рис. 3.28, б), а секция с индуктивностью 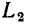 и конденсатор С — другую (для упрощения анализа пренебрегаем взаимной индуктивностью между секциями катушки). Таким образом, индуктивная катушка не полностью входит в первую ветвь контура. При перемещении скользящего контакта вдоль катушки или при изменении места расположения отвода изменяется коэффициент включения индуктивности, определяющий, какая часть суммарной индуктивности катушки
и конденсатор С — другую (для упрощения анализа пренебрегаем взаимной индуктивностью между секциями катушки). Таким образом, индуктивная катушка не полностью входит в первую ветвь контура. При перемещении скользящего контакта вдоль катушки или при изменении места расположения отвода изменяется коэффициент включения индуктивности, определяющий, какая часть суммарной индуктивности катушки 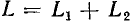 включена в первую ветвь:
включена в первую ветвь:
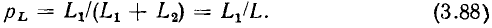
Коэффициент включения индуктивности может изменяться в пределах от нуля (на рисунке при крайнем нижнем положении подвижного контакта) до единицы (при крайнем верхнем положении). В последнем случае рассматриваемый колебательный контур вырождается в параллельный колебательный контур основного вида.
В связи с тем что одна из ветвей параллельного колебательного контура с неполным включением индуктивности представляет собой последовательное включение конденсатора С и индуктивной катушки 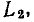 в контуре этого вида наряду с резонансом токов имеет место резонанс напряжений. Очевидно, что частота резонанса напряжений
в контуре этого вида наряду с резонансом токов имеет место резонанс напряжений. Очевидно, что частота резонанса напряжений 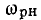 должна быть выше, чем частота резонанса токов
должна быть выше, чем частота резонанса токов 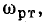 так как для выполнения условия резонанса токов необходимо, чтобы сопротивление ветви, содержащей
так как для выполнения условия резонанса токов необходимо, чтобы сопротивление ветви, содержащей 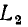 и С, носило емкостной характер, что, как известно, имеет место только на частотах ниже частоты резонанса напряжений.
и С, носило емкостной характер, что, как известно, имеет место только на частотах ниже частоты резонанса напряжений.
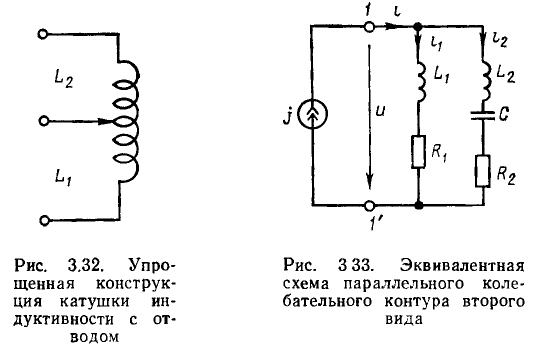
Рассмотрим особенности частотных характеристик параллельного колебательного контура с неполным включением индуктивности и влияние коэффициента включения индуктивности 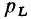 на параметры контура. Для анализа используем эквивалентную схему контура, в которой индуктивные катушки и конденсатор представлены их последовательными схемами замещения (рис. 3.33). Сопротивления
на параметры контура. Для анализа используем эквивалентную схему контура, в которой индуктивные катушки и конденсатор представлены их последовательными схемами замещения (рис. 3.33). Сопротивления 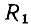
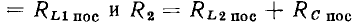 представляют собой соответственно сопротивление потерь индуктивной катушки
представляют собой соответственно сопротивление потерь индуктивной катушки 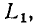 а также суммарное сопротивление потерь индуктивной катушки
а также суммарное сопротивление потерь индуктивной катушки 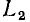 и конденсатора С.
и конденсатора С.
Комплексное входное сопротивление рассматриваемого контура в точках 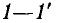 определяется выражением
определяется выражением
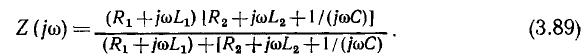
Когда элементы контура обладают высокой добротностью, а частота внешнего воздействия близка к частоте резонанса токов, выражение (3.89) можно привести к более простому виду:
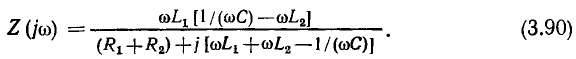
На частоте резонанса токов мнимая составляющая 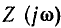 должна равняться нулю, что возможно только при выполнении условия
должна равняться нулю, что возможно только при выполнении условия
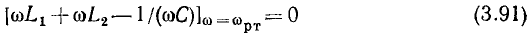
или
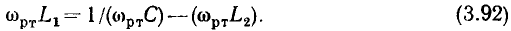
Решая уравнение (3.91), находим выражение для частоты резонанса токов:
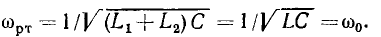
Таким образом, частота резонанса токов параллельного колебательного контура 2-го вида не зависит от коэффициента включения индуктивности и совпадает с резонансной частотой последовательного колебательного контура, построенного из тех же элементов, что и рассматриваемый колебательный контур.
В то время как частота резонанса токов 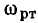 зависит от суммарной индуктивности контура
зависит от суммарной индуктивности контура 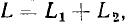 частота резонанса напряжений
частота резонанса напряжений 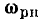 определяется только индуктивностью второй ветви
определяется только индуктивностью второй ветви 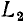 и, следовательно, зависит от коэффициента включения индуктивности:
и, следовательно, зависит от коэффициента включения индуктивности:
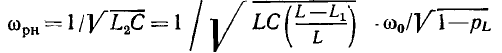
С уменьшением коэффициента включения индуктивности частота 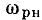 уменьшается, оставаясь большей, чем
уменьшается, оставаясь большей, чем 
Подставляя (3.92) в (3.90), найдем сопротивление рассматриваемого контура на частоте резонанса токов:
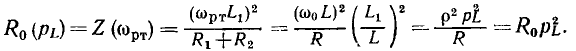
Здесь 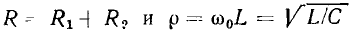 — суммарное сопротивление потерь и характеристическое сопротивление рассматриваемого контура, равные соответственно сопротивлению потерь и характеристическому сопротивлению последовательного колебательного контура, составленного из тех же элементов;
— суммарное сопротивление потерь и характеристическое сопротивление рассматриваемого контура, равные соответственно сопротивлению потерь и характеристическому сопротивлению последовательного колебательного контура, составленного из тех же элементов; 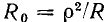 — резонансное сопротивление параллельного контура основного вида. Таким образом, резонансное сопротивление контура с неполным включением индуктивности
— резонансное сопротивление параллельного контура основного вида. Таким образом, резонансное сопротивление контура с неполным включением индуктивности 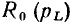 меньше, чем резонансное сопротивление контура основного типа
меньше, чем резонансное сопротивление контура основного типа 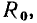 причем при
причем при 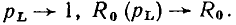
Амплитудно-частотные и фазо-частотные характеристики параллельного колебательного контура рассматриваемого типа приведены на рис. 3.34. На частотах ниже 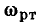 входное сопротивление контура определяется в основном сопротивлением ветви 1 и имеет резистивноиндуктивный характер. На частоте резонанса токов сопротивление контура достигает максимального значения
входное сопротивление контура определяется в основном сопротивлением ветви 1 и имеет резистивноиндуктивный характер. На частоте резонанса токов сопротивление контура достигает максимального значения 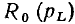 и имеет чисто резистивный характер. На частотах выше
и имеет чисто резистивный характер. На частотах выше 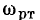 сопротивление контура определяется в основном параметрами ветви 2, причем при
сопротивление контура определяется в основном параметрами ветви 2, причем при 
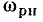 сопротивление контура имеет резистивно-емкостной характер, а на частотах выше частоты резонанса напряжений — резистивноиндуктивный. На частоте резонанса напряжений входное сопротивление контура имеет чисто резистивный характер и достигает минимального значения, определяемого сопротивлением потерь второй ветви.
сопротивление контура имеет резистивно-емкостной характер, а на частотах выше частоты резонанса напряжений — резистивноиндуктивный. На частоте резонанса напряжений входное сопротивление контура имеет чисто резистивный характер и достигает минимального значения, определяемого сопротивлением потерь второй ветви.
Покажем, что добротность параллельного колебательного контура с неполным включением индуктивности не зависит от коэффициента включения и равна добротности последовательного колебательного контура, составленного из тех же элементов. Пусть контур настроен на частоту источника сигнала, а напряжение и ток на входе контура определяются соотношениями
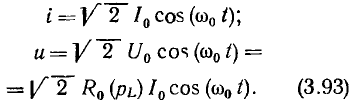
Токи ветвей контура i и 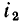 на резонансной частоте имеют одинаковые действующие значения
на резонансной частоте имеют одинаковые действующие значения
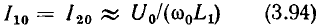
и отличаются по фазе на угол 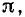 а напряжение на емкости
а напряжение на емкости 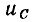 отстает по фазе от тока второй ветви на угол
отстает по фазе от тока второй ветви на угол 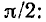
–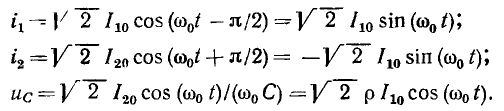
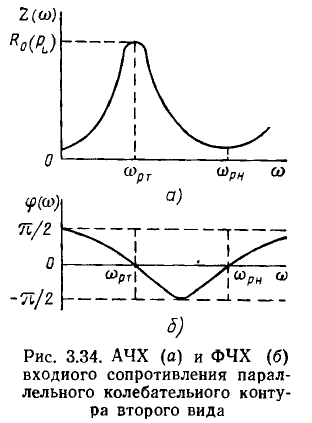
и энергию, потребляемую контуром за период Т:
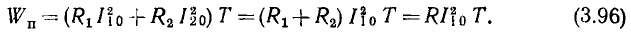
Подставляя (3.95) и (3.96) в (3.43), получим выражение для добротности параллельного колебательного контура с неполным включением индуктивности:
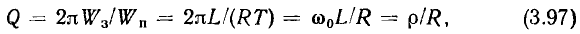
которое совпадает с выражением для добротности параллельного контура основного типа и соответственно с выражением для добротности последовательного колебательного контура, построенного из тех же элементов. Далее, используя (3.93), (3.94) и (3.97), найдем, что на резонансной частоте действующие значения токов ветвей контур; превышают действующее значение входного тока контура в 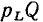 раз
раз
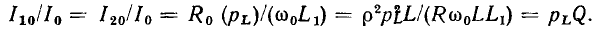
Итак, важнейшие параметры параллельного колебательного контура 2-го вида (частота резонанса токов, характеристическое сопротивление и добротность) не зависят от коэффициента включения индуктивности 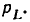 В то же время резонансное сопротивление контура является функцией
В то же время резонансное сопротивление контура является функцией 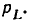
Указанная особенность параллельного колебательного контура широко используется на практике при согласовании его с источником энергии. Согласование осуществляют путем надлежащего выбора значения коэффициента включения, причем при изменении 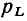 настройка контура и ширина его полосы пропускания, определяемая эффективной добротностью, не изменяются.
настройка контура и ширина его полосы пропускания, определяемая эффективной добротностью, не изменяются.
Наличие ярко выраженного минимума в АЧХ контура с неполным включением индуктивности может быть использовано для подавления колебаний, частота которых близка к 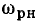 рассматриваемого контура.
рассматриваемого контура.
Параллельный колебательный контур третьего вида
Колебательный контур этого типа по своим свойствам в значительной степени подобен параллельному колебательному контуру второго вида. Используя эквивалентную схему контура, приведенную на рис. 3.35, нетрудно показать, что частота резонанса токов 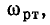 характеристическое сопротивление р и добротность Q параллельного колебательного контура с неполным включением емкости совпадают с резонансной частотой, характеристическим сопротивлением и добротностью последовательного колебательного контура, построенного из тех же элементов и, следовательно, обладающего теми же суммарной емкостью
характеристическое сопротивление р и добротность Q параллельного колебательного контура с неполным включением емкости совпадают с резонансной частотой, характеристическим сопротивлением и добротностью последовательного колебательного контура, построенного из тех же элементов и, следовательно, обладающего теми же суммарной емкостью 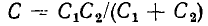 и суммарным сопротивлением
и суммарным сопротивлением 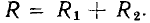
Частота резонанса напряжений
рассматриваемого контура определяется параметрами элементов второй ветви 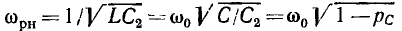
и зависит от коэффициента включения емкости
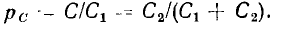
Резонансное сопротивление контура с неполным включением емкости так же, как и резонансное сопротивление контура с неполным включением индуктивности, пропорционально квадрату коэффициента включения
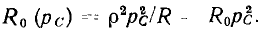
Здесь 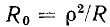 — резонансное сопротивление параллельного контура основного вида, обладающего той же индуктивностью L, суммарной емкостью С и суммарными сопротивлением R, что и рассматриваемый контур АЧХ и ФЧХ входного сопротивления параллельного колебательного контура с неполным включением емкости приведены на рис. 3.36. На частотах ниже
— резонансное сопротивление параллельного контура основного вида, обладающего той же индуктивностью L, суммарной емкостью С и суммарными сопротивлением R, что и рассматриваемый контур АЧХ и ФЧХ входного сопротивления параллельного колебательного контура с неполным включением емкости приведены на рис. 3.36. На частотах ниже 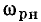 входное сопротивление обеих ветвей контура имеет резистивно-емкостной характер; на частоте резонанса напряжений входное сопротивление контура имеет чисто резистивный характер и достигает минимального значения, определяемого в основном сопротивлением потерь второй ветви; на частотах
входное сопротивление обеих ветвей контура имеет резистивно-емкостной характер; на частоте резонанса напряжений входное сопротивление контура имеет чисто резистивный характер и достигает минимального значения, определяемого в основном сопротивлением потерь второй ветви; на частотах 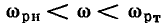 входное сопротивление контура имеет резистивно-индуктивный характер; при
входное сопротивление контура имеет резистивно-индуктивный характер; при 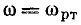 входное сопротивление контура имеет чисто резистивный характер и его модуль достигает максимального значения
входное сопротивление контура имеет чисто резистивный характер и его модуль достигает максимального значения 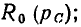 на частотах выше частоты резонанса токов входное сопротивление контура определяется в основном параметрами первой ветви и имеет резистивно-емкостной характер.
на частотах выше частоты резонанса токов входное сопротивление контура определяется в основном параметрами первой ветви и имеет резистивно-емкостной характер.
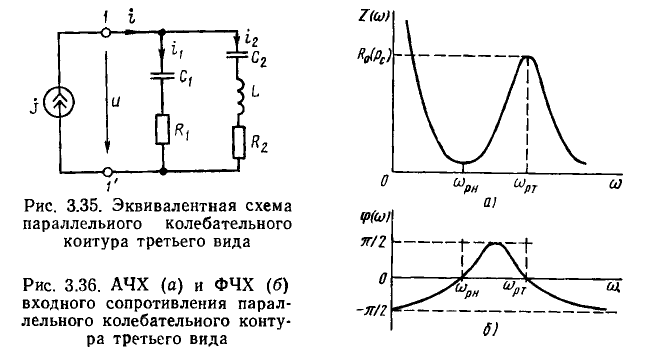
Связанные колебательные контуры
Общие представления о связанных контурах:
Два контура-электрической цепи называются связанными, если возбуждение колебаний в одном из них приводит к возникновению колебаний в другом. Каждый из связанных контуров может быть либо колебательным (если он содержит индуктивные катушки и конденсаторы), либо апериодическим (если он содержит реактивные элементы только одного типа). Наибольший практический интерес представляют связанные колебательные контуры, так как их избирательные свойства лучше, чем избирательные свойства одиночных колебательных контуров.
В зависимости от типа элемента, через который осуществляется взаимодействие между контурами, различают контуры с трансформаторной, индуктивной, емкостной и комбинированной (индуктивно-емкостной) связями. По способу включения элемента связи связанные контуры подразделяются на контуры с внешней связью и контуры с внутренней связью. Принципиальные электрические схемы связанных колебательных контуров некоторых типов приведены на рис. 3.37.
Внешнее воздействие на связанные колебательные контуры обычно задается в виде напряжения источника энергии Г, включенного в один из контуров, называемый первичным. В качестве реакции связанных контуров на внешнее действие рассматривают ток или напряжение одного из элементов другого контура, называемого вторичным.
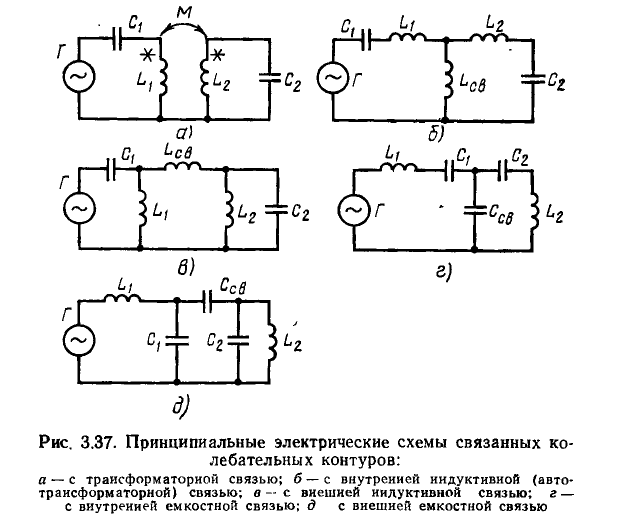
Каждому типу связанных колебательных контуров можно поставить в соответствие так называемый четырехполюсник связи (рис. 3.38), который получается из исходных контуров при их размыкании и устранении из контуров всех элементов, имеющих другой характер по сравнению с элементом связи.
Назовем коэффициентом передачи из первичного контура во вторичный 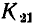 комплексный коэффициент передачи соответствующего четырехполюсника связи по напряжению от зажимов 1—1′ к зажимам 2—2′ (при холостом ходе на зажимах 2—2′)
комплексный коэффициент передачи соответствующего четырехполюсника связи по напряжению от зажимов 1—1′ к зажимам 2—2′ (при холостом ходе на зажимах 2—2′)
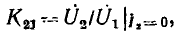
а коэффициентом передачи из вторичного контура в первичный — комплексный коэффициент передачи четырехполюсника связи по напряжению от зажимов 2 –2′ к зажимам 1—1′ (при холостом ходе на зажимах 1—1′)
Можно убедиться, что коэффициенты передачи  связанных контуров, схемы которых приведены на рис. 3.37, а—д, а соответствующие четырехполюсники связи — на рис. 3.38, а—д, являются действительными числами и не зависят от частоты.
связанных контуров, схемы которых приведены на рис. 3.37, а—д, а соответствующие четырехполюсники связи — на рис. 3.38, а—д, являются действительными числами и не зависят от частоты.
Среднее геометрическое из коэффициентов передачи  называется коэффициентом связи между контурами
называется коэффициентом связи между контурами

Коэффициент связи не зависит от частоты и используется для количественной оценки степени связи между контурами.
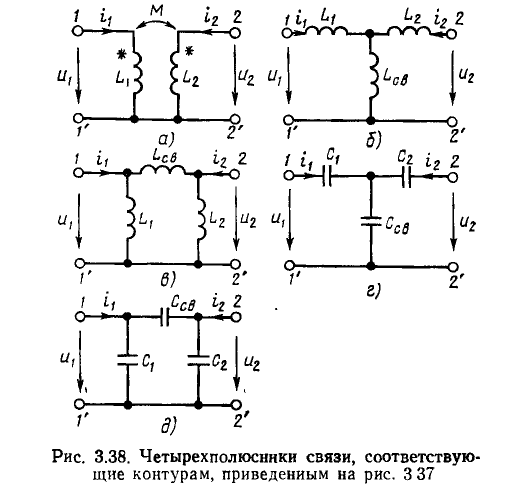
Для контуров с трансформаторной связью (см. рис. 3.37, а) при определении коэффициентов передачи 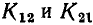 можно воспользоваться компонентным уравнением связанных индуктивностей (2.165)
можно воспользоваться компонентным уравнением связанных индуктивностей (2.165)
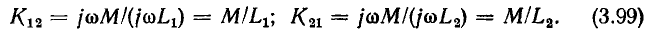
Подставляя (3.99) в (3.98), можно установить, что коэффициент связи между контурами с трансформаторной связью равен коэффициенту связи между входящими в эти контуры индуктивностями:

Анализируя четырехполюсники связи, найдем выражения для коэффициентов связи между контурами с внутренней индуктивной (автотрансформаторной) связью (см. рис. 3.37, б)
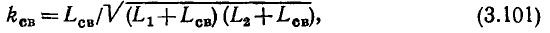
с внешней индуктивной связью (см. рис. 3.37, в)
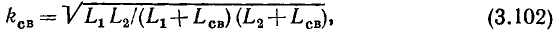
с внутренней емкостной связью (см. рис. 3.37, г)
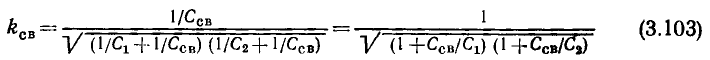
и с внешней емкостной связью
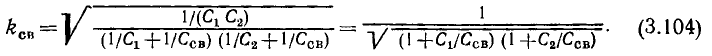
Из выражений (3.100)—(3.104) видно, что значение коэффициента связи между контурами 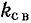 не может превышать единицы, причем с увеличением параметра элемента связи
не может превышать единицы, причем с увеличением параметра элемента связи 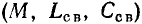 происходит увеличение
происходит увеличение 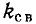 между контурами с трансформаторной, автотрансформаторной и внешней емкостной связями и уменьшение коэффициента связи между контурами с внешней индуктивной и внутренней емкостной связями.
между контурами с трансформаторной, автотрансформаторной и внешней емкостной связями и уменьшение коэффициента связи между контурами с внешней индуктивной и внутренней емкостной связями.
Схемы замещения связанных контуров
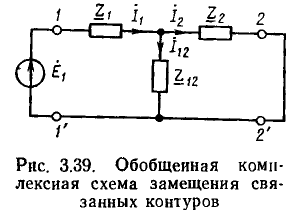
Для изучения процессов в связанных контурах различных типов воспользуемся их обобщенной комплексной схемой замещения (рис. 3.39), на которой 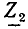 — компексное сопротивление элементов, входящих только во вторичный контур;
— компексное сопротивление элементов, входящих только во вторичный контур; 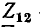 — комплексное сопротивление связи. Соответствие между элементами обобщенной схемы замещения и элементами контуров с внутренней индуктивной и внутренней емкостной связями устанавливается из сравнения рис. 3.39 с рис. 3.37, б, г; сопротивление
— комплексное сопротивление связи. Соответствие между элементами обобщенной схемы замещения и элементами контуров с внутренней индуктивной и внутренней емкостной связями устанавливается из сравнения рис. 3.39 с рис. 3.37, б, г; сопротивление 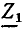 включает в себя внутреннее сопротивление источника энергии Г, а также комплексные сопротивления индуктивной катушки
включает в себя внутреннее сопротивление источника энергии Г, а также комплексные сопротивления индуктивной катушки 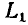 и конденсатора
и конденсатора 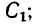 сопротивление
сопротивление 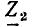 равно сумме комплексных сопротивлений индуктивной катушки
равно сумме комплексных сопротивлений индуктивной катушки 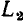 и конденсатора
и конденсатора 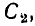 а сопротивление
а сопротивление 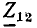 представляет собой комплексное сопротивление элемента связи индуктивной катушки
представляет собой комплексное сопротивление элемента связи индуктивной катушки 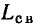 или конденсатора
или конденсатора 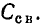 Чтобы обобщенную схему замещения можно было применять для анализа контуров с внешней индуктивной или емкостной связями, эти контуры должны быть (с помощью преобразования треугольник—звезда) заменены эквивалентными контурами с внутренней индуктивной или емкостной связями. Контуры с трансформаторной связью также можно преобразовать в эквивалентные им контуры с. внутренней индуктивной связью, используя рассмотренную ранее схему замещения связанных индуктивностей (см. рис. 2.49. в).
Чтобы обобщенную схему замещения можно было применять для анализа контуров с внешней индуктивной или емкостной связями, эти контуры должны быть (с помощью преобразования треугольник—звезда) заменены эквивалентными контурами с внутренней индуктивной или емкостной связями. Контуры с трансформаторной связью также можно преобразовать в эквивалентные им контуры с. внутренней индуктивной связью, используя рассмотренную ранее схему замещения связанных индуктивностей (см. рис. 2.49. в).
Воспользуемся обобщенной схемой замещения (рис. 3.39) для определения токов первичного и вторичного контуров. Уравнения баланса токов и напряжений рассматриваемой цепи имеют вид

Исключая из уравнений (3.105) ток сопротивления связи 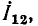 преобразуем их к более удобному виду
преобразуем их к более удобному виду
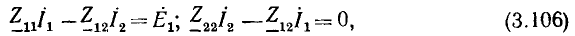
где 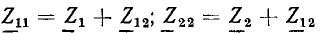 — соответственно собственные сопротивления первичного и вторичного контуров, равные сумме всех сопротивлений, входящих в каждый из контуров. Решая уравнения (3.106) относительно токов первичного и вторичного контуров, получаем
— соответственно собственные сопротивления первичного и вторичного контуров, равные сумме всех сопротивлений, входящих в каждый из контуров. Решая уравнения (3.106) относительно токов первичного и вторичного контуров, получаем
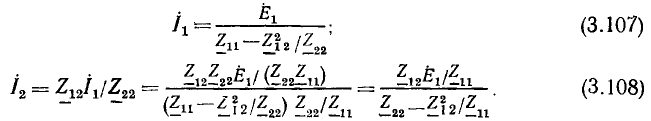
Рассмотрим более подробно структуру полученных выражений. Величина, стоящая в знаменателе выражения (3.107), имеет физический смысл входного сопротивления системы связанных контуров относительно точек 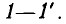 Эта величина отличаеся от собственного сопротивления первичного контура
Эта величина отличаеся от собственного сопротивления первичного контура 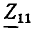 на некоторую добавку —
на некоторую добавку — 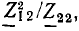 учитывающую влияние вторичного контура на процессы, протекающие в первичном. Нетрудно убедиться, что при размыкании вторичного контура —
учитывающую влияние вторичного контура на процессы, протекающие в первичном. Нетрудно убедиться, что при размыкании вторичного контура — 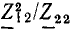 будет равно нулю и ток первичного контура будет равен
будет равно нулю и ток первичного контура будет равен 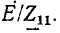 Аналогичным образом, величина —
Аналогичным образом, величина — 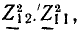 стоящая в знаменателе выражения (3.108), отражает влияние первичного контура на процессы, протекающие во вторичном контуре. Величины
стоящая в знаменателе выражения (3.108), отражает влияние первичного контура на процессы, протекающие во вторичном контуре. Величины
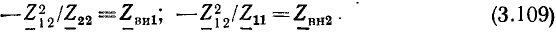
получили название вносимых сопротивлений.
Влияние первичного контура на процессы во вторичном контуре отражается не только введением в него некоторого дополнительного сопротивления 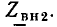 По аналогии с величиной, стоящей в числителе выражения (3.107), числитель выражения (3.108) может рассматривать как э. д. с. некоторого источника
По аналогии с величиной, стоящей в числителе выражения (3.107), числитель выражения (3.108) может рассматривать как э. д. с. некоторого источника

внесенного во вторичный контур под влиянием первичного. Напряжение вносимого источника 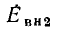 численно равно пряжению на сопротивлении связи
численно равно пряжению на сопротивлении связи 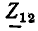 при разомкнутом вторичном контуре.
при разомкнутом вторичном контуре.
С учетом (3.109), (3.110) выражения для токов 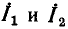 могут быт записаны в единообразной форме
могут быт записаны в единообразной форме
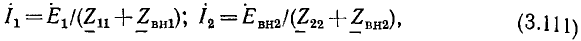
им можно поставить в соответствие эквивалентные схемы первичного и вторичного контуров, изображенные на рис. 3.40.
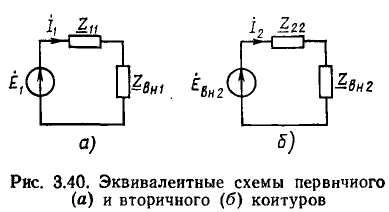
Представляя собственные сопротивления контуров в алгебраической форме
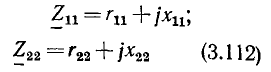
и полагая, что комплексное сопротивление связи имеет чисто реактивный характер
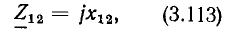
преобразуем выражения (3.109) к виду
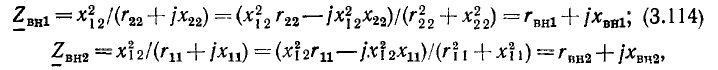
откуда
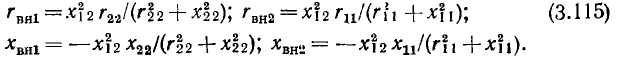
Из выражений (3.115) видно, что вещественные составляющие вносимых сопротивлений всегда положительны, а знаки реактивных составляющих вносимых сопротивлений 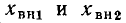 противоположны знакам реактивных составляющих собственных сопротивлений вторичного и первичного контуров
противоположны знакам реактивных составляющих собственных сопротивлений вторичного и первичного контуров 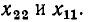 Если, например, при каком-то значении частоты внешнего воздействия собственное сопротивление первичного контура
Если, например, при каком-то значении частоты внешнего воздействия собственное сопротивление первичного контура 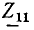 имеет резистивно-емкостной характер, то на этой же частоте сопротивление, вносимое во вторичный контур
имеет резистивно-емкостной характер, то на этой же частоте сопротивление, вносимое во вторичный контур 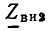 будет иметь резистивно-индуктивный характер.
будет иметь резистивно-индуктивный характер.
Используя (3.112)—(3.114), выразим токи первичного и вторичного контуров через вещественные и мнимые составляющие сопротивлений элементов обобщенной схемы замещения связанных контуров:
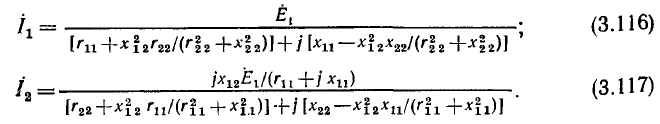
Настройка связанных контуров
Настройка системы связанных колебательных контуров заключается в выборе таких значений параметров элементов контуров, при которых ток вторичного контура достигает максимального значения при заданных частоте и действующем значении напряжения источника энергии. Настройку связанных контуров можно осуществлять как за счет изменения параметров реактивных элементов, входящих в один или в разные контуры, так и за счет совместного изменения параметров реактивных элементов контуров и параметров элементов связи. Рассмотрим основные способы настройки связанных контуров.
Настройку на первый частный резонанс осуществляют путем изменения параметров реактивных элементов, входящих только в первичный контур. Параметры элементов, входящих только во вторичный контур, и параметры элементов связи при настройке на первый частный резонанс не изменяются. Значение индуктивности 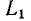 или емкости
или емкости 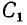 выбирают таким образом, чтобы сумма реактивной составляющей собственного сопротивления первичного контура
выбирают таким образом, чтобы сумма реактивной составляющей собственного сопротивления первичного контура 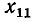 и реактивной составляющей сопротивления, вносимого в первый контур
и реактивной составляющей сопротивления, вносимого в первый контур 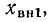 была равна нулю:
была равна нулю:
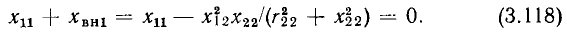
Этот способ настройки соответствует настройке на резонансную частоту контура, эквивалентного первичному (рис. 3.40, а). Входное сопротивление такого контура относительно зажимов, к которым подключен источник энергии, имеет чисто резистивный характер, а действующее значение тока первичного контура — максимально:
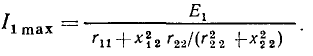
Как видно из выражения (3.108), ток вторичного контура прямо пропорционален току первичного контура, поэтому максимуму тока 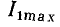 соответствует максимум тока
соответствует максимум тока 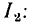
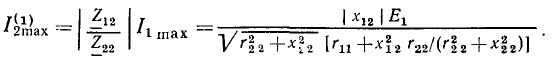
При настройке на второй частный резонанс максимальное значение тока вторичного контура получают путем изменения параметров реактивных элементов, входящих только во вторичный контур. Значение индуктивности 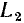 или емкости
или емкости 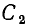 выбирают таким образом, чтобы обеспечить равенство нулю суммы реактивных составляющих собственного и вносимого сопротивлений вторичного контура:
выбирают таким образом, чтобы обеспечить равенство нулю суммы реактивных составляющих собственного и вносимого сопротивлений вторичного контура:
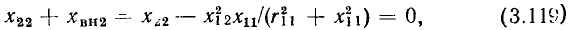
что соответствует настройке на частоту источника контура, эквивалентного вторичному. Действующее значение тока вторичного контура в этом случае
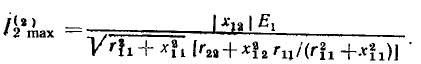
Настройку связанных контуров на первый или второй частные резонансы обычно выполняют только в тех случаях, когда конструкция устройства позволяет производить изменение параметров реактивных элементов только одного из контуров. Если можно изменять параметры реактивных элеменов, входящих в разные контуры, при фиксированном значении сопротивления связи, то производят настройку контуров на индивидуальный резонанс. Параметры реактивных элементов в этом случае выбирают так, чтобы обеспечить равенство нулю мнимой составляющей собственного сопротивления каждого из контуров при разомкнутом другом контуре:

Из выражений (3.115) видно, что выполнение условия (3,120) обеспечивает равенство нулю мнимых составляющих сопротивлений, вносимых в каждый из контуров:

Таким образом, при настройке связанных колебательных контуров на идеальный резонанс одновременно выполняются условия настройки контуров на первый и второй частные резонансы (3.118), (3.119).
Подставляя (3.120), (3.121) в выражение (3.117), найдем действующее значение тока вторичного контура при настройке на индивидуальный резонанс: 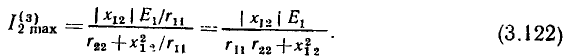
Настройка связянных контуров на первый и второй частные или на индивидуальный резонансы позволяет получить максимальное значение тока вторичного контура, соответствующее некоторому заданному значению сопротивления связи, однако не позволяет достигнуть наибольшего возможного (максимум максиморум) значения тока 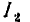 .
.
Если настройка связанных контуров на первый или второй частные резонансы сопровождается последующим выбором оптимального сопротивления связи, то говорят о настройке контуров на сложный резонанс. Определим оптимальное сопротивление связи при сложном резонансе резонансе 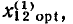 соответствующее случаю, когда связанные контуры предварительно настроены на первый частный резонанс. Приравнивая к нулю первую производную по
соответствующее случаю, когда связанные контуры предварительно настроены на первый частный резонанс. Приравнивая к нулю первую производную по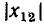 тока вторичного контура, настроенного на первый частный резонанс, получаем
тока вторичного контура, настроенного на первый частный резонанс, получаем
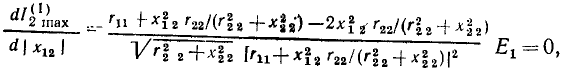
откуда
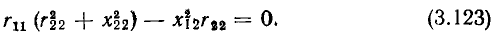
Решая уравнение (3.123), находим оптимальное сопротивление связи
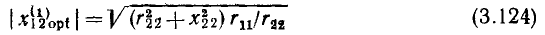
и соответствующее ему действующее значение тока вторичного контура
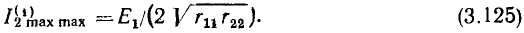
Если связанные контуры были предварительно Настроены на второй частный резонанс, то оптимальное сопротивление связи 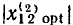 и действующее значение тока вторичного контура
и действующее значение тока вторичного контура 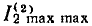 при настройке на сложный резонанс определяются выражениями:
при настройке на сложный резонанс определяются выражениями:
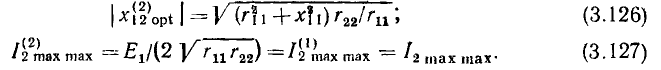
Итак, наибольшее возможное значение тока вторичного контура при настройке на сложный резонанс не зависит от того, какой из контуров был предварительно настроен на частный резонанс.
Наибольший практический интерес представляет настройка связанных колебательных контуров на полный резонанс, которая выполняется в два этапа: на первом этапе связанные контуры настраивают на индивидуальный резонанс, а затем выбирают оптимальное сопротивление связи между ними. Анализируя выражение (3.122), найдем 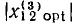 и действующее значение тока вторичного контура, соответствующие настройке контура на полный резонанс:
и действующее значение тока вторичного контура, соответствующие настройке контура на полный резонанс:
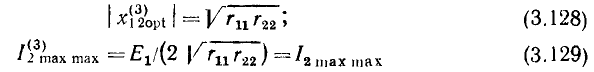
Из выражений (3.124)—(3.129) следует, что как при настройке на сложный резонанс, так и при настройке на полный резонанс во вторичном контуре достигается одно и то же значение тока 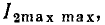 однако в последнем случае это имеет место при меньшем значении сопротивления связи.
однако в последнем случае это имеет место при меньшем значении сопротивления связи.
Зависимость тока вторичного контура от абсолютного значения сопротивления связи при настройке на полный или сложный резонансы иллюстрируется кривыми, приведенными на рис. 3.41, в. Как следует из выражений (3.110), (3.115), с ростом сопротивления связи э. д. с., вносимая во вторичный контур, возрастает по линейному закону (рис. 3.41, а), а вещественная составляющая вносимого во вторичный контур сопротивления — по квадратичному (рис. 3.41,6). При сопротивлении связи, меньшем оптимального, суммарное сопротивление вторичного контура 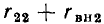 определяется в основном собственным сопротивлением вторичного контура
определяется в основном собственным сопротивлением вторичного контура 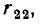 поэтому с ростом сопротивления связи происходит увеличение тока вторичного контура (рис. 3.41, в). При сопротивлении связи, большем оптимального, суммарное сопротивление вторичного контура определяется в основном сопротивлением, вносимым во вторичный контур
поэтому с ростом сопротивления связи происходит увеличение тока вторичного контура (рис. 3.41, в). При сопротивлении связи, большем оптимального, суммарное сопротивление вторичного контура определяется в основном сопротивлением, вносимым во вторичный контур 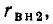 которое с увеличением
которое с увеличением 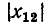 растет быстрее, чем вносимая в контур э. д. с. Вследствие этого при сопротивлении связи, большем
растет быстрее, чем вносимая в контур э. д. с. Вследствие этого при сопротивлении связи, большем 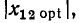 дальнейший рост
дальнейший рост 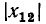 приводит к уменьшению тока вторичного контура.
приводит к уменьшению тока вторичного контура.
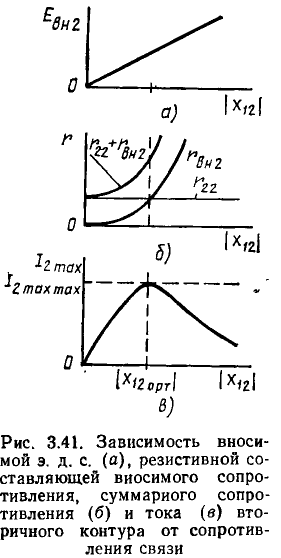
Найдем значение коэффициента связи между контурами 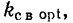 соответствующее настройке контуров на полный резонанс. Анализ выражений (3.101) и (3.103) показывает, что для контуров с. внутренней емкостной и индуктивной связями коэффициент связи между контурами равен отношению сопротивления связи к среднему геометрическому реактивных сопротивлений того же типа обоих контуров. Если связанные контуры настроены на индивидуальный резонанс, то с учетом (3.120) сопротивление емкостных элементов каждого из них равно по абсолютному значению сопротивлению индуктивных элементов и приблизительно равно характеристическому сопротивлению контура. Таким образом, для контуров с внутренней емкостной и индуктивной связями можно записать
соответствующее настройке контуров на полный резонанс. Анализ выражений (3.101) и (3.103) показывает, что для контуров с. внутренней емкостной и индуктивной связями коэффициент связи между контурами равен отношению сопротивления связи к среднему геометрическому реактивных сопротивлений того же типа обоих контуров. Если связанные контуры настроены на индивидуальный резонанс, то с учетом (3.120) сопротивление емкостных элементов каждого из них равно по абсолютному значению сопротивлению индуктивных элементов и приблизительно равно характеристическому сопротивлению контура. Таким образом, для контуров с внутренней емкостной и индуктивной связями можно записать
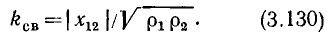
Выражение (3.130) можно использовать и при расчетах связанных контуров других типов, предварительно преобразовав их в эквивалентные контуры с внутренней связью. При настройке связанных контуров на полный резонанс (3.130) принимает вид
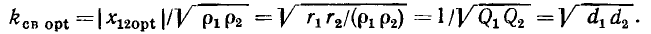
Если первичный и вторичный контуры имеют одинаковую добротность 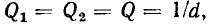 то оптимальный коэффициент связи между контурами, соответствующий настройке на полный резонанс, равен затуханию контура d:
то оптимальный коэффициент связи между контурами, соответствующий настройке на полный резонанс, равен затуханию контура d:

Величина

получила название параметра связи. Как видно из выражения (3.131), при настройке связанных контуров на полный резонанс А = 1.
Частотные характеристики связанных контуров
Рассмотрим зависимость тока вторичного контура от частоты для случая, когда параметры обоих контуров одинаковы:
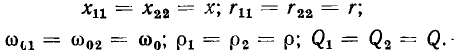
Собственные сопротивления первичного и вторичного контуров в этом случае могут быть представлены в следующей форме:
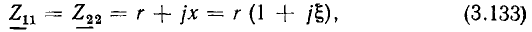
где 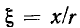 — обобщенная расстройка.
— обобщенная расстройка.
Подставляя (3.113), (3.133) в (3.108), найдем выражения для комплексного действующего значения
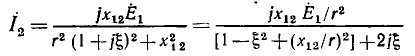
и действующего значения
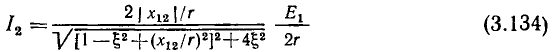
тока вторичного контура. Принимая во внимание, что 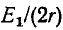 есть наибольшее возможное значение тока вторичного контура
есть наибольшее возможное значение тока вторичного контура
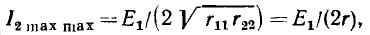
a 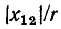 с учетом соотношений (3.130) и (3.132) приблизительно равно параметру связи
с учетом соотношений (3.130) и (3.132) приблизительно равно параметру связи
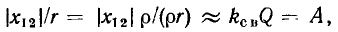
выражение (3.134) можно записать в более компактной форме
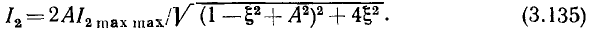
Очевидно, что экстремумы функции 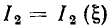 совпадают с экстремумами знаменателя выражения (3.135). Приравнивая нулю первую производную знаменателя по
совпадают с экстремумами знаменателя выражения (3.135). Приравнивая нулю первую производную знаменателя по 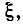 получим
получим 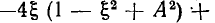
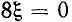 или
или
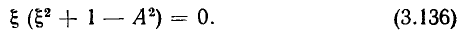
Уравнение (3.136) имеет три решения:
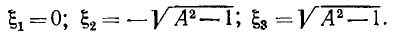
Первое из них соответствует случаю, когда 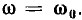 Второе и третье решения имеют физический смысл только при
Второе и третье решения имеют физический смысл только при 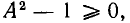 т. е. когда параметр связи не меньше некоторого критического значения
т. е. когда параметр связи не меньше некоторого критического значения 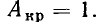
Таким образом, при больших значениях параметра связи 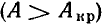 функция
функция 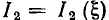 имеет три экстремума, а при малых значениях параметра связи
имеет три экстремума, а при малых значениях параметра связи  — один. При
— один. При 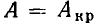 все три решения уравнения (3.136) совпадают и функция
все три решения уравнения (3.136) совпадают и функция 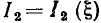 имеет один экстремум. Отметим, что критическое значение параметра связи соответствует оптимальной связи между контурами при настройке на полный резонанс.
имеет один экстремум. Отметим, что критическое значение параметра связи соответствует оптимальной связи между контурами при настройке на полный резонанс.
Зависимость нормированного тока вторичного контура
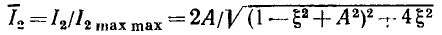
от обобщенной расстройки 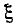 показана на рис. 3.42.
показана на рис. 3.42.
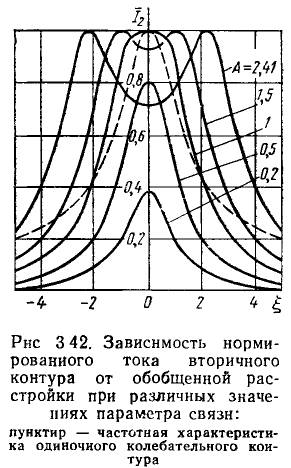
При слабой связи между контурами  частотные характеристики
частотные характеристики 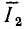 имеют вид «одногорбых» кривых, причем максимальное значение тока вторичного контура, достигаемое на резонансной частоте
имеют вид «одногорбых» кривых, причем максимальное значение тока вторичного контура, достигаемое на резонансной частоте 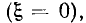 меньше, чем
меньше, чем 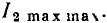 С увеличением параметра связи вплоть до
С увеличением параметра связи вплоть до 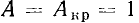 значения тока
значения тока 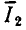 в максимуме увеличиваются, а кривые остаются «одногорбыми». При А=
в максимуме увеличиваются, а кривые остаются «одногорбыми». При А=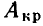 ток вторичного контура на резонансной частоте
ток вторичного контура на резонансной частоте 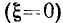 равен
равен 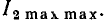 При дальнейшем увеличении связи между контурами ток вторичного контура на резонансной частоте
При дальнейшем увеличении связи между контурами ток вторичного контура на резонансной частоте  начнет уменьшаться и частотные характеристики
начнет уменьшаться и частотные характеристики 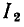 приобретут вид «двугорбых» кривых. Максимальное значение тока
приобретут вид «двугорбых» кривых. Максимальное значение тока 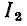
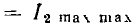 достигается на частотах связи, соответствующих обобщенным расстройкам
достигается на частотах связи, соответствующих обобщенным расстройкам 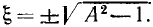 Физически существование максимумов тока
Физически существование максимумов тока 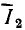 на частотах связи объясняется тем, что на них реактивная составляющая собственного сопротивления каждого из контуров компенсируется реактивной составляющей вносимого сопротивления. С увеличением параметра связи А при сильной связи между контурами
на частотах связи объясняется тем, что на них реактивная составляющая собственного сопротивления каждого из контуров компенсируется реактивной составляющей вносимого сопротивления. С увеличением параметра связи А при сильной связи между контурами 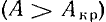 максимальное значение тока вторичного контура, достигаемое на частотах связи, остается равным
максимальное значение тока вторичного контура, достигаемое на частотах связи, остается равным 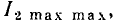 расстояние между максимумами увеличивается, а значение тока
расстояние между максимумами увеличивается, а значение тока 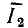 на резонансной частоте
на резонансной частоте  в соответствии с кривой, изображенной на рис. 3.41, в, уменьшается. При А > 2,41 значение
в соответствии с кривой, изображенной на рис. 3.41, в, уменьшается. При А > 2,41 значение 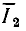 на резонансной частоте упадет ниже
на резонансной частоте упадет ниже 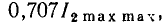 при этом полоса пропускания связанных контуров распадется на два участка.
при этом полоса пропускания связанных контуров распадется на два участка.
По сравнению с одиночными колебательными контурами связанные контуры обладают существенно лучшими избирательными свойствами, форма их нормированных АЧХ намного ближе к прямоугольной и имеет большую крутизну склонов на границах полосы пропускания.
Дополнительное удобство состоит в возможности плавно изменять ширину полосы пропускания за счет изменения коэффициента связи между контурами. Это обусловило широкое применение связанных контуров в различных радиотехнических устройствах.
Временные и частотные характеристики линейных электрических цепей
Свойства электрических цепей удобно изучать по их реакции на воздействия, изменение которых во времени описывается простейшими законами. Как показано далее, кроме упрощения собственно анализа, по реакции на эти воздействия оказывается возможным найти реакцию цепи на произвольное воздействие.
Определение:
Простейшие воздействия, реакция на которые полностью характеризуют все свойства цепи, называются типовыми, или испытательными воздействиями.
В теории электрических цепей в качестве типовых используются прямоугольные однополярные импульсные воздействия и отрезок гармонического колебания.
Определение:
Однополярным прямоугольным импульсом напряжения или тока называется такое однополярное воздействие, значение которого на некотором конечном интервале времени неизменно и вне этого интервала равно нулю.
Единичный скачок (ступенчатое воздействие)
Единичный скачок ( ступенчатое воздействие, или перепад )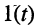 определяется функцией Хэвисайда
определяется функцией Хэвисайда (15.1). Единичный скачок, как и всякое иное воздействие, может появиться на входе цепи как в момент
(15.1). Единичный скачок, как и всякое иное воздействие, может появиться на входе цепи как в момент 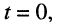 принятый за начало отсчёта времени, так и спустя некоторое время
принятый за начало отсчёта времени, так и спустя некоторое время 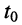 относительно начала отсчёта. В первом случае говорят, что скачок (воздействие) является незадержанным (рис. 15.1, а), а во втором — задержанным на
относительно начала отсчёта. В первом случае говорят, что скачок (воздействие) является незадержанным (рис. 15.1, а), а во втором — задержанным на 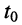 (рис. 15.1, б).
(рис. 15.1, б).
 Хэвисайд О. (1850—1925) — английский физик.
Хэвисайд О. (1850—1925) — английский физик.
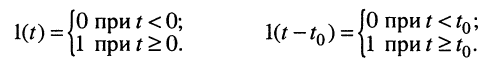 (15.1)
(15.1)
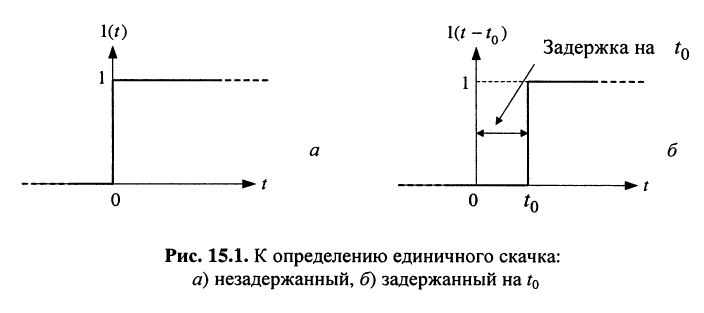
В соответствии с определением (15.1) произведение любой ограниченной во времени функции 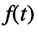 на функцию Хэвисайда представляет собой саму функцию при
на функцию Хэвисайда представляет собой саму функцию при 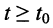 и равно нулю при
и равно нулю при 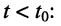
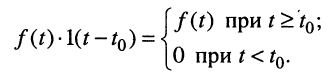 (15.2)
(15.2)
По этой причине функцию Хэвисайда используют для аналитического представления внешних воздействий, значения которых равны нулю до коммутации (момента подключения) и скачкообразно изменяются в момент коммутации.
Реализация скачка (перепада) напряжения и тока изображена на рис. 15.2: замыкание ключа соответствует коммутации источника напряжения (рис. 15.2, а), а размыкание ключа — коммутации источника тока (рис. 15.2, в) с электрической цепью. Схемные изображения источников ступенчатых воздействий напряжения и тока показаны на рис. 15.2, б и г соответственно, где напряжение источника напряжения и ток источника тока могут быть представлены через функцию Хэвисайда 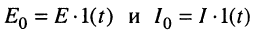 соответственно.
соответственно.
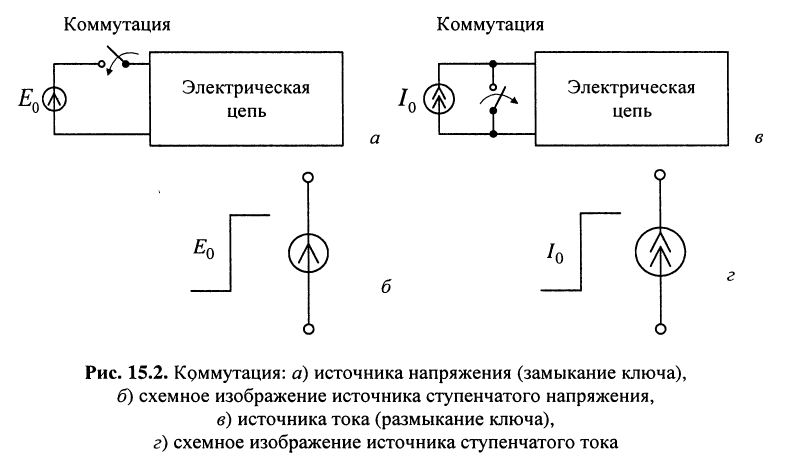
Единичный импульс ( -функция, функция Дирака)
-функция, функция Дирака)
Пусть на цепь в момент 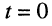 воздействует прямоугольный импульс
воздействует прямоугольный импульс 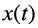 высоты X и длительностью
высоты X и длительностью 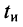 (рис. 15.3, а). Такой импульс называется видеоимпульсом. Его можно представить в виде разности двух одинаковых по высоте скачков, один из которых задержан (сдвинут) на
(рис. 15.3, а). Такой импульс называется видеоимпульсом. Его можно представить в виде разности двух одинаковых по высоте скачков, один из которых задержан (сдвинут) на 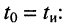
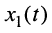 (рис. 15.3,6) и
(рис. 15.3,6) и 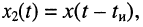 причём
причём

Рассмотрим видеоимпульс 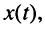 длительность которого
длительность которого 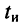 и высота
и высота 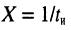 (рис. 15.4, а). Ясно, что площадь такого импульса равна 1 и не зависит от его длительности, поскольку уменьшение длительности импульса приводит к увеличению его высоты.
(рис. 15.4, а). Ясно, что площадь такого импульса равна 1 и не зависит от его длительности, поскольку уменьшение длительности импульса приводит к увеличению его высоты.
Определение:
Импульс бесконечно малой длительности 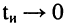 и бесконечно большой высоты
и бесконечно большой высоты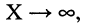 площадь которого равна единице, называется единичным импульсом.
площадь которого равна единице, называется единичным импульсом.
Единичный импульс (рис. 15.4,6) определяется функцией 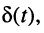 которая называется
которая называется 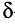 -функцией, или функцией Дирака
-функцией, или функцией Дирака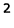 :
:
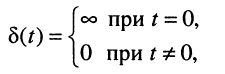 (15.3)
(15.3)
а её задержанный вариант имеет вид:
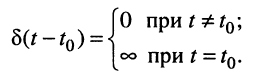 (15.4)
(15.4)
Задержанная на 
 -функция
-функция 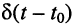 показана на рис. 15.4, в.
показана на рис. 15.4, в.
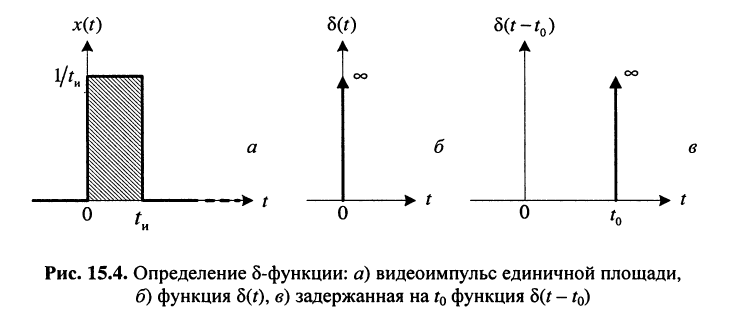
Из определения 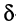 -функции следуют её свойства:
-функции следуют её свойства:
при всех значениях 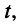 не равных
не равных 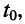 она равна нулю;
она равна нулю;
при 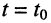 принимает бесконечно большое значение;
принимает бесконечно большое значение;
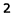 Поль Адриен Морис Дирак (1902—1984) — английский физик, Нобелевский лауреат по физике, 1933 г. (совместно с Э. Шредингером).
Поль Адриен Морис Дирак (1902—1984) — английский физик, Нобелевский лауреат по физике, 1933 г. (совместно с Э. Шредингером).
интеграл от 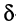 -функции равен единице:
-функции равен единице:
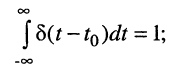 (15.5)
(15.5)
для любой непрерывной на всей оси 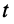 функции
функции 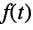 имеет место равенство
имеет место равенство
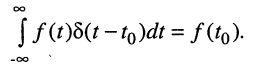 (15.6)
(15.6)
Важно:
свойство, отображаемое равенством (15.6), называется фильтрующим (избирательным, селективным) свойством 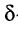 -функции, смысл которого заключается в том, что
-функции, смысл которого заключается в том, что 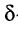 -функция ставит в соответствие каждой функции
-функция ставит в соответствие каждой функции 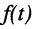 число
число 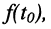 т. е. выбирает то значение функции
т. е. выбирает то значение функции 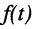 , которое приходится на момент
, которое приходится на момент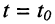 (рис. 15.5).
(рис. 15.5).
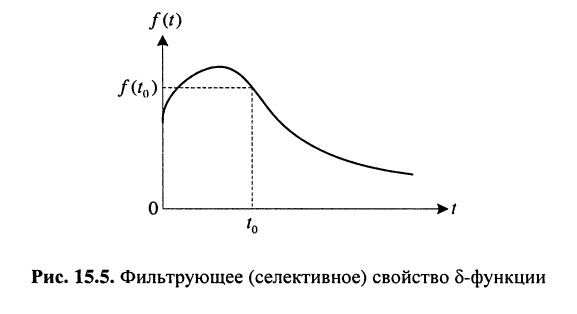
Генерирование единичного импульса согласно его определению неосуществимо, однако его моделью могут служить очень короткие однополярные импульсы, создаваемые источниками импульсного напряжения или тока, схемные изображения которых показаны на рис. 15.6.
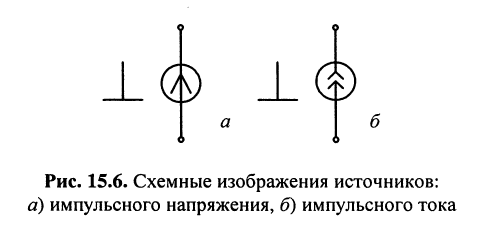
Связь между единичным скачком и единичным импульсом
Во многих приложениях появляется необходимость перехода от единичного скачка 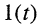 к единичному импульсу
к единичному импульсу 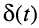 и наоборот. Установим связь между этими воздействиями, помня, что они представляются функциями Хэвисайда и Дирака.
и наоборот. Установим связь между этими воздействиями, помня, что они представляются функциями Хэвисайда и Дирака.
Представим единичный импульс 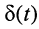 в виде предельного перехода разности двух единичных скачков высотой
в виде предельного перехода разности двух единичных скачков высотой 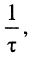 сдвинутых относительно друг друга на время
сдвинутых относительно друг друга на время 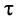 (рис. 15.7):
(рис. 15.7):
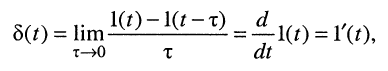 (15.7)
(15.7)
т. е. единичный импульс (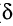 -функция) равен производной единичного скачка (функции Хэвисайда). Отсюда ясно, что единичный скачок равен интегралу от
-функция) равен производной единичного скачка (функции Хэвисайда). Отсюда ясно, что единичный скачок равен интегралу от 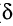 -функции:
-функции:
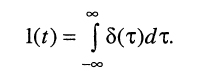 (15.7а)
(15.7а)
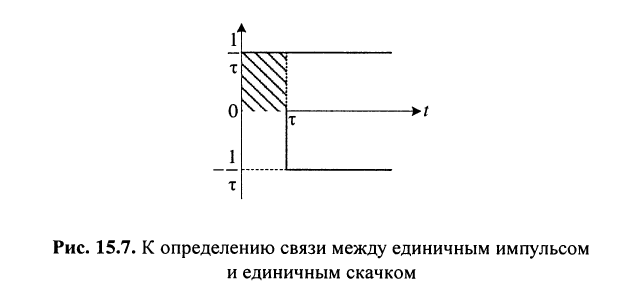
Отрезок гармонического колебания
Отрезок гармонического колебания (рис. 15.8) определяется функцией вида
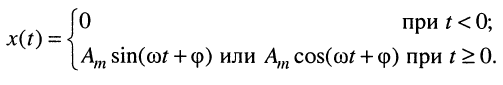 (15.8)
(15.8)
Важно:
воздействия в виде отрезков гармонического колебания не являются периодическими, поскольку вблизи точки разрыва 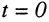 условие периодичности
условие периодичности
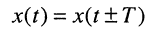
не выполняется.
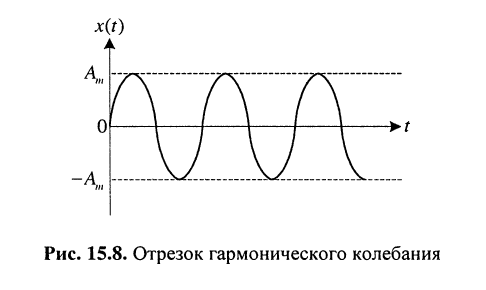
Описание процессов с помощью интегро-дифференциальных уравнений
В предыдущих лекциях рассматривались принципы анализа электрических цепей при воздействии постоянных или гармонических токов и напряжений. Если воздействие произвольное, то найти реакцию цепи с применением, например, метода комплексных амплитуд, невозможно. В таком случае необходимо использовать временное описание цепи в виде интегро-дифференциальных уравнений с учётом определения мгновенных токов и напряжений на реактивных элементах. Рассмотрим два примера.
Пример 15.1.
Найти ток 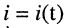 в последовательном колебательном контуре (рис. 15.9, а) при произвольном воздействии
в последовательном колебательном контуре (рис. 15.9, а) при произвольном воздействии 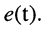
Решение. Согласно второму закону Кирхгофа для последовательного колебательного контура справедливо следующее равенство:
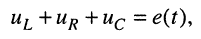
где напряжения на элементах цепи являются функциями времени 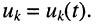 Выразив напряжения на элементах через ток в цепи
Выразив напряжения на элементах через ток в цепи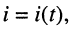 получим неоднородное линейное интегро-дифференциальное уравнение с постоянными коэффициентами:
получим неоднородное линейное интегро-дифференциальное уравнение с постоянными коэффициентами:
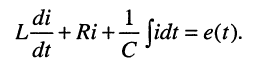 (15.9)
(15.9)
Чтобы освободиться от интеграла, продифференцируем уравнение (15.9). Тогда получим неоднородное линейное дифференциальное уравнение второго порядка
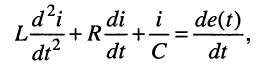 (15.10)
(15.10)
которое необходимо решить относительно тока 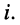
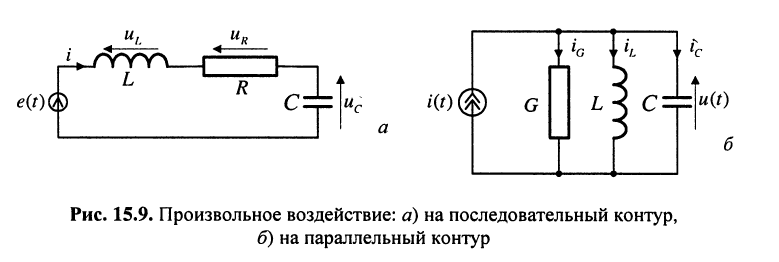
Пример 15.2.
Найти напряжение 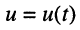 на параллельном колебательном контуре (рис. 15.9, б) при произвольном воздействии
на параллельном колебательном контуре (рис. 15.9, б) при произвольном воздействии 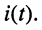
Решение. Согласно первому закону Кирхгофа для параллельного колебательного контура справедливо следующее равенство:
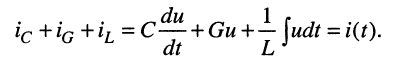 (15.11)
(15.11)
Освободимся от интеграла в (15.11) путём его дифференцирования. Тогда, как и в примере 15.1, получим неоднородное линейное дифференциальное уравнение второго порядка относительно напряжения 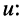
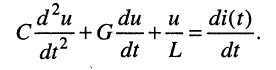 (15.12)
(15.12)
Видно, что уравнения (15.10) и (15.12) имеют одинаковый вид и дуальны, что является следствием дуальности последовательного и параллельного контуров. Решения этих уравнений определяют законы изменения тока и напряжения в последовательном и параллельном контурах соответственно.
Если отвлечься от физической сущности входящих в уравнения (15.10) и (15.12) коэффициентов и переменных, эти уравнения можно записать в обобщённом виде
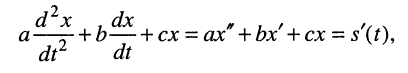 (15.13)
(15.13)
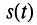 — воздействие;
— воздействие;
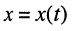 — искомый ток или напряжение;
— искомый ток или напряжение;
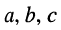 — коэффициенты, соответствующие значениям реактивных и активных элементов.
— коэффициенты, соответствующие значениям реактивных и активных элементов.
Из математического анализа известно, что любое дифференциальное уравнение имеет бесконечное число решений. Для получения единственного решения согласно теореме существования и единственности необходимо задать начальные условия, т. е. начальные значения переменной 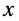 и всех её производных. Физически это означает характеристику состояния электрической цепи на момент подачи воздействия
и всех её производных. Физически это означает характеристику состояния электрической цепи на момент подачи воздействия 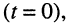 а именно — значения токов и напряжений, действующих в цепи. (Состоянием цепи или системы называют множество свойств и функций системы в данный момент времени.) Чаще всего при анализе процессов в электрических цепях используют нулевые начальные состояния цепи (системы) в момент
а именно — значения токов и напряжений, действующих в цепи. (Состоянием цепи или системы называют множество свойств и функций системы в данный момент времени.) Чаще всего при анализе процессов в электрических цепях используют нулевые начальные состояния цепи (системы) в момент 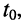 или нулевые начальные условия.
или нулевые начальные условия.
Определение:
Нулевыми начальными условиями называется такое состояние электрической цепи в момент 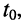 при котором значения всех напряжений на ёмкостях и токов в индуктивностях равны нулю:
при котором значения всех напряжений на ёмкостях и токов в индуктивностях равны нулю: 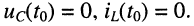
Смысл нулевых начальных условий состоит в том, что цепь к моменту приложения воздействия, т. е. к моменту коммутации, находится в состоянии покоя. Отсюда следует признак нулевых начальных условий:
нулевому воздействию соответствует нулевая реакция.
Импульсная характеристика и интеграл свёртки
Определение:
Импульсной характеристикой цепи 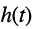 называется реакция цепи на единичный импульс (
называется реакция цепи на единичный импульс (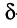 -функцию) при нулевых начальных условиях (рис. 15.10, а).
-функцию) при нулевых начальных условиях (рис. 15.10, а).
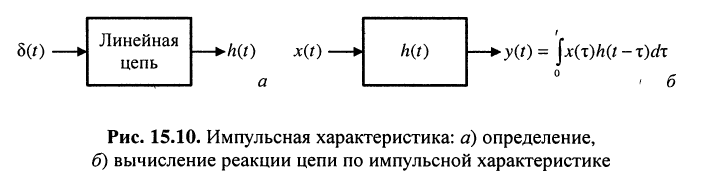
Импульсная характеристика является основной характеристикой линейной электрической цепи, поскольку её знание позволяет определить реакцию цепи 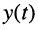 на произвольное воздействие
на произвольное воздействие 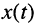 (рис. 15.10, б).
(рис. 15.10, б).
Получим формулу для вычисления реакции цепи по её импульсной характеристике, для чего воспользуемся свойствами инвариантности во времени (стационарности), однородности и аддитивности (наложения) линейных систем (см. лекцию 1). При выводе формулы будем последовательно (с помощью знака 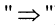 ) записывать соответствия между воздействием и реакцией:
) записывать соответствия между воздействием и реакцией:
по определению реакция на 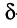 -функцию является импульсной характеристикой
-функцию является импульсной характеристикой
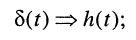
согласно свойству инвариантности во времени (стационарности) линейных систем воздействию, задержанному на время 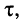 соответствует реакция, задержанная на это же время
соответствует реакция, задержанная на это же время
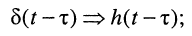
по свойству однородности линейных систем умножению воздействия на величину x(t) соответствует реакция, умноженная на ту же величину
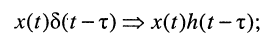
на основании свойства аддитивности (наложения) линейных систем интегралу от воздействия соответствует интеграл от реакции (заметим, что собственно интегрирование обладает свойством аддитивности)
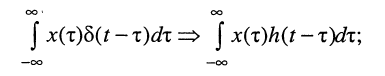
в полученном соответствии слева согласно свойству фильтрации 5-функции имеем воздействие в момент 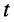
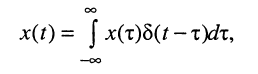
а справа имеем реакцию в момент t
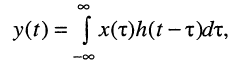
наконец, для физически реализуемых систем время воздействия, а потому и время реакции, ограничено отрезком 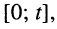 поэтому окончательно получаем:
поэтому окончательно получаем:
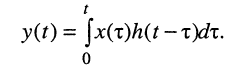 (15.14)
(15.14)
Можно показать, что справедливо равенство:
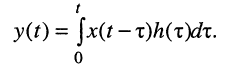 (15.14 а)
(15.14 а)
Выражения (15.14) называются уравнениями свёртки, или просто свёрткой, а интеграл, стоящий справа, — интегралом свёртки. Для свёртки 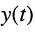 двух функций
двух функций 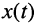 и
и 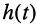 принята следующая краткая запись:
принята следующая краткая запись:
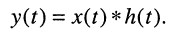 (15.15)
(15.15)
Переходная характеристика и интеграл Дюамеля
Определение:
Переходной характеристикой цепи 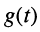 называется реакция цепи на единичный скачок
называется реакция цепи на единичный скачок 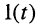 (функцию Хэвисайда) при нулевых начальных условиях (рис. 15.11, а).
(функцию Хэвисайда) при нулевых начальных условиях (рис. 15.11, а).
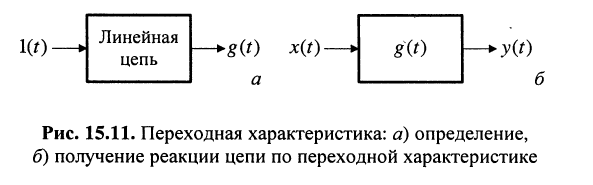
Переходная характеристика, как и импульсная характеристика, позволяет определить реакцию цепи 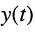 на произвольное воздействие
на произвольное воздействие 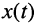 (рис. 15.11,6). Кроме того, знание переходной характеристики позволяет изучить процессы, происходящие в цепи при переходе цепи из одного установившегося режима к другому, и определить длительность такого процесса, который называется переходным процессом, а сопутствующие ему токи и напряжения на отдельных участках цепи — переходными напряжениями и токами. Причина этого явления заключается в том, что накопление энергии электрического (в ёмкостях) и магнитного (в индуктивностях) полей не может происходить мгновенно. Необходимая длительность переходного процесса определяется назначением цепи, хотя обычно стремятся к достижению минимально возможной длительности.
(рис. 15.11,6). Кроме того, знание переходной характеристики позволяет изучить процессы, происходящие в цепи при переходе цепи из одного установившегося режима к другому, и определить длительность такого процесса, который называется переходным процессом, а сопутствующие ему токи и напряжения на отдельных участках цепи — переходными напряжениями и токами. Причина этого явления заключается в том, что накопление энергии электрического (в ёмкостях) и магнитного (в индуктивностях) полей не может происходить мгновенно. Необходимая длительность переходного процесса определяется назначением цепи, хотя обычно стремятся к достижению минимально возможной длительности.
Чтобы получить формулу для вычисления реакции цепи по её переходной характеристике, предварительно выразим переходную характеристику через импульсную характеристику 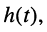 для чего воспользуемся формулой свёртки (15.14, а), когда известна импульсная характеристика
для чего воспользуемся формулой свёртки (15.14, а), когда известна импульсная характеристика 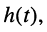 а воздействием является единичный скачок
а воздействием является единичный скачок 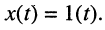 При этих условиях получаем формулу для переходной характеристики
При этих условиях получаем формулу для переходной характеристики
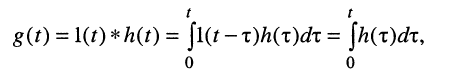 (15.16)
(15.16)
откуда
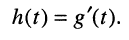 (15.17)
(15.17)
Полученная связь справедлива при нулевых начальных условиях, когда 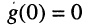 (рис. 15.12, а). При ненулевых начальных условиях (рис. 15.12,6), когда
(рис. 15.12, а). При ненулевых начальных условиях (рис. 15.12,6), когда 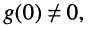 переходную характеристику можно представить в виде суммы:
переходную характеристику можно представить в виде суммы:
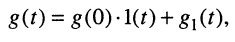 (15.18)
(15.18)
где
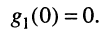
Тогда для импульсной характеристики согласно (15.8) и (15.17) получим:
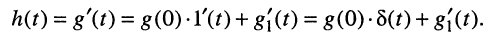 (15.19)
(15.19)

Подставив импульсную характеристику (15.19) в (15.14, а), получаем реакцию цепи 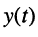 на воздействие
на воздействие 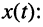
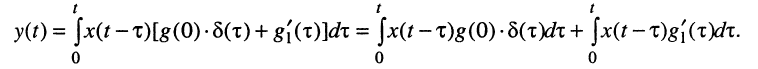
Рассмотрим первый интеграл полученного выражения. Он содержит константу 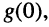 которую можно вынести за знак интеграла. Оставшийся интеграл будет равен
которую можно вынести за знак интеграла. Оставшийся интеграл будет равен 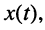 поскольку
поскольку 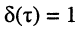 только при
только при 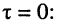
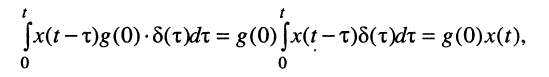
поэтому окончательно имеем:
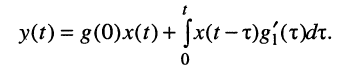 (15.20)
(15.20)
Можно получить другую форму интеграла (15.20):
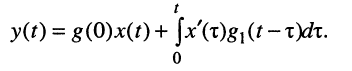 (15.20a)
(15.20a)
Интегралы (15.20) называются интегралами Дюамеля, которые позволяют вычислить реакцию цепи по переходной характеристике как при нулевых, так и при ненулевых условиях.
Выводы:
Описание линейных электрических цепей в операторной р – области
Преобразование Лапласа и его свойства:
Классический метод анализа колебаний в электрических цепях, основанный на применении комплексных амплитуд, эффективен при невысоком порядке сложности цепи, а воздействие является либо гармонической функцией времени, либо постоянно. Если же воздействие произвольно, то задача анализа сводится к решению неоднородной системы обыкновенных линейных дифференциальных и интегро-дифференциальных уравнений при известных начальных условиях. Это решение само по себе является далеко не простой процедурой.
Значительно облегчает задачу анализа процессов в электрических цепях операторный метод, основанный на применении преобразования Лапласа. Операторный метод переводит решение из области функций действительного переменного t (т. е. из временной области) в область комплексного переменного р (т. е. в операторную область), в результате чего система дифференциальных уравнений сводится к системе алгебраических уравнений, решать которые значительно легче. Преобразование Лапласа подобно методу комплексных амплитуд, когда операции над функциями времени замещаются операциями над их изображениями, или символами.
Определение преобразования Лапласа
Пусть функция 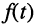 — кусочно-непрерывная однозначная функция времени
— кусочно-непрерывная однозначная функция времени 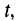 которая тождественно равна нулю при отрицательных значениях
которая тождественно равна нулю при отрицательных значениях 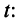
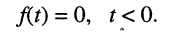 (16.1)
(16.1)
и, кроме того, имеем комплексную переменную
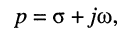 (16.2)
(16.2)
называемую оператором. (В математической литературе для обозначения оператора вместо р применяется буква s ).
При этих условиях вводится пара взаимно однозначных преобразований:
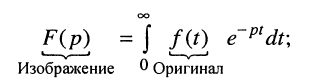 (16.3)
(16.3)
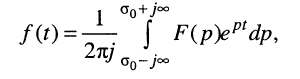 (16.4)
(16.4)
из которых первое называют преобразованием Лапласа 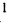 F(p) функции
F(p) функции 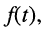 а второе — обратным преобразованием Лапласа.
а второе — обратным преобразованием Лапласа.
Преобразуемая функция 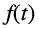 называется оригиналом, а функция
называется оригиналом, а функция 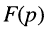 — её изображением. Преобразование (16.3) ставит в соответствие оригиналу
— её изображением. Преобразование (16.3) ставит в соответствие оригиналу 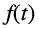 его изображение
его изображение 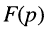 . С представлением о преобразовании связано понятие об отображении, в связи с чем также говорят, что функция времени
. С представлением о преобразовании связано понятие об отображении, в связи с чем также говорят, что функция времени 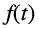 отображается в комплексную плоскость оператора
отображается в комплексную плоскость оператора 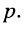
Преобразования (16.3) и (16.4) кратко записывают с помощью следующей символики:
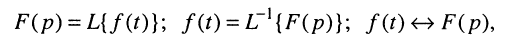
0 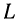 — оператор прямого преобразования Лапласа, или L-преобразование;
— оператор прямого преобразования Лапласа, или L-преобразование;
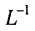 — оператор обратного преобразования Лапласа, или обратное
— оператор обратного преобразования Лапласа, или обратное 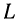 -преобразование;
-преобразование;
О знак 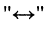 —символ однозначного взаимного соответствия, или отображения, этот символ показывает, что каждому оригиналу
—символ однозначного взаимного соответствия, или отображения, этот символ показывает, что каждому оригиналу 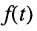 соответствует одно-единственное изображение
соответствует одно-единственное изображение 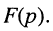
Заметим, что преобразование Лапласа существует, во-первых, только для функций 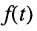 удовлетворяющих указанным ранее требованиям, и, во-вторых, для таких значений
удовлетворяющих указанным ранее требованиям, и, во-вторых, для таких значений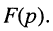 когда при
когда при 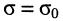 интеграл (16.3) сходится абсолютно:
интеграл (16.3) сходится абсолютно:
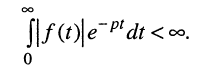
В ряде справочников приводятся таблицы преобразования Лапласа—Карсона, которое отличается от преобразования Лапласа только наличием множителя 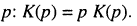
Однако на практике нет необходимости заботиться о выполнении указанных ограничений, поскольку используемые в теории цепей функции всегда преобразуемы по Лапласу.
Процедура применения преобразования Лапласа схожа с процедурой, используемой в символическом методе, по сути дела также являющемся отображением:
- Оригинал, или пространство оригиналов, переводится в р-область с помощью преобразования (16.3).
- Находятся решения в р-области, являющиеся L-изображениями решений в пространстве оригиналов.
- Полученные решения в р-области переводятся в пространство оригиналов с помощью обратного преобразования (16.4).
Использование преобразования Лапласа наиболее эффективно для решения интегро-дифференциальных уравнений с постоянными коэффициентами.
Основные свойства преобразования Лапласа
1. Свойство линейности
Пусть функция 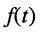 представляет собой сумму N взвешенных функций
представляет собой сумму N взвешенных функций 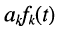
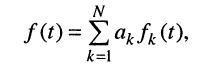
тогда согласно определению её L-изображение имеет вид:
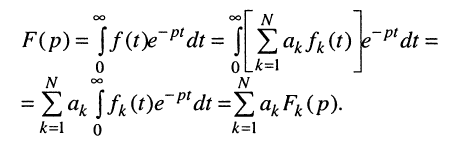 (16.5)
(16.5)
Таким образом, L-изображение суммы взвешенных функций равно сумме L-изображений этих функций с теми же весовыми коэффициентами.
2. Теорема запаздывания (задерживания)
Найдём преобразование Лапласа функции 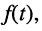 задержанной по времени на
задержанной по времени на 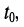 т. е. функции
т. е. функции 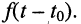 По определению имеем:
По определению имеем:
Произведём в интеграле замену переменной 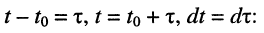
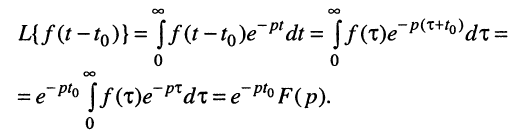 (16.6)
(16.6)
Следовательно, L-изображение задержанной функции 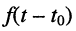 есть изображение исходной функции
есть изображение исходной функции 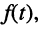 умноженное на экспоненту
умноженное на экспоненту 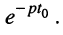
3. Теорема свёртки
Найдём L-изображение свёртки функций 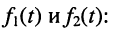
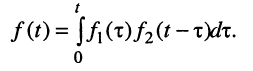
По определению имеем:
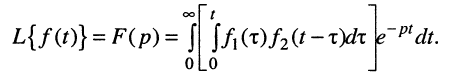
Поменяем местами операции интегрирования с учётом переменных, по которым осуществляется интегрирование, и получим:
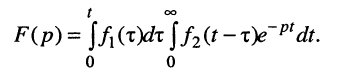
Второй интеграл в полученном выражении является L-изображением задержанной на 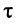 функции
функции 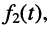 и согласно тереме запаздывания можно записать:
и согласно тереме запаздывания можно записать:
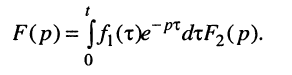 (16.7)
(16.7)
Последний интеграл представляет собой L-изображение функции 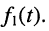 Действительно, поскольку функция
Действительно, поскольку функция 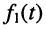 существует только на интервале
существует только на интервале 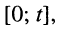 ничто не мешает верхний предел
ничто не мешает верхний предел 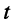 интегрирования заменить бесконечностью — и тогда получим преобразование Лапласа (16.3). Следовательно, выражение (16.8) представляет собой произведение L-изображений свёртываемых функций
интегрирования заменить бесконечностью — и тогда получим преобразование Лапласа (16.3). Следовательно, выражение (16.8) представляет собой произведение L-изображений свёртываемых функций 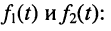
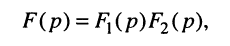
причём результат не зависит от порядка записи свёртываемых функций.
4. Теорема смещения
Покажем, что смещение изображения на некоторую величину 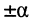 соответствует умножению оригинала на экспоненту
соответствует умножению оригинала на экспоненту 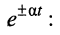
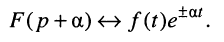 (16.9)
(16.9)
Действительно,
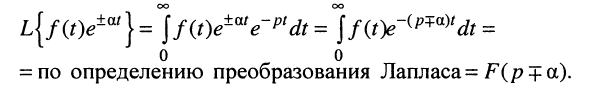
5. Теорема подобия (изменения масштаба аргумента)
Умножению аргумента оригинала на постоянное число 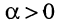 соответствует деление аргумента изображения и самого изображения на это же число.
соответствует деление аргумента изображения и самого изображения на это же число.
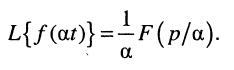 (16.10)
(16.10)
Покажем это. По определению имеем:
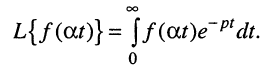
Произведём замену переменной:
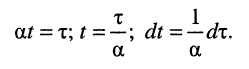
Подставляя полученные соотношения в L-изображение оригинала и вынося
при этом за знак интеграла константу 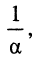 приходим к выражению (16.11):
приходим к выражению (16.11):
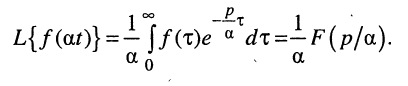
L-изображения типовых функций, операций дифференцирования и интегрирования
Изображение константы А:
Изображение константы имеет вид:
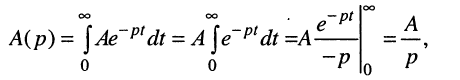 (16.11)
(16.11)
откуда следует, что L-изображение константы равно отношению константы к оператору 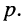
Изображение 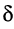 -функции
-функции
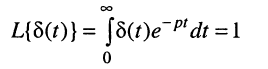 (16.12)
(16.12)
соответствует определению 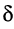 -функции, которая равна 1 только при
-функции, которая равна 1 только при 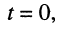 а при остальных значениях
а при остальных значениях 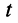 функция равна нулю.
функция равна нулю.
Изображение единичного скачка (функции Хэвисайда)
Согласно формуле (16.6) получаем:
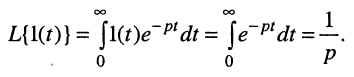 (16.13)
(16.13)
Изображение взвешенной экспоненты:
Как увидим в дальнейшем, большое практическое значение имеет взвешенная экспонента вида 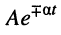 (рис. 16.1), L-изображение которой равно:
(рис. 16.1), L-изображение которой равно:
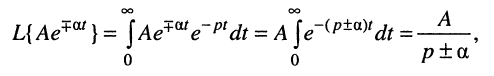 (16.14)
(16.14)
где следует быть внимательным к соответствию между знаком показателя степени экспоненты и знаком в знаменателе изображения.
Изображение отрезка синусоиды
Найдём L-изображение отрезка синусоиды 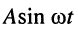 на интервале
на интервале 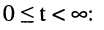
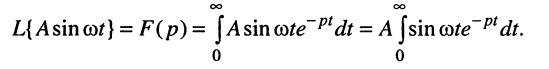
Представим синус через экспоненциальные функции согласно формуле Эйлера
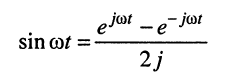
и воспользуемся свойством линейности преобразования Лапласа; тогда получим:
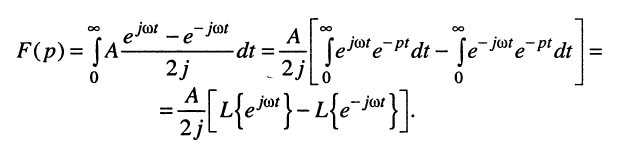
Для записи изображений экспонент воспользуемся свойством (16.14):
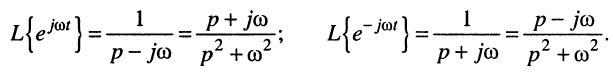
Подставим эти изображения в предыдущую формулу:
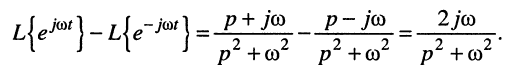
Теперь окончательно получаем:
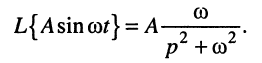 (16.15)
(16.15)
Изображение отрезка косинусоиды
Поступая так же, как в предыдущем пункте, нетрудно получить:
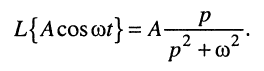 (16.16)
(16.16)
Знание изображений типовых функций позволяет получить L-изображения более сложных функций, являющихся различными комбинациями типовых. В приводимой далее таблице соответствий табл. 16.1 даны преобразования Лапласа основных операций и рациональных функций.
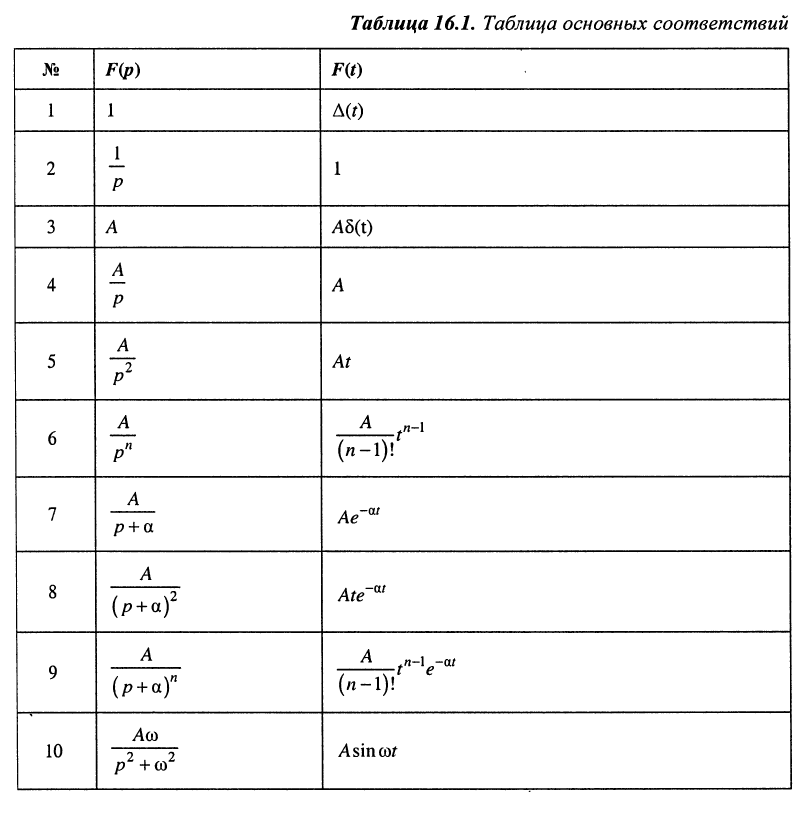
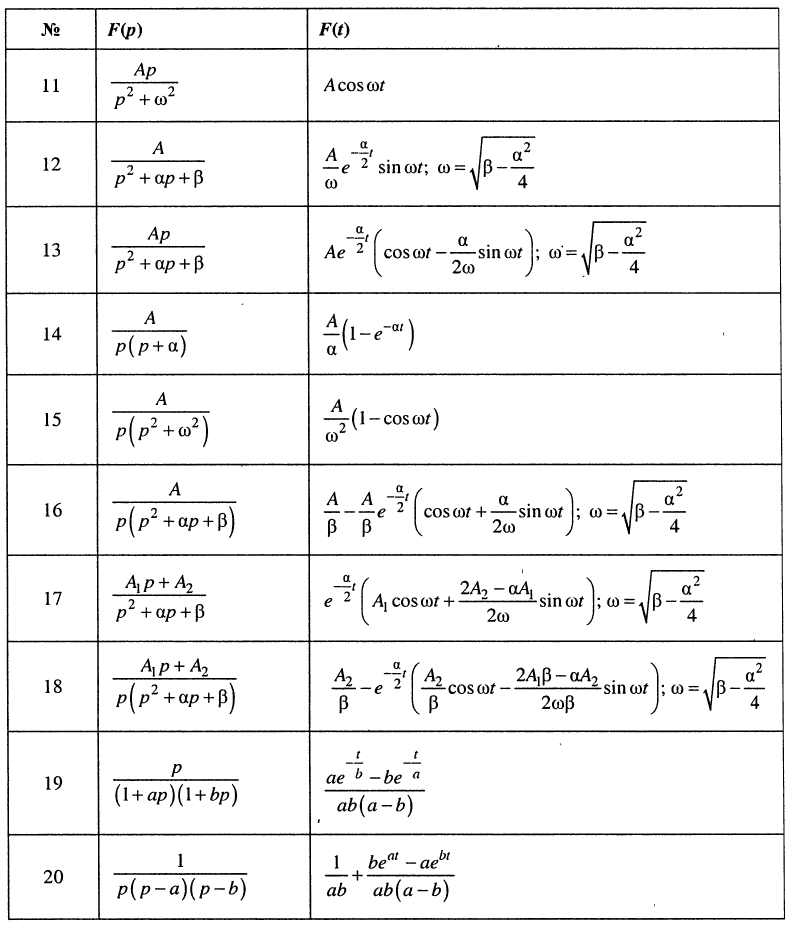
Подробные таблицы преобразований Лапласа приводятся в разнообразных руководствах, учебных пособиях и справочниках как по теории электрических цепей, так и в математических справочниках.
L-изображения операций дифференцирования и интегрирования
L-изображение операции дифференцирования:
Пусть функция 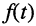 имеет L-изображение
имеет L-изображение 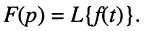 Поставим задачу найти L-изображение производной
Поставим задачу найти L-изображение производной
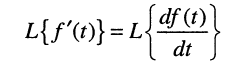
этой функции:
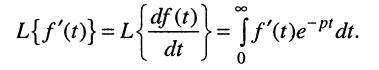
Произведём интегрирование по частям:
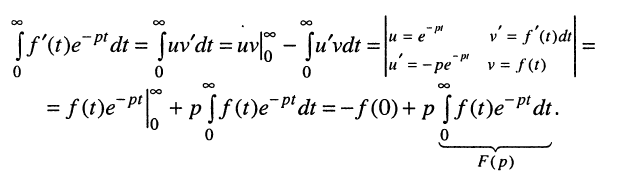 (16.17)
(16.17)
Интеграл в последней сумме (16.17) представляет собой L-изображение функции 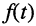 , поэтому справедлива окончательная запись:
, поэтому справедлива окончательная запись:
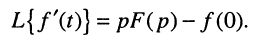 (16.18)
(16.18)
Если имеют место нулевые начальные условия, когда 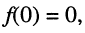 получаем L-изображение первой производной:
получаем L-изображение первой производной:
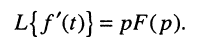 (16.19)
(16.19)
Применяя аналогичный подход для вывода L-изображений высших производных при ненулевых начальных условиях, нетрудно получить:
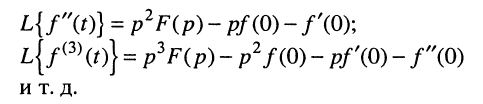
Тогда для производной и-го порядка можно записать:
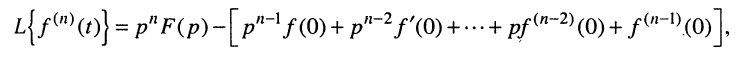
откуда следует общая формула L-изображений высших производных при ненулевых начальных условиях:
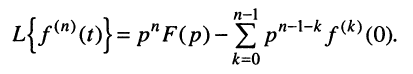 (16.20)
(16.20)
Смысл полученной формулы состоит в том, что весьма непростая операция дифференцирования в пространстве оригиналов заменяется элементарными операциями умножения и суммирования в пространстве изображений, причём коэффициентами многочлена порядка n – 1 являются начальные значения оригинала 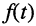 и всех его производных порядка до n – 1 включительно.
и всех его производных порядка до n – 1 включительно.
Выражение (16.20) особенно полезно при решении дифференциальных уравнений.
При нулевых начальных условиях, когда начальные значения оригинала и всех его производных порядка до п – 1 включительно равны нулю, получаем формулу:
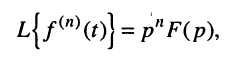 (16.21)
(16.21)
т. е. L-изображение дифференцируемой функции представляется умножением изображения функции на степень оператора, равную порядку производной.
Важно:
использование соответствий (16.20) и (16.21) возможно только в том случае, когда наивысшая встречающаяся производная 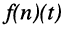 существует в каждой точке
существует в каждой точке 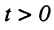 и обладает L-изображением.
и обладает L-изображением.
L-изображение операции интегрирования:
Если дифференцированию оригинала соответствует умножение изображения на р (16.19), то при нулевых начальных условиях интегрированию оригинала на отрезке времени 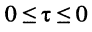 соответствует деление изображения на р:
соответствует деление изображения на р:
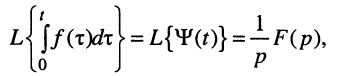 (16.22)
(16.22)
где
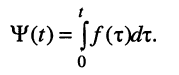
Покажем справедливость соотношения (16.22), для чего продифференцируем интеграл по t. Тогда получим подынтегральную функцию
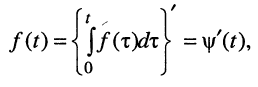
к которой применим правило определения изображения производной (16.19)
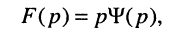
откуда
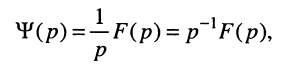 (16.23)
(16.23)
что подтверждает верность выражения (16.22).
Замечание:
Поскольку при нулевых начальных условиях операции дифференцирования (интегрирования) оригинала соответствует операция умножения (деления) её изображения на оператор 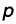 , то оператор
, то оператор 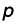 часто называют оператором дифференцирования, а оператор
часто называют оператором дифференцирования, а оператор 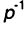 — оператором интегрирования.
— оператором интегрирования.
Обратное преобразование Лапласа
Задача получения оригинала 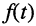 по его известному изображению
по его известному изображению 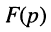 может быть решена с помощью интеграла (16.4):
может быть решена с помощью интеграла (16.4):
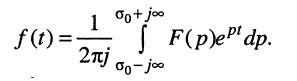
Однако применение этого интеграла весьма и весьма ограничено, поскольку в большинстве случаев этот интеграл не берётся. Тем не менее, получить оригинал по его изображению можно, не прибегая к интегралу (16.4). Для получения обратного преобразования Лапласа наиболее широко применяются два метода: табличный метод и разложение на сумму простых дробей (теорема разложения).
1. Табличный метод:
Метод основан на использовании табличных однозначных соответствий между оригиналами и изображениями с применением свойств преобразования Лапласа.
Пример 16.1.
Пусть известно изображение
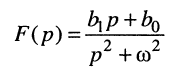
и требуется найти оригинал 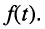
Решение. Обратимся к таблице соответствий (табл. 16.1) и увидим, что такой табличной функции нет. Однако в той же таблице имеются соответствия 10 и 11 (см. (16.15) и (16.16)), у которых знаменатели одинаковые, а именно:
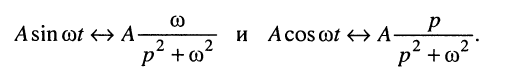
Чтобы использовать эти соответствия, представим изображение (16.24) в виде суммы двух дробей с одинаковыми знаменателями:
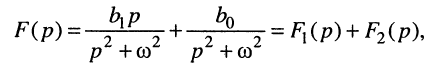
где
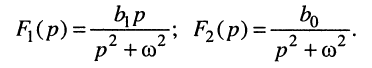
Следовательно, по свойству линейности искомый оригинал будет представлять собой сумму двух оригиналов:
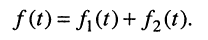
Согласно полученным в разд. 16.2.1 табличным соответствиям имеем:
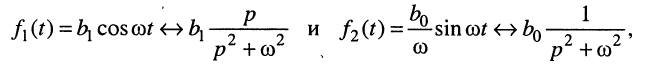
откуда следует:
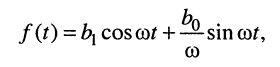
или
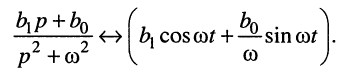
2. Метод разложения на сумму простых дробей (теорема разложения)
Пусть L-изображение некоторого оригинала 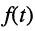 представляет собой дробно-рациональную функцию
представляет собой дробно-рациональную функцию
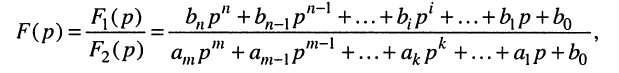 (16.25)
(16.25)
где 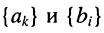 — вещественные коэффициенты и порядок
— вещественные коэффициенты и порядок 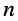 полинома в числителе не превышает порядка
полинома в числителе не превышает порядка 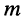 полинома в знаменателе. Такие функции применяются при синтезе пассивных электрических цепей (см. лекцию 30). Обратимся к знаменателю (16.25): уравнение, получаемое приравниванием полинома знаменателя нулю,
полинома в знаменателе. Такие функции применяются при синтезе пассивных электрических цепей (см. лекцию 30). Обратимся к знаменателю (16.25): уравнение, получаемое приравниванием полинома знаменателя нулю,
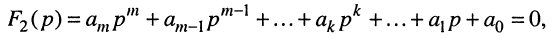
называется характеристическим уравнением. Пусть корни 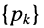 характеристического уравнения простые и не равны корням уравнения, получаемого приравниванием нулю полинома числителя. При этих условиях дробь (16.25) можно представить в виде суммы простых дробей:
характеристического уравнения простые и не равны корням уравнения, получаемого приравниванием нулю полинома числителя. При этих условиях дробь (16.25) можно представить в виде суммы простых дробей:
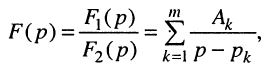
где 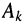 — коэффициенты разложения, имеющие тот же тип, что и корни
— коэффициенты разложения, имеющие тот же тип, что и корни 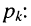 вещественному корню соответствует вещественный коэффициент разложения, комплексному корню — комплексный коэффициент разложения.
вещественному корню соответствует вещественный коэффициент разложения, комплексному корню — комплексный коэффициент разложения.
Знание корней 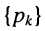 полинома
полинома 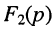 и коэффициентов разложения
и коэффициентов разложения 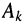 позволяет из (16.26) получить обратное преобразование Лапласа функции
позволяет из (16.26) получить обратное преобразование Лапласа функции 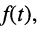 для чего воспользуемся свойством линейности преобразования:
для чего воспользуемся свойством линейности преобразования:
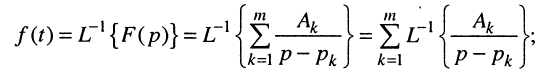 (16.27)
(16.27)
в результате остаётся только найти обратное L-преобразование дроби, стоящей в скобках; но эта дробь представляет собой L-преобразование взвешенной экспоненты (16.14):
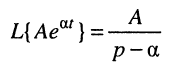
при 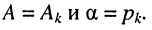 Подставляя взвешенную экспоненту с указанными параметрами в (16.27), получаем:
Подставляя взвешенную экспоненту с указанными параметрами в (16.27), получаем:
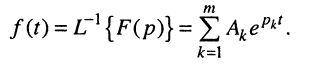 (16.28)
(16.28)
Здесь значения 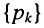 известны, и для окончательного решения задачи необходимо вычислить коэффициенты разложения
известны, и для окончательного решения задачи необходимо вычислить коэффициенты разложения 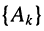 , что можно выполнить двумя способами, рассматриваемыми далее.
, что можно выполнить двумя способами, рассматриваемыми далее.
3. Метод производной знаменателя:
Для определения 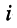 -го коэффициента разложения
-го коэффициента разложения 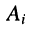 умножим обе части (16.26) на
умножим обе части (16.26) на 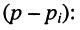
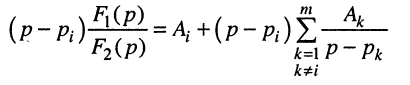 (16.29)
(16.29)
и устремим 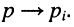 Тогда правое слагаемое обращается в нуль:
Тогда правое слагаемое обращается в нуль:
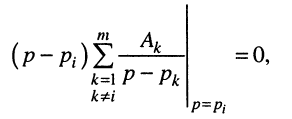
и коэффициент 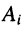 оказывается равным:
оказывается равным:
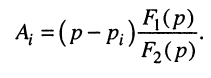
Перейдём в полученном выражении к пределу:
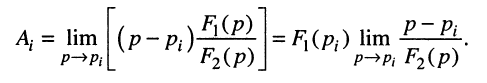 (16.30)
(16.30)
В уравнении (16.30) при 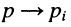 под знаком предела множитель и знаменатель
под знаком предела множитель и знаменатель 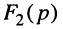 обращаются в нуль, образуя неопределённость вида 0/0, которую раскроем по правилу Лопиталя путём дифференцирования по
обращаются в нуль, образуя неопределённость вида 0/0, которую раскроем по правилу Лопиталя путём дифференцирования по 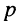 числителя и знаменателя:
числителя и знаменателя:
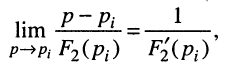
в результате чего из (16.30) имеем:
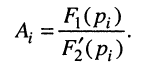 (16.31)
(16.31)
В полученном выражении величина 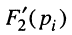 представляет собой значение производной полинома
представляет собой значение производной полинома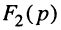 по комплексной переменной
по комплексной переменной 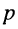 при
при 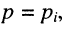 причём неравенство
причём неравенство 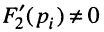 является принципиальным, поскольку полином
является принципиальным, поскольку полином 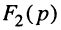 согласно принятому предположению, имеет только простые корни.
согласно принятому предположению, имеет только простые корни.
Аналогичным образом можно получить любой из коэффициентов 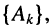 что даёт возможность перейти от индекса
что даёт возможность перейти от индекса 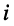 к индексу к и записать,(16.31) в виде:
к индексу к и записать,(16.31) в виде:
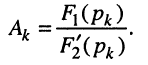
Если один из корней характеристического уравнения равен нулю (пусть это будет 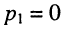 ), тогда соответствующий коэффициент разложения вычисляется по простой формуле:
), тогда соответствующий коэффициент разложения вычисляется по простой формуле:
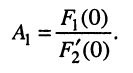 (16.33)
(16.33)
Пример 16.2.
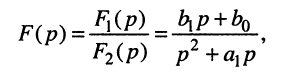 (16.34)
(16.34)
найдём оригинал 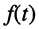 по его изображению, воспользовавшись изложенной методикой.
по его изображению, воспользовавшись изложенной методикой.
Решение. Здесь характеристическое уравнение
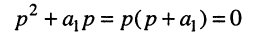
имеет два простых вещественных корня: 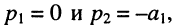 поэтому разложение функции (16.34) согласно (16.26) получает вид:
поэтому разложение функции (16.34) согласно (16.26) получает вид:
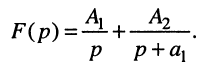
Для вычисления коэффициентов разложения 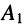 и
и 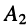 запишем производную знаменателя (16.34):
запишем производную знаменателя (16.34):
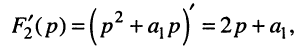
после чего коэффициенты разложения в соответствии с (16.32) оказываются равными:
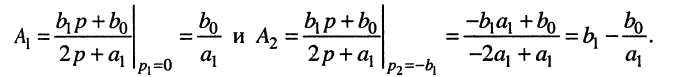 (16.36)
(16.36)
Подставляя полученные коэффициенты и значения корней 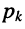 в (16.32), получаем оригинал:
в (16.32), получаем оригинал:
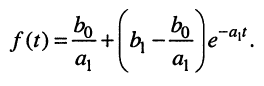 (16.37)
(16.37)
4. Метод неопределённых коэффициентов
Рассмотренный метод получения коэффициентов разложения требует вычисления производной знаменателя, что не всегда бывает удобным. В большинстве же практических случаев можно воспользоваться известным из математики методом неопределённых коэффициентов, при котором рациональная дробь также представляется в виде суммы простых дробей (16.26), а дальнейшие вычисления осуществляются в следующем порядке:
Пример 16.3.
Найдём решение задачи, поставленной в предыдущем примере, методом неопределённых коэффициентов.
Решение. Для решения задачи вновь обратимся к формуле (16.35):
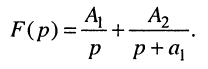
Приведём дроби к общему знаменателю:
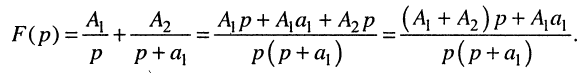 (16.38)
(16.38)
Равенство дробей (16.38) и (16.34) означает равенство их знаменателей и числителей, но знаменатели равны, поэтому приравняем числители
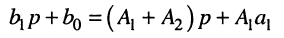
и коэффициенты при одинаковых степенях р:
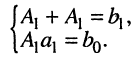
Нетрудно проверить, что решение этой системы даёт те же коэффициенты (16.36), а потому и тот же итоговый результат (16.37).
- Частотные методы анализа и расчёта электрических цепей
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Гармонические напряжения и токи
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре

Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):

Рис.1. Вращающийся вектор
С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
![]()
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
![]()
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
![]()
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат)
и тогда
![]()
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
![]()
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.
2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)

Рис.2. Комплексное число на комплексной плоскости
Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как ![]() .
.
На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна

На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли

При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:
1) показательная форма в виде
![]()
2) тригонометрическая форма в виде
![]()
3) алгебраическая форма
![]()
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.
Например, имеем комплексное число в показательной форме вида
![]()
в тригонометрической форме записи это запишется как
![]()
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
![]()
![]()
В итоге получим
![]()
где ![]()
При переходе от алгебраической формы к показательной комплексное число вида
![]()
переходит к показательному виду по следующим преобразованиям
![]()
а угол

Таким образом, и получим
![]()
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
-
-
- Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
- В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
- При необходимости составляют комплексные уравнения по выбранному методу решения.
- Решают уравнения относительно комплексного значения искомой величины.
- Если требуется, записывают мгновенные значения найденных комплексных величин.
-
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.

Рис.3. Схема с последовательным соединением элементов
Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):

Рис.4. Схема с комплексными обозначениями
По закону Ома ток в цепи равен
![]()
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как

Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида ![]() при φ = 0° равно
при φ = 0° равно
![]()
Соответственно, комплекс входного напряжения в показательной форме запишется как

Полное комплексное сопротивление цепи в общем виде

Находим комплексное сопротивление индуктивности
![]()
Находим комплексное сопротивление емкости

Соответственно, общее комплексное сопротивление цепи

Ток в цепи

Комплексные напряжения на элементах

Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство ![]()
Проверяем

С небольшим расхождением из-за округлений промежуточных вычислений всё верно.
Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
-
- Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.

Рис.5.Цепь однофвзного синусоидального тока
Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что

Комплексное сопротивление первой ветви:
![]()
Комплексное сопротивление второй ветви:

Комплексное сопротивление третьей ветви:

Общее сопротивление цепи

Откуда
![]()
![]() — нагрузка носит активно-индуктивный характер
— нагрузка носит активно-индуктивный характер
2. Находим действующие значения токов в ветвях:

Рис.6. Схема с обозначенными комплексными токами

Действующие значения, соответственно,
![]()
3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:
![]()
