Загрузить PDF
Загрузить PDF
При измерении чего-либо можно предположить, что есть некоторое «истинное значение», которое лежит в пределах диапазона значений, которые вы нашли. Для расчета более точной величины нужно взять результат измерения и оценить его при прибавлении или вычитании погрешности. Если вы хотите научиться находить такую погрешность, выполните следующие действия.
-

1
Выражайте погрешность правильно. Допустим, при измерении палки ее длина равна 4,2 см плюс-минус один миллиметр. Это означает, что палка примерно равна 4,2 см, но на самом деле может быть немного меньше или больше этого значения — с погрешностью до одного миллиметра.
- Запишите погрешность как: 4,2 см ± 0,1 см. Вы также можете переписать это как 4,2 см ± 1 мм, так как 0,1 см = 1 мм.
-

2
Всегда округляйте значения измерений до того же знака после запятой, что и в погрешности. Результаты измерений, которые учитывают погрешность, как правило, округляются до одной или двух значащих цифр. Наиболее важным моментом является то, что нужно округлить результаты до того же знака после запятой, что и в погрешности, чтобы сохранить соответствие.
- Если результат измерения 60 см, то и погрешность следует округлять до целого числа. Например, погрешность этого измерения может быть 60 см ± 2 см, но не 60 см ± 2,2 см.
- Если результат измерения 3,4 см, то погрешность округляется до 0,1 см. Например, погрешность этого измерения может быть 3,4 см ± 0,7 см, но не 3,4 см ± 1 см.
-

3
Найдите погрешность. Допустим, вы измеряете линейкой диаметр круглого шара. Это сложно, так как из-за кривизны шара будет трудно померить расстояние между двумя противоположными точками на его поверхности. Скажем, линейка может дать результат с точностью до 0,1 см, но это не значит, что вы можете измерить диаметр с той же точностью.[1]
- Изучите шар и линейку, чтобы получить представление о том, с какой точностью вы можете измерить диаметр. У стандартной линейки четко видна разметка по 0,5 см, но, возможно, вы сможете измерить диаметр с большей точностью, чем эта. Если вы думаете, что сможете измерить диаметр с точностью до 0,3 см, то погрешность в этом случае равна 0,3 см.
- Измерим диаметр шара. Допустим, вы получили результат около 7,6 см. Просто укажите результат измерения вместе с погрешностью. Диаметр шара составляет 7,6 см ± 0,3 см.
-

4
Рассчитайте погрешность измерения одного предмета из нескольких. Скажем, вам даны 10 компакт-дисков (CD), при этом размеры каждого одинаковы. Допустим, вы хотите найти толщину всего одного CD. Эта величина настолько мала, что погрешность практически невозможно вычислить. Тем не менее, чтобы вычислить толщину (и ее погрешность) одного CD, вы можете просто разделить результат измерения (и его погрешность) толщины всех 10 CD, сложенных вместе (один на другого), на общее количество CD.[2]
- Допустим, что точность измерения стопки CD с помощью линейки 0,2 см. Итак, ваша погрешность ± 0,2 см.
- Допустим, толщина всех CD равна 22 см.
- Теперь разделим результат измерения и погрешность на 10 (число всех CD). 22 см/10 = 2,2 см и 0,2 см/10 = 0,02 см. Это означает, что толщина одного компакт-диска 2,20 см ± 0,02 см.
-

5
Измерьте несколько раз. Для повышения точности измерений, будь то измерение длины или времени, замерьте искомую величину несколько раз. Вычисление среднего значения из полученных значений увеличит точность измерения и расчета погрешности.
Реклама
-

1
Проведите несколько измерений. Допустим, вы хотите найти, сколько времени падает мяч с высоты стола. Чтобы получить наилучшие результаты, измерьте время падения насколько раз, например, пять. Потом нужно найти среднее значение из пяти полученных значений измерений времени, а затем для наилучшего результата добавить или вычесть среднеквадратичное отклонение.[3]
- Допустим, в результате пяти измерений получены результаты: 0,43 с, 0,52 с, 0,35 с, 0,29 с и 0,49 с .
-

2
Найдите среднее арифметическое. Теперь найдите среднее арифметическое путем суммирования пяти различных результатов измерений и разделив результат на 5 (количество измерений). 0,43 + 0,52 + 0,35 + 0,29 + 0,49 = 2,08 с. 2,08 / 5 = 0,42 с. Среднее время 0,42 с.
-

3
Найдите дисперсию полученных значений. Для этого, во-первых, найдите разницу между каждой из пяти величин и средним арифметическим. Чтобы сделать это, вычтите из каждого результата 0,42 с.[4]
-
- 0,43 с – 0,42 с = 0,01 с
- 0,52 с – 0,42 с = 0,1 с
- 0,35 с – 0,42 с = -0,07 с
- 0,29 с – 0,42 с = -0,13 с
- 0,49 с – 0,42 с = 0,07 с
- Теперь сложите квадраты этих разниц: (0,01) 2 + (0,1) 2 + (-0,07) 2 + (-0,13) 2 + (0,07) 2 = 0,037 с.
- Найти среднее арифметическое этой суммы можно, разделив ее на 5: 0,037 / 5 = 0,0074 с.
-
-

4
Найдите среднеквадратичное отклонение. Чтобы найти среднеквадратичное отклонение, просто возьмите квадратный корень из среднего арифметического суммы квадратов. Квадратный корень из 0,0074 = 0,09 с, так что среднеквадратичное отклонение равно 0,09 с.[5]
-

5
Запишите окончательный ответ. Чтобы сделать это, запишите среднее значение всех измерений плюс-минус среднеквадратичное отклонение. Поскольку среднее значение всех измерений равно 0,42 с, а среднеквадратичное отклонение 0,09 с, то окончательный ответ 0,42 с ± 0,09 с.
Реклама
-

1
Сложение. Чтобы сложить величины с погрешностями, сложите отдельно величины и отдельно погрешности.[6]
- (5 см ± 0,2 см) + (3 см ± 0,1 см) =
- (5 см + 3 см) ± (0,2 см + 0,1 см) =
- 8 см ± 0,3 см
-

2
Вычитание. Чтобы вычесть величины с погрешностями, вычтите величины и сложите погрешности.[7]
- (10 см ± 0,4 см) – (3 см ± 0,2 см) =
- (10 см – 3 см) ± (0,4 см + 0,2 см) =
- 7 см ± 0,6 см
-

3
Умножение. Чтобы умножить величины с погрешностями, перемножьте величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности (в процентах).[8]
Рассчитать можно только относительную погрешность, а не абсолютную, как и в случае со сложением и вычитанием. Чтобы узнать относительную погрешность, разделите абсолютную погрешность на измеренное значение, затем умножьте на 100, чтобы выразить результат в процентах. Например:- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
Следовательно: - (6 см ± 0,2 см) х (4 см ± 0,3 см) = (6 см ± 3,3 % ) x (4 см ± 7,5 %)
- (6 см x 4 см) ± (3,3 + 7,5) =
- 24 см ± 10,8 % = 24 см ± 2,6 см
- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
-

4
Деление. Чтобы разделить величины с погрешностями, разделите величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности.[9]
- (10 см ± 0,6 см) ÷ (5 см ± 0,2 см) = (10 см ± 6 %) ÷ (5 см ± 4 %)
- (10 см ÷ 5 см) ± (6 % + 4 %) =
- 2 см ± 10 % = 2 см ± 0,2 см
-

5
Возведение в степень. Для того, чтобы возвести в степень величину с погрешностью, возведите величину в степень, а относительную погрешность умножьте на степень.[10]
- (2,0 см ± 1,0 см)3 =
- (2,0 см)3 ± (50 %) x 3 =
- 8,0 см3 ± 150 % или 8,0 см3 ±12 см3
Реклама
Советы
- Вы можете дать погрешность как для общего результата всех измерений, так и для каждого результата одного измерения в отдельности. Как правило, данные, полученные из нескольких измерений, менее достоверны, чем данные, полученные непосредственно из отдельных измерений.
Реклама
Предупреждения
- Точные науки никогда не работают с «истинными» величинами. Хотя правильное измерение, скорее всего, даст величину в пределах погрешности, нет никакой гарантии, что это будет так. Научные измерения допускают возможность ошибок.
- Погрешности, описанные здесь, применимы только для случаев нормального распределения (распределения Гаусса). Другие распределения вероятностей требуют других решений.
Реклама
Об этой статье
Эту страницу просматривали 104 724 раза.
Была ли эта статья полезной?
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) – это истинное значение, а (triangle a) – погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? 
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
Оценка погрешности
прямых многократных измерений
При
оценке погрешности прямых многократных
измерений рекомендуется принять
следующий порядок выполнение операций.
-
Проводятся
измерения заданного физического
параметра n
раз в
одинаковых условиях,
и результаты записываются в таблицу. -
Если
результаты некоторых измерений резко
отличаются по своему значению от
остальных измерений, то они как промахи
отбрасываются, если после проверки не
подтверждаются. -
Вычисляется
среднее арифметическое
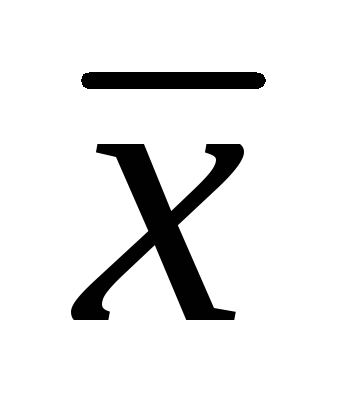 изn
изn
одинаковых измерений. Оно принимается
за наиболее вероятное значение измеряемой
величины
![]() .
.
(8)
-
Находятся
абсолютные погрешности отдельных
измерений

-
Вычисляются
квадраты абсолютных погрешностей
отдельных измерений (Δхi)2 -
Определяется
средняя квадратичная ошибка среднего
арифметического
 .
.
-
Задается
значение доверительной вероятности
Р. В лабораториях практикума принято
задавать Р=0,95.
|
n |
Р |
n |
Р |
||||||
|
0,8 |
0,9 |
0,95 |
0,98 |
0,8 |
0,9 |
0,95 |
0,98 |
||
|
3 |
1,9 |
2,9 |
4,3 |
7,0 |
6 |
1,5 |
2,0 |
2,6 |
3,4 |
|
4 |
1,6 |
2,4 |
3,2 |
4,5 |
7 |
1,4 |
1,9 |
2,4 |
3,1 |
|
5 |
1,5 |
2,1 |
2,8 |
3,7 |
8 |
1,4 |
1,9 |
2,4 |
3,9 |
-
Находится
коэффициент Стьюдента
 для
для
заданной доверительной вероятности α
и числа произведенных измерений
(см.табл.) -
Определяется
случайная погрешность
![]() .
.
-
Определяется
суммарная погрешность
![]() ,
,
где δх – приборная
погрешность, Δх – случайная
погрешность.
-
Оценивается
относительная погрешность результата
измерений
![]() .
.
-
Записывается
окончательный результат в виде
![]() ,
,
с α=… Е=…%.
Окончательный
результат измерений рекомендуется
представлять в следующем виде
![]() ,
,
Р=…, Е=…(7)
Следует
иметь в виду, что сами формулы теории
ошибок справедливы для большого число
измерений. Поэтому значение случайной,
а следовательно, и суммарной погрешности
определяется при малом n
с большой ошибкой. При вычислении Δх
при числе измерений
![]() рекомендуется
рекомендуется
ограничиваться одной значащей цифрой,
если она больше 3 и двумя, если первая
значащая цифра меньше 3. Например, если
Δх=
0,042, то отбрасываем 2 и пишем Δх=0,04,
а если Δх=0,123,
то пишем Δх=0,12.
Число
разрядов результата и суммарной
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
вычисляется вначале на один разряд
больше, чем измерение, а при записи
результата его значение уточняется до
числа разрядов суммарной ошибки.
Оценка погрешности
косвенных многократных измерений
При
оценке погрешности косвенных многократных
измерений
![]() ,
,
являющейся функцией других независимых
величин![]() ,
,
можно использовать два способа.
Первый
способ используется,
если величина y
определяется при различных условиях
опыта. В этом случае для каждого из
значений
![]() вычисляется
вычисляется![]() ,
,
а затем определяется среднее арифметическое
из всех значенийyi
![]() .
.
Систематическая
(приборная) погрешность находится на
основании известных приборных погрешностей
всех измерений по формуле. Случайная
погрешность в этом случае определяется
как ошибка прямого измерения.
Второй
способ применяется,
если данная функция y
определяется
несколько раз при одних и тех же измерений.
В этом случае величина
![]() рассчитывается
рассчитывается
по средним значениям![]() ..
..
Систематическая (приборная) погрешность,
как и при первом способе, находится на
основании известных приборных погрешностей
всех измерений по формуле
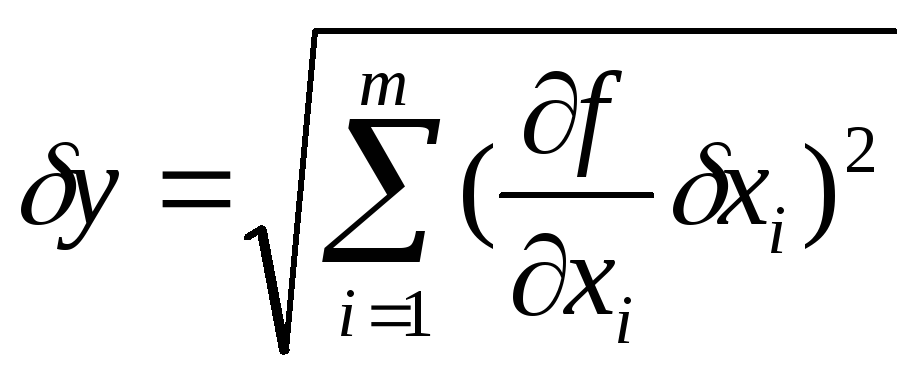 ,
,
где
![]() – приборные ошибки прямых измерений
– приборные ошибки прямых измерений
величины![]() ,
,![]() –
–
частные производные функции по переменной![]() .
.
Для
нахождения случайной погрешности
косвенного измерения вначале рассчитываются
средние квадратичные ошибки среднего
арифметического отдельных измерений.
Затем находится средняя квадратичная
ошибка величины y.
Задание доверительной вероятности α,
нахождение коэффициента Стьюдента
![]() ,
,
определение случайной и суммарной
ошибок осуществляются так же, как и в
случае прямых измерений. Аналогичным
образом представляется результат всех
расчетов в виде
![]() ,
,
с Р=… Е=…%.
Пример,
получим формулу для расчета систематической
погрешности при измерении объема
цилиндра. Формула вычисления объема
цилиндра имеет вид
![]() .
.
Частные
производные по переменным d
и
h
будут равны
![]() ,
,
![]()
![]() .
.
Таким
образом, формула для определения
абсолютной систематической погрешности
при измерении объема цилиндра имеет
следующий вид
![]() ,
,
где
![]() и
и![]() приборные
приборные
ошибки при измерении диаметра и высоты
цилиндра
Пример:
Определить
погрешность мощности, которая рассеивается
в резисторе по формуле
![]() со
со
следующими величинами тока и сопротивления
резистору, которые определяются прямым
измерением: R
= 1,10 ± 0.05 Ом ; I = 1,20 ± 0.05 A. Результаты
приведены со средними квадратичными
отклонениями средних арифметических
R
и
I.
Оценка истинного (среднего) значения
мощности:
![]() Вт
Вт
Для
оценки точности полученного значения
вычисляем частичные производные и
частичные погрешности косвенных
измерений:
![]() =
=
1,22·0,05=0,072 А2 Ом;
![]() =2·1,2·1,1·0,05=
=2·1,2·1,1·0,05=
0,132 А2 Ом
Среднее
квадратичное отклонение косвенного
измерения мощности , которое вычислено
за формулой составляет
![]() =0,15 А2 Ом =0,15 Вт.
=0,15 А2 Ом =0,15 Вт.
Р
= 1,58 ± 0.15 Вт.
Соседние файлы в папке Точность измерений
- #
- #
- #
- #
- #
- #
Как найти абсолютную и относительную погрешность
При измерении какой-либо величины всегда есть некоторое отклонение от истинного значения, поскольку ни один прибор не может дать точного результата. Для того, чтобы определить возможные отклонения полученных данных от точного значения, используют понятия относительной и абсолютной погрешности.

Вам понадобится
- – результаты измерений;
- – калькулятор.
Инструкция
В первую очередь, проведите несколько измерений прибором одной и той же величины, чтобы иметь возможность посчитать действительное значение. Чем больше будет проведено измерений, тем точнее будет результат. Например, взвесьте яблоко на электронных весах. Допустим, вы получили результаты 0,106, 0,111, 0,098 кг.
Теперь посчитайте действительное значение величины (действительное, поскольку истинное найти невозможно). Для этого сложите полученные результаты и разделите их на количество измерений, то есть найдите среднее арифметическое. В примере действительное значение будет равно (0,106+0,111+0,098)/3=0,105.
Для расчета абсолютной погрешности первого измерения вычитайте из результата действительное значение: 0,106-0,105=0,001. Таким же образом вычислите абсолютные погрешности остальных измерений. Обратите внимание, независимо от того, получится результат с минусом или с плюсом, знак погрешности всегда положительный (то есть вы берете модуль значения).
Чтобы получить относительную погрешность первого измерения, разделите абсолютную погрешность на действительное значение: 0,001/0,105=0,0095. Обратите внимание, обычно относительная погрешность измеряется в процентах, поэтому умножьте полученное число на 100%: 0,0095х100%=0,95%. Таким же образом считайте относительные погрешности остальных измерений.
Если истинное значение уже известно, сразу принимайтесь за расчет погрешностей, исключив поиск среднего арифметического результатов измерений. Сразу вычитайте из истинного значения полученный результат, при этом вы найдете абсолютную погрешность.
Затем делите абсолютную погрешность на истинное значение и умножайте на 100% – это будет относительная погрешность. Например, количество учеников 197, но его округлили до 200. В таком случае рассчитайте погрешность округления: 197-200=3, относительная погрешность: 3/197х100%=1,5%.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Измерительные каналы систем автоматизации могут включать в себя несколько средств измерений различных типов, например датчики, измерительные преобразователи, модули аналогового и частотного ввода и вывода [1]. Погрешность такой системы желательно определять экспериментальным путём [2], однако это не всегда возможно или целесообразно. В таких случаях используют расчётный метод.
Исходные данные для расчёта
Исходными данными для расчёта погрешности измерительных каналов являются [3]:
-
метрологические характеристики средств измерений;
-
погрешность метода измерений (методическая погрешность);
-
характеристики влияющих величин (например, окружающая температура, влажность);
-
характеристики измеряемого сигнала.
ГОСТ 8.009-84 [4] для всех типов средств измерений устанавливает следующий комплекс метрологических характеристик, который указывается в эксплуатационной документации на средства измерений:
-
систематическая составляющая основной погрешности;
-
среднеквадратическое отклонение случайной составляющей основной погрешности;
-
дополнительная погрешность для каждой из влияющих величин;
-
динамическая погрешность.
Некоторые средства измерений обладают гистерезисом – для них, кроме перечисленных погрешностей, указывается случайная составляющая основной погрешности, вызванной гистерезисом.
Основная погрешность может быть указана без разделения её на части (на систематическую, случайную и погрешность от гистерезиса), и этот вариант является наиболее распространённым. Случайную составляющую указывают в случае, когда она больше 10% от систематической [4].
Дополнительная погрешность указывается в виде функции влияния внешнего фактора на основную погрешность или её составляющие: систематическую и случайную. Обычно эта функция представляет собой линейную зависимость, и тогда указывается только коэффициент влияния, например 0,05%/°С.
Динамическая погрешность указывается с помощью одной из следующих характеристик: импульсная, переходная, амплитудно-частотная и фазочастотная, амплитудно-фазовая характеристика, передаточная функция. Для минимально-фазовых цепей указывается только амплитудно-частотная характеристика, поскольку фазочастотная однозначно может быть получена из амплитудно-частотной характеристики.
Для расчёта методической погрешности могут быть указаны сопротивления проводов, среднеквадратическое значение или спектральная плотность помех в них, ёмкость, индуктивность и сопротивление источника сигнала, а также другие факторы, которые возникают при создании системы, включающей средства и объект измерений.
Характеристики измеряемого сигнала задаются в виде функции от времени или функции спектральной плотности. Для случайного входного сигнала задаётся спектральная плотность мощности или автокорреляционная функция. Во многих случаях для оценки погрешности бывает достаточно знания скорости нарастания входного сигнала.
Коэффициент корреляции
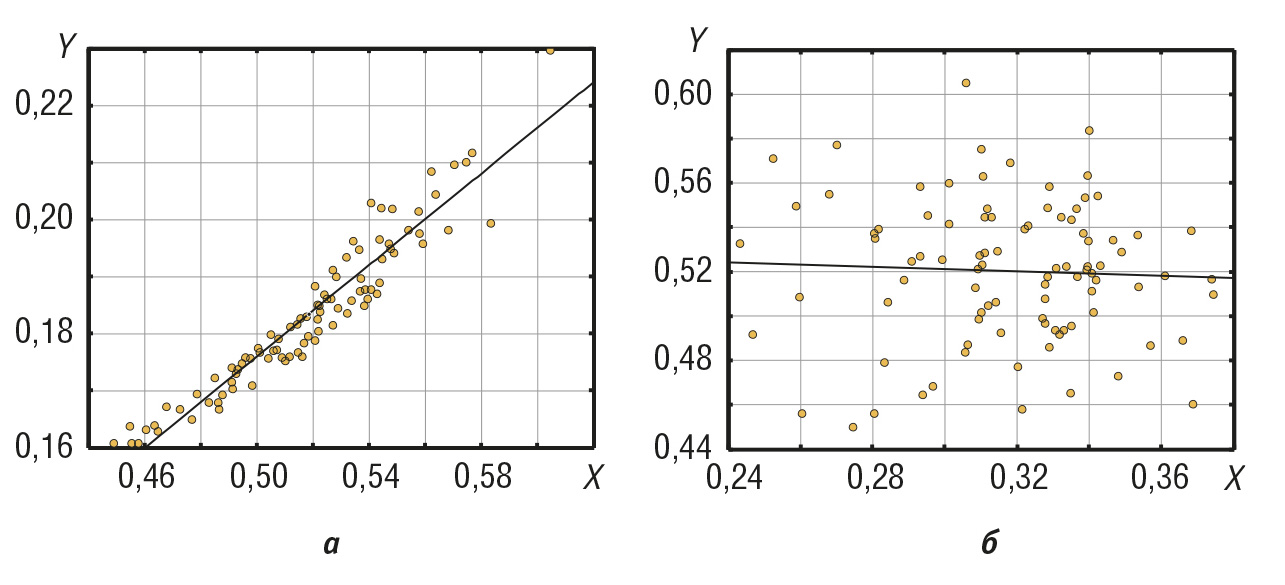
При расчёте погрешности измерительного канала возникает задача суммирования погрешностей средств измерений, которые являются случайными величинами. Способ суммирования будет различным в зависимости от того, являются ли случайные величины статистически зависимыми. Понятие статистической зависимости иллюстрирует рис. 1: если с ростом одной случайной величины X в среднем увеличивается (или уменьшается) и вторая (Y), то между этими величинами имеется статистическая зависимость. Для её количественного описания используются понятия ковариации или коэффициента корреляции.
Рассмотрим суммирование двух случайных погрешностей X и Y с нулевым математическим ожиданием (то есть центрированных случайных величин). Дисперсия суммы двух случайных величин по определению равна математическому ожиданию квадрата их суммы:
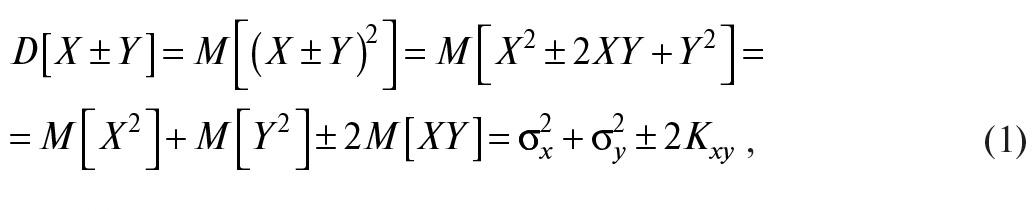
где D[•] и M[•] – операторы дисперсии и математического ожидания; σx, σy – среднеквадратические отклонения случайных величин X и Y. Величина

называется ковариацией («совместной вариацией») случайных величин X и Y.
Ковариацию дискретных случайных величин можно оценить по их дискретным значениям X = {x1,…xN} и Y = {y1,…yN} с помощью формулы среднего арифметического:

Коэффициентом корреляции Rxy называют отношение ковариации к произведению среднеквадратических отклонений σx и σy случайных величин X и Y:
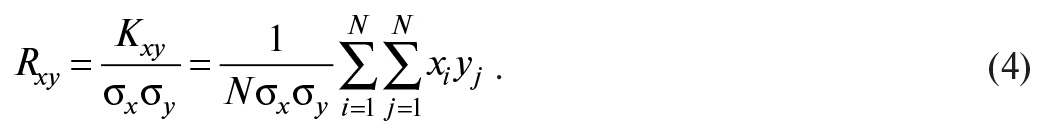
Когда случайные величины независимы, их коэффициент корреляции равен нулю (Rxy = 0), и такие величины называются некоррелированными. Если коэффициент корреляции равен единице (Rxy = 1), то между величинами X и Y имеется не статистическая, а функциональная зависимость.
Используя понятие среднеквадратического отклонения σx = √D[X], уравнение (1) можно записать в виде:
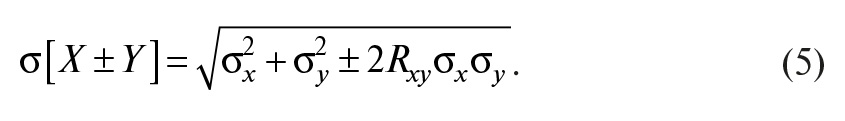
Здесь знак минус используется, когда случайные величины вычитаются, например, если находится разность напряжений двух измерительных каналов. При этом наличие корреляции между каналами частично уменьшает погрешность разности.
В случае когда случайные величины статистически независимы (Rxy = 0), выражение (5) упрощается:

Такое суммирование называют геометрическим, поскольку оно выполняется аналогично нахождению гипотенузы прямоугольного треугольника.
Если коэффициент корреляции Rxy = +1, то
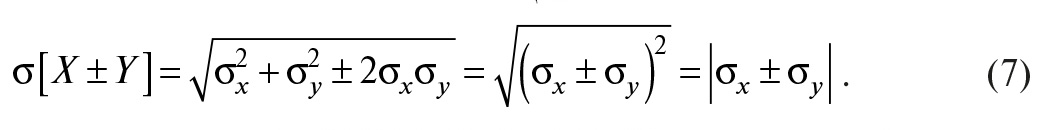
Если коэффициент корреляции равен Rxy = –1, то
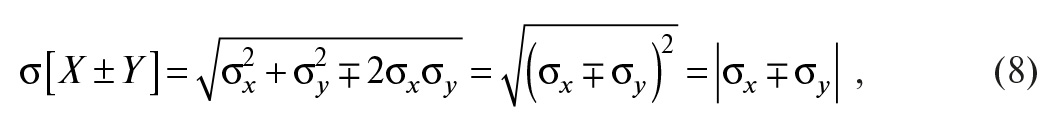
это означает, что при нахождении суммы случайных величин отрицательный коэффициент корреляции уменьшает итоговую погрешность, а при нахождении разности – увеличивает.
Если случайные величины не центрированы и имеют математические ожидания mx и my, то коэффициент корреляции можно оценить как
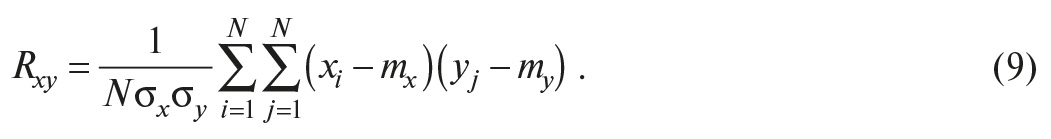
На рис. 1 показаны примеры статистической зависимости между случайными величинами при сильной (а) и слабой (б) корреляции. Точки на графике (значения случайной величины) могут группироваться очень близко к прямой линии, которая аппроксимирует эту зависимость, и тогда статистическая зависимость приближается к детерминированной. Степень отличия статистической зависимости от детерминированной характеризуют коэффициентом корреляции Rxy.
Прямая линия, проведённая таким образом, что сумма квадратов отклонений значений случайной величины от этой линии минимальна, называется линией среднеквадратической регрессии. Тангенс угла наклона этой линии называется коэффициентом регрессии. Уравнение линии регрессии можно получить методом наименьших квадратов; оно имеет вид [1]:
y = A(x – mx) + my,
где A – коэффициент регрессии. Коэффициент регрессии вычисляется через коэффициент корреляции Rxy и среднеквадратические отклонения σy и σx как

Коэффициент корреляции приобретает ясный физический смысл, если статистические переменные центрировать (вычесть математическое ожидание) и нормировать на величину среднеквадратического отклонения. Поскольку среднеквадратические отклонения нормированных величин равны единице, то коэффициент корреляции (9) становится равен тангенсу наклона линии среднеквадратической регрессии.
Статистическая зависимость между погрешностями средств измерений в общем случае нелинейная, однако этой нелинейностью обычно пренебрегают.
Точечные и интервальные оценки погрешности
Погрешности средств измерений и измерительных каналов средств автоматизации могут быть выражены двумя различными способами: с помощью точечных оценок и с помощью интервальных. К точечным оценкам относятся математическое ожидание погрешности и среднеквадратическое отклонение. В качестве интервальной оценки используют интервал погрешности, который охватывает все возможные значения погрешности измерений с вероятностью P. Она называется доверительной вероятностью, или надёжностью оценки погрешности.
Предел допускаемой погрешности можно рассматривать как точечную оценку или как интервальную для доверительной вероятности, равной единице.
Интервальная оценка является более гибкой, поскольку она позволяет указать погрешность измерений в зависимости от того, какая требуется вероятность реализации этой погрешности для конкретных условий эксплуатации средства измерений.
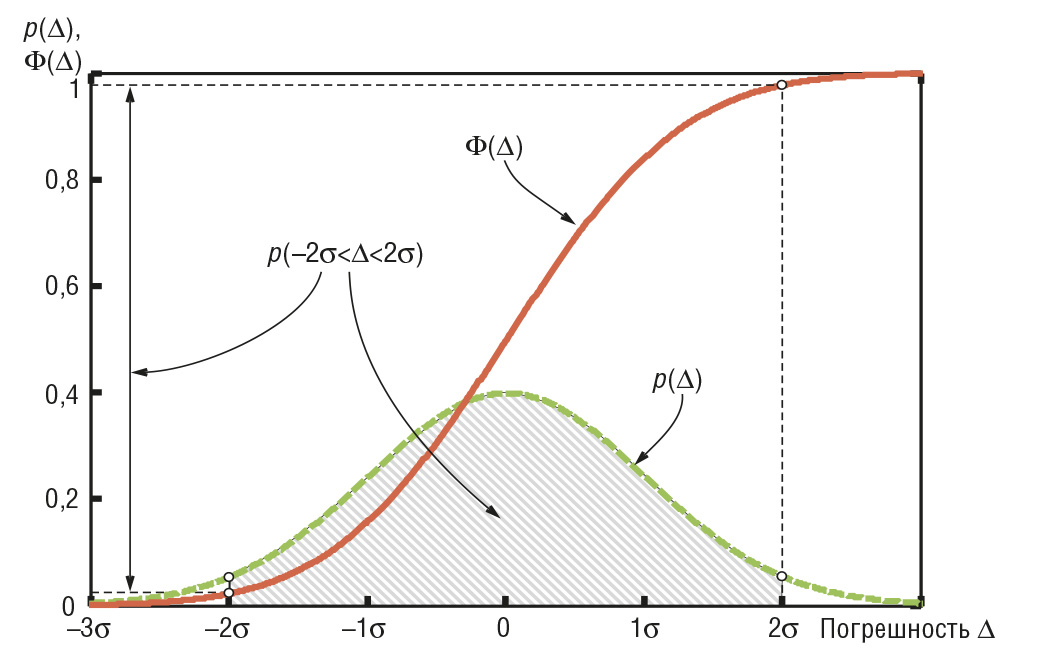
Смысл интервальной оценки погрешности иллюстрирует рис. 2. Здесь использованы следующие обозначения: ∆ – по-грешность измерения; р(∆) – плотность распределения по-грешностей; Φ(∆) – функция распределения погрешностей,
.jpg)
Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины ∆ описывается функцией
.jpg)
где σ – среднеквадратическая погрешность.
Если погрешность измерения ∆ находится внутри интервала ∆1 < ∆ < ∆2, то вероятность этого события вычисляется как
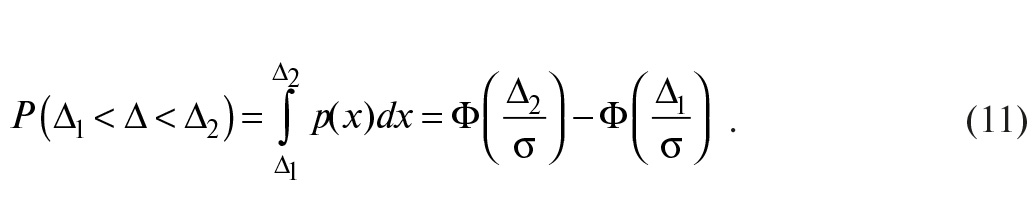
В наиболее типичном случае симметричных границ (–∆0 < ∆ < ∆0) получим
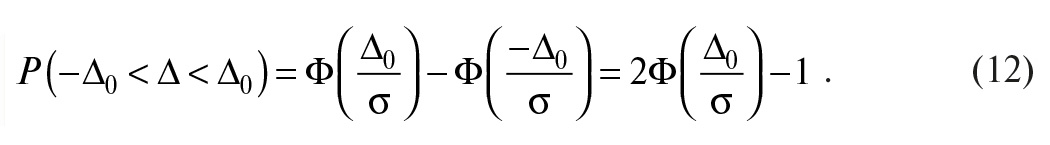
Здесь использовано свойство симметрии функции распределения для закона Гаусса.
Таким образом, если задан интервал –∆0 < ∆ < ∆0, который содержит в себе погрешность измеряемого параметра ∆, то вероятность того, что погрешность ∆ не выходит за границы интервала, можно найти по формуле (12) для нормального закона распределения. Вероятность P(–∆0 < ∆ < ∆0) называют также надёжностью оценки погрешности и обозначают символом γ:

Для вычисления функции распределения удобно использовать пакеты Mathcad, MATLAB. С их помощью из формулы (13) несложно найти величину доверительного интервала [–∆0, +∆0], если задана величина надёжности γ.
Для ∆0 = σ доверительная вероятность равна γ = 68,3%, для ∆0 = 2σ она уже равна γ = 95,3%, для ∆0 = 3σ составляет γ = 99,7% и для ∆0 = 4σ достигает γ = 99,994%.
Для увеличения надёжности оценки погрешности измерений или для сужения доверительного интервала при заданной надёжности можно использовать усреднение результатов многократных измерений. Поскольку оценка среднеквадратической погрешности результата усреднения σср равна [1], где σx – среднеквадратическая погрешность средства измерений, N – количество однократных измерений, то, подставив в (13) вместо σ величину σср, получим

Эта формула позволяет найти количество однократных измерений N, которое необходимо усреднить для получения требуемого доверительного интервала [–∆0, +∆0] при заданной надёжности γ или требуемой надёжности γ при заданном доверительном интервале [–∆0, +∆0]. Поскольку формула (14) задана в неявном виде, для нахождения требуемых неизвестных следует воспользоваться математическими пакетами для компьютерных вычислений.
Следует иметь в виду, что повышение точности путём усреднения результатов многократных измерений имеет множество ограничений [1].
Проблемой использования интервального метода оценки погрешности является необходимость знания закона распределения погрешностей.
Отметим, что доверительные интервалы, полученные из рассеяния множества измерений, никак не учитывают систематическую погрешность измерений. Интересные примеры из истории определения расстояния до Солнца, заряда электрона и др. приводятся в книге [5]. Ученые, которые делали эти выдающиеся измерения, указывали доверительные вероятности для оценки точности своих измерений. Однако ни одна из этих оценок не выдержала испытания временем: каждое новое, более точное измерение не укладывается в предсказанный ранее доверительный интервал. Это связано с тем, что систематическую погрешность или наличие ошибки в постановке эксперимента, в учёте факторов, о существовании которых мы не знаем, оценить невозможно, не имея более точного измерительного прибора.
Погрешность метода измерений
Для выполнения автоматизированных измерений используют датчики и измерительные преобразователи, измерительные модули ввода аналоговых сигналов, обработку результатов измерений на компьютере или в контроллере. При этом на погрешность результата измерений оказывают влияние следующие факторы:
-
сопротивление кабелей;
-
соотношение между входным импедансом средства измерений и выходным импедансом датчика;
-
качество экранирования и заземления, мощность источников помех;
-
погрешность метода косвенных, совместных или совокупных измерений;
-
наличие внешних влияющих факторов, если они не учтены в дополнительной погрешности средства измерений;
-
погрешность обработки результатов измерений программным обеспечением.
Все погрешности, которые не могут быть учтены в процессе сертификационных испытаний и внесены в паспорт средства измерений, а появляются в конкретных условиях применения, относятся к методическим. В отличие от них, инструментальные погрешности нормируются в процессе производства измерительного прибора и заносятся в его эксплуатационную документацию. Таким образом, если в состав смонтированной автоматизированной измерительной системы входят средства измерений с нормированными погрешностями, то погрешность, вызванная ранее перечисленными факторами, является методической. Если же выполняется сертификация всей измерительной системы, то методические погрешности могут быть учтены в погрешности всей системы, и тогда они переходят в разряд инструментальных.
Для расчёта или измерения методической погрешности трудно дать общие рекомендации. Каждый конкретный случай требует отдельного рассмотрения.
Погрешность программного обеспечения
Погрешность программного обеспечения (ПО) [6, 7] оценивается как разность между результатами измерений, полученными данным ПО и эталонным ПО. Под эталонным по-нимается программное обеспечение, высокая точность которого доказана многократными испытаниями и тестированием. Понятие эталонного ПО является условным и определяется соглашением между заказчиком аттестации и исполнителем. В качестве эталонного может быть использовано ра-нее аттестованное ПО.
К основным источникам погрешностей ПО относятся:
-
ошибки записи исходного текста программы и ошибки трансляции программы в объектный код;
-
ошибки в алгоритме решения измерительной задачи;
-
ошибки в таблицах для линеаризации нелинейных характеристик преобразования;
-
применение неустойчивых или медленно сходящихся алгоритмов при решении плохо обусловленных измерительных задач;
-
ошибки преобразования форматов данных;
-
ошибки округления и др.
Надёжность (достоверность) ПО обеспечивается средствами защиты от несанкционированных изменений, которые могут явиться причиной появления не учтённых при аттестации погрешностей.
Достоверность измерений
В процессе выполнения измерений могут появиться грубые ошибки (промахи), которые делают измерения недостоверными, несмотря на применение очень точных измерительных приборов. Здесь под достоверностью понимается степень доверия к полученным результатам. Достоверность может быть низкая при наличии погрешностей, о существовании которых экспериментатор не догадывается. Достоверность при использовании автоматизированных измерительных систем снижается с ростом их сложности и существенно зависит от квалификации персонала проектирующей и монтажной организаций.
Главным методом обеспечения достоверности является сопоставление результатов измерения одной и той же величины разными, не связанными друг с другом способами. Например, после монтажа системы измерения температуры в силосе элеватора следует сравнить показания автоматизированной системы и автономного контрольного термометра, чтобы убедиться в правильности показаний автоматизированной системы.
Приведём несколько примеров, иллюстрирующих случаи, когда, несмотря на применение точных средств измерений, получаются совершенно ошибочные данные, вводящие человека в заблуждение.
Пример 1. Для измерения температуры воздуха в теплице использован датчик температуры с погрешностью ±0,5°С. Однако датчик установлен таким образом, что в некоторые часы на него падают прямые лучи солнца, которые нагревают датчик, но не изменяют температуру воздуха. При этом погрешность измерения температуры воздуха может составить +5°С, что позволяет квалифицировать результат измерения как недостоверный.
Пример 2. Для измерения температуры в силосах элеватора установлены точные датчики и сделан тщательный монтаж, но расположенный на крыше элеватора ретранслятор сотовой связи оказался незамеченным, и не было принято достаточных мер для защиты от помех. При этом погрешность измерения температуры может составить ±10°С вслед-ствие помех, наведённых передатчиком в сигнальных кабелях системы.
Пример 3. В автоматизированной системе для измерения параметров продукции использован модуль ввода с погрешностью ±0,05%, однако при наладке системы программист по ошибке установил частоту помехоподавляющего режекторного фильтра не 50, а 60 Гц. Проведённые приёмо-сдаточные испытания системы не позволили выявить эту ошибку.
В результате погрешность измерений вследствие наведённой помехи с частотой 50 Гц может повыситься до ±10% вместо ожидаемых ±0,05%.
Пример 4. Во время выполнения измерений ваш коллега разговаривал по сотовому телефону. Наводка сигнала от передатчика сотового телефона может повысить погрешность измерений в несколько раз.
Пример 5. При монтаже системы заземлили экран сигнального кабеля с двух сторон. Проведённые приёмо-сдаточные испытания не позволили выявить эту ошибку. Погрешность может увеличиться в несколько раз по сравнению с ожидаемой.
Пример 6. В процессе эксплуатации системы нарушился контакт в цепи заземления, что привело к эпизодическому повышению уровня помех в измерительной цепи. В статье [8] описан пример, когда плохо затянутый болт в цепи заземления приводил к сбоям системы автоматики, причину которых искали несколько лет.
Пример 7. При расчёте погрешности средств измерений была проигнорирована динамическая погрешность, поскольку исходные данные для её расчёта не были указаны в эксплуатационной документации на средство измерения и не были выявлены в процессе приёмо-сдаточных испытаний ввиду сложности постановки эксперимента, отсутствия времени и приборов для контроля величины погрешности. Во время эксплуатации системы фактическая погрешность в несколько раз превысила расчётную.
В приведённых примерах сложно обнаружить наличие погрешности в процессе сдачи системы в эксплуатацию, она может появляться в особых условиях эксплуатации. Это приводит к снижению достоверности измерений, несмотря на высокую инструментальную точность использованных технических средств.
Общий подход к решению проблемы заключается в применении второй, независимой системы или методики измерений для обнаружения ошибок. Можно использовать также целый комплекс мер, включая подбор персонала, соблюдение графика поверки, тщательность выполнения типовых и сертификационных испытаний системы, соблюдение методики измерений и обслуживания измерительной системы.
Термин «достоверность» иногда используется во втором его значении – для указания вероятности того, что измеренное значение находится в заданном доверительном интервале [9] при условии, что все промахи и ошибки измерительной системы и методики измерений исключены. Количественным выражением достоверности в данном случае является доверительная вероятность [1]. Следует различать эти два значения одного и того же термина.
Методы суммирования погрешностей
Перед суммированием все погрешности делятся на следующие группы:
-
систематические и случайные;
-
в группе случайных – на коррелированные и некоррелированные;
-
аддитивные и мультипликативные;
-
основные и дополнительные.
Такое деление необходимо потому, что систематические и случайные погрешности, а также коррелированные и некоррелированные суммируются по-разному, а аддитивные по-грешности нельзя складывать с мультипликативными.
Если некоторые погрешности указаны в виде доверительных интервалов, то перед суммированием их нужно представить в виде среднеквадратических отклонений [1].
Дополнительные погрешности могут складываться с основными либо перед суммированием погрешностей, либо на заключительном этапе, в зависимости от поставленной задачи. Второй вариант часто предпочтительнее, поскольку он позволяет оценивать погрешность всего измерительного канала в зависимости от величины внешних влияющих факторов в конкретных условиях эксплуатации.
При последовательном соединении нескольких средств измерений погрешности, проходя через измерительный канал с передаточной функцией (функцией преобразования) f(x), могут усиливаться или ослабляться. Для учёта этого эффекта используют коэффициенты влияния, которые определяются как .
.jpg)
Все погрешности перед суммированием приводят к выходу (или входу) измерительного канала путём умножения (деления) на коэффициент влияния. В дальнейшем будем предполагать, что такое приведение уже выполнено.
Погрешности средств измерений являются случайными величинами, поэтому при их суммировании в общем случае необходимо учитывать соответствующие законы распределения. На практике пользуются более грубыми упрощёнными методами, разработанными математической статистикой.
Математическое ожидание погрешностей средств измерений, как правило, равно нулю. Если это не так, то его (в виде поправки) складывают с систематической составляющей погрешности. В средствах автоматизации введение поправки выполняется автоматически с помощью микроконтроллера, входящего в состав средств измерений. Математическое ожидание случайной составляющей всегда равно нулю, поскольку при нормировании метрологических характеристик его относят к систематической составляющей.
Наиболее полное определение итоговой погрешности измерительного канала состояло бы в нахождении функции распределения суммы нескольких погрешностей измерения. Однако функция распределения суммы случайных величин находится с помощью операции свёртки [10], что приводит к значительным практическим трудностям. Поэтому для оценки итоговой погрешности ограничиваются только суммированием дисперсий погрешностей.
Погрешности суммируют по однородным группам, затем находят общую погрешность, используя геометрическое суммирование для случайных погрешностей и алгебраическое для детерминированных.
Существует три способа суммирования погрешностей:
-
алгебраический (15)

где i – номер погрешности, N – их количество;
-
геометрический

где σi – среднеквадратическое значение i-й погрешности;
-
с учётом корреляции
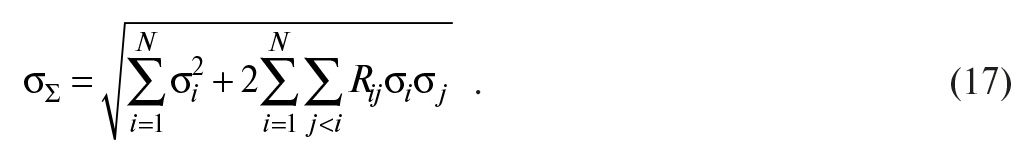
В этой формуле j ≠ i потому, что члены с j = i уже учтены в сумме NΣi=1 σi2 , а граница j < i установлена для того, чтобы суммировать только члены, лежащие ниже диагонали корреляционной матрицы, поскольку вследствие её симметричности Rijσiσj + Rjiσjσi = 2Rijσiσj.
При Rij = +1 выражение (17) переходит в формулу алгебраического суммирования:
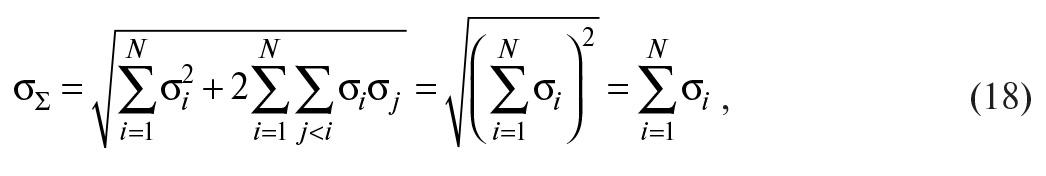
где σi складываются со своими знаками, то есть коррелированные погрешности с противоположными знаками частично взаимно компенсируются, если их коэффициент корреляции равен единице.
При Rij = –1 погрешности вычитают попарно в соответствии с (8):
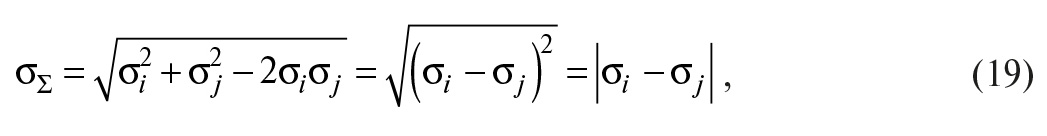
то есть при отрицательной корреляции погрешности частично компенсируются, если они имеют один и тот же знак.
Учитывая, что получить удовлетворительные оценки коэффициентов корреляции довольно трудно, используют следующий приём: при |Rij| ≥ 0,7 считают, что |Rij| = 1, при |Rij| < 0,7 полагают |Rij| = 0 [9, 10].
Систематические погрешности
В наиболее типовом случае систематические составляющие основных погрешностей средств измерений суммируются геометрически по формуле (16), поскольку они являются случайными величинами.
Формулы геометрического суммирования были получены для среднеквадратических погрешностей [1]. Поэтому, если комплекс метрологических характеристик средств измерений включает предел допускаемых значений систематической составляющей основной погрешности ∆os без указания среднеквадратического значения (по ГОСТ 8.009-84 [4]), то соответствующее ему среднеквадратическое значение находят в соответствии с рекомендациями РД 50-453-84 [11] по формуле

Эта формула справедлива, если нет оснований полагать, что функция распределения данной погрешности является несимметричной и имеет несколько максимумов.
Метрологическая инструкция МИ 2232-2000 [12] рекомендует иную формулу – половину предела допускаемой погрешности.
Выбор способа суммирования систематических составляющих основных погрешностей не является однозначным, и это связано с отсутствием полной информации о законе распределения. Дело в том, что причиной существования основной погрешности является как технологический разброс параметров электронных компонентов, так и нескомпенсированная нелинейность. Технологический разброс обычно является случайным, и на этом основании систематическая составляющая погрешности может рассматриваться как случайная величина на множестве средств измерений одного и того же типа. Поэтому в формулах для расчёта погрешностей она учитывается геометрически. Однако нелинейность передаточной характеристики средства измерений (нелинейность АЦП, нормирующих усилителей, термопар) у всех экземпляров приборов одного типа будет иметь примерно один и тот же вид, величину и знак. Например, погрешность, вызванная нелинейностью, в начале шкалы может быть положительной, в середине шкалы – отрицательной, у верхнего предела шкалы – опять положительной, и так для всех экземпляров приборов одного типа. Поэтому погрешности, обусловленные нелинейностью, должны суммироваться алгебраически.
В современных модулях аналогового ввода используется автоматическая калибровка, позволяющая уменьшить случайную компоненту систематической погрешности, и в этом случае преобладающей является детерминированная погрешность нелинейности.
Поскольку ГОСТ 8.009-84 [4] не предусматривает нормирование таких тонких нюансов поведения погрешностей, выбор способа суммирования начинает зависеть не от технических, а от политических факторов. Если фактическая погрешность окажется выше расчётной и это повлечёт за собой угрозу жизни людей, большой экономический ущерб, техногенную катастрофу и т. п. [12], то суммирование погрешностей выполняют алгебраически, причём используют не среднеквадратические отклонения, а пределы допустимых значений погрешности.
Если известен знак систематической погрешности, то его учитывают при суммировании.
Для наиболее ответственных применений следует использовать средства измерений, для которых указана погрешность без разделения на случайную и систематическую компоненты, поскольку в этом случае погрешность указана с доверительной вероятностью, равной единице. Если же ис-пользуются средства измерений, для которых указана случайная составляющая, то для них рассчитывают величину погрешности при доверительной вероятности, равной единице. Это условие существенно завышает требования к точности средства измерений.
Алгебраическое суммирование часто даёт слишком завышенную оценку погрешности. Поэтому МИ 2232-2000 [12] предусматривает промежуточный вариант между формулами геометрического и алгебраического суммирования:

где K – поправочный коэффициент, равный 1,2 для наиболее важных параметров устройств аварийной защиты и блокировки, контроля за соблюдением требований техники безопасности и экологической безопасности, контроля характеристик готовой продукции [12].
Для конкретных экземпляров приборов могут быть указаны не номинальные характеристики (имеющие одну и ту же величину для всех приборов данного типа), а индивидуальные. В этом случае систематическая погрешность является не случайной, а детерминированной величиной, поэтому должна учитываться в итоговой погрешности измерительного канала алгебраически.
Случайные составляющие погрешностей
Случайные составляющие основной погрешности средств измерений по ГОСТ 8.009-84 [4] задаются своими среднеквадратическими отклонениями, поэтому их суммирование выполняется непосредственно по формуле геометрического суммирования (16).
Если случайная погрешность является коррелированным случайным процессом [1] и задана в виде функции автокорреляции R(t) или спектральной плотности мощности S(f), то сначала находят среднеквадратическое значение случайной составляющей погрешности. Для этого используют формулу:

где fв – верхняя граничная частота полосы пропускания всего измерительного канала или цифрового фильтра, используемого при обработке полученных данных. Если задана функция автокорреляции, то спектральную плотность мощности находят по формуле, учитывающей корреляцию [1].
Случайная составляющая погрешности может быть уменьшена в несколько раз (в зависимости от величины фликкер-шума) путём усреднения результатов многократных измерений [1].
Дополнительные погрешности
Дополнительные погрешности задаются в виде функции влияния внешних факторов (температуры, влажности, напряжения питания) на основную погрешность измерения, или, в случае линейной функции влияния, они характеризуются коэффициентом влияния. Например, может быть задано, что основная погрешность увеличивается на +0,05% при изменении напряжения питания на +20%.
Если задан диапазон изменения влияющих величин, в качестве их математического ожидания для расчётов с помощью функции влияния берут их среднее значение [11].
Среднеквадратическое отклонение дополнительной погрешности для линейной функции влияния находят по формуле [11]:

где Kξ – коэффициент влияния внешнего фактора; ξ1, ξ2 – нижняя и верхняя границы изменения влияющей величины.
Дополнительная погрешность может увеличивать как систематическую, так и случайную составляющую основной погрешности. Для этого функции влияния задаются раздельно на каждую составляющую.
Если известно, что дополнительные погрешности нескольких средств измерений коррелируют (например, синхронно возрастают при увеличении напряжения питания в сети или температуры окружающей среды), то такие погрешности суммируют как коррелированные величины с учётом коэффициента корреляции в соответствии с (17) – (19).
Дополнительные погрешности считаются несущественными, если их сумма составляет менее 17% от наибольшего возможного значения инструментальной погрешности в рабочих условиях эксплуатации [4].
Динамические погрешности
Динамическая погрешность при известном входном сигнале является детерминированной. Она обычно приводит к занижению показаний измерительного прибора. Суммирование таких погрешностей выполняется алгебраически.
Подробнее об оценке динамической погрешности см. [1, 10].
Динамическая погрешность считается несущественной, если она составляет менее 17% от наибольшего возможного значения инструментальной погрешности в рабочих условиях эксплуатации [4].
Нахождение итоговой погрешности
После суммирования погрешностей по группам, как это было описано ранее, результат измерения обычно выражают в виде:

где x0 – измеренное значение; ∆ – сумма всех погрешностей, которые складывались алгебраически, то есть детерминированных погрешностей (детерминированные погрешности могут быть прибавлены к измеренной величине в качестве поправки); σ – сумма всех случайных погрешностей, которые складывались геометрически, в том числе с учётом корреляционных связей:
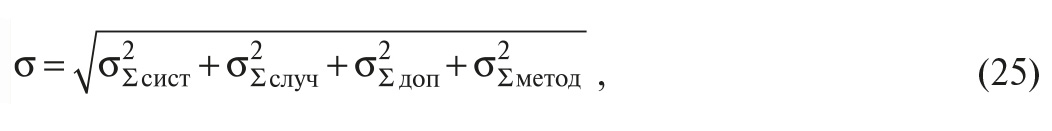
где σΣсист – сумма всех систематических погрешностей измерительного канала; σΣслуч – сумма всех случайных погрешностей; σΣдоп – сумма всех дополнительных погрешностей; σΣметод – сумма всех случайных составляющих методических погрешностей, включая погрешность программного обеспечения. Детерминированные составляющие методических погрешностей учитываются в слагаемом ∆.
Вместо среднеквадратического отклонения может быть указан предел допустимых значений. Однако должно быть явно указано, какая именно оценка погрешности использована, поскольку доверительные вероятности для предела допустимых значений (единица) и для среднеквадратического отклонения (0,68) существенно отличаются.
Случайная, систематическая и дополнительная погрешности могут быть указаны раздельно. МИ 1317-2004 [13] рекомендует «вместе с результатом измерений представлять характеристики его погрешности или их статистические оценки». Поэтому состав характеристик погрешности может быть выбран в каждом конкретном случае индивидуально, в зависимости от смысла решаемой задачи.
При выполнении многократных измерений результат должен также содержать указание на количество измерений, использованных при усреднении, и интервал времени, в течение которого были выполнены измерения [13].
Поскольку выражение для суммы дисперсий случайных величин (1) получено независимо от закона распределения, геометрическое суммирование погрешностей даёт правильное значение дисперсии независимо от законов распределения отдельных составляющих. Однако при этом ничего нельзя сказать о функции распределения суммарной погрешности, в том числе о надёжности (доверительной вероятности) полученного результата. Тем не менее, поскольку при суммировании пяти и более погрешностей закон распределения суммы близок к нормальному независимо от законов распределения отдельных слагаемых [10], то, зная среднеквадратическое отклонение итоговой погрешности, можно использовать нормальный закон распределения для указания доверительного интервала и доверительной вероятности результата измерений.
Нахождение погрешности измерительного канала в условиях недостатка исходных данных
При оценке погрешности измерительных каналов средств автоматизации следует по возможности использовать экспериментальный метод. Однако в случаях когда это невозможно или экономически нецелесообразно, делают расчёт по изложенной ранее методике. Типичной проблемой, которая при этом возникает, является отсутствие некоторых исходных данных. В этой ситуации метрологическая инструкция МИ 2232-2000 [12] рекомендует использовать следующие «значения по умолчанию»:
-
среднеквадратическое значение погрешности принимается равным половине предела допускаемых значений погрешности;
-
математическое ожидание основной и дополнительной погрешности принимается равным нулю;
-
корреляция между отдельными составляющими погрешности отсутствует;
-
случайная составляющая погрешности измерений является некоррелированной случайной величиной (белым шумом) или вырождается в систематическую погрешность;
-
функции распределения внешних влияющих величин предполагаются равномерными или нормальными;
-
считается, что инерционные свойства средств измерений не оказывают влияния на погрешность измерений. ●
Литература
-
Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. – М. : Горячая линия – Телеком, 2009. – 608 с.
-
МИ 2440-97. ГСИ. Методы экспериментального определения и контроля характеристик погрешности измерительных каналов измерительных систем и измерительных комплексов (взамен МИ 2313-94).
-
ГОСТ 23222-88. Характеристики точности выполнения предписанной функции средств автоматизации. Требования к нормированию. Общие методы контроля.
-
ГОСТ 8.009-84. Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерений.
-
Тутубалин В.Н. Теория вероятностей и случайных процессов. Основы математического аппарата и прикладные аспекты. – М. : Изд-во МГУ, 1992. – 400 с.
-
МИ 2955-2005. ГСИ. Типовая методика аттестации программного обеспечения средств измерений и порядок её проведения.
-
МИ 2891-2004. ГСИ. Общие требования к программному обеспечению средств измерений.
-
Burleson J. Wiring and grounding to prevent power quality problems with industrial equipment // Textile, Fiber and Film Industry Technical Conference, 8–9 May 1991. – Pp. 5/1–5/6.
-
Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. – Л. : Энергоатомиздат, 1991. – 304 с.
-
Орнатский П.П. Теоретические основы информационно-измерительной техники. – 2-е изд. – Киев : Вища школа, 1983. – 455 с.
-
РД 50-453-84. Методические указания. Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчёта.
-
МИ 2232-2000. ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Оценивание погрешности измерений при ограниченной исходной информации.
-
МИ 1317-2004. ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров (взамен ГОСТ 8.011-72, МИ 1317-86).
