Как найти наименьший положительный период функции онлайн – Сайт, где вы сможете решить свои вопросы

Онлайн калькулятор для определения периодичности функции. Периодическая функция – это функция повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (периода функции) на всей области определения.

Периодичная функция может иметь и несколько периодов, самый маленький положительный из них называется основным.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

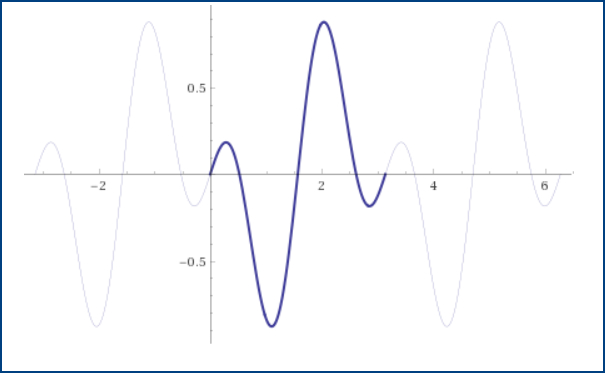
Типичная школьная задача – нахождение периода функции. Теперь вы можете решить эту быстро онлайн с помощью нашего калькулятора. Для это надо только ввести команду «period» и функцию для которой надо найти период. Кроме того что будет выведен период, если он есть, будет еще и график построен (как на рисунке слева) на котором будет показана величина периода.

Чтобы воспользоваться онлайн сервисом нажмите значок копирования, чтобы добавить команду из примера в окно ввода команд для обработки изображений.

Пример команды, которая находит период функции одной переменной. Ключевое слово – «period».

period y=sin(x)*cos(3x)

Пример команды, которая позволяет найти период функции двух переменных. Период определяется для каждой переменной отдельно.

period of f(x,y)=sin(x)*cos(3y)

Пример функции у которой нет периода (будет выведено сообщение «function not periodic»).

period y=sin(x)*cos(3x)+x^2

Пишите в комментарии примеры функция для которых вы нашли период с помощью нашего калькулятора.

Похожие публикации

2019-11-01 • Просмотров [ 45970 ]

Источник

наименьший положительный период функции онлайн

Вы искали наименьший положительный период функции онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найти наименьший положительный период функции онлайн калькулятор, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение.
Например, «наименьший положительный период функции онлайн».

наименьший положительный период функции онлайн

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как наименьший положительный период функции онлайн,найти наименьший положительный период функции онлайн калькулятор,найти период функции онлайн,период функции онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и наименьший положительный период функции онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти период функции онлайн).

Где можно решить любую задачу по математике, а так же наименьший положительный период функции онлайн Онлайн?

Решить задачу наименьший положительный период функции онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать – это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Источник

При построении графиков, для выполнения анализа функции может понадобиться знание периода функции. Даже в механике, получив уравнение колебаний может возникнуть задача о периоде колебаний.

Для тех кто забыл или не знает математику, напомним, что период это длина интервала, через который функция повторяется. Или можно записать так: если существует такая величина (Tneq0), что (fleft(x+Tright)=fleft(xright)), то функция будет периодической. На графике периодичной функции есть повторяющиеся участки. Можно посмотреть пример, приведенный на рисунке. Один период функции выделен. Но, достаточно теории. Наших читателей интересует как быстро и правильно найти период функции. Особенно, если это не простая функция. Ответ – это можно сделать с помощью решателя. Вводите команду period, а затем ту функцию, период которой вам надо найти. И жмете кнопку “решить”. Вы получите не только значение периода, если он есть, но и график самой функции, на котором будет отмечен период. Пример команды и функции приведен ниже.

period y=sin(x)*cos(3x)

Похожие публикации: алгебра, математика

Источник

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, $y = sin x, , y = tg x$ — периодические функции.

Дадим определение периодической функции:

Функция $y=f(x)$ называется периодической, если существует такое число $T$ , не равное нулю, что для любого $x$ из ее области определения $f(x + T) = f(x).$

Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа $T$ . Число $T$ называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.

Например, $y = sin x, , y = cos x, , y = tg x, , y = ctg x$ — периодические функции.

Для функций $y = sin x$ и $y = cos x$ период $T = 2pi$ ,

Для функций $tg x$ и $y = ctg x$ период $T = pi.$

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция $y = fleft(xright)$ определена для всех действительных чисел. Ее период равен двум и $f(1)=5.$ Найдите значение выражения $3f(7) - 4 f(-3).$

График функции ${y = }fleft(xright)$ может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции ${y = }fleft(xright)$ . Поскольку период функции равен 2, значения функции в точках $3, 5, 7dots 1 + 2k$ будут также равны пяти. Здесь k — целое число.

Как ведет себя функция ${y = }fleft(xright)$ в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

Значения функции ${y = }fleft(xright)$ в точках -3 и 7 равны пяти. Мы получим: $3fleft(7right)4fleft(-3right)=3cdot 5-4cdot 5=-5.$

2. График четной периодической функции $y = fleft(xright)$ совпадает с графиком функции $zleft(xright)=2(x-1)^2$ на отрезке от 0 до 1; период функции $y = fleft(xright)$ равен 2. Постройте график функции $y = fleft(xright)$ и найдите f(4 ).

Построим график функции $zleft(xright)=2(x-1)^2$ при $xin [0;1].$

Поскольку функция $y = { f}left({ x}right)$ четная, ее график симметричен относительно оси ординат. Построим часть графика при $xin [-1;0],$ симметричную части графика от 0 до 1.

Период функции $y = fleft(xright)$ равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем $f(4)$

$f(4)= f (0 + 2cdot 2) = f(0) = 2.$

3. Найдите наименьший положительный период функции $fleft(xright)={sin 3x+{cos 5x}}$

Наименьший положительный период функции $y={sin x}$ равен $2pi.$

График функции $y=sin 3x$ получается из графика функции $y={sin x}$ сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Значит, у функции $y={sin 3x}$ частота в 3 раза больше, чем у функции $y={sin x}$ , а наименьший положительный период в 3 раза меньше и равен $frac{{rm 2}pi }{{rm 3}}$ . Значит, на отрезке $2pi$ укладывается ровно 3 полных волны функции $y={sin 3x}.$

Рассуждая аналогично, получим, что для функции $y={cos 5x}$ наименьший положительный период равен $frac{{rm 2}pi }{{rm 5}}.$ На отрезке $2pi$ укладывается ровно 5 полных волн функции $y={cos 5x}.$

Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции $fleft(xright)={sin 3x+{cos 5x}}$ равен $2pi$ .

4. Период функции $fleft(xright)$ равен 12, а период функции $gleft(xright)$ равен 8. Найдите наименьший положительный период функции $zleft(xright)=fleft(xright)+gleft(xright).$

По условию, период функции $fleft(xright)$ равен 12. Это значит, что все значения $fleft(xright)$ повторяются через 12, через $24, 36, 48 ... 12n$ . Если мы выберем любую точку $x_0$ на графике функции $fleft(xright),$ то через $12, 36, 48dots 12n$ значение функции будет такое же, как и в точке $x_0.$

Аналогично, все значения функции $gleft(xright)$ повторяются через $8, 16, 24, 32dots 8k$ . В этих точках значения $gleft(xright)$ будут такие же, как и в точке $x_0.$

На каком же расстоянии от точки $x_0$ расположена точка, в которой значение функции $zleft(xright)=fleft(xright)+gleft(xright)$ такое же, что и в точке $x_0$ ? Очевидно, на расстоянии $T = 12n = 8k.$ Это значит, что число $T$ делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, $T = 24$ .

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Периодические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

наименьший положительный период функции онлайн

Где можно решить любую задачу по математике, а так же наименьший положительный период функции онлайн Онлайн?

Вам также может понравиться

Как найти комнату в хабаровске

Как составить заявку на кредит чтобы одобрили

Поставил светодиодные лампы в поворотники стали быстро моргать как исправить

Добавить комментарий Отменить ответ