Инфоурок
›
Математика
›Другие методич. материалы›Формулы площади и объема 5 класс математика
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Булатова Айгуль Рустемовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 5 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 24224
-
Всего материалов:
1
Определение прямоугольника и параллелепипеда
Прямоугольник – одна из самых простых плоских фигур, а прямоугольный параллелепипед – такая же простая фигура, но в пространстве (рис. 1). Они очень похожи.
Так же похожи, как круг и шар.

Рис. 1. Прямоугольник и параллелепипед
Вычисление площади
Разговор про площади начинают с площади прямоугольника, а про объемы – с объема прямоугольного параллелепипеда.
Если мы умеем находить площадь прямоугольника, то это нам позволяет найти площадь любой фигуры.
Вот эту фигуру мы можем разбить на 3 прямоугольника и найти площадь каждого, а значит, и всей фигуры (рис. 2).
Даже если фигура не разбивается точно на прямоугольники, это можно сделать с любой точностью и площадь посчитать приблизительно.
Площадь этой фигуры (рис. 3) примерно равна сумме площадей семи прямоугольников. Неточность получается за счет верхних маленьких фигур. Если увеличить число прямоугольников, то неточность уменьшится.
То есть прямоугольник – это инструмент для вычисления площадей любых фигур.
Вычисление объема
Такая же ситуация, когда речь идет об объемах.
Любую фигуру можно выложить прямоугольными параллелепипедами, кирпичиками. Чем мельче будут эти кирпичики, тем точнее мы сможем посчитать объем (рис. 4, рис. 5).

Рис. 4. Вычисление площади с помощью прямоугольных параллелепипедов
Прямоугольный параллелепипед является инструментом для вычисления объемов любых фигур.

Рис. 5. Вычисление площади с помощью маленьких параллелепипедов
Формула площади прямоугольника
Давайте немного вспомним.
Квадрат со стороной 1 единица (рис. 6) имеет площадь в 1 квадратную единицу. Исходная линейная единица может быть любой: сантиметр, метр, километр, миля.
Например, 1 см2 – это площадь квадрата со стороной 1 см.

Рис. 6. Квадрат и прямоугольник
Площадь прямоугольника – это количество таких квадратов, которые в него поместятся (рис. 6).
Уложим единичные квадраты в длину прямоугольника в один ряд. Получилось 5 штук.
В высоту помещается 3 квадрата. Значит, всего помещается три ряда, в каждом по пять квадратов.
Итого площадь равна ![]() .
.
Понятно, что нет нужды каждый раз внутри прямоугольника размещать единичные квадраты.
Достаточно умножить длину одной стороны на длину другой.
![]()
Или в общем виде:
![]()
Объем прямоугольного параллелепипеда
Очень похоже обстоят дела с объемом прямоугольного параллелепипеда.
Объем куба со стороной 1 единица – это 1 кубическая единица. Опять же, исходные линейные величины могут быть любыми: миллиметры, сантиметры, дюймы.
Например, 1 см3 – это объем куба со стороной 1 см, а 1 км3 – это объем куба со стороной 1 км.
Найдем объем прямоугольного параллелепипеда со сторонами 7 см, 5 см, 4 см (рис. 7).

Рис. 7. Прямоугольный параллелепипед
Решение
Объем нашего прямоугольного параллелепипеда – это количество единичных кубов, помещающихся в него.
Уложим на дно ряд единичных кубиков со стороной 1 см вдоль длинной стороны. Поместилось 7 штук. Уже по опыту работы с прямоугольником мы знаем, что на дно поместится всего 5 таких рядов, по 7 штук в каждом. То есть всего:
![]()
Назовем это слой. Сколько таких слоев мы можем уложить друг на друга?
Это зависит от высоты. Она равна 4 см. Значит, укладывается 4 слоя в каждом по 35 штук. Всего:
![]()
А откуда у нас появилось число 35? Это 7![]() 5. То есть количество кубиков мы получили перемножением длин всех трех сторон.
5. То есть количество кубиков мы получили перемножением длин всех трех сторон.
![]()
Но это и есть объем нашего прямоугольного параллелепипеда.
![]()
Ответ: 140 ![]()
Теперь мы можем записать формулу и в общем виде (рис. 8).

Рис. 8. Объем параллелепипеда
![]()
Объем прямоугольного параллелепипеда со сторонами ![]() ,
, ![]() ,
, ![]() равен произведению всех трех сторон.
равен произведению всех трех сторон.
Если длины сторон даны в сантиметрах, то объем получится в кубических сантиметрах (см3).
Если в метрах, то объем в кубических метрах (м3).
Аналогично объем может быть измерен в кубических миллиметрах, километрах и т. д.
Задача 1
Стеклянный куб со стороной 1 м наполнен водой целиком. Какова масса воды (рис. 9)?

Рис. 9. Куб
Решение
Куб является единичным. Сторона – 1 м. Объем – 1 м3.
![]()
Если мы знаем, сколько весит 1 кубический метр воды (сокращенно говорят кубометр), то задача решена.
Но если мы этого не знаем, то нетрудно посчитать.
Длина стороны ![]() .
.
Посчитаем объем в дм3.
![]()
Но 1 дм3 имеет отдельное название, 1 литр. То есть у нас 1000 литров воды.
Нам всем известно, что масса одного литра воды равна 1 кг. То есть у нас 1000 кг воды, или 1 тонна.
![]()
Понятно, что такой куб, наполненный водой, не под силу передвинуть ни одному обычному человеку.
Ответ: 1 т.
Задача 2

Рис. 10. Холодильник
Холодильник имеет высоту 2 метра, ширину 60 см и глубину 50 см. Найти его объем.
Решение
Прежде чем мы воспользуемся формулой объема – произведение длин всех сторон – необходимо перевести длины в одинаковые единицы измерения.
Мы можем перевести все в сантиметры.
Соответственно, и объем мы получим в кубических сантиметрах.
![]()
Ответ: ![]()
Думаю, вы согласитесь, что в кубических метрах объем более понятен.
Человек на глаз плохо отличает число с пятью нулями от числа с шестью нулями, а ведь одно в 10 раз больше, чем другое.
Как перевести единицы объема?
Часто нам нужно перевести одну единицу объема в другую. Например, кубометры в кубические дециметры. Тяжело запомнить все эти соотношения. Но этого и не нужно делать. Достаточно понять общий принцип.
Например, сколько кубических сантиметров в кубическом метре?
Давайте посмотрим, сколько кубиков со стороной 1 сантиметр поместится в куб со стороной 1 м (рис. 11).

Рис. 11. Куб
В один ряд укладывается 100 штук (ведь в одном метре 100 см).
В один слой укладывается 100 рядов или ![]() кубиков.
кубиков.
Всего помещается 100 слоев.
Всего ![]()
Таким образом, ![]()
То есть если линейные величины связаны соотношением «в одном метре 100 см», то чтобы получить соотношение для кубических величин, нужно возвести 100 в 3 степень (![]() ). И не нужно каждый раз чертить кубы.
). И не нужно каждый раз чертить кубы.
Заодно мы увидели соотношение и для единиц площади. В одном квадратном метре ![]() квадратных сантиметров. В одном слое у нас было 10 000 кубиков.
квадратных сантиметров. В одном слое у нас было 10 000 кубиков.
Задачи
Сколько в одном кубическом километре кубических метров?
![]()
![]()
![]()
Ответ: 1 млрд м3.
Каждый кубометр воды весит 1 т. Значит, кубический километр воды весит 1 млрд тонн. Такими единицами пользуются при измерении количества воды в морях и океанах.
Какова масса одного кубического сантиметра воды?
Мы знаем массу одного литра, это 1 кг, но 1 литр – это кубический дециметр.
![]()
Так как ![]() , то
, то ![]() . Но это значит, что 1
. Но это значит, что 1 ![]() весит:
весит:
![]()
Для одной тысячной существует приставка «милли-» (помним, что миллиметр – это одна тысячная метра), эту приставку используют и здесь.
![]()
То есть иными словами мы можем сказать, что один миллилитр воды имеет массу 1 г.
Заключение
Сегодня на уроке мы узнали, как найти площадь и объем. А также научились переводить одну единицу объема в другую.
Список литературы
- Виленкин Н. Я., Жохов В. И. Учебник по математике 5 класс. – 2008.
- Зубарева И. И., Мордкович А. Г. Математика. 5 класс. – М.: Мнемозина, 2013.
- Никольский С. М., Потапов М. К. Учебник по математике 5 класс. – 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «festival.1september.ru» (Источник)
- Интернет-портал «granddecor12.ru» (Источник)
- Интернет-портал «classcenter.ru» (Источник)
Домашнее задание
- Как найти объем параллелепипеда?
- Найдите объем прямоугольного параллелепипеда, если его длина, ширина и высота соответственно равны: 5 м, 6 м, 7 м.
ПЕРИМЕТР
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.
Чаще всего периметр обозначается буквой P.
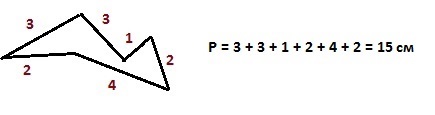
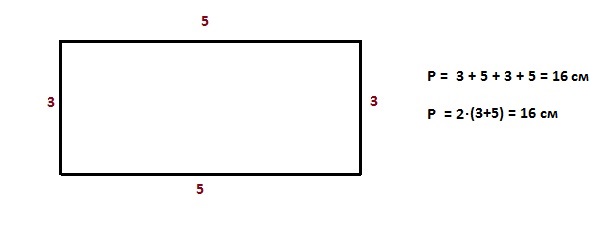
Периметр прямоугольника – удвоенная сумма длины и высоты – 2∙(a+b)
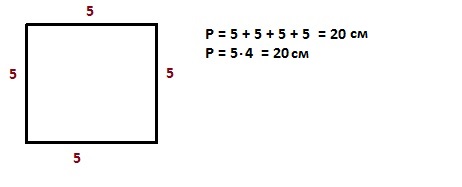
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.
ПЛОЩАДЬ
Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.
В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.
Чаще всего площадь обозначается буквой S.
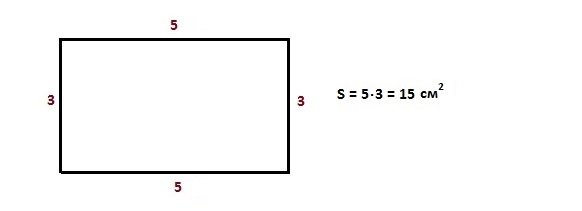
Площадь прямоугольника – произведение длины на высоту.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Разделим этот прямоугольник на квадраты
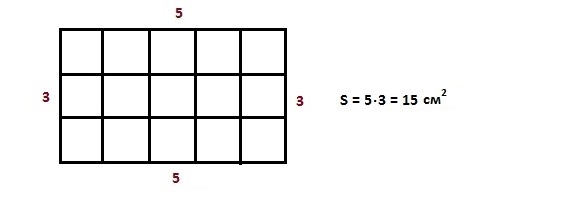
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.
Площадь квадрата – произведение длины стороны на саму себя.
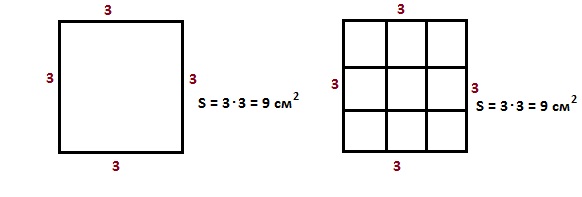
СОСТАВНЫЕ ФИГУРЫ
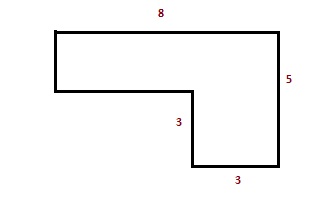
Разделим эту фигуру на прямоугольник и квадрат
Высота прямоугольника составит 5 – 3 = 2
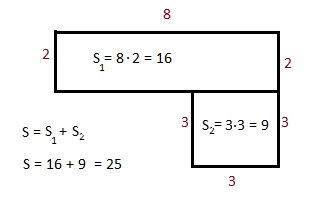
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА
Фигуры с одной и той же площадью могут иметь разный периметр
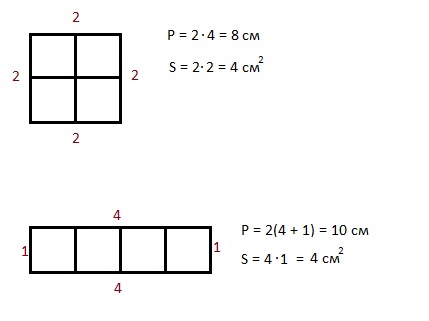
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?
Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.
Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.
ОБЪЁМ
Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.
1 л = 1 дм3
Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.
Чаще всего объём обозначается буквой V.
Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.
Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты

Зная объём и две стороны, мы можем найти третью сторону:
c = (V:a):b = V:S
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
ЗАДАЧИ
Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.
x = 10 см – ширина
1. Найдём длину
y = 10 + 6 = 16 см
2. Найдём периметр
P = 2∙(10+16) = 52 см
3. Найдём площадь
S = 10∙16 = 160 см2
Ответ: P = 52 см, S = 160 см2
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?
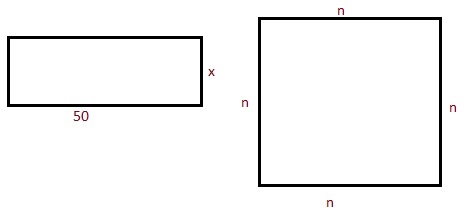
1. Вычислим сторону квадрата
4∙n = 80 – периметр
n = 20 см
2. Вычислим площадь квадрата
20∙20 = 400 см2
3. Вычислим ширину прямоугольника
50∙x = 400 см2
x = 8 см
Ответ: 8 см
Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?
1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм
1. Переведём длину прямоугольника в дм
x = 15∙10 = 150 дм
2. Найдём ширину прямоугольника
150∙y = 7500
y = 7500:150 = 50 дм
Ответ: 50 дм
Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.
1. Найдите площадь этого прямоугольника.
2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.
3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.
1. Найдём ширину прямоугольника
x = 60:3 = 20 см
2. Найдём площадь прямоугольника
S = 60∙20 = 1200 см
2. Найдём периметр прямоугольника
P = 2∙(60+20) = 160 см
3. Найдём сторону квадрата
y = 160:4 = 40 см
4. Найдём площадь квадрата
Sкв = 40∙40 = 1600 см2
5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:
Sкв2 = 1200:12 = 100 см2
6. Найдём сторону такого квадрата
Площадь квадрата = 100 см2
Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см
7. Найдём периметр такого квадрата
P = 10∙4 = 40 см
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.
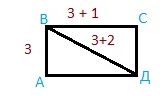
1. Найдём сторону ВС
ВС = 3+1 = 4
2. Найдём диагональ ВД
ВД = 3+2 = 5
3. Найдём периметр АВСД
P = 2∙(3+4) = 14 см
4. Найдём площадь АВСД
Sавсд = 3∙4 = 12 см2
5. Найдём периметр треугольника АВД
Pавд = 3 + 5 + 4 = 13 см
6. Найдём площадь треугольника АВД
Треугольник АВД занимает половину площади прямоугольника АВСД
Sавд = Sавсд:2
Sавд = 12:2 = 6 см2
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?
Решение
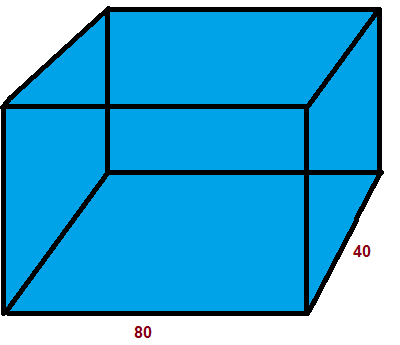
1. Переведём литры в кубические дециметры
1 л = 1 дм3, 160 л = 160 дм3
2. Переведём стороны аквариума в дециметры
1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм
3. Найдём высоту аквариума
V = a∙b∙c, a = 8, b = 4
c = (V:a):b
c = (160:8):4 = 5 дм
c = 5∙10 = 50 см
Ответ: 50 см
Напомним, что измерить отрезок означает подсчитать, сколько
единичных отрезков в нём укладывается. Измерить площадь фигуры означает
подсчитать, сколько единичных квадратов в ней укладывается. Измерить объём
фигуры означает подсчитать, сколько единичных кубов в ней укладывается.
Теперь сформулируем некоторые свойства произвольных фигур.
Итак, каждая плоская фигура или пространственное тело имеют форму
и размеры.
Равные фигуры – это фигуры, равные по
размерам и имеющие одинаковую форму.
Так, например, следующие прямоугольник и квадрат имеют равные
площади (в каждом из них укладывается одинаковое число единичных квадратов), но
при этом они не равны, так как имеют разные формы.
Или, например, два круга имеют одну и ту же форму, но очевидно,
что их размеры не совпадают. Значит, эти два круга не равны между собой.
А вот два отрезка одинаковой длины являются равными фигурами.
Две фигуры называют равными, если они совпадают при
наложении. Посмотрите, на листе бумаги изображены фигуры. Если их вырезать и
совместить, то мы увидим, что они совпадают при наложении. А значит, эти фигуры
равны.
Если две различные плоские фигуры можно разрезать на одинаковые
части, то эти фигуры будут иметь равные площади. Такие фигуры называют равносоставленными.
Давайте возьмём прямоугольник и разрежем его на два треугольника.
Сложим из полученных фигур новую фигуру – треугольник. Полученный треугольник и
прямоугольник – равносоставленные фигуры, так как состоят из одного и того же
набора плоских фигур.
Прямоугольник и треугольник, составленные из частей
прямоугольника, имеют одинаковую площадь.
Фигуры, имеющие равные площади, называют равновеликими.
Плоские равновеликие многоугольники также являются
равносоставленными.
Таким образом, можно сказать, что многоугольник всегда можно
перекроить в любой другой многоугольник с такой же площадью.
Давайте следующий четырёхугольник разделим на три части. Получили
два треугольника и квадрат.
Теперь переложим один треугольник вот таким образом…
В результате получим прямоугольник, площадь которого равна площади
исходного четырёхугольника.
Объёмные тела, составленные из одинаковых частей, имеют одинаковый
объём.
В отличие от многоугольников, два многогранника, имеющие
одинаковый объём, не всегда можно разделить на одинаковые части.
Теперь возьмём прямоугольник со сторонами длиной 2 см и 3 см.
Этот прямоугольник состоит из 6 квадратов. Площадь каждого
квадрата равна 1 см2. Тогда площадь всего прямоугольника равна 6 см2.
Давайте увеличим каждую сторону данного прямоугольника в 2 раза.
Тогда получим прямоугольник со сторонами 4 см и 6 см. Несложно посчитать, что полученный
прямоугольник состоит из 24 квадратов, а значит, его площадь равна 24 см2.
. Получается, что площадь прямоугольника увеличилась в 4 раза.
При увеличении длины каждой стороны прямоугольника в 2 раза
площадь увеличилась в , то есть в 4 раза.
Таким образом, если, не меняя формы плоской фигуры, увеличить её
размеры в раз, то её площадь увеличится в
раз.
Возьмём куб с длиной ребра 2 см. Найдём объём этого куба. Для
этого посчитаем, сколько кубиков с ребром 1 см в нём поместится. Итак, на дно
куба помещается 2 ряда из 2 единичных кубиков. Тогда на дне куба помещается
слой из , то есть из 4 кубиков. Чтобы заполнить весь куб, в него надо
вложить ещё 1 слой из 4 кубиков. Получается, что весь куб можно заполнить , то есть 8 кубиками. Поэтому объём нашего куба равен 8 см3.
А теперь давайте увеличим ребро куба, например, в 2 раза. Тогда
получим куб с длиной ребра 4 см. Найдём объём этого куба. На дно куба помещается
4 ряда из 4 единичных кубиков. Тогда на дне куба помещается слой из , то есть из 16 кубиков. Чтобы заполнить весь куб, в него надо
вложить ещё 3 слоя из 16 кубиков. Получается, что весь куб можно заполнить , то есть 64 кубиками. Поэтому объём этого куба равен
см3.
. Получается, что объём куба увеличился в 8 раз.
При увеличении длины ребра куба в 2 раза объём куба увеличился в , то есть в 8 раз.
Таким образом, если, не меняя формы тела, увеличить его размеры в раз, то его объём увеличится в
раз.
Отметим, что площадь фигуры и объём тела не всегда удобно находить
так, как мы это делали выше. Так, например, вычислить площадь участка или объём
комнаты было бы удобнее с помощью некоторых формул. Ещё в начальной школе мы
узнали, что площадь прямоугольника равна произведению его длины и ширины.
Если и
– длины соседних сторон прямоугольника (в
каких-то единицах), то его площадь равна квадратных единиц.
В буквенном виде формулу для вычисления площади прямоугольника
записывают так:
– площадь,
,
– длины соседних сторон прямоугольника. При вычислениях важно
помнить, что длина и ширина прямоугольника должны быть выражены в одних и тех
же единицах измерения.
Так, площадь прямоугольника со сторонами 2 см и 3 см равна (см2).
А сейчас посмотрите на следующий рисунок.
На нём изображён квадрат со стороной 4 см. Давайте вычислим его
площадь. Так как квадрат – это прямоугольник, у которого все стороны равны, то воспользуемся
формулой площади прямоугольника. (см2).
Так как у квадрата все стороны равны, то его площадь находят по
формуле:
Теперь познакомимся с формулой для вычисления объёма
прямоугольного параллелепипеда.
Если ,
и
– длина, ширина и высота прямоугольного параллелепипеда, то его
объём равен кубических единиц.
В буквенном виде формулу для вычисления объёма прямоугольного
параллелепипеда записывают так:
– объём,
,
,
– измерения прямоугольного параллелепипеда. Отметим, что при
вычислениях важно помнить, что длина, ширина и высота прямоугольного
параллелепипеда должны быть выражены в одинаковых единицах измерения.
Куб – это прямоугольный параллелепипед, у которого все рёбра равны
между собой, то его объём вычисляют по формуле:
Например, объём куба с длиной ребра 2 см равен (см3).
А теперь давайте с вами решим несколько задач.
Задание первое. Выясните, являются
ли квадрат со стороной 6 см и прямоугольник со сторонами 9 см и 4 см
равновеликими фигурами?
Решение.
Задание второе. Найдите площадь фигуры,
изображённой на рисунке.
Решение.
Запомните! Площадь фигуры равна
сумме площадей фигур, из которых она состоит.
Задание третье. Найдите объём комнаты,
если её длина равна 7 м, ширина равна 4 м, а высота стен равна 3 м.
Решение.
Тема урока: «Обобщающий урок по теме «Площади и объёмы»
(5 класс, математика)
Цели (задачи) урока:
образовательные:
Совершенствовать умение работать с формулами, находить площади фигур и объёмы тел, оперировать различными величинами.
Способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
воспитательные:
Воспитывать культуру поведения при фронтальной и индивидуальной работе, формирование положительной мотивации, способность к самооценке на основе критерия успешности учебной деятельности.
развивающие:
– Регулятивные УУД: умение планировать своё действие в соответствии с поставленной задачей; высказывать своё предположение.
– Коммуникативные УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
– Познавательные УУД: умение ориентироваться в своей системе знаний, находить ответы на вопросы используя свой жизненный опыт и информацию, полученную на уроке.
Результаты урока
Предметные
Уметь работать с формулами, находить площади фигур и объёмы тел, оперировать различными величинами.
Метапредметные
Уметь определять планировать своё действие в соответствии с поставленной задачей;
высказывать своё предположение (Регулятивные УУД).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД).
Уметь ориентироваться в своей системе знаний, находить ответы на вопросы используя свой жизненный опыт и информацию, полученную на уроке. (Познавательные УУД).
Личностные
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Оборудование урока
Доска, мультимедиа проектор, ноутбук, презентация «Площади и объемы», карточки.
Учебник: Математика. 5 класс: учеб. для общеобразовательных учреждений /Н.Я.Виленкин и др. – 22-е изд., стер. – М.: Мнемозина, 2015. – 280 с..
Тип урока
Урок обобщения и систематизации.
Контроль, самоконтроль на уроке
Фронтальная работа, индивидуальная и самостоятельная работа, взаимопроверка, работа в группах и в парах.
Ход урока
Здравствуйте, ребята. Сегодня мы заканчиваем изучение одного из разделов нашего учебника и готовимся к контрольной работе.
Внимание на экран:
– Отгадайте пожалуйста следующие ребусы (Слайд 2 «площадь», Слайд 3 «объем»)
– Сформулируйте тему урока.( Слайд 4«Площади и объемы»)
-Какие цели сегодняшнего урока? Подготовится контрольной работе ,а что это значит?. (Слайд 5)
- закрепить навыки нахождения объёма прямоугольного параллелепипеда, куба;
- сформировать умение самостоятельно анализировать условие задания;
- сформировать навыки применения полученных знаний в практической деятельности;
- развивать логическое мышление;
- развивать творческую деятельность;
- закрепить навыки нахождение площади прямоугольника, квадрата;
- развивать грамотную математическую речь;
воспитывать усердие, целеустремлённость, самостоятельность.
1) Найдите одинаковые фигуры(Слайд 6)
2) Как найти площадь прямоугольника?( Слайд 7)
Формулу запишите на доске
Вычислите площадь прямоугольника: 21 кв. см., 24 кв..см?
Формулу запишите на доске
3) Как найти площадь квадрата?(слайд 8)
Вычислите площадь квадрата:16 кв. см.
Вычислите площадь не закрашенной области фигуры: 9кв. м
4)Поясните рисунок
Площадь всей фигуры равна сумме площадей её частей (Слайд 9)
Площадь треугольника равна половине площади всего прямоугольника(Слайд10)
5) Найдите площади фигур: 8 кв.см,14 кв.см (слайд 11)
Сгруппируйте данные единицы измерения(слайд 12,13)
6) Повторение единицы измерения площадей (Слайд 14)
1 см2 = 100 мм2
1 дм2 = 100 см2 = 10 000 мм2
1 м2 = 100 дм2 = 10 000 см2 = 1 000 000 мм2
1 км2 = 100 га = 1 000 000 м2 = 100 000 000 дм2
1 а = 100 м2 = 10 000 дм2 = 1 000 000 см2
1 га = 10 000 м2 = 1 000 000 дм2
Если длина и ширина прямоугольника измерены в разных единицах, то их надо выразить в одних единицах
Откроем тетради запишем число и тему урока.
7) Выразите и запишите только ответы в тетрадях(Слайд15)
а) в квадратных метрах:19 а, 25 га,3 а 59 м2
б) в арах: 38 га, 3 га 12 а, 3200 м2
8) Ребята проверьте себя (слайд 16)
а) 1900м2, 250000м2,359м2
б) 3800а, 312а, 32а
8) Приведите примеры предметов, имеющих форму прямоугольного параллелепипеда. (Ответ: спичечный коробок, деревянный брусок, кирпич…) (Слайд 17)
9) Сколько граней, вершин и ребр имеет прямоугольный параллелепипед?(слайд 18)
10 ) Как найти объём параллелепипеда? Вычислите.(Слайд 19)
Формулу запишите на доске
11) Как найти объём куба?
Формулу запишите на доске
Вычислите объем куба и фигуры(Слайд 20)
-А теперь ребята будем решать задачи.
–Открываем стр. 116 учебника находим №762. (Слайд 21)
– Каждый читает условие задачи и приступает решению ?
-Кто напишет решение задачи?
Пол покрасили масляной краской два раза. В первый раз на каждый квадратный метр пошло 125 г краски, а во второй – 75 г. Сколько понадобится краски, если длина комнаты 6 м, а ширина 5 м?
Решение: 1) – площадь комнаты
2) – расход краски на 1
3)
Ответ: 6 кг краски понадобится, чтобы покрасить пол.
12) Находим стр.128 №827 (Слайд 22)
Читаем каждый про себя задачу.
-Кто хочет к доске?
-,,,,…..
– На доске запишем решение.
-Остальные пишут решение в тетрадях.
Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см?
Решение: 1) – уровень воды
2)
Ответ: 162 л воды надо влить в аквариум.
13) Физкультминутка (Слайд 23,24)
-Давайте и мы с вами немного разомнёмся… Встаньте пожалуйста радом со своим рабочим местом и потянемся вверх столько раз, какова площадь прямоугольника, приседаем столько раз, каков объем куба. Молодцы! Присаживайтесь на свои места.
– Перед вами маленькая самостоятельная работа (Слайд 25), состоящая из трёх заданий. Всю работу вы выполняете в тетрадях, а на листочках указываете только ответ.
|
1 Вариант |
2 Вариант |
|
№1. Выразите в квадратных метрах: 15 а, 9 га №2 Длина прямоугольника равна 90 м, что в 3 раза больше ширины. Найдите площадь прямоугольника. №3 Дан прямоугольный параллелепипед. Его длина равна 12 см, ширина в 3 раза меньше длины, а высота на 2 см больше ширины. Найдите объём параллелепипеда. |
№1 Выразите в арах: 16 га, 1500 №2 Ширина прямоугольника равна 80 м, что в два раза больше длины. Найдите площадь прямоугольника. №3. Дан прямоугольный параллелепипед. Его ширина равна 7 см, длина в 2 раза больше ширины, высота на 5 см меньше длины. Найдите объём параллелепипеда. |
|
Ответы: №1 1500 №2 2700 №3 288 |
Ответы: №1 1600 а, 15 а №2 3200 №3 882 |
А теперь отложите ручки в сторону и обменяйтесь с соседом по парте листочкам и мы проверим вашу работу.
(Учитель зачитывает ответы (Слайд26), а ребята проверяют друг у друга. 1 правильно решенный номер – «3», два – «4», три – «5».)
Возьмите в руки карандаши и поставьте своему соседу соответствующую отметку.
Молодцы! А теперь соберите листочки и положите, пожалуйста, ко мне на стол. Спасибо.
-Ребята запишем домашнее задание.
Составить кроссворд по теме «Площади и объёмы»
(Этап рефлексии)
И так ребята подведем итог сегодняшнего урока
-Доволен ли вы тем, как прошел урок?
– Было ли вам интересно?
-Как вы думаете сумели ли вы показать свои знания?
-Готовы ли теперь к контрольной работе ?
-У каждого из вас на парте лежит бумага. Укажите ,пожалуйста, тот пункт которые соответствует вам и положите на край парты. Спасибо.
-Какие вы сегодня молодцы!
-Спасибо за урок!
