2.2. Бюджетные ограничения для потребителя
Потребительский выбор всегда осуществляется в рамках ресурсных, или бюджетных ограничений. Предположим, покупатель потребляет только два товара: ананасы (а) и бисквиты (b). Рыночная цена ананасов – Ра, а бисквитов – Рb. Пусть сумма денег,
которую может израсходовать потребитель – I. Бюджетное ограничение
потребителя требует, чтобы сумма денег, затраченная на оба товара, не
превышала общей суммы денег, которую может израсходовать потребитель. Тогда
потребителю доступны все товарные наборы, которые стоят не дороже I. Это
доступное потребителю множество товаров – бюджетное
множество можно записать в виде:
PaQa
+ PbQb ≤ I,
где Qa –
количество товара а, а Qb –
количество товара b в потребительском
наборе, PaQa – сумма денег, расходуемая потребителем на
товар а, PbQb
-– сумма денег, расходуемая на товар b.
Предположим, для
простоты, что потребитель тратит на покупку товаров сумму I полностью. Тогда все наборы из
бюджетного множества, стоимость которых точно равна I, будут лежать на бюджетной линии, которая должна удовлетворять требованию
PaQa + PbQb = I (1)
Пример.
Предположим, что ваш недельный бюджет, который вы можете использовать на
покупку двух товаров ананасов и бисквитов составляет 120 руб. и вы эту сумму
расходуете полностью. Пусть цена ананаса, Pa =10 руб., а цена
бисквита, Pb = 8 руб. Тогда вашим бюджетным ограничением будет:
10Qa +
8Qb = 120
Изобразим графически бюджетное множество и
бюджетную линию (рис. 2-7).
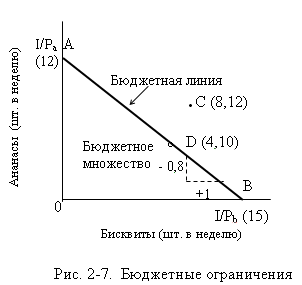 Вам, как потребителю, доступны все наборы, лежащие внутри бюджетного
Вам, как потребителю, доступны все наборы, лежащие внутри бюджетного
множества и на его границе АВ. Если бюджет
расходуется полностью, то выбранный вами набор представляет одна из
точек бюджетной линии АВ (За пределами бюджетной линии находятся недоступные
комбинации благ. Так, набор в точке С недоступен, поскольку для его
приобретения требуется 176 руб. (= 10·8
+ 8·12). Поэтому
бюджетная линия называется также границей
потребительских возможностей.
Составим уравнение бюджетной линии.
Это линейное уравнение типа: y = c + dx (2)
где y –количество первого
товара (ананасов), то есть Qa,
x – количество второго товара
(бисквитов) то есть Qb,
c – это вертикальное пересечение бюджетной линией оси ординат в
точке А (если x=0, то y = c),
d – это наклон линии, который
равен отношению вертикального изменения y
к горизонтальному изменению х.
Определим значение c
применительно к нашей задаче. Это количество ананасов (Qa), которое
в состоянии купить потребитель на всю сумму (I) , если он не будет покупать бисквиты вообще: с = I/Pa.
В нашем примере с = 120/10 = 12
(точка А).
Найдём, чему
равен наклон бюджетной линии d.
Наклон = – ∆Qa/∆Qb,
или: – ОА/ОВ.
ОА –это вертикальное пересечение, равное I/Pa.
ОВ –
это горизонтальное пересечение бюджетной линией оси абсцисс. ОВ показывает,
сколько бисквитов может купить потребитель на всю сумму (I), если он не
покупает ананасов вообще. ОВ = I/Рb. В нашем примере в точке В
потребитель покупает 15 бисквитов (=120/8). Таким образом,
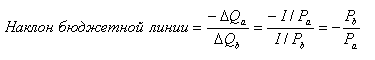 (3)
(3)
Наклон бюджетной
линии в нашем примере составит: – 0,8 (= – 12/ 15 или – 8/10).
Подставим найденные значения с и d в
уравнение (2). Уравнение бюджетной линии
выглядит:
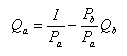 (4)
(4)
![]() Вопрос к аудитории (пример): Какое количество ананасов может позволить себе потребитель, если он решил купить 10 бисквитов?
Вопрос к аудитории (пример): Какое количество ананасов может позволить себе потребитель, если он решил купить 10 бисквитов?
![]() Ответ (нажмите, чтобы увидеть):
Ответ (нажмите, чтобы увидеть):
4 ананаса = (120/10 − 8 × 10/10)
Уравнение бюджетной линии (4) легко можно получить путём чисто формального преобразования уравнения бюджетного ограничения (1). Но для нас было важно вывести и определить смысл наклона бюджетной линии.
Наклон бюджетной линии (3) показывает от какого количества одного блага
(ананасов) должен при существующих
ценах отказаться потребитель, чтобы включить в свой набор дополнительную
единицу другого блага (бисквиты). В нашем примере он равен – 0,8. Это означает,
что потребитель должен пожертвовать 0,8 ананаса, чтобы купить ещё один бисквит.
Для приобретения бисквита нужно 8 рублей (цена 1 бисквита). Их потребитель
получит, если откажется от покупки 0,8 ананасов (именно такое количество
ананасов можно было купить на 8 руб. при цене 1 ананаса в 10 руб.). Но то
количество блага, которым приходится жертвовать ради получения данного блага
есть не что иное как альтернативная стоимость (opportunity cost), или издержки
приобретения данного блага. (Напомним, что альтернативная стоимость – это не особый вид издержек, а правильный
взгляд на любые издержки. Деньги, которые мы тратим, чтобы что-нибудь купить,
являются издержками только потому, что существуют другие вещи, которые мы могли
бы купить на эти деньги). Отсюда следует важный вывод, который будет нам
полезен потом, при нахождении потребительского оптимума: наклон бюджетной линии отражает предельные издержки приобретения
дополнительной единицы блага.
Из уравнения (3) также видно, что наклон
бюджетной линии показывает соотношение цен товаров, входящих в потребительский
набор, точнее, отношение цены замещающего товара (бисквит), к цене
замещаемого товара (ананас).
При изменении цен товаров и дохода изменяется множество товаров,
доступное потребителю и, следовательно, положение бюджетной линии.
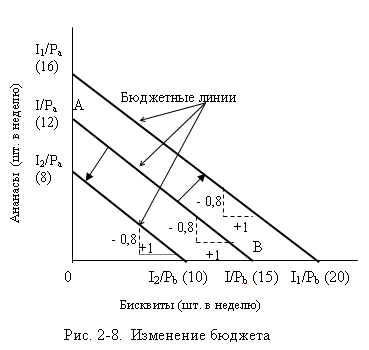
Изменение дохода при тех же товарных ценах
ведёт к параллельному сдвигу бюджетной линии. Её наклон не меняется – ведь
соотношение цен остаётся прежним. На рис.2-8 отражены два случая – изменение
бюджета (мы продолжаем наш пример) с I = 120 руб. до I1 = 160
руб., и с с I = 120 руб. до I2 = 160
руб. В случае увеличения суммы, предназначенной для расходов, бюджетная линия
сдвигается вверх, в случае уменьшения – вниз.
В случае изменения цен при неизменном доходе положение бюджетной линии
также меняется. Рассмотрим два случая.
Первый. Если изменяется цена одного товара, а
бюджет и цена второго товара те
же, то бюджетная линия меняя наклон (соотношение цен изменилось!)
поворачивается вокруг точки пересечения бюджетной линии с координатной осью, на
которой показывается количество товара, цена которого не претерпела изменения.
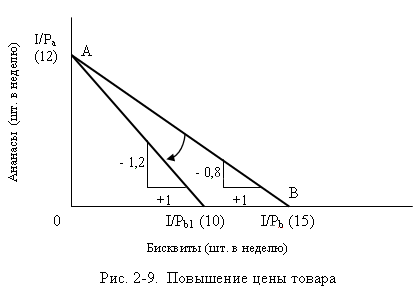
Пусть цена бисквитов повышается с Pb = 8 до Pb1 = 12 руб.
(см. рис. 2-9).
Тогда, максимальное количество бисквитов, которое может купить
потребитель на свой доход I = 120 руб. уменьшается с 15 штук до 10. Максимально
возможное количество другого товара в наборе (ананасов) по-прежнему равно 12,
ведь ни его цена, ни доход не изменились. Наклон бюджетной линии увеличился (по
модулю) с Pb/Pa = – 0,8 до Pb1/Pa =
– 1,2 (= -12/10).
Если бюджетная линия стала круче, значит
цена товара, показываемого по горизонтальной оси, снизилась. Если же
произойдёт понижение цены, то бюджетная линия повернётся вокруг точки А направо
и её наклон уменьшится. Если бюджетная
линия стала более пологой то это означает, что относительная цена товара по
горизонтальной оси понизилась.
Если обе цены изменяются в одинаковой пропорции, а бюджет остаётся тем
же, то наклон бюджетной линии не меняется, но происходит её параллельный сдвиг
– верх, если цены понизились и вниз,
если цены повысились. Если наряду с ценами в такой же пропорции изменяется
бюджет потребителя, то бюджетная линия останется в прежнем положении. Значение
для наклона и положения бюджетной линии имеет относительное, а не абсолютное
изменение цен.
На бюджетное
ограничение потребителя кроме цен и бюджета (дохода) оказывают также влияние
налоги, субсидии, рационирование благ правительством. Бюджетная линия может
прерываться, становится ломаной. Её конкретная форма зависит от обстоятельств.
Мы вернёмся к этому вопросу на лекции после рассмотрения потребительского
оптимума, а также на семинарах при решении различных задач.
Кривые
безразличия позволяют выявить
потребительские предпочтения, однако
при этом не учитываются: цены товаров
и доход потребителя. Они не определяют,
какой именно набор товаров потребитель
считает для себя наиболее выгодным.
Эту информацию дает нам бюджетное
ограничение, показывающее все комбинации
благ, которые могут быть куплены
потребителем при данном доходе и данных
ценах.
Пусть
I
– доход
потребителя, РX
– цена блага Х,
РY
– цена блага Y,
а Х
и Y
составляют, соответственно, нужные
количества благ. Для упрощения
предположим, что потребитель не делает
никаких сбережений и весь свой доход
расходует на приобретение только двух
товаров Х
и Y.
Уравнение
бюджетного ограничения будет иметь
вид: I=PX·X+PY·Y.
Бюджетное ограничение имеет достаточно
простой смысл: доход потребителя равен
сумме его расходов на покупку товаров
X
и Y.
Преобразуем уравнение бюджетного
ограничения к следующему виду:
![]() .
.
Бюджетная
линия (линия бюджетного ограничения)
– это прямая,
точки которой показывают наборы благ,
при покупке которых доход потребителя
тратится полностью.
Т
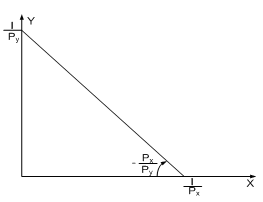
Рис. 2.7. Бюджетное
ограничение
очки пересечения бюджетной линии
с осями координат можно получить
следующим образом. Если потребитель
весь свой доход расходует только на
покупку товараX,
то он сможет приобрести
![]() единиц этого товара, аналогично
единиц этого товара, аналогично![]() – единиц
– единиц
товара Y
(рис. 2.7). Наклон бюджетной линии равен
![]() коэффициенту при X в уравнении бюджетной
коэффициенту при X в уравнении бюджетной
линии. Экономический смысл данного
наклона состоит в измерении альтернативной
стоимости товаров, в данном случае
стоимости одной единицы товараX
в единицах товара Y.
Например,
товар X
– столовое вино ценой 20 тыс. руб. за
бутылку, а Y
– безалкогольный напиток ценой 5 тыс.
руб. за бутылку. Тогда, купив на одну
бутылку меньше вина, потребитель имеет
дополнительные 20 тыс. руб. для покупки
четырех дополнительных бутылок
безалкогольного напитка, т.е. альтернативная
стоимость одной бутылки вина составляет
четыре бутылки безалкогольного напитка.
И

Рис. 2.8. Сдвиг
бюджетного
ограничения
при росте дохода
з уравнения бюджетной линии![]() следует, что бюджетная линия имеет
следует, что бюджетная линия имеет
отрицательный наклон; угол ее наклона
определяется соотношением цен, а
отдаленность от начала координат –
величиной бюджета.
Если
при фиксированных ценах благ изменяется
бюджет потребителя, то происходит
параллельный сдвиг бюджетной линии.
Наклон бюджетной линии не изменится,
поскольку он определяется только
соотношением цен. При увеличении дохода
и неизменных ценах будет наблюдаться
параллельный сдвиг бюджетной линии
вверх (рис. 2.8).
Е

Рис. 2.9. Влияние
на бюджетное ограничение изменений
цены товара X
сли при фиксированном бюджете и
неизменной цене благаY
цена блага X
изменяется, то изменяется
наклон бюджетной линии (рис. 2.9). Происходит
поворот бюджетной линии вокруг точки
пересечения бюджетной линии с вертикальной
осью координат: угол наклона уменьшается
при удешевлении товара (снижении цены
на величину a)
и увеличивается – при его подорожании
(росте цены на величину a).
Это объясняется изменением максимального
количества потребления товара X.
Соседние файлы в предмете Микроэкономика
- #
- #

|
������ 14. ���������� ����������� ��������� ���������� ������������ �����������. ��������� ����� � ���������� ������ �� ������� ������� ������������ �����������. ���������� ������ ��������� ��� ������������, �.�. ��������� ���� ��������� ����������� �������� �������. ����������, ������ �����, ��� ����������� ����������� � ������ ������ �������� ������, ��������, � 1000 ���. �������, ��� ��������� ��� ����� � �������� ����� ������ ���������� ���������: ����� ������ �� ��� ������ ����������� �������, ����� – ��������� �� ���������, � ����� ������ ���� ������� (�������, ���, ������� �� ������� ������ � �����), ���� ����� �������, � �� ��������� ������ ��� ����-������, ��� ���� ��������. ����� �������, ��� ����������� ����� ������ ����� ����� �������, ��������������� ���� ������ �������� ����������: ����� ������� �� ������ ����� �� ��������� ����� �����, ����������� � ������������ ����������� – 1000 ���. ������������ ��� ������� � ����� ����� ����. ����� ����������� ����������� � ������� ������� ��������� ������� �. �������, ��� ���������� � ������ ������ ���������� �� ���������� �������� ����� ������ (���� �� ������ ����������, ����� � ���� ��� �������� �� ������� ���������), ����� ����, ��� ����������� � ������� ������� ������� �� ����� ����������� ����� � �������� ������. �����, ��� ��� ���������� ����, ����������� ����� ���������� ����� ����� ������� � = (x1, x2, …, xn), ��������������� ���������� �������:
��� x1, x2, …, xn — ���������� ������ ������� 1, 2,…, n, ������������� ������������; , P2,…, Pn — ���� ���� �������; � — ������������� ����� �����������. ��������� (1) ���������� ��������� ������������ �����������. ��������, ��� ����������� ������ ������� ���������� ��� ������������� ������, ����� ��������������� ����� ��������� ����� �������� (������� �� ����� � � Y). ����� ��������� ����������� ����� ��� ��� ���� ����� ����������� ��������� �������� �������, ��������������� ����������� (2) � ����������� ������������ �������, ��� ����������, ��������, ���������� � ������������ ������� ������� ����� ���������, �.�. ����� �����, ����������� ���������� (3), ����� �������� ��������� �����. ������ ������ ����� ������ �������������: �����������, ��� ��������� ����������� �� ����� �������� �� ���� ������-���� ������, ����� ����������� �� ���� ����������� �� ������� ���� ����� ����������� ������� ������ (����� �������, �� ����� ���������� ����������� ����������� �� ������� ������). � ����� ����, ������ ���� �����������, ����� ���� ���������� ����������� �� ����� ��������� ��������������� ������� (��������� �������, ������, �����, ������� ������� � �.�.) ���� ����� ������, ����� ��������� ������ ������ ���� �����������, ��������, �� ������ �������� ��� ������������� ������� ����� �� �������� � ��������� ���� �� ��� ������. ����� �������, ���� ������� ��������� ��� ����������� ��� ����� �������, �������� ������ ��������. �������� ������ � ��������� (3) � ��������� ����������� ��������� ����� ����������. �������, ��� ��������� (3) ����� ������������� � ��������� ��������� �������� �, �X � �Y, �� ������ �������������, ���������, ��������� (4) ������������ ����� ��������� ������ ����� (���� y = ax + b), ��� �/�Y — ��������� ����, � –�X/�Y — ����������� ��� ���������� �. ��������� ����� �������������� ������������ ����� ������ ����� ���� ����� ��, ������������ �� ���. 1.
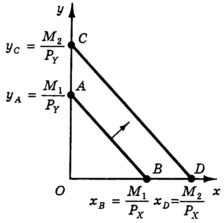
���������� ����� � � � (����� ����������� ��������� ����� � ����� ���������) ������������� ������������ ���������� ������� � � Y, ������� ����� ���������� �����������, �������� ���� ���� ����� ������ �� ����� � ��� ������ �� ����� Y. ���, �������� ����� � yA = �/�Y. ������ ������� ������ Y ����� ������ �����������, ����� ����������� �� ������������ ������ X. ����������� ������� �������� ����� � xB = = �/�X. ����� ������ ����������� �� ��������� ����� ����� ������� � = (xc, yc) ����� ��� ����������� ����� ����� �� ��������� �, ��� � ������ � = (0, �/�Y) � � = (�/�X, 0). ������ ������, ��������� ����� – ��� �������������� ����� �����, ��������������� ��� ������ �������, ������� ����� ���������� �����������, ��������� ������������ ���� ����� � ��� ������ ����� ������� �X � �Y. ��� ����� �� ���. 1, ��������� ����� ����� ������������� ������. ����� �������� ��������� ����� ������ ���������: ��������� ������ �������, ����������� �� ��������� �����, ����� ���������� ���������, ���������� ������ ������� ������ ������ �������� ���� �� ���� ���������� ����������� ������� ������. ��������, ��� ������ ������ ����� ��������������� ������������� ��� ���������� � � ��������� ���� ������. �������������, ������ ��������� ����� ��������������� ��������� �X/�Y (��. (4)). ���� “�����” ��� ��� � ��������� �� ������������� ������ ��������� ����� (��� ��� ���� ������� — ������������� ��������, �. �. �X > 0, �Y > 0, �� �������� �X/�Y �������������). ������ ��������� ����� �����, ����� �������, ����������� ��� �������, ������� � ��������������� ������. ������ ����, ��� �����, �������� ���������� ���������, ��������� �� ������������ �����, ��� ��������� ����������� �� �������� �������� �� �������� ���� �������. ������, ����� �� ��� ����� �������� ��������� �����, ���������� ���������� ��������� ���� ������� �������, ��������������� ���������� �����������.. ��������� ������ ����������� �� ����� ���� �������������� ���������� (x i 0, y i 0), ��������� ��������� ������������ ����� �������������� �� ���. 2 ����������� ���, ������������ ��������� ������ � ����� ���������.
��������� �������� ����� ������ ������� �������� �������� ������� ����������� �� ��������� ��� � ������, ��� ����������, ��������, �����������, ��� ���������� ��� ��������� ��� � ������� ������� ���������� ���������. ������ � ��������� ������. ����� ������������� ����� ����������� ��������� �1. ����� ��������� ����� ����������� ���������� (����� �� �� ���. 3)
����������� ������, ��� ����� ����������� ���������� � �1 �� � ���� ������� �������� �����������. ����� ��������� ����� ��������� ����� ����� ���
������� ��������� ����������, ��� ����������� ��� ���������� � � ��������� (6) ������� ����� ��, ��� � � ��������� (5), � ������, �� ��������� ������ ��������� �����, ������� ������������ ������������ ���. ���� ���������� ���������� ����� ����������� ��������� ����� � ����� ���������: ����� ��������� ����� ���������� ��� y � ����� � � ��������� yc = �2/PY, � ��� x — � ����� D � ��������� xD = = �2/PX. ����� �������, ���������� ������ ��� ���������� ����� �������� � ������������� ������ ��������� ����� ����� (� �������� ������ �������������� � ������������� ������ ��������� ����� ����, �������������� ���� ����������� ��������). �������� ������ � �������������� ��������� ����� ��, ����������� ���������� (5), � ���������� ��� ���� ������ ������ � ��������� ��������: ����� ������ ��������� ���� ���� ������ ������ � (��������, ���������� � PX �� PX1), � �� ����� ��� ���� ������ Y � ����� ����������� ��������� �����������. ����� ����� ��������� ����������� ������ ���
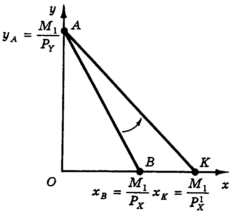
� ���� ������ ����������� ��� ���������� � ��������� � –PX/PY �� –PX1/PY, � �������������, ��������� � ������ ��������� �����. ���������� ��������� ����� ����������� ��������� ����� � ���� y — ����� �. ��������� ����� �1, � ���� PY �� ����������, ����������� ��������� ����� ������� ������������ ������ Y ��-�������� ���������� �1/PY ������ ������ Y. � �� �� ����� ����� ����������� ��������� ����� � ���� � ���������� ������ (���. 4).
���� �������������� ��������� ����� ���������� ��� � � ����� � � ��������� xB = �1/PY, �� “�����” ��������� ����� (��� ���� PX1 < PX ���������� ��� � � ����� K � ��������� xk = �1/PX1. ����� �������, ��������� ���� ������ � �����������, ����������� ����� ������, ������������ ���� ���� ����� �� ����� X, ������ ������� ���������� ������ ����� ������. ����� �������, ���������� ���� ������ � �������� � �������� ��������� ����� ������ ������� ������� ������ ����� ����������� ��������� ����� � ���� y (� ���������� ���� ������ � — � ������������ �������� �� ������� �������). |
Евгения Кузнецова
Эксперт по предмету «Экономика»
преподавательский стаж — 8 лет
Задать вопрос автору статьи
Бюджетное ограничение
Определение 1
Теория поведения потребителя рассматривает понятие бюджетного ограничения, которое представляет собой ограничение при выборе потребителя из комбинации двух товаров, определяемое доходом потребителя, а также ценой на товар.
Определение 2
Потребительский набор – комбинация доступных для покупателя благ, при его ограничении в бюджете. Бюджетное ограничение можно представить в виде графика, который представляет собой прямую линию.
Способность покупателя к удовлетворению своих потребностей, то есть тот вопрос, который предъявляется им на рынке, зависит от двух факторов:
- Доход, который находится в распоряжении у покупателя,
- Цена блага, которая хочет купить покупатель.
Бюджетное ограничение потребителя записывается в виде формулы:
$P_1Q_1 + P_2Q_2 ≤ R$
где $P_1 P_2$ — цены на блага $Q_1$ и $Q_2, R$ — доход покупателя.
Бюджетная линия
В том случае, когда покупатель полностью израсходует свой бюджет на товары $Q_1$ и $Q_2$, то мы получим равенство:
$P_1Q_1 + P_2Q_2 = R$
При преобразовании этого равенства, можно получить уравнение бюджетной линии, которое имеет следующий вид:
$Q_2=frac{R}{P_2}-frac{P_1}{P_2 cdot Q_1}$
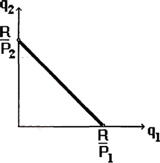
С помощью бюджетной линии можно увидеть, какой набор комбинаций блага $Q_1$ и $Q_2$ может приобрести покупатель, расходуя при этом весь свой бюджет.
«Модель бюджетного ограничения» 👇
Отношение $frac{P_1}{P_2}$ показывает наклон бюджетной линии.
При функционировании многотоварной экономики в условиях учета сбережений потребителей, это уравнение в общем виде представляет собой:
$P_1Q_1 + P_2Q_2 + … +P_nQ_n + сбережения = R$
Смещение бюджетной линии
Изменение в области бюджетных линий могут происходить под влиянием факторов, которые представляют собой:
- Изменение в доходах потребителя,
- Изменение в ценах на товары.
Если доход увеличится с $R_1$ до $R_2$ при стабильных ценах, то в данной ситуации покупателем может быть приобретено большее количество одного и другого блага. При этом угол наклона бюджетной линии останется прежним, так как цена не меняется, но произойдет смещение самой линии вверх и вправо (параллельно). Если же доход снизится, то линия будет смещаться вниз и влево (рис. 2).
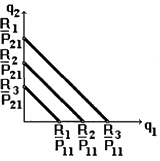
В случае изменения цены на какое-либо благо при стабильном доходе и ценах на другие блага, бюджетная линия изменит свой наклон. Если цена $P_1$ на благо $Q_1$ увеличится, то наклон угла бюджетной линии уменьшится (рис.3).
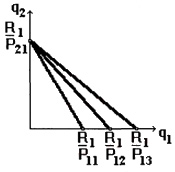
В соответствии с уравнением бюджетной линии можно отметить некоторые свойства бюджетных ограничений потребителей:
- Если произойдет одновременное увеличение в n раз и цены ($P_1$, $P_2$), и доходов ($R$), то положение бюджетной линии останется прежней, как и область бюджетного ограничения.
- Если цены увеличатся в n раз, это будет равнозначно уменьшению доходов покупателей в это же количество раз.
Точка оптимума
Карту безразличия можно представить в виде графического изображения вкусов и предпочтений потребителей.
С помощью бюджетной области отражается вся совокупность доступных потребителям благ, так называемая покупательная способность. В результате объединения данных графиков, можно найти ответ на вопрос, какой набор товаров или услуг будет более нужным и лучшим для покупателей.
Товарный набор, с помощью которого происходит максимизация совокупной полезности потребителя, представляет собой точку потребительского равновесия (точка оптимума), которая лежит в точке, где касается бюджетная линия и кривая безразличия. Э то происходит в том случае, если товар желателен для потребителя, то есть обладает положительной предельной полезностью.
Для определения оптимального потребительского набора необходимо выполнение следующих условий:
- равновесная комбинация товаров всегда будет лежать на бюджетной линии, а не под, это означает, что для того, что бы максимизировать полезность, потребителю необходимо полное использование имеющегося дохода
- при достижении точки равновесия угол наклона кривой безразличия будет равен углу наклона бюджетной линии.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Бюджетное ограничение (budget constraint) показывает все комбинации благ, которые могут быть куплены потребителем при данном доходе и данных ценах. Бюджетное ограничение указывает, что общий расход должен быть равен доходу. Увеличение или уменьшение дохода вызывает сдвиг бюджетной линии.
Бюджетная линия (budget line) — это прямая, точки которой показывают наборы благ, при покупке которых выделенный доход тратится полностью. Бюджетная линия пересекает оси координат в точках, показывающих максимально возможные количества благ, которые можно приобрести на данный доход при определенных ценах. Для каждой бюджетной линии можно построить кривую безразличия, которая будет иметь с бюджетной линией точку касания.
Наклон линии бюджетного ограничения
Если I — доход потребителя, Рх — цена блага Х, Рy – цена блага Y, а Х и Y составляют купленные количества благ, то уравнение бюджетного ограничения можно записать следующим образом:
I = Рх × Х + Рy × Y
При Х = 0, Y = I / Рy , т.е. весь доход потребителя расходуется на благо Y. При Y = 0, Х = I / Рх, т.е. мы находим количество блага Х, которое потребитель может купить по цене Рх.
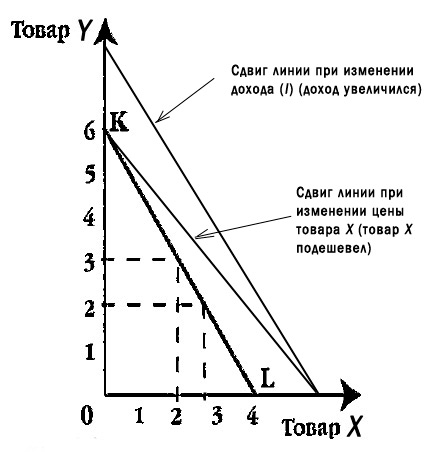
Как видно на графике, потребитель имеет фиксированный доход. Допустим он тратит 6 руб. в день. При этои товар X стоит 1,5 руб, а товар Y – 1 руб. Если потратить все деньги на товар X, то, как видно из графика, можно купить 4 ед. , а если все деньги потратить на товар Y, то можно купить 6 ед. При этом потребителю не обязательно покупать только товар X или товар Y, он может израсходовать свои деньги на любую из возможных комбинаций данных товаров в пределах своего дохода в 6 руб., что и показывает бюджетная линия.
Нужно отметить, что при изменении дохода потребителя (I), бюджетная линия может сдвигаться параллельно старой линии, а при изменении цены на один из товаров сдвиг будет непараллельным, что продемонстрировано на графике.
При одновременном использовании кривых безразличия и бюджетной линии можно найти равновесие потребителя.