Скорость, путь и время являются важными характеристиками любого механического движения. Они связаны между собой формулами:
- $upsilon = frac{S}{t}$
- $S = upsilon t$
- $t = frac{S}{upsilon}$
Данные формулы описывают равномерное движение. При неравномерном движении мы говорим о средней скорости: $upsilon_{ср} = frac{S}{t}$.
Чтобы полноценно научиться использовать вышеупомянутые определения и величины, в данном уроке мы рассмотрим решение разнообразных задач. Вы научитесь вычислять скорость, среднюю скорость, время и путь, переводить единицы измерения скорости из одних в другие, узнаете, как использовать графики этих величин.
Задача №1
Выразите в метрах в секунду ($frac{м}{с}$) скорости: $60 frac{км}{ч}$; $90 frac{км}{ч}$; $300 frac{км}{ч}$; $120 frac{м}{мин}$.
Дано:
$upsilon_1 = 60 frac{км}{ч}$
$upsilon_2 = 90 frac{км}{ч}$
$upsilon_3 = 300 frac{км}{ч}$
$upsilon_4 = 120 frac{м}{мин}$
Показать решение и ответ
Скрыть
Решение:
Для перевода скорости в метры в секунду нам нужно:
- перевести километры в метры ($1 space км = 1000 space м$)
- выразить часы или минуты в секундах ($1 space мин = 60 space с$; $1 space ч = 60 space мин = 3600 space с$)
Тогда,
$upsilon_1 = 60 frac{км}{ч} = 60 frac{1000 space м}{3600 space c} = frac{1000 space м}{60 space c} approx 16.7 frac{м}{с}$.
При вычислениях старайтесь увидеть величины, которые можно сократить (как 60 и 3600).
Если мы вычислим множитель $frac{1000 space м}{3600 space c}$, то получим, что $1 frac{км}{ч} = frac{}{3.6} frac{м}{с}$.
Вы можете каждый раз последовательно переводить величины (километры в метры и часы в секунды) или просто разделить скорость, выраженную в километрах в час на $3.6$ и получить скорость в метрах в секунду. Рекомендуется идти первым путем, потому что второй способствует потере точности.
Переведем следующие две скорости в единицы СИ:
$upsilon_2 = 90 frac{км}{ч} = 90 frac{1000 space м}{3600 space c} = 1000 cdot 0.025 frac{м}{с} = 25 frac{м}{с}$,
$upsilon_3 = 300 frac{км}{ч} = 300 frac{1000 space м}{3600 space c} = frac{1000 space м}{12 space c} approx 83.3 frac{м}{с}$.
Теперь переведем скорость, выраженную в метрах в минуту в метры в секунду:
$upsilon_4 = 120 frac{м}{мин} = 120 frac{м}{60 space c} = 2 frac{м}{с}$.
Ответ: $upsilon_1 approx 16.7 frac{м}{с}$; $upsilon_2 = 25 frac{м}{с}$; $upsilon_1 approx 83.3 frac{м}{с}$; $upsilon_4 = 2 frac{м}{с}$.
Задача №2
Пуля, выпущенная из винтовки, долетела до цели, находящейся на расстоянии $1 space км$, за $2.5 space с$. Найдите скорость пули.
Дано:
$S = 1 space км$
$t = 2.5 space с$
СИ:
$S = 1000 space м$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета скорости:
$upsilon = frac{S}{t}$.
Перед вычислениями не забывайте переводить единицы измерения величин в СИ!
Рассчитаем скорость:
$upsilon = frac{1000 space м}{2.5 space с} = 400 frac{м}{с}$.
Ответ: $upsilon = 400 frac{м}{с}$.
Задача №3
Пароход, двигаясь против течения со скоростью $14 frac{км}{ч}$, проходит расстояние между двумя пристанями за $4 space ч$. За какое время он пройдет то же расстояние по течению, если его скорость в этом случае равна $5.6 frac{м}{с}$?
Дано:
$upsilon_1 = 14 frac{км}{ч}$
$t_1 = 4 space ч$
$upsilon_2 = 5.6 frac{м}{с}$
$t_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Найдем расстояние между двумя пристанями:
$S = upsilon_1 t_1$,
$S = 14 frac{км}{ч} cdot 4 space ч = 56 space км = 56 space 000 space м$.
Обратите внимание, что мы изначально не перевели единицы измерения в СИ (километры в час в метры в секунду и часы в секунды), потому что удобнее это сделать после расчета расстояния $S$. Таким образом мы сохраняем более высокую точность вычислений.
Итак, мы знаем расстояние и скорость движения парохода по течению. Теперь мы можем рассчитать время движения парохода по течению:
$t_2 = frac{S}{upsilon_2}$,
$t_2 = frac{56 space 000 space м}{5.6 frac{м}{с}} = 10 space 000 space с$.
Ответ: $t_2 = 10 space 000 space с$.
Задача №4
Автомобиль проехал равномерно участок дороги длиной $3.5 space км$ за $3 space мин$. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак “скорость не более $50 frac{км}{ч}$”?
Дано:
$S = 3.5 space км$
$t = 3 space мин$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
После того, как мы рассчитаем скорость движения автомобиля, нам нужно будет сравнить ее со скоростным ограничением в $50 frac{км}{ч}$. Для того чтобы это сделать, нужно, чтобы скорость тоже была выражена в километрах в час.
Так как водитель двигался равномерно, рассчитывать скорость его движения мы будем по формуле:
$upsilon = frac{S}{t}$.
Путь $S$ у нас и так выражен в километрах, а время — в минутах. Поэтому, перед рассветом скорости переведем время из минут в часы:
$t = 3 space мин = frac{3}{60} cdot ч = 0.05 space ч$.
Теперь мы можем рассчитать скорость движения автомобиля:
$upsilon = frac{3.5 space км}{0.05 space ч} = 70 frac{км}{ч}$.
Получается, что водитель нарушил правила дорожного движения, ведь $70 frac{км}{ч} > 50 frac{км}{ч}$.
Ответ: нарушил.
Задача №5
Росток бамбука за сутки вырастает на $86.4 space см$. На сколько он вырастает за $1 space мин$?
Дано:
$S = 86.4 space см$
$t = 1 space сут$
$t_1 = 1 space мин$
$S_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Переведем сутки в минуты:
$t = 1 space сут = 24 space ч = 24 cdot 60 space мин = 1440 space мин$.
Рассчитаем скорость роста бамбука, выраженную в сантиметрах в минуту:
$upsilon = frac{86.4 space см}{1440 space мин} = 0.06 frac{см}{мин}$.
Понятие скорости в физике определяет расстояние, которое тело проходит в единицу времени. В нашем случае полученную скорость роста мы можем описать так:
бамбук вырастает на расстояние, равное $0.06 space см$, за $1 space мин$.
Значит,
$S_1 = 0.06 space см = 0.6 space мм$.
Ответ: $S_1 = 0.6 space мм$.
Задача №6
Самолет, летящий со скоростью $300 frac{км}{ч}$, в безветренную погоду пролетел расстояние между аэродромами A и B за $2.2 space ч$. Обратный полет из-за встречного ветра он совершил за $2.5 space ч$. Определите скорость ветра.
Дано:
$upsilon_1 = 300 frac{км}{ч}$
$t_1 = 2.2 space ч$
$t_2 = 2.5 space ч$
$upsilon_в — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала вычислим расстояние между аэродромами, которое пролетает самолет:
$S = upsilon_1 t_1$,
$S = 300 frac{км}{ч} cdot 2.2 space ч = 660 space км$.
Теперь рассчитаем скорость, с которой самолет совершил обратный полет:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{660 space км}{2.5 space ч} = 264 frac{км}{ч}$
Если бы ветра не было, то скорость самолета составила бы $300 frac{км}{ч}$. Но ветер направлен противоположно движению самолеты, вектор его скорости противоположно направлен вектору скорости самолета. Поэтому мы можем записать, что скорость самолета, летящего при встречном ветре, равна разности скорости самолета в безветренной обстановке и скорости ветра:
$upsilon_2 = upsilon_1 — upsilon_в$.
Рассчитаем скорость ветра:
$upsilon_в = upsilon_1 — upsilon_2$,
$upsilon_в = 300 frac{км}{ч} — 264 frac{км}{ч} = 36 frac{км}{ч}$,
или в СИ $upsilon_в = 36 cdot frac{1000 space м}{3600 space с} = 10 frac{м}{с}$.
Ответ: $upsilon_в = 10 frac{м}{с}$.
Определите по графику равномерного движения, изображенному на рисунке 1:
- скорость движения
- путь, пройденный телом в течение $4.5 space с$
- время, в течение которого пройден путь, равный $15 space м$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитывается по формуле:
$upsilon = frac{S}{t}$.
Выберем на графике такую точку, данные которой мы можем точно определить. Например, в момент времени, равный $4 space с$, был пройден путь, равный $16 space м$.
Используя эти данные, рассчитаем скорость:
$upsilon = frac{16 space м}{4 space с} = 4 frac{м}{с}$.
Найдем путь, пройденный телом в течение $4.5 space с$. Если мы взглянем на график, то в этот момент времени тело прошло путь, приблизительно равный $18 space м$. Давайте проверим точность этих данных с помощью вычислений:
$S = upsilon t$,
$S = 4 frac{м}{с} cdot 4.5 space с = 18 space м$.
Используя график, мы не можем точно определить время, в течение которого пройден путь, равный $15 space м$. Поэтому вычислим его:
$t = frac{S}{upsilon}$,
$t = frac{15 space м}{4 frac{м}{с}} = 3.75 space с$.
Ответ: $4 frac{м}{с}$, $18 space м$, $3.75 space с$.
Задача №8
Средняя скорость велосипедиста на всем пути равна $40 frac{км}{ч}$. Первую половину пути он ехал со скоростью $60 frac{км}{ч}$. С какой скоростью велосипедист проехал остаток пути?
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$upsilon_1 = 60 frac{км}{ч}$
$S_1 = S_2 = frac{1}{2}S$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу средней скорости при неравномерном движении:
$upsilon_{ср} = frac{S}{t}$.
Общее время движения $t$ мы можем представить в виде суммы $t_1 + t_2$, где $t_1$ — это время движения на первой половине пути, а $t_2$ — время движения на второй половине пути:
$upsilon_{ср} = frac{S}{t_1 + t_2}$.
Время мы можем выразить через скорость на данном участке пути и пройденный за это время путь:
$t_1 = frac{S_1}{upsilon_1} = frac{frac{1}{2}S}{upsilon_1} = frac{S}{2 upsilon_1}$,
$t_2 = frac{S_2}{upsilon_2} = frac{frac{1}{2}S}{upsilon_2} = frac{S}{2 upsilon_2}$,
$upsilon_{ср} = frac{S}{frac{S}{2 upsilon_1} + frac{S}{2 upsilon_2}} = frac{S}{frac{S(upsilon_1 + upsilon_2)}{2 upsilon_1 upsilon_2}} = frac{2 upsilon_1 upsilon_2}{upsilon_1 + upsilon_2}$.
Теперь выразим отсюда скорость $upsilon_2$, с которой велосипедист двигался вторую половину пути:
$2 upsilon_1 upsilon_2 = upsilon_{ср} upsilon_1 + upsilon_{ср} upsilon_2$,
$2 upsilon_1 upsilon_2 — upsilon_{ср} upsilon_2 = upsilon_{ср} upsilon_1$,
$upsilon_2 cdot (2 upsilon_1 — upsilon_{ср}) = upsilon_{ср} upsilon_1$,
$upsilon_2 = frac{upsilon_{ср} upsilon_1}{2 upsilon_1 — upsilon_{ср}}$.
Рассчитаем эту скорость:
$upsilon_2 = frac{40 frac{км}{ч} cdot 60 frac{км}{ч}}{2 cdot 60 frac{км}{ч} — 40 frac{км}{ч}} = frac{2400 frac{км}{ч}}{80} = 30 frac{км}{ч}$.
Ответ: $upsilon_2 = 30 frac{км}{ч}$.
Задача №9
На рисунке 2 дан график пути движения поезда. Определите скорости движения на участках, изображенных отрезками графика OA, AB и BC. Какой путь пройден поездом в течении $3 space ч$ с начала его движения?
Дано:
$t = 3 space ч$
$upsilon_1 — ?$, $upsilon_2 — ?$, $upsilon_3 — ?$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы определить скорость на каждом участке пути, мы будем выбирать удобную нам точку на графике и проводить вычисления.
Определим скорость движения поезда на участке OA. В момент времени, равный $1 space ч$, пройденный поездом путь составил $40 space км$:
$upsilon_1 = frac{S_1}{t_1}$,
$upsilon_1 = frac{40 space км}{1 space ч} = 40 frac{км}{ч}$.
Участок графика AB параллелен оси времени, пройденный путь не изменяется. Значит скорость здесь равна нулю: $upsilon_2 = 0 frac{км}{ч}$.
Определим скорость движения поезда на участке BC. По наклону прямой графика мы видим, что скорость после остановки изменилась. За время с $2 space ч$ до $3 space ч$, пройденный путь изменился с $60 space км$ до $80 space км$. Значит, за $1 space ч$ поезд прошел путь, равный $20 space км$:
$upsilon_3 = frac{S_3}{t_3}$,
$upsilon_3 = frac{20 space км}{1 space ч} = 20 frac{км}{ч}$.
Теперь нам нужно найти путь, пройденный поездом за $3 space ч$ с момента начала движения. Этот путь будет складываться из трех составляющих на разных участках:
$S = S_1 + S_2 + S_3$.
Путь $S_2$, соответствующий участку AB будет равен нулю, так как на нем скорость движения равна нулю.
Тогда, используя данные графика и рассчитанные значения скоростей, мы можем записать:
$S = S_1 + S_3 = upsilon_1 t_1 + upsilon_3 t_3$,
$S = 40 frac{км}{ч} cdot 1.5 space ч + 20 frac{км}{ч} cdot 1 space ч = 80 space км$.
Ответ: $upsilon_1 = 40 frac{км}{ч}$, $upsilon_2 = 0 frac{км}{ч}$, $upsilon_3 = 20 frac{км}{ч}$, $S = 80 space км$.
Задача №10
От одной и той же станции в одном и том же направлении отправляются два поезда. Скорость первого $30 frac{км}{ч}$, второго $40 frac{км}{ч}$. Второй поезд отправляется через $10 space мин$ после первого. После сорокаминутного движения первый поезд делает пятиминутную остановку, потом продолжает двигаться дальше с прежней скоростью.
Определите графически, когда и на каком расстоянии от станции второй поезд догонит первый. Графическое решение проверьте вычислением.
Дано:
$upsilon_1 = 30 frac{км}{ч}$
$upsilon_2 = 40 frac{км}{ч}$
$t_{01} = 0 space мин$
$t_{02} = 10 space мин$
$t_1 = 40 space мин$
$t_{1о} = 5 space мин$
$t — ?$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала займемся построением графика движения поездов.
По оси $x$ мы будем откладывать время, а по оси $y$ — расстояние. Время оставим в $мин$, а расстояние будем отмечать в $км$.
Построим график движения первого поезда (рисунок 3). Он начинает свое движение в момент времени $t_{01} = 0 space мин$.
Движется он со скоростью $30 frac{км}{ч}$ в течение $t_1 = 40 space мин$. Переведем эту скорость в $frac{км}{мин}$ и вычислим, какое расстояние этот поезд пройдет за указанное время:
$upsilon_1 = 30 frac{км}{ч} = 30 frac{км}{60 space мин} = 0.5 frac{км}{мин}$,
$S_1 = upsilon_1 t_2$,
$S = 0.5 frac{км}{мин} cdot 40 space мин = 20 space км$.
Поставим эту точку на графике и соединим с началом координат.
Далее поезд сделал остановку. Этот участок графика будет параллелен оси времени — значение пройденного пути остается постоянным, ведь поезд никуда не двигается.
Далее поезд продолжает движение с прежней скоростью. Без вычислений мы можем провести из точки, соответствующей концу остановки, прямую параллельную первой части графика.
Теперь построим тут же график движения для второго поезда (рисунок 4).
Он начинает свое движение не из начала координат, а из точки, соответствующей времени $t_{02} = 10 space мин$.
Он движется со скоростью $40 frac{км}{ч}$. Это означает, что за $1 space ч = 60 space мин$ он проходит путь, равный $40 space км$. Отметим эту точку на координатной плоскости и соединим с точкой начала движения.
Итак, графически мы получили, что
- Второй поезд догонит первый в момент времени $t = 40 space мин$
- Поезда встретятся на расстоянии $S = 20 space км$ от места отправления
Теперь подтвердим полученные данные вычислениями. Поезда встретятся друг с другом, пройдя определенный путь $S$. Это случится через определенное время $t$:
$S = S_1 = S_2$,
$S_1 = upsilon_1 t$,
$S_2 = upsilon_2 (t — t_{02})$.
Найдем это время:
$upsilon_1 t = upsilon_2 (t — t_{02})$,
$upsilon_2 t — upsilon_1 t = upsilon_2 t_{02}$,
$t (upsilon_2 — upsilon_1) = upsilon_2 t_{02}$,
$t = frac{upsilon_2 t_{02}}{upsilon_2 — upsilon_1}$.
Перед расчетом переведем $мин$ в $ч$: $t_{02} = 10 space мин = frac{10}{60} space ч = frac{1}{6} space ч$.
Теперь рассчитаем время встречи двух поездов:
$t = frac{40 frac{км}{ч} cdot frac{1}{6} space ч}{40 frac{км}{ч} — 30 frac{км}{ч}} = frac{4}{6} space ч = frac{2}{3} space ч = 40 space мин$.
Используя полученное значение времени и скорость движения первого поезда, рассчитаем расстояние, на котором встретятся поезда:
$S = upsilon_1 t$,
$S = 30 frac{км}{ч} cdot frac{2}{3} space ч = 20 space км$.
Ответ: $t = 40 space мин$, $S = 20 space км$.
Задача №11
Поезд прошел $25 space км$ за $35 space мин$, причем первые $10 space км$ он прошел в течение $18 space мин$, вторые $10 space км$ в течение $12 space мин$, а последние $5 space км$ за $5 space мин$. Определите среднюю скорость поезда на каждом участке и на всем пути.
Дано:
$S = 25 space км$
$t = 35 space мин$
$S_1 = 10 space км$
$t_1 = 18 space мин$
$S_2 = 10 space км$
$t_2 = 12 space мин$
$S_3 = 5 space км$
$t_3 = 5 space мин$
$upsilon_{1ср} — ?$, $upsilon_{2ср} — ?$, $upsilon_{3ср} — ?$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Переведем время из $мин$ в $ч$:
- $t = 35 space мин = frac{35}{60} space ч = frac{7}{12} space ч$
- $t_1 = 18 space мин = frac{18}{60} space ч = frac{3}{10} space ч = 0.3 space ч$
- $t_2 = 12 space мин = frac{12}{60} space ч = frac{1}{5} space ч = 0.2 space ч$
- $t_3 = 5 space мин = frac{5}{60} space ч = frac{1}{12} space ч$
Теперь рассчитаем среднюю скорость на каждом участке пути:
- $upsilon_{1ср} = frac{S_1}{t_1}$,
$upsilon_{1ср} = frac{10 space км}{0.3 space ч} approx 33.3 frac{км}{ч}$ - $upsilon_{2ср} = frac{S_2}{t_2}$,
$upsilon_{2ср} = frac{10 space км}{0.2 space ч} = 50 frac{км}{ч}$ - $upsilon_{3ср} = frac{S_3}{t_3}$,
$upsilon_{3ср} = frac{5 space км}{frac{1}{12} space ч} = 60 frac{км}{ч}$
Рассчитаем среднюю скорость на на всем пути:
$upsilon_{ср} = frac{S}{t}$,
$upsilon_{ср} = frac{25 space км}{frac{7}{12} space ч} approx 42.9 frac{км}{ч}$
Ответ: $upsilon_{1ср} approx 33.3 frac{км}{ч}$, $upsilon_{2ср} = 50 frac{км}{ч}$, $upsilon_{3ср} = 60 frac{км}{ч}$, $upsilon_{ср} approx 42.9 frac{км}{ч}$.
Задачи на движение с решениями
Используемые формулы в 7 классе по теме «Задачи на движение (прямолинейное равномерное)»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Путь |
s |
м, км |
s = v * t |
Время |
t |
с, ч |
t = s / v |
Скорость |
v |
м/с, км/ч |
v = s / t |
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Задача № 1.
Ласточка летит со скоростью 36 км/ч. Какой путь она преодолеет за 0,5 ч?

Задача № 1.
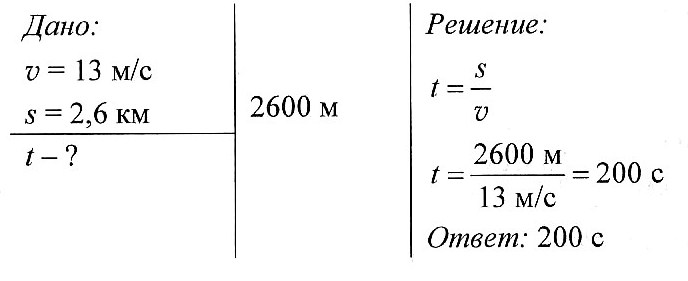
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?
Задача № 3.
Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь — до 16 м/с. Сможет ли голубь обогнать автомобиль?
Решение. Чтобы сравнить скорости движения тел, надо перевести их в одинаковые единицы измерения. Перевод скорости из одних единиц в другие выполняют следующим образом. 160 км = 160000 м, 1 ч = 3600 с. Следовательно, за 1 с автомобиль пройдет путь 160000 : 3600 = 44 (м), значит:

Ответ: Голубь не обгонит автомобиль, так как 16 м/с < 44 м/с.
Задача № 4.
Вдоль дороги навстречу друг другу летят скворец и комнатная муха. На рисунке представлены графики движения скворца (I) и мухи (II). Пользуясь графиком, определите:
1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи?

Решение.
1. Скорость движения скворца определим по формуле v=S/t. Выберем на графике произвольное время и определим, какое расстояние за это время пролетел скворец. Видно, что за 5 с скворец пролетел 100 м. Тогда

Аналогично найдем скорость движения мухи:

2. Точка А (точка пересечения графиков движения) соответствует моменту встречи. Скворец и муха встретятся через 4 секунды.
3. Скворец до места встречи пролетит расстояние SI = 80 м. Муха пролетит расстояние SII = 100 м — 80 м = 20 м.
Ответ: 1) скворец 20 м/с, муха 5 м/с, 2) через 4 с, 3) скворец 80 м, муха 20 м
Задача № 5.
Определите среднюю скорость движения плота, если за 20 минут он переместился на 900 м. Скорость выразить в км/ч.

Ответ: Средняя скорость плота 2,7 км/ч.
Задача № 6.
Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?
ОТВЕТ: 1 мин.
Решение. Стоящий на эскалаторе человек за 1 мин перемещается на половину длины эскалатора, а бегущий — перемещается на полторы длины эскалатора. Следовательно, идущий по неподвижному эскалатору человек за 1 мин перемещается как раз на длину эскалатора.
Задача № 7.
Моторная лодка за 3 ч проходит расстояние от города до поселка, расположенного ниже по течению реки. Сколько времени займет обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения?
ОТВЕТ: 5 ч.
Решение. Обозначим скорость течения v. При движении по течению скорость лодки относительно берега равна 5v, а при движении против течения ее скорость равна 3v. Следовательно, время движения против течения в 5/3 раза больше, чем время движения по течению.
Задача № 8 (повышенной сложности).
Рыбак плыл по реке на лодке, зацепил шляпой за мост, и она свалилась в воду. Через час рыбак спохватился, повернул обратно и подобрал шляпу на 4 км ниже моста. Какова скорость течения? Скорость лодки относительно воды оставалась неизменной по модулю.
ОТВЕТ: 2 км/ч.
Решение. Удобно рассматривать движение шляпы и лодки относительно воды, потому что относительно воды шляпа неподвижна, а скорость лодки, когда она плывет от шляпы и к шляпе, по модулю одна и та же — так, как это было бы в озере. Следовательно, после поворота рыбак плыл к шляпе тоже 1 ч, т. е. он подобрал шляпу через 2 ч после того, как уронил ее. По условию за это время шляпа проплыла по течению 4 км, откуда следует, что скорость течения 2 км/ч.
Задача № 9 (олимпиадного уровня).
Из городов А и Б навстречу друг другу по прямому шоссе одновременно выехали два велосипедиста. Скорость первого 10 км/ч, скорость второго 15 км/ч. Одновременно с велосипедистами из города А вылетела ласточка. Она долетает до второго велосипедиста, разворачивается, Долетает до первого велосипедиста и летает так между ними до тех пор, пока велосипедисты не встретятся. Какой путь пролетела ласточка, если скорость ее движения 50 км/ч, а расстояние между городами 100 км? Временем разворота ласточки можно пренебречь.
ОТВЕТ: 200 км.
Решение. Расстояние между велосипедистами каждый час уменьшается на 25 км. Поскольку начальное расстояние между ними 100 км, они встретятся через 4 ч. Все это время ласточка будет летать со скоростью 50 км/ч, следовательно, ее путь составит 200 км.
Алгоритм решения задач на движение
При решении других задач прямолинейного равномерного движения в общем виде нужно придерживаться следующего алгоритма: 1) выбрать систему отсчёта; 2-3) определить начальные координаты и значения скоростей движения тел в этой системе отсчёта; 4) записать зависимости координат тел от времени; 5) записать в виде уравнения условие задачи; 6) объединить уравнения; 7) решить эти уравнения; 8) провести анализ полученного результата (после чего выяснить, имеет ли полученный результат физический смысл); 9) если в условии задачи даны числовые значения, необходимо подставить их в полученное выражение и получить числовой ответ.
Анализ полученного результата заключается в исследовании зависимости искомой величины от входящих в ответ величин.
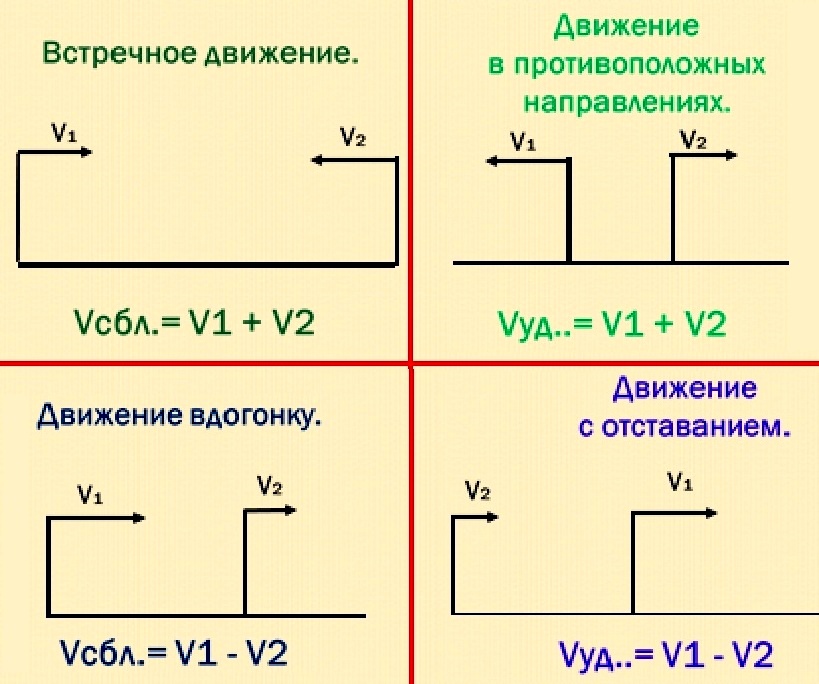
Не стоит забывать и про направление движения в зависимости от типа задачи (встреча, погоня, обгон, отставание)
Конспект урока «Задачи на движение с решением».
Следующая тема: «Задачи на плотность, массу и объем«.
Содержание:
Путь и перемещение:
Вы знаете, что любой вид движения совершается по определенной траектории.
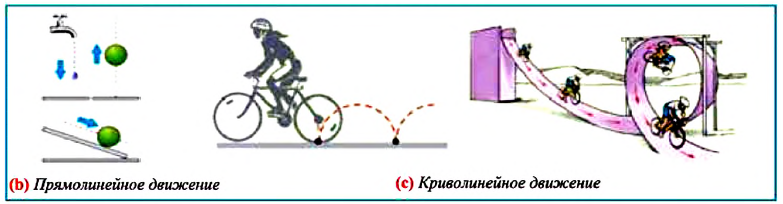
Траектория – это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.
Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, – криволинейным (с).
Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой 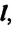
Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.
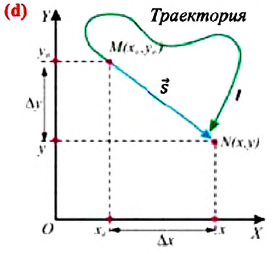
Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком 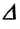 (буква греч. алфавита) перед этой величиной.
(буква греч. алфавита) перед этой величиной.
Изменение координат материальной точки во время движения
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается 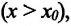 то изменение координаты по этой оси будет положительным:
то изменение координаты по этой оси будет положительным: 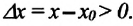 Координата же муравья по оси У уменьшается
Координата же муравья по оси У уменьшается 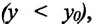 поэтому изменение его координаты по этой оси будет отрицательным:
поэтому изменение его координаты по этой оси будет отрицательным: 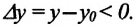
Изменение радиус-вектора материальной точки во время движения
На следующем рисунке представлены радиус-векторы 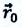 и
и 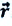 начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор
начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор 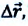 соединяющий концы этих радиус-векторов
соединяющий концы этих радиус-векторов 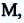 называют перемещением данной материальной точки за промежуток времени
называют перемещением данной материальной точки за промежуток времени 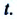 Согласно правилу сложения векторов:
Согласно правилу сложения векторов:  Из последнего выражения получается,
Из последнего выражения получается, 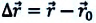 или
или 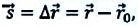 где
где 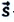 — перемещение материальной точки.
— перемещение материальной точки.
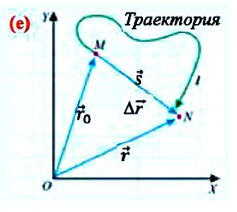
Перемещение – это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.
Векторная величина – это величина, определяемая, кроме числового значения (модуля), также и направлением.
К вектору перемещения, как векторной величине, можно применить известные действия над векторами – сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.
Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).
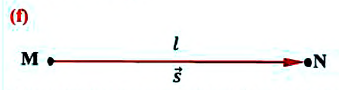
Материальная точка прошла расстояние 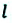 от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения:
от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения: 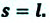

Материальная точка прошла расстояние 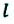 от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку
от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку 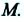 В этом случае материальная точка прошла путь, равный
В этом случае материальная точка прошла путь, равный 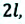 а модуль перемещения равен нулю:
а модуль перемещения равен нулю:

Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение 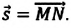 Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения
Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения 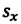 и
и 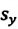 (h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки:
(h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки:
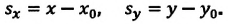
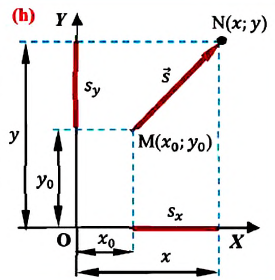
Одинаковы ли путь и перемещение
Задача:
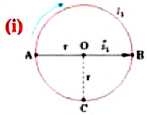
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Дано:
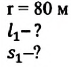
Решение:
Пройденный путь 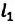 равен длине дуги:
равен длине дуги: 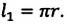
Модуль перемещения же равен диаметру окружности: 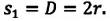
Вычисление:
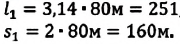
Что такое путь и перемещение
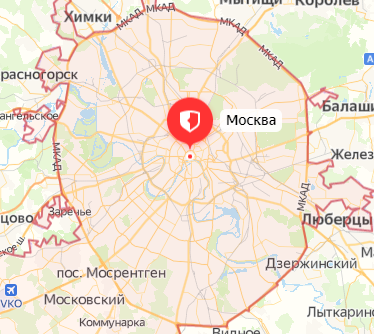
Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь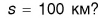
Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.
Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.
Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.
А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
Обозначим перемещение символом 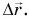 На рисунке 38 вектор
На рисунке 38 вектор 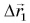 — это перемещение автобуса из Минска в Мытищи, вектор
— это перемещение автобуса из Минска в Мытищи, вектор 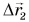 — из Мытищь в Балашиху, а вектор
— из Мытищь в Балашиху, а вектор 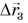 — из Минска в Борисов.
— из Минска в Борисов.
Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.
Можно ли сравнивать путь S, пройденный телом, с его перемещением 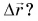 Нельзя, поскольку путь S — скаляр, а перемещение
Нельзя, поскольку путь S — скаляр, а перемещение 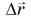 — вектор.
— вектор.
Сравнивать путь S можно с модулем перемещения 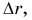 который является скалярной величиной. Равен ли путь модулю перемещения?
который является скалярной величиной. Равен ли путь модулю перемещения?
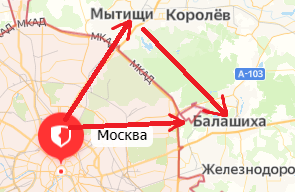
В рассматриваемом примере путь, пройденный автобусом за два часа, 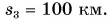 Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова:
Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова: 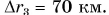 Путь автобуса больше модуля его перемещения:
Путь автобуса больше модуля его перемещения: 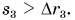
Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.
Следовательно, путь всегда не меньше модуля перемещения:
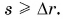
Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:
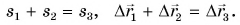
Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.
Равен ли при этом модуль 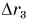 сумме модулей
сумме модулей 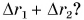 Ответьте самостоятельно.
Ответьте самостоятельно.
Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.
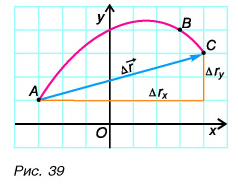
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 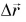 на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:
на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:
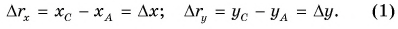
Главные выводы:
- Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
- Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
- Путь не меньше модуля перемещения тела за то же время.
- Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.
Пример:
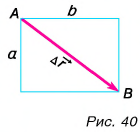

Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.
Решение
Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:
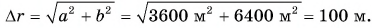
Путь конькобежца: 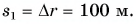
Путь пешехода: 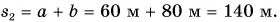
Ответ: 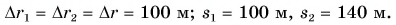
- Заказать решение задач по физике
Траектория движения
Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.
Так, в безоблачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел (рис. 7.3).

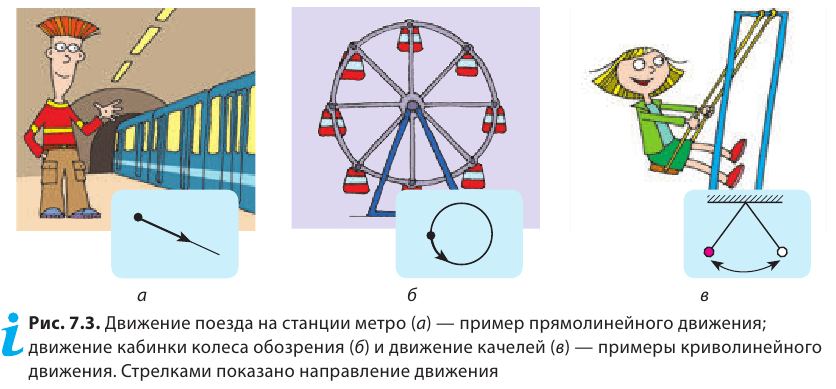
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
Чем путь отличается от перемещения
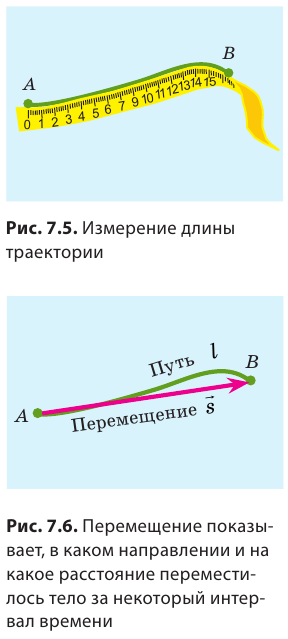
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):
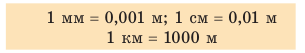
Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
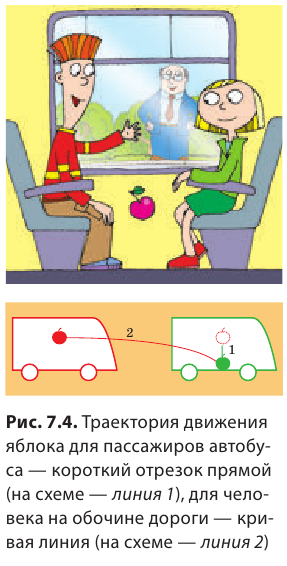
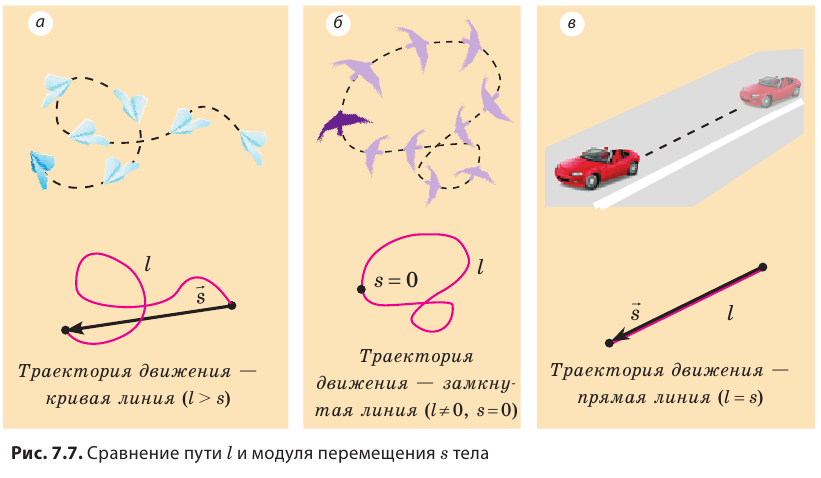
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом 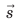 . Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.
. Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.
Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
Итоги:
Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 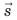 — это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).
— это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).
Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
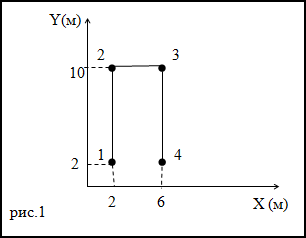
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 – 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В физике следует различать траекторию, путь и перемещение.
Определение 1
Траектория – форма линии, описываемая телом. Ее длина представляет собой путь и является скалярной величиной. Перемещением же называется вектор, соединяющий точки начала и конца пути, и направленный от начала к концу.
Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) – в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).
При движении без ускорения путь равен произведению скорости на расстояние:
$S = v cdot (t_2 – t_1) = v cdot Delta t$,
где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $Delta t$ – время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.
Замечание 1
Поскольку скорость – векторная величина, равномерным можно считать только движение по прямой, т.к. при изменении направления движения вектор не остается неизменным даже при сохранении его длины.
Если равноускоренное движение начато с нулевой скорости и известно ускорение, то формула пути имеет вид
$S = frac{a cdot t^{2}}{2}$
где $a$ – ускорение тела.
Объединив два условия, получим общую формулу нахождения пути при равноускоренном движении с произвольной начальной скоростью:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$.
Если движение не равномерное и известна средняя скорость движения, то путь можно выразить и другим способом:
$S = v_{ср.} cdot Delta t$,
где $v_{ср.}$ – средняя скорость движения.
На практике движение бывает равномерным или равноускоренным лишь на небольших фрагментах пути, поэтому для вычисления его длины траекторию разбивают на участки, где тело движется по простым закономерностям, вычисляют длину каждого из них и суммируют. Если известна траектория, то ее разбивают на фрагменты, каждый из которых имеет простую геометрическую форму. Сложив их длины, можно найти путь.
Пример 1
Найти путь, пройденный при движении с ускорением 2 $м/с^2$ в течение 20 с, если скорость на момент начала измерения была равна 10 м/с.
Подставим в формулу численные значения:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$
$S = frac{2 cdot 20^2}{2} + 10 cdot 20 = 600 м$.
Ответ: длина пути составила 600 метров.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
