Загрузить PDF
Загрузить PDF
Чтобы визуализировать соединение каналов, нужно представить цепь элементов. Элементы должны добавляться последовательно в один ряд. Должен существовать только один путь, по которому будут течь электроны и заряды. Когда у вас будет базовая идея о том, что такое соединение каналов или соединение цепей, вы сможете научиться рассчитывать суммарный ток.
-

1
Для начала нужно понять, что такое ток. Ток — это поток электрически заряженных частиц (электронов), то есть, это поток заряда за единицу времени. Но что такое заряд и что такое электрон? Электрон — это отрицательно заряженная частица. Заряд — это свойство материи, то есть вещества, которое используется для классификации положительных и отрицательных зарядов. Также, как и магниты, похожие заряды отталкиваются, а разные притягиваются.
- Мы можем иллюстрировать это с помощью воды. Вода состоит из молекул H2O — это два атома водорода и один атом кислорода, соединённые вместе. Мы знаем, что атом кислорода и атомы водорода при соединении образуют воду — молекулу H2O.
- Поток воды состоит из миллионов молекул. Мы можем сравнить текущую воду с током, молекулу с электроном, а заряд с атомами.
-

2
Узнайте, что такое напряжение или разность потенциалов. Напряжение — это определённая сила, которая заставляет ток течь. Чтобы лучше понять напряжение, мы используем для примера батарейку. Внутри батарейки есть много химикатов, которые реагируют между собой, образуя химические реакции, что влечёт за собой накопление электронов в положительном контакте на батарейке.
- Теперь, если мы подключим проводник, например, провод – от положительного терминала к отрицательному к терминалу батарейки, электроны будут накапливаться и начнут двигаться, чтобы отстраниться друг от друга, потому, что мы уже сказали, что похожие заряды отталкиваются.
- К тому же, из за закона сохранения энергии, который утверждает, что суммарный результативный заряд изолированной системы должен оставаться постоянным, электроны начнут пытаться балансировать, то есть, уравновесить заряды, меняя большую концентрацию электронов на маленькую концентрацию электронов, то есть, положительный терминал, на отрицательный терминал.
- Это движение электронов вызывает разницу потенциалов в каждом терминале батарейки, что мы можем назвать напряжением.
-

3
Теперь мы должны понять, что такое сопротивление. Сопротивление — это противостояние определённых элементов потоку зарядов.
- Резистор, то есть, элемент указывающий (оказывающий) сопротивление, находится в разных частях цепи, чтобы регулировать поток частиц или электронов.
- Если резистора – частицы оказывающей сопротивление нет, электроны не регулируются и цепь может получать слишком большой заряд, что может повредить её.
Реклама
-

1
Сейчас мы найдём общее сопротивление тока(у). Представьте себе трубочку, из которой вы пьете воду. Ущипните её несколько раз, что вы увидите? Поток Воды уменьшится. Когда вы щипали трубочку, вы создавали сопротивление. Таким образом вы блокировали поток воды. Если вы поставите прищепки в ряд, вы создадите серию резисторов для определённого потока в данной системе. Из этого примера мы можем посчитать суммарное сопротивление резисторов:
- Rсуммарное = R1+ R2 + R3.
-

2
Найдите общее напряжение резисторов. Чаще всего общее напряжение уже дано в условиях задачи, но если вам даны только индивидуальные напряжения, мы можем рассчитать суммарное с помощью такого уравнения:
- Vсуммарное = V1 + V2 + V3.
- Но почему это так? Если мы опять используем аналогию с трубочкой, мы увидим, что после того, как мы ущипнём трубочку, вам понадобится прилагать более усилий, чтобы вытягивать из неё воду. Общее количество усилий, которые вы прилагаете, зависит от индивидуальной силы и каждого резистора потока.
- Сила, которую нужно приложить – это напряжение, поскольку оно направляет поток воды или ток. Таким образом, по логике вещей, общее напряжение можно узнать, сложив индивидуальные напряжения каждого резистора.
-

3
Найдите суммарный ток этой системы. Используя аналогию с трубочкой и прищепками, подумайте, изменилось ли количество воды. Оно не изменилось. Скорость с которой вы получаете воду, изменилась, но общее количество воды — нет. Если вы посмотрите на количество воды, которое входит и выходит из трубочки, вы увидите, что изменилась скорость, но не количество. Таким образом, мы можем сказать что:
- I1 = I2 = I3 = I.
-

4
Помните закон Ома? Его можно применять в этом случае. У нас немного данных, поэтому мы можем использовать закон Ома по отношению к напряжению, току и сопротивлению:
- V = I * R.
-

5
Попробуйте рассмотреть это на примере. Три резистора R1 = 10 Ом, R2 = 2 Ом, R3 = 9 Ом, соединены в цепь. Общее напряжение 2.5 Вольт применяется к электрической цепи (приложено к данному участку цепи). Посчитайте суммарный ток в электрической цепи. Сначала посчитаем общее сопротивление:
- Rсуммарное = 10 Ом R2 + 2 Ом R3 + 9 Ом.
- Таким образом, Rсуммарное = 21 Ом.
-

6
Используем закон ома для подсчёта суммарного тока.
- Vсуммарное = Iсуммарное * Rсуммарное.
- Iсуммарное = Vсуммарное / Rсуммарное.
- Iсуммарное = 2.5 вольт / 21 Ом.
- Iсуммарное = 0.1190 Ампер.
Реклама
-

1
Для начала нужно понять, что такое параллельная электроцепь. Параллельная электроцепь состоит из элементов, соединённых параллельно. Это используется с помощью проводов, которые создают путь, по которому идёт ток.
-

2
Найдите суммарное напряжение. Мы определились с терминологией в предыдущей части статьи. Теперь можем перейти сразу к расчётам. Возьмём в качестве примера трубу разделённую на 2 пути с различными диаметрами. чтобы вода протекла по обеим частям трубы, нужно использовать неодинаковые силы, так? не так. Нужно использовать достаточно силы, чтобы вода текла по трубе. Таким образом, используя аналогию с водой, мы можем рассчитать суммарное напряжение для тока:
- Vсуммарное = V1 + V2 + V3
-

3
Найдём суммарное сопротивление. Например, вам нужно регулировать поток воды в трубах. Как мы заблокируем трубы? Поставим один блок на каждый путь или несколько блоков по всей цепи труб? Нужно сделать последнее. Чтобы создать сопротивление, необходимо поставить несколько резисторов. Их нужно подключить, чтобы они регулировали поток электрического тока. Их нужно подключить цепью, а не параллельно, таким образом, выведем уравнение:
- 1/Rсуммарное = (1/R1)+(1/R2)+(1/R3).
-

4
Вычисление суммарного тока. Вернёмся у своему примеру. Вода течёт из источника по направлению к нам через разделённые трубы. Применим ту же схему к току. Поскольку, есть несколько путей, по которым идёт заряд, мы можем сказать, что он разделён. Оба пути не обязательно получают одинаковое количество заряда, всё зависит от сопротивления и материала из которого сделаны элементы. Таким образом, уравнение суммарного тока — это сумма всех токов для всех путей:
- Iсуммарное = I1 + I2 + I3.
- Мы не можем использовать эту формулу, так как мы не знаем индивидуального тока. Используем закон Ома.
Реклама
-

1
Давайте попробуем решить это на примере. Четыре резистора разделены на два пути, которые соединены параллельно. На первом пути R1 = 1Ом, R2 = 2 Ом, а на втором пути R3 = 0.5 Ом, R4 = 1.5 Ом. Резисторы на каждом пути соединены систематически цепью. Напряжение первого пути 3 Вольта. Найдите суммарный ток.
-

2
Для начала найдём общее сопротивление. Поскольку резисторы на каждом пути соединены, мы сложим сопротивления на каждом пути.
- Rсумарное = R1 + R2.
- Rсумарное = 1 Ом + 2 Ом.
- Rсумарное = 3 Ом.
- Rсумарное = R3 + R4 (для второго пути).
- Rсумарное = 0.5 Ом + 1.5 Ом.
- R = 2 Ом.
-

3
Подставим значения в наше уравнение для параллельной цепи. Поскольку пути соединены параллельно, мы подставим значения в уравнение:
- (1/Rсуммарное) = (1/Rсуммарное 1-й путь) + (1/Rсуммарное 2-й путь).
- (1/Rсуммарное) = (1/3 Ом) + (1/2 Ом).
- (1/Rсуммарное) = 5/6.
- (1/Rсуммарное) = 1.2 Ом.
-

4
Найдите общее напряжение. Рассчитаем суммарное напряжение, это будет сумма всех напряжений:
- Vсуммарное = V1 = 3V.
-

5
Используем закон Ома, чтобы найти суммарный ток. Теперь мы можем посчитать суммарный ток с помощью закона Омв.
- Vсуммарное = Iсуммарное*Rсуммарное.
- Iсуммарное = Vсуммарное/Rсуммарное.
- Iсуммарное = 3 Вольта / 1.2 Ом.
- Iсуммарное = 2.5 А.
Реклама
Советы
- Общее сопротивление параллельной электрической цепи всегда меньше, чем сопротивление каждого отдельного резистора.
- Терминология:
- Электрическая цепь — составленная из элементов (резисторов, индукторов и конденсаторов) цепь, соединённая проводами, через которые протекает ток.
- Резистор — элемент, который оказывает сопротивление току.
- Ток — поток заряженных частиц по проводам, измеряется в амперах (А).
- Напряжение — работа выполненная на единицу заряда, измеряется в вольтах (В).
- Сопротивление — измерение сопротивления элемента электрическому току. Единица — Ом(Омега).
Реклама
Об этой статье
Эту страницу просматривали 13 433 раза.
Была ли эта статья полезной?
Download Article
Download Article
The easiest way to picture a series circuit connection is a chain of elements. The elements are added consequently and in the same line. There is only one path wherein the electrons and charges can flow. Once you have a basic idea of what a series circuit connection involves, you can learn how to calculate total current.
-

1
Familiarize yourself with what current is. Current is the flow of electrically charged carriers like electrons or the flow of charge per unit of time. But what is a charge and what is an electron? An electron is a negatively charged particle. A charge is a property of matter that is used to classify whether a thing is positive or negatively charged. Like magnets, alike charges repel and opposites attract.[1]
- We can illustrate this by using water. Water is composed of the molecule, H2O – which stands for 2 atoms of Hydrogen and 1 atom of Oxygen bonded together. We know that the oxygen atom and hydrogen atoms make up the molecule, H2O.
- A flowing body of water is composed of millions and millions of this molecule. We can compare the flowing body of water to the current; the molecule to electron; and the charge to the atoms.
-

2
Understand what voltage refers to. Voltage is the “force” that drives the current to flow. To best illustrate voltage; we will use the battery as an example. Inside the battery is a series of chemical based reactions which create a buildup of electrons in the positive terminal of the battery.[2]
- If we now connect a medium (eg a wire) from the positive terminal to the negative terminal of the battery, the electron buildup will now move to get away from each other because as we said, alike charges repel.
- In addition, because of the law of conservation of charge, which states that the net charge of an isolated system should remain constant, the electrons will try to balance the charges by going from the higher concentration of electrons to the lower concentration of electrons or positive terminal to the negative terminal, respectively.
- This movement causes a potential difference in each of the terminals which we can now call voltage.
Advertisement
-

3
Know what resistance is. Resistance, on the other hand, is the opposition of certain elements to flow of charge.[3]
- Resistors are elements with significant resistance. They are placed in certain parts of a circuit to regulate the flow of charge or electrons.
- If there are no resistors, the electrons are not regulated, the equipment may receive too much charge and it will be damaged or cause a fire due to overcharging.
Advertisement
-

1
Find the total resistance of the circuit. Imagine a straw you are drinking from. Pinch it several times. What do you notice? The water flowing will be lessened. Those pinches are the resistors. They block the water which is the current. Since the pinches are in a straight line, they are in series. Drawing from this example, the total resistance of resistors in a series is:[4]
- R(total) = R1 + R2 + R3.
-

2
Identify the total voltage of the resistor. Most of the time, the total voltage is readily given, but in cases where individual voltages are given, we can use the equation:[5]
- V(total) = V1 + V2 + V3.
- But why is this so? Using the straw analogy again, after pinching the straw, what do you expect? You need more effort to get water through the straw. The total effort you are delivering is brought about by the individual force the individual pinches need.
- The “force” you need is the voltage, because it drives the flow of water or the current. Therefore it is only logical that the total voltage is brought about by adding up the individual voltages across each resistor.
-

3
Calculate the total current of the system. Using the straw analysis again, even in the presence of pinches, did the amount of water you get change? No. Although the speed at which you are getting the water changes, the amount of water you can drink is fixed. And if you look closer at the amount of water entering and leaving, the pinches are the same because of the fixed speed the water is flowing, therefore, we can say that:[6]
- I1 = I2 = I3 = I(total)
-

4
Remember Ohm’s law. But it doesn’t stop there! Remember we don’t have any of this data, so we can use the Ohm’s Law which relates voltage, current and resistance:[7]
- V = IR.
-

5
Try working with an example. Three resistors, R1 = 10Ω R2=2Ω R3 = 9Ω, are connected in series. A total voltage of 2.5V is applied to the circuit. Compute for the total current of the circuit. First let’s compute for the total resistance:[8]
- R(total) = 10Ω R2 + 2Ω R3 + 9Ω
- Therefore R(total) = 21Ω
-

6
Use Ohm’s Law for computing the total current:[9]
- V(total) = I(total) x R(total).
- I(total) = V(total) / R(total).
- I(total) = 2.5V / 21Ω.
- I(total) = 0.1190A.
Advertisement
-

1
Understand what a parallel circuit is. Like it name, a parallel circuit contains elements that are arranged in a parallel way. This makes use of multiple wiring arrangements creating paths wherein current can travel.[10]
-

2
Compute for the total voltage. Since we have sorted out the terminologies in a previous section, we can now go directly to the computations. Take for an example a pipe split into two paths with different diameters. For the water to flow into both of the pipes, do you need to use unequal forces in each of the pipes? No. You just need enough force for the water to flow. Therefore, using the analogy that the water is the current and the force is the voltage, we can say that:[11]
-
V(total) = V1 + V2 + V3.[12]
-
V(total) = V1 + V2 + V3.[12]
-

3
Compute for the total resistance. Say you want to regulate the water flowing in the pipes. How will you block the pipes? Do you put just one blockage on each path or do you put multiple blockages arranged consecutively to control the water flow? You would need to do the latter. For resistances, this analogy is the same. Resistors connected in series regulate current far better than those arranged in a parallel way. The equation for the total resistance in a parallel circuit is:[13]
- 1/R(total) = (1/R1) + (1/R2) + (1/R3).
-

4
Compute for the total current. Going back to our example, the water flowing from the source to the split path is divided. The same is applicable for current. Since there are multiple paths where charges can flow, it can be said that to be split. The pathways do not necessarily receive equal amounts of charge. It is dependent on the resistances and the materials the elements have in each path. Therefore, the equation of the total current is just the summation of all the currents in all of the paths:[14]
- I(total) = I1 + I2 + I3.
- Of course, we can’t use this yet because we do not have the individual currents. In this case Ohm’s Law can also be used.
Advertisement
-

1
Try an example. 4 resistors divided into two paths which are connected in parallel. Path 1 contains, R1 = 1Ω R2=2Ω while Path 2 contains, R3 = 0.5Ω R4=1.5Ω. The resistors in each path are connected in series. The voltage applied in path 1 is 3V. Find the total current.
-

2
Find the total resistance. Since the resistors in each path are connected in series, we will find solve for the total resistance in each path.
- R(total 1&2) = R1 +R2.
- R(total 1&2) = 1Ω + 2Ω.
- R(total 1&2) = 3Ω.
- R(total 3&4) = R3 + R4.
- R(total 3&4) = 0.5Ω + 1.5Ω.
- R(total 3&4) = 2Ω.
-

3
Plug in the equation for parallel connection. Now, we since the paths are connected in parallel, we will now use the equation for parallel connection
- (1/R(total)) = (1/R(total 1&2)) + (1/R(total 3&4)).
- (1/R(total)) = (1/3Ω) + (1/2Ω).
- (1/R(total)) = ⅚.
- R(total) = 1.2Ω.
-

4
Find the total voltage. Now compute for the total voltage. Since the total voltage is equal to all the voltages:
- V(total) = V1 = 3V.
-

5
Use Ohm’s law to find the total current. Now, we can compute for the total current using Ohm’s Law.
- V(total) = I(total) x R(total).
- I(total) = V(total)/R(total).
- I(total) = 3V/1.2Ω.
- I(total) = 2.5A.
Advertisement
Add New Question
-
Question
How do you calculate resistors connected in a series?

Series resistors’ value is the value of all added together. 1 Ohm+2 Ohm = 3 Ohm total, for example.
-
Question
What is the formula for a total current?

Gabeericwolf
Community Answer
IT = VT/RT or I total = V total / R total or the total current = the total voltage / the total resistance.
-
Question
A street lamp is rated at 240V and 120W. How do I calculate the current through the lamp when it is working at its recommended power?

The answer is 0.5 amps. Using the P=IxE formula, I=P/E so plugging the numbers in gives 120W/240V=0.5 Amps
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
The total resistance for the parallel circuit is always smaller than ANY of the resistance of the resistors.
-
Terminologies:
- Circuit – composed of elements (e.g. resistors, capacitors, and inductors) connected by wires and wherein current can pass through.
- Resistors – elements that can reduce or resist current
- Current – flow of charge into wires; unit: Ampere, A
- Voltage – work done per unit charge; unit: Voltage, V
- Resistance – measurement of the opposition of an element to electric current; unit: Ohm, Ω
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To find the total current in both series and parallel circuits, start by calculating the total resistance. For series circuits, the total resistance is equal to resistor 1 plus resistor 2 plus resistor 3 and so forth. For parallel circuits, the inverse of the total resistance is equal to the inverse of resistor 1 plus the inverse of resistor 2 and so forth. Calculate the total voltage of the circuit next. In both series and parallel circuits, the total voltage is equal to the sum of the individual voltages. Once you have worked out the total resistance and voltage, use Ohm’s Law to calculate the total current in the circuit. In Ohm’s Law, the total current is equal to the total voltage divided by the total resistance. In a series circuit, the current is the same through all of the components in the circuit, whereas in a parallel circuit, the total current is only equal to the individual current in that branch of the circuit. For more information on calculating the total current, like how to understand the difference between voltage and current, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 375,257 times.
Did this article help you?
Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
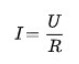
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
Общие схемы типов соединений представлены на рисунке 1.
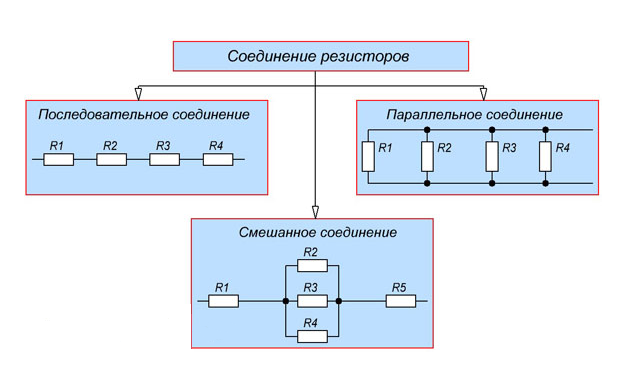
Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
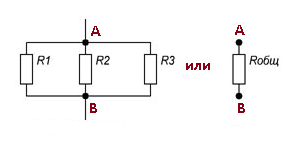
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
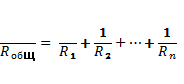
и рассчитывается по формуле:
![]()
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
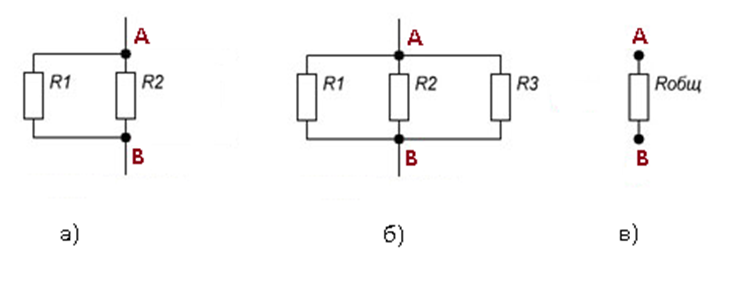
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
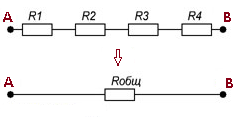
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
![]()
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
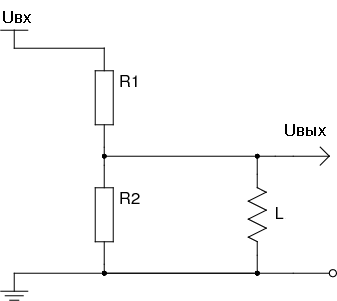
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
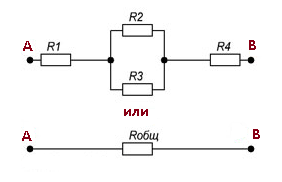
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
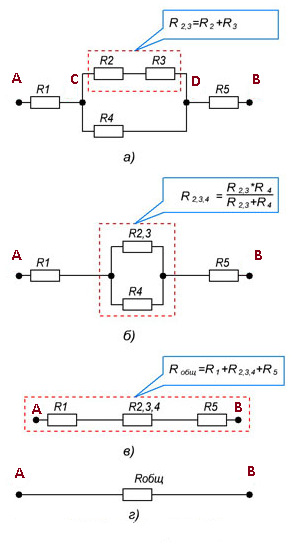
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Для расчета электрической цепи применяют два закона Кирхгофа. (Скорее их можно отнести не к законам, а к правилам. Но в большинстве учебников пишут именно о “законах” Кирхгофа. Поэтому и здесь будем обращаться к законам).
Первый закон Кирхгофа
Первый закон Кирхгофа применяют к узлам электрической цепи и выражают баланс токов в них. Первый закон Кирхгофа гласит:
Алгебраическая сумма токов сходящихся в узле электрической цепи равна 0.
Под словом “алгебраическая” имеется в виду, что учитывается знак перед током: “плюс” или “минус”.
В общем виде первый закон Кирхгофа можно записать как:
Для примера возьмем узел, в котором протекают токи, указанные стрелками (далее рассмотрим это все на конкретных схемах).
Токи, втекающие и вытекающие из узла, берутся с противоположными знаками. Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Будем считать токи положительными, если они втекают в узел, а вытекающие из узла – отрицательными. Тогда первый закон Кирхгофа для узла, представленного на рисунке 2, запишется:
I1-I2+I3+I4=0
Это выражение можно записать и в следующем виде:
I2=I1+I3+I4;
Ток I2 мы перенесли за знак равенства, его знак поменялся на противоположный (был с “минусом”, стал с “плюсом”).
Остальные токи мы не переносим, поэтому их знаки не меняются.
Согласно последнему выражению, первый закон Кирхгофа можно сформулировать по-другому:
Сумма токов, втекающих (подходящих) в узел, равна сумме токов, вытекающих (отходящих) из узла.
Все это говорит о том, что в узле эти токи не остаются и заряд в узле не накапливается.
Для более полного понимания, представим электрическую цепь (схему электрической цепи), для которой запишем первый закон Кирхгофа.
Запишем для этой цепи первый закон Кирхгофа для узла “a” (о том, как определить количество уравнений по первому и второму законам Кирхгофа, рассмотрим в конце ).
I1+I2-I3=0 или I3=I1+I2.
Второй закон Кирхгофа
Этот закон применяется к контурам электрической цепи и выражает баланс напряжений в них. Второй закон Кирхгофа звучит так:
Алгебраическая сумма ЭДС в замкнутом контуре (с учетом направления обхода контура) равна алгебраической (учитывается знак “+” или “-“) сумме падений напряжений на всех сопротивлениях (элементах) этого контура.
Для того, чтобы правильно составить уравнения по второму закону Кирхгофа, нужно пользоваться следующим правилом:
ЭДС берется со знаком “+”, если ее действие совпадает с направлением обхода контура. Напряжение на элементе контура берется со знаком “+”, если направление тока через данный элемент совпадает с направлением обхода контура. Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
Запишем второй закон Кирхгофа для цепи, представленной ниже:
Выбираем направление обхода контура по часовой стрелке. В данном случае направление тока и направление обхода контура совпадают, поэтому I·R1 и I·R2 взяли со знаком “+”. А также совпадает направление обхода контура и действие ЭДС, поэтому ЭДС также записали со знаком “+”.
Возьмем еще один пример.
Запишем для этой цепи второй закон Кирхгофа. Обход выбираем по часовой стрелке (указали обход контура на схеме круговой стрелкой внутри контура). Как видим, направление обхода контура и направление тока I1 совпадают, а ток I2 направлен напротив обхода контура.
Следовательно, падение напряжения на резисторе R1 запишется со знаком “+”, т. е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
Направление действия ЭДС совпадает с обходом контура, поэтому ЭДС E берем со знаком “+”.
Запишем второй закон Кирхгофа для этой цепи:
I1·R1-I2·R2=E
Ну и напоследок рассмотрим сложную электрическую цепь, состоящую из нескольких источников и резисторов.
Введем произвольно направление токов в ветвях, а также укажем на схеме в виде круговых стрелок направление обхода контуров.
Токи в ветвях направили произвольно, обход контура выбрали по часовой стрелке, а также узлы в этой схеме обозначили буквами a и b. Для того, чтобы понять, как и сколько уравнений по первому и второму законам Кирхгофа нужно составить для данной цепи, необходимо посчитать количество ветвей, узлов и независимых контуров.
Подробно вышесказанные понятия электрической цепи мы рассмотрим в следующих статьях. А пока вкратце.
Узел – это место соединения трех и более ветвей в электрической цепи (в данном случае таких узлов два. Это узлы “a” и “b”.
Ветвь – это участок электрической цепи, который образуется одним или несколькими последовательно соединенными элементами и через все эти элементы протекает один и тот же ток.
Контур – это любой замкнутый путь электрической цепи, проходящий по двум или нескольким ветвям.
Так же есть такое понятие как независимый контур.
Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
На рисунке 9 будет три контура, два из которых независимые. Если контур 1 независимый, контур 2 независимый(таким образом все три ветви этой схемы цепи вошли в эти независимые контуры). Тогда контур 3 уже независимым не будет, поскольку все ветви “заняты” остальными двумя контурами.
Или если контур 1 независимый (он включает в себя ветви с элементами E и R1). Контур 3 независимый (он включает в себя ветви с элементом E и ветвь с элементом R3. Элемент R3 ранее не входил в первый независимый контур), поэтому контур 3 считается независимым.
Получается, что все ветви “заняты”. Тогда контур 2 независимым уже не будет, поскольку в него не входят ветви или ветвь ранее не входящую в другие контура. Все ветви вошли в ранее независимые контуры 1 и 3.
В цепи на рисунке 9, в общем случае, три ветви, два узла и два независимых контура. Общее количество уравнений по законам(правилам) Кирхгофа составляется столько, сколько ветвей в схеме цепи за вычетом количества ветвей, где есть источник тока (именно источник тока, а не ЭДС). В нашей схеме нет источников тока, следовательно, составляются три уравнения по законам Кирхгофа. Теперь осталось определить, сколько уравнений нужно составить по первому и второму законам Кирхгофа. Общее количество уравнений будет три. Формула для определения количества уравнений по первому закону Кирхгофа следующая:
N1з.к.=Ny-1, где Ny – количество узлов.
Ny=2, тогда
N1.з.к.=Ny-1=2-1=1
Т. е. по первому закону Кирхгофа составляется одно уравнение для данной цепи, а общее количество уравнений – три. Таким образом, мы получаем, что по второму закону Кирхгофа нужно составить два уравнения. Или для определения количества уравнений по второму закону Кирхгофа есть формула:
N2.з.к.=Nв-(Ny-1), где Nв – количество ветвей
Nв=3, тогда:
N2.з.к.=3-(2-1)=2
По второму закону Кирхгофа составляется два уравнения. Составим систему, состоящую из трех уравнений. Одно уравнение по первому закону Кирхгофа (это уравнение составляется для любого узла a или b) и двух уравнений по второму закону Кирхгофа для двух любых независимых контуров, например, составим для контуров 1 и 2.
Неизвестными в данной системе являются токи I1, I2 и I3. Решая данную систему, находят эти неизвестные.
О том, как решаются задачи с более сложными цепями, мы поговорим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
Содержание:
Расчет электрических цепей постоянного тока:
Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.
Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.
Законы Кирхгофа
Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:

В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I1 + I2 — I4 — I7 = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I1 + I2 = I4 + I7. (4.2)
Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:

Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V1. Потенциал каждой последующей точки выразим относительно точки предыдущей: V2 = V1 + Е1; V3 = V2 — I1R1; V4 = V3 — I4R4; V5 = V4 — E3; V6 = V5 + I6R6; V1 = V6 — I3R3.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре
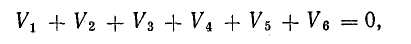
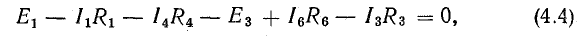
или
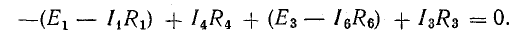
В этом уравнении напряжения ветвей
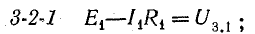
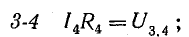
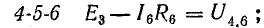
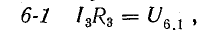
поэтому 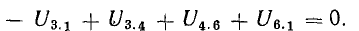
В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде:
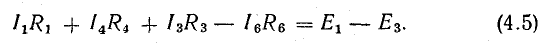
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура:

Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.
Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.
При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1
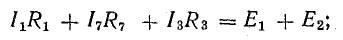
для 3-4-6-3
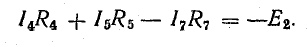
Неразветвленная электрическая цепь
Элементы неразветвленной электрической цепи соединены между собой последовательно.
Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.
Общий случай последовательного соединения
Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):
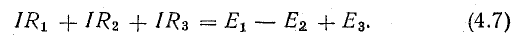
Ток в цепи

При обходе контура видно, что относительно направления обхода э. д. с. Е1 и Е3 направлены одинаково, т. е. согласно, а э. д. с. Е2 — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E1 и Е3 вырабатывают электрическую энергию, а элемент с э. д. с. Е2 ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е1 и Е3 разряжаются, а источник Е2 заряжается.
В элементах цепи, характеризующихся сопротивлениями R1, R2 и R3, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.
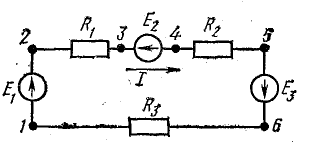
Рис. 4.1. Схема неразветвленной электрической цепи
Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е2 в левую часть:
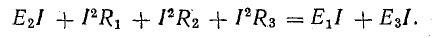
Получим уравнение баланса мощности – для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.
Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а.
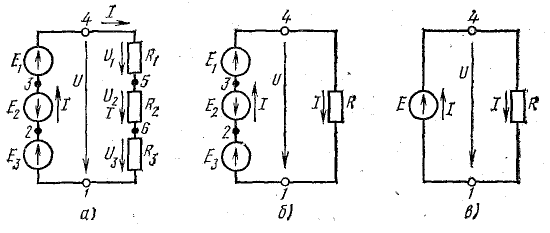
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи
Последовательное соединение пассивных элементов
Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)].
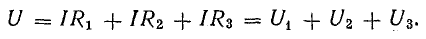
Вынеся I за скобку, получим
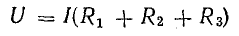
или
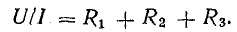
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:
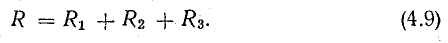
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:

т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.
Последовательное соединение источников э.д.с.
Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1 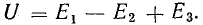
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной)

и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.
Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле

где Еn — э. д. с. одного элемента; n — число элементов в батарее.
Согласно составленной эквивалентной схеме (рис. 4.2, в),
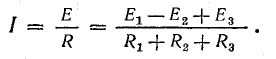
Потенциальная диаграмма
В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е1, а при переходе от точки 2 к точке 3 — снижается на величину U2.3 = IR1. При переходе от точки 3 к точке 4 потенциал понижается на величину U3.4 = —E2.
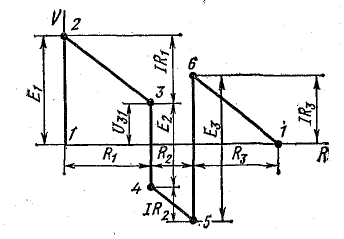
Рис. 4.3. Потенциальная диаграмма электрической цепи
Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.
Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.
Потенциалы точек цепи найдены согласно равенствам
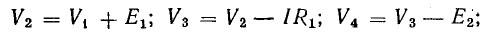
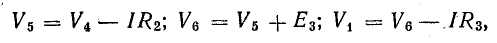
причем потенциал точки 1 принят равным нулю.
Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
Задача 4.3.
Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора Eг = 120 В; внутреннее сопротивление rг = 1,0 Ом, э. д. с. батареи Еа = 72 В, внутреннее сопротивление rа = 3 Ом, R1 = 16 Ом, R2 = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково.
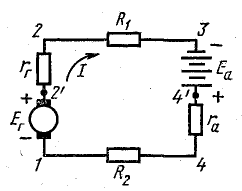
Рис. 4.4. К задаче 4.3
Эквивалентная э. д. с. цепи
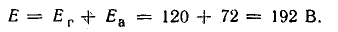
Эквивалентное внутреннее сопротивление
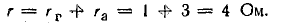
Эквивалентное сопротивление нагрузки
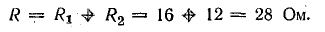
Ток в цепи
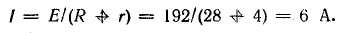
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора
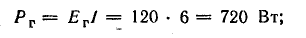
аккумуляторной батареи
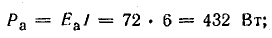
потерь внутри генератора
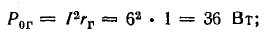
потерь внутри аккумуляторной батареи
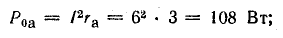
потребления в резисторе R1
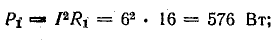
потребления в резисторе R2
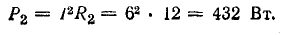
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления)

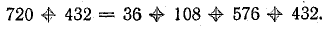
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V1 = 0:
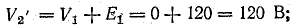
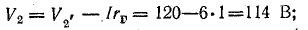
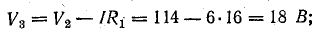
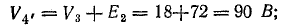
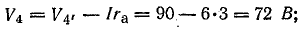
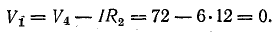
Потенциальная диаграмма показана на рис. 4.5.
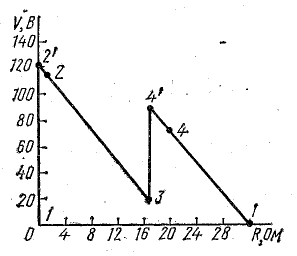
Рис. 4.5. Потенциальная диаграмма.
Разветвленная электрическая цепь с двумя узлами
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.
Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.
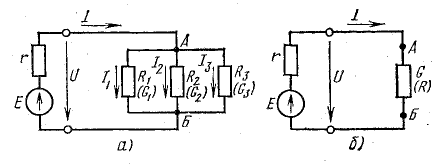
Рис. 4.7. Преобразование схемы с параллельным соединением приемников
Параллельное соединение пассивных элементов
Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R1, R2, R3 и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа: 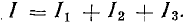
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей:
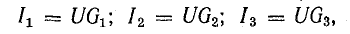
где
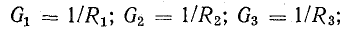
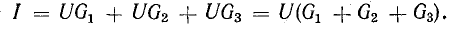
Разделим это уравнение на U:
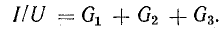
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению:

Этот вывод можно распространить на любое число n параллельно соединенных приемников:

При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.
Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).
Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства
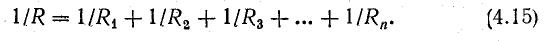
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле
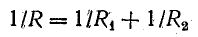
или

Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле 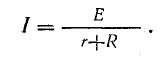
Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.
Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома:
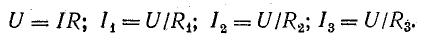
Параллельное соединение источников энергии
В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).
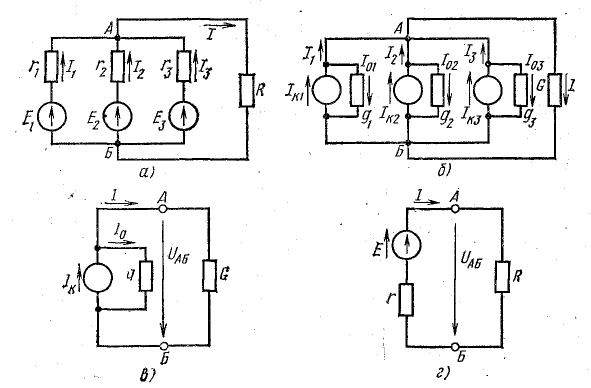
Рис. 4.8. Преобразование схемы с параллельным соединением источников
В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.
Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):

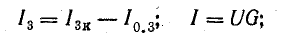


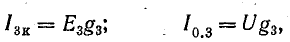
где U = Uаб — напряжение между узловыми точками А и Б.
По первому закону Кирхгофа, для узла А
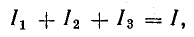
или
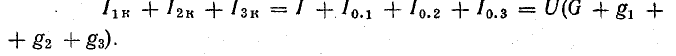
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания
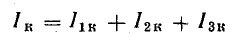
и внутренней проводимостью
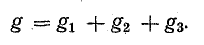
Для схемы рис. 4.8, в
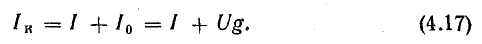
Напряжение между узлами
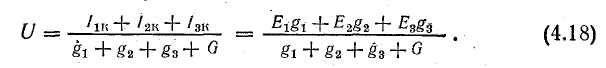
Токи в ветвях можно определить по следующим формулам:
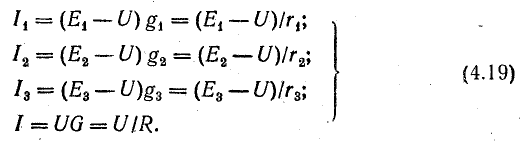
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.
Общий ток в этом случае определяется произведением тока одного источника In на число параллельно включенных источников:

Величина тока каждого источника ограничена его номинальным значением Iном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.
От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g:
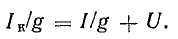
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то Iкr = Ir + U.
Но Iкr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.
Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.
Общий случай параллельного соединения источников и приемников электрической энергии
Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).
Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.
Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви).
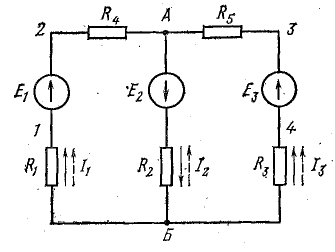
Рис. 4.9. Схема с двумя узлами
В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид

Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).
Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
Задача 4.8.
Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R1 = 30 Ом, R2 = 20 Ом, R3 = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б:
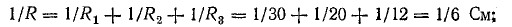
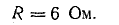
Ток в неразветвленной части цепи
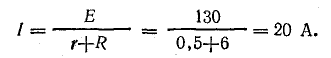
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках:
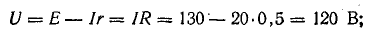
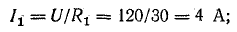
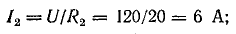
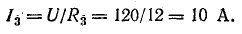
Проверим правильность определения токов по уравнению (4.1):
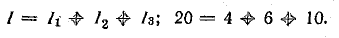
Мощность передачи энергии приемникам
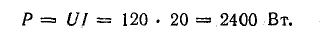
К. п. д. источника
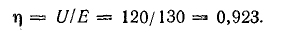
Задача 4.10.
Для схемы, изображенной на рис. 4.7, а, известны: R1 = 10 Ом; R2 = 15 Ом; R3 = 6 Ом, r = 0,5 Ом, l3 = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома:
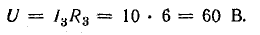
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях:
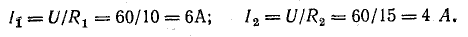
Ток в неразветвленной части цепи
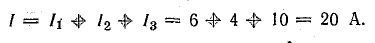
Э. д. с. источника
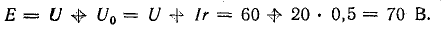
Мощность источника
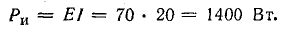
Мощность потребления энергии приемниками
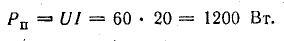
К. п. д. источника
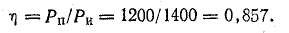
Задача 4.12.
Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E1 = 120 В; E2 = 80 В; E3 = 60 В; r1 = 0,5 Ом; r2 = 0,4 Ом; r3 = 0,2 Ом; R1 = 2 Ом; R2 = 15,6 Ом; R3 = 12,4 Ом; R4 = 7,5 Ом; R5 = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем UАБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей:
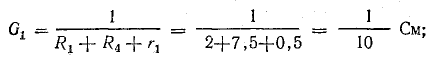
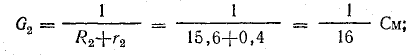
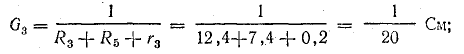
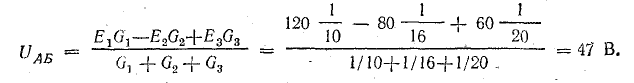
Токи в ветвях:
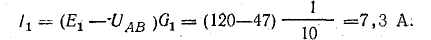
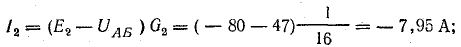
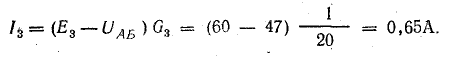
Токи l1 и l3 положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l2 противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.
Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P1.1 = E1I1 = 120 • 7,3 = 876 Вт; P1.2 = Е2I2 = 80 • 7,95 = 636 Вт; Р1.3 = E3I3 = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.
При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е2 и I2 сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.
Мощность потерь внутри источников: 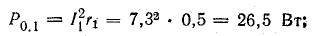
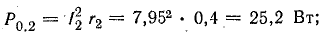
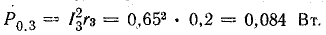
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников:
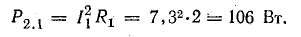
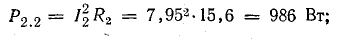
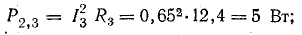
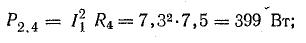
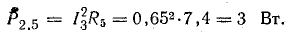
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.
Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
Определение эквивалентных сопротивлений
На схеме рис. 4.10, а сопротивления R3 и R4 включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I3 = I4. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму 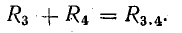
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R2 и R3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):
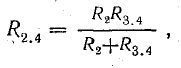
и получить более простую схему (рис. 4.10, в).
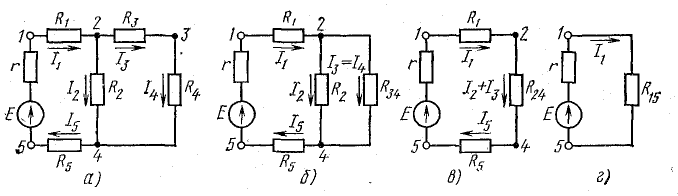
Рис. 4.10. К методу эквивалентных сопротивлений
В схеме рис. 4.10, в сопротивления R1, К2.4, К5 соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
Определение токов
В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что
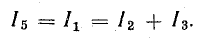
Кроме того, напряжение между точками 2 и 4
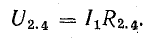
Зная это напряжение, легко определить токи I2 и I3 = I4:
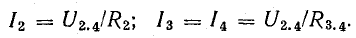
После определения токов I1 и I5 напряжение U2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V4 известным (например, равным нулю), а V2 найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I1 =I5:
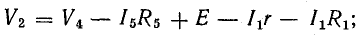
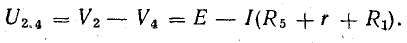
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.
Треугольник и звезда сопротивлений
Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).
В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.
К узловым точкам a, b, c присоединен треугольник сопротивлений Rab, Rbc, Rca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений Ra, Rb, Rc (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.
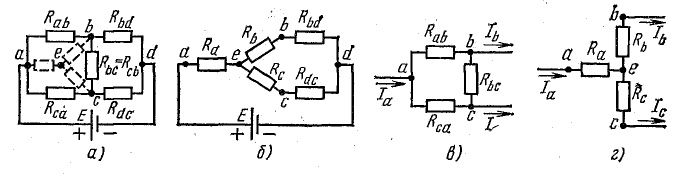
Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления Rb и Rbd соединены между собой последовательно, так же как b сопротивления Rc и Rdc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором Ia = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями Rbc и Rab + Rca
Общее сопротивление между этими точками
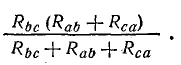
В схеме звезды между точками b и c включены последовательно сопротивления Rb и Rc. Общее сопротивление между этими точками Rb + Rc.
По условиям эквивалентности напряжение между точками b и c и токи Ib и Ic в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е.
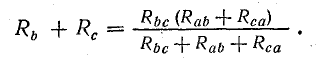
Полагая Ib =0, а затем Ic = 0, получим:
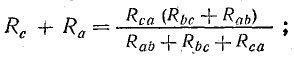
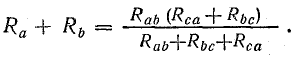
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника:
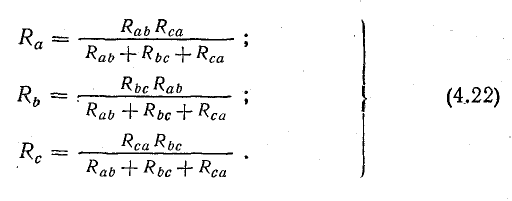
Преобразование звезды сопротивлений в эквивалентный треугольник
Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.
При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б:
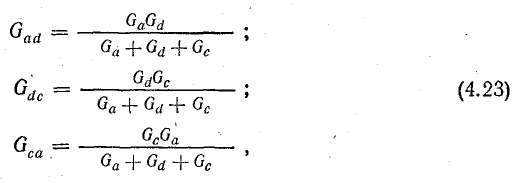
где Gad; Gdc; Gca — проводимости сторон треугольника; Ga; Gd; Gc — проводимости лучей звезды.
Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.
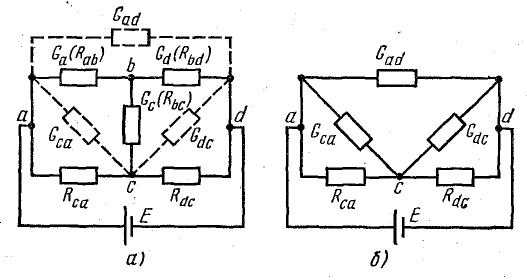
Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
