Как найти площадь треугольника

О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.

Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
[spoiler title=”источники:”]
http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika
http://mozgan.ru/Geometry/AreaTriangle
[/spoiler]
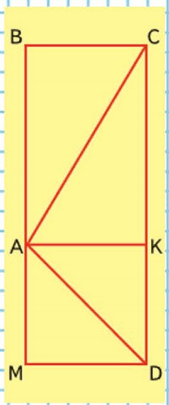
Найди площадь и периметр треугольника ACD.

reshalka.com
Математика 4 класс Моро. Часть 1. Сложение и вычитание. Номер №318
Решение
Отрезок AC делит прямоугольник ABCK на 2 равных треугольника ABC и ACK, и отрезок AD делит квадрат MAKD на 2 равных треугольника MAD и DAK, поэтому:
S
A
C
D
=
S
A
C
K
+
S
D
A
K
=
S
M
B
C
D
:
2
;
S
M
B
C
D
=
M
B
∗
B
C
=
8
∗
3
=
24
(
с
м
2
)
;
Значит,
S
A
C
D
=
24
:
2
=
12
(
с
м
2
)
.
P
A
C
D
=
42
+
58
+
80
=
180
(
м
м
)
=
18
с
м
.
- Ответы к учебнику Моро 4 класс 1 часть (2015 г)
- Ответы к учебнику Моро 4 класс 2 часть (2015 г)
- Главная страница
7. Реши уравнения.

8. 1) Найди площадь прямоугольника ВСКЕ и площадь прямоугольника АЕКD.

Измерим линейкой стороны фигур.
ВС=КЕ = 2 см, СК = ВЕ = 2 см. Значит площадь ВСКЕ = 2 • 2 = 4 см².
КD = АЕ = 3 см, ЕК = АD = 2 см. Значит площадь АЕКD = 3 • 2 = 6 см².
2) Найди двумя способами площадь прямоугольника АВСD.
1-й способ:
Площадь прямоугольника АВСD можно найти сложив площади ВСКЕ и АЕКD.
4 + 6 = 6 см².
2-й способ:
Площадь прямоугольника АВСD можно найти перемножив его длину и ширину.
АВ = СD = ВЕ + АЕ = 2 + 3 = 5 см, ВС = АD = 2 см.
5 • 2 = 10 см².
9. 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной ОК (рис. 1); с общей стороной NP (рис. 2).
Общая сторона OK есть у трёх фигур: треугольника OKD, четырехугольника OKEA и пятиугольника OKCBF.
Площадь треугольника OKD = (OD • KD) : 2 = (2 см • 3 см) : 2 = 6 см² : 2 = 3 см²
Площадь четырехугольника OKEA = EKDA — OKD = 4 см • 3 см — 3 см² = 12 см² — 3 см² = 9 см²
Площадь пятиугольника OKCBF = ABCD — OKD= 4 см • 4 см — 3 см² = 16 см² — 3 см² = 13 см²
Общая сторона NP есть у четырёх фигур: треугольника NPS, квадрата NPLS, треугольника NPT и прямоугольника NPTM.
Площадь квадрата NPLS = NP • LS = 3 см • 3 см = 9 см²
Площадь треугольника NPS = NPLS : 2 = 9 см² : 2 = 4,5 см² (или можно выразить в миллиметрах — 9 см² = 900 мм², площадь треугольника NPS = 900 мм² : 2 = 450 мм²)
Площадь прямоугольника NPTM = NP • NM = 3 см • 2 см = 6 см²
Площадь треугольника NPT = NPTM : 2 = 6 см² : 2 = 3 см²
2) Узнай, площадь какой фигуры меньше: прямоугольника ВСКЕ или треугольника ОKD — и на сколько квадратных сантиметров.
Площадь прямоугольника BCKE = BC • CK = 4 см • 1 см = 4 см²
Площадь треугольника OKD = (OD • KD) : 2 = (2 см • 3 см) : 2 = 6 см² : 2 = 3 см²
4 см² > 3 см², значит площадь прямоугольника BCKE больше площади треугольника OKD.
4 см² — 3 см² = 1 см². Площадь прямоугольника BCKE больше площади треугольника OKD на 1 см².
На сколько 9 меньше, чем 72?
72 — 9 = 63, значит 9 меньше, чем 72 на 63.
Во сколько раз 6 меньше, чем 54?
54 : 6 = 9, значит 6 меньше, чем 54 в 9 раз.
Задание на полях
54 —> 6 —> 42 —> 100 —>25
- Ответы к учебнику Моро 4 класс 1 часть (2015 г)
- Ответы к учебнику Моро 4 класс 2 часть (2015 г)
- Главная страница
Как найти площадь треугольника 3 класс Моро?
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне. где – длина стороны, – высота, проведенная к ней.
Что нужно сделать чтобы найти площадь треугольника?
Площадь треугольника, формула. Треугольник образуется соединением отрезками трех точек, не лежащих на одной прямой. При этом точки называются вершинами треугольника, а отрезки – его сторонами. Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h):
Как вычислить площадь треугольника?
Как найти площадь треугольника
- Первый способ. Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними (рис. …
- Второй способ. Чтобы найти площадь треугольника, нужно сторону умножить на высоту, проведенную к этой стороне (рис. …
- Третий способ. …
- Четвертый способ. …
- Пятый способ.
Как найти площадь треугольника по сторонам?
1. Площадь треугольника через две стороны и угол между ними. S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.
Как вычислить квадратуру в треугольнике?
что обозначает, что площадь треугольника равна произведению длины его основания и высоты поделенной на два.
Как посчитать кв метры крыши?
S=CxD. Длину и ширину скатов можно замерить, не поднимаясь на крышу. Просто измерьте длину и ширину здания и прибавьте к ним величину всех свесов. Если по каким-либо причинам измерить величину ската нельзя, то вычислите ее по теореме Пифагора, сняв размеры высоты крыши и проекцию одного из скатов.
Как найти площадь равностороннего треугольника?
Треугольник называется равносторонним, если все его три стороны равны. Площадь равностороннего треугольника вычисляется как половина как половина произведения его основания на высоту. где a – сторона равностороннего треугольника.
Как высчитать квадратуру крыши?
Как рассчитать площадь простой крыши дома?
- Предположим, размеры дома — 12 х 10.
- Длина стропил — 5 метров.
- Типовая длина свеса — 0,5 м.
- Определяем площадь поверхности одного из скатов: S = (12+0,5+0,5) х (5+0,5) = 71,5 кв. м.
- Так как у здания 2 ската, то полученное число умножаем на 2: 71,5 х 2 = 143 кв. м.
Как посчитать площадь 4 х скатной крыши?
Взяв во внимание, что каждый элемент проекции находится под углом, следует умножить его площадь на принятый косинус угла наклона скатов. После сложения всех полученных результатов получим площадь четырехскатной крыши.
Как рассчитать площадь крыши конвертом?
Например, расчет металлочерепицы для крыши-конверта:
- Общую площадь кровли делим на полезную площадь листа, округляем в большую сторону и добавляем запас;
- Суммируем длины всех карнизов. Из общей длины карнизной планки вычитаем 10 сантиметров, необходимые для нахлеста.
Сколько нужно профнастила на крышу?
Количество листов для каждого ската считается по такой формуле:
- Количество листов = ширина ската/полезная ширина листа …
- Количество листов = 12/1,1 = 10,9. …
- Результат: для крыши необходимо 11 листов профнастила Bulat® 20R длиной 5м. …
- Профнастил в м2 = 11 * 5 * 1,16 = 63,8.
Как рассчитать количество профнастила?
Чтобы рассчитать количество листов профнастила, необходимое для покрытия 30 метров, требуется эту длину поделить на полезную ширину профлиста (допустим, она равна 1140 мм). Полученный показатель – 26,32 округляем в большую сторону и делаем вывод, что для такого забора нам необходимо 27 листов профнастила.
Как рассчитать сколько нужно доски на крышу?
Как рассчитать материалы на крышу Для того, чтобы высчитать его вес, необходимо умножить плотность дерева на объем элемента. Объем высчитывается по формуле: V=C*L, где C — это сечение бруса, а L — его длина.
Сколько стоит один лист профнастила?
Низкая цена на профнастил!!! C года дешевая цена на профнастил для забора!!!
| Наименование | Цена |
|---|---|
| Профнастил для забора с20 толщина 0,4 мм | 717 руб за лист размером 2х1,15 |
| Профнастил для забора цена за лист С8-1150 полиэстер сталь 0,45 мм | 882 руб за лист размером 2х1,15 |
Сколько стоит один лист для забора?
Купить профлист для забора: цена за лист от 217 руб.
Сколько стоит профлист 6 метров?
от 667.
Какие бывают размеры профлиста для забора?
Стандартные размеры профлиста для забора – высота 2 метра, которая считается классической. Также в стандартные рамки входит высота от 1,8 до 2,5 метра. Длина пролета традиционно – 3-3,5 метра. Меньше 3 м длину делать неэкономно, поскольку это увеличит количество столбов.
Какой высоты бывает профлист?
Ее показатель может варьироваться от 0,4 до 14 мм. Стандартные виды имеют высоту до 2 м. Параметры оцинкованного профиля указаны в ГОСТе основные требования к материалу обозначены в ГОСТе ГОСТ описывает качество листов с полимерным слоем.
Какой высоты бывает профнастил для забора?
Стандартные размеры профлиста для забора – высота 2 метра, которая считается классической. Также в стандартные рамки входит высота от 1,8 до 2,5 метра. Заборный профнастил высотой выше 2,5 м изготавливаются индивидуально на заказ и используется нечасто. Длина пролета традиционно – 3-3,5 метра.
Какой длины бывает профнастил?
В зависимости от производителя средняя ширина профнастила может колебаться в пределах 1150-1080 мм (для ПС-10, имеющего высоту волны 10 мм.) Производители предлагают профнастил толщиной от 0,3 до 1 мм. На российском рынке наиболее распространены листы, имеющие толщину в 0,45-0,5 мм.
Как определить профнастил?
Расшифровка маркировки профлистов
- – Цифра, стоящая сразу после буквенного обозначения, указывает на высоту гофра в мм. В данном примере 8 мм.
- – Вторая цифра — толщина профнастила (0,55 мм).
- – Третья — монтажная ширина листа (1150 мм).
- – Последняя — длина листа (12 000 мм).
Сколько квадратов в 1 Профлисте?
Профлист, размеры листа которого составляют 118 см в ширину, 2 метра в высоту. Количество – 27 штук (27 *1,18 * 2 = 63, 72 квадратных метра профилированного листа).
Как правильно стыковать профнастил на заборе?
Стыковать между собой листы нужно так, чтобы сверху оказалась волна, край которой загибается книзу. Если верхним окажется загнутый вверх край, вода будет попадать в щель. Это категорически неприемлемо при монтаже крыш.
Урок
по геометрии.
4
класс
Учитель: Карташева Елена Евгеньевна
Тема урока: « Площадь прямоугольного
треугольника»
Тип урока: Урок
открытия новых знаний.
Цели урока:
– Повторить определения геометрических
фигур.
– Дать учащимся представление о
прямоугольном треугольнике, вывести формулу нахождения площади прямоугольного
треугольника, формировать способность к использованию ее для решения задач.
– Тренировать навыки решения задач на
нахождение площади прямоугольника и прямоугольного треугольника.
– Развивать математическую речь, мышление,
внимание, познавательный интерес.
– Воспитывать самостоятельность,
аккуратность в работе.
Оборудование: компьютер,
интерактивная доска, технологические карты учащихся,
модели прямоугольников, карточки с формулами.
У каждого учащегося: ножницы, прямоугольник со сторонами: 4 см на 6 см,
линейка, фломастеры, клей
Структура
урока: 1)
Организационный момент
2) Актуализация знаний
3) Постановка проблемы
4)
« Открытие» детьми нового знания
5) Физкультминутка
6) Первичное закрепление
7) Самостоятельная работа с самопроверкой в классе
8) Рефлексия деятельности
Ход
урока
1. Организационный момент. ( кадр 1)
Улыбнитесь друг другу. Ваши улыбки
располагают к приятному общению. Спасибо! Сегодня на уроке мы будем работать в
группах, в каждой группе будет технолог, ученик который будет помогать и
контролировать выполнение технологического процесса.
2. Актуализация знаний.
Разминка: ( кадр 2)
1. Как называется фигура, у
которой противоположные стороны равны?
2. Какой угол называется
развернутым?
3. Что такое треугольник?
4. Какой треугольник называется
прямоугольным?
5. Чему равна сумма углов треугольника?
6. Дайте определение геометрии как
науки.
7. В каких единицах измеряется площадь?
8.Что обозначает слово « ЭВРИКА»
?
( « Эврика» – воскликнул
древнегреческий философ и ученый АРХИМЕД, когда нашел решении задачи.
Слово « Эврика» означает – нашёл, открытие).
3. Постановка проблемы. Геометрическая
площадка. ( кадр 3)
– Назовите какие фигуры вы видите?
– Оставлю только треугольник и
прямоугольник. Наш урок тесно будет связан с
понятием
« площадь», кто может предположить тему нашего урока? Формулу
нахождения площади прямоугольника мы знаем, значит, тема нашего урока: «
Нахождение площади треугольника». (прямоугольного) Поможет нам в этом
прямоугольник. Чему равна площадь прямоугольника?
– Работа в тетрадях. Запись числа,
классная работа. Каждая группа получает карточку с задачей на нахождение
площади прямоугольника.
Задачи
1 группа
–
Ширина прямоугольника 8 см, его длина в 2
раза больше. Найдите площадь прямоугольника.
2 группа –
Длина прямоугольника 12см, что в 2 раза больше
его ширины. Найдите площадь прямоугольника.
3 группа –
Длина прямоугольника 15см, его ширина
составляет 1/3 часть длины. Найдите площадь прямоугольника.
Проверка результатов. ( кадр 4)
4. « Открытие» учащимися новых
знаний. Нахождение формулы площади прямоугольного треугольника.
Сейчас мы выполним практическую работу для
того, чтобы найти формулу площади прямоугольного треугольника.
Мы будем использовать ножницы, не
забудьте, разрезаем лист, касаясь парты.
– Какая фигура лежит перед вами? ( прямоугольник)
Какими свойствами обладает эта фигура? ( все углы прямые, противоположные
стороны равны) Возьмите прямоугольник, проведите диагональ, разрежьте.
Какие 2 фигуры получились? (треугольники, прямоугольные). Равные ли эти
треугольники? (да) Что нужно сделать, чтобы найти площадь треугольника?
(площадь прямоугольника (ахв) : 2, запишите формулу в технологическую карту.
5. Физкультминутка
6. Первичное закрепление материала.
Работа в тетрадях. Начертите прямоугольный
треугольник со сторонами 3см и 6 см
 3см
3см
3см
6 см
Найдите его площадь по формуле!!! Что
нужно сделать для её нахождения? ( достроить прямоугольник), решение : 3
х 6 : 2= 9 см2
7. Нахождение площади треугольника и
прямоугольника ( связь с жизненными задачами и ситуациями)
У всех ребят макет горки. Нужно найти
площадь занимаемой ею поверхности на листе.
![]() 4см
4см

9см
Решение: 4 х 9 : 2 = 18см2
8. Рефлексия урока. Таблица
9. Домашнее задание
Технологическая карта
урока
![]() 1.
1.
– « нашёл, открыл» – АРХИМЕД
![]() 2. –
2. –
формула нахождения площади
прямоугольника![]() 3. –
3. –
формула нахождения площади
прямоугольного треугольника
4. Рефлексия
|
Было |
|
|
|
Было |
||
|
Теперь я |
Технологическая карта урока
![]() 1.
1.
– « нашёл, открыл» – АРХИМЕД
![]() 2. –
2. –
формула нахождения площади
прямоугольника
![]() 3. –
3. –
формула нахождения площади
прямоугольного треугольника
4. Рефлексия
|
Было |
|
|
|
Было |
||
|
Теперь я |

