Как найти область сходимости функциональных рядов

Лекция
4 1

4.1.
Функциональные ряды: основные понятия,
область сходимости 1

4.2.
Степенные ряды: основные понятия,
теорема Абеля 2

4.3.
Свойства степенных рядов 5

4.4.
Формула Тейлора 5

4.1. Функциональные ряды: основные понятия, область сходимости

Определение
1.
Ряд, члены которого являются функциями
одной
или нескольких независимых переменных,
определёнными
на некотором множестве,
будем называть функциональным
рядом.

Рассмотрим
функциональный ряд,
члены которого являются функциями одной
независимой переменной х.
Сумма первых n
членов ряда

является частичной суммой данного
функционального ряда. Общий член

есть функция от х,
определенная в некоторой области. Если
положить
,
получим числовой ряд
,
и если он сходится, т.е. существует предел
частичных сумм этого ряда,
где

− сумма числового ряда, тогда говорят,
что

− точка сходимости функционального
ряда
,
а если числовой ряд

расходится, то

называется точкой расходимости
функционального ряда.

Определение
2.
Областью
сходимости
функционального ряда

называется множество всех таких значений
х,
при которых функциональный ряд сходится.
Область сходимости, состоящая из всех
точек сходимости, обозначается
.
Отметим, что
.

Будем
говорить, что функциональный ряд сходится
в области
,
если для любого

он сходится как числовой, при этом его
сумма будет некоторой функцией

(это так называемая предельная
функция
последовательности
:
).

Как
находить область сходимости функционального
ряда
?
Можно использовать признак, аналогичный
признаку Даламбера. Для ряда

составляем

и рассматриваем предел при фиксированном
х:
.
Тогда

является решением неравенства

и решением уравнения

(берем только те решения уравнения, в
которых соответствующие числовые ряды
сходятся).

Пример
1.
Найти область сходимости ряда
.

Решение.
Обозначим
,
.
Составим и вычислим предел
,
тогда область сходимости определяется
неравенством

и уравнением
.
Исследуем дополнительно сходимость
исходного ряда в точках, являющимися
корнями уравнения: а) если
,
,
то получается расходящийся ряд
;
б) если
,
,
то ряд

сходится условно (по признаку Лейбница,
пример 1, лекция 3).
Таким образом,
область сходимости

ряда

имеет вид:
.

4.2. Степенные ряды: основные понятия, теорема Абеля

Рассмотрим
частный случай функционального ряда,
так называемый степенной
ряд:
,
где
.

Определение
3.
Степенным
рядом
называется функциональный ряд вида
,
где

−
постоянные числа, называемые
коэффициентами
ряда.

Степенной
ряд есть «бесконечный многочлен»,
расположенный по возрастающим степеням
.
(Любой числовой ряд

является частным случаем степенного
ряда при
.)

Рассмотрим
частный случай степенного ряда при
:
.
Выясним, какой вид имеет область
сходимости данного ряда
.

Теорема
1 (теорема Абеля).
1) Если степенной ряд
(*)
сходится в точке
,
то он абсолютно сходится при всяком х,
для которого справедливо неравенство
.
2)
Если же степенной ряд расходится при
,
то он расходится при всяком х,
для
которого
.

Доказательство.
1) По условию степенной ряд сходится в
точке
,
т е. сходится числовой ряд
(**),
а значит, по необходимому признаку
сходимости его общий член стремится к
0, т.е.
.
Следовательно, существует такое число
,
что все члены ряда ограничены этим
числом:
.

Рассмотрим
теперь любое х,
для которого
,
и составим ряд из абсолютных величин:
.
Запишем этот ряд в другом виде: т.к.
,
то
(***).

Из
неравенства

получаем
,
т.е. ряд
(****)
состоит из членов, которые больше
соответствующих членов ряда (***). Ряд

представляет собой сходящийся ряд
геометрической прогрессии с знаменателем
,
причем
,
т.к.
.
Следовательно, ряд (***) сходится при
.
Таким образом, степенной ряд

абсолютно сходится.

2)
Пусть теперь ряд

расходится при
,
иными словами, расходится числовой ряд
.
Докажем, что для любого х
()
ряд расходится. Доказательство ведется
от противного. Пусть при некотором
фиксированном

()
ряд сходится, тогда он сходится при всех

(см. первую часть данной теоремы), в
частности, при
,
что противоречит условию 2 теоремы.
Теорема доказана.

Следствие.
Теорема Абеля позволяет судить о
расположении точки сходимости степенного
ряда.
Если точка

является точкой сходимости степенного
ряда, то интервал

заполнен точками сходимости; если точкой
расходимости является точка
,
то бесконечные интервалы

заполнены точками расходимости (см.
рис. 1).

Рис.
1.

Можно
показать, что существует такое число
,
что при всех

степенной ряд

абсолютно сходится, а при

− расходится. Будем считать, что если
ряд сходится только в одной точке 0, то
,
а если ряд сходится при всех
,
то
.

Определение
4.
Интервалом
сходимости
степенного ряда

называется такой интервал
,
что при всех

этот ряд сходится и притом абсолютно,
а для всех х,
лежащих вне этого интервала, ряд
расходится. Число R
называется радиусом
сходимости
степенного ряда.

Замечание.
На концах интервала

вопрос о сходимости или расходимости
степенного ряда решается отдельно для
каждого конкретного ряда.

Покажем
один из способов определения интервала
и радиуса сходимости степенного ряда.

Рассмотрим
степенной ряд

и обозначим
.
Составим ряд из абсолютных величин его
членов:

и применим к нему признак
Даламбера.

Пусть
существует
,
где
.
По признаку Даламбера ряд сходится,
если
,
и расходится, если
.
Отсюда ряд сходится при
,
тогда интервал сходимости:
.
При

ряд расходится, т.к.
.
Используя обозначение
,
получим формулу для определения радиуса
сходимости степенного ряда:
,
где

− коэффициенты степенного ряда. Если
окажется, что предел
,
то полагаем
.

Для
определения интервала и радиуса
сходимости степенного ряда также можно
использовать радикальный признак Коши,
радиус сходимости ряда определяется
из соотношения
.

Определение
5.
Обобщенным
степенным рядом называется ряд вида
.
Его также называют рядом по степеням
.
Для такого ряда интервал сходимости
имеет вид:
,
где

− радиус сходимости.

Покажем,
как находится радиус сходимости для
обобщенного степенного ряда.

,
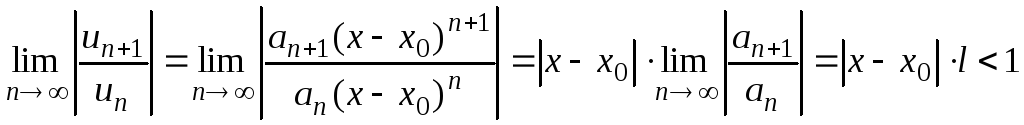т.е.
,
где
.

Если
,
то
,
;
если
,
то

и область сходимости
.

Пример
2.
Найти область сходимости ряда
.

Решение.
Обозначим
.
Составим предел
.
Решаем неравенство:
,

,
следовательно, интервал сходимости
имеет вид:
,
причем R
= 5. Дополнительно исследуем концы
интервала сходимости: а)
,
,
получаем ряд
,
который
расходится;
б)
,

,
получаем ряд
,
который сходится условно. Таким образом,
область сходимости:
,
.

Пример
3.
Ряд

расходится для всех
,
т.к.

при
,
радиус сходимости
.

Пример
4.
Ряд

сходится при всех
,
радиус сходимости
.

Пример 1:

Найти область сходимости ряда:

Решение от преподавателя:

Пример 2:

Найти область сходимости ряда:

Решение от преподавателя:

Пример 3:

Найти область сходимости ряда:

Решение от преподавателя:

Областью сходимости степенного ряда является интервал (-R;R), где: 

R – радиус сходимости. Вычислим его: 

x₁ = 2 – 1 = 1 
x₂ = 2 + 1 = 3 
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (1;3) 
Теперь проверим сходимость ряда на концах этого интервала. 
Пусть x = 1 
Получаем ряд: 

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. 
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется 

б) По второму признаку Лейбница предел ряда должен стремится к 0. 

Второе условие Лейбница выполняется. 
Ряд сходится, значит, x = 1 – точка сходимости. 
При x = 3 
получаем ряд: 

числовой знакоположительный ряд. 
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл: 

Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 3 – точка расходимости. 
Таким образом, данный степенной ряд является сходящимся при x [1;3) 

Пример 4:

Исследовать область сходимости функционального ряда:

Решение от преподавателя:

Пример 5:

Найти область сходимости степенного ряда:

Решение от преподавателя:

Пример 6:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом члены ряда не определены при х=-3/11, а если х≠-3/11, то

      

при любом х – ряд расходится всюду.

Пример 7:

Найти область сходимости ряда:

Решение от преподавателя:

Областью сходимости степенного ряда является интервал (-R;R), где: 

R – радиус сходимости. Вычислим его: 

x1 = -1 – 2 = -3 
x2 = -1 + 2 = 1 
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-3;1) 
Теперь проверим сходимость ряда на концах этого интервала. 
Пусть x = -3 
Получаем ряд: 

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. 
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется 
1<2<3 
б) По второму признаку Лейбница предел ряда должен стремится к 0. 

Второе условие Лейбница не выполняется. 
Ряд расходится, значит, x = -3 – точка расходимости. 
При x = 1 
получаем ряд: 

числовой знакоположительный ряд. 
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:

Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 1 – точка расходимости. 
Таким образом, данный степенной ряд является сходящимся при x (-3;1) 

Пример 8:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом

       

Следовательно, ряд сходится, если

       

и расходится, если

       

Если x=4/9, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).

Если x=2/3, то ряд принимает вид – такой ряд расходится (по признаку сравнения, т.к. и ряд  расходится (гармонический ряд)).

Окончательно получаем область сходимости исходного ряда: [4/9;2/3).

Пример 9:

Найдите множество абсолютной (условной) сходимости ряда:

Решение от преподавателя:

Пример 10:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом

       

Следовательно, ряд сходится, если

       

и расходится, если

       

Если x=-3/7, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).

Если x=-1/7, то ряд принимает вид  – такой ряд также сходится (обобщенный гармонический ряд с параметром p=11>1).

Окончательно получаем область сходимости исходного ряда: [-3/7;-1/7].

Пример 11:

Найдите множества абсолютной (условной) сходимости ряда

Решение от преподавателя:

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. 

 Проверяем выполнение признака Лейбница:

Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю, то ряд сходится.

Ряд знакочередующийся. Составим ряд из абсолютных величин членов данного ряда

По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется

Второе условие Лейбница выполняется. 

Данный ряд сходится, так как удовлетворяет условиям признака Лейбница для знакочередующихся рядов.

Следовательно, ряд условно сходящийся.

Следовательно, сходится условно и исходный ряд.

Область сходимости ряда:(-∞; +∞)

Пример 12:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид – обобщенный гармонический ряд с параметром .

Такой ряд сходится, если

       

Однако и поэтому  при любом х – ряд всюду расходится.

Пример 13:

Найти область сходимости ряда:

Решение от преподавателя:

По признаку Лейбница ряд расходится

Т. о., область сходимости имеет вид (-1; 1)

Пример 14:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом

     

Следовательно, ряд сходится, если

       

и расходится, если

       

Если x=1/6, то ряд принимает вид  – такой ряд расходится (не выполнено необходимое условие сходимости).

Если x=3/2, то ряд принимает вид  – такой ряд также расходится (также не выполнено необходимое условие сходимости).

Окончательно получаем область сходимости исходного ряда: .

Пример 15:

Найти область сходимости ряда:

Решение от преподавателя:

Функциональные и степенные ряды

Возьмем последовательность натуральных чисел n{n} и поставим каждому n{n} в соответствие функцию fn(x)f_n (x). Если функции fn(x)f_n (x) определены на некотором множестве x∈Ex in E, E⊂RE subset R, то на множестве EE определено выражение:

f1(x)+f2(x)+f3(x)+…+fn(x)+…,f_1 (x)+f_2 (x)+f_3 (x)+ ldots +f_n (x)+ ldots,

состоящее из функций fn(x)f_n (x), которое называется функциональным рядом.

В общем виде функциональный ряд записывается как:

∑n=1∞fn(x)sumlimits_{n=1}^{infty} f_n(x)

Примеры функциональных рядов

1+cos⁡x2!+cos⁡2×3!+cos⁡3×4!+…+cos⁡nx(n+1)!+…=∑n=1∞cos⁡nx(n+1)!1+frac{cos x}{2!}+frac{cos 2x}{3!}+frac{cos 3x} {4!} +ldots +frac{cos nx}{(n+1)!}+ldots=sumlimits_{n=1}^{infty}frac{cos nx} {(n+1)!}

ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}

Степенные ряды являются одним из видов функциональных рядов и в общем виде записываются как:

a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k

где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,

x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,

RR – радиус сходимости степенного ряда.

Примеры степенных рядов

12+2!(x−5)4+3!(x−5)28+…+(n+1)!(x−5)n2n+1+…=∑n=0∞(n+1)!(x−5)n2n+1frac{1}{2}+frac{2!(x-5)}{4}+frac{3!(x-5)^2}{8}+ldots +frac{(n+1)!(x-5)^n}{2^{n+1}}+ldots =sum limits_{n=0} ^{infty} frac{(n+1)!(x-5)^n}{2^{n+1}}

ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}

Сходимость степенных рядов

Сумму SnS_n первых nn членов степенного ряда называют nn–й частичной суммой:
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)nS_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n

Если при определенном значении x∈Ex in E существует конечный предел:

lim⁡n→∞Sn(x)=S(x)limlimits_{n to infty } S_n (x) = S (x)

то ряд называется сходящимся, а значение S(x)S(x) называют суммой ряда. Если сходится ряд, составленный из абсолютных величин его членов, то такой ряд называется абсолютно сходящимся.
Если степенной ряд сходится в точке x=x1x=x_1, то он сходится абсолютно и при:

∣x∣<∣x1∣|x|<|x_1 |

Если степенной ряд расходится в точке x=x2x=x_2, то он расходится и при:

∣x∣>∣x2∣|x|>|x_2 |

Интервалом сходимости степенного ряда является:

(x0−R,x0+R)(x_0-R,x_0+R)

Здесь RR – радиус сходимости степенного ряда. Степенной ряд расходится при:

∣x−x0∣>R|x-x_0 |>R

Для граничных точек интервала

∣x−x0∣>R|x-x_0 |>R

степенной ряд может, как сходится, так и расходится, для чего требуется дополнительное изучение.

Основные признаки сходимости

Приведем основные признаки, используемые для определения сходимости степенных рядов.

1-й признак сравнения

Пусть даны два ряда с положительными членами:

∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n

причем, un≤vnu_n le v_n для всех номеров, начиная с некоторого nn. Тогда:

1. Если ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n сходится, то сходится и ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n

2. Если ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n расходится, то расходится и ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n

2-й признак сравнения

Пусть даны два ряда с положительными членами:

∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n

и существует конечный и отличный от нуля предел:

lim⁡n→∞unvn≠0limlimits_{n to infty } dfrac{ u_n }{ v_n }ne 0

Тогда ряды

∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n

сходятся или расходятся одновременно.

Признак Лейбница для знакочередующихся рядов

При исследовании степенных рядов на сходимость часто используется признак Лейбница для знакочередующихся рядов. Ряд, содержащий как положительные, так и отрицательные члены, называют знакопеременным.

Ряд вида:

b1−b2+b3−b4+…+(−1)n+1bn+1+…=∑k=1∞(−1)k+1bk+1b_1-b_2+b_3-b_4+ ldots +{(-1)}^{n+1}b_{n+1}+ldots=sumlimits_{k=1} ^ {infty}{(-1)}^{k+1}b_{k+1},

когда любые два соседних члена имеют противоположные знаки, называется знакочередующимся.

Очевидно, каждый знакочередующийся ряд является знакопеременным.
В случае, когда выполняется два условия:

b1>b2>b3>b4>…>bn>…b_1>b_2>b_3>b_4> ldots >b_{n}> ldots, т.е когда члены ряда по модулю монотонно убывают

и

lim⁡n→∞an=0limlimits_{n to infty }{a_n}=0, т.е. когда общий член ряда стремится к нулю при n→∞n to infty, ряд сходится. Если, помимо этого, сходится ряд

b1+b2+b3+b4+…+bn+1+…=∑k=1∞bk+1b_1+b_2+b_3+b_4+ ldots + b_{n+1}+ldots=sumlimits_{k=1} ^ {infty} b_{k+1}

составленный из модулей исходного ряда, то такой ряд называют абсолютно сходящимся. Если признак Лейбница выполняется, но, при этом, ряд из абсолютных значений не сходится, то такой ряд называют условно сходящимся.

Признак Даламбера

Пусть дан ряд с положительными членами

∑n=1∞unsum limits_{n=1} ^{infty} u_n

и существует конечный предел

lim⁡n→∞un+1un=1limlimits_{n to infty } dfrac{ u_{n+1} }{ u_n }=1

Тогда, если l<1l<1, то данный ряд сходится; если же l>1l>1, то – расходится. Если l=1l=1 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.

Признак Коши

Пусть дан ряд с положительными членами

∑n=1∞unsum limits_{n=1} ^{infty} u_n

такой, что существует конечный предел

lim⁡n→∞unn=1limlimits_{n to infty } sqrt [n] { u_n }=1

Тогда, если l<1l<1, то ряд сходится. В случае, если l>1l>1, то ряд расходится. Если же l=1l=1, то вопрос о сходимости рядя требует дополнительного исследования.

Интегральный признак сходимости

Пусть дан ряд с положительными членами

∑n=1∞unsum limits_{n=1} ^{infty} u_n

для которого существует положительная, непрерывная и монотонно убывающая на промежутке [1,+∞)[1, +infty) функция f(x)f(x) такая, что f(n)=an,n=1,2,…f(n)=a_n, n=1,2, ldots

Тогда данный ряд и несобственный интеграл ∫0∞f(x)dxintlimits_0^infty f(x) dx сходятся или расходятся одновременно.

Примеры исследования степенных рядов

Пример 1

Найти область сходимости ряда

∑n=1∞(x−1)n+12n(n+1)sum limits_{n=1} ^{infty} dfrac{(x-1)^{n+1}}{2^n {(n+1)}}

Используем признак Даламбера. Учитывая, что

∣an+1an∣=∣(x−1)(n+1)+12n+1(n+1+1):(x−1)n+12n(n+1)∣=∣(x−1)n+2(x−1)n+1⋅2n2n+1⋅n+1n+2∣=∣x−1∣2⋅n+1n+2Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x-1)^{(n+1)+1}}{2^{n+1}(n+1+1)}: dfrac {(x-1)^{n+1}}{2^n(n+1)}Bigr|= Bigl| dfrac {(x-1)^{n+2}}{(x-1)^{n+1}}cdot dfrac {2^n}{2^{n+1}}cdot dfrac {n+1}{n+2}Bigr|=dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}

находим:

lim⁡n→∞∣an+1an∣=lim⁡n→∞(∣x−1∣2⋅n+1n+2)=∣x−1∣2⋅lim⁡n→∞1+1n1+2n=∣x−1∣2limlimits_{n to infty }Bigl| dfrac{a_{n+1}}{a_n} Bigr|= limlimits_{n to infty} left(dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}right)= dfrac {|x-1|}{2} cdot limlimits_{n to infty }dfrac{1+dfrac{1}{n}}{1+dfrac{2}{n}}=dfrac {|x-1|}{2}

Для определения требуемых значений xx решаем неравенство:

∣x−1∣2<1⇔−1<x−12<1⇔−2<x−1<2⇔−1<x<3dfrac{|x-1|}{2}<1 Leftrightarrow -1<dfrac{x-1}{2}<1 Leftrightarrow -2<x-1<2 Leftrightarrow -1<x<3

Таким образом, при x∈(−1,3)x in (-1,3) ряд сходится абсолютно, а при $ x notin (-1,3) $ ряд расходится. Это означает, что (−1,3)(-1,3) – интервал сходимости данного ряда.

Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−1x=-1 и x=3x=3.

При x=3x=3 получаем ряд

∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(3−1)n+12n(n+1)=∑n=1∞2n+12n(n+1)=∑n=1∞2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(3-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2}{n+1}

Применим 2-й признак сравнения и проведем сравнение этого ряда с гармоническим:

∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}

Получаем:

lim⁡n→∞(2n+1:1n)=lim⁡n→∞(2nn+1)=lim⁡n→∞(21+1n)=2≠0limlimits_{n to infty }left( dfrac{2}{n+1}:dfrac{1}{n}right)= limlimits_{n to infty }left( dfrac{2n}{n+1}right)=limlimits_{n to infty }left( dfrac{2}{1+dfrac{1}{n}}right)=2 ne 0

Как известно, гармонический ряд расходится. Так как полученный предел отличен от нуля, то ряды

∑n=1∞2n+1sum limits_{n=1} ^{infty} dfrac{2}{n+1} и ∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}

сходятся или расходятся одновременно. В данном случае, они расходятся, и, следовательно, исходный ряд при x=2x=2 расходится.

При x=−1x=-1 получаем ряд

∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(−1−1)n+12n(n+1)=∑n=1∞(−2)n+12n(n+1)=∑n=1∞(−1)n+1⋅(2)n+12n(n+1)=∑n=1∞(−1)n+1⋅2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(-1-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-1)^{n+1}cdot (2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{ (-1)^{n+1}cdot 2}{n+1}

Как было показано, этот ряд не является абсолютно сходящимся, так как ряд, составленный из абсолютных значений:

∑n=1∞∣(−1)n+1⋅2n+1∣=∑n=1∞2n+1sum limits_{n=1} ^{infty}Bigl| dfrac{ (-1)^{n+1}cdot 2}{n+1} Bigl|=sum limits_{n=1} ^{infty} dfrac {2}{n+1}

расходится.

Используя признак Лейбница, выясним сходимость данного знакочередующегося ряда. Очевидно, что неравенство:

bn>bn+1⇔2n+1>2(n+1)+1⇔2n+1>2n+2b_n>b_{n+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{(n+1)+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{n+2}

выполнено для всех n=1,2,3,…n=1,2,3, ldots

Выполняется и второе условие:

lim⁡n→∞an=lim⁡n→∞3n+2=0limlimits_{n to infty } a_n = limlimits_{n to infty } dfrac{3}{n+2}=0

Оба условия признака Лейбница выполнены. Это означает, что знакочередующийся ряд

∑n=1∞(−1)n+13n+2sum limits_{n=1} ^{infty} (-1)^{n+1} dfrac {3}{n+2}

сходится. Так как этот ряд не является абсолютно сходящимся, то знакочередующийся ряд сходится условно.
Таким образом, областью сходимости исходного ряда является промежуток:

x∈[−1,3)x in [-1,3)

Пример 2

Найти область сходимости ряда

∑n=2∞(x+3)nnln⁡3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}

Используем признак Даламбера. Учитывая, что

∣an+1an∣=∣(x+3)n+1(n+1)ln⁡3(n+1):(x+3)nnln⁡3n∣=∣(x+3)n+1(x+3)n⋅nn+1⋅ln⁡3nln⁡3(n+1)∣=∣x+3∣⋅nn+1⋅ln⁡3nln⁡3(n+1)Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(n+1)ln^3{(n+1)}}: dfrac {(x+3)^n}{nln^3{n}}Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(x+3)^n}cdot dfrac {n}{n+1}cdot dfrac {ln^3{n}}{ln^3{(n+1)}}Bigr|=|x+3| cdot dfrac{n}{n+1} cdot dfrac{ln^3{n}}{ln^3{(n+1)}}

находим c помощью правила Лопиталя:

lim⁡n→+∞∣an+1an∣=lim⁡n→+∞(∣x+3∣⋅nn+1⋅ln⁡3nln⁡3(n+1))=∣x+3∣⋅lim⁡n→∞11+1n⋅(lim⁡n→∞ln⁡nln⁡(n+1))3=∣x+3∣⋅lim⁡n→∞1n1n+1=∣x+3∣limlimits_{n to +infty } Bigl| dfrac {a_{n+1}}{a_n}Bigr| = limlimits_{n to +infty } left( |x+3| cdot dfrac {n}{n+1}cdot dfrac{ln^3{n}}{ln^3{(n+1)}} right)=|x+3| cdot limlimits_{n to infty } dfrac {1}{1+dfrac{1}{n}} cdot {left(limlimits_{n to infty } dfrac {ln{n}}{ln{(n+1)}}right)}^3= |x+3| cdot limlimits_{n to infty } dfrac{dfrac{1}{n}}{dfrac{1}{n+1}}=|x+3|

Для определения требуемых значений x решаем неравенство:

∣x+3∣<1⇔−1<x+3<1⇔−4<x<−2|x+3|<1 Leftrightarrow -1<x+3<1 Leftrightarrow -4<x<-2

Таким образом, при x∈(−4,−2)x in (-4,-2) ряд сходится абсолютно, а при x∉(−4,−2)x notin (-4,-2) ряд расходится. Это означает, что (−4,−2)(-4,-2) – интервал сходимости данного ряда.

Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−4x=-4 и x=−2x=-2.

При x=−4x=-4 получаем ряд

∑n=2∞(x+3)nnln⁡3n=∑n=2∞(−4+3)nnln⁡3n=∑n=2∞(−1)nnln⁡3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-4+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}

Воспользуемся интегральным признаком. Возьмем функцию:

f(x)=1xln⁡3xf(x)=dfrac{1}{x ln^3{x}}

Очевидно, что для любых x1>x2>2x_1>x_2>2:

1x2ln⁡3×2>1x1ln⁡3×1⇒f(x2)>f(x1)dfrac{1}{x_2 ln^3{x_2}}>dfrac{1}{x_1 ln^3{x_1}} quad Rightarrow quad f(x_2 )>f(x_1 )

Найдем неопределенный интеграл

∫dxxln⁡3x=∫d(ln⁡x)xln⁡3x=(−12)(ln⁡x)−2+C=−12ln⁡2x+Cint dfrac {dx}{x ln^3 {x}}=int dfrac {d(ln{x})}{x ln^3 {x}}=left( -dfrac{1}{2}right)(ln{x})^{-2}+C= -dfrac{1}{2 ln^2{x}}+C

Далее:

∫2∞f(x)dx=∫2∞dxxln⁡3x=lim⁡d→+∞∫2ddxxln⁡3x=lim⁡d→+∞(−12ln⁡2x∣2d)=lim⁡d→+∞(−12ln⁡2d+12ln⁡22)=12ln⁡22intlimits_2^infty f(x) dx=intlimits_2^infty dfrac {dx}{x ln^3 {x}}=limlimits_{d to +infty }intlimits_2^d dfrac{dx}{xln^3 {x}}=limlimits_{d to +infty }left( -dfrac{1}{2 ln^2{x}}Bigr|_2^d right) = limlimits_{d to +infty } left(-dfrac{1}{2 ln^2{d}}+dfrac{1}{2 ln^2{2}} right) = dfrac{1}{2 ln^2{2}}

Таким образом, несобственный интеграл сходится. Это значит, что ряд

∑n=2∞1nln⁡3nsum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}

также сходится, а ряд

∑n=2∞(−1)nnln⁡3nsum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}

сходится абсолютно.

При x=−2x=-2 получим ряд

∑n=2∞(x+3)nnln⁡3n=∑n=2∞(−2+3)nnln⁡3n=∑n=2∞1nln⁡3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-2+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}

Как было показано, этот ряд сходится абсолютно. Следовательно, область сходимости исходного ряда – промежуток [−4,−2][-4, -2].

Тест по теме “Степенные ряды”

Область сходимости функционального ряда