


2.5.2*. На покоящийся шар налетает шар такой же массы. Найдите угол разлета шаров после нецентрального упругого удара.
Решение.
Рассмотрим векторный треугольник импульсов тел (см. рис.)

$vec{p_0} = vec{p_1} + vec{p_2}$.
Воспользуемся теоремой косинусов
$p_1^2 + p_2^2 + 2p_1p_2cosalpha = p_0^2$. (1)
Здесь $p_0$ – модуль начального импульса шара до взаимодействия, $p_1, p_2$ – модули импульсов шаров после соударения, $alpha$ – угол разлета шаров.
Так как кинетическая энергия равна $E = frac{mv^2}{2}$, а импульс тела $p = mv$, то $E = frac{p^2}{2m}$. (2)
Воспользовавшись уравнение связи кинетической энергии и импульса тела (2) запишем закон сохранения кинетической энергии при упругом столкновении шаров:
$frac{p_0^2}{2m_1} = frac{p_1^2}{2m_1} + frac{p_2^2}{2m_2}$. (3)
По условию задачи $m_1 = m_2 = m$,
тогда уравнение (3) примет вид
$p_0^2 = p_1^2 + p_2^2$. (4)
Решая совместно уравнения (1) и (4) получаем
$2p_1p_2cosalpha = 0 Rightarrow cosalpha = 0 Rightarrow alpha = frac{pi}{2}$,
Ответ: угол разлета шаров после нецентрального упругого удара равен $frac{pi}{2}$
Столкновение двух
частиц называется упругим,
если оно не сопровождается изменением
их внутреннего состояния. Поэтому при
описании упругого соударения в законе
сохранения энергии внутреннюю энергию
тел можно не учитывать.
Выберем лабораторную
систему отсчета, где одна из частиц
обладает импульсом
![]()
,
а вторая покоится (![]()
)
и запишем законы сохранения энергии и
импульса:
![]()
![]()
.
(14.17)
Выразим
![]()
из закона сохранения импульса и подставим
в закон сохранения энергии:
![]()
Введя угол
![]()
между векторами
и
![]()
,
выразим
![]()
:
![]()
.
(14.18)
Полученный
результат можно интерпретировать
геометрически с помощью векторных
диаграмм, построенных для различных
соотношений масс сталкивающихся частиц:
![]()
;
![]()
и
![]()
.
Обозначим
![]()
,
(14.19)
где
![]()
приведенная
масса,
![]()
скорость
налетающей частицы (вторая частица
покоится
![]()
),
и проведем окружность
радиусом
![]()
.
Построим вектор
![]()
.
Из (14.19) следует
![]()
.
(14.20)
Направленный
отрезок
![]()
на диаграмме изображает импульс
налетающей частицы до рассеяния. При
этом точка
лежит внутри
(если
![]()
),
вне
(если
![]()
)
или на
окружности
(если
![]()
).


Из (14.20) видно,
что
![]()
складывается из отрезков
![]()
и
,
пропорциональных массам сталкивающихся
частиц,
![]()
и
![]()
,
соответственно.
В свою очередь
из (14.18) следует, что диаметр окружности,
равный
![]()
,
будучи умноженным
на
![]()
,
дает вектор
(см. рисунок:
![]()
как
угол, вписанный в окружность).
Из уравнения
(14.17) следует, что вектору
на диаграмме соответствует отрезок,
направленный из точки
в точку
.
Тогда
![]()
угол
отклонения 1-ой частицы (налетающей) от
её первоначального направления движения
после столкновения.
Угол
![]()
угол разлета
1 и 2-ой частиц после столкновения.
Возможные
направления рассеяния первой частицы
определяются вращением вектора
вокруг точки
.
При этом конец вектора
(точка
)
всегда должен лежать на окружности
радиусом
![]()
.
При
угол рассеяния
![]()
может принимать значения от
![]()
до
![]()
,
а угол разлета
![]()
изменяется от
![]()
до
.
При
очевидно, что существует максимальный
угол отклонения налетающей частицы
![]()
,
определяемый точкой касания вектором
![]()
окружности:
![]()
.
угол разлета
в этом случае изменяется от
до
.
Угол
![]()
соответствует центральному удару, или
лобовому столкновению частиц.
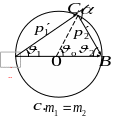
При
все точки начала и конца векторов лежат
на
окружности. Угол
![]()
,
т.е. разлет частиц происходит под
прямым углом. В
этом случае
![]()
.
Исключением
является лобовое столкновение, при
котором
![]()
.
Тот же
результат можно получить аналитически,
решая
совместно
уравнения законов сохранения энергии
и импульса:
![]()
,
.
Возводя в
квадрат второе уравнение и сравнивая
с первым, легко убедиться, что совместно
эти уравнения могут быть удовлетворены
лишь при указанных значениях углов.
На всех рисунках
центральный угол
представляет собой угол поворота первой
частицы в системе центра инерции. Из
рисунков видно, что углы
![]()
и
![]()
связаны с углом
соотношениями:
![]()
,
![]()
.
Модули скоростей
частиц после столкновения выражаются
через угол
и скорость налетающей частицы следующим
образом:
![]()
,
![]()
,
где
![]()
.
1.15. Рассеяние
частиц.
15.1. Рассеяние
частицы на силовом центре.
Формула
Резерфорда.
Рассмотрим
снова рассеяние частицы на силовом
центре.
Если на налетающую
частицу действуют силы отталкивания,
то, как мы установили в § 13, её движение
всегда инфинитно, а траектория частицы
– гипербола.
Для
рассмотрения задачи введем



![]()
![]()
прицельное
расстояние – длина


перпендикуляра,
опущенного из
рассеивающего
центра на направление
касательной
к траектории (асимптоту гиперболы)
находящейся
на бесконечно большом удалении

от
центра частицы,


![]()

![]()
угол
рассеяния частицы,


![]()
![]()
масса
частицы,

![]()
скорость
налетающей частицы на
бесконечно
большом удалении от центра.
Угол
определяет наклон асимптот гиперболы,
по которой движется рассеиваемая частица
(см. рисунок и уравнение (13.17)), к оси
и связан с углом рассеяния
очевидным
соотношением
![]()
(15.1)
Значение угла
может быть найдено из уравнения (13.17),
если положить, что частица находится
на бесконечно большом удалении от
рассеивающего центра (![]()
).
В этом случае уравнение (13.17) приводится
к виду:
![]()
и
![]()
.
(15.1а)
Тогда, с учетом
(15.1) и (15.1а),
![]()
.
Учитывая (13.5),
получаем
![]()
.
(15.2)
На бесконечно
большом расстоянии от рассеивающего
центра (![]()
,
![]()
),
полная энергия и момент импульса частицы
равны
![]()
.
(15.3)
Подставляя эти
величины в выражение (15.2), получаем
формулу, связывающую угол рассеяния
с прицельным параметром
:
![]()
.
(15.4)
Заметим, что
при движении частицы в поле притяжения
(![]()
)
связь между углом рассеяния и прицельным
параметром получается точно такой же,
т.е. также выражается формулой (15.4).
Задача о
рассеянии на силовом центре имеет важное
практическое значение. Однако, формулу
(15.4) не удается непосредственно
использовать для описания результатов
эксперимента, т.к. она написана для
определенного прицельного параметра
и определяет индивидуальное отклонение
частицы. В эксперименте же мы имеем дело
не с отдельной частицей, а наблюдаем
рассеяние целого пучка одинаковых
частиц, падающих на рассеивающий центр
с одинаковыми
скоростями
![]()
,
но с разными
значениями прицельного параметра
.
Следовательно, и рассеиваются частицы
под разными углами
.
Поэтому в физике
вводится другая, очень важная,
характеристика процесса рассеяния –
сечение
или эффективное
сечение.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи на непрямой упругий удар практически не рассматриваются в курсе школьной физики. В то же время такие задачи встречаются в заданиях олимпиад различного уровня, в том числе вузовских олимпиад, включаемых в перечень Министерства образования, призеры которых имеют право засчитывать свой результат как высший балл по ЕГЭ. В связи с этим представляется целесообразным рассматривать задачи на непрямой упругий удар на школьном факультативе по физике, что в течение ряда лет и делается в Лицее научно-инженерного профиля города Королева. Кроме того, на факультативе имеется возможность систематизировано изложить подходы к решению данных задач, разбросанных по различным задачникам и учебным пособиям. Представляется, что данная статья может быть полезной как для учителей физики школ с углубленным изучением предмета, так и для абитуриентов.
Задача 1. На покоящийся шар налетает шар такой же массы. Найдите угол разлета шаров после нецентрального упругого удара. [1,2]
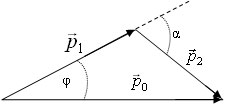 Решение. Используя теорему косинусов для треугольника импульсов, представленного на рисунке, запишем закон сохранения импульса в виде:
Решение. Используя теорему косинусов для треугольника импульсов, представленного на рисунке, запишем закон сохранения импульса в виде:
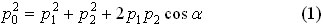
где p0 – модуль импульс налетающего шара до удара, p1 – модуль импульса налетающего шара после удара, p2 – модуль импульса покоящегося шара после удара, α – угол разлета шаров. Закон сохранения энергии запишем также через импульсы шаров:
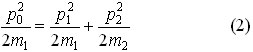
Если m1 = m2, то из уравнений (1) и (2) следует, что cosα = 0 и α = π/2.
Ответ: α = π/2.
Задача 2. Тяжелая частица массы m1 сталкивается с покоящейся легкой частицей массы m2. На какой наибольший угол может отклониться тяжелая частица в результате упругого удара? [1]
Решение. Запишем закон сохранения импульса в виде (рисунок к задаче 1):
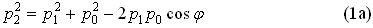
где p0 – модуль импульса налетающей частицы до удара, p1 – модуль импульса налетающей частицы после удара, p2 – модуль импульса покоящейся частицы после удара, φ – искомый угол отклонения налетающей частицы. Закон сохранения энергии запишем также через импульсы частиц:

Из второго уравнения выразим

И подставим в (1а). Тогда
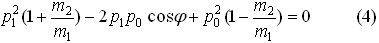
Детерминант уравнения (4) должен быть больше или равен нуля:
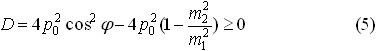
Отсюда получаем ограничение на угол отклонения налетающей частицы:

Максимальный угол отклонения имеет место, когда детерминант равен нулю. Для этого угла 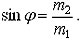
Ответ: 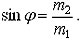
Важным обстоятельством при упругом нецентральном ударе является то, что ввиду отсутствия сил трения, силы взаимодействия соударяющихся тел направлены по нормали к поверхности их соприкосновения.
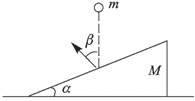
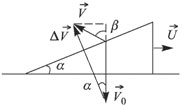
Задача 3. На горизонтальном столе покоится клин массой М = 4 кг. Сверху на клин падает шарик массой m = 1 кг. Определить угол при основании клина α, если известно, что после упругого удара о клин шарик отскочил под углом β = 45° к вертикали. Трением пренебречь.[3]
Решение. Поскольку смещения шарика и клина за время соударения пренебрежимо малы (удар, как обычно, считается мгновенным), а также из-за отсутствия трения, силы взаимодействия шарика и клина направлены по нормали к наклонной плоскости. Следовательно, изменение импульса шарика при ударе также будет направлено по нормали к наклонной плоскости клина (смотри рисунок, где через V0 и V обозначены скорости шарика до и после удара соответственно, U — скорость клина после удара). Из рисунка видно, что
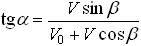
Используя закон сохранения импульса в проекции на горизонтальное направление и закон сохранения кинетической энергии при упругом ударе, получаем следующие равенства:
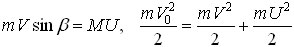
Отсюда
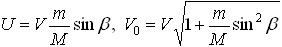
Объединяя записанные выражения, получаем ответ.
Ответ:
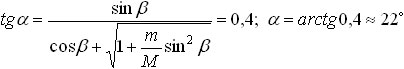
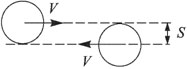
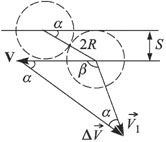
Задача 4. Два одинаковых шара радиусами R летят навстречу друг другу с одинаковыми скоростями как показано на рисунке. Расстояние между линиями движения центров шаров S = R. На какой угол β повернется вектор скорости каждого из шаров после удара? Удар считать упругим, шары – идеально гладкими. [3]
Решение. Обозначим через 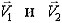 скорости шаров после удара. Используя законы сохранения импульса и энергии
скорости шаров после удара. Используя законы сохранения импульса и энергии
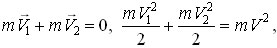
находим, что V1 = V2 = V, т.е. модули скоростей шаров после удара останутся прежними. Из предположения о кратковременности удара вытекает, что приращение импульса каждого из шаров направлено по линии, соединяющей центры шаров в момент удара. Из рисунка видно, что
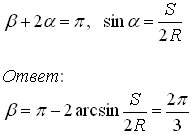
Задачи для самостоятельного решения.
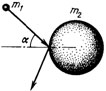 1. [1] Частица массы m1 налетает на шар массы m2. Направление ее движения составляет угол α с нормалью к поверхности шара. Под каким углом к этой нормали отскочит от шара частица, если шар сначала покоился, а удар упругий?
1. [1] Частица массы m1 налетает на шар массы m2. Направление ее движения составляет угол α с нормалью к поверхности шара. Под каким углом к этой нормали отскочит от шара частица, если шар сначала покоился, а удар упругий?
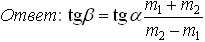
2. [1] При упругом столкновении налетающей частицы с покоящейся первая полетела под углом α к направлению первоначального движения, а вторая – под углом β. Найдите отношение масс этих частиц.
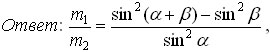 m1 – масса налетающей частицы.
m1 – масса налетающей частицы.
3. [1] Частица массы m1 налетела со скоростью v на неподвижную частицу массы m2, которая после упругого удара полетела под углом α к первоначальному направлению движения налетающей частицы. Определите скорость частицы массы m2 после удара.
![]()
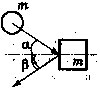
4. [2] По центру неподвижного кубика, лежащего на гладкой горизонтальной поверхности, наносят удар шариком той же массы, так, что начальная скорость шарика v направлена под углом α к оси симметрии кубика. Определить скорость v1 и v2 шарика и кубика после удара. Под каким углом β к оси симметрии кубика полетит шарик после удара?
Ответ: v1 = v sinα; v2 = v cosα; β = π/2
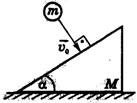 5. [2] Шариком массой m наносят удар по клину. Масса клина M, угол при основании α. Удар абсолютно упругий. Трением можно пренебречь. Определить скорость шарика v и скорость клина u после удара, если скорость шарика перед ударом равна v0 и направлена: а) перпендикулярно поверхности клина; б) по вертикали; в) по горизонтали.
5. [2] Шариком массой m наносят удар по клину. Масса клина M, угол при основании α. Удар абсолютно упругий. Трением можно пренебречь. Определить скорость шарика v и скорость клина u после удара, если скорость шарика перед ударом равна v0 и направлена: а) перпендикулярно поверхности клина; б) по вертикали; в) по горизонтали.
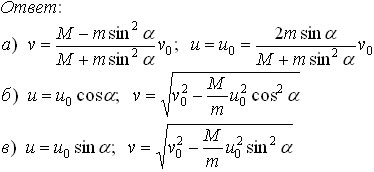
Литература:
- Задачи по физике: Учеб. пособие/ И.И. Воробьев, П.И. Зубков, Г.А. Кутузова и др.; Под ред. О.Я. Савченко. − 2-е изд., перераб. − М.: Наука. Гл. ред. физ.-мат. лит. 1988. – 416 с.
- Дмитриев С.Н., Васюков В.И., Струков Ю.А. Физика: Сборник задач для поступающих в вузы. Изд. 7-е, доп. М: Ориентир. 2005. – 312 с.
- Драбович К.Н., Макаров В.А., Чесноков С.С. Физика. Практический курс для поступающих в университеты. – М.: ФИЗМАТЛИТ, 2006. – 544 с. – ISBN 5-9221-0652-Х.
Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.
Применение такого вида задач используется в технике и физике элементарных частиц.
Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.
При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.
Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.
Абсолютно неупругий удар. Скорость
Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.
Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.
Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1.21.1, m – горизонтально летящая пуля с v→ скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.
Если скорость ящика с пулей обозначить как u→, тогда, используя формулу сохранения импульса, получаем:
mv=(M+m)u; u=mM+mv.
Когда пуля застревает в песке, то механическая энергия теряется:
∆E=mv22-(M+m)u22=MM+m·mv22.
M (M + m) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда
∆EE0=MM+m=11+mM.
Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.
Когда m << М ∆EE0→12, тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆EE0→0, только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим (m>>М), отношение принимает вид ∆EE0→0.
Расчет движения маятника производится по закону сохранения механической энергии. Получаем
(M+m)u22=(M+m)gh; u2=2gh.
В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что
v=M+mm2gh.
При известной высоте h возможно определение скорости пули v.
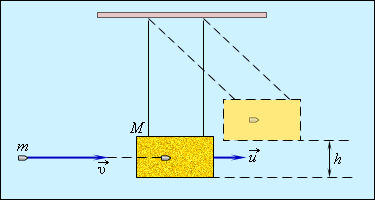
Рисунок 1.21.1. Баллистический маятник.
Абсолютно упругий удар
Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.
Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1.21.2.
Центральный удар – это соударение, когда скорости шаров направлены по линии центра.
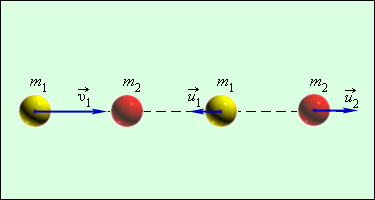
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров.
Встречаются случаи, когда массы m1 и m2 не равны. Тогда, используя закон сохранения механической энергии, получаем
m1v122=m1v122+m2v222.
За v1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v2=0 скорость второго шара, u1 и u2 – скорости после столкновения.
Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:
m1v1=m1u1+m2u2.
Полученная система из двух уравнений позволяет найти неизвестные скорости u1 и u2 шаров после столкновения.
u1=m1-m2v1m1+m2; u2=2m1v1m1+m2.
Если массы равны, то есть, тогда происходит остановка первого шара (u1=0), а второй продолжает движение u2=v1. происходит обмен скоростями и импульсами.
При наличии нулевой скорости второго шара (v2≠0), задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v1’=v1–v2. После определения скорости шаров v1 и v2 производится переход к «неподвижной» системе.
С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.
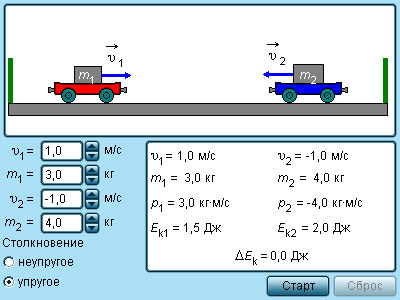
Рисунок 1.21.3. Модель упругие и неупругие соударения.
При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.
Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1.21.4.
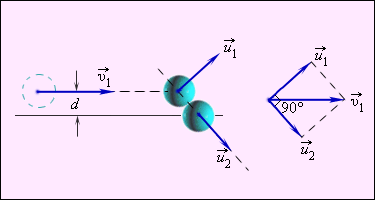
Рисунок 1.21.4. Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.
Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v1 и v2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d, изображенное на рисунке 1.21.4.
Предельное расстояние
Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v1→ летящего шара.
При одинаковых массах шаров векторы v1→ и v2→ имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m1=m2=m, тогда определение примет вид
v1→=u1→+u2→; v12=u12+u22.
Первое равенство значит, что векторы v1→, u1→, u2→ образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u1→ и u2→, равняется 90 градусов.
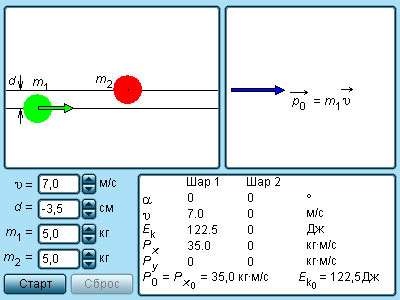
Рисунок 1.21.5. Модель соударения упругих шаров
Упругое соударение
Соударение — это столкновение двух тел.
При соприкосновении тела обмениваются энергией и импульсом.
После соударения они двигаются со скоростями, которые отличаются по направлению и величине от их скоростей до столкновения.
При лобовом центральном соударении центры масс обоих тел двигаются вдоль одной линии.
Силы взаимодействия, возникающие при соударении, параллельны направлению движения.
Если применить к такой системе двух тел закон сохранения импульса, то полный импульс системы будет равен алгебраической сумме импульсов обоих тел.
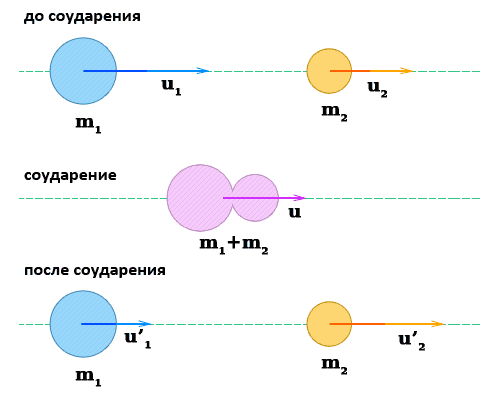
Упругое соударение
При упругом соударении на протяжении кратковременного соприкосновения тела двигаются с общей скоростью,
затем они разлетаются и продолжают двигаться с разными скоростями.
Если
| m1 | масса первого тела, | кг |
|---|---|---|
| m2 | масса второго тела, | кг |
| u1 | скорость первого тела до соударения, | метр/секунда |
| u2 | масса второго тела до соударения, | метр/секунда |
| u`1 | скорость первого тела после соударения, | метр/секунда |
| u`2 | масса второго тела после соударения, | метр/секунда |
то из закона сохранения импульса следует
[ m_1 u_1 + m_2 u_2 = m_1 u`_1 + m_2 u`_2 ]
или
[ m_1 (u_1 – u`_1) = m_2 (u`_2 – u_2) ]
Из закона сохранения энергии получаем
[ frac{m_1 u_1 ^2}{2} + frac{m_2 u_2 ^2}{2} = frac{m_1 u`_1 ^2}{2} + frac{m_2 u`_2 ^2}{2} ]
или
[ m_1 (u_1 ^2 – u`_1 ^2) = m_2 (u`_2 ^2 – u_2 ^2) ]
подставив формулу разность квадратов получим
[ m_1 (u_1 – u`_1)(u_1 + u`_1) = m_2 (u`_2 – u_2)(u`_2 + u_2) ]
воспользовавшись законом сохранения импульса, находим
[ u_1 + u`_1 = u`_2 + u_2 ]
Сумма скоростей до и после соударения одинакова при любом соударении тел.
Из формулы (6) следует
[ u`_2 = u`_1 + u_1 – u_2 ]
[ u`_1 = u`_2 + u_2 – u_1 ]
Подставив эти выражения в видоизмененный закон сохранения импульса, получим
[ m_1 (u_1 – u`_1) = m_2 (u`_1 + u_1 – u_2 – u`_2) ]
[ m_1 (u_1 – u_2 – u`_2 + u_1) = m_2 (u`_2 – u_2) ]
откуда, разрешив относительно u`1 и u`2 найдем
[ u`_1 = frac{ (m_1 – m_2) u_1 + 2 m_2 u_2 }{ m_1 + m_2 } ]
[ u`_2 = frac{ (m_2 – m_1) u_2 + 2 m_1 u_1 }{ m_1 + m_2 } ]
Упругое соударение, вычислить скорости тел после упругого соударения
Упругое соударение |
стр. 477 |
|---|
