Вытекающая за единицу времени от куда-либо жидкость, будет иметь импульс
mv=Qv=ρv2S=2ρghSmv=Qv=rho {{v}^{2}}S=2rho ghS
По закону сохранения импульса должен измениться импульс сосуда с жидкостью. Это приведет к тому, что на сосуд со стороны жидкости будет действовать сила давления в направлении, противоположном направлению скорости истечения жидкости:
FR=2ρghS{{F}_{R}}=2rho ghS
Силу FRF_R называют силой реакции вытекающей жидкости, или реактивной силой.
Cила возникающая при истекании рабочего тела и действующая на сосуд в направлении, противоположном направлению скорости истечения.
Из формулы FRF_R следует, что сила реакции вытекающей жидкости вдвое больше силы давления на пробку, которая бы закрывала отверстие. Это объясняется тем, что при истечении жидкости через отверстие происходит перераспределение давления внутри жидкости в сосуде. При этом напротив отверстия давление на стенки сосуда оказывается большим, чем вблизи отверстия, где скорость движения жидкости близка к скорости истечения через отверстие.
Реактивная сила в винтовых движителях
На действии реактивной силы основано применение винтов на самолетах и кораблях для создания силы тяги. При быстром вращении винта самолета воздух отталкивается назад к хвосту лопастями самолета, меняя свой импульс. В свою очередь, воздух действует на винт и на связанный с ним корпус самолета с силой, которая придает ему импульс.
Действием реактивной силы на винт вертолета со стороны воздуха объясняется возникновение подъемной силы.
При вращении вокруг вертикальной оси винт вертолета предоставляет прилегающим к нему слоям воздуха импульс, направленный вниз. Эти массы воздуха, в свою очередь, действуют на винт и соединенный с ним корпус вертолета с силой реакции, направлена вверх Если эта сила равна весу вертолета или превышает ее, то вертолет летит в воздухе или поднимается вверх.
Реактивная сила в изогнутой трубе
Реактивная сила реакции возникает также и тогда, когда скорость течения постоянна по величине, но меняется по направлению. Так, при стационарном потоке жидкости по трубе постоянного сечения, которая согнута под некоторым углом (рис. 1), жидкость к изгибу трубы за единицу времени переносит импульс
K1→=ρv1Sv1→overrightarrow{{{K}_{1}}}=rho {{v}_{1}}Soverrightarrow{{{v}_{1}}}
После сгиба трубы за единицу времени подвижной жидкостью переносится импульс
K2→=ρv1Sv2→overrightarrow{{{K}_{2}}}=rho {{v}_{1}}Soverrightarrow{{{v}_{2}}}
Поскольку труба устойчивого сечения, то v1=v2v_1 = v_2. Изменение импульса движущейся жидкости за единицу времени будет равнятся действующей силе, которая обусловила это изменение, то есть
F→=ΔK→=K1→−K2→=ρvS(v2→−v1→)overrightarrow{F}=Delta overrightarrow{K}=overrightarrow{{{K}_{1}}}-overrightarrow{{{K}_{2}}}=rho vS(overrightarrow{{{v}_{2}}}-overrightarrow{{{v}_{1}}})
Рис. 1
Сила FF обусловлена действием трубы на движущуюся жидкость. По третьему закону Ньютона, со стороны жидкости на трубу будет действовать сила реакции F1=−FF_1 = -F.
На реактивной силе такого типа основывается действие турбин.
В турбинах через изогнутые трубы (сопла), закрепленных на общей оси вращения в плоскости, перпендикулярной оси, пропускают жидкость или газ в направлении от их приосевых концов к внешним. При движении жидкости или газа по изогнутым форсунках возникает сила реакции, момент которой и приводит турбину во вращательное движение. Газовые турбины широко используются в авиации (турбовинтовые и турбореактивные двигатели).
Гидравлические турбины используются в основном в стационарных условиях для приведения в движение генераторов электрического тока. Благодаря высокой экономичности, компактности, надежности и возможности достижения больших мощностей турбины практически вытеснили поршневые паровые машины в современной энергетике.
Тест по теме «Реактивная сила»
Асламазов Л. Закон сохранения импульса. Реактивная сила // Квант. — 1979. — № 10. — С. 49-53.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Одна из возможных формулировок второго закона Ньютона утверждает, что изменение импульса (количества движения) механической системы равно импульсу внешних сил:
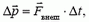 (1)
(1)
где 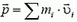 — полный импульс системы,
— полный импульс системы, 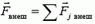 — векторная сумма внешних сил, действующих на систему.
— векторная сумма внешних сил, действующих на систему.
Для замкнутой (изолированной) системы 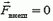 и, следовательно,
и, следовательно,
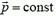 (2)
(2)
— суммарный импульс системы есть величина постоянная. Это — закон сохранения импульса. Он позволяет найти конечные скорости взаимодействующих тел, образующих изолированную систему, не вдаваясь в детали взаимодействия.
Следует помнить, что уравнение (2) — векторное, и ответ может существенно зависеть от направления начальных скоростей тел.
Задача 1. По гладкой горизонтальной поверхности движется тележка массой M со скоростью 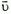 (рис. 1). В нее стреляют из ружья, причем пуля массой m, летящая со скоростью
(рис. 1). В нее стреляют из ружья, причем пуля массой m, летящая со скоростью 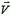 , застревает в тележке. Какой станет скорость тележки после попадания в нее пули в случае: а) когда скорость пули направлена горизонтально, так же как скорость тележки, б) когда скорость пули направлена вертикально вниз?
, застревает в тележке. Какой станет скорость тележки после попадания в нее пули в случае: а) когда скорость пули направлена горизонтально, так же как скорость тележки, б) когда скорость пули направлена вертикально вниз?
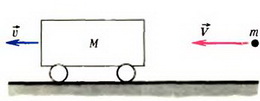
а
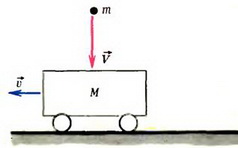
б
Рис. 1
Воспользуемся законом сохранения импульса в проекции на направление первоначального движения тележки.
В случае а) получим:
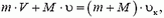
откуда конечная скорость тележки
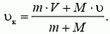
Как видно, после попадания пули скорость тележки увеличилась.
В случае б) начальный импульс пули не дает проекции на горизонтальное направление, следовательно,
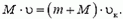
Отсюда
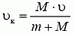
— конечная скорость тележки уменьшилась.
Векторный характер закона сохранения импульса в ряде случаев приводит к неожиданным результатам.
Задача 2. Две одинаковые лодки, в которых находятся два одинаковых спортсмена, движутся по инерции (почти без трения) с одинаковыми скоростями параллельно друг другу пи поверхности озера (рис. 2). Начинает идти дождь. Спортсмен, сидящий в первой лодке, вычерпывает воду из лодки и выливает ее в сторону, а спортсмен во второй лодке спит. Какая из лодок быстрее пройдет одно и то же расстояние? В направлении, перпендикулярном к килю, лодки двигаться не могут.

Рис. 2
Как следует из решения задачи 1, при попадании в лодку воды массой m, начальная скорость которой направлена вертикально (дождь!), скорость лодки уменьшается и становится равной по модулю
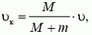
где M — масса лодки, υ — модуль ее начальной скорости. Отсюда видно, что изменение скорости лодки
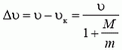
тем меньше, чем больше отношение M/m. Поскольку масса дождя, попавшего в лодки, одна и та же, уменьшение скорости будет большим у той лодки, из которой спортсмен вычерпывает воду. Заметим также, что при выбросе воды в сторону скорость лодки не меняется, так как киль не дает ей двигаться в перпендикулярном направлении.
Таким образом, вторая лодка, в которой спортсмен спит, быстрее пройдет заданное расстояние и первой окажется у финиша.
Если система незамкнутая, изменение ее импульса всегда связано с действием внешних сил.
Задача 3. Пучок частиц, имеющих скорость 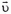 и массу m, падает на пластину площадью S; при этом он частично поглощается, а частично упруго отражается (рис. 3). Какая сила действует на пластину, если концентрация частиц в пучке равна n, а доля поглощенных частиц α? Рассмотреть также случай, когда пластина сама движется со скоростью
и массу m, падает на пластину площадью S; при этом он частично поглощается, а частично упруго отражается (рис. 3). Какая сила действует на пластину, если концентрация частиц в пучке равна n, а доля поглощенных частиц α? Рассмотреть также случай, когда пластина сама движется со скоростью 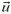 : а) навстречу пучку, б) в том же направлении, что и налетающие частицы.
: а) навстречу пучку, б) в том же направлении, что и налетающие частицы.
Рис. 3.
Вначале рассмотрим случай неподвижной пластины. Каждая частица, поглощаемая пластиной, передает ей импульс 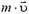 . За время Δt до пластины долетают те частицы, которые находятся в объеме
. За время Δt до пластины долетают те частицы, которые находятся в объеме 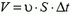 (υ — модуль скорости частиц), то есть
(υ — модуль скорости частиц), то есть
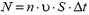 частиц.
частиц.
Из них поглощается
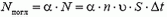 частиц.
частиц.
и, следовательно, пластине передается импульс
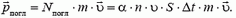
В соответствии с формулой (1) на пластину действует сила 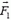 , модуль которой равен
, модуль которой равен
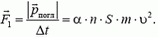
При упругом отражении частицы модуль ее скорости, а значит, и модуль импульса частицы не меняются, однако направление вектора импульса меняется на противоположное. Поэтому изменение импульса частицы

Число частиц, отраженных от пластины за время Δt, равно
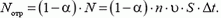
Следовательно, при отражении частиц пластине передается импульс
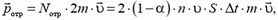
что приводит к появлению силы 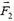 , действующей на пластину. Ее модуль
, действующей на пластину. Ее модуль
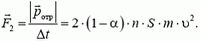
Полная сила, действующая на пластину, равна по модулю
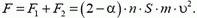 (3)
(3)
Для того чтобы найти силу, действующую на движущуюся пластину, перейдем в систему координат, движущуюся со скоростью 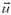 . В этой системе скорость частиц увеличивается при движении пластины навстречу пучку:
. В этой системе скорость частиц увеличивается при движении пластины навстречу пучку: 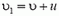 и уменьшается при движении пластины в обратном направлении:
и уменьшается при движении пластины в обратном направлении: 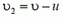 (здесь υ, u, υ1 и υ2 — модули соответствующих скоростей). В остальном все остается таким же, как в случае неподвижной пластины. Следовательно, сила, действующая на пластину, находится по формуле (3), в которой следует υ заменить на υ1 или υ2:
(здесь υ, u, υ1 и υ2 — модули соответствующих скоростей). В остальном все остается таким же, как в случае неподвижной пластины. Следовательно, сила, действующая на пластину, находится по формуле (3), в которой следует υ заменить на υ1 или υ2:
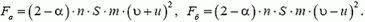
В первом случае сила возрастает, во втором—уменьшается.
Особый интерес представляет случай возникновения так называемой реактивной силы 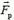 , когда из системы с некоторой скоростью
, когда из системы с некоторой скоростью 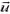 выбрасывается часть Δm ее массы. В соответствии с формулой (2)
выбрасывается часть Δm ее массы. В соответствии с формулой (2)
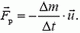
Величину 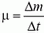 , равную массе вещества, выбрасываемого за единицу времени, называют обычно расходом вещества.
, равную массе вещества, выбрасываемого за единицу времени, называют обычно расходом вещества.
Задача 4. В воздушном шарике, удерживаемом нитью, в том месте, где крепится нить, появилось отверстие сечением S (рис. 4). Как изменилось натяжение нити, если скорость истечения газа из шарика равна υ? Плотность газа ρ.
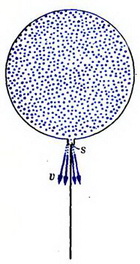
Рис. 4.
Изменение 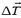 натяжения нити равно по модулю реактивной силе, возникающей при вытекании газа из шарика (изменением выталкивающей силы и веса шарика в начальный момент, пока изменение объема шарика мало, можно пренебречь). За время Δt вытекает объем газа
натяжения нити равно по модулю реактивной силе, возникающей при вытекании газа из шарика (изменением выталкивающей силы и веса шарика в начальный момент, пока изменение объема шарика мало, можно пренебречь). За время Δt вытекает объем газа 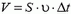 , его масса
, его масса 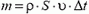 . Следовательно, расход газа
. Следовательно, расход газа 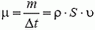 и реактивная сила
и реактивная сила
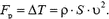
Задача 5. Закрепленный воздушный вентилятор потребляет мощность N, его КПД равен η. Какая реактивная сила действует на вентилятор во время его работы? Диаметр лопастей вентилятора D, плотность воздуха ρ.
Обозначим через υ модуль скорости воздушного потока, создаваемого вентилятором. Тогда масса воздуха, приводимого в движение за время Δt, равна 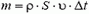 , где
, где 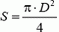 — площадь сечения воздушного потока (рис. 5), а его кинетическая энергия —
— площадь сечения воздушного потока (рис. 5), а его кинетическая энергия —
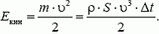
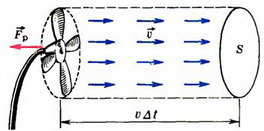
Рис. 5
Следовательно, мощность вентилятора
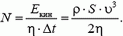
Отсюда можно найти скорость потока воздуха:
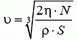
и реактивную силу, действующую на вентилятор:
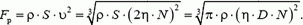
Если механическая система движется с постоянной скоростью, так что изменение ее импульса происходит только вследствие выброса массы, для нахождения реактивной силы удобнее перейти в систему отсчета, связанную с движущимся телом.
Задача 6. На горизонтальной поверхности стоит сосуд с водой, закрытый легким подвижным поршнем, на котором лежит тяжелый груз массой M (рис. 6). У дна сосуда имеется отверстие сечением s, через которое вытекает вода. Какова установившаяся скорость движения сосуда, если сила трения между сосудом и поверхностью пропорциональна скорости сосуда, причем коэффициент пропорциональности равен k. Площадь сечения сосуда S.
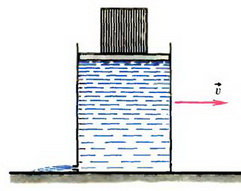
Рис. 6
Искомая скорость (точнее, ее модуль υ) определяется из условия равенства модулей силы трения и реактивной силы, действующей на сосуд:
Fтр = k·υ = Fp.
Чтобы найти реактивную силу, перейдем в систему отсчета, движущуюся со скоростью 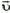 . В этом системе сосуд неподвижен. Для определения модуля u скорости истечения воды воспользуемся законом сохранения энергии.
. В этом системе сосуд неподвижен. Для определения модуля u скорости истечения воды воспользуемся законом сохранения энергии.
При вытекании небольшого количества воды массой Δm изменение кинетической энергии воды 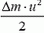 равно изменению потенциальной энергии воды Δm·g·h (h — высота уровня воды в сосуде) и груза M·g·Δh (Δh — перемещение груза, равное изменению уровня воды):
равно изменению потенциальной энергии воды Δm·g·h (h — высота уровня воды в сосуде) и груза M·g·Δh (Δh — перемещение груза, равное изменению уровня воды):
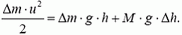
Изменение уровня воды в сосуде Δh выражается через массу Δm вытекающей воды: 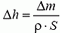 . Подставляя это выражение в закон сохранения энергии и сокращая на Δm, для скорости u истечения воды получим
. Подставляя это выражение в закон сохранения энергии и сокращая на Δm, для скорости u истечения воды получим
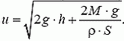
Если груз достаточно тяжелый (то есть его масса много больше массы воды в сосуде: 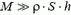 ), первым слагаемым под корнем можно пренебречь. В таком случае скорость истечения воды практически постоянна, и равна
), первым слагаемым под корнем можно пренебречь. В таком случае скорость истечения воды практически постоянна, и равна
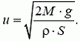
Теперь можно найти реактивную силу, действующую на сосуд:
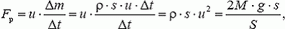
и скорость движения сосуда:
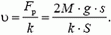
Задача 7. Из ракеты массой М, движущейся со скоростью 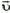 , выбрасывается порция топлива m со скоростью
, выбрасывается порция топлива m со скоростью 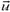 относительно ракеты. Какой станет скорость ракеты? Какую скорость будет иметь ракета после выброса двух таких порций, трех порций, k порций (рис. 7)?
относительно ракеты. Какой станет скорость ракеты? Какую скорость будет иметь ракета после выброса двух таких порций, трех порций, k порций (рис. 7)?
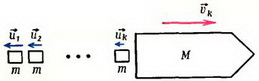
Рис. 7.
Воспользуемся законом сохранения импульса. Удобнее написать его в системе отсчета, движущейся с первоначальной скоростью ракеты 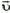 (так как скорость выброса топлива
(так как скорость выброса топлива 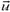 задана относительно ракеты). В проекции на направление движения ракеты получим
задана относительно ракеты). В проекции на направление движения ракеты получим
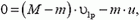
откуда скорость ракеты
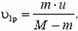
В неподвижной системе отсчета скорость ракеты после выброса первой порции топлива равна по модулю
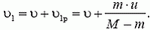
Выброс второй порции топлива будем рассматривать в системе, движущейся со скоростью 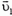 (на рисунке 7 выброс топлива показан в неподвижной системе отсчета). Из закона сохранения импульса имеем
(на рисунке 7 выброс топлива показан в неподвижной системе отсчета). Из закона сохранения импульса имеем
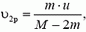
а в неподвижной системе
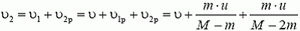
Легко видеть, что после k выбросов скорость ракеты будет равна
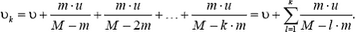
Для сравнения найдем также скорость ракеты 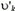 при одноразовом выбросе топлива массой k·m с той же скоростью
при одноразовом выбросе топлива массой k·m с той же скоростью 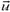 относительно ракеты. Для этого опять воспользуемся законом сохранения импульса, только запишем его сразу относительно неподвижной системы отсчета:
относительно ракеты. Для этого опять воспользуемся законом сохранения импульса, только запишем его сразу относительно неподвижной системы отсчета:
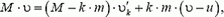
откуда
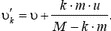
Легко видеть, что 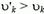 . Такой результат связан с предположением, что скорость выброса топлива из ракеты в неподвижной системе отсчета постоянна и равна υ – u. В действительности по мере ускорения ракеты скорость выброса топлива уменьшается (постоянна скорость выброса относительно ракеты). Поэтому первая формула для υk более точно описывает реальную ситуацию.
. Такой результат связан с предположением, что скорость выброса топлива из ракеты в неподвижной системе отсчета постоянна и равна υ – u. В действительности по мере ускорения ракеты скорость выброса топлива уменьшается (постоянна скорость выброса относительно ракеты). Поэтому первая формула для υk более точно описывает реальную ситуацию.
Упражнения
1. Нейтрон массой m0 поглощается ядром неподвижного атома массой m. Известно, что энергия возбужденного атома может отличаться от энергии основного состояния только на определенное значение Е0. С какой скоростью двигался нейтрон?
2. Ракета, запущенная вертикально вверх, взрывается в высшей точке своего подъема. При взрыве образуются три осколка равной массой. Один осколок падает в месте старта ракеты. Два других падают на Землю в один и тот же момент. Показать, что эти осколки приземляются на одном и том же расстоянии от места старта ракеты.
3. С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально со скоростью 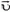 ? Масса змеи М, ее длина L.
? Масса змеи М, ее длина L.
4. Лестница, на которой находится человек, уравновешена противовесом на веревке, перекинутой через блок. Масса человека равна массе лестницы, а масса блока и трение пренебрежимо малы. Человек, находящийся вначале на высоте h от пола, поднимается по лестнице на n ступенек. На какой высоте от пола он окажется после этого, если расстояние между ступеньками равно l?
5. На конце соломинки, лежащей на гладком столе, сидит кузнечик. С какой наименьшей скоростью он должен прыгнуть, чтобы попасть на другой конец соломинки? Трение между столом и соломинкой отсутствует. Масса соломинки М, ее длина l. Масса кузнечика m.
6. Скорость истечения газов из сопла ракеты равна 300 м/с относительно ракеты. Может ли такой двигатель разогнать ракету до скорости 600 м/с?
7. При испытании реактивного снаряда, установленного в хвосте самолета для защиты его от нападения сзади, был обнаружен удивительный факт: при пуске снаряд разворачивался и догонял самолет. Как можно объяснить это явление?
Ответы
1. 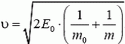
2. Указание. Воспользуйтесь законом сохранения импульса.
3. 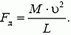
4. 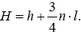
5. 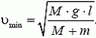
6. Может (реактивная сила определяется значением скорости истечения газов относительно ракеты).
7. Непосредственно после вылета из ракеты снаряд движется в ту же сторону, что и ракета, то есть вперед. Через некоторое время стабилизаторы разворачивают снаряд, затем под действием реактивной силы он разгоняется и может догнать самолет.
Выберите два верных утверждения, которые соответствуют содержанию текста. Запишите в ответ их номера.
1. Модуль реактивной силы зависит только от скорости расхода топлива.
2. Модуль реактивной силы зависит от скорости истечения газов из сопла двигателя и от скорости расхода топлива.
3. Ракета начальной массой 800 т, стартовав из неподвижного положения, сожгла половину топлива, в результате чего ею была достигнута скорость 2,5 км/с. Когда её скорость достигнет значения 7,5 км/с ее масса будет равна 300 т.
4. Ракета начальной массой 800 т, стартовав из неподвижного положения, сожгла половину топлива, в результате чего ею была достигнута скорость 2,5 км/с. Когда её скорость достигнет значения 7,5 км/с ее масса будет равна 200 т.
5. Ракета начальной массой 800 т, стартовав из неподвижного положения, сожгла половину топлива, в результате чего ею была достигнута скорость 2,5 км/с. Когда её скорость достигнет значения 7,5 км/с ее масса будет равна 100 т.
Сила тяги, теория и онлайн калькуляторы
Сила тяги
Понятие сила тяги
Определение
Понятие «сила тяги» часто встречается в задачах по физике, когда речь идеи о механической мощности или движении транспорта.
Вообще говоря, это гипотетическая сила, которая вводится для удобства при решении задач.
Поясним эту мысль. Рассмотрим движение автобуса. Сила тяги (обозначим ее как ${overline{F}}_t$) в этом случае является силой трения покоя, которая действует на нижние точки колес со стороны поверхности шоссе. Для реализации движения автобуса по дороге колеса транспортного средства вращает двигатель так, чтобы сила трения была направлена в сторону перемещения (рис.1). В этом случае силу тяги определим как силу трения, которая возникает между ведущими колесами и поверхностью, по которой колеса катятся. Если сила трения отсутствует (колесо находится на льду), то автобус не двигается с места, так как колеса проскальзывают. Трение, которое появляется между колесами и поверхностью дороги создает поступательное перемещение.
Так как сила тяги зависит от силы трения, то для увеличения величины $F_t $ следует увеличить трение. Трение увеличивается при росте коэффициента трения и (или) с увеличением силы нормального давления, которое зависит от массы тела.
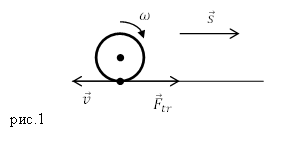
Возникает вопрос о необходимости введения некоей силы тяги вместо того, чтобы использовать привычную силу трения. При выделении из внешних сил, которые действуют на наш автобус силы тяги и силы сопротивления движению уравнения движения имеют универсальный вид, и, используя силу тяги, просто выражается полезная механическая мощность ($N$):
[N={overline{F}}_tcdot overline{v}left(1right),]
где $overline{v}$ – скорость движения тела (у нас автобуса).
Отметим, что у силы тяги нет четко определенной формулы, как, например, у гравитационной силы или силы Архимеда и других сил. Ее часто вычисляют, используя второй закон Ньютона и рассматривая все силы, которые действуют на тело.
Реактивная сила тяги
Уравнения движения тел переменной массы и формулу для вычисления реактивной силы получил первым И.В. Мещерский в 1897 г. Формула реактивной силы является основой для расчета силы тяги ракетных и турборакетных двигателей всех систем.
Пусть ракета перемещается со скоростью $overline{v}$ относительно Земли. Вместе с ней с такой же скоростью движется часть топлива, которая сгорает в ближайшую секунду. При сгорании продукты горения этой части топлива получают дополнительную скорость $overline{u}$ относительно ракеты. Относительно Земли они имеют скорость $overline{v}-overline{u}$. При этом сама ракета увеличивает скорость. После выброса продукты горения не взаимодействуют с ракетой. Поэтому систему ракета плюс продукты горения топлива рассматривают как систему из двух тел, которые взаимодействуют при горении по законам неупругого удара. Пусть реактивный двигатель ракеты каждую секунду выбрасывает массу $mu $ продуктов горения топлива. Используя закон сохранения импульса и второй закон Ньютона получают, что модуль реактивной силы тяги двигателя ($R$) ракеты равен:
[R=mu u left(2right).]
Формула (2) показывает, что реактивная сила, которая действует на тело переменной массы, пропорциональна массе отделяющихся частиц за единицу времени и скорости движения этих частиц относительно тела.
Примеры задач с решением
Пример 1
Задание. Сила тяги, действующая на тело, находящееся на наклонной плоскости (рис.2) направлена вдоль этой плоскости вверх (рис.2). Какова ее величина, если масса тела равна $m$, угол наклона плоскости $alpha , $ускорение движения тела $a$? Коэффициент трения тела о плоскость равен $mu $. Тело движется с постоянной скоростью в гору.
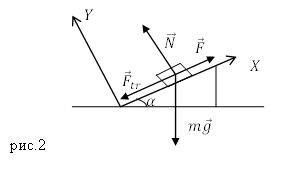
Решение. Запишем второй закон Ньютона для сил, действующих на тело, учтем, что тело движется равномерно:
[moverline{g}+overline{N}+overline{F}+{overline{F}}_{tr}=0left(1.1right).]
Запишем проекции уравнения (1.1) на оси X и Y:
[left{ begin{array}{c}
X: -mg{sin alpha + }F-F_{tr}=0left(1.2right);; \
Y: N-mg{cos alpha =0left(1.3right). } end{array}
right.]
Сила трения связана с силой нормального давления как:
[F_{tr}=mu N left(1.4right).]
Выразим из (1.3) $N$, используем выражение (1.4), получим из (1.2) силу тяги:
[-mg{sin alpha + }F-mu mg{cos alpha }=0to F=mu mg{cos alpha }+mg{sin alpha . }]
Ответ. $F=mg(mu {cos alpha }+{sin alpha ). }$
Пример 2
Задание. Ракету, массой (в начальный момент времени) равной $M,$ запустили вертикально вверх. Относительная скорость выброса продуктов горения равна $u$, расход горючего составляет $mu $. Каким будет ускорение ракеты через время $t$ после старта, если сопротивление воздуха не учитывать, поле силы тяжести считать однородным.
Решение. Сделаем рисунок.
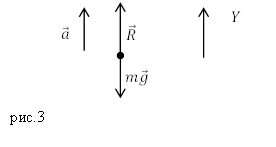
На ракету (из условий задачи) будут действовать две силы: сила тяжести и реактивная сила тяги. Запишем уравнение движения ракеты:
[moverline{g}+overline{R}=moverline{a}left(2.1right).]
В проекции на ось Y уравнение (2.1) запишем как:
[R-mg=ma left(2.2right).]
Реактивная сила тяги может быть найдена как:
[R=mu u left(2.3right).]
Учитывая равенство (2.3) уравнение преобразуем к виду:
[mu u-mg=mato a=frac{mu u-mg}{m}left(2.4right).]
Масса ракеты в момент времени $t$ равна:
[m=M-mu tleft(2.5right).]
Подставим (2.5) в (2.4) имеем:
[a=frac{mu u-left(M-mu tright)g}{M-mu t}=frac{mu u}{M-mu t}-g.]
Ответ. $a=frac{mu u}{M-mu t}-g.$
Читать дальше: скорость.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание:
Реактивное движение:
Одним из наиболее ярких проявлений и практического применения закона сохранения импульса является реактивное движение. Это движение, которое возникает, когда от системы отделяется и движется с некоторой скоростью относительно нее какая-то ее часть. В живой природе так движется осьминог (рис. 121), выбрасывая воду.
Типичным примером реактивного движения может служить движение ракет.

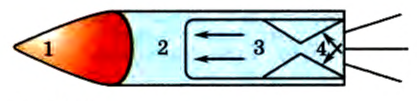
На рисунке 122 схематично представлено устройство ракеты. В головной ее части 1 помещается полезный груз. Это может быть боезаряд, навигационное оборудование для управления движением боевой ракеты. В космическом корабле в головной части помещаются космонавты, научные приборы, система обеспечения жизнедеятельности, система навигационного оборудования и т. п. В части 2 находится запас топлива и окислителя, а также различные системы управления. Топливо и окислитель подаются в камеру сгорания 3, где топливо сгорает и превращается в газ, имеющий высокую температуру. Реактивное сопло 4 формирует реактивную струю, движущуюся с большой скоростью относительно ракеты. Газ в камере и все остальное, что составляет ракету, можно рассматривать как систему двух взаимодействующих тел.
Будем пока считать, что силы притяжения к Земле отсутствуют. Тогда ракета представляет собой замкнутую систему, и перед стартом ее общий импульс относительно Земли равен нулю. Газ, вырывающийся из сопла, имеет определенный импульс. Поэтому оставшаяся часть ракеты по закону сохранения импульса получает импульс, равный по модулю импульсу газа, но противоположный по направлению. На рисунке 122 стрелками показаны силы давления газа, сообщающие ракете этот импульс.
Закон сохранения импульса позволяет оценить скорость ракеты и силу, действующую на нее. Предположим, что за некоторый промежуток времени Δt из сопла вырывается масса газа Δm со скоростью  относительно ракеты, тогда, обозначив массу ракеты через M, по закону сохранения импульса можно записать:
относительно ракеты, тогда, обозначив массу ракеты через M, по закону сохранения импульса можно записать:
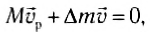
где 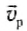 — скорость ракеты.
— скорость ракеты.
Величину 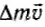 можно переписать следующим образом:
можно переписать следующим образом:
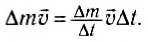
Но 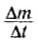 — масса газа, которая выбрасывается из ракеты в единицу времени. Нетрудно убедиться, что величина
— масса газа, которая выбрасывается из ракеты в единицу времени. Нетрудно убедиться, что величина 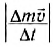 имеет размерность силы, и она называется реактивной силой. Реактивная сила равна произведению массы газа, вырывающегося из сопла в единицу времени, и скорости струи газа.
имеет размерность силы, и она называется реактивной силой. Реактивная сила равна произведению массы газа, вырывающегося из сопла в единицу времени, и скорости струи газа.
Следовательно, чтобы реактивная сила была максимальной, нужно повышать скорость газовой струи. В современных ракетах она может достигать 4,5 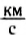 .
.
Уравнение (1) можно записать в виде
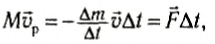 (2)
(2)
где в правой части стоит импульс реактивной силы 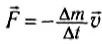 , который увеличивает скорость ракеты. Из (2) следует, что скорость ракеты направлена в сторону, противоположную скорости выбрасываемых газов.
, который увеличивает скорость ракеты. Из (2) следует, что скорость ракеты направлена в сторону, противоположную скорости выбрасываемых газов.
Вследствие вылета газов масса ракеты все время уменьшается. Так что масса космического корабля, которая может быть выведена на орбиту искусственного спутника Земли, составляет малую долю его первоначальной массы. Например, при скорости космического корабля, равной первой космической, точный расчет показывает, что для одноступенчатых ракет при скорости вылета газов относительно ракеты 2 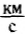 отношение массы топлива к полезной массе равно 55. Если скорость газовой струи 3
отношение массы топлива к полезной массе равно 55. Если скорость газовой струи 3 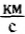 , то отношение масс равно 14.
, то отношение масс равно 14.
Ракеты известны давно. Впервые о них упоминается в китайских хрониках 1150 г. Естественно, что такое интересное явление, как движение ракет, изучалось многими учеными. Так, в 1650 г. в Амстердаме вышла книга «Великое искусство артиллерии» генерал-лейтенанта польской армии К. Семеновича, уроженца Беларуси. В ней была глава, посвященная описанию движения ракет и их конструкций. Эта книга практически одновременно была переведена на основные европейские языки.
Большой вклад в теорию движения ракет внесли русские ученые И. В. Мещерский и К. Э. Циолковский. В 1903 г. К. Э. Циолковский впервые предложил и теоретически обосновал идею использования ракет для космических полетов. Им была получена формула, сейчас носящая его имя, позволяющая оценить запас топлива, который должен быть в ракете, чтобы она стала искусственным спутником Земли. В 1904 г. И. В. Мещерским было получено уравнение, с помощью которого можно описать движение ракет.
Идея К. Э. Циолковского была осуществлена советскими учеными под руководством С. П. Королева. Первый в истории искусственный спутник Земли массой 84 кг был запущен с помощью ракеты в Советском Союзе 4 октября 1957 г. Первым человеком, который совершил космический полет, был гражданин СССР Ю. А. Гагарин. 12 апреля 1961 г. он облетел земной шар за 108 мин на корабле-спутнике «Восток».
Советские ракеты первыми достигли Луны, первыми облетели Луну и сфотографировали ее невидимую с Земли сторону, первыми достигли планеты Венера.
В 1969 г. американский астронавт Н. Армстронг впервые в истории человечества ступил на поверхность другого небесного тела — Луны. Американские астронавты совершили несколько полетов на Луну с выходом на ее поверхность и длительным (до трех земных суток) сроком пребывания на ней.
Началось практическое освоение космоса. Ряд стран запустили искусственные спутники Земли, предназначенные для связи, телевидения, наблюдения за погодой, научных и других целей. Так, с помощью приборов, установленных на искусственных спутниках Земли, был обнаружен дрейф континентов. Было доказано, что расстояние между побережьями Африки и Америки увеличивается на несколько сантиметров в год.
Белорусские ученые тоже внесли свой вклад в освоение космоса. Группа ученых под руководством академика Л. И. Киселевского создала ряд научных приборов, побывавших в космосе. Ученые Института тепломассообмена HAIl Беларуси рассчитали тепловую защиту космических кораблей. Командирами космических кораблей типа «Союз» и орбитальных станций «Салют» были и уроженцы Беларуси, летчики-космонавты, дважды Герои Советского Союза П. И. Климук и В. В. Коваленок.
Главные выводы
- Изменение скорости ракеты обусловлено действием реактивной силы, создаваемой струей газа, вытекающей из сопла.
- Движение ракет (реактивное движение) объясняется выполнением закона сохранения импульса.
- Реактивная сила равна произведению массы газа, вырывающегося из сопла в единицу времени, и скорости струи газа относительно ракеты.
Что такое реактивное движение
Мы уже знаем, что тела образуют замкнутую систему, если взаимодействуют только друг с другом. Не изменяя механического состояния системы в целом, взаимодействие может приводить к изменению механического состояния тел, составляющих систему.
В качестве примера рассмотрим резиновый шарик с газом, лежащий на столе. Его можно считать замкнутой системой, поскольку сила тяжести, сила Архимеда и сила реакции стола компенсируют друг друга. Механическое состояние такой системы не изменяется. Если же в стенке шарика сделать отверстие, через которое газ будет выходить наружу, он начнет двигаться в направлении, противоположном направлению вытекания газа (рис. 2.55). Такое перераспределение массы системы в пространстве вызывает изменение скоростей обеих ее частей (системы).

Подобное наблюдается и в случае, когда с неподвижной лодки, находящейся на воде, бросить весло (или другой предмет определенной массы) в направлении кормы. Следствием такого действия будет перемещение лодки в противоположном направлении.
Движение резинового шарика, из которого вытекает газ, и движение лодки, из которой выбрасывают весло, происходят вследствие отделения от системы какой-то ее части.
Движение, происходящее вследствие отделения от системы ее части с некоторой скоростью, называют реактивным.
Примеры реактивного движения можно найти и в природе. Так, кальмар для осуществления быстрого перемещения набирает воду в полость своей мантии и резким сокращением мышц выбрасывает ее наружу (рис. 2.56).
Среди растений известен так называемый «бешеный» огурец. При созревании плода его семена выбрасываются наружу в одну сторону, а оболочка отлетает в другую (рис. 2.57).

Человек освоил принцип реактивного движения и применяет его в реактивных летательных аппаратах – ракетах и самолетах.
Основная часть ракеты – реактивный двигатель, имеющий камеру сгорания и сопло – отверстие, через которое выходят газы, образовавшиеся при сгорании топлива (рис. 2.58).
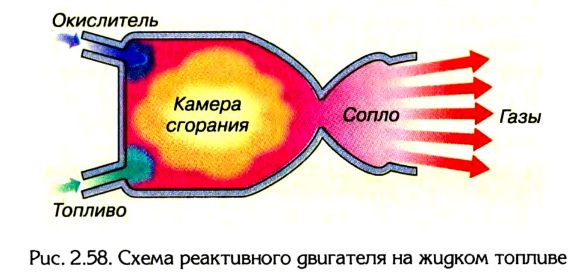
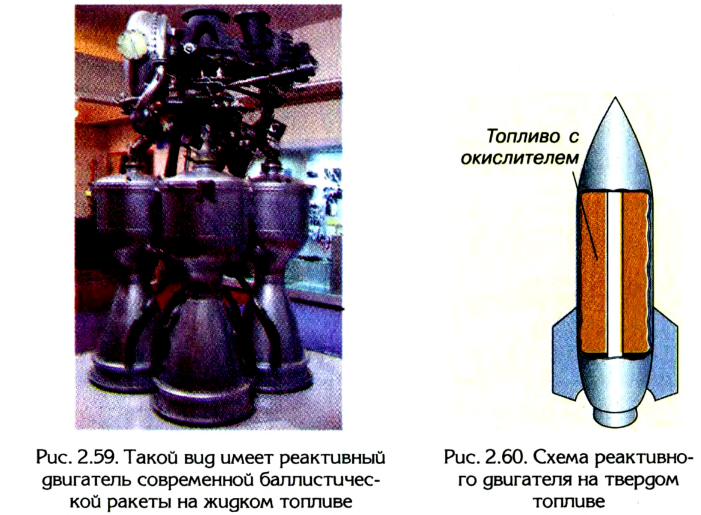
Если двигатель работает на жидком топливе, специальные насосы подают топливо и окислитель с баков, расположенных на ракете, в камеру сгорания, в результате чего происходит быстрое сгорание топлива и выброс газов через сопло (рис. 2.59).
Существуют ракеты, у которых топливо и окислитель находятся непосредственно в камере сгорания в твердом состоянии (рис. 2.60). При сгорании топлива образуется раскаленный газ, создающий давление на стенки и дно камеры. Там, где камера сгорания переходит в сопло, такое давление отсутствует.
Сила давления на дно камеры сгорания является реактивной силой тяги двигателя, изменяющей импульс ракеты.
Чем дольше работает двигатель, тем большую скорость набирает ракета. Измерить силу давления газов на дно камеры сгорания по многим причинам очень сложно. Поэтому движение ракеты рассчитывают по закону сохранения импульса.
Если ракету с топливом считать замкнутой системой, то ее начальный импульс в системе, связанной с ее центром масс, равен нулю. Как только начинает работать двигатель, раскаленные газы выходят из сопла, приобретают определенный импульс 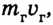 а ракета –
а ракета – 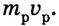
Расчеты на основании закона сохранения импульса показывают, что увеличить скорость ракеты можно увеличив или массу топлива, или скорость вытекания газов, поскольку 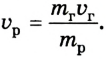
Устройства, использующие принцип реактивного движения, широко применяются в современной жизни: реактивные самолеты, военная и космическая техника и пр.
Значительный вклад в развитие реактивной техники сделали украинские ученые и инженеры, среди которых следует назвать генерала царской армии по происхождению украинца А.Д. Засядько, изобретателя Н.И. Кибальчича, академика В.П. Глушко и др. Украина принадлежит к немногим странам, которые создают современную ракетную технику для освоения космоса. На «Южмаше» в Днепропетровске создают ракеты «Зенит», при помощи которых на околоземную орбиту выводят искусственные спутники различного назначения.
- Заказать решение задач по физике
Определение реактивного движения
Интересный и важный случай практического использования закона сохранения импульса – это реактивное движение. Так называют движение тела, возникающее при отделении от тела с определенной скоростью некоторой его части.
Реактивное движение осуществляют, например, ракеты. Любая ракета – это система двух тел. Она состоит из оболочки и топлива, которое в ней находится. Оболочка имеет форму трубы, один конец которой закрыт, а второй открыт и обеспечен трубчатой насадкой с отверстием особенной формы – реактивным соплом.
Топливо при запуске ракеты сжигается и превращается в газ высокого давления и высокой температуры. Благодаря высокому давлению этот газ с большой скоростью вырывается из сопла ракеты. Оболочка ракеты движется при этом в противоположную сторону (рис. 290).

Перед стартом ракеты ее общий импульс (оболочки и топлива) в системе координат, связанной с Землей, равен нулю, ракета не движется относительно Земли. В результате взаимодействия газа и оболочки, которая выбрасывает газ, она приобретает определенный импульс. Будем считать, что сила притяжения практически не влияет на движение, поэтому оболочку и топливо можно рассматривать как замкнутую систему и их общий импульс должен и после запуска остаться равным нулю. Оболочка, в свою очередь, благодаря взаимодействию с газом приобретает импульс, который равен по модулю импульсу газа, но противоположно направленного. Вот почему в движение приходит не только газ, но и оболочка ракеты. В ней могут быть размещены научные приборы для исследований, средства связи. В ракете может размещаться космический корабль, в котором находятся космонавты или астронавты.
Закон сохранения импульса дает возможность определить скорость движения ракеты (оболочки).
Допустим сначала, что весь газ, который образуется при сгорании горючего, выбрасывается из ракеты сразу, а не вытекает постепенно.
Обозначим всю массу газа, в который превращается топливо в ракете, через 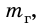 , а скорость газа – через
, а скорость газа – через 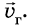 . Массу и скорость движения оболочки обозначим через
. Массу и скорость движения оболочки обозначим через 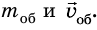 По закону сохранения импульса сумма импульсов оболочки и газа после запуска должна быть такой же, как до запуска ракеты, то есть должна быть равна нулю. Следовательно,
По закону сохранения импульса сумма импульсов оболочки и газа после запуска должна быть такой же, как до запуска ракеты, то есть должна быть равна нулю. Следовательно, 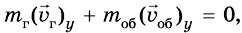 или
или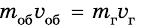 (координатная ось Оу выбрана в направлении движения оболочки). Отсюда определим скорость движения оболочки:
(координатная ось Оу выбрана в направлении движения оболочки). Отсюда определим скорость движения оболочки:
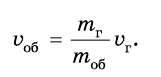
Из формулы видно: чем больше скорость вытекания газа и чем больше отношение массы топлива к массе оболочки, тем скорость движения оболочки ракеты больше. Поэтому достаточно большую скорость оболочка получит в том случае, если масса топлива намного больше массы оболочки. Например, чтобы скорость движения оболочки была по абсолютному значению в 4 раза больше скорости вытекания газа, необходимо, чтобы масса топлива была во столько же раз больше массы оболочки, то есть оболочка должна составлять пятую часть всей массы ракеты на старте. Ведь «полезная» часть ракеты – это сама оболочка.
С создания ракет началось активное освоение космоса. Украинский авиаконстуктор Сергей Павлович Королев и его коллеги создали ракету-носитель «Восток», и 12 апреля 1961 г. человек вышел в космическое пространство. Это был Юрий Гагарин.

Украина входит в состав космических государств мира благодаря высокому уровню научно-технического и производственного потенциала, участию в международной космической деятельности.
В марте 1999 г. состоялся первый пуск украинской ракеты-носителя «Зенит-ЗвЬ» по международной программе «Морской старт». Украина вместе с США, Норвегией и Россией стала участницей грандиозного проекта запусков с плавучего космодрома в Мировом океане.
В декабре 2004 г. были выведены в космос спутники дистанционного зондирования Земли серии «Сич», «Сич-1М» и первый украинский малогабаритный космический аппарат «МС-1-ТК».
За 15 лет работы Национального космического агентства Украины (сейчас Государственное космическое агентство Украины) и предприятий украинской космической отрасли было обеспечено более 100 пусков ракет-носителей и выведено в космос более 180 космических аппаратов.
В октябре 2016 г. с о. Уоллопс (штат Вирджиния, США) состоялся успешный запуск модернизированной ракеты-носителя среднего класса Antares-230 с транспортным космическим кораблем Cygnus. Главным разработчиком ракеты-носителя является американская компания Orbital АТК, а основную конструкцию ее первой ступени создали украинские госпредприятия космической отрасли КБ «Южное» им. М.К. Янгеля и ПО «Южный машиностроительный завод им. А.М. Макарова» (г. Днепр) в кооперации с предприятиями «Хартрон-АРКОС» (г. Харьков), «Хартрон-ЮКОМ» (г. Запорожье), «ЧЕЗАРА», «РАПИД» (г. Чернигов) и т. п.
Украинские специалисты занимались модернизацией первой степени ракеты-носителя Antares, адаптируя эту степень к новому, более эффективному двигателю.
Грузовой корабль Cygnus доставил на Международную космическую станцию свыше 2 т груза (образцы для проведения научных экспериментов, научные инструменты и продовольствие), а также оборудование для вывода в космическое пространство миниатюрных спутников. Астронавт-ка NASA Кейт Рубине сделала снимки стыковки корабля с Международной космической станцией, которые были опубликованы на официальной странице астронавтов агентства в Twitter (рис. 291).

Примеры решения задачи
Пример №1
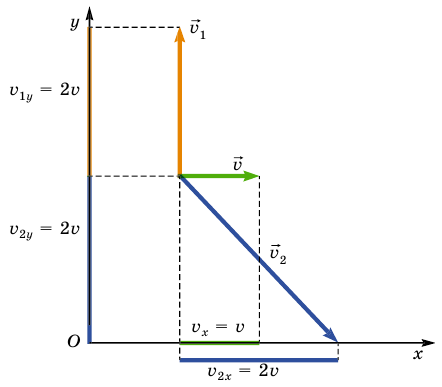
Снаряд разорвался в верхней точке траектории на два осколка одинаковой массы. Скорость движения снаряда непосредственно перед взрывом была 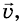 а скорость движения одного из осколков сразу после взрыва
а скорость движения одного из осколков сразу после взрыва  и направлена вертикально вверх. Вычислите значение и направление скорости
и направлена вертикально вверх. Вычислите значение и направление скорости  второго осколка в момент взрыва.
второго осколка в момент взрыва.
Решение:
Поскольку при взрыве снаряда возникают большие внутренние силы и время их действия очень мало, то внешней силой притяжения можно пренебречь и считать систему на время взрыва замкнутой. По закону сохранения импульса: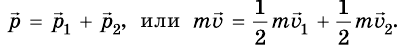
Перепишем это уравнение в проекциях на координатные оси:
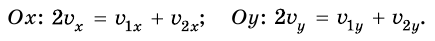
Учитывая, что по условию задачи 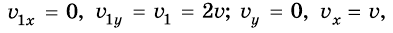
получим: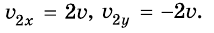
Тогда 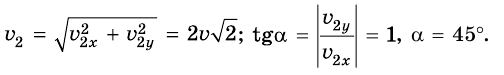
Второй осколок полетит со скоростью 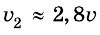 вниз под углом а = 45° к горизонту.
вниз под углом а = 45° к горизонту.
Пример №2
Мальчик массой 50 кг движется от носовой части к корме лодки массой 150 кг со скоростью 0,6 м/с относительно лодки. С какими скоростями движутся при этом лодка и мальчик относительно воды? Сопротивлением воды пренебречь.
Дано:
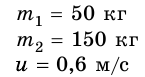
Решение:
Поскольку равнодействующая сил притяжения и архимедовой силы, действующих на лодку, равна нулю, система тел «лодка-мальчик» является замкнутой. Силой сопротивления воды, возникающей при движении лодки, пренебрежем, поскольку при малых скоростях эта сила небольшая. Применим закон сохранения импульса относительно системы отсчета, связанной с неподвижной водой. Импульс системы до начала движения мальчика равен нулю.
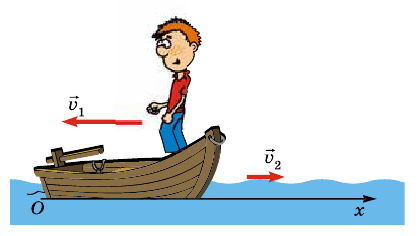
За положительное направление оси Ох выберем направление движения лодки. Относительно воды проекция импульса лодки на ось Ох равна 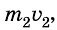 , а импульса мальчика
, а импульса мальчика 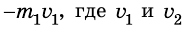 – соответственно скорости движения мальчика и лодки относительно воды. Из закона сложения скоростей следует, что
– соответственно скорости движения мальчика и лодки относительно воды. Из закона сложения скоростей следует, что 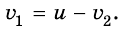
Запишем теперь закон сохранения импульса:
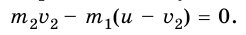
Отсюда скорости лодки и мальчика относительно воды равны:
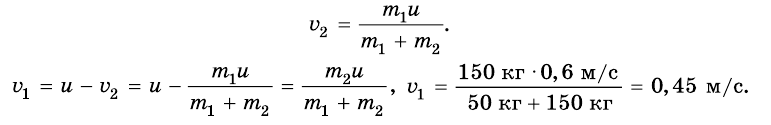
Ответ: скорость движения лодки равна 0,15 м/с, а скорость движения мальчика 0,45 м/с.
- Освоение космоса – история, этапы и достижения с фотографиями
- Закон сохранения механической энергии в физике
- Релятивистская механика в физике
- Теория относительности Эйнштейна
- Гравитационные силы в физике
- Центр тяжести в физике (центр масс)
- Импульс тела в физике
- Замкнутая система в физике
