Свойства ромба:
1. Ромб – частный случай параллелограмма
2. Противоположные стороны – параллельны
3. Все четыре стороны – равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы диагоналей через сторону и угол, ( D d):
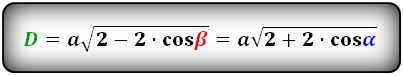
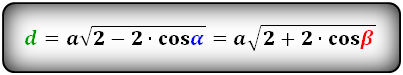
Формулы диагоналей через сторону и половинный угол, (D d):
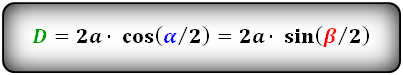
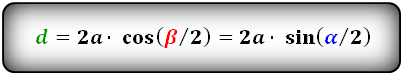
Формулы диагоналей через сторону и другую диагональ, (D d):


Формулы диагоналей через угол и другую диагональ, (D d):
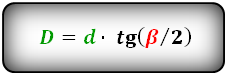
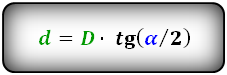
Формулы диагоналей через площадь (D d):
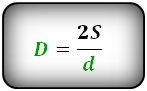
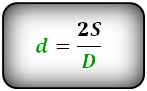
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 23 ноября 2011
-
Обновлено: 13 августа 2021
Каким способом высчитать диагональ:
Способ расчёта
Введите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Ромб – это параллелограмм у которого все стороны равны.
Свойства ромба:
- Диагонали ромба делят его углы пополам.
- Cумма углов прилежащих к одной стороне равна 180°.
- Диагонали ромба пересекаются под прямым углом (90°).
- Диагонали ромба в точке пересечения делятся попалам.
- Диагонали ромба являются биссектрисами его углов.
Диагональ – это отрезок, соединяющий несмежные вершины многоугольника или многогранника.
Формулы расчёта диагонали ромба
Длину диагоналей ромба можно посчитать несколькими способами. В зависимости от известных данных, для расчёта применяют следующие формулы:
Через сторону и другую диагональ
D
d
a
a
a
a
D = sqrt{4a^2 – d^2}
d = sqrt{4a^2 – D^2}
- D – большая диагональ ромба
- d – меньшая диагональ ромба
- a – сторона ромба
Через сторону и угол
D
d
a
a
a
a
α
β
- D – большая диагональ
- d – меньшая диагональ ромба
- a – сторона ромба
- α – острый угол ромба (от 0° до 90°)
- β – тупой угол ромба (от 90° до 180°)
D = a sqrt{2 + 2 cdot cos alpha}
D = a sqrt{2 – 2 cdot cos beta}
d = a sqrt{2 – 2 cdot cos alpha}
d = a sqrt{2 + 2 cdot cos beta}
Через угол и вторую диагональ
D = d cdot tg ( dfrac{beta}{2} )
d = D cdot tg ( dfrac{alpha}{2} )
- D – большая диагональ ромба
- d – меньшая диагональ ромба
- α – острый угол ромба (от 0° до 90°)
- β – тупой угол ромба (от 90° до 180°)
Через площадь и вторую диагональ
D = dfrac{2 cdot S}{d}
d = dfrac{2 cdot S}{D}
- D – большая диагональ ромба
- d – меньшая диагональ ромба
- S – площадь ромба
Похожие калькуляторы:
Войдите чтобы писать комментарии
|
Начнем с того что у ромба две диагонали.
Одна большая D, а другая маленькая d. Рассмотрим способы нахождения большой диагонали D.
Также D находится по площади ромба и малой диагонали: D=(2*S)/d; Рассмотрим способы нахождения меньшей диагонали d.
Малую диагональ d тоже можно найти через площадь ромба и большую диагональ: d=(2*S)/D; автор вопроса выбрал этот ответ лучшим Alexsandr82 5 лет назад У ромба есть две диаганали: большая (d1) и малая (d2), а также углы а – острый угол ромба (в ромбе два острых угла и оба равны между собой), и b – тупой угол (их тоже два и они тоже равны). Если нам известна сторона ромба (x) и один из углов то мы можем найти любую диагональ по формулам: d1 = 2x*cos(a/2) d2 = 2x*sin(a/2) Или d1 = 2x*sin(b/2) d2 = 2x*cos(b/2) Кроме этого если нам извесна площадь ромба и одна из диагоналей мы можем найти вторую диагональ по формулам: d1 = 2S/d2 d2 = 2S/d1 Если нам дан радус вписанной в ромб окружности и любой из углов мы также можем рассчитать диагональ ромба: d1 = 2r/sin(a/2) d2 = 2r/sin(b/2) Где r – радиус вписанной окружности. Знаете ответ? |
Диагонали ромба
Диагональ
Ромб — частный случай параллелограмма, у которого все стороны равны, а противоположные — параллельны. Отрезки, соединяющие противоположные вершины ромба, называются его диагоналями. Они пересекаются между собой под прямым углом и делятся в точке пересечения пополам. Диагонали делят ромб на два равнобедренных треугольника и четыре одинаковых прямоугольных треугольника, у которых гипотенузой является сторона ромба (а), углом — половина угла ромба, сторонами (катетами) — половина диагоналей. Используя тригонометрические отношения находим катеты треугольника как произведение гипотенузы на синус и косинус половины известного угла. Чтобы найти второй угол, нужно из 180 градусов вычесть величину известного нам угла. Диагонали D, d ромба через сторону и половинный угол определяем по формуле:
где D — большая диагональ, d — меньшая диагональ ромба, a — сторона ромба, углы ромба α,β. Чтобы найти диагонали D, d через сторону и угол, воспользуемся формулами:
D = 2a × cos (α/2) = 2a × sin (β/2)
d = 2a × cos (β/2) = 2a × sin (α/2)
Если даны угол и сторона ромба, можно определить его высоту, как произведение стороны на синус угла. Произведение высоты на сторону ромба позволит определить его площадь. Площадь ромба через две его диагонали равна половине их произведений. Если известна площадь ромба и одна из его диагоналей, можно найти другую диагональ. Так как в ромбе все стороны равны, то его периметр равен произведению одной стороны на количество всех его сторон — четыре.
![]()
Рассчитать диагонали ромба зная стороны и угол
- Диагональ прямоугольника
- Диагональ квадрата
- Диагональ куба
- Диагональ прямоугольного параллелепипеда
- Диагонали ромба
- Диагонали параллелограмма
- Диагонали трапеции
Добавить в закладки
Диагонали ромба
Сторона а
Угол (градусы) α
Знаков после запятой
Поделиться в социальных сетях:
или https://correctcalc.ru/formula-diagonali/diagonali-romba/ скопировать ссылку на страницу
Ромб является четырехугольником, который параллелограмм, сохраняет всю свою силу, но, кроме того, является равносторонним. Поскольку все стороны Ромба равны и из свойства параллелограммы их противоположные уголки тоже равны, диагональ Ромба не только пересекает точку, разделяющую их на два равных части каждой, но всегда будет пересекаться друг с другом.
0 Комментариев |
; ; ; ; ;
Войти
Наш сайт использует файлы cookie, чтобы улучшить работу сайта, повысить его эффективность и удобство. Продолжая использовать сайт correctcalc.ru, вы соглашаетесь на использование файлов cookie.

