Как найти корень в математике формула – Сайт, где вы сможете решить свои вопросы

Квадра́тный ко́рень из числа $a$ (корень 2-й степени) — число $x$ , дающее $a$ при возведении в квадрат^[1]: ${displaystyle xcdot x=a.}$ Равносильное определение: квадратный корень из числа $a$ — решение уравнения ${displaystyle x^{2}=a.}$ Операция вычисления значения квадратного корня из числа $a$ называется «извлечением квадратного корня» из этого числа.

Наиболее часто под $x$ и $a$ подразумеваются вещественные числа, но существуют и обобщения ^[⇨] для комплексных чисел и других математических объектов, например, матриц и операторов.

У каждого положительного вещественного числа существуют два противоположных по знаку квадратных корня. Например, квадратными корнями из числа 9 являются ${displaystyle +3}$ и ${displaystyle -3,}$ у обоих этих чисел квадраты совпадают и равны 9. Это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня, значение которого при $ageqslant 0$ всегда неотрицательно (а на положительных $a$ — положительно); арифметический корень из числа $a$ обозначается с помощью знака корня (радикала)^[2]^[3]: ${sqrt {a}}$ .

Пример для вещественных чисел: ${displaystyle {sqrt {16}}=4,}$ потому что ${displaystyle { 4}^{2}=16.}$

Если требуется учесть двузначность корня, перед радикалом ставится знак плюс-минус^[2]; например, так делается в формуле решения квадратного уравнения $ax^{2}+bx+c=0$ :

${displaystyle x_{1,2}={frac {-bpm {sqrt {b^{2}-4ac}}}{2a}}}$

Например, √25 = 5, поскольку

25 = 5 ⋅ 5, или

5² (5 «в квадрате»)

История[править | править код]

Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков. Среди таких задач^[4]:

Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.
Нахождение стороны квадрата, площадь которого задана.
Решение квадратных уравнений.

Вавилонская глиняная табличка YBC 7289 с пометками. Диагональ отображает приближение ${sqrt {2}}$ четырьмя 60-ричными цифрами, 1 24 51 10

Вавилонская глиняная табличка YBC 7289 из вавилонской коллекции Йельского университета была создана между 1800 и 1600 годами до н. э. и демонстрирует √2 и √2/2 соответственно в шестидесятиричной системе счисления: 1;24,51,10 и 0;42,25,35 на квадрате, пересечённом двумя диагоналями^[5]. (1;24,51,10) по основанию 60 соответствует 1,41421296, что является правильным значением с точностью до 5 десятичных знаков: ${displaystyle 1+24/60+51/60^{2}+10/60^{3}=1{,}41421296.}$ Вавилонские математики (II тысячелетие до н. э.) разработали для извлечения квадратного корня особый численный метод^[6], изложенный ниже^[⇨]. Аналогичные задачи и методы встречаются в древнекитайской «Математике в девяти книгах»^[7].

Древние греки сделали важное открытие: ${sqrt {2}}$ — иррациональное число. Детальное исследование, выполненное Теэтетом Афинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально^[8].

Средневековые европейские математики (например, Кардано) обозначали квадратный корень^[9] символом R_x, сокращение от слова «radix». Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов (то есть алгебраистов), в 1525 году^[10]. Происходит этот символ от стилизованной первой буквы того же слова «radix». Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт («Геометрии», 1637) для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.

После появления формулы Кардано (XVI век) началось применение в математике мнимых чисел, понимаемых как квадратные корни из отрицательных чисел^[11]. Основы техники работы с комплексными числами разработал в XVI веке Рафаэль Бомбелли, который также предложил оригинальный метод вычисления корней (с помощью цепных дробей). Открытие формулы Муавра (1707) показало, что извлечение корня любой степени из комплексного числа всегда возможно и не приводит к новому типу чисел^[12].

Комплексные корни произвольной степени в начале XIX века глубоко исследовал Гаусс, хотя первые результаты принадлежат Эйлеру^[13]. Чрезвычайно важным открытием (Галуа) стало доказательство того факта, что не все алгебраические числа (корни многочленов) могут быть получены из натуральных с помощью четырёх действий арифметики и извлечения корней^[14].

Квадратные корни из чисел[править | править код]

Рациональные числа[править | править код]

При рациональных $a$ уравнение $x^2=a$ не всегда разрешимо в рациональных числах. Более того, такое уравнение, даже при положительном $a$ , разрешимо в рациональных числах тогда и только тогда, когда и числитель и знаменатель числа $a$ , представленного в виде несократимой дроби, являются квадратными числами.

Непрерывная дробь для корня из рационального числа всегда является периодической (возможно, с предпериодом), что позволяет, с одной стороны, легко вычислять хорошие рациональные приближения к рациональным числам с помощью линейных рекурсий, а с другой стороны ограничивает точность приближения: $|{sqrt {r}}-p/q|>{frac {1}{Cq^{2}}}$ , где $C$ зависит от $r$ ^[15]^[16]. Верно и то, что любая периодическая непрерывная дробь является квадратичной иррациональностью.

Примеры разложения корней из натуральных чисел от 2 до 10 в непрерывные дроби:

${sqrt {2}}$	= [1; 2, 2, …]
$sqrt{3}$	= [1; 1, 2, 1, 2, …]
${displaystyle {sqrt {4}}}$	= [2]
${sqrt {5}}$	= [2; 4, 4, …]
${sqrt {6}}$	= [2; 2, 4, 2, 4, …]
${displaystyle {sqrt {7}}}$	= [2; 1, 1, 1, 4, 1, 1, 1, 4, …]
${displaystyle {sqrt {8}}}$	= [2; 1, 4, 1, 4, …]
${displaystyle {sqrt {9}}}$	= [3]
${sqrt {10}}$	= [3; 6, 6, …]

Действительные (вещественные) числа[править | править код]

Для любого положительного числа $a$ существуют ровно два вещественных корня, которые равны по модулю и противоположны по знаку^[17].

Неотрицательный квадратный корень из неотрицательного числа $a$ называется арифметическим квадратным корнем и обозначается с использованием знака радикала^[3]: ${sqrt a}$ .

Основные свойства вещественного квадратного корня (все подкоренные выражения считаются неотрицательными):

К комплексным числам, учитывая двузначность корня, все эти свойства неприменимы (см. ниже пример ошибки).

Комплексные числа[править | править код]

Квадратных корней из любого ненулевого комплексного числа всегда ровно два, они противоположны по знаку. Для корней в комплексной области понятие арифметического корня не вводится, знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней. В последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Распространённая ошибка:

${displaystyle -1=({sqrt {-1}})^{2}={sqrt {(-1)^{2}}}={sqrt {1}}=1}$ (что, конечно, неверно)

Ошибка возникла из-за того, что комплексный квадратный корень является двузначной функцией, и его нельзя использовать в арифметических действиях.

Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если

${displaystyle a=|a|e^{iphi }}$ ,

то (см. Формула Муавра)

${displaystyle {sqrt {a}}={sqrt {|a|}}cdot e^{i(phi +2pi k)/2}}$ ,

где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом, в итоге получаются два различных результата.

Существует и чисто алгебраическое представление для корня из $a+bi$ ; оба значения корня имеют вид ${displaystyle pm (c+di)}$ где:

${displaystyle c={sqrt {frac {a+{sqrt {a^{2}+b^{2}}}}{2}}}}$

${displaystyle d=operatorname {sgn}(b){sqrt {frac {-a+{sqrt {a^{2}+b^{2}}}}{2}}}}$

Здесь sgn — функция «знак». Формула легко проверяется возведением ${displaystyle c+di}$ в квадрат^[18].

Пример: для квадратного корня из ${displaystyle 3+4i}$ формулы дают два значения: ${displaystyle 2+i;;-2-i.}$

Квадратный корень как элементарная функция[править | править код]

Квадратный корень является элементарной функцией и частным случаем степенной функции ${displaystyle x^{alpha }}$ с $alpha=1/2$ . Арифметический квадратный корень является гладким при ${displaystyle x>0,}$ в нуле же он непрерывен справа, но не дифференцируем^[19].

Производная функции квадратного корня вычисляется по формуле:

${displaystyle {frac {d({sqrt {x}})}{dx}}={frac {1}{2{sqrt {x}}}}}$

Как функция комплексного переменного корень — двузначная функция, два листа которой соединяются в нуле (см. подробнее Комплексный анализ).

В элементарной геометрии[править | править код]

Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того^[20].

В информатике[править | править код]

Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).

Применение[править | править код]

Квадратные корни используются повсеместно в математике и естественных науках, например:

Алгоритмы нахождения квадратного корня[править | править код]

Разложение в ряд Тейлора[править | править код]

${displaystyle {sqrt {1+x}}=sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+textstyle {frac {1}{2}}x-{frac {1}{8}}x^{2}+{frac {1}{16}}x^{3}-{frac {5}{128}}x^{4}+dots ,}$ при ${displaystyle |x|leqslant 1}$ .

Грубая оценка[править | править код]

Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:

Если D нечётно, D = 2n + 1, тогда используем ${sqrt {S}}approx 2cdot 10^{n}.$

Если D чётно, D = 2n + 2, тогда используем ${sqrt {S}}approx 6cdot 10^{n}.$

Два и шесть используются потому, что ${displaystyle {sqrt {sqrt {1cdot 10}}}={sqrt[{4}]{10}}approx 2}$ и ${sqrt {{sqrt {10cdot 100}}}}={sqrt[ {4}]{1000}}approx 6,.$

При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку $2^{{leftlfloor D/2rightrfloor }}$ (здесь D это число двоичных цифр).

Геометрическое извлечение квадратного корня[править | править код]

Построение для геометрического извлечения квадратного корня

Так как треугольники ${displaystyle Delta ABH}$ и ${displaystyle Delta BCH}$ подобны по признаку подобия треугольников по 2 равным углам, то ${displaystyle {frac {|AH|}{|BH|}}={frac {|BH|}{|HC|}},~}$ откуда ${displaystyle |BH|^{2}=|AH|cdot |HC|}$ и ${displaystyle |BH|={sqrt {|AH|cdot |HC|}}.}$

В частности, если ${displaystyle |AH|=1}$ , а ${displaystyle |HC|=x}$ , то $|BH|={sqrt {x}}$ ^[21].

Итерационный аналитический алгоритм[править | править код]

Данный способ был известен уже в Древнем Вавилоне. Он позволяет найти приближённое значение квадратного корня с любой точностью,

Последовательные приближения рассчитываются по формуле:
${displaystyle {begin{cases}x_{0}=a\x_{n+1}={frac {1}{2}}left(x_{n}+{frac {a}{x_{n}}}right)end{cases}}}$
тогда $lim _{{nto infty }}x_{n}={sqrt {a}}$

Этот метод сходится очень быстро. Например, если для ${sqrt {5}}$ взять начальное приближение ${displaystyle x_{0}=2,}$ то получим:

${displaystyle x_{1}={frac {9}{4}}=2{,}25; x_{2}={frac {161}{72}}=2{,}23611dots ; x_{3}={frac {51841}{23184}}=2{,}2360679779dots }$

В заключительном значении верны все приведённые цифры, кроме последней.

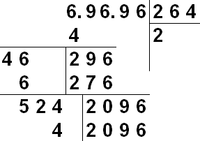
Столбиком[править | править код]

Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.

Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа N с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости группы дополняются нулями — целая часть дополняется слева, дробная справа. Так, 31234,567 можно представить как 03 12 34, 56 70. В отличие от деления, снос производится такими группами по 2 цифры.

Записать число N (в примере — 69696) на листке.
Найти $a$ , квадрат которого меньше или равен группе старших разрядов числа N (старшая группа — самая левая, не равная нулю), а квадрат $a+1$ больше группы старших разрядов числа. Записать найденное $a$ справа от N (это очередная цифра искомого корня). (На первом шаге примера $a^{2}=2^{2}=2cdot 2=4<6$ , а $(a+1)^{2}=3^{2}=3cdot 3=9>6$ ).
Записать квадрат $a$ под старшей группой разрядов. Провести вычитание из старшей группы разрядов N выписанного квадрата числа $a$ и записать результат вычитания под ними.
Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число, равное уже найденным цифрам результата (мы их выписываем справа от N), умноженное на 20. Назовём это число $b$ . (На первом шаге примера это число просто есть $b=2cdot 20=40$ , на втором $b=26cdot 20=520$ ).
Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа N справа от результата вычитания. Назовем $c$ число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число $c=296$ , на втором $c=2096$ ). Если сносится первая группа после десятичной точки числа N, то нужно поставить точку справа от уже найденных цифр искомого корня.
Теперь нужно найти такое $a$ , что $(b+a)cdot a$ меньше или равно $c$ , но $(b+(a+1))cdot (a+1)$ больше, чем $c$ . Записать найденное $a$ справа от N как очередную цифру искомого корня. Вполне возможно, что $a$ окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как $(40+6)cdot 6=46cdot 6=276<296$ , но $(40+7)cdot 7=47cdot 7=329>296$ ) Если число найденных цифр уже удовлетворяет искомой точности, прекращаем процесс вычисления.
Записать число $(b+a)cdot a$ под $c$ . Провести вычитание столбиком числа $(b+a)cdot a$ из $c$ и записать результат вычитания под ними. Перейти к шагу 4.

Наглядное описание алгоритма:

Вариации и обобщения[править | править код]

Квадратный корень из $a$ определяется как решение уравнения ${displaystyle x^{2}=a,}$ и его в принципе можно определить не только для чисел, но и всюду, где такое уравнение имеет смысл. В общей алгебре применяется следующее формальное определение:

Чаще всего рассматривают такие обобщения в алгебраических кольцах.

Если кольцо есть область целостности, то квадратных корней из ненулевого элемента может быть либо два, либо ни одного. В самом деле, если имеются два корня $a,b,$ то ${displaystyle a^{2}=b^{2},}$ откуда: ${displaystyle (a-b)(a+b)=0}$ , то есть, в силу отсутствия делителей нуля, ${displaystyle a=pm b}$ . В более общем случае, когда в кольце имеются делители нуля или оно некоммутативно, число корней может быть любым.

В теории чисел рассматривается конечное кольцо вычетов по модулю $m$ : если сравнение ${displaystyle x^{2}equiv a{pmod {m}}}$ имеет решение, то целое число $a$ называется квадратичным вычетом (в противном случае — квадратичным невычетом). Решение указанного сравнения вполне аналогично извлечению квадратного корня в кольце вычетов^[22].

Корни для кватернионов имеют много общего с комплексными, но есть и существенные особенности. Квадратный кватернионный корень обычно имеет 2 значения, но если подкоренное выражение — отрицательное вещественное число, то значений бесконечно много. Например, квадратные корни из $-1$ образуют трёхмерную сферу, определяемую формулой^[23]:

${ai+bj+ckmid a^{2}+b^{2}+c^{2}=1},.$

Для кольца квадратных матриц доказано, что если матрица положительно определена, то положительно определённый квадратный корень из матрицы существует и единственен^[24]. Для матриц других типов корней может быть сколько угодно (в том числе ни одного).

Квадратные корни вводятся также для функций^[25], операторов^[26] и других математических объектов.

См. также[править | править код]

Быстрый инверсный квадратный корень
Вложенные радикалы
День квадратного корня
Кубический корень

Примечания[править | править код]

↑ Математическая энциклопедия (в 5 томах), 1982.
↑ ¹ ² Элементарная математика, 1976, с. 49.
↑ ¹ ² Корн Г., Корн Т. Справочник по математике, 1970, с. 33.
↑ История математики, 1970—1972, Том I, С. 42—46.
↑ Analysis of YBC 7289 (англ.). ubc.ca. Дата обращения: 19 января 2015. Архивировано 12 марта 2020 года.
↑ История математики, 1970—1972, Том I, С. 47.
↑ История математики, 1970—1972, Том I, С. 169—171.
↑ Башмакова И. Г. Становление алгебры (из истории математических идей). — М.: Знание, 1979. — С. 23. — (Новое в жизни, науке, технике. Математика, кибернетика, № 9).
↑ Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 81. — 208 с. — (История науки и техники).
↑ Знаки математические // Математическая энциклопедия. — М.: Советская Энциклопедия, 1982. — Т. 2. Архивировано 20 ноября 2012 года.
↑ История математики, 1970—1972, Том I, С. 296—298.
↑ История математики, 1970—1972, Том III, С. 56—59.
↑ История математики, 1970—1972, Том III, С. 62.
↑ Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I. — С. 58—66.
↑ Теорема Лиувилля о приближении алгебраических чисел
↑ Хинчин, 1960.
↑ Фихтенгольц, 4.
↑ Cooke, 2008.
↑ Фихтенгольц, 2.
↑ Курант, Роббинс, 2000.
↑ Курант, Роббинс, 2000, с. 148.
↑ Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — С. 71. — 180 с. Архивировано 4 ноября 2011 года.
↑ Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
↑ См., например: Гантмахер Ф. Р. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, или: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
↑ См., например: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, или: * Каплан И. А. Практические занятия по высшей математике. — Харьков: Изд-во ХГУ, 1966.
↑ См., например: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, или: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.

Литература[править | править код]

Воеводин В. В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. — Санкт-Петербург: БХВ-Петербург, 2006.
Ершов Л. В., Райхмист Р. Б. Построение графиков функций. — Москва: Просвещение, 1984.
Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье. — М.: Наука, 1976. — 591 с.
История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М.: Наука, 1970—1972.
Корень // Математическая энциклопедия (в 5 томах). — Москва: Советская Энциклопедия, 1982. — Т. 3.
Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд.. — Москва: Наука, 1970. — 720 с.
Курант Р., Роббинс Г. ГЛАВА III Геометрические построения. Алгебра числовых полей // Что такое математика?. — Москва: МЦНМО, 2000.
Понятов А. Откуда вырос арифметический корень? // Наука и жизнь. — 2022. — № 8. — С. 81—89.
Фихтенгольц Г. М. Введение, § 4 // [Мат. анализ на EqWorld Курс дифференциального и интегрального исчисления]. — Т. 1.
Фихтенгольц Г. М. Глава 2, § 1 // [Мат. анализ на EqWorld Курс дифференциального и интегрального исчисления]. — Т. 1.
Халмош П. Гильбертово пространство в задачах. — Москва: Мир, 1970.
Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. — Москва: Мир, 1983.
Хинчин А. Я. §§ 4, 10 // Цепные дроби. — Москва: ГИФМЛ, 1960.
Cooke, Roger. Classical algebra: its nature, origins, and uses (англ.). — John Wiley and Sons, 2008. — P. 59. — ISBN 0-470-25952-3.

Ссылки[править | править код]

Алгоритмы вычисления квадратного корня (англ.). Дата обращения: 12 октября 2006. Архивировано 19 ноября 2010 года.
Соловьев Ю. Старый алгоритм. Дата обращения: 6 ноября 2006. Архивировано 3 марта 2016 года.

Источник

Загрузить PDF

До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.

1
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число.^[1] Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
2
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b.^[2] Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
  - √(25 х 16)
  - √25 х √16
  - 5 х 4 = 20
3
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
  - √147
  - = √(49 х 3)
  - = √49 х √3
  - = 7√3
4
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
  - Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 – мы были правы.
5
Еще один способ – разложите подкоренное число на простые множители. Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
  - √88
  - = √(2 х 44)
  - = √ (2 х 4 х 11)
  - = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
  - = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Реклама

При помощи деления в столбик

1
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как “7 95 20 78 91 82, 47 89 70”.
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде “7 80, 14”. Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
2
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4 < 7, то есть 2² < 7 и n = 2. Напишите 2 сверху справа – это первая цифра в искомом квадратном корне. Напишите 2×2=4 справа снизу; вам понадобится это число для последующих вычислений.
3
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
4
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере второй парой чисел является “80”. Запишите “80” после 3. Затем, удвоенное число сверху справа дает 4. Запишите “4_×_=” снизу справа.
5
Заполните прочерки справа. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 – слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа – это вторая цифра в искомом квадратном корне числа 780,14.
6
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
7
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением “_×_=”.
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите “54_×_=” снизу справа.
8
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 – 4941 = 173.
9

Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).

Реклама

Понимание процесса

1

Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
2

Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C – третьей и так далее.
3

Задайте букву для каждой пары первых цифр. Обозначим через S_a первую пару цифр в значении S, через S_b – вторую пару цифр и так далее.
4

Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
5
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S_a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa < (A+1)²). В нашем примере, S1 = 7, и 2² ≤ 7 < 3²; таким образом A = 2.
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8 < 7×(d+1). В этом случае d будет равно 1.
6
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C – цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B². Запомните, что 10A+B – это такое число, у которого цифра B означает единицы, а цифра A – десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² – это площадь всего квадрата, 100A² – площадь большого внутреннего квадрата, B² – площадь малого внутреннего квадрата, 10A×B – площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
7

Вычтите A² из S_a. Для учета множителя 100 снесите одну пару цифр (S_b) из S: вам нужно, чтобы “SaSb” было равным общей площади квадрата, и из нее вычтите 100A² (площадь большого квадрата). В результате получите число N1, стоящее слева в шаге 4 (N = 380 в нашем примере). N1 = 2×10A×B + B² (площадь двух прямоугольников плюс площадь малого квадрата).
8

Выражение N1 = 2×10A×B + B² можно записать как N1 = (2×10A + B) × B. В нашем примере вам известно значение N1 (=380) и A(=2) и необходимо вычислить B. Скорее всего, B не является целым числом, поэтому необходимо найти наибольшее целое B, удовлетворяющее условию: (2×10A + B) × B ≤ N1. При этом B+1 будет слишком большим, поэтому N1 < (2×10A + (B+1)) × (B+1).
9

Решите уравнение. Для решения умножьте A на 2, переведите результат в десятки (что эквивалентно умножению на 10), поместите B в положение единиц, и умножьте это число на B. Это число (2×10A + B) × B и это выражение абсолютно идентичны записи “N_×_=” (где N=2×A) сверху справа в шаге 4. А в шаге 5 вы находите наибольшее целое B, которое ставится на место прочерков и соответствует неравенству: (2×10A + B) × B ≤ N1.
10

Вычтите площадь (2×10A + B) × B из общей площади (слева в шаге 6). Так вы получите площадь S-(10A+B)², которая еще не учитывалась (и которая поможет вычислить следующие цифры).
11

Для вычисления следующей цифры C повторите процесс. Слева снесите следующую пару цифр (Sc) из S для получения N2 и найдите наибольшее C, удовлетворяющее условию (2×10×(10A+B)+C) × C ≤ N2 (что эквивалентно двукратному написанию числа из пары цифр “A B” с соответствующим “_×_=”, и нахождению наибольшего числа, которое можно подставить вместо прочерков).

Реклама

Советы

Перемещение десятичного разделителя при увеличении числа на 2 цифры (множитель 100), перемещает десятичный разделить на одну цифру в значении квадратного корня этого числа (множитель 10).
В нашем примере, 1,73 может считаться остатком: 780,14 = 27,9² + 1,73.
Данный метод верен для любых чисел.
Записывайте процесс вычисления в том виде, который вам наиболее удобен. Например, некоторые записывают результат над исходным числом.
Альтернативный метод с использованием непрерывных дробей включает формулу: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x + …))). Например, для вычисления квадратного корня из 780,14, целым числом, квадрат которого близок к 780,14 будет число 28, поэтому z=780,14, x=28, y=-3,86. Подставляя эти значения в уравнение и решая его в упрощении до х+у/(2x), уже в младших членах получаем результат 78207/2800 или около 27,931(1), а в следующих членах 4374188/156607 или около 27,930986(5). Решение каждого последующего члена добавляет около 3 цифр к дробной доли по сравнению с предыдущем членом.

Предупреждения

Не забудьте разделить число на пары, начиная с дробной части числа. Например, разделяя 79520789182,47897 как “79 52 07 89 18 2,4 78 97″, вы получите бессмысленное число.

Источники

Об этой статье

Эту страницу просматривали 926 223 раза.

Была ли эта статья полезной?

Источник

Из этой статьи вы узнаете:

что такое «извлечение корня»;
в каких случаях он извлекается;
принципы нахождения значения корня;
основные способы извлечения корня из натуральных и дробных чисел.

Что такое «извлечение корня»

Для начала введем определение «извлечение корня».

Определение 1

Извлечение корня — процесс нахождения значения корня.

При извлечении корня n-ной степени из числа a, мы находим число b, n-ная степень которого равняется a. Если мы нашли такое число b, можно утверждать, что корень извлечен.

Замечание 1

Выражения «извлечение корня» и «нахождение значения корня» равнозначны.

В каких случаях извлекается корень?

Определение 2

Корень n-ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n-ной степени некоторого числа b.

Пример 1

4=2×2, следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2

Определение 3

Когда корень n-ной степени из числа a невозможно представить в виде n-ной степени числа b, то такой корень не извлекается, либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.

Пример 2

2≈1,4142.

Принципы нахождения значения корня и способы их извлечения

Использование таблицы квадратов, таблицы кубов и т.д.
Разложение подкоренного выражения (числа) на простые множители
Извлечение корней из дробных чисел
Извлечение корня из отрицательного числа
Поразрядное нахождение значения корня

Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.

Определение 4

Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: bnn=b, которое является справедливым для любого неотрицательного числа b.

Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.

Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).

Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.

Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.

И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.

Таблица квадратов

Таблица квадратов	единицы
0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2041
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.

Таблица кубов

Таблица кубов		единицы
0	1	2	3	4	5	6	7	8	9
десятки	0	0	1	8	27	64	125	216	343	512	729
1	1000	1 331	1 728	2 197	2 744	3 375	4 096	4 913	5 832	6 859
2	8000	9 261	10 648	12 167	13 824	15 625	17 576	19 683	21 952	24 389
3	27000	29 791	32 768	35 937	39 304	42 875	46 656	50 653	54 872	59 319
4	64000	68 921	74 088	79 507	85 184	91 125	97 336	103 823	110 592	117 649
5	125000	132 651	140 608	148 877	157 464	166 375	175 616	185 193	195 112	205 379
6	216000	226 981	238 328	250 047	262 144	274 625	287 496	300 763	314 432	328 509
7	343000	357 911	373 248	389 017	405 224	421 875	438 976	456 533	474 552	493 039
8	512000	531 441	551 368	571 787	592 704	614 125	636 056	658 503	681 472	704 969
	729000	753 571	778 688	804 357	830 584	857 375	884 736	912 673	941 192	970 299

Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.

Разложение подкоренного числа на простые множители

Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.

Определение 5

Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.

Пример 3

Извлечем квадратный корень из 144.

Разложим 144 на простые множители:

Таким образом: 144=2×2×2×2×3×3=(2×2)2×32=(2×2×3)2=122. Следовательно, 144=122=12.

Также при использовании свойств степени и корней можно записать преобразование немного по-другому:

144=2×2×2×2×3×3=24×32=24×32=22×3=12

144=12 – окончательный ответ.

Извлечение корней из дробных чисел

Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.

Определение 6

Следуя свойству корня из частного, справедливым является следующее равенство:

pqn=pnqn. Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.

Пример 4

Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.

Необходимо извлечь кубический корень из 474,552. Первым делом, представим десятичную дробь в виде обыкновенной: 474,552 = 474552/1000. Из этого следует: 47455210003=474552310003. Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:

474552=2×2×2×3×3×3×13×13×13=(2×3×13)3=783 и 1000=103, то

4745523=7833=78 и 10003=1033=10.

Завершаем вычисления: 474552310003=7810=7,8.

Извлечение корня из отрицательных чисел

Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа -a и нечетного показателя корня 2n-1 справедливо равенство:

-a2×n-1=-a2×n-1

Определение 7

Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.

Пример 5

-122092435. Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:

-122092435=12209243-5

Затем следует заменить смешанное число обыкновенной дробью:

12209243-5=3125243-5

Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:

3125243-5=-312552435

Вычисляем корни в числителе и знаменателе:

-312552435=-555355=-53=-123

Краткая запись решения:

-122092435=12209243-5=3125243-5=-312552435=-555355=-53=-123.

Ответ: -122092435=-123.

Поразрядное нахождение значения корня

Бывают случаи, когда под корнем находится число, которое не получается представить в виде n-ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.

В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.

Пример 6

Как это происходит, разберем на примере извлечения квадратного корня из 5.

Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0,1,2,…,9, вычисляя при этом 02, 12, …, 92 до необходимого значения, которое больше, чем подкоренное число 5. Все это удобно представить в виде таблицы:

Возможное значение корня	0	1	2	3
Это значение в степени	0	1	4	9

Значение ряда единиц равняется 2 (так как 22<5, а 23>5). Переходим в разряду десятых — будем возводить в квадрат числа 2,0, 2,1, 2,2,…,2,9, , сравнивая полученные значения с числом 5.

Возможное значение корня	2,0	2,1	2,2	2,3
Это значение в степени	4	4,41	4,84	5,29

Поскольку 2,22<5, а 2,32>5, то значение десятых равняется 2. Переходим к нахождению значения сотых:

Возможное значение корня	2.20	2,21	2,22	2,23	2,24
Это значение в степени	4,84	4,8841	4,8294	4,9729	5,0176

Таким образом, найдено значение корня из пяти — 2,23. Можно находить значения корня дальше:

2,236, 2,2360, 2, 23606, 2,236067,…

Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.

Источник

Что такое арифметический квадратный корень

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа (a) называется такое неотрицательное число, квадрат которого равен (a). ( (sqrt{a}=x, {{x}^{2}}=a; x, age 0)).

А почему же число ( a) (число под корнем) должно быть обязательно неотрицательным?

Например, чему равен ( sqrt{-9})?

Так-так, попробуем подобрать. Может, три?

Проверим: ( {{3}^{2}}=9), а не ( -9).

Может, ( left( -3 right))?

Опять же, проверяем: ( {{left( -3 right)}^{2}}=9).

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!

Число или выражение под знаком корня должно быть неотрицательным!

Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!

Ведь в определении сказано, что «квадратным корнем из числа( a)называется такое неотрицательное число, квадрат которого равен( a)».

Но подождите! В самом начале мы разбирали пример ( {{x}^{2}}=4) и один из ответов был отрицательным числом!

Мы подбирали числа, которые можно возвести в квадрат и получить при этом ( displaystyle 4). Ответом были ( displaystyle 2) и ( displaystyle -2)

А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?

Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.

К примеру, ( displaystyle {{x}^{2}}=4) (квадратное уравнение) не равносильно выражению ( x=sqrt{4}) (арифмитический квадратный корень).

Из ( {{x}^{2}}=4) следует, что

( left| x right|=sqrt{4}), то есть ( x=pm sqrt{4}=pm 2) или ( {{x}_{1}}=2); ( {{x}_{2}}=-2)

(не помнишь почему так? Почитай тему «Модуль числа»!)

А из ( x=sqrt{4}) следует, что ( x=2).

Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как ( 2), так и ( x=-2).

Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

Запись иррациональных чисел с помощью квадратного корня

А теперь попробуй решить такое уравнение ( {{x}^{2}}=3).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: ( {{0}^{2}}=0) – не подходит.

Двигаемся дальше ( displaystyle x=1); ( displaystyle {{1}^{2}}=1) – меньше трех, тоже отметаем.

А что если ( displaystyle x=2)?

Проверим: ( displaystyle {{2}^{2}}=4) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между ( displaystyle 1) и ( displaystyle 2), а также между ( displaystyle -2) и ( displaystyle -1).

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции ( displaystyle y={{x}^{2}}) и отметим на нем решения.

Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!

Извлечем корень из ( displaystyle 3), делов-то!

Ой-ой-ой, выходит, что ( sqrt{3}=1,732050807568ldots ) Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. ( sqrt{3}) и ( -sqrt{3}) уже сами по себе ответы.

Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.

Деление корней

С умножением корней разобрались, теперь приступим к свойству деления.

Напомню, что формула в общем виде выглядит так:

( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b>0).

А значит это, что корень из частного равен частному корней.

Ну что, давай разбираться на примерах:

( displaystyle frac{sqrt{12}}{sqrt{3}}=sqrt{frac{12}{3}}=sqrt{4}=2)

Вот и вся наука. А вот такой пример:

( displaystyle frac{sqrt{12}}{3}=frac{sqrt{12}}{sqrt{9}}=sqrt{frac{12}{9}}=sqrt{frac{4}{3}}=frac{2}{sqrt{3}})

Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.

А что, если попадется такое выражение:

( displaystyle sqrt{frac{144}{225}}=?)

Надо просто применить формулу в обратном направлении:

( displaystyle sqrt{frac{144}{225}}=frac{sqrt{144}}{sqrt{225}}=frac{12}{15}=frac{4}{5}=0,8)

А вот такой примерчик:

( displaystyle sqrt{0,16}=sqrt{frac{16}{100}}=frac{4}{10}=0,4)

Еще ты можешь встретить такое выражение:

( displaystyle sqrt{5frac{19}{25}}=?)

Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!

( displaystyle sqrt{5frac{19}{25}}=sqrt{frac{144}{25}}=frac{12}{5}=2,4)

Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.

Возведение в степень

А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа ( displaystyle a) – это число, квадратный корень которого равен ( displaystyle a).

Так вот, если мы возводим число, квадратный корень которого равен ( displaystyle a), в квадрат, то что получаем?

Ну, конечно, ( displaystyle a)!

Рассмотрим на примерах:

( displaystyle {{left( sqrt{12} right)}^{2}}=12)

( displaystyle {{left( sqrt{17} right)}^{2}}=17)

Все просто, правда? А если корень будет в другой степени? Ничего страшного!

Придерживайся той же логики и помни свойства и возможные действия со степенями.

Забыл?

Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.

Вот, к примеру, такое выражение:

( displaystyle {{left( sqrt{5} right)}^{6}}={{left( {{left( sqrt{5} right)}^{2}} right)}^{3}}={{5}^{3}}=125)

В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:

( displaystyle {{left( sqrt{5} right)}^{7}}={{left( sqrt{5} right)}^{6}}cdot sqrt{5}=125sqrt{5})

С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:

( displaystyle sqrt{{{3}^{2}}}=sqrt{9}=3)

Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:

( displaystyle sqrt{{{3}^{6}}}=sqrt{{{left( {{3}^{3}} right)}^{2}}}={{3}^{3}}=27)

( displaystyle sqrt{{{3}^{5}}}=sqrt{{{3}^{4}}cdot 3}=sqrt{{{left( {{3}^{2}} right)}^{2}}cdot 3}={{3}^{2}}cdot sqrt{3}=9sqrt{3})

Ну как, все понятно? Тогда реши самостоятельно примеры:

( displaystyle sqrt{{{left( -3 right)}^{2}}})
( displaystyle sqrt{{{6}^{6}}})
( displaystyle {{left( sqrt{8} right)}^{7}})

А вот и ответы:

Извлечение корней из больших чисел

До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!

( displaystyle sqrt{98}=sqrt{49cdot 2}=sqrt{49}cdot sqrt{2}=7sqrt{2})

Можно было пойти по иному пути и разложить на другие множители:

( displaystyle sqrt{98}=sqrt{7cdot 14})

Что дальше? А дальше раскладываем на множители до самого конца:

( displaystyle sqrt{98}=sqrt{7cdot 14}=sqrt{7cdot 7cdot 2}=sqrt{{{7}^{2}}cdot 2}=7sqrt{2})

Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.

Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:

( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12})

Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:

А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):

( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12}=sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6})

Разве это конец? Не останавливаемся на полпути!

( displaystyle begin{array}{l}sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6}=sqrt{5cdot 3}cdot sqrt{3cdot 12cdot 5}cdot sqrt{2cdot 3cdot 2}=\=sqrt{5cdot 3}cdot sqrt{3cdot 2cdot 2cdot 3cdot 5}cdot sqrt{2cdot 3cdot 2}end{array})

На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:

( displaystyle begin{array}{l}sqrt{5cdot 3cdot 3cdot 2cdot 2cdot 3cdot 5cdot 2cdot 3cdot 2}=sqrt{5cdot 5cdot 3cdot 3cdot 3cdot 3cdot 2cdot 2cdot 2cdot 2}=\=sqrt{25}cdot sqrt{81}cdot sqrt{16}=5cdot 9cdot 4=180end{array})

Вот и все, не так все и страшно, правда?

( displaystyle sqrt{15}cdot sqrt{54}cdot sqrt{10}=?)

Получилось ( displaystyle 90)? Молодец, все верно!

А теперь попробуй вот такой пример решить:

( displaystyle sqrt{4225}=?)

А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.

Источник

Приветствую Вас, уважаемые Читатели! Сегодня продолжаем цикл статей, посвященных основам школьной математики, которые неплохо бы знать каждому взрослому человеку. Поговорим о квадратном корне и его свойствах. Поехали!

Источник: http://clipart-library.com/img1/1156351.png

Итак, квадратный корен – это частный случай корня n-ной степени при n=2. Как и у любого математического понятия у квадратного корня есть определение, например:

Квадратный корень из числа а – это решение указанного выше уравнения. Обратите внимание на +-, а также на то, что цифру “2” при записи знака радикала по умолчанию опускают.

У каждого положительного числа есть два противоположных квадратных корня, например, для 16 – это 4 и -4. В школьном курсе математики ограничиваются неотрицательными числами под знаком квадратного корня, но мы же знаем, что извлечь его можно и из отрицательного числа, перейдя к комплексным числам.

Кстати, арифметическим квадратным корнем из неотрицательного числа называется именно то значение, которое больше нуля.

График квадратного корня

Квадратный корень на области своего определения является монотонной возрастающей функцией. График его выглядит так:

Источник: https://otvet.imgsmail.ru/download/45720838_53f458062dcde8834277f3810ebdd18c_800.jpg

Квадратный корень занимает особое место в геометрических построениях с помощью циркуля и линейки: в общем виде возможно построить только такие отрезки, длина которых описывается выражениями содержащими основные арифметические операции и квадратный корень.

В языках программирования общепринятой записью операции извлечения квадратного корня является запись sqrt(x).

Как извлечь квадратный корень ?

Извлечение квадратного корня – очень важный с алгоритмической точки зрения процесс. Поэтому следует различать алгоритмы, которые могут быть в жизненных ситуациях от тех, которые применяются при высокоскоростной обработке данных.

Можно извлечь и так. Источник: https://belnaviny.by/wp-content/uploads/2019/06/belnaviny.by-v-kobrinskom-rajone-likvidiruyut-posledstviya-uragana.jpg

Например, квадратный корень можно считать как на калькуляторе, так и в столбик, ведь никаких требований к скорости вычислений не предъявляется.

В практических задачах всё по-другому. Например, некоторые алгоритмы извлечения квадратного корня подразумевают нахождение первоначальной грубой оценки:

Для нечетных D в выражении 6 поменяется на 2, а само D = 2n+1

Оценка действительно очень грубая, но для еще бОльших чисел она даёт неплохой быстрый старт для итеративных алгоритмов.

Естественно, квадратный корень не ограничивается только числами. Существуют и применяются его расширения, например для матриц.

Наиболее точный алгоритм вычисления квадратного корня использовался еще в древнем Вавилоне, но в математике он известен под названием “итеративная формула Герона”:

Всё, что нужно знать о квадратном корне. Вспоминаем математику

Источник

История[править | править код]

Квадратные корни из чисел[править | править код]

Рациональные числа[править | править код]

Действительные (вещественные) числа[править | править код]

Комплексные числа[править | править код]

Квадратный корень как элементарная функция[править | править код]

В элементарной геометрии[править | править код]

В информатике[править | править код]

Применение[править | править код]

Алгоритмы нахождения квадратного корня[править | править код]

Разложение в ряд Тейлора[править | править код]

Грубая оценка[править | править код]

Геометрическое извлечение квадратного корня[править | править код]

Итерационный аналитический алгоритм[править | править код]

Столбиком[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

При помощи деления в столбик

Понимание процесса

Советы

Предупреждения

Похожие статьи

Источники

Об этой статье

Была ли эта статья полезной?

Что такое «извлечение корня»

В каких случаях извлекается корень?

Принципы нахождения значения корня и способы их извлечения

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов

Таблица кубов

Разложение подкоренного числа на простые множители

Извлечение корней из дробных чисел

Извлечение корня из отрицательных чисел

Поразрядное нахождение значения корня

Что такое арифметический квадратный корень

Запись иррациональных чисел с помощью квадратного корня

Деление корней

Возведение в степень

Извлечение корней из больших чисел

График квадратного корня

Как извлечь квадратный корень ?

Вам также может понравиться

Как исправить ошибки в своем сайте на главной странице

Как найти координаты прямого восхождения

Как найти парня в симс 4 подростку

Добавить комментарий Отменить ответ