Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 28 человек из 14 регионов




- Сейчас обучается 249 человек из 63 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
ТЕМА ПИРАМИДА Кониченко Елена Михайловна учитель 1 категории школа № 4 им. А.Н. Кесаева г. Севастополь
-

2 слайд
ЦЕЛИ УРОКА : а) образовательные: познакомить учащихся с понятием –пирамида; познакомить учащихся с элементами пирамиды; научить учащихся находить грани, ребра, вершины пирамиды; научить учащихся выполнять построение пирамиды и ее развертки; научить учащихся вычислять длину ребер пирамиды; б) развивающие: развитие пространственного воображения; формирование способности сравнивать геометрические фигуры, обобщать полученные знания, формирование логического мышления; в) воспитательные: привитие навыка аккуратности при построении чертежа; активизация интереса учащихся к получению новых знаний; воспитание трудолюбия. Тип урока: изучение нового материала.
-

3 слайд
УСТНЫЙ СЧЕТ Вычислите и запишите результаты по возрастанию чисел. Поставьте соответствующие буквы и прочитайте название темы урока. 1) 20 x 7 4) 23 + 47 7) 100 – 10 – 50 : 7 x 90 : 5 x 16 + 1900 + 33 – 90 : 100 = … М = … И = … Д 2) 100 – 77 5) 620 + 190 8) 54 : 6 x 3 : 90 + 34 + 51 x 20 x 2 : 12 – 180 – 56 = … И = … П = … А 3) 200 : 4 6) 4 x 40 + 70 + 260 x 5 : 6 – 240 – 45 = … А = … Р
-

4 слайд
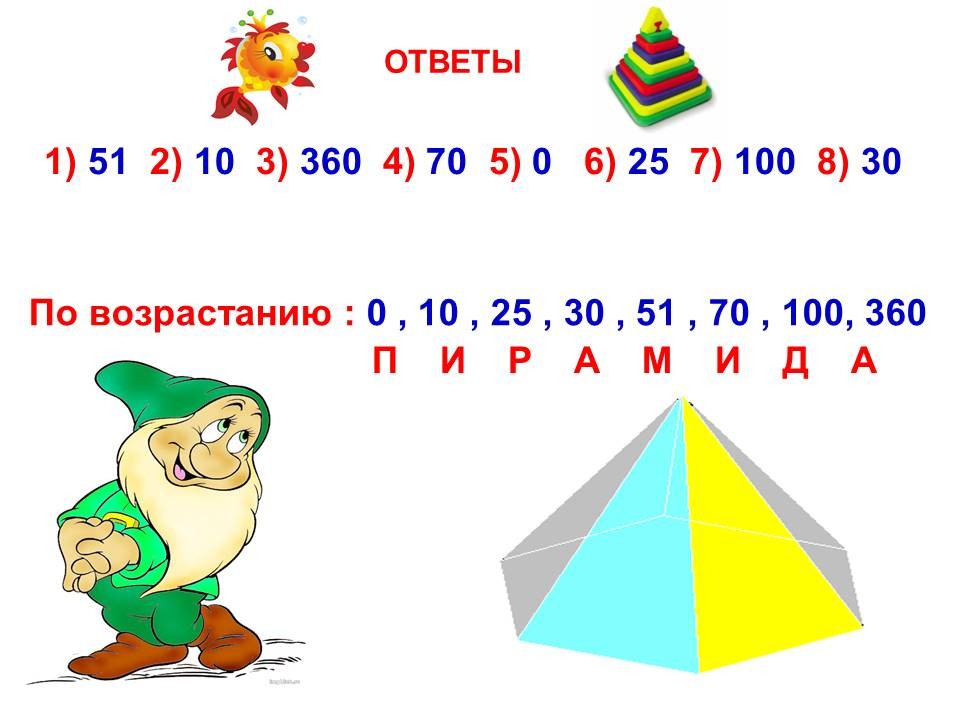
ОТВЕТЫ 1) 51 2) 10 3) 360 4) 70 5) 0 6) 25 7) 100 8) 30 По возрастанию : 0 , 10 , 25 , 30 , 51 , 70 , 100, 360 П И Р А М И Д А
-

5 слайд
Назовите представленные на картинках предметы: 1) 2) 3) 4)
-

6 слайд
Все эти предметы дают представление о пирамиде:
-

-

8 слайд
Многоугольники Назовите виды многоугольников на рисунках: 1 2 3 4 5 6 7 8
-

9 слайд
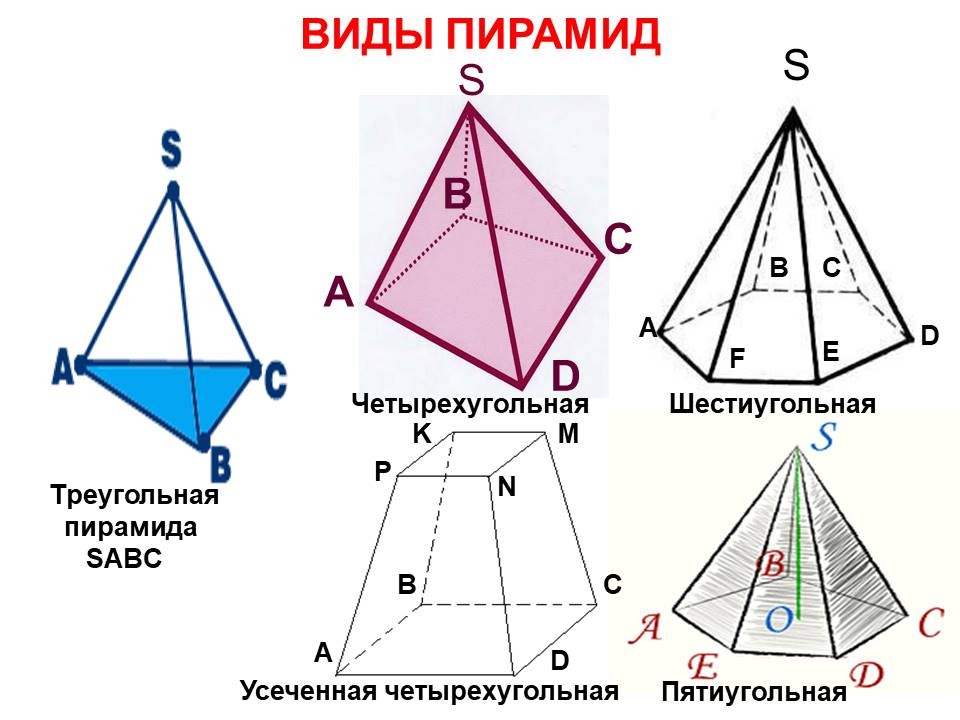
ВИДЫ ПИРАМИД S S Треугольная пирамида SABC Четырехугольная Шестиугольная Пятиугольная Усеченная четырехугольная A B C D A B C D E F A B C D P K M N
-

10 слайд
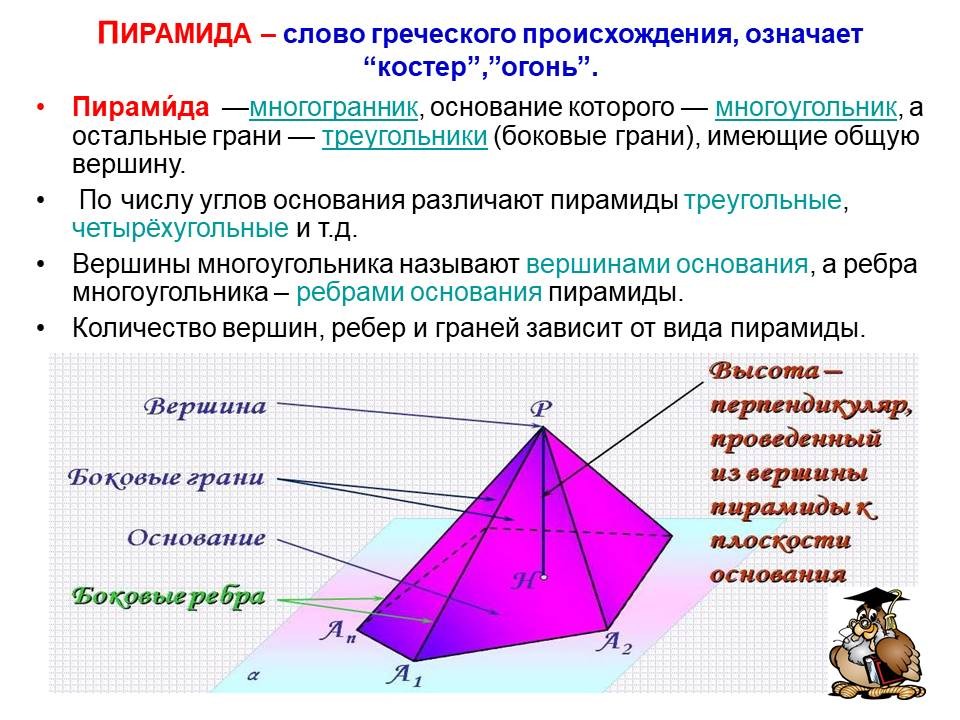
ПИРАМИДА – слово греческого происхождения, означает “костер”,”огонь”. Пирами́да —многогранник, основание которого — многоугольник, а остальные грани — треугольники (боковые грани), имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т.д. Вершины многоугольника называют вершинами основания, а ребра многоугольника – ребрами основания пирамиды. Количество вершин, ребер и граней зависит от вида пирамиды.
-

11 слайд
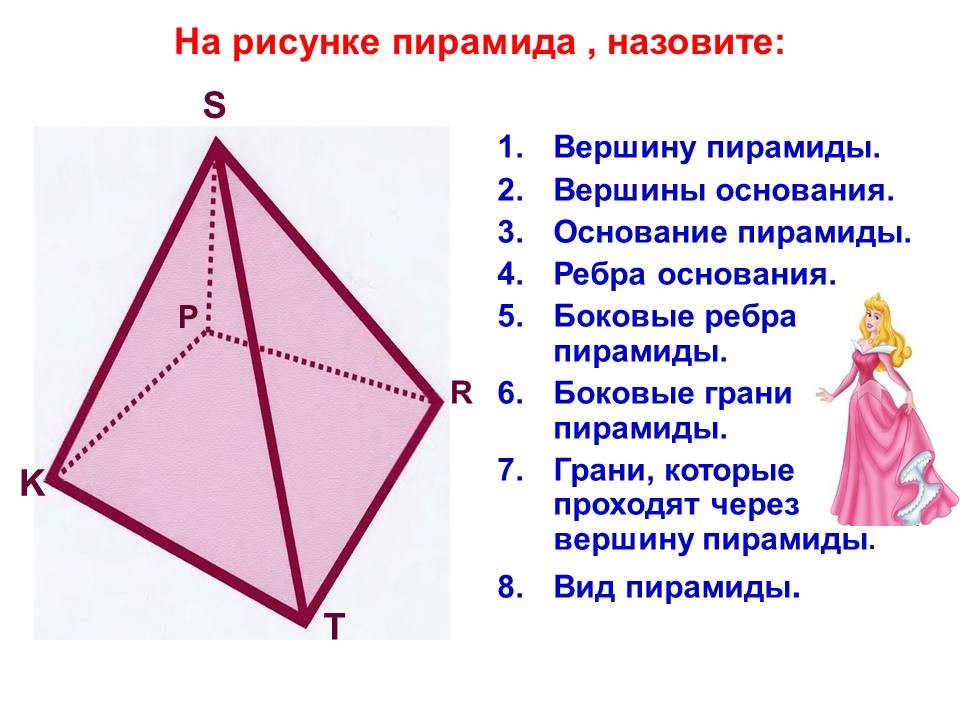
На рисунке пирамида , назовите: Вершину пирамиды. Вершины основания. Основание пирамиды. Ребра основания. Боковые ребра пирамиды. Боковые грани пирамиды. Грани, которые проходят через вершину пирамиды. Вид пирамиды. S K P R T
-

12 слайд
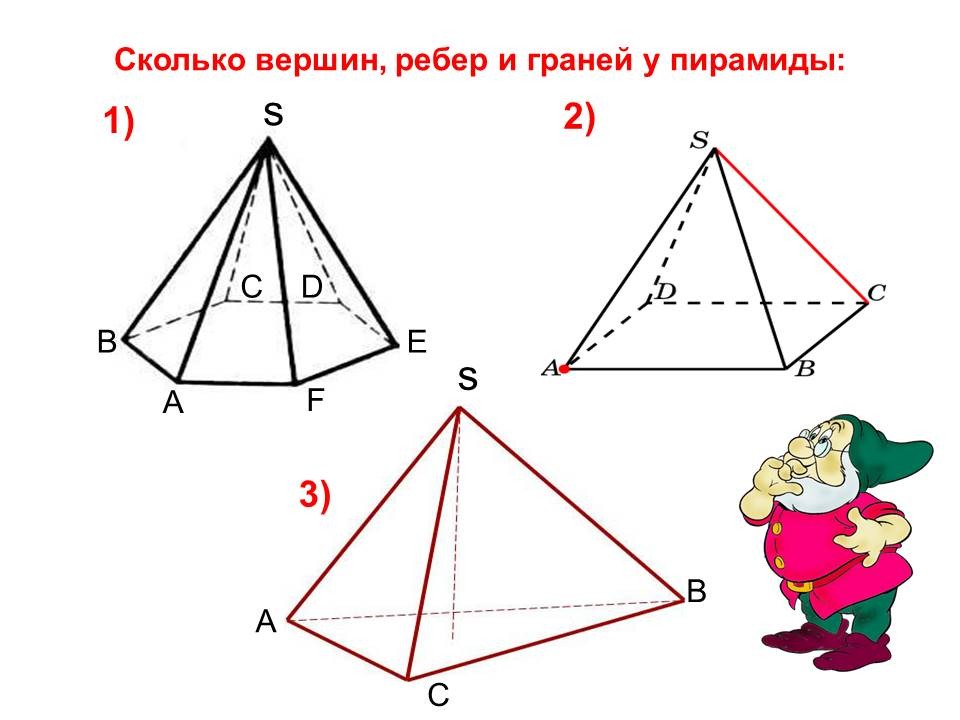
Сколько вершин, ребер и граней у пирамиды: s s A B C A B C D E F 1) 2) 3)
-

13 слайд
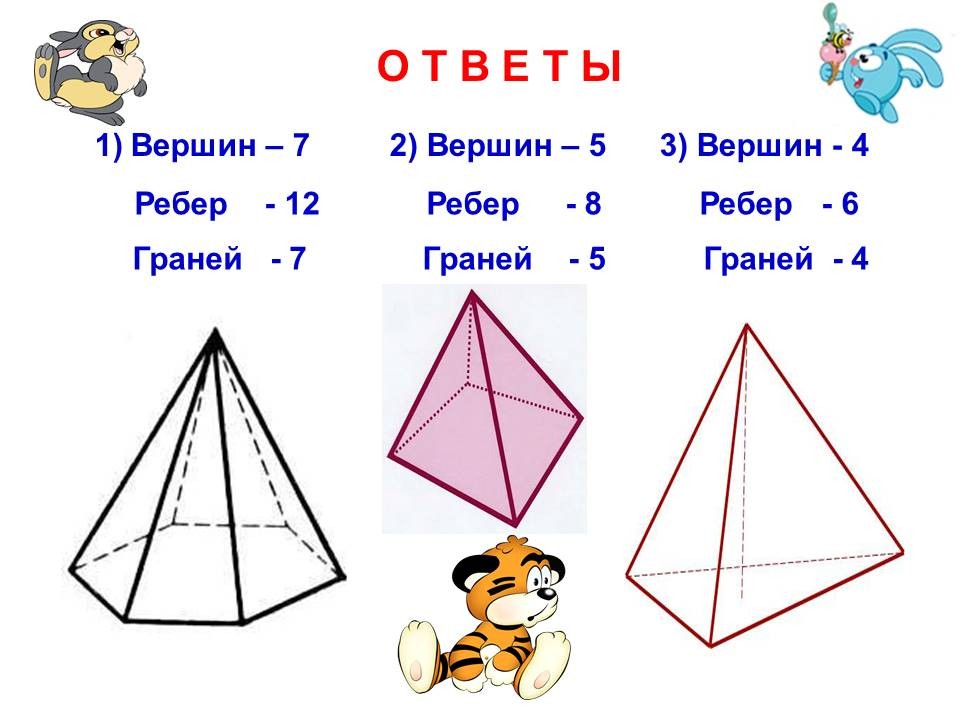
О Т В Е Т Ы Вершин – 7 2) Вершин – 5 3) Вершин – 4 Ребер – 12 Ребер – 8 Ребер – 6 Граней – 7 Граней – 5 Граней – 4
-

14 слайд
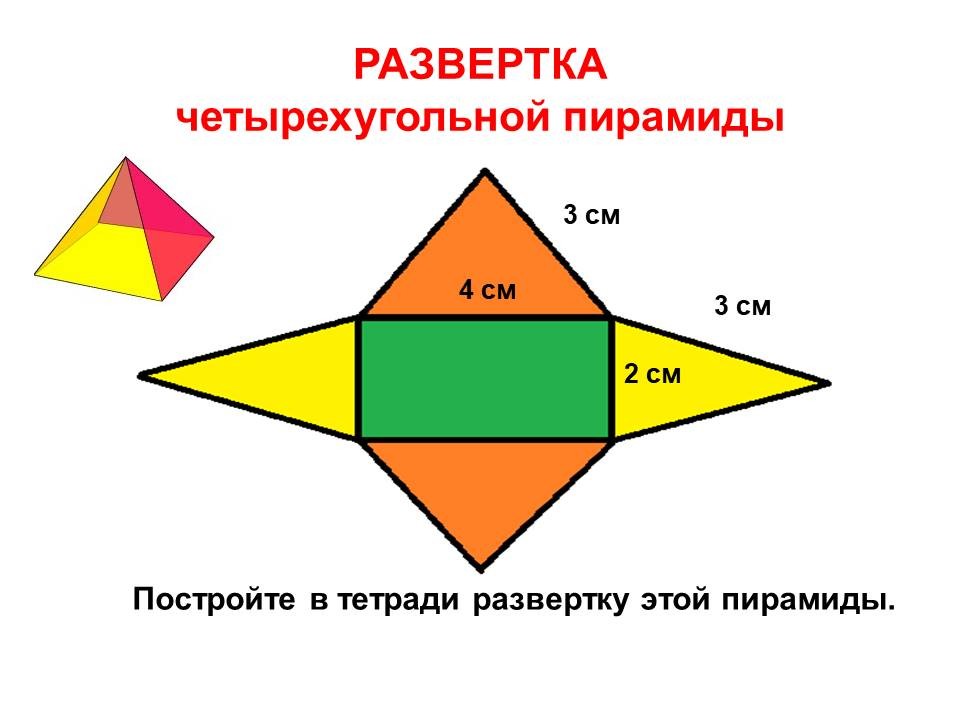
РАЗВЕРТКА четырехугольной пирамиды 3 см 3 см 4 см 2 см Постройте в тетради развертку этой пирамиды.
-

15 слайд
ФИЗКУЛЬТМИНУТКА Потрудились-отдохнем, Встанем, глубоко вздохнем. Руки в стороны, вперед, Влево, вправо, поворот. Три наклона, прямо встать. Руки вниз и вверх поднять. Руки плавно опустили, Всем улыбки подарили.
-

16 слайд
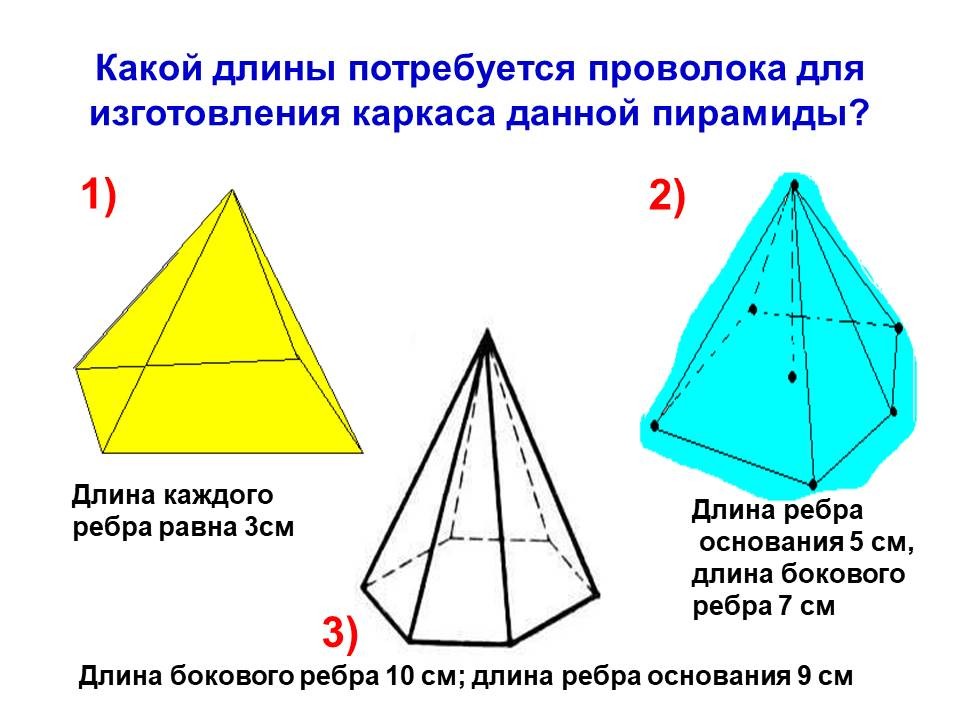
Какой длины потребуется проволока для изготовления каркаса данной пирамиды? 1) 2) 3) Длина каждого ребра равна 3см Длина ребра основания 5 см, длина бокового ребра 7 см Длина бокового ребра 10 см; длина ребра основания 9 см
-

17 слайд
ОТВЕТЫ: 1) 8 x 3 = 24 ( см ) 2) 5 x 5 + 5 x 7 = 25 + 35 = 60 ( см ) 3) 6 x 9 + 6 x 10 = 54 + 60 = 114 ( см )
-

18 слайд
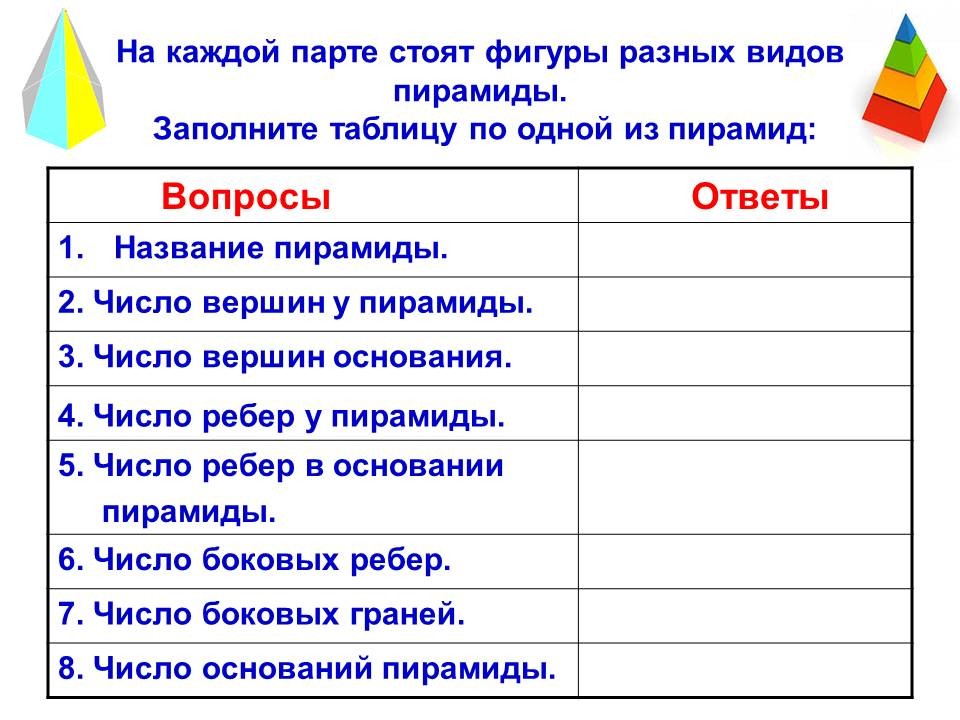
На каждой парте стоят фигуры разных видов пирамиды. Заполните таблицу по одной из пирамид:
-

19 слайд
Задание: по данным своей таблицы заполните пропуски в тексте Число вершин пирамиды на ________ больше числа вершин в ее основании. Ребер боковых граней _________, сколько их в основании. Число боковых граней _________ числу сторон основания.
-

20 слайд
Проверьте свои выводы: Число вершин пирамиды на единицу больше числа вершин в ее основании. Ребер боковых граней столько же, сколько их в основании. Число боковых граней равно числу сторон основания.
-

21 слайд
ПИРАМИДЫ вокруг нас
-

-

23 слайд
Спасибо за урок .
Краткое описание документа:
•ЦЦели презентацииа)образовательные:
•познакомить учащихся с понятием –пирамида;
•познакомить учащихся с элементами пирамиды;
•научить учащихся находить грани, ребра, вершины пирамиды;
•научить учащихся выполнять построение пирамиды и ее развертки;
•научить учащихся вычислять длину ребер пирамиды;
•б) развивающие:
•развитие пространственного воображения;
•формирование способности сравнивать геометрические фигуры, обобщать полученные знания, формирование логического мышления;
•в) воспитательные:
•привитие навыка аккуратности при построении чертежа;
•активизация интереса учащихся к получению новых знаний;
•воспитание трудолюбия.
•
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 119 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
-
Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
5 из 5
- 18.11.2014
- 5556
- 19
Рейтинг:
4 из 5
- 18.11.2014
- 13959
- 164
- 18.11.2014
- 1877
- 0
Рейтинг:
4 из 5
- 18.11.2014
- 5793
- 259
Рейтинг:
5 из 5
- 18.11.2014
- 9388
- 162
- 18.11.2014
- 1339
- 0
- 18.11.2014
- 3783
- 11
Цели урока:
Познавательные:
Познакомить учащихся с геометрическим телом –
пирамидой.
Обучающие:
- Уметь из данных многогранников находить
пирамиду, - Уметь находить основание и боковые грани
пирамиды, - Уметь давать название пирамидам.
Развивающие:
- Развитие логического мышления, умения
самостоятельно работать, умения говорить и
слушать
Воспитательные:
- Выработка привычки к постоянной занятости
каким-либо полезным делом, - Воспитание отзывчивости, трудолюбия,
аккуратности.
Оборудование: модели многогранников,
карточки для устного счета, линейка, цветные
мелки.
План урока
- Организационный момент 3 мин
- Устная работа 7 мин
- Объяснение нового материала 10 мин
- Отработка нового материала 15 мин
- Резерв
- Итоги урока 2 мин
- Домашнее задание 3 мин
Ход урока
I. Организационный момент
II. Устная работа
Решить устно:
А 46-113/8
М 42•2/3
Д 10:6
П 2•19
И 14+237/8
А 2/3+3/8
Р 82-45
И 8:1/3
Составьте слово, расположив ответы примеров в
порядке убывания, и вы узнаете тему нашего урока.
Работа в парах. Из предложенных
геометрических тел найдите многогранники.
Почему выбранные вами многогранники являются
многогранниками? С какими многогранниками вы уже
знакомы?
(На каждую парту выдаются модели
геометрических тел).
III. Объяснение нового материала
Как уже вы знаете, тема нашего урока
“Пирамида”, поэтому мы сегодня должны
познакомиться с этим геометрическим телом.
( В тетрадях записывается число, классная
работа, тема урока).
“Пирамида” – слово греческого
происхождения, означает “костер”, “огонь”.
Где вы встречались с пирамидой?
Ответы: На уроках истории (пирамида Хеопса).
В архитектуре (крыши домов, музей современного
искусства в Париже). Также можно встретить
пирамиду в виде сувениров, свечей, упаковки.
Одним из интересных фактов является то, что
продукты, находящиеся в упаковке в виде пирамиды,
лучше и дольше сохраняются.
Важным и интересным семейством многогранником
являются пирамиды.
(Работа с моделями пирамид).
У пирамиды различают боковые грани –
треугольники, сходящиеся в одной вершине и основание
– многоугольник, противолежащий этой вершине. В
основании пирамиды может лежать многоугольник с
любым количеством сторон. Называют пирамиду по
числу сторон ее основания: треугольная,
четырехугольная, шестиугольная и т.д.
(Продемонстрировать)
Простейшей пирамидой и даже простейшим
многогранником является треугольная пирамида,
которая называется тетраэдром . Тетраэдр
изображен в учебнике на с.314 рис. 275; начертите ее в
тетради. Обозначьте ее.
- Какую форму имеют ее грани? ( Треугольники).
- Сколько граней у пирамиду? (4) Назовите их.
- Сколько боковых граней у пирамиды? ( 3) Назовите
их. - Назовите основание пирамиды.
- Сколько ребер у пирамиды? (6) Назовите их.
- Сколько боковых ребер у пирамиды? ( 3) Назовите
их. - Сколько вершин? (4) Назовите их.
- Сколько ребер выходит из каждой вершины? (3)
Каждую грань можно считать основанием. Ни у
одного многогранника не может быть меньшего
числа граней, вершин или ребер, чем у треугольной
пирамиды.
IY. Отработка нового материала
Работа в группах.
(У каждой группы на столе пирамида, таблица и
текст к таблице).
Заполнить таблицу.
|
Вопросы |
Ответы |
| 1. Число вершин пирамиды. | |
| 2. Число вершин основания пирамиды. |
|
| 3. Число ребер у пирамиды. | |
| 4. Число ребер боковых граней пирамиды. |
|
| 5. Число ребер в основании пирамиды. |
|
| 6. Число боковых граней. | |
| 7. Число сторон основания. | |
| 8. Название пирамиды. |
По данным таблицы заполните пропуски в тексте.
Число вершин пирамиды на _______________ больше числа
вершин в ее основании.
Ребер боковых граней _________________, сколько их в
основании.
Число боковых граней _________________ числу сторон
основания.
После выполнения группами задания проверить
выводы.
Ответы:
Число вершин пирамиды на единицу больше
числа вершин в ее основании.
Ребер боковых граней столько же , сколько
их в основании.
Число боковых граней равно числу сторон
основания.
Работа с классом.
1. С. 314 №1264 (рис. а и в).
2. Назовите пирамиду на рис. 276. Укажите ее
основание и боковые грани. Начертите пирамиду в
тетради.
3. С.314 №1267.
4. Нужно изготовить каркасную модель
треугольной пирамиды, все ребра которой равны 7
см. Сколько потребуется проволоки?
Ответ:(6•7=42)
Y. Резерв. №1265, 1271(1)
YI. Итоги урока
С чем мы сегодня познакомились и что вы узнали
нового?
(Каждый ученик высказывается по данному
вопросу).
YII. Домашнее задание
П. 10.4, на “3” №1264 (рис. б), 1266;
на “4” №1264 (рис. б), 1266, №1268;
на “5” №1264 (рис. б), 1266, №1268, №1270.
Как нарисовать пирамиду

Умение рисовать простые геометрические фигуры — это базовый навык для любого художника.
Пирамида имеет грани и грани, такие как куб или призма , и соответственно способы изображения всех этих геометрических фигур очень близки.

Как и в уроке по рисованию куба, начните с переднего нижнего угла, изобразив его двумя прямыми линиями. Очень важно помнить, что мы изображаем объемный объект. Имея это в виду, гораздо проще построить правильные трехмерные геометрические фигуры.

Теперь, следуя той же методике, изобразите дальнюю половину нижнего основания пирамиды. Напомним еще раз, что крайне важно учитывать правила линейной перспективы и воздушная перспектива, чтобы рисунок пирамиды получился правильным и естественным.

Чтобы пирамида получилась ровной и пропорциональной, нам нужно найти центральную вертикальную ось. Для этого изобразите две линии, выходящие из углов и пересекающиеся в центре основы. Не забывайте, что линии должны быть очень светлыми, ведь это всего лишь конструктивные линии, которые в дальнейшем будут стираться.

Итак, длинной прямой вертикальной линией изобразите центральную ось, которая начинается в точке, указанной на предыдущем этапе. Не забывайте, что эта линия также будет стерта в будущем, поэтому постарайтесь сделать ее максимально светлой, едва заметной.

Теперь изобразите четыре линии, которые идут от углов, поднимаются и соединяются в одной точке наверху. Не забывайте, что по законам воздушной перспективы передний край должен быть самым темным, а линии на расстоянии должны быть намного светлее.

Теперь аккуратно избавьтесь от всех линий построения, которые мы создали на первых этапах, и придайте изображению более законченный и чистый вид. Напомним, что для того, чтобы проверить пропорциональность художественного произведения, нужно посмотреть на него в зеркало, и тогда все ошибки будут заметны.

Чтобы пирамида приобрела по-настоящему объемный и реалистичный вид, нужно изобразить тени. С помощью равномерной штриховки начните изображать тени, как это сделано на изображении. Не забывайте также, что штриховку следует изображать с учетом форм и объемов геометрической фигуры.

Продолжайте добавлять тени, делая их темнее и контрастнее там, где это необходимо. На этом же этапе добавьте тон к светлой стороне и изобразите отбрасываемую тень так, чтобы геометрическая фигура не выглядела зависшей в воздухе, а спокойно стояла на поверхности.

Урок, как нарисовать пирамиду, закончен. Посмотрите на свои работы и сравните их с изображением. Если вы обнаружите какие-либо неточности и ошибки, то вернитесь к тому этапу, на котором вы допустили ошибку, и попробуйте исправить ее.
Если ваша работа выглядит правильно и вы не обнаружили ошибки, не спешите расслабляться. Как мы уже говорили ранее, если вы научитесь рисовать хотя бы полчаса в день, вы постепенно поднимете свои навыки рисования до невероятного уровня.













 Назад Вперёд
Назад Вперёд
Учебник: Математика 5 класс. Г.В.Дорофеев, И.Ф.Шарыгин, С.В.Суворова и др. ФГОС.
Тип урока: урок применения полученных знаний в практике.
Форма урока: урок-исследование.
Цель урока: организация работы по формированию знаний и исследованию пирамиды, построение развёртки и моделирование пирамиды.
Задачи: определить элементы пирамиды, исследовать особенности пирамиды, изучить виды пирамид, построить развёртку пирамиды, изготовить модель пирамиды.
Образовательные: продолжить изучение основных элементов пирамиды, научить учащихся находить грани, рёбра, вершины пирамиды, познакомить с развёрткой пирамиды и научить моделировать пирамиду.
Развивающие: развивать пространственное воображение, формировать способности сравнивать геометрические фигуры, обобщать полученные знания, формировать логическое мышление и навыки грамотной математической речи.
Воспитательные: прививать навыки аккуратности при построении чертежа, воспитывать положительную мотивацию к учению, умение выслушивать товарища, высказывать свою точку зрения, активизация интереса учащихся к получению новых знаний, воспитание трудолюбия.
Оборудование: компьютер с проектором, презентация, ролик, карточки, учебники, модели пирамид, развертки пирамид, ножницы, картон, клей, раздаточный материал.
Планируемые образовательные результаты:
Личностные
Метапредметные
Предметные
Умение выдвигать гипотезы и отстаивать свою позицию. Находчивость и активность при выполнении исследовательской работы. Осознание личной ответственности за общее дело. Умение признавать собственные ошибки.
Регулятивные
Коммуникативные
Познавательные
Формулировать определение пирамиды, распознавать пирамиду на чертежах, рисунках, в окружающем мире; определять количество граней, ребер, вершин пирамиды; моделировать пирамиду, используя трубочки и пластилин; моделировать пирамиду из разверток.
Умение определять тему, цель, организовать выполнение заданий учителя, преодолевать трудности на пути достижения цели, адекватно их оценивая, уметь контролировать свое время при выполнении задания.
Умение работать в составе группы, планировать успешное сотрудничество, аргументировать свою точку зрения, задавать вопросы с целью получения нужной информации
Вырабатывать умение работать с различными источниками информации, работать с таблицами, дополнять их необходимыми данными, структурировать учебный материал, грамотно формулировать выводы, делать умозаключения, представлять результаты работы классу.
Узнать ещё
Чертеж — первый и очень важный шаг в решении геометрической задачи. Каким должен быть рисунок правильной пирамиды?
Сначала вспомним свойства параллельного проектирования:
— параллельные отрезки фигуры изображаются параллельными отрезками;
— сохраняется отношение длин отрезков параллельных прямых и отрезков одной прямой.
Рисунок правильной треугольной пирамиды
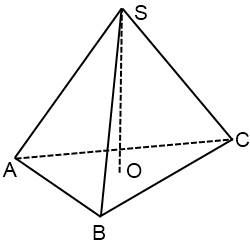
Сначала изображаем основание. Поскольку при параллельном проектировании углы и отношения длин не параллельных отрезков не сохраняются, правильный треугольник в основании пирамиды изображается произвольным треугольником.
Центр правильного треугольника — точка пересечения медиан треугольника. Поскольку медианы в точке пересечения делятся в отношении 2:1, считая от вершины, мысленно соединяем вершину основания с серединой противолежащей стороны, приблизительно делим ее на три части, и на расстоянии 2 частей от вершины ставим точку. Из этой точки вверх проводим перпендикуляр. Это — высота пирамиды. Перпендикуляр рисуем такой длины, чтобы боковое ребро не закрывало изображение высоты.
Рисунок правильной четырехугольной пирамиды
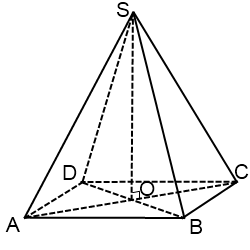
Рисунок правильной четырехугольной пирамиды также начинаем с основания. Поскольку параллельность отрезков сохраняется, а величины углов — нет, то квадрат в основании изображается параллелограммом. Желательно острый угол этого параллелограмма делать поменьше, тогда боковые грани получаются больше. Центр квадрата — точка пересечения его диагоналей. Проводим диагонали, из точки пересечения восстанавливаем перпендикуляр. Этот перпендикуляр — высота пирамиды. Выбираем длину перпендикуляра таким образом, чтобы боковые ребра не сливались между собой.
Рисунок правильной шестиугольной пирамиды
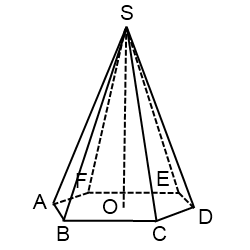
Поскольку при параллельном проектировании параллельность отрезков сохраняется, основание правильной шестиугольной пирамиды — правильный шестиугольник — изображаем шестиугольником, у которого противолежащие стороны параллельны и равны. Центр правильного шестиугольника — точка пересечения его диагоналей. Чтобы не загромождать рисунок, диагонали не проводим, а находим эту точку приблизительно. Из нее восстанавливаем перпендикуляр — высоту пирамиды — так, чтобы боковые ребра не сливались между собой.
Конспект урока: Прямоугольный параллелепипед. Пирамида
Призма
Прямоугольный параллелепипед. Пирамида
План урока
- Прямоугольный параллелепипед
- Куб
- Пирамида
Цели урока
- Знать элементы прямоугольного параллелепипеда, пирамиды.
- Уметь выделять элементы многогранников.
Разминка
- Какие геометрические фигуры на плоскости вы знаете?
- Назовите предметы, похожие по форме на кирпич.
Прямоугольный параллелепипед
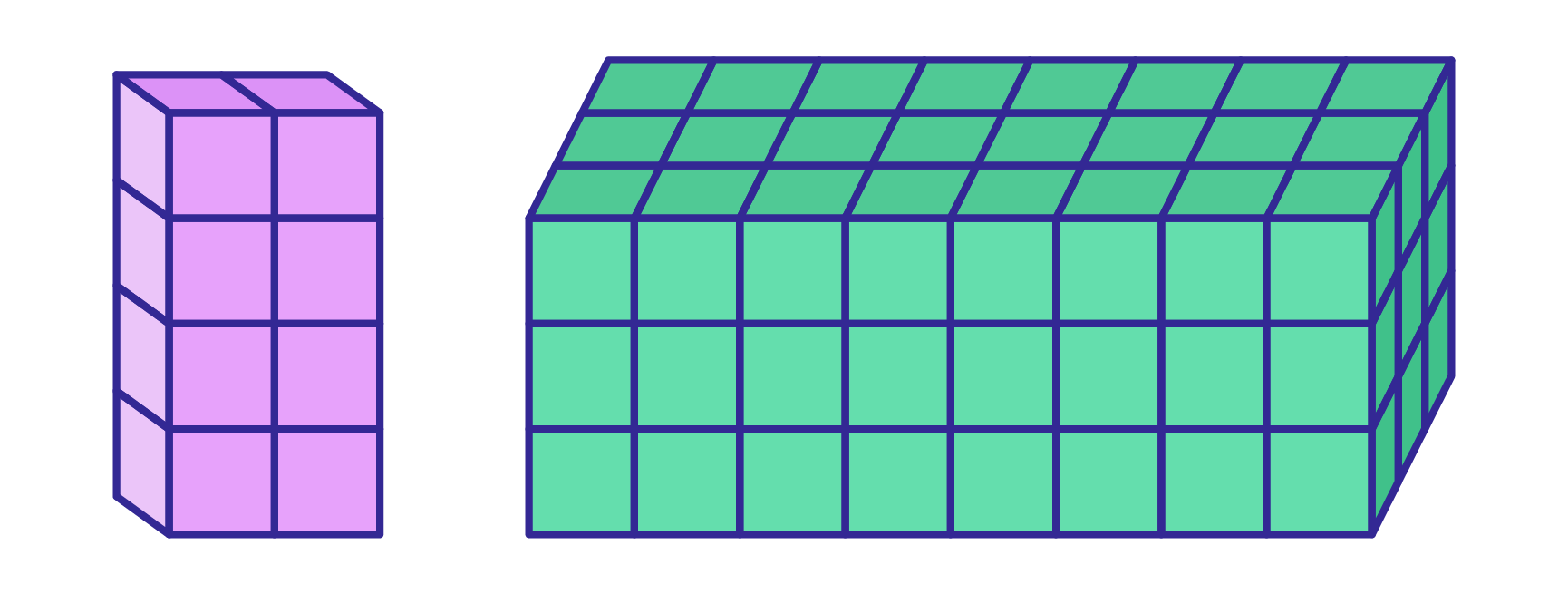
Рис. 1. Прямоугольные параллелепипеды
Если из одинаковых кубиков сложить такие фигуры, как на рис. 1, то они будут иметь форму прямоугольного параллелепипеда.
Такая форма часто встречается в предметах, которые нас окружают. Например, чемодан, ящик, плитка шоколада и др. предметы имеют форму прямоугольного параллелепипеда.
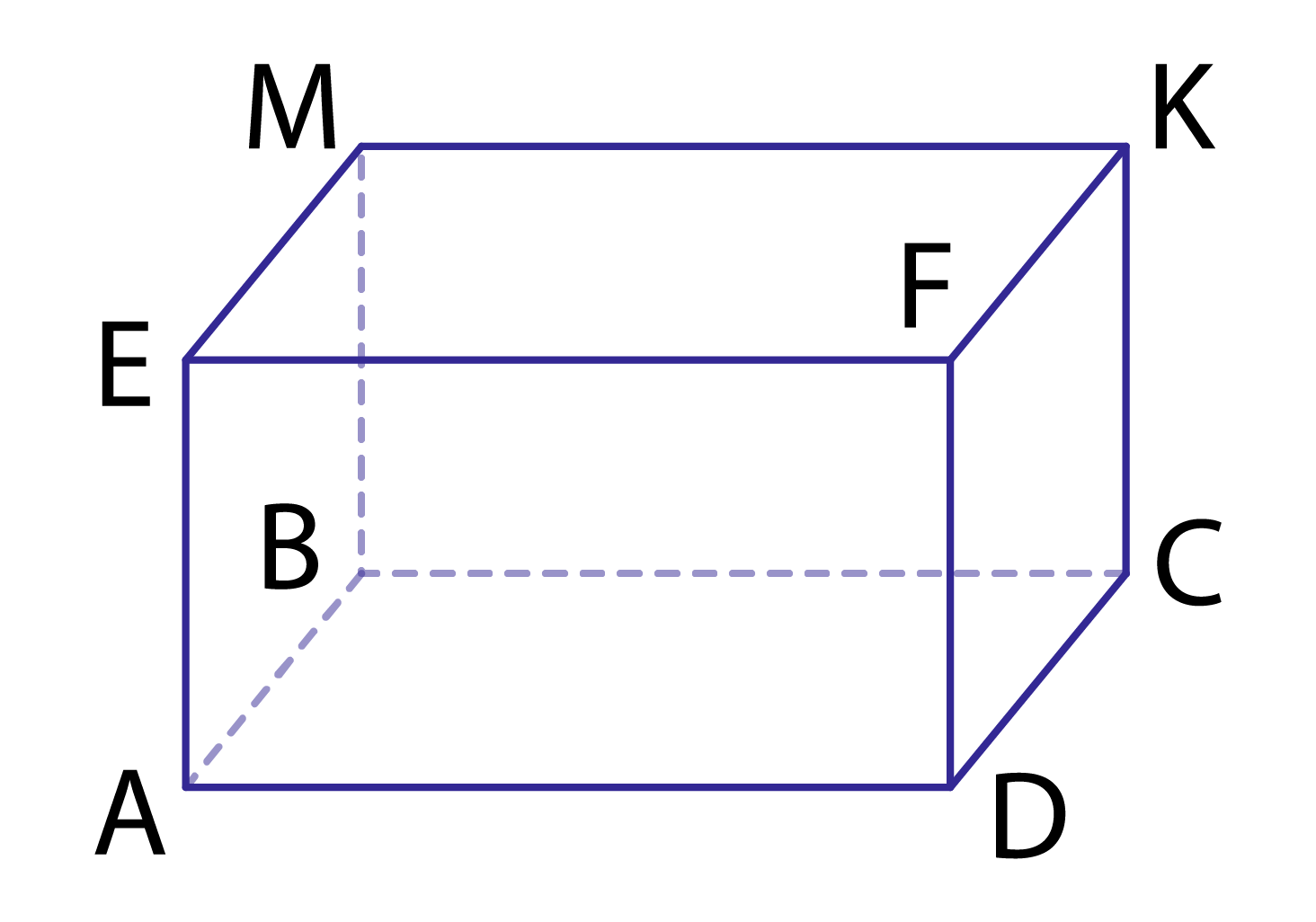
Рис. 2. Прямоугольный параллелепипед
На рис. 2 изображен прямоугольный параллелепипед ABCDEMKF. Он составлен из 6 прямоугольников, которые называются гранями. Стороны граней называются ребрами параллелепипеда, а их вершины — вершинами параллелепипеда.
Перечислим элементы этой фигуры:
- 8 вершин: точки A, B, C, D, E, M, K и F;
- 12 ребер: отрезки AB, BC, CD, AD, AE, BM, CK, DF, EF, EM, MK и FK;
- 6 граней: прямоугольники ABCD, AEMB, BMKC, DFKC, AEFD, EMKF.
Грани, не имеющие общих вершин, называются противолежащими, например, ABCD и EMKF. Грани ABCD и EMFK называют основаниями прямоугольного параллелепипеда.
Противолежащие грани прямоугольного параллелепипеда равны.
Ребра, выходящие из одной вершины, называются
измерениями прямоугольного параллелепипеда
.
Их называют длина, ширина и высота. Например, в вершине D (рис. 2) сходятся три ребра: AD (длина), СD (ширина) и DF (высота).
Прямоугольный параллелепипед, у которого все измерения равны, называют кубом. Поверхность куба состоит из шести равных квадратов.
Лена решила сделать коробочку для подарка своими руками. Для этого она хочет обклеить картонную коробку цветной бумагой. Сколько бумаги потребуется Лене?
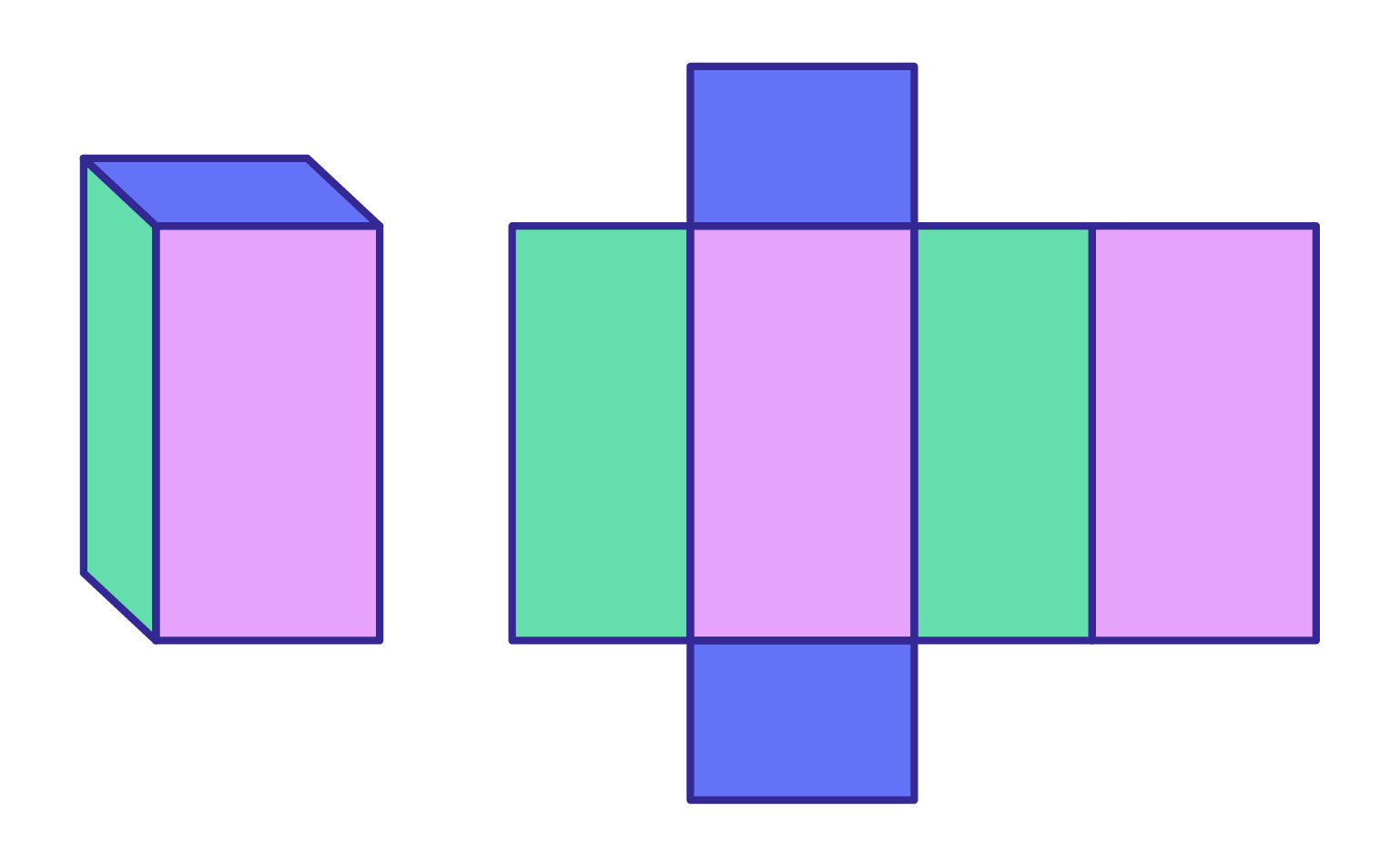
Рис. 3. Развертка прямоугольного параллелепипеда
Получается, что Лене нужно вырезать 6 прямоугольников из цветной бумаги такого же размера (мы уже с вами понимаем, что речь идет о площади каждого прямоугольника), как и грани коробки. Другими словами, нужно найти площадь всех граней прямоугольного параллелепипеда. Эта площадь имеет особое название —
площадь
поверхности
параллелепипеда
.
На рис. 3 справа от прямоугольного параллелепипеда изображена фигура, состоящая из граней этого параллелепипеда.
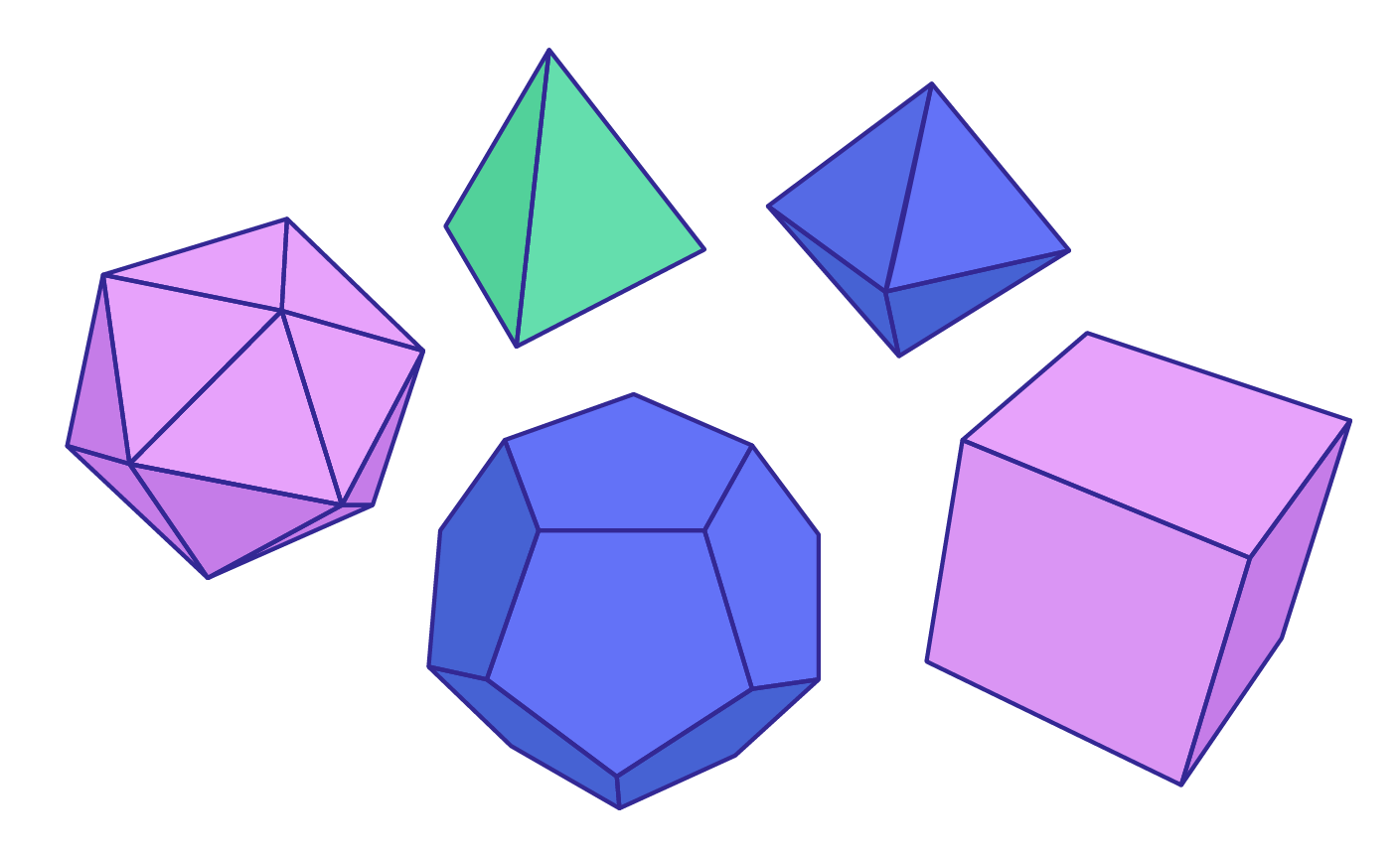
Рис. 4. Многогранники
Причем грани расположены в том порядке, в котором они находятся по соседству в фигуре слева. Такое изображение называется
разверткой фигуры
. Если мы сделаем загибы по линии ребер и совместим соседние грани, то получим прямоугольный параллелепипед.
Прямоугольный параллелепипед является разновидностью многогранника — фигуры, состоящей из нескольких многоугольников (см. рис. 4). Сами многогранники — геометрические тела.
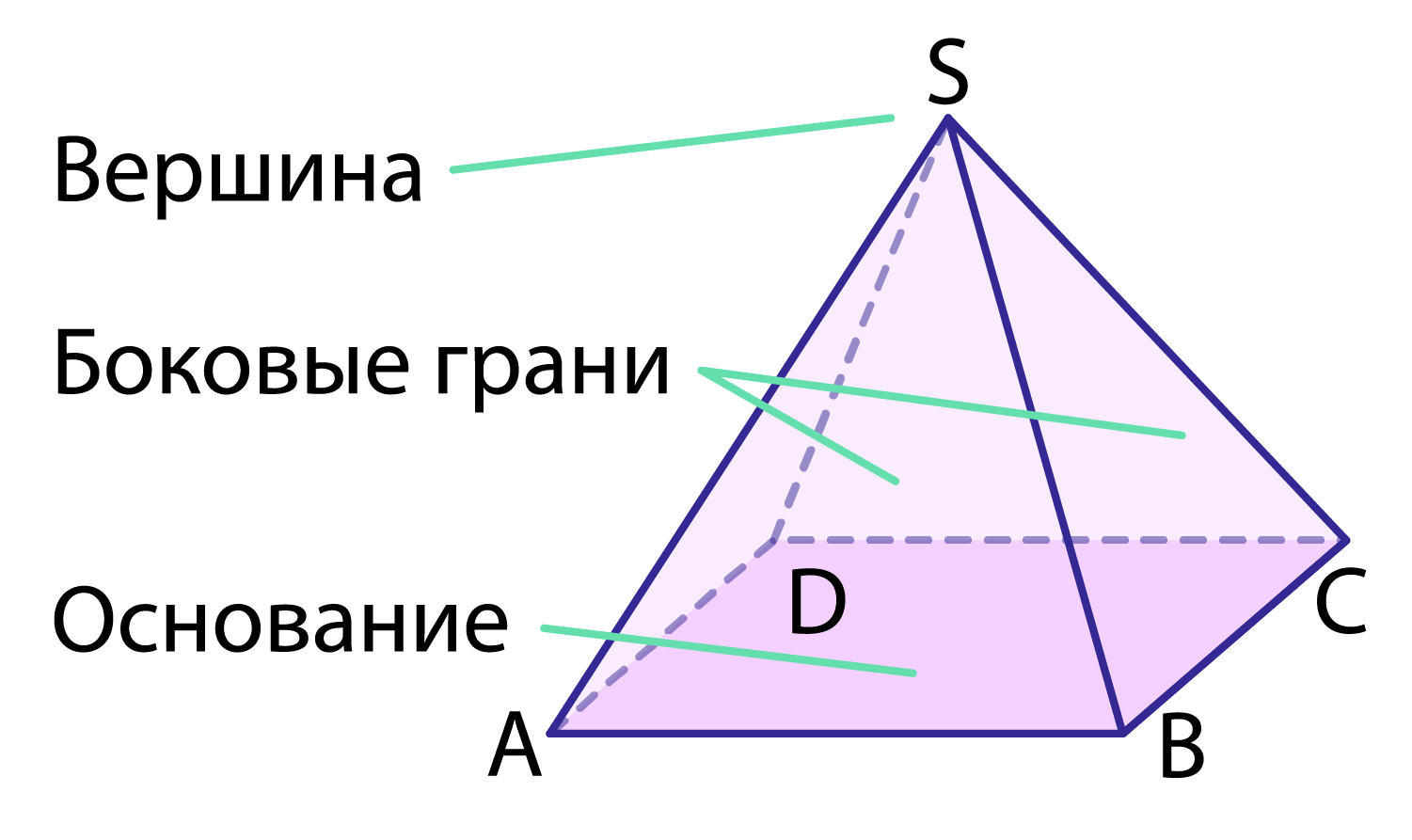
Рис. 5. Пирамида
Пирамида
Еще из курса истории Древнего мира вам знакомо название «пирамида». Но это не только одно из чудес света, но и название геометрической фигуры. На рис. 5 изображена четырехугольная пирамида SABCD. Поверхность пирамиды состоит из боковых граней треугольников, имеющих общую вершину S, и основания. На рис. 5 четырехугольник ABCD — основание, поэтому и пирамиду назвали четырехугольной. Если бы в основании лежал треугольник, то ее называли бы треугольной и т.д.
Точка S называется вершиной пирамиды.
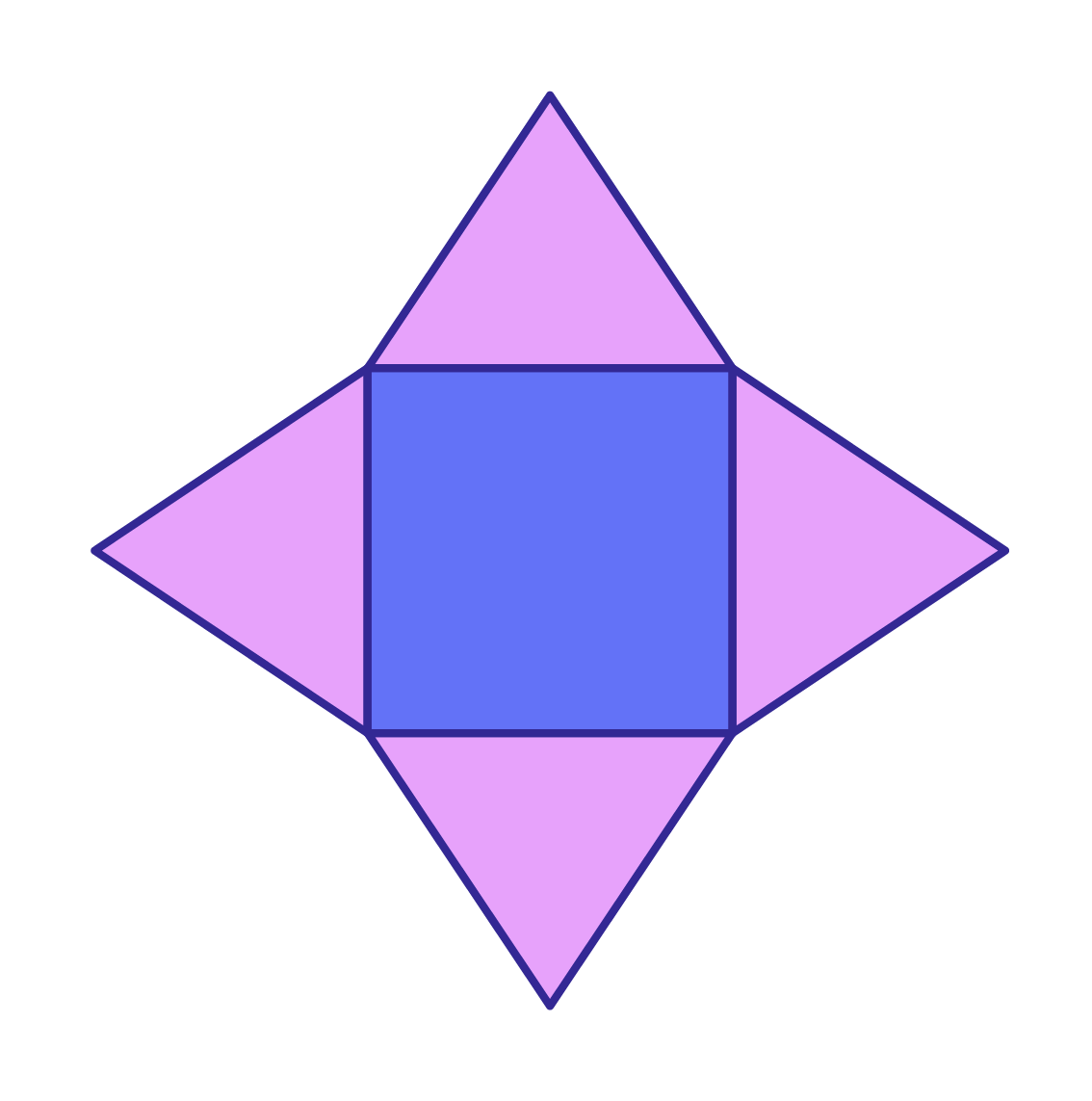
Рис. 6. Развертка пирамиды
Ребра, выходящие из этой вершины, называются боковыми. Ребра, которые являются сторонами основания — ребра основания.
На рис. 7 представлена развертка пирамиды, состоящая из квадрата и четырех треугольников.
1. В пирамиде SABCD, боковые грани — равносторонние треугольники со стороной, равной 7 см. Чему равна сумма длин всех рёбер пирамиды?
2. Назовите грани и ребра прямоугольного параллелепипеда, имеющие вершину K.
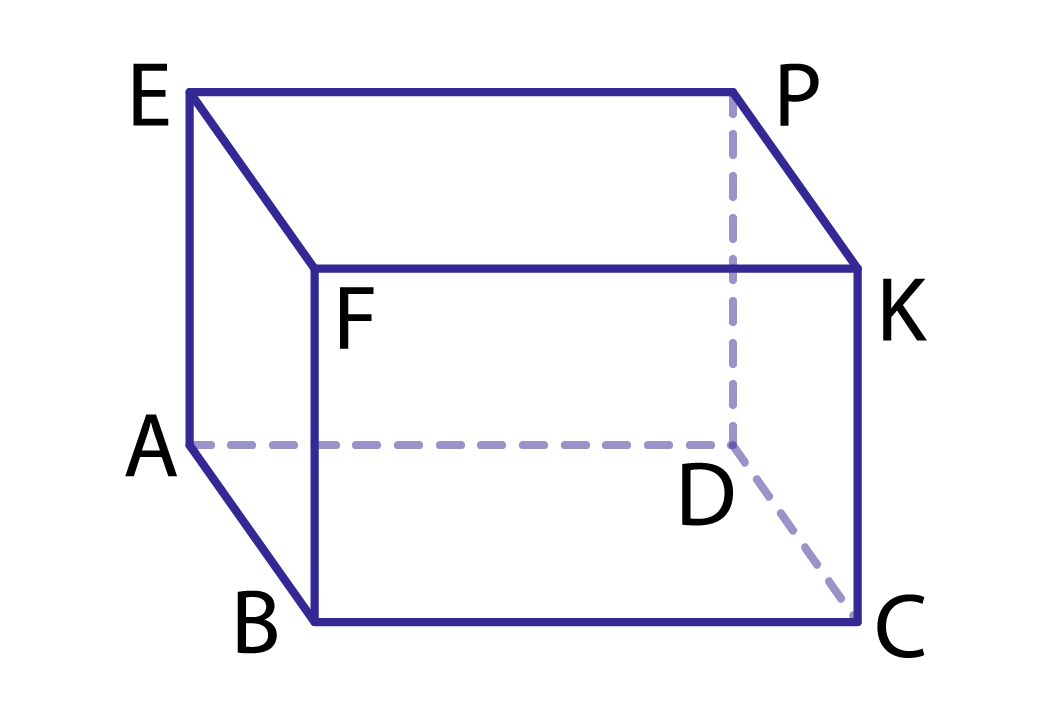
Рис. 7. Упражнение
1. Что такое многоугольник?
2. Как называются фигуры из которых состоит многоугольник?
3. Какая фигура является гранью прямоугольного параллелепипеда?
4. Сколько у прямоугольного параллелепипеда ребер?
5. Что такое пирамида?
6. Сколько граней у шестиугольной пирамиды?
7. Что такое развертка?
Ответы
1. 56 см.
2. Ребра KC, KF, KP
Грани BFKC, EFKP, KCDP.
Предыдущий урок
Объем прямоугольного параллелепипеда
Объем
Следующий урок
Угол. Обозначение углов. Виды углов. Измерение углов
Общие геометрические сведения
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие предметы дают представление о прямоугольном параллелепипеде?
Коробка, кирпич, спичечный коробок, ящик, пакет молока или сока, платяной шкаф и т.д.
2. Из каких фигур состоит поверхность прямоугольного параллелепипеда?
Из шести прямоугольников.
3. Сколько граней имеет прямоугольный параллелепипед?
Шесть граней.
4. Сколько пар противолежащих граней имеет прямоугольный параллелепипед?
У прямоугольного параллелепипеда три паны противолежащих граней.
5. Каким свойством обладают противолежащие грани прямоугольного параллелепипеда?
Противолежащие грани прямоугольного параллелепипеда равны.
6. Как называют стороны граней прямоугольного параллелепипеда?
Стороны граней прямоугольного параллелепипеда называют рёбрами.
7. Как называют вершины граней прямоугольного параллелепипеда?
Вершины граней прямоугольного параллелепипеда называют вершинами.
8. Сколько вершин имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет 8 вершин.
9. Сколько рёбер имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет 12 рёбер.
10. Какое общее название имеют длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину?
Измерения.
11. Какие названия измерений прямоугольного параллелепипеда используют для их различия?
Длина, ширина, высота.
12. Какую фигуру называют кубом?
Куб — это прямоугольный параллелепипед, у которого все измерения равны.
13. Из каких фигур состоит поверхность куба?
Из шести равных квадратов.
14. Из каких фигур состоит поверхность пирамиды?
Поверхность пирамиды состоит из боковых граней — треугольников, имеющих общую вершину, и основания.
15. Какую пирамиду называют треугольной? Четырёхугольной?
Треугольной пирамидой называют пирамиду, у основания которой три стороны, то есть основание является треугольником.
Четырехугольной пирамидой называют пирамиду, у основания которой четыре стороны, то есть основание является четырёхугольником.
16. Что называют вершиной пирамиды?
Вершиной пирамиды называют общую вершину боковых граней.
17. Что называют рёбрами основания пирамиды?
Стороны основания пирамиды называют рёбрами основания пирамиды.
18. Что называют боковыми рёбрами пирамиды?
Боковыми рёбрами пирамиды называют стороны боковых граней, не принадлежащие основанию.
Решаем устно
1. Вычислите:
- 13 • 4 • 25 = 13 • (4 • 25) = 13 • 100 = 1 300
- 4 • 5 • 78 • 5 = (4 • 5) • 78 • 5 = (20 • 5) • 78 = 100 • 78 = 7 800
- 125 • 943 • 8 = (125 • 8) • 943 = 1 000 • 943 = 943 000
2. Упростите выражение:
- 3a • 16b = 48 ab
- 4m •9n •5k = 180 mnk
- 7a •2b •50c •8d = 5600 abcd
3. Раскройте скобки:
- 2(a + b) = 2a + 2b
- (3 — b) • 5 = 3 • 5 — b • 5 = 15 — 5b
- 6m(7n + 8p) = 6m • 7n + 6m • 8p = 42 mn + 48 mp
4. Найдите периметр прямоугольника, площадь которого равна 28 см², а одна из его сторон — 7 см.
1) 28 : 7 = 4 (см) — длина второй стороны прямоугольника.
2) (4 + 7) • 2 = 11 • 2 = 22 (см) — периметр прямоугольника.
Ответ: периметр равен 22 см.
5. В магазине разложили 6 ц яблок в ящики так, что в каждом ящике оказалось по 12 кг яблок. Сколько ящиков заполнили яблоками?
6ц = 600 кг.
600 : 12 = 50 (ящиков) — заполнили яблоками.
Ответ: 50 ящиков.
6. Во сколько раз площадь квадрата, сторона которого равна 6 см, больше площади квадрата со стороной 2 см?
1) 6 • 6 = 36 (см²) — площадь квадрата со стороной 6 см.
2) 2 • 2 = 4 (см²) — площадь квадрата со стороной 2 см.
3) 36 : 2 = 18 (раз) — площадь квадрата со стороной 6 см больше площади квадрата со стороной 2 см.
Ответ: в 18 раз.
Упражнения
598. На рисунке 169 изображён прямоугольный параллелепипед ABCDMNKP. Назовите:
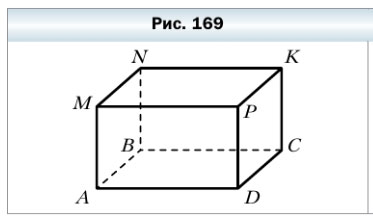
1) грани, которым принадлежит вершина С — ABCD, NKCB, PKCD
2) рёбра, равные ребру ВС — AD, MP, NK
3) верхнюю грань — MNKP
4) вершины, принадлежащие нижней грани — A, B, C, D
5) грани, имеющие общее ребро AM — AMNB, AMPD
6) грань, равную грани DPKC — AMNB
599. Измерения прямоугольного параллелепипеда MNKPEFST (рис. 170) равны 9 см, 5 см и 6 см. Вычислите сумму длин всех его рёбер и площадь его поверхности.
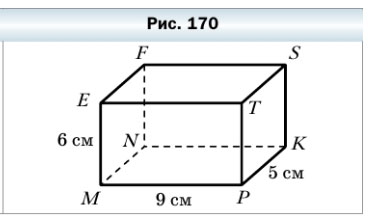
В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:
- рёбро EM = FN = SK = TP = 6 см
- рёбро MP = ET = FS = NK = 9 см
- рёбро PK = MN = EF = TS = 5 см
6 • 4 + 9 • 4 + 5 • 4 = 24 + 36 + 20 = 80 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.
Поверхность прямоугольного параллелепипеда состоит из 6 граней:
- площадь грани EFST = MNKP = 5 • 9 = 45 см²
- площадь грани EFNM = TSKP = 6 • 5 = 30 см²
- площадь грани ETPM = FSKN = 9 • 6 = 54 см²
45 • 2 + 30 • 2 + 54 • 2 = 90 + 60 + 108 = 258 (см²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.
Ответ: длина всех рёбер 80 см, площадь поверхности 258 см².
600. Найдите сумму длин всех рёбер прямоугольного параллелепипеда, измерения которого равны 13 см, 16 см, 21 см.
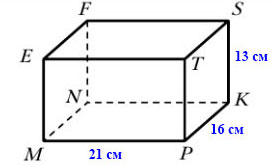
В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:
- рёбро EM = FN = SK = TP = 13 см
- рёбро MP = ET = FS = NK = 21 см
- рёбро PK = MN = EF = TS = 16 см
13 • 4 + 16 • 4 + 21 • 4 = 52 + 64 + 84 = 200 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.
Ответ: длина всех рёбер 200 см.
601. Найдите площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м, 11 м.
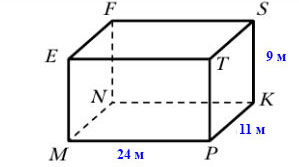
Поверхность прямоугольного параллелепипеда состоит из 6 граней:
- площадь грани EFST = MNKP = 24 • 11 = 264 м²
- площадь грани EFNM = TSKP = 9 • 11 = 99 м²
- площадь грани ETPM = FSKN = 24 • 9 = 216 м²
264 • 2 + 99 • 2 + 216 • 2 = 528 + 198 + 432 = 1 158 (м²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.

Ответ: площадь поверхности 1 158 м².
602. Вычислите площадь поверхности и сумму длин всех рёбер куба (рис. 171), ребро которого равно 5 см.
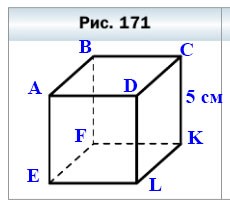
В кубе ABCDEFKL всего 12 рёбер и они все равны 5 см.
5 • 12 = 60 (см) — длина всех рёбер куба ABCDEFKL.
Поверхность куба состоит из 6 граней и они все равны 5 • 5 = 25 см²
25 • 6 = 150 (см²) — площадь поверхности куба ABCDEFKL.
Ответ: длина всех рёбер 60 см, площадь поверхности 150 см².
603. Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.

В кубе ABCDEFKL всего 12 рёбер и они все равны 7 см.
7 • 12 = 84 (см) — длина всех рёбер куба ABCDEFKL.
Поверхность куба состоит из 6 граней и они все равны 7 • 7 = 49 см²
49 • 6 = 294 (см²) — площадь поверхности куба ABCDEFKL.
Ответ: длина всех рёбер 84 см, площадь поверхности 294 см².
604. На рисунке 172 изображена пирамида МАВС. Укажите:
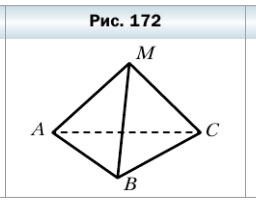
1) основание пирамиды — ABC
2) вершину пирамиды — M
3) боковые грани пирамиды — AMB, AMC, BMC
4) боковые рёбра пирамиды — AM, BM, CM
5) рёбра основания пирамиды — AB, BC, AC
605. На рисунке 173 изображена пирамида SABCD. Укажите:

1) основание пирамиды — ABCD
2) вершину пирамиды — S
3) боковые грани пирамиды — ADS, DCS, CBS, ABS
4) боковые рёбра пирамиды — AS, BS, CS, DS
5) рёбра основания пирамиды — AB, BC, CD, DA
606. На рисунке 174 изображена развёртка прямоугольного параллелепипеда.
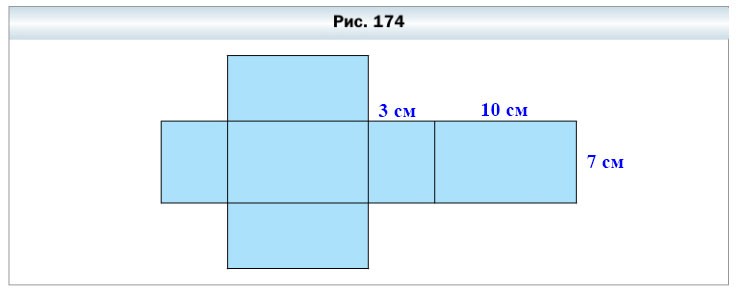
1) Из скольких прямоугольников состоит развёртка? — из 6 прямоугольников.
2) Сколько пар равных прямоугольников содержит развёртка? — 3-х пары равных прямоугольников.
3) Какова площадь этой развёртки, если измерения параллелепипеда равны 10 см, 7 см и 3 см?
S = (10 • 7) • 2 + (3 • 10) • 2 + (7 • 3) • 2 = 70 • 2 + 30 • 2 + 21 • 2 = 140 + 60 + 42 = 242 см²
607. Вычислите площадь поверхности прямоугольного параллелепипеда, развёртка которого изображена на рисунке 175.
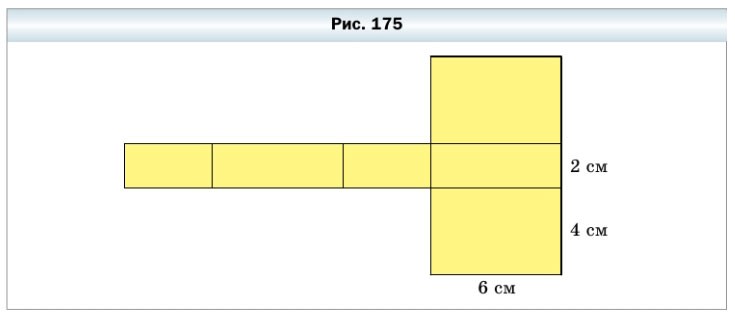
S = (6 • 4) • 2 + (6 • 2) • 2 + (4 • 2) • 2 = 24 • 2 + 12 • 2 + 8 • 2 = 48 + 24 + 16 = 88 см²
Ответ: площадь поверхности равна 88 см².
608. Высота прямоугольного параллелепипеда равна 20 см, что на 5 см больше его ширины и в 3 раза меньше его длины. Вычислите площадь поверхности параллелепипеда.

1) 20 — 5 = 15 (см) — ширина прямоугольного параллелепипеда.
2) 20 • 3 = 60 (см) — длина прямоугольного параллелепипеда
3) (60 • 20) • 2 + (60 • 15) • 2 + (20 • 15) • 2 = 1 200 • 2 + 900 • 2 + 300 • 2 = 2 400 + 1 800 + 600 = 4 800 (см²) — площадь поверхности прямоугольного параллелепипеда.
Ответ: S = 4 800 см².
609. Сумма длин всех рёбер прямоугольного параллелепипеда равна 28 см. Найдите сумму длин трёх его рёбер, имеющих общую вершину.
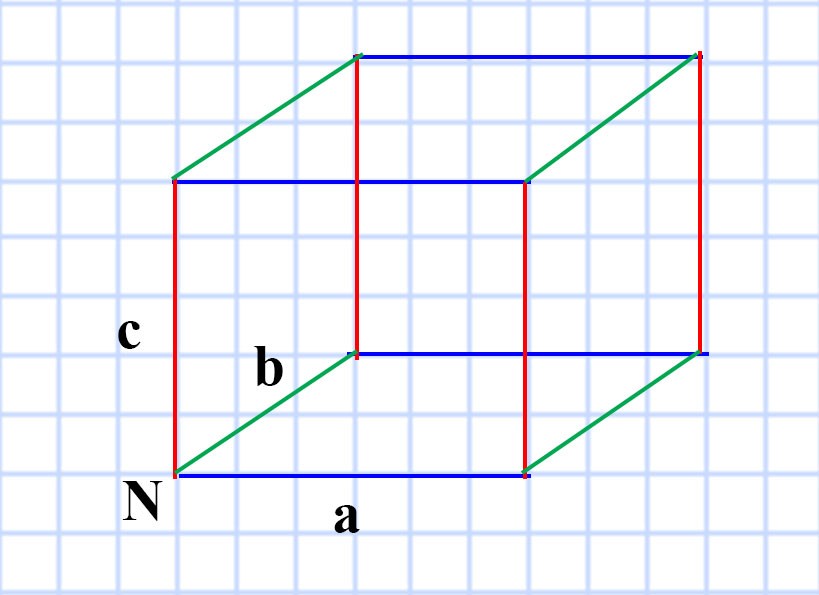
В прямоугольном параллелепипеде всего 12 ребер. Причём:
- 4 ребра равны длине a — рёбра синего цвета
- 4 ребра равны ширине b — рёбра зелёного цвета
- 4 ребра равны ширине c — рёбра красного цвета
Мы знаем, что сумма длин всех рёбер этого прямоугольного параллелепипеда равна 28 см.
Значит, можно записать:
4a + 4b + 4с = 28
4 (a + b + с ) = 28
a + b + с = 28 : 4
a + b + с = 7 (см)
Так как рёбра a, b и с сходятся в общей вершине N, то искомая сумма длин трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину равна 7 см.
Ответ: 7 см.
610. Прямоугольный параллелепипед и куб имеют равные площади поверхностей. Длина параллелепипеда равна 18 м, что в 2 раза больше, чем его ширина, и на 8 м больше, чем его высота. Найдите ребро куба.

1) 18 : 2 = 9 (м) — ширина параллелепипед.
2) 18 — 8 = 10 (м) — высота параллелепипеда.
3) (18 • 9) • 2 + (18 • 10) • 2 + (10 • 9) • 2 = 162 • 2 + 180 • 2 + 90 • 2 = 324 + 360 + 180 = 864 (м²) — площадь поверхности параллелограмма.
Значит площадь поверхности куба равна 864 м². Так как у куба всего 6 граней и все они одинаковы, то можно найти площадь грани куба.
4) 864 : 6 = 144 (м²) — площадь грани куба.
Для того, чтобы найти длину ребра куба, надо подобрать такое число, квадрат которого будет равняться числу 144. Это число 12 (12 • 12 = 144).
Значит длина ребра куба равна 12 м.
Ответ: 12 метров.
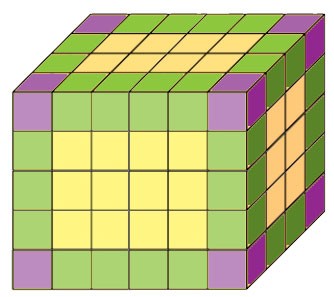
611. Брусок, имеющий форму прямоугольного параллелепипеда с измерениями 4 см, 5 см и 6 см, покрасили со всех сторон и разрезали на кубики с ребром 1 см. Сколько получилось кубиков, у которых:
1) окрашено три грани — 8 кубиков (фиолетовые), которые расположены по вершинам прямоугольного параллелепипеда.
2) окрашено две грани — 36 кубков (зелёные), которые расположены по рёбрам параллелепипеда, но не являются его вершинами (4 • 4 + 3 • 4 + 2 • 4 = 16 + 12 + 8 = 36):
- по 4 кубика на 4 рёбрах длиной 6 см
- по 3 кубика на 4 рёбрах длиной 5 см
- по 2 кубика на 4 рёбрах длиной 4 см
3) окрашено одна грань — 52 кубика (жёлтые), которые не примыкают ни к вершинам, ни к рёбрам параллелепипеда (12 • 2 + 8 • 2 + 6 • 2 = 24 + 16 + 12 = 52):
- 4 • 3 = 12 кубиков на двух гранях размерами 6 см х 5 см
- 4 • 2 = 8 кубиков на двух гранях размерами 6 см х 4 см
- 3 • 2 = 6 кубиков на двух гранях размерами 5 см х 5 см
Упражнения для повторениях
612. Скорость космического корабля «Восток», на котором Юрий Гагарин совершил свой полёт, равна 8 км/с.
1) За сколько минут он пролетал 960 км?
960 : 8 = 120 (с) — нужно кораблю для преодоления 960 км.
120 с = 2 мин
Ответ: 2 минуты.
2) Какое расстояние он пролетал за 1 ч?
1 ч = 60 мин = 3 600 с
8 • 3 600 = 28 800 (км) — пролетает корабль за 1 час.
Ответ: 28 800 км.
613. Из листа картона можно вырезать шесть одинаковых квадратов. Сколько листов картона надо для того, чтобы вырезать 50 таких квадратов?
50 = 6 • 8 + 2
Значит нужно 8 + 1 = 9 листов.
Ответ: 9 листов.
614. Поезд отправился со станции в 16 ч со скоростью 54 км/ч. В 19 ч с этой же станции в противоположном направлении отправился второй поезд. В 24 ч расстояние между ними было равно 642 км. С какой скоростью двигался второй поезд?

1) 24 — 16 = 8 (часов) — двигался первый поезд.
2) 54 • 8 = 432 (км) — проехал первый поезд за 8 часов.
3) 24 — 19 = 5 (часов) — двигался второй поезд.
4) 642 — 432 = 210 (км) — проехал второй поезд за 5 часов.
5) 210 : 5 = 42 (км/ч) — скорость второго поезда.
Ответ: 42 км/ч.
615. Решите уравнение:

Задача от мудрой совы
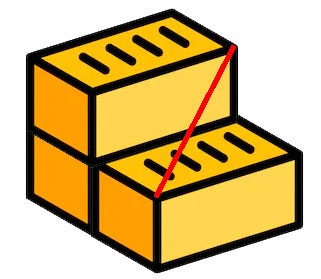
616. Как с помощью линейки измерить диагональ кирпича, имея ещё несколько таких кирпичей? (Диагональ параллелепипеда — это отрезок, соединяющий две его вершины, не принадлежащие одной грани.)
Для этого нам потребуется как минимум 3 кирпича:
- Сложим кирпичи лесенкой
- Линейкой измерим расстояние так, как показано на рисунке.
- Измеренное расстояние будет точно соответствовать длине диагонали кирпича.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
