Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 марта 2021 года; проверки требуют 4 правки.
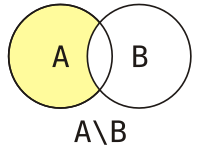
Ра́зность двух мно́жеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество.
Обычно разность множеств 


но иногда можно встретить обозначение 

Пусть 

Это множество часто называют дополнением множества 

Обычно предполагается, что рассматриваются подмножества одного и того же множества, которое, в этом случае называют универсумом, скажем, 




С учётом данного замечания, оказывается, что 




Также применяется и операторная запись вида 




Операция разности множеств не является по определению симметричной по отношению ко входящим в неё множествам. Симметричный вариант теоретико-множественной разности двух множеств описывается понятием симметрической разности.
Примеры[править | править код]
Свойства[править | править код]
Пусть 
- Вычитание множества из самого себя даёт в результате пустое множество:
- Свойства пустого множества относительно разности:
- Разность двух множеств содержится в уменьшаемом:
- Разность множеств равна пустому множеству тогда и только тогда, когда уменьшаемое содержится в вычитаемом:
- Законы де Моргана в алгебре множеств формулируются следующим образом:
Компьютерные реализации[править | править код]
В пакете Mathematica операция реализована с помощью функции Complement. В пакете MATLAB она же реализована с помощью функции setdiff.
В языке программирования Pascal (а также в его объектном расширении Object Pascal) операция разности множеств представлена оператором «−», обоими операндами и результатом выполнения которого являются значения типа set.
В языке программирования Python операция реализована с помощью метода diff над объектом типа set.
Дополнение множества[править | править код]
Определение[править | править код]
Если из контекста следует, что все рассматриваемые множества являются подмножествами некоторого фиксированного универсума 
Свойства[править | править код]
- Операция дополнения является унарной операцией на булеане
.
- Законы дополнения:[1]
-
- В частности, если оба
и
непусты, то
является разбиением
.
- Операция дополнения является инволюцией:
- Законы де Моргана:
- Законы разности множеств:
Кодировка[править | править код]
| Графема | Название | Юникод | HTML | LaTeX |
|---|---|---|---|---|
| ∁ | COMPLEMENT | U+2201 | ∁
|
complement
|
См. также[править | править код]
- Операции над множествами
Литература[править | править код]
- Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. — М.: Физматлит, 2004. — 256 с.
- Куратовский К., Мостовский А. Теория множеств / Пер. с англ. М. И. Кратко, под ред. А. Д. Тайманова. — М.: Мир, 1970. — С. 16, 20—22.
Примечания[править | править код]
- ↑ Ильин В. А., Садовничий В. А., Сендов Бл. Х.. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 66. — 672 с. — ISBN 5-482-00445-7.
Пересечение, объединение и разность множеств
- Пересечение множеств
- Объединение множеств
- Универсум и отрицание
- Свойства операций пересечения и объединения
- Разность множеств
- Формулы включений и исключений
- Примеры
Пересечение множеств
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
$$ A cap B = {x|x in Bbb A и x in Bbb B } $$

Если множества не пересекаются, то $A cap B = varnothing $ – пустое множество в пересечении. Если $B subseteq A$ – подмножество, то $A cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A cap B$ = {f|f-квадрат}.
Если A = ${n|n⋮3, n in Bbb N }$ – натуральные числа, кратные 3, B = ${n|n⋮5, n in Bbb N }$ – натуральные числа, кратные 5, то $A cap B = {n|n⋮15, n in Bbb N}$ – натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A cap B = varnothing$.
Объединение множеств
Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:
$$ A cup B = { x|x in Bbb A или x in Bbb B } $$

Если $B subseteq A$ – подмножество, то $A cap B = A$ – объединением будет большее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cup B$ = {1;3;5;7;9;11}.
Если $A = {x|x^2-4 = 0, x in Bbb R}, B = {x|x+3 = 2, x in Bbb R }, то A cup$ B = {-2;-1;2}
Если $A = {n│n in Bbb Z }$- все целые числа, $B = {x|x = frac{a}{b}, a in Bbb Z, b in Bbb N }$ – все дроби, то $A cup B = {x│x in Bbb Q}$ – множество рациональных чисел. Заметим, что в данном случае $A subset B$.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:

Примеры универсумов:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Отрицание (абсолютное дополнение) множества A – множество всех элементов универсума, не принадлежащих A:
$$ bar{A} = {x|x notin A } $$
Читается «не A».
У отрицания есть любопытное свойство: $bar{bar{Α}} = Α $(два раза «нет» – это «да»).

Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $bar{A} = {1;2;6;7}$
Если U = ${x|x in Bbb R}$ – все действительные числа, A = ${x|x gt 0, x in Bbb R }$ – все положительные действительные числа, то $ bar{A} = {x|x le 0, x in Bbb R}$.
Свойства операций пересечения и объединения
$A cap B = B cap A$
$ A cup B = B cup A $
$(A cap B) cap C = A cap (B cap C)$
$ (A cup B) cup C = A cup ( B cup C) $
$(A cup B) cap C = (A cap C) cup (B cap C)$
$ (A cap B) cup C = (A cup C) cap (B cup C) $
$A cap A = A$
$ A cup A = 0 $
Взаимодействие с отрицанием, пустым множеством и универсумом
$A cap bar{A} = varnothing $
$A cap U = A$
$A cap varnothing = varnothing$
$A cup bar{A} = U $
$A cup U = U$
$A cup varnothing = A$
$ overline{(A cap B)} = bar{A} cup bar{B} $
$ overline{(A cup B)} = bar{A} cap bar{B} $
$ (A cup B) cap A = A $
$ (A cap B) cup A = A $
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
$$ AB = {x|x in Bbb A , x notin B} $$
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:


Получается, что отрицание – частный случай разности: $ bar{A} = {x|x in Bbb U, x notin A } $= UA
«Не A» – это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A cup B)$?

Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A cup B) = n(A)+ n(B)-n(A cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.

Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A cap B)+n(A cap C)+n(B cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A cap B cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A cup B cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A cap B)+n(A cap C)+n(B cap C) )+n(A cap B cap C) $$
Примеры
Пример 1. Найдите пересечение данных множеств:
а) A = {0;5;8;10},
B = {3;6;8;9}
$A cap B$ = {8}
$б) A = {x|x lt 3, x in Bbb R}, $
$ B = {x|x gt 1, x in Bbb R} $
$A cap B = {x|1 lt x lt 3, x in Bbb R}$ – отрезок
$в) A = {x|x lt 3, x in Bbb R}, $
$ B = {x|x gt 1, x in Bbb N} $
$A cap B = {x|1 lt x lt 3, x in Bbb N } или A cap B = {2}$ – одна точка
г) A = {f|f-правильный многоугольник},
B = {f|f-четырехугольник}
$A cap B = {f|f-квадрат}$
Пример 2. Найдите объединение данных множеств:
а) A = {0;5;8;10}, B = {3;6;8;9}
$A cup B$ = {0;3;5;6;8;9;10}
б) A = {1;2}, B = {1;2;3;4}
$A subset B$ – строгое подмножество
$A cup B $ = B = {1;2;3;4}
$в) A = {x|x lt 1, x in Bbb R}, B = {x|x gt 1,x in Bbb R} $
$A cup B = {x|x neq 1, x in Bbb R }$
$г) A = {n│n⋮3, n in Bbb Z}, B = {n|n⋮9,n in Bbb N} $
$B subset A$ – строгое подмножество
$ A cup B = A = {n│n⋮3, n in Bbb Z} $
Пример 3. Найдите отрицание данного множества на данном универсуме:
а) U = {1;2;3;4;5}, A = {2;3}
$ bar{A} = {1;4;5}$
б) U = ${x│x in Bbb Q }$, A = ${ frac{4}{5}, frac{7}{8} }$
$ bar{A} = {x|x neq frac{4}{5}, x neq frac{7}{8}, x in Bbb Q} $
$в) U = {x│x in Bbb R}, A = {x|x ge 2, x in Bbb R} $
$bar{A} = {x|x lt 2, x in Bbb R}$
г) U = { 0;1}, A = { 0}
$ bar{A} = {1}$
Пример 4. Найдите обе разности данных множеств:
а) A = {0;1;2;3;4}, B = {2;4}
AB = {0;1;3}, $BA = {∅}$
б) A = {0;1;3}, B = {2;4;6}
AB = {0;1;3}, BA = {2;4;6}
$в) A = {x|x gt 1, x in Bbb R}, $
$ B = {x|x lt 3, x in Bbb R} $
AB $ = {x|x ge 3, x in Bbb R}$
BA $ = {x|x le 1,x in Bbb R} $
$ г*) A = {(x,y)|x gt 0, x in Bbb R, y in Bbb R} $
$ B = {(x,y)|x le 5, x in Bbb R, y in Bbb R} $
AB $ = {(x,y)|x gt 5, x in Bbb R, y in Bbb R} $
BA $ = {(x,y)|x le 0, x in Bbb R, y in Bbb R} $
Пример 5. Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?

n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42
$ n(A cap B) = 8, n(B cap C) = 5, n(A cap C) = 10 $
$n(A cap B cap C) = 3$
Всего программистов:
$ n(A cup B cup C) = n(A)+n(B)+n(C)- $
$ (n(A cap B)+n(B cap C)+n(A cap C) )+n(A cap B cap C) $
$n(A cup B cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$
Число не умеющих программировать:
$n(U)-n(A cup B cup C) = 100-80 = 20$
Ответ: 20 человек
«Теория систем и системный анализ»
И. Б. Родионов
Лекция 13: Операции над множествами. Упорядоченное множество
1. Объединение множеств
Объединение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X или Y, т.е. принадлежат X или принадлежат Y.
Объединение X и Y обозначается через X∪Y
Формально x∈X∪Y ⇔ x∈X или x∈Y
Пример 1. Если X={1,2,3,4,5} и Y={2,4,6,8}, то
X∪Y={1,2,3,4,5,6,7,8}
Пример 2. Если X={x:x — отл.гр.}, и Y={x:x — gib.}, то
X∪Y={x:x — или отл., или gib}.
Пример 3. Если X — множество точек левого круга и Y — множество точек правого круга, то
X∪Y — заштрихованная область, ограниченная обоими кругами.
Понятие объединения можно распространить и на большее число множеств, на систему множеств. Обозначим через М={X1,X2, …,Xn} совокупность n множеств X1,X2, …,Xn, называемую иногда системой множеств. Объединение этих множеств
∪Xi=∪(X∈M), Х=X1∪X2∪…∪Xn
представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств данной системы М.
Для объединенных множеств справедливы:
- X∪Y = Y∪X — коммутативный закон
- (X∪Y)∪Z = X∪(Y∪Z) = X∪Y∪Z — ассоциативный закон,
справедливость которых вытекает из того, что левая и правая части равенств состоят из одних и тех же элементов.
Очевидно, что X∪∅ = X. Отсюда можно видеть, что ∅ играет роль нуля в алгебре множеств.
2. Пересечение множеств
Пересечение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству X, так и множеству Y.
Пересечение множеств обозначается X∩Y.
Формально x∈X∩Y ⇔ x∈X и x∈Y
Пример 4. X={1,2,3,4,5} Y={2,4,6,8} X∩Y = {2,4}
Пример 5. Если Х — множество точек левого круга, а Y — множество точек правого круга, то X∩Y представляет собой заштрихованную область, являющуюся общей частью обоих кругов.
Множества X и Y называются непересекающимися (дизъюнктными), если они не имеют общих элементов, то есть если X∩Y=∅.
Пример 7. {1,2,3} и {4,5,6}
В отличие от алгебры чисел, где могут быть три возможности: a<b, a=b, b<a между двумя множествами X и Y может быть одно из 5 cотношений:
X=Y; X⊂Y; Y⊂X; X∩Y=∅ и X и Y находятся в общем положении.
Говорят, что множества X и Y находятся в общем положении, если выполняются три условия:
- существует элемент множества X, не принадлежащий Y;
- существует элемент множества Y, не принадлежащий X;
- существует элемент, принадлежащий как X, так и Y.
Аналогично объединению понятие пересечения можно распространить на систему множеств:
∩X=∩Xi=X1∩X2∩…∩Xn
Пересечение множеств представляет собой множество, элементы которого принадлежат каждому из множеств системы М.
Для пересечения множеств справедливы:
- X∩Y=Y∩X — коммутативный закон
- (X∩Y)∩Z = X∩(Y∩Z) = X∩Y∩Z — ассоциативный закон
Заметим также, что имеет место соотношение X∩∅=∅.
Пример 8. A={a,b}, B={b,c}, C={a,c}.
A∩B∩C=∅, хотя A∩B={b}, B∩C={c}
3. Разность множеств
Разность множеств определена только для двух множеств. Разностью множеств X и Y называется множество, состоящее из всех тех и только тех элементов, которые принадлежат X и не принадлежат Y.
Обозначается: XY.
Формально: x∈XY ⇔ x∈X и x∉Y
Пример 9. (см. Пример 1) X={1,2,3,4,5}, Y={2,4,6,8}, XY={1,3,5}, YX={6,8}
Разность множеств не обладает свойством коммутативности.
XY≠YX
Если AB=∅, то A⊂B — поставить ? обратно
при A∩B≠∅
4. Универсальное множество
Роль нуля в алгебре множеств играет пустое множество. А нет ли такого множества, которое играет роль «1», т.е. удовлетворяет условию: X∪I = X, что означает, что пересечение или «общая часть» множества I и множества X для любого множества X совпадает с самим этим множеством. Это возможно лишь в том случае, если множество I содержит все элементы, из которых может состоять множество X, так что любое множество X полностью содержится в множестве I.
Множество I, удовлетворяющее этому условию, называется полным, или универсальным, или единичным.
Если при некотором рассмотрении участвуют только подмножества некоторого фиксированного множества, то это самое большое множество будем считать универсальным и обозначать I.
Пример 12 (Пример 1). I — множество целых чисел
Пример 13 (Пример 2). I — множество студ. гр.
Пример 14 (Пример 3). I — лист бумаги, доска
Универсальное множество обычно обозначают графически в виде множества точек прямоугольника, а отдельные множества в виде отдельных областей внутри этого прямоугольника. Изображение множеств в виде областей в прямоугольнике, представляющем универсальное множество, называется диаграммой Эйлера-Венна.
Универсальное множество обладает интересным свойством, которое не имеет аналогии в обычной алгебре, а именно, для любого множества X справедливо соотношение X∪I = I.
5. Дополнение множества
Множество, определяемое из соотношения X¯ = IX, называется дополнением множества X (до универсального множества I).
На диаграмме множество X¯ представляет собой незаштрихованную область.
Формально: X = {x: x∈I и x∉X}.
Из определения следует, что X и X¯ не имеют общих элементов. Х∩X¯=∅.
Кроме того, не имеется элементов I, которые не принадлежали бы ни X, ни X¯ (его дополнению), так как те элементы, которые не принадлежат X, принадлежат X¯ (его дополнению). Следовательно, Х∪X¯=I.
Из симметрии данной формулы относительно Х и X¯ следует не только то, что X¯ является дополнением Х, но и что Х является дополнением X¯. Но дополнение X¯ есть X¯ ¯. Таким образом, X¯ ¯=X¯.
С помощью операции дополнения представим разность множеств:
XY = {x: x∈X и x∉Y} ={ x: x∈X и x∈Y¯ }, т.е. XY= Х∩Y¯.
Порядок выполнения операций:
- дополнение;
- пересечение;
- объединение, разность.
Для изменения порядка используют скобки.
6. Разбиение множества
Одной из наиболее часто встречающихся операций над множествами является операция разбиения множества на систему подмножеств.
Так, система курсов данного факультета является разбиением множества студентов факультета; система групп данного курса является разбиением множества студентов курса.
Пример. Продукция предприятия: — высший сорт, I, II, брак.
Рассмотрим некоторое множество M и систему множеств
М = {X1, X2, …, Xn}
Система множеств M называется разбиением множества M, если она удовлетворяет следующим условиям:
-
Любое множество X из M является подмножеством множества М
∀X∈M: X⊆M;
-
Любые два множества X и Y из М являются непересекающимися
∀X∈М, ∀Y∈M: X≠Y → X∩Y=∅.
-
Объединение всех множеств, входящих в разбиение, дает множество M
X1∪X2∪…∪ Xn=M.
7. Тождества алгебры множеств
С помощью операций объединения, пересечения и дополнения из множеств можно составлять различные алгебраические выражения.
Если алгебраические выражения V(X,Y,Z) и S(X,Y,Z) представляют собой одно и то же множество, то их можно приравнять друг другу, получая алгебраическое тождество вида V(X,Y,Z) = S(X,Y,Z)
- (X∪Y)∩Z = (X∩Z)∪(Y∩Z) (аналогичное дистрибутивному закону (a+b)c=(a+c)(b+c) в обычной алгебре).
- (X∩Y)∪Z = (X∪Z)∩(Y∪Z)
- Если Y⊆X, то X∩Y=Y, X∪Y=X. Действительно, все элементы множества Y являются в то же время и элементами множества X. Значит пересечение этих множеств, то есть общая множеств Х и Y совпадает с Y. В объединение множеств X и Y множество Y не внесет ни одного элемента, который уже не входил бы в него, будучи элементом множества Х. Следовательно, X∪Y совпадает с X.
- Пусть в примере 3 Y=X. Тогда, учитывая, что X⊆X, то X∩Х=Х, X∪Х=X. (идемпотентность).
- Докажем тождество (X∪Y)¯=X¯∩Y¯. Предположим, что х∈(X∪Y)¯, то есть х∉X∪Y. Это значит, что х∉X и х∉Y, то есть и x&isinX¯ и x&isinY¯;. Следовательно, x∈X¯∩Y¯. Предположим теперь, что y∈X¯∩Y¯, то есть y∈X¯ и y∈Y¯. Это значит, что y∉X и y∉Y, то есть что y∉X∪Y. Следовательно, y∈(X∪Y)¯.
- Тождество (X∩Y)¯=X¯∪Y¯. Обычно тождества 5) и 6) называются тождествами де-Моргана.
- (AB)∩C=(A∩C)B=(A∩C)(B∩C)
- AB=A(A∩B)
- A=(A∩B)∪(AB)
Дополнение к занятию «операции над множествами»
Множество элементов, принадлежащих или A, или B, называют симметричной разностью или дизьюнктивной суммой.
S = A⊕B = (AB)∪(BA) = (A∩B¯)∪(A¯∪B) = (A∪B)∩(A∩B)¯
Для симметрической разности выполняются следующие законы:
- 1) A⊕B = B ⊕A — коммутативность,
- 2) A⊕(B⊕С) = (A⊕B)⊕С — ассоциативность,
- 3) A⊕∅ = А=∅⊕A — существование нейтрального элемента,
- 4) A ⊕А = ∅
- 5) A∩(B⊕С) = (A∩B)⊕(А∩С) — дистрибутивность относительно пересечения.
Упорядоченное множество
Упорядоченным множеством (или кортежем) называется последовательность элементов, то есть совокупность элементов, в которой каждый элемент занимает определенное место. Сами элементы — компоненты кортежа.
Пример 1. Множество людей, стоящих в очереди, множество слов в фразе, алфавит. Во всех этих множествах место каждого элемента является вполне определенным и не может быть произвольно изменено.
Число элементов кортежа называется его длиной. Обозначают кортеж скобками «< >», иногда круглыми «( )». А=<a1, a2, …, an>. Кортежи длины 2 называются упорядоченными парами, 3 — тройками, n-ками.
Частный случай: кортеж длины 1 — <a>
кортеж длины 0 — < > или ∧ — пустой кортеж.
Отличие кортежа и обыкновенного множества: в кортеже могут быть одинаковые элементы.
Упорядоченные множества, элементами которых являются вещественные числа, будем называть векторами или точками пространства (n-мерного).
Так, кортеж <a1, a2> может рассматриваться как точка на плоскости или вектор, проведенный из начала координат в данную точку. Тогда компоненты a1, a2 — проекции вектора на оси 1 и 2.
Пр1 <a1, a2> = a1, Пр2 <a1, a2> = a2, Прi <a1, a2, a3>= ai, Пр12 <a1, a2, a3>= <a1, a2> — двухэлементный кортеж. Проекция кортежа на пустое множество осей — пустой кортеж.
Обобщая эти понятия, будем рассматривать упорядоченное n-элементное множество вещественных чисел (a1, …, an) как точку в воображаемом n–мерном пространстве (иногда называемом гиперпространством), или как n-мерный вектор. При этом компоненты n-элементного кортежа а будем рассматривать как проекции этого кортежа на соответствующие оси.
Прi a = ai, i=1,2,…,n
Прi,j,…,l a = <ai, aj, …, al>, i=1,2,…,n
Два вектора равны, если они имеют одинаковую длину и соответствующие координаты их равны.
<a1, …, am> = <b1, …, bn> ⇔ m = n и a1 = b1, b1 = b2, …
Компонентами кортежа (вектора) могут быть также компоненты кортежи (векторы):
Пример. Слова в предложении,
A = < <a1, a2>, <a1, a3>, <a2, a3> >
Прямое произведение множеств
Прямым (декартовым) произведением множеств X и Y называется множество, состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству X, а вторая принадлежит множеству Y.
Формально: X*Y = {<x,y>: x∈X, y∈Y}
Пример 2. Пусть X=<1,2>, Y=<1,3,4>
Тогда X*Y={<1,1>,<1,3>,<1,4>,<2,1>,<2,3>,<2,4> } См. рис. а).
Пример 3. Пусть X и Y — отрезки вещественной оси. Прямое произведение X*Y изображается заштрихованным прямоугольником. См. рис. б).
Прямое произведение изменяется при изменении порядка сомножителей т.е.
X*Y ≠ Y*X
Прямое произведение множеств X1, X2, …, Xn — это множество, обозначаемое X1*X2*…*Xn и состоящее из всех тех и только тех кортежей длины n, правая компонента которых принадлежит X1, вторая — X2 и т.д.
Очевидно X*Y = ∅ ⇔ X = ∅ или Y = ∅.
Аналогично X1*X2*…*Xn = ∅ тогда и только тогда, когда хотя бы одно из множеств X1, X2, …, Xn является пустым.
Частным случаем прямого произведения является понятие степеней (декартовых) множества — прямое произведение одинаковых множеств
Ms=M*M*…*M, M1=M, M0=∧.
Обычно R — множество вещественных чисел, тогда R2=R*R — вещественная плоскость и R3=R*R*R — трехмерное вещественное пространство.
Пример. A={a,b,c,d,e,f,g,h}, B={1,2,3, …,8}
Тогда A*B ={a1, a2, a3, …, h7, h8} — множество обозначающее все 64 клеток шахматной доски.
Пример. Пусть A — конечное множество, элементами которого являются символы (буквы, цифры, знаки препинания и т.д.). Такие множества обычно называют алфавитами. Элементы множества an называются словами длины n в алфавите A. Множество всех символов в алфавите A — это множество A* = ∪Ai = A1∪A2∪A3… . При написании слов не принято пользоваться ни запятыми, ни скобками, ни разделителями.
СЛОВО ⇔ <С,Л,О,В,О>
Теорема. Пусть a1, a2, …, an — конечные множества и |a1| = m1, |a2|=m2, …, |an|=mn. Тогда мощность множества a1*a2*a3*…*an равна произведению мощностей a1, a2, …, an
|a1*a2*…*an|=|a1|*|a2|*|a3|*…*|an|= m1*m2*…*mn
Следствие |an|=|A|n
Проекция множества.
Операция программирования множества тесно связана с операцией проектирования кортежа и может применяться лишь к таким множествам, элементами которых являются кортежи одинаковой длины.
Пусть M — множество, состоящее из кортежей длины S. Тогда пролинией множества M будем называть множество пролиний всех кортежей из М
Пример. Пусть М={<1,2,3,4,5>,<2,1,3,5,5>,<3,3,3,3,3>,<3,2,3,4,3>}
тогда Пр2М={2,1,3}, Пр3M={3}, Пр4M={4,5,3}, Пр24M={<2,4>,<1,5>,<3,3>}, Пр13M={<1,3>,<2,3>,<3,3>}, Пр15M={<1,5>,<2,5>,<1,3>}, Пр25M={<2,5>,<1,5>,<3,3>,<2,3>}.
Очевидно что если М=Х*Y то Пр1М=Х, Пр2М=Y
и если Q⊆Х*Y то Пр1Q⊆Х и Пр2Q⊆Y
Пример. V={<a,b,d>,<c,b,d>,<d,b,b>}
Пр1V={a,c,d}
Пр2V={b}
Пр3V={d,b}
Пр12V={<a,b>,<c,b>,<d,b>}
Пр23V={<b,d>,<b,b>}
Пр13V={<a,d>,<c,d>,<d,b>}
Пусть V — множество векторов одинаковой длины S.
ПрiV ={Прiv/v∈Y}, Прii…ikv = { Прii…ikv/v∈Y}.
Если V =A1*A2*…*An, то Прii…ikV=Ai1*Ai2*…*Aik.
В общем случае ПрiV — вовсе не обязательно прямое произведение: оно может быть подмножеством.
Для того, чтобы рассчитать разность множеств, нужно определить, что обозначает это понятие. Третье множество, которое получается из «вычитания» одного множества (A) из другого (U) и состоит из элементов одного из двух множеств, исключая общие элементы, называется разностью множеств (U и A). Записывается следующим образом: UA. Результат во многом зависит от того, какое множество «вычитают».
Пример
Дано множество U={2,5,6,7,9} и множество A={4,5,7,8,9}.
• Разность множеств UA={2,6}, так как 5, 7 и 9 входят в множество (А).
• И наоборот, разность множеств AU={4,8}, так как те же 5, 7, и 9 входят в множество (U).
Если элементы множеств не совпадают, то разность будет аналогична элементам «уменьшаемого» множества.
Пример
Дано множество U={2,5,6,7,9} и множество A={1,3,4,8}.
• Разность множеств UA={2,5,6,7,9}
• И наоборот, разность множеств AU={1,3,4,8}.
Если все элементы обоих множеств аналогичны, в результате получится пустое множество.
Для расчета разности множеств оптимальный выход – воспользоваться онлайн калькулятором. На практике разность множеств применяют в 3D графике, например: создание объемного кольца. Или для поиска IP-адресов, которые находятся в различных наборах (множествах) данных.
Лекция 4. Вычитание
множеств, дополнение подмножества.
Определение. Разностью множеств
А и В называется множество, содержащее те и только те элементы, которые
принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А В. Таким образом, по определению
разности А В = { х | х ∈
А и х ∉В}.
Например, если А = { a , c , k , m , n }
и В = { a , b , c , d , e }, то
А В = { k , m , n }.
Если
изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств
является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством
множества А. В этом случае разность множеств А и В называют дополнением подмножества
В до множества А и обозначают В’А. Дополнение можно изобразить
как показано на рис. 5. Если В – подмножество универсального множества U, то
дополнение подмножества В до U обозначают В’.

Например, если В – множество однозначных
натуральных чисел, то В’– множество неоднозначных натуральных чисел, если С –
множество равнобедренных треугольников, то С’ – множество треугольников, у
которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству
обладают рядом свойств.
1) (А В) С = (А С)
В.
2) (А∪В)
С = (А С) ∪ (В С).
3) (А В) ∩ С = (А ∩С)
(В ∩ С).
4) (А ∪
В)’ = А’ ∩ В’.
5) (А ∩ В)’ = А’ ∪В’.
Задания для самостоятельной работы по теме:
1.
Найдите разность множеств А и В, если
а) А = {1,2, 3,4,
5, 6}, В = {2, 4, 6, 8, 10};
б) А =
{1,2,3,4,5,6},В={1,3,5};
в) А =
{1,2,3,4,5,6},В={6,2,3,4,5,1}.
2. В
каких случаях, выполняя упражнение 1, вы находили дополнение множества В до
множества А?
3.
Из каких чисел состоит дополнение:
а) множества натуральных
чисел до множества целых;
б) множества целых чисел
до множества рациональных;
в) множества рациональных
чисел до множества действительных.




















