Доходность активов – формула ее расчета будет рассмотрена нами далее – нагляднее всего отражается в виде коэффициента рентабельности. Изучим специфику исчисления этого показателя.
Коэффициент рентабельности — основной показатель доходности активов
В общем случае доходность активов предприятия рассчитывается посредством исчисления коэффициента их рентабельности. Этот показатель предполагает расчет доходности с учетом реальных (отраженных в официальной финансовой отчетности) показателей по всем типам активов, что используются в целях финансирования хозяйственных операций предприятия.
Доходность активов с использованием рассматриваемого коэффициента отражается наглядно — в формате, близком к отражению годовых процентов по вкладу в банке (или инвестпроекту.) Зная соответствующий коэффициент, инвестор сразу может сопоставить его с аналогичным показателем по другим бизнесам и выберет среди предприятий наиболее привлекательное с точки зрения собственного участия в финансировании деятельности.
Коэффициент рентабельности активов: формула
Рассматриваемый коэффициент, если анализируемый период соответствует налоговому году, вычисляется по формуле:
КРА = ЧП / А,
где:
КРА — коэффициент рентабельности активов;
ЧП — чистая прибыль за год;
А — величина активов фирмы по состоянию на конец года.
При необходимости формулу можно приспособить и к иным периодам. В этом случае она будет выглядеть так:
КРА (ПЕРИОД) = ЧП (ПЕРИОД) / ((А1 + А1) / 2),
где:
КРА (ПЕРИОД) — коэффициент рентабельности за анализируемый период;
ЧП (ПЕРИОД) — чистая прибыль за период;
А1 — стоимость активов на начало периода;
А2 — стоимость активов на конец периода.
Показатель ЧП для приведенных формул берется из строки 2400 отчета о финрезультатах, а показатель А — из строки 1600 бухбаланса (если указанная отчетная документация сформирована в рамках годовой отчетности). В случае расчетов за иные периоды данные берутся из промежуточной отчетности (если таковая составляется) или из оборотно-сальдовых ведомостей за анализируемый период.
Какой может быть оптимальная величина коэффициента рентабельности активов?
Всё зависит от отраслевой специфики и масштабов предприятия. Так, в сфере промышленности соответствующий показатель составляет порядка 1–5%, что, как правило, ниже, чем рентабельность активов в сфере услуг или ИТ-разработки. Рентабельность активов стартапов и малых бизнесов обычно выше, чем у крупных предприятий, много лет присутствующих на рынке.
Итоги
Основной показатель доходности активов предприятия — коэффициент их рентабельности. Для его расчета берутся показатели по чистой прибыли и стоимости активов, соответственно, по отчету о финрезультатах и бухгалтерскому балансу.
Ознакомиться со спецификой иных показателей рентабельности, применяемых в рамках анализа результатов хозяйственной деятельности организации, вы можете в статьях:
- «Как рассчитать рентабельность продукции?»;
- «Как определить рентабельность производства (формула)?».
#статьи
- 5 май 2023
-
0
Рентабельность активов: что показывает и по какой формуле её рассчитывать
Бывает, что бизнес вкладывает деньги в развитие, но прибыль при этом не растёт. Объясняем, почему так происходит и как это контролировать.
Иллюстрация: Polina Vari для Skillbox Media

Рассказывает просто о сложных вещах из мира бизнеса и управления. До редактуры — пять лет в банке и три — в оценке имущества. Разбирается в Excel, финансах и корпоративной жизни.
Рентабельность активов (ROA) — показатель успешности бизнеса. С его помощью можно понять, насколько эффективно бизнес использует свои ресурсы. Следить за ним важно всем предпринимателям и руководителям.
Из этой статьи Skillbox Media вы узнаете, как рассчитать, оценить и изменить показатель.
- Что такое рентабельность активов
- По какой формуле её рассчитывать
- Как определить рентабельность активов по балансу
- Как анализировать показатели рентабельности активов
- Как их увеличить
- Как узнать больше об управлении финансами в бизнесе
Рентабельность активов — это финансовый показатель отношения прибыли бизнеса к стоимости его активов. Его рассчитывают, чтобы понять, эффективно ли бизнес использует ресурсы.
Рентабельность активов показывает, сколько копеек приносит каждый рубль, вложенный в активы бизнеса. Например, какую прибыль предпринимателю даёт его недвижимость, оборудование или транспорт — насколько эффективно их используют в бизнес-процессах.
Разберём на примере. Предположим, что один цветочный бизнес заработал за год 10 миллионов рублей, второй — 15 миллионов. Может показаться, что во втором случае компания работала эффективнее. Но прежде чем делать такой вывод, нужно узнать, сколько стоят активы этих компаний, и рассчитать ROA.
Допустим, стоимость активов первой компании — 30 миллионов рублей, стоимость активов второй — 53 миллиона. ROA в первом случае будет равна 33%, во втором — 28%.
Получается, первый цветочный бизнес работал с большей отдачей. Собственник первой компании вложил в бизнес 30 миллионов и получил с них 10 миллионов. Собственник второй компании вложил 53 миллиона, а получил 15 миллионов.
Формула для расчёта рентабельности активов выглядит так:
ROA = Прибыль до налогообложения / Стоимость активов × 100%
Разберём, что означают эти показатели, и рассчитаем ROA на примере.
Прибыль до налогообложения — выручка, очищенная от всех расходов бизнеса, кроме налогов.
Выручка — все деньги, которые бизнес заработал в результате своей деятельности. Расходы — все деньги, которые бизнес потратил, чтобы эту выручку получить.
Активы — вся собственность бизнеса в денежном выражении. Например, недвижимость, оборудование, транспорт, сырьё и материалы, деньги в кассе, дебиторская задолженность. Чтобы посчитать стоимость активов, используют их рыночную стоимость.
Допустим, фермерское хозяйство продало сельхозпродукции на 11 миллионов рублей. Это его выручка. Расходы за год составили 5,3 миллиона — это зарплаты работникам, сырьё и материалы, деньги на содержание животных, амортизация техники. Тогда прибыль до уплаты налогов будет равна: 11 млн рублей − 5,3 млн рублей = 5,7 млн рублей.
Активы фермерского хозяйства — сельскохозяйственная недвижимость, техника, животные, земельные участки — стоят 21 миллион рублей.
Отсюда ROA = 5,7 млн рублей / 21 млн рублей × 100% = 27%.
Это значит, что каждый рубль, вложенный в активы бизнеса, приносит фермеру 27 копеек прибыли.
Для расчёта рентабельности активов чаще всего используют бухгалтерскую отчётность — бухгалтерский баланс (форма 1 отчётности) и отчёт о финансовых результатах (форма 2).
Формула расчёта рентабельности активов по балансу (по формам бухгалтерской отчётности) выглядит так:
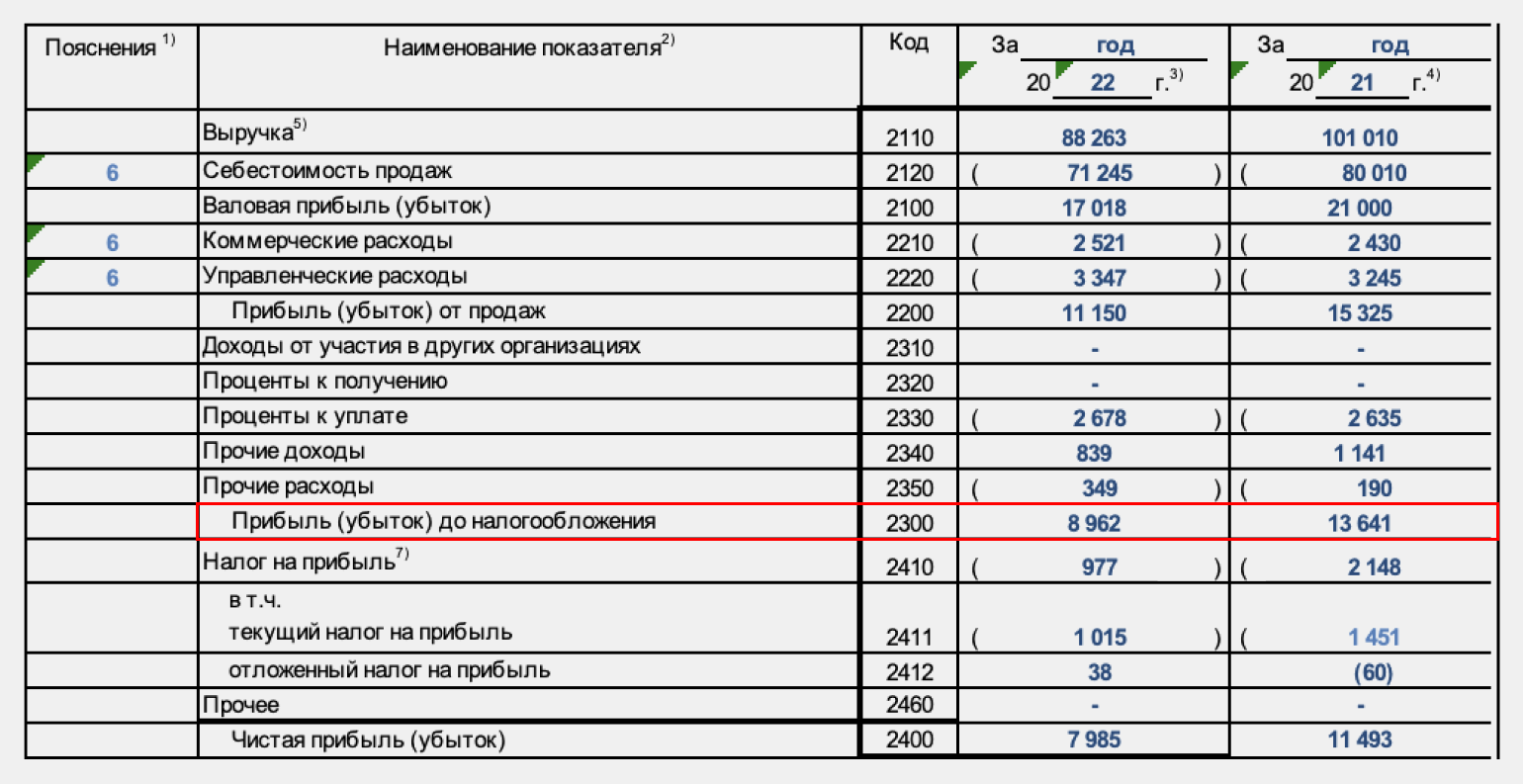
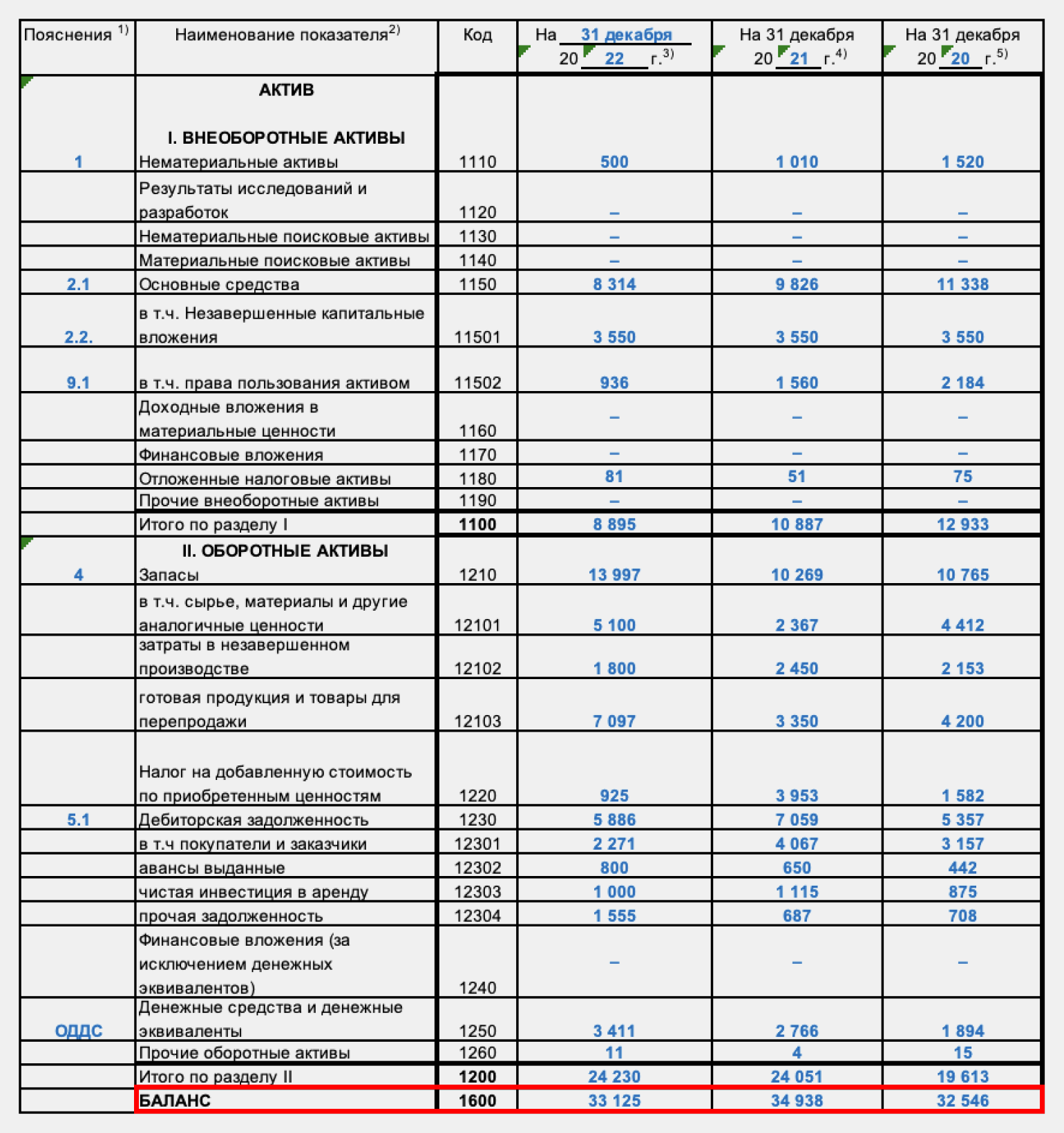
ROA = Строка 2300 формы 2 / (Строка 1600 НП формы 1 + Строка 1600 КП формы 1) / 2 × 100%
- Строка 2300 формы 2 — прибыль до налогообложения, отражённая в отчёте о финансовых результатах.
- Строка 1600 НП формы 1 — стоимость активов на начало периода, отражённая в бухгалтерском балансе.
- Строка 1600 КП формы 1 — стоимость активов на конец периода, отражённая в бухгалтерском балансе.
Скриншот: «Главбух» / Skillbox Media
Скриншот: «Главбух» / Skillbox Media
Также для расчёта ROA можно использовать другие документы — например, данные управленческого учёта или собственные финансовые отчёты компании. Это зависит от того, какую отчётность ведёт бизнес.
Сам по себе показатель ROA ничего не даёт. Чтобы понять, приемлем он для бизнеса или нет, его нужно анализировать. Например, отслеживать в динамике — каждый квартал, полугодие или год — или сравнивать с конкурентами.
Если рентабельность активов растёт, значит бизнес эффективно использует ресурсы в своих процессах. И наоборот, если ROA снижается, значит, снижается и эффективность использования ресурсов.
Если компания увеличивает стоимость активов, но прибыль при этом не растёт и ROA уменьшается, — значит, нет смысла расширять бизнес дальше, ничего при этом не меняя в его процессах. Если компания увеличивает стоимость активов и вместе с этим увеличивается показатель их рентабельности — значит, наращивание активов приводит к росту прибыли, бизнес можно расширять.
Также ROA компании можно сравнивать с показателями конкурентов. Так можно понять общую эффективность ведения бизнеса. При этом в числе конкурентов должны быть только конкуренты из той же отрасли с сопоставимой стоимостью активов.
Если рентабельность активов компании ниже, чем у аналогичных конкурентов, — нужно искать причины и исправлять их. Подробнее об этом говорим ниже.
Мы выяснили, что рентабельность активов зависит от двух показателей — прибыли компании и стоимости её активов. Соответственно, чтобы увеличить ROA, нужно повышать прибыль и оптимизировать активы.
Вот некоторые способы увеличения прибыли:
- снизить себестоимость продукции — например, внедрить более экономичные решения производства, использовать материалы вторично или найти поставщиков с более выгодными условиями сотрудничества;
- пересмотреть ассортимент — производить и продавать только наиболее рентабельные товары;
- увеличить объём продаж;
- повысить цены.
Чтобы оптимизировать активы, можно:
- продать объекты, которыми компания больше не пользуется, — например, лишнюю недвижимость;
- отремонтировать технику или заменить её новой;
- сократить дебиторскую задолженность.
Также позитивно влияют на рентабельность активов изменения в управлении процессами компании — например, их автоматизация.
- Рентабельность активов (ROA) — отношение прибыли бизнеса к стоимости его активов. Она показывает, сколько копеек приносит каждый рубль, вложенный в активы.
- Показатели ROA нужно отслеживать в динамике — сравнивать с показателями бизнеса за предыдущие периоды или с показателями конкурентов.
- Если бизнес наращивает активы, но его прибыль при этом не растёт и ROA падает, значит, нет смысла расширяться дальше — лучше пересмотреть бизнес-процессы.
- Чтобы увеличить рентабельность активов, нужно увеличивать прибыль компании и оптимизировать активы. Например, можно продать ненужную технику, попросить дебиторов об оплате долгов, увеличить цены на свою продукцию.
- Если вы только начали знакомиться с финансовыми показателями бизнеса — прочитайте статью о рентабельности. В ней мы рассказали, какие бывают виды рентабельности, как их рассчитывать и анализировать.
- Также в Skillbox Media есть отдельные статьи о рентабельности продаж, рентабельности продукции и рентабельности собственного капитала.
- Эффективность бизнеса можно определить с помощью показателя маржинальности. Подробнее об этом рассказали в статье о маржинальности, марже и наценке.
- Управление финансами — базовая функция любого бизнеса. Понимая основы управления финансами, можно эффективно распоряжаться ресурсами компании. Прочитайте материал о финансовом менеджменте, чтобы понять, как он устроен в компаниях.
- За расчёт и анализ рентабельности может отвечать финансовый менеджер. Это перспективная профессия, с которой можно зарабатывать от 100 тысяч рублей. Освоить её можно на курсе Skillbox «Профессия Финансовый менеджер». Курс будет интересен также предпринимателям, которые хотят более эффективно управлять финансами бизнеса.

Научитесь: Профессия Финансовый менеджер
Узнать больше
Инвестиции03 декабря 2021 в 08:0025 538
Как получать дивиденды ежемесячно: пошаговая инструкция
Преимущества и недостатки дивидендной инвестиционной стратегии и параметры выбора ценных бумаг
Что такое дивиденды
Кто решает, когда и сколько платить дивидендов?
Сколько можно заработать на дивидендах?
Плюсы и минусы дивидендной стратегии
Как собрать дивидендный портфель
Как собрать портфель из акций
Шаг 1. Составляем порядок выплат
Шаг 2. Отбираем эмитентов
Шаг 3. Изучаем компании
Как собрать портфель из ETF и REIT
Что ещё нужно учитывать при покупке дивидендных бумаг
Ошибки при составлении дивидендного портфеля
Что такое доходные активы?
Прибыльные активы — это приносящие доход инвестиции, которые принадлежат или удерживаются бизнесом, учреждением или физическим лицом. Эти активы также имеют базовую стоимость и способность приносить дополнительные средства сверх собственной стоимости для держателя инвестиций. Это позволяет держателю инвестиций поддерживать активы в качестве источника дохода или продавать активы за единовременную сумму, исходя из внутренней стоимости.
Понимание доходных активов
Прибыльные активы включают акции, облигации, доход от сдачи в аренду собственности, депозитные сертификаты (CD) и другие счета или инструменты для получения процентов или дивидендов. Они могут обеспечивать стабильный доход, что особенно полезно для достижения долгосрочных целей, таких как пенсионное планирование. Прибыльные активы отражают только часть общих активов отдельного лица или учреждения.
Сопровождение зарабатываемых активов
Некоторые приносящие доход активы, такие как депозитные сертификаты, не требуют дополнительных усилий после первоначального инвестирования. Доход создается за счет выплаты процентов или дивидендов и является частью основной схемы конкретного типа инвестиций. Эти инвестиции практически не требуют обслуживания и обычно не требуют дополнительных вложений со стороны держателя инвестиций.
Другие приносящие доход активы, такие как аренда недвижимости, требуют постоянных усилий с точки зрения времени и денег. Например, сдаваемая в аренду собственность требует текущего обслуживания, улучшения собственности, налогов, страхования и общего управления недвижимостью. Некоторые из этих усилий могут быть эффективно переданы на аутсорсинг за плату третьей стороне, например, фирме по управлению недвижимостью.
Фирмы по управлению недвижимостью берут на себя ответственность за повседневные операции, связанные с арендой собственности. Это может включать поиск и проверку потенциальных арендаторов, управление любым техническим обслуживанием, сбор арендной платы и рекламу собственности. Гонорары фирмы обычно выплачиваются за счет части полученного дохода от аренды. В случаях, когда недвижимость пустует, плата за управление может потребоваться непосредственно от владельца.
Получение активов и налоговые обязательства
Доход от приносящих доход активов должен быть указан в соответствующих налоговых декларациях.В случае дохода, полученного от различных ценных бумаг, инвестиционные учреждения присылают годовые отчеты для целей налоговой отчетности, которые включают общую сумму полученных процентов и / или дивидендов. Также должен быть указан доход от сдачи в аренду.
Определенные расходы, связанные с обслуживанием активов, таких как арендуемая недвижимость, могут квалифицироваться как налоговые вычеты.Сюда могут входить некоторые текущие расходы, такие как коммунальные услуги и налоги, а также некоторые переменные затраты, такие как затраты, связанные с ремонтом объекта недвижимости.
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
- Коэффициент вариации — coefficient of variation.
- Коэффициент Шарпа — Sharpe ratio.
- Коэффициент информации — information ratio.
- Коэффициент Сортино — Sortino ratio.
- Коэффициент Трейнора — Treynor ratio.
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
(Pt + 1 − Pt + CF) / Pt,
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
Бытовой пример: инвестор купил акцию за 100 $ и продал за 150 $, а за время владения получил 3 $ дивидендов. Доходность по формуле выше будет считаться так:
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
Например, акции Apple 31 декабря 2016 стоили 27,4 $, а 30 сентября 2020 — 115,6 $. Посчитаем общую доходность за этот период:
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
((1 + r1) × (1 + r2) × (1 + r3) × (1 + rn))1/n − 1,
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
Например, инвестор купил акцию компании за 100 $ и владел ею 3 года. За первый год стоимость акции выросла на 20%, во второй год — упала на 10% по отношению к прошлому периоду, а за третий год акции прибавили в цене 30%. Общая годовая доходность за эти три года будет считаться так:
((1 + 20%) × (1 − 10%) × (1 + 30%))1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
(20% − 10% + 30%) / 3
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному: акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
| Покупка | Первый год | Второй год | Третий год | Четвертый год | |
|---|---|---|---|---|---|
| Акция A | 100 $ | 140 $ (+40%) | 150 $ (+7%) | 125 $ (−17%) | 180 $ (+44%) |
| Акция B | 100 $ | 70 $ (−30%) | 120 $ (+71%) | 100 $ (−17%) | 180 $ (+80%) |
Четвертый год
180 $ (+44%)
Четвертый год
180 $ (+80%)
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Актив A:
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%)1/4 = 15,8%.
Актив B:
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%)1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность)(365 / Количество дней владения активом) − 1
Например, инвестор купил акцию компании за 100 $, держал ее 714 дней, а на 715-й день продал и получил доходность 74% за весь период владения. Общая годовая доходность за рассматриваемый период будет считаться так:
(1 + 74%)(365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива)(1 / Количество периодов) − 1
Например, инвестор купил 20 акций по 200 $ и решил удерживать их 2 года. За этот период компания каждый год выплачивала 1 $ дивидендов на акцию. На момент продажи цена акции составила 270 $. В этом случае общая годовая доходность будет такой:
((270 × 20 + 2 × 20) / 200 × 20)(1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Итак, в общем виде мы рассмотрели понятия доходности и риска. Теперь я построю диаграмму «риск-доходность», чтобы проанализировать, какие активы показывают оптимальное отношение риска к доходности. Простыми словами, по диаграмме можно понять, какой актив дает максимальную доходность на единицу риска.
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
6 крупнейших по весу компаний в портфеле Berkshire Hathaway на 30.09.2020
| Компания | Тикер | Вес актива в портфеле |
|---|---|---|
| Apple | AAPL | 47,78% |
| Bank of America | BAC | 10,63% |
| Coca-Cola | KO | 8,63% |
| American Express | AXP | 6,64% |
| Moody’s | MCO | 3,12% |
| US Bancorp | USB | 2,07% |
Вес актива в портфеле
47,78%
Вес актива в портфеле
10,63%
Вес актива в портфеле
8,63%
Вес актива в портфеле
6,64%
Вес актива в портфеле
3,12%
Вес актива в портфеле
2,07%
В расчетах для повышения точности я опираюсь на ежедневные котировки акций с 2012 по 2020 год — данные и расчеты представлены в гугл-таблице.
Еще для расчетов нам понадобится бенчмарк и безрисковая ставка. Бенчмарк — это портфель, с которым мы будем сравнивать эффективность наших активов. Обычно в качестве бенчмарка берут индекс на широкий рынок США — я взял ETF SPDR S&P 500.
Безрисковая ставка нужна для расчета показателей эффективности инвестиций: в ряде этих показателей она используется как доходность от вложения в безрисковый актив, то есть актив, риск наступления дефолта по которому стремится к нулю. Конечно, абсолютно безрисковых активов не существует, поэтому в качестве безрисковой ставки часто используют процентную ставку по государственным облигациям или определяют ее равной нулю. В качестве безрисковой ставки (RFR, risk-free rate) я взял 10-летние казначейские облигации США — 10-Year Treasury Constant Maturity Rate.
Шаги будут такие:
- Берем дневные доходности активов.
- Рассчитываем по ним среднюю годовую доходность и стандартное отклонение — как делали в разделе с расчетом риска.
- Строим карту «риск-доходность».
Показатели доходности и риска
| Компания | Тикер | Среднегодовая доходность | Стандартное отклонение |
|---|---|---|---|
| Apple | AAPL | 30,2% | 28,6% |
| Bank of America | BAC | 18,4% | 31,1% |
| Coca-Cola | KO | 10,0% | 18,3% |
| American Express | AXP | 15,0% | 29,3% |
| Moody’s | MCO | 27,1% | 27,7% |
| US Bancorp | USB | 10,8% | 26,1% |
| ETF S&P 500 | SPY | 15,5% | 16,8% |
| 10-Y Treasury Bonds | DGS10 | 2,1% | 0,0% |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Среднегодовая доходность
2,1%
Стандартное отклонение
0,0%
Теперь строим карту по данным из таблицы: данные по среднегодовой доходности откладываем по вертикали, а по стандартному отклонению (риску) — по горизонтали.
Из диаграммы выше можно сделать ряд выводов относительно соотношения доходности и риска активов, определить наиболее предпочтительные и исключить наиболее убыточные из них: например, можно сделать вывод, что акции AAPL дают большую доходность, чем BAC и AXP, но при этом риск инвестирования в AAPL ниже.
Но зачастую неочевидно, какой из активов лучше, — в таком случае на помощь приходят показатели оценки соотношения риска и доходности.
Считаем индикаторы привлекательности активов
Индикаторы привлекательности активов приводят данные из таблицы выше к одному знаменателю: мы можем посчитать конкретные показатели для каждой бумаги и сравнить их. Разберем основные показатели.
Коэффициент вариации показывает величину риска, приходящуюся на единицу доходности. Он рассчитывается по следующей формуле:
CV = σ / r̄,
где σ — стандартное отклонение доходности актива,
r̄ — среднее арифметическое доходности актива.
Коэффициент вариации применяется для сравнения активов с разными доходностями и стандартными отклонениями. Применение показателя позволяет ранжировать активы по степени их рискованности. Чем больше значение показателя, тем выше риск инвестиций.
Коэффициент вариации для рассматриваемых акций
| Тикер | Среднегодовая доходность | Стандартное отклонение | Коэффициент вариации |
|---|---|---|---|
| AAPL | 30,2% | 28,6% | 0,95 |
| MCO | 27,1% | 27,7% | 1,03 |
| SPY | 15,5% | 16,8% | 1,09 |
| BAC | 18,4% | 31,1% | 1,70 |
| KO | 10,0% | 18,3% | 1,82 |
| AXP | 15,0% | 29,3% | 1,95 |
| USB | 10,8% | 26,1% | 2,40 |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Коэффициент вариации
0,95
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Коэффициент вариации
1,03
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Коэффициент вариации
1,09
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Коэффициент вариации
1,70
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Коэффициент вариации
1,82
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Коэффициент вариации
1,95
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Коэффициент вариации
2,40
Можно сделать вывод относительно того, какой из активов несет больше или меньше риска. Теперь мы видим, что инвестиции в AAPL выгоднее не только инвестиций в BAC и AXP, но и вообще в любой из рассматриваемых активов: на единицу риска тут приходится наибольшая доходность. Самый рискованный актив — USB: на 1% доходности приходится 2,4% стандартного отклонения.
Коэффициент Шарпа показывает, во сколько раз избыточная доходность от инвестирования в портфель по сравнению с безрисковым активом выше уровня риска инвестиций. Избыточная доходность показывает, насколько доходность инвестиционного портфеля выше доходности безрискового актива, в роли которого чаще всего выступают государственные облигации.
Коэффициент Шарпа определяется по следующей формуле:
R̄x − R̄f / σx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σx — стандартное отклонение доходности актива за сопоставимый период.
Рассмотрим пример. Предположим, что средняя доходность по акции составляет 30% годовых при 20% стандартного отклонения, а средняя доходность по государственным облигациям США (безрисковый актив) равна 3% годовых. Тогда коэффициент Шарпа для нашей акции будет считаться так:
(30% − 3%) / 20% = 1,35
Это значение показателя говорит о высокой инвестиционной привлекательности нашей акции: доходность по ней выше доходности безрискового актива и превышает уровень риска.
Из формулы видно, что коэффициент Шарпа измеряет вознаграждение в виде средней избыточной доходности на единицу риска. Также следует отметить, что коэффициент был создан для анализа портфелей, а не отдельных инструментов, но все же его следует учитывать при отборе активов в портфель: он позволяет сделать вывод об эффективности вложения.
Критерии эффективности инвестиций на основе коэффициента Шарпа
| Критерий | Вывод по активу |
|---|---|
| Коэффициент Шарпа > 1 | Доходность инвестиций выше доходности безрискового актива и превышает уровень риска |
| 1 > коэффициент Шарпа > 0 | Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности |
| Коэффициент Шарпа < 0 | Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив |
Коэффициент Шарпа > 1
Доходность инвестиций выше доходности безрискового актива и превышает уровень риска
1 > коэффициент Шарпа > 0
Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности
Коэффициент Шарпа < 0
Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив
Рассмотрим результаты расчетов по коэффициенту Шарпа для акций в нашем примере.
Коэффициент Шарпа у акций из портфеля Баффетта
| AAPL | 0,98 |
| MCO | 0,90 |
| SPY | 0,79 |
| BAC | 0,52 |
| AXP | 0,44 |
| KO | 0,43 |
| USB | 0,33 |
Коэффициент информации характеризует соотношение риска-доходности актива или портфеля по сравнению с бенчмарком. Коэффициент расчетами напоминает коэффициент Шарпа, только вместо безрисковой ставки используется определенный эталон — бенчмарк. Бенчмарком могут выступать широкие рыночные индексы — MSCI, S&P 500, отраслевые индексы — DJA, собственноручно разработанные бенчмарки и так далее.
Иными словами, коэффициент информации — это отношение сверхдоходности к стандартному отклонению этой сверхдоходности у актива и бенчмарка. Коэффициент помогает понять, выгодно ли инвестировать в актив или набор активов — или проще и безопасней инвестировать в актив, выбранный бенчмарком. В нашем случае в качестве бенчмарка мы взяли ETF на S&P 500.
Формула выглядит так:
R̄x − R̄m / σx − m,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄m — средняя доходность бенчмарка за сопоставимый период,
σx − m — стандартное отклонение разности доходности актива и бенчмарка за сопоставимый период.
На примере AAPL и S&P 500 все будет выглядеть так:
В числителе: считаем разницу между средней доходностью акции AAPL (30,2% годовых) и средней доходностью индекса S&P 500 (15,5% годовых).
В знаменателе: сначала считаем разницу между дневными доходностями акции AAPL и индекса S&P 500, а потом по полученной совокупности дневных сверхдоходностей определяем стандартное отклонение и приводим дневное значение стандартного отклонения к годовому, перемножив дневное стандартное отклонение на корень из 252. Перемножаем на 252, так как в году 252 торговых дня. В нашей таблице этот расчет произведен на листе «Дневная доходность».
Итого получается:
(30,2% − 15,5%) / 21,28% = 0,69. Значение показателя выше 0,5 говорит о хорошей инвестиционной привлекательности акции.
Следует отметить, что этот коэффициент показывает эффективность активного управления, — при пассивном управлении, если мы просто покупаем индексный фонд и держим его, коэффициент будет равен нулю.
Чем больше значение коэффициента, тем выше избыточная «отдача» от инвестирования в определенный актив или портфель по сравнению с бенчмарком. Значение коэффициента информации в диапазоне от 0,5 до 0,74 считается хорошим, значение от 0,75 до 0,99 считается очень хорошим, а значение свыше 0,99 считается отличным. Ниже представлены результаты расчетов коэффициента информации для рассматриваемых акций.
Коэффициент информации у рассматриваемых акций
| AAPL | 0,69 |
| MCO | 0,63 |
| BAC | 0,13 |
| SPY | 0 |
| AXP | −0,02 |
| KO | −0,36 |
| USB | −0,26 |
Можно заметить, что для SPY (ETF на S&P 500) коэффициент информации равен нулю, так как он отражает движение рынка и не подразумевает сверхдоходности за активное управление. Напротив, хорошее значение коэффициента имеют акции AAPL и MCO, у которых на 1% стандартного отклонения сверхдоходности приходится 0,69 и 0,63% сверхдоходности соответственно. В случае с KO, AXP и USB отрицательные значения коэффициента связаны с отрицательными избыточными доходностями относительно бенчмарка.
Коэффициент Сортино — показатель, напоминающий коэффициент Шарпа, он отличается лишь расчетом риска. В коэффициенте Сортино для расчета риска учитываются только доходности актива ниже определенного уровня — чаще всего этот уровень определяется как доходность безрискового актива за сопоставимый период либо нулевая ставка.
Предполагается, что положительные отклонения доходностей — выше доходности безрискового актива — не несут риск, так как повышают доходность актива, — соответственно, учитывать их при расчете риска не нужно. Таким образом, для расчета стандартного отклонения необходимо выбрать только те дневные доходности, значение которых будет ниже доходности безрискового актива за этот же день. В нашей таблице все посчитано на листе «Кф. Сортино». Вот по какой формуле этот коэффициент рассчитывается:
R̄x − R̄f / σxd,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σxd — стандартное отклонение доходности актива ниже заданного уровня.
Для примера рассмотрим логику, по которой фильтруются доходности для расчета риска по коэффициенту Сортино.
Месячные доходности акции и безрискового актива
| Период | Доходность акции | Доходность безрискового актива | Отфильтрованная доходность |
|---|---|---|---|
| 1 месяц | 0,16% | 0,18% | 0,16% |
| 2 месяц | −2,54% | 0,18% | −2,54% |
| 3 месяц | 0,29% | 0,18% | 0,00% |
| 4 месяц | 0,00% | 0,18% | 0,00% |
| 5 месяц | 2,24% | 0,18% | 0,00% |
| 6 месяц | −11,80% | 0,18% | −11,80% |
| 7 месяц | 14,10% | 0,18% | 0,00% |
| 8 месяц | 8,36% | 0,18% | 0,00% |
| 9 месяц | −2,14% | 0,18% | −2,14% |
| 10 месяц | 9,67% | 0,18% | 0,00% |
| 11 месяц | 7,00% | 0,18% | 0,00% |
| 12 месяц | 0,90% | 0,18% | 0,00% |
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,16%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,54%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−11,80%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,14%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
В последней колонке оказались лишь те значения доходности акции, которые были ниже доходности безрискового актива за соответствующий период. Затем с помощью формулы стандартного отклонения рассчитываем риск по отфильтрованной доходности — он составит 3,54%. Среднемесячная доходность по акции — 2,19%, а среднемесячная доходность по безрисковому активу — 0,18%. Таким образом, коэффициент Сортино для акции из примера считается так:
(2,19% − 0,18%) / 3,54% = 0,57. Значение показателя ниже единицы указывает на то, что актив не обеспечивает должного уровня доходности на единицу нисходящего риска.
Чем больше значение коэффициента, тем выше вероятность безубыточности вложения и тем большей инвестиционной привлекательностью обладает рассматриваемый актив. Минимально допустимое значение показателя, определяющее инвестиционную привлекательность актива, — 1. Таким образом, на примере портфеля Баффетта допустимая и большая привлекательность у AAPL, MCO и SPY, а остальные же активы по коэффициенту Сортино непривлекательны, потому что не обеспечивают должного уровня доходности на единицу нисходящего риска.
Коэффициент Сортино у рассматриваемых акций
| AAPL | 1,59 |
| MCO | 1,40 |
| SPY | 1,19 |
| BAC | 0,86 |
| AXP | 0,73 |
| KO | 0,66 |
| USB | 0,53 |
Коэффициент Трейнора — еще один показатель, напоминающий коэффициент Шарпа и отличающийся только расчетом риска. В качестве риска берется коэффициент бета акции — он отражает волатильность актива по отношению к рынку. Коэффициент Трейнора показывает отношение сверхдоходности к рыночному риску.
Для расчета коэффициента бета акции используется следующая формула — рассчитанную бета акции можно найти на Yahoo Finance в разделе Summary на странице акции:
где σxm — ковариация между доходностью актива (портфеля) и доходностью рынка,
σm2 — дисперсия доходности рынка.
Методика расчета коэффициента бета акции раскрыта на листе «Дневная доходность» нашей таблицы, в столбце «Рыночный риск».
Коэффициент бета, находящийся в диапазоне от 0 до 1, свидетельствует о том, что акция движется в целом в одном направлении с рынком: если фондовый индекс растет, то растет и акция. Но значение коэффициента меньше 1 говорит о том, что актив менее чувствителен к движению рынка.
Коэффициент бета, равный 1, говорит о том, что движение актива полностью повторяет движение фондового индекса. Можно заметить, что значение 1 наблюдается у SPY, то есть у рыночного индекса.
Коэффициент бета больше 1 говорит о том, что динамика акции коррелирует с движением индекса, но при этом акция более чувствительно реагирует на любое движение рыночного индекса.
Коэффициент бета у рассматриваемых акций
| BAC | 1,38 |
| MCO | 1,26 |
| AXP | 1,26 |
| AAPL | 1,14 |
| SPY | 1,00 |
| USB | 1,15 |
| KO | 0,69 |
Зная коэффициент бета, доходность актива и доходность безрискового актива, мы можем рассчитать коэффициент Трейнора по следующей формуле:
R̄x − R̄f / βx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
βx — коэффициент бета актива.
Допустим, необходимо рассчитать коэффициент Трейнора для акции USB — US Bancorp. Переходим на страницу компании на Yahoo Finance и находим Beta — 1,14 на момент написания статьи. Далее для расчета коэффициента Трейнора достаточно найти разницу между среднегодовой доходностью акции — 10,8% и среднегодовой доходностью безрискового актива — 2,1% и поделить полученное значение на бета акции.
Для акции USB:
(10,8% − 2,1%) / 1,14 = 0,076
Значение показателя выше нуля указывает на то, что инвестирование в актив более привлекательно, чем в рыночный индекс. Если коэффициент ниже нуля, то целесообразнее вкладывать в рыночный индекс, так как актив проигрывает рынку по соотношению риска и доходности. Таким образом, все акции портфеля инвестиционно привлекательны по этому показателю.
Коэффициент Трейнора у рассматриваемых акций
| AAPL | 0,24 |
| MCO | 0,20 |
| SPY | 0,13 |
| BAC | 0,12 |
| KO | 0,11 |
| AXP | 0,10 |
| USB | 0,08 |
Выводы
Теперь мы можем собрать сводную таблицу и оценить инвестиционную привлекательность активов на примере акций из портфеля Баффетта.
По данным из таблицы можно сделать вывод, что из рассмотренных активов наиболее привлекательны для инвестора Apple (AAPL), Moody’s (MCO) и SPDR S&P 500 (SPY).
Но важно помнить: кроме расчета индикаторов нужно оценивать перспективы отрасли и самой компании — и только когда картина собрана целиком, можно решать, инвестировать ли в компанию.
