Поправляю Алексея:
Точно так же, как и на других языках. Уменьшить год на единицу, получить целую часть от деления на сто и к результату прибавить единицу.
.386
.model flat, stdcall
option casemap:none
include windows.inc
include kernel32.inc
include msvcrt.inc
includelib kernel32.lib
includelib msvcrt.lib
.stack 100h
.data
tPrompt db ‘Введите четырёхзначный номер года: ‘,0
tError db ‘Ошибка! Повторите ввод. ‘,13,10,0
tResult db ‘%d век. ‘,0
fInput db ‘%dn’,0
Year dd ?
.code
N76070897:
invoke crt_printf,addr tPrompt
invoke crt_scanf,addr fInput,addr Year
cmp Year,1000
jb Error
cmp Year,9999
ja Error
mov eax,Year
dec eax
cdq
mov ecx,100
div ecx
inc eax
invoke crt_printf,addr tResult,eax
invoke crt__flushall
invoke crt_scanf,addr fInput+2
invoke ExitProcess,NULL
Error:
invoke crt_printf,addr tError
jmp N76070897
end N76070897

![]()
0
жека
#
12 февраля 2017 в 13:27
круто ваще помогли спасибо
![]()
0
Ласточка
#
28 мая 2017 в 15:20
![]()
0
I.X.Sh
#
22 июня 2017 в 16:44
![]()
0
Bek
#
19 августа 2017 в 12:22
![]()
0
Яна
#
9 сентября 2017 в 19:27
![]()
0
Саня
#
19 сентября 2017 в 17:38
![]()
0
Владимир
#
20 сентября 2017 в 19:50
![]()
0
В’ячеслав
#
26 октября 2017 в 13:33
Круто спасибос респект уважуха
![]()
0
Iness
#
1 ноября 2017 в 12:05
![]()
0
Ямал
#
22 января 2018 в 08:30
А есть такая же таблица, но только с веками до нашей эры?
![]()
![]()
0
Настя
#
14 мая 2020 в 15:02
![]()
0
Биба
#
14 марта 2018 в 12:39
Спасибо, теперь я знаю сколько веков моей маме))))
![]()
0
Daria
#
18 марта 2018 в 15:38
А есть такаежа таблица,но только с веками до нашей эры?
![]()
![]()
0
Константин
#
24 декабря 2018 в 19:11
В днях и месяцах рубежом является 1ца, а в часах, годах, веках итд 0. Не правильно ли переход в следующий век начинать с нуля, а не с 1цы, как у вас? Т.е 0-99…2000-2099 итд?
![]()
Википедия:
Распространено заблуждение, проявляющееся в неверной интерпретации года, с которого начинаются десятилетия, века и тысячелетия современного григорианского календаря. В юлианском и григорианском календарях нет нулевого года. Первое тысячелетие начинается 1 годом и заканчивается 1000 годом. Любой век нашей эры начинается годом, номер которого оканчивается 01, и заканчивается годом, кратным 100, то есть оканчивающимся на 00. Таким образом, любой век длится с XY01 года по X(Y+1)00 год. Аналогично тысячелетие длится с X001 года по (X+1)000 год.
https://ru.wikipedia.org/wiki/0_%D0%B3%D0%BE%D0%B4
![]()
0
Валима Губайдуллина
#
6 января 2019 в 10:37
Крутоооо! А то мучаюсь,не могу определить какой это век!)
![]()
0
Игорь
#
28 февраля 2019 в 15:58
Очень сильно помогли,спасибо большое)
![]()
0
Владимир
#
10 сентября 2019 в 09:20
Не мешало бы сделать такую же таблицу и по десятилетиям, а то у народа каша в голове. ХХ век теперь начинается сотыми (1900-и), а заканчивается «лихими девяностыми» плюс еще один неприкаянный 2000-й год. Несмотря на то, что век математически состоит из десяти десятилетий и у каждого десятилетия есть свой порядковый номер.ш
![]()
0
максим
#
4 октября 2019 в 11:27
![]()
0
Игорь
#
4 декабря 2019 в 18:16
Ковалев Игорь
Если мне не изменяет память, в журнале «Оракул» № 1 за 2000 (или 2001) год, в разделе «Письма читателей» поместили выдержку из письма жителя Ростова-наДону
(фамилию не помню). Тема была такая , мол — наступило новое тысячелетие — третье. То есть в новой эре (н.э.) мы прожили уже 2000 лет, а от чего идет отсчет?
От рождества Христова. Но (внимание — так пишет автор) ПЕРВЫЕ 10 ВЕКОВ БЫЛИ НЕ ПО 100 ЛЕТ, А ПО 60 ЛЕТ (как минут в часе, секунд в минуте). То есть первое
тысечелетие длилось фактически 600 лет. И только на Никейском соборе в 1035 году постановили отныне каждый век считать по 100 лет. Поэтому, когда мы
встречаем 2001 год, то от Рождества прошло 1600 лет, и звезда, которая вспыхнула при появлении младенца Христа, не находится 2000 назад. Еще автор пишет,
что этот факт якобы широко известен в узких кругах ученых людей (например — в документах в хранилищах Ватикана), но почему-то все человечество считает иначе.
Меня заинтересовало это письмо и я стараюсь найти либо подтверждение либо опровержение такому факту в истории. Особенно когда появился Интернет. Но нигде
нет никакой информации на эту тему. Может кто-то встречал что-нибудь подобное?
![]()
0
Марина
#
27 января 2020 в 15:20
Спасибо огромное. Вы облегчели мне жизнь(。・ω・。)ノ♡.Теперь буду знать.
![]()
0
выа
#
12 мая 2020 в 17:45
![]()
0
tim
#
17 сентября 2021 в 16:15
а теперь до нашей эры, пожалуйста . Для шестого класса
![]()
![]()
0
Х
#
8 марта 2022 в 13:48
![]()
0
Ольга Сумська
#
29 сентября 2022 в 19:15
я не понимаю прикола 4 и 5
При выводе формулы примем следующие обозначения: К — календарное число месяца; М — коэффициент месяца; J — полный номер года н. э.; Д — порядковый номер года в столетии; Г’ — сдвиг дней недели по годам; Г — коэффициент года; В — коэффициент века; С — число полных прошедших столетий; [] — целая часть частного от деления (неполное частное); | | — остаток от деления, причем если делимое меньше делителя, остаток равен делимому; d — порядковый номер дня недели (0 — воскресенье, вс; 1 — понедельник, пн; 2 — вторник, вт; 3 — среда, ср; 4 — четверг, чт; 5 — пятница, пт; 6 — суббота, сб).
День недели календарной даты определяется как остаток от деления суммы чисел К, М, Г и В на 7:
d = |(K+ M + Г+В) / 7 | (1)
Сделаем предположение, что 1 января 1 г. п. э. был понедельник (= 1). Тогда для дат января первого года день недели будет определяться по формуле
d = |К / 7 |.
Так как в январе 31 день, то день недели в феврале первого года определится по формуле
d = |(К + (31–28)) / 7 | = |(K + 3) / 7 |.
Здесь 28 — ближайшее к 31 число, кратное семи, которое мы вычитаем для упрощения вычислений.
Так как в феврале первого года 28 дней, то день недели в марте определяется так же, как и в феврале. В марте 31 день, поэтому для апреля получим формулу
d = |(К + 3 + (31–28)) / 7 | = |(K + 6) / 7 |.
Аналогично получим формулы для остальных месяцев. В этих формулах числа, прибавляемые к календарному числу К, суть коэффициенты месяцев М, которые мы свели в табл. 9.

Таким образом, день недели для первого года н. э. будет определяться по формуле
d = |(K + M) / 7 |. (2)
Объединив повторяющиеся в табл. 9 значения М для разных месяцев, получим табл. 10.

Так как в простом году 52 недели и один день (365 = 52×7 + 1), то для второго года н. э. календарная формула примет вид
d = |(K + M + 1) / 7 |.
а для третьего
d = |(К + М + 2) / 7 |.
Следующий год (четвертый) — високосный; в нем 366 дней (за счет увеличения числа дней в феврале: 29 вместо 28). Поэтому для 4 г. н. э. календарная формула принимает вид для января и февраля
d = |(K = M + 3) / 7 |.
а для месяцев с марта по декабрь
d = |(K = M + 4) / 7 |.
В табл. 11 приведены коэффициенты М для високосных (вис.) и невисокосных — простых (пр.) лет. Так как сдвиг дней недели по годам Г’ в четырехлетиях 1–4, 5–8, 9–12 и т. д. происходит одинаково, составим таблиц значений Г’ для J от 1 до 60 лет (табл. 12). Мы видим, что в каждом следующем четырехлетии значение сдвига Г’ «увеличивается» на 5. Это позволяет выразить его для високосных годов (Jвис) в виде формулы
Г’ = |(5(Jвис:4) — 1) / 7)|

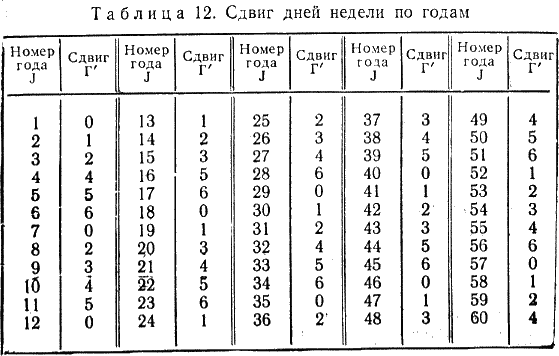
а для простых (Jnp) в виде формулы
Г’ = |(5 (Jвис: 4) — 1 + (Jпр — Jвис)) / 7 |,
где Jвс — ближайший меньший високосный год [53], а так как
Jвис: 4 = [Jпр: 4],
(3)
то общей формулой для Г’ для простых и високосных годов будет
Г’ =|(J + [J: 4] — 1) / 7 |. (3)

Упростим формулу (3), убрав в ней «—1». Чтобы сумма М + Г в формуле (1) осталась неизменной, уменьшим на единицу значения коэффициентов М в табл. 11 (при этом 0 считается равным 7). Новые значения коэффициентов М приведены в табл. 13, а формула (3) примет вид
Г’ = |(J + [J: 4]) / 7 |.
(4)
В формуле (4) полный порядковый номер года J, выражающийся для нашего времени четырехзначными числами, усложняет вычисления. Если обозначить число тысяч буквой а, число сотен — буквой Ь, число десятков — буквой с и число единиц — буквой f, то номер года J можно записать в виде
J= 1000а + 100b + 10с + f
и тогда
[J: 4] = 250а + 25b + [(10с + f): 4],
а
J + [J: 4] = 100a + 100b + 10c + f + 250a + 25b + [(10c + f): 4] = 1250а+ 125b + 10c + f + [(10c + f): 4].
Так как
|(1250a + 125b) / 7 | = |(7×170a + 60a + 7×17b + 6b) / 7 | = |6(10a + b) / 7 |.
то
(J + [J: 4]) / 7 = 10c + f + |(10с + f): 4 | + 6 (10а + Ь) / 7.
Если же учесть, что 10а + b = С — это число полных прошедших столетий (например, для 1986 г. С = 19 = 10×1 + 9), а 10с + f = Д — порядковый номер года в столетии, то формула (4) примет вид
Г’ = |(Д + [Д: 4]) / 7 | + |6c / 7 |. (5)
Значения второго слагаемого с течением веков циклически повторяются (см. табл. 14); это коэффициент века В. Первое же слагаемое будет коэффициентом года Г,
Г’ = |(Д + [Д: 4]) / 7 |. (6)
Следует учитывать, что порядковый номер Д года J в столетии имеет значения от 1 до 100, и поэтому для всех вековых лет, например 1800, 1900, 2000 гг. и т. д., Д = 100. Для I в. (годы 1–100) число полных прошедших столетий С = 0, для II в. (годы 101–200) С = 1 и т. д.
В табл. 14 приведены значения коэффициента века В (по старому стилю) для н. э.; из нее следует, что повторяемость юлианского. календаря происходит через 700 лет.

В начале изложения мы условно приняли, что первый день нашей эры (1 января 1 года первого века) был понедельником. Установим теперь значения коэффициентов М, которые дадут возможность правильно определять дни недели. Для этого используем точную дату какого-либо известного события.

Например, что 9 января 1905 г. было воскресенье («Кровавое воскресенье»). Для этой даты d = 0, К = 9, Г = |(5 + [5: 4]) / 7 | = 6, а В = 2. Подставляя эти данные в формулу (1), получим 0 = | (9 = M + 6 + 2) / 7 |, откуда М = — |17 / 7 | = —3. (Если для коэффициента М получается отрицательное значение, то его следует заменить положительным, прибавляя ближайшее большее число, кратное 7. В нашем случае —3 + 7 = 4.) Коэффициенты остальных месяцев можно установить исходя из сравнения с табл. 13. Вообще же их можно вычислить, взяв табель-календарь любого года. Окончательные значения М приведены в табл. 15. Теперь можно определить, каким днем недели было 1 января 1 г. н. э. Для этой легендарной даты К = 1, М = 4, Г = |(1 + [1: 4] / 7 | = 1 и В = 0, следовательно, d = |(1+ 4 + 1 + 0) / 7 | = 6 — суббота.
В новом стиле все вековые годы, кроме тех, число столетий в номере которых делится на 4 (например, 1600, 2000, 24 000 гг. и т. д.), невисокосные. Поэтому коэффициенты века В для этих годов будут другими.
Для определения значений поправок к коэффициенту века В для нового стиля следует учитывать, что при реформе юлианского календаря было принято следующую после четверга 4 октября 1582 г. дату считать пятницей 15 октября.
При этих условиях для 15 октября 1582 г. (С = 15) получаем d = 5, К =15, М = 4 и Г = |(82 + [82: 4]) / 7 | = 4.
Подставляя эти значения в формулу (1), получим 5 = |(15 + 4 + 4 +В) / 7 |, откуда В = |–18/7 | = |–14/7 | = 3.
Для юлианского календаря коэффициент века B = |(6C + P) / 7 |, а для григорианского к нему надо найти поправку Р, определяемую из соотношения
B = |(6c +P) / 7 |.
Так как в этих вычислениях применяется правило остатков, то формула преобразуется к виду
P = |(B + 6С) / 7 |.
В табл. 16 приведены эти поправки Р и коэффициенты века В для нового стиля с XVI по XXIII вв. Как видно из таблицы, коэффициенты В имеют всего четыре значения 3, 2, 0 и 5, которые циклически повторяются через 400 лет.

С введением григорианского календаря появились особые простые вековые годы 1700, 1800, 1900; для которых коэффициент года Г, определяемый по формуле (6), необходимо уменьшать на единицу, т. е. для этих лет
Г = |(100+ [100:4])/7 | = 5. (7)
Что касается вековых лет, число сотен которых кратно четырем, например, 1600, 2000 и т. д., то для нового стиля они остаются високосными, и коэффициент года для них определяется по общему правилу:
Г = |(100 + [100:4]/7 | = 6.
Итак, порядковый номер d дня недели любой календарной даты задается формулой (1) (см. с. 102). Значение коэффициента месяца М берется из табл. 15, коэффициент года Г вычисляется по формуле (6) или (7), а значение коэффициента века В берется для старого стиля из табл. 14, а для нового из табл. 16. Напомним еще раз, что если сумма К + М + Г + В меньше семи, то остаток от деления на семь равен самой сумме. То же правило действует при делении на четыре.

Многие люди затрудняются ответить на вопрос: «Как определить век по году, в котором произошло то или иное событие?» В общем-то, тут нет ничего сложного. Сейчас вы сами это увидите.
Наша эра
Для событий, произошедших во временном отрезке нашей эры (т.е. все, что было от наших дней до периода чуть более двух тысяч лет назад), век вычисляется следующим образом: у значения года отбрасываются две последние цифры, и к результату прибавляется единица. Допустим, нам нужно узнать, в каком веке началась Великая Отечественная война. Это произошло в 1941 г. Отбрасываем две последние цифры (41) и к оставшимся цифрам (19) прибавляем единицу. Получается число 20. Т.е. Великая Отечественная война началась в ХХ веке. Другой пример — Вещий Олег умер в 912 г. Какой век это был? Отбрасываем цифры 12, к девятке прибавляем один и понимаем, что киевский князь умер в десятом веке.
Тут нужно внести одно уточнение. Век — это промежуток длиной в сто лет. Если последние две цифры года — 01, то это первый год начала века. Если 00 — последний год столетия. Таким образом, в нашем правиле есть исключение. Если последние две цифры года — нули, то единицу мы не прибавляем. Как определить такой век по году? Например, Пий VII стал Папой Римским в 1800 году. В каком веке это произошло? Отбрасываем последние две цифры даты, но держим в уме, что это нули, и ничего не прибавляем. Получаем 18. Пий VII стал Папой Римским в XVIII веке. И уже в следующем году наступил век XIX. Мы разобрались с определением того, какой век какой год включает в себя, относительно нашей эры. А если речь идет о событиях, произошедших раньше?
До нашей эры
Тут все несколько сложнее. От 1 года до 100 года до н.э – это первый век до н.э. От 101 до 200 – второй, и так далее. Таким образом, чтобы определить век по году до рождества Христова, надо отбросить последние две цифры года и прибавить единицу. И точно так же, при последних цифрах в два нуля – ничего не прибавляем. Пример: Карфаген разрушен в 146 году до н. э. Как определить век по году в этом случае? Отбрасываем последние две цифры (46) и прибавляем единицу. Получаем второй век до н.э. И не забудем про наше исключение: катапульты изобрели в 400 году до н.э. Отбрасываем две последние цифры, держим в уме, что это нули, и ничего не прибавляем. Получается, что катапульты были изобретены в 4 веке до нашей эры. Все просто!

Тысячелетие
Раз уж мы разобрались, как определить век по году, давайте попробуем заодно научиться определять тысячелетие. Тут тоже нет ничего сложного. Только отбрасывать придется не две, а три последние цифры даты, а прибавлять по-прежнему 1.
Пример: Александр Второй отменил крепостное право в 1861 году. В каком тысячелетии он это сделал? Отбрасываем три последние цифры (861) и к оставшейся единице прибавим еще одну. Ответ: второе тысячелетие. Исключения тут тоже есть. Если последние три цифры – нули, то единица не прибавляется.
Национальная валюта «сомони» была введена в Таджикистане в 2000 году. То есть это произошло во втором тысячелетии.

Именно поэтому те, кто в 2000 году праздновал наступление третьего тысячелетия и 21-го века, заблуждались — эти события произошли лишь в следующем году.
Если вы поняли всю эту несложную арифметику, то теперь точно знаете, как определить век по году или даже узнать номер тысячелетия.

- Как определять век
- Что такое третье веко
- Какой сейчас год по-старославянски
При определении порядкового номера века могут возникнуть две сложности.
Первая – обозначать век принято римскими цифрами, но далеко не все умеют их правильно читать. Разобраться с римскими цифрами поможет следующая табличка соответствия знаков в римской записи числа арабским цмфрам:
Дальше все просто: складываем все десятки (Х) и пятерки (V), прибавляем единички, расположенные в конце записи числа, отнимаем единички расположенные в другом месте.
XIX – десяток две и одна единичка не в конце записи, т.е. 10 + 10 – 1 = 19 – обозначение девятнадцатого века;
ХIV – десятка одна, пятерка одна и одна единичка не в конце записи, т.е. 10 + 5 – 1 = 14 – обозначение четырнадцатого века;
XVII – десятка одна, пятерка одна и две единички в конце записи, т.е. 10 + 5 + 1 + 1 = 17 – обозначение семнадцатого века.
Второй момент, который надо помнить при определении века, что в арабской записи числа последние две цифры номер года, а предыдущие — номер века, но номер столетия на единицу больше обозначающего числа.
1932 – номер века обозначают цифры 19, следовательно, век двадцатый;
345 – номер века 3, следовательно, век четвертый.
![]()
Если перед нами есть дата, написанная арабскими цифрами (1.2.3.4.5.6.7.8.9.0) то определить, к какому веку дата относится, очень легко.
Если дата до 1000, например, 678 год, то смотрим на первую цифру -6 и добавляем один, получается седьмой век.
Если же дата написана четырехзначной цифрой, например, 1645, то смотреть надо на первые две цифры и опять добавлять один., значит, в нашей дате 16+1=17 , получается, что это семнадцатый век.
Смотрите, последние две цифры — это годы текущего века, все цифры что перед ними — это номер прошедшего века.
Например, год 22333 будет обозначать 224-й век ( 223+1=224).
![]()
Определить легко. Берем год. Например, 1703 (год основания города Санкт-Петербурга), берем первые две цифры (17) и прибавляем к ним один. Получается, что город был основан в восемнадцатом веке.
Другой пример: 998 год. Берем первую цифру и прибавляем к ней один. Получается, что десятый век.
![]()
Определяется век по первым цифрам заданного года.
Например, год 1905, это год первой русской революции, двадцатый век.
Или время Французской революции, которая была в 1848 году, это век девятнадцатый.
То есть от годов плюс один.
Сейчас 2016, а век 21-й.
![]()
Один век, это столетие, но к нему требуется добавить плюс один.
Например, в 1900 году пошёл уже двадцатый век, в 2000 уже пошел двадцать первый век.
Так что к году потребуется прибавить единичку, чтобы узнать, какой век.
![]()
Один век — это сто лет. Для того, чтобы определить, какому веку соответствует интересующая вас дата (интересующий вас год), то нужно взять эту дату (к примеру, 1641 — ый год), разделить это число на 100 (1 век — 100 лет) и прибавить единицу (1). Получаем: 1641/100 + 1 = 17,41. Цифры после запятой нам не нужны (мы не округляем, а просто отбрасываем). Получается, что 1641 год это 17 век.
Сейчас 2016 год. Делим на сто и прибавляет единицу и получается, что мы сейчас живем в 21 — ом веке.
![]()
Век — единица времени, которая измеряется 100 годами. Прошло 100 лет — прошел век.
Чтобы по годам определить век, нам надо знать или видеть первые две цифры года, к которым нужно будет добавить 1. Например, возьмем теперешний 2016 год. Первые две цифры — это цифра 20. Добавляем к цифре 20 единицу (20+1=21) и получаем 21 век.
Если же взять года до нашей или в начале нашей эры, то разобраться в вопросе, а какой же тогда будет век, поможет таблица ниже:

Когда-то — в школьные годы — для меня было очень трудно определить век по году. Поэтому мне пришлось поковыряться с данной темой. Итак, если взять 1945 год, то это будет двадцатый век. Все годы после 1900 года принадлежат следующему после 19-го века. Ведь если начать считать с нуля, то первый, и последующие годы относятся к первому веку. И так до сотого года. Сто первый год — второй век. И так далее. Так что если взять 986 год, то он будет десятым веком. А если назвать 1236 год, то это получается (12+1=) 13 век.
Итак, век наступает с первым годом после нулевого года.
Если упростить, то к первым двум цифрам нужно прибавить один и получим век, например: 1552 — первые цифры — 15. Прибавляем 1 и получаем 16 (шестнадцатый) век.
Integer30. Дан
номер некоторого года (целое положительное число). Определить соответствующий
ему номер столетия, учитывая, что, к примеру, началом 20 столетия был 1901 год.
Используется операция div деления нацело
или mod – взятие остатка от целочисленного деления.
Очевидно, что для определения номера столетия необходимо
находить целую часть при делении на 100. Но вот что делить? Возьмем, к примеру,
любой год N с диапазона [1901, 1999] – это все года XX столетия кроме 2000 г.
Чтобы получить для таких чисел 20 столетие (число 20), необходимо, очевидно, N
разделить на 100 и откинуть остаток (получим 19), а потом добавить 1; одним
словом, вычислить значение N div 100 +. Но если так поступить с годом 2000 (который мы не включили в
1
промежуток выше), то мы получим уже число 21, а это неверно, так как 2000 год –
это ещё XX столетие.
Тогда как быть? Можно поступить так: сначала отнимаем 1 от N,
делим на 100, а к результату прибавляем 1: (N-1). Действительно, если приглядеться на это
div 100 + 1
выражение, то видно, что при граничных 1901 и 2000 оно дает число 20. И даже
для 1 года н.э. по формуле получим (1-1) div 100 + 1 = 0 div 100
+ 1 = 0 + 1 = 1 (год) ⇒ 1 столетие.
Наконец, хочу напомнить, как в конце 1999 года разгорелся жаркий
спор о следующем 2000 годе. Люди не знали, вернее, не понимали, как считать его
– концом 20 столетия или началом 21 столетия. Здесь всё просто: поскольку
началом нашей эры является 1 год (а не нулевой год – его не существует), то все
года, оканчивающиеся на цифру 1, тоже будут началом – десятилетия, столетия,
тысячелетия…, а все года с окончанием 0 будут концом – десятилетия, столетия
и т.д. Таким образом, 2000 год был последним годом 20 столетия, а 1 января 2001
года наступил XXI век.
var
N: word;
begin
write('Введите номер года: ');
readln(N);
writeln;
{ Определяем номер столетия: }
N := (N - 1) div 100 + 1;
writeln('Номер столетия: ', N);
readln
end.
§ 24. Исследование календарных формул
Начиная с 1873 года календарные формулы публиковались в разных странах. Входящие в них элементы имели различные обозначения и порядок расположения. Для возможности исследования формул мы свели их в таблицу (табл. 17) в хронологическом порядке с одинаковыми условными обозначениями (см. § 23) и расположением элементов К, М, Г и В.
В большинстве формул коэффициент месяца М дается в виде таблицы с готовыми значениями — числами от 0 до 6. В некоторых формулах (Перевощиков, Дроздов и Перельман) вместо готовых значений коэффициента месяца М используется число дней от начала года R. Это усложняет вычисления. Также усложняет вычисления примененное Целлером и Каменьщиковым определение коэффициента месяца М в зависимости от порядкового номера месяца в году m (при этом январь и февраль високосного года считаются 13-м и 14-м месяцами предыдущего года). Формулы отличаются еще и тем, что при вычислении коэффициента года в одних вводится полный номер года J, а в других его порядковый номер в столетий Д, что упрощает вычисления.
В табл. 18 приведены значения коэффициента месяца М для формул, представленных в табл. 17. Проверка показала, что все формулы дают правильные ответы для всех дат за исключением простых (невисокосных) вековых лет по новому стилю, — т. е. годов 1700, 1800, 1900, 2100, 2200, 2300 и т. д. Для этих годов необходимо уменьшать на единицу коэффициент года Г (см. формулу (7)).
§ 25. Постоянные табель-календари. Табель-календарь И. Я. Голуба
Определение дня недели значительно упрощается с помощью постоянных табель-календарей. Если подсчитать для каждого года и месяца заданного столетия величины Е, представляющие остатки от деления на 7 (т. е. числа от 0 до 6) суммы коэффициентов месяца М, года Г и века В,
Е = |(M + Г + B)/7 |,
и свести их в таблицу, то определение дня недели выразится формулой
d = |(К + Е)/7 |,
где К — календарное число месяца.
Каждый замечал, что распределение дней недели по числам года повторяется. Эта повторяемость имеет определенную закономерность. Так, если номер года в столетии при делении на 4 дает в остатке 1 (год, следующий за високосным), то следующий год с тем же распределением дней недели повторится через 6 лет, если же остаток 2 или 3, то следующий такой же год будет через 11 лет. Так, для 1985 г. (85 = 21 × 4 + 1) это будет год 1991, а для годов 1986 и 1987 (соответственно 21 × 4 + 2 и 21 × 4 + 3) — годы 1997 и 1998. Високосные годы с одинаковым распределением дней педели повторяются только через 28 лет. В юлианском календаре ровно через 100 лет даты отступают по дням недели на одну позицию назад, и полная повторяемость дней педели происходит через 700 лет. В григорианском календаре столетия начинаются только с воскресенья, субботы, четверга и вторника, и здесь полный цикл завершается по прошествии 400 лет.
В книге А. В. Буткевича и М. С. Зеликсона (см. список литературы) представлена обширная коллекция из 60 постоянных табель-календарей без их математического обоснования и подробного анализа. Рассмотрим их отличия. Часть из них рассчитана на старый стиль (юлианский календарь), а часть на новый стиль (григорианский календарь). Следует отметить, что табель-календарь на XX в. по новому стилю совпадает с календарем для XIX в. по старому стилю.
Другое отличие состоит в том, что в одних календарях для определения порядкового номера дня недели приходится находить остатки от деления на 7 суммы К + Е, а в других день недели определяется по таблице готовых значений этой суммы. Сумма К + Е имеет значения от 1 до 37, при этом значениям 1, 8, 15, 22, 29 и 36 соответствует один день недели, значениям 2, 9, 16, 23, 30, 37 — следующий и т. д. Такая таблица дается в ряде вечных календарей.
Еще одно отличие заключается в том, что в одних календарях приводятся 12 столбцов значений Е, а а других 7. Это следует из таблиц 11, 13, 15, в которых можно объединить также январь простого года и октябрь, январь високосного года и апрель, июль и т. д.
Остается определить, па какие сроки целесообразно издавать постоянные табель-календари. В книге А. В. Буткевича и М. С. Зеликсона такие календари подразделяются на краткосрочные со сроком действия от одного до 25 лет, среднесрочные (от 34 до 200 лет) и долгосрочные (200–3000 лет). По нашему мнению, наименьший срок, на который нужно рассчитывать постоянные табель-календари, — это столетие. Предлагаем постоянный табель-календарь на XX в. по новому стилю (табл. 19), состоящий из частей А и Б. Он пригоден также для XIX в. по старому стилю. Если к нему добавить таблицу поправок (табл. 20), то он будет пригоден для 1–2000 гг. по старому стилю и для 1501–2301 гг. по новому стилю. Для определения дня недели нужно взять значение Е на пересечении номера года в столетии с колонкой месяца для високосного или невисокосного года в части А и прибавить к нему число месяца К. По полученной сумме в части Б найдем день недели.
Пример 1. Определить, в какой день недели было 9 мая 1945 г. В части А слева находим число 45. Справа против него в колонке «май» находим число 1, которое прибавляем к календарному числу: 9 + 1 = 10. Эту сумму находим во втором слева вертикальном столбце части Б, и против нее в последнем крайнем столбце читаем «ср», т. е. «среда».
Пример 2. Определить, в какой день недели было 9 января 1905 г. (старый стиль). По аналогии с первым примером слева в части А находим 05 (левый крайний столбец) и против него в колонке «янв.» читаем «6», а так как это событие задано календарной датой старого стиля, вычитаем единицу, т. е. 9 + 6–1 = 14. Эту сумму (14) находим в части Б (второй слева столбец) и против 14 в правом крайнем столбце находим ответ «вс», т. е. воскресенье («Кровавое воскресенье»).
Пример 3. Определить, в какой день недели будет 7 ноября в 2017 г. — столетие Великой Октябрьской социалистической революции. Найдя в части А число 17 (две последние цифры номера заданного года), против него в вертикальном столбце «нояб.» читаем цифру 3.2017 г. относится к XXI в., поэтому вычитаем единицу. Получим 7 + 3–1 = 9, и против этого числа в части Б (вторая колонка) в правом крайнем столбце читаем «вт». Следовательно, 100-летие Великого Октября будет во вторник.
Пример 4. Определить, какой будет день недели 1 мая 2000 г., являющегося високосным. В части А находим две последние цифры века-в данном случае «00», и против них в колонке «май» читаем «0». Следовательно, 1 + 0 = 1. В первой строке части Б находим «пн», т. е. понедельник.
ПРИЛОЖЕНИЯ
1. Число выходных и рабочих дней в СССР в 1988–2000 гг.
(в скобках со знаком «плюс» указано число праздничных дней, не совпадающих в данном году с субботой и воскресеньем)
СПИСОК ЛИТЕРАТУРЫ
Ахслис Элизабет. Мировой календарь: Пер. с англ. А. В. Буткевича и Ю. Г. Переля//Природа. — 1963. —№ 3. — С. 46–48.
Бакулин П. И., Блинов Н. С. Служба точного времени. — М.: Наука, 1968, 320 с.
Бережков Н. Г. Общая формула определения дня недели по числу месяца в январских годах нашей эры и в сентябрьских, мартовских и ультрамартовских годах от сотворения мира//Проблемы источниковедения. — 1958. — Вып. 6.
При выводе формулы примем следующие обозначения: К — календарное число месяца; М — коэффициент месяца; J — полный номер года н. э.; Д — порядковый номер года в столетии; Г’ — сдвиг дней недели по годам; Г — коэффициент года; В — коэффициент века; С — число полных прошедших столетий; [] — целая часть частного от деления (неполное частное); | | — остаток от деления, причем если делимое меньше делителя, остаток равен делимому; d — порядковый номер дня недели (0 — воскресенье, вс; 1 — понедельник, пн; 2 — вторник, вт; 3 — среда, ср; 4 — четверг, чт; 5 — пятница, пт; 6 — суббота, сб).
День недели календарной даты определяется как остаток от деления суммы чисел К, М, Г и В на 7:
d = |(K+ M + Г+В) / 7 | (1)
Сделаем предположение, что 1 января 1 г. п. э. был понедельник (= 1). Тогда для дат января первого года день недели будет определяться по формуле
d = |К / 7 |.
Так как в январе 31 день, то день недели в феврале первого года определится по формуле
d = |(К + (31–28)) / 7 | = |(K + 3) / 7 |.
Здесь 28 — ближайшее к 31 число, кратное семи, которое мы вычитаем для упрощения вычислений.
Так как в феврале первого года 28 дней, то день недели в марте определяется так же, как и в феврале. В марте 31 день, поэтому для апреля получим формулу
d = |(К + 3 + (31–28)) / 7 | = |(K + 6) / 7 |.
Аналогично получим формулы для остальных месяцев. В этих формулах числа, прибавляемые к календарному числу К, суть коэффициенты месяцев М, которые мы свели в табл. 9.

Таким образом, день недели для первого года н. э. будет определяться по формуле
d = |(K + M) / 7 |. (2)
Объединив повторяющиеся в табл. 9 значения М для разных месяцев, получим табл. 10.

Так как в простом году 52 недели и один день (365 = 52×7 + 1), то для второго года н. э. календарная формула примет вид
d = |(K + M + 1) / 7 |.
а для третьего
d = |(К + М + 2) / 7 |.
Следующий год (четвертый) — високосный; в нем 366 дней (за счет увеличения числа дней в феврале: 29 вместо 28). Поэтому для 4 г. н. э. календарная формула принимает вид для января и февраля
d = |(K = M + 3) / 7 |.
а для месяцев с марта по декабрь
d = |(K = M + 4) / 7 |.
В табл. 11 приведены коэффициенты М для високосных (вис.) и невисокосных — простых (пр.) лет. Так как сдвиг дней недели по годам Г’ в четырехлетиях 1–4, 5–8, 9–12 и т. д. происходит одинаково, составим таблиц значений Г’ для J от 1 до 60 лет (табл. 12). Мы видим, что в каждом следующем четырехлетии значение сдвига Г’ «увеличивается» на 5. Это позволяет выразить его для високосных годов (Jвис) в виде формулы
Г’ = |(5(Jвис:4) — 1) / 7)|


а для простых (Jnp) в виде формулы
Г’ = |(5 (Jвис: 4) — 1 + (Jпр — Jвис)) / 7 |,
где Jвс — ближайший меньший високосный год [53], а так как
Jвис: 4 = [Jпр: 4],
(3)
то общей формулой для Г’ для простых и високосных годов будет
Г’ =|(J + [J: 4] — 1) / 7 |. (3)

Упростим формулу (3), убрав в ней «—1». Чтобы сумма М + Г в формуле (1) осталась неизменной, уменьшим на единицу значения коэффициентов М в табл. 11 (при этом 0 считается равным 7). Новые значения коэффициентов М приведены в табл. 13, а формула (3) примет вид
Г’ = |(J + [J: 4]) / 7 |.
(4)
В формуле (4) полный порядковый номер года J, выражающийся для нашего времени четырехзначными числами, усложняет вычисления. Если обозначить число тысяч буквой а, число сотен — буквой Ь, число десятков — буквой с и число единиц — буквой f, то номер года J можно записать в виде
J= 1000а + 100b + 10с + f
и тогда
[J: 4] = 250а + 25b + [(10с + f): 4],
а
J + [J: 4] = 100a + 100b + 10c + f + 250a + 25b + [(10c + f): 4] = 1250а+ 125b + 10c + f + [(10c + f): 4].
Так как
|(1250a + 125b) / 7 | = |(7×170a + 60a + 7×17b + 6b) / 7 | = |6(10a + b) / 7 |.
то
(J + [J: 4]) / 7 = 10c + f + |(10с + f): 4 | + 6 (10а + Ь) / 7.
Если же учесть, что 10а + b = С — это число полных прошедших столетий (например, для 1986 г. С = 19 = 10×1 + 9), а 10с + f = Д — порядковый номер года в столетии, то формула (4) примет вид
Г’ = |(Д + [Д: 4]) / 7 | + |6c / 7 |. (5)
Значения второго слагаемого с течением веков циклически повторяются (см. табл. 14); это коэффициент века В. Первое же слагаемое будет коэффициентом года Г,
Г’ = |(Д + [Д: 4]) / 7 |. (6)
Следует учитывать, что порядковый номер Д года J в столетии имеет значения от 1 до 100, и поэтому для всех вековых лет, например 1800, 1900, 2000 гг. и т. д., Д = 100. Для I в. (годы 1–100) число полных прошедших столетий С = 0, для II в. (годы 101–200) С = 1 и т. д.
В табл. 14 приведены значения коэффициента века В (по старому стилю) для н. э.; из нее следует, что повторяемость юлианского. календаря происходит через 700 лет.

В начале изложения мы условно приняли, что первый день нашей эры (1 января 1 года первого века) был понедельником. Установим теперь значения коэффициентов М, которые дадут возможность правильно определять дни недели. Для этого используем точную дату какого-либо известного события.

Например, что 9 января 1905 г. было воскресенье («Кровавое воскресенье»). Для этой даты d = 0, К = 9, Г = |(5 + [5: 4]) / 7 | = 6, а В = 2. Подставляя эти данные в формулу (1), получим 0 = | (9 = M + 6 + 2) / 7 |, откуда М = — |17 / 7 | = —3. (Если для коэффициента М получается отрицательное значение, то его следует заменить положительным, прибавляя ближайшее большее число, кратное 7. В нашем случае —3 + 7 = 4.) Коэффициенты остальных месяцев можно установить исходя из сравнения с табл. 13. Вообще же их можно вычислить, взяв табель-календарь любого года. Окончательные значения М приведены в табл. 15. Теперь можно определить, каким днем недели было 1 января 1 г. н. э. Для этой легендарной даты К = 1, М = 4, Г = |(1 + [1: 4] / 7 | = 1 и В = 0, следовательно, d = |(1+ 4 + 1 + 0) / 7 | = 6 — суббота.
В новом стиле все вековые годы, кроме тех, число столетий в номере которых делится на 4 (например, 1600, 2000, 24 000 гг. и т. д.), невисокосные. Поэтому коэффициенты века В для этих годов будут другими.
Для определения значений поправок к коэффициенту века В для нового стиля следует учитывать, что при реформе юлианского календаря было принято следующую после четверга 4 октября 1582 г. дату считать пятницей 15 октября.
При этих условиях для 15 октября 1582 г. (С = 15) получаем d = 5, К =15, М = 4 и Г = |(82 + [82: 4]) / 7 | = 4.
Подставляя эти значения в формулу (1), получим 5 = |(15 + 4 + 4 +В) / 7 |, откуда В = |–18/7 | = |–14/7 | = 3.
Для юлианского календаря коэффициент века B = |(6C + P) / 7 |, а для григорианского к нему надо найти поправку Р, определяемую из соотношения
B = |(6c +P) / 7 |.
Так как в этих вычислениях применяется правило остатков, то формула преобразуется к виду
P = |(B + 6С) / 7 |.
В табл. 16 приведены эти поправки Р и коэффициенты века В для нового стиля с XVI по XXIII вв. Как видно из таблицы, коэффициенты В имеют всего четыре значения 3, 2, 0 и 5, которые циклически повторяются через 400 лет.

С введением григорианского календаря появились особые простые вековые годы 1700, 1800, 1900; для которых коэффициент года Г, определяемый по формуле (6), необходимо уменьшать на единицу, т. е. для этих лет
Г = |(100+ [100:4])/7 | = 5. (7)
Что касается вековых лет, число сотен которых кратно четырем, например, 1600, 2000 и т. д., то для нового стиля они остаются високосными, и коэффициент года для них определяется по общему правилу:
Г = |(100 + [100:4]/7 | = 6.
Итак, порядковый номер d дня недели любой календарной даты задается формулой (1) (см. с. 102). Значение коэффициента месяца М берется из табл. 15, коэффициент года Г вычисляется по формуле (6) или (7), а значение коэффициента века В берется для старого стиля из табл. 14, а для нового из табл. 16. Напомним еще раз, что если сумма К + М + Г + В меньше семи, то остаток от деления на семь равен самой сумме. То же правило действует при делении на четыре.

