Энергия характеризует способность тела совершать работу. Натянутая тетива лука, сжатая пружина, поднятый с земли камень, сжатый газ при определённых условиях могут совершать работу.
Потенциальной энергией обладают:
1. тела, поднятые над поверхностью земли (например, камень при падении с высоты образует на земле воронку);
2. упруго деформированные тела (например, человек натягивает тетиву лука и выпускает стрелу);
3. сжатые газы (расстояние между молекулами газа уменьшается, и увеличивается сила отталкивания между ними).
Слово «потенциальный» (potentia) на латинском языке означает «возможность».
Огромной потенциальной энергией обладают воды водопада. Потенциальная энергия воды совпадает с работой силы притяжения Земли.
Потенциальная энергия накапливается в водах рек. Сила притяжения Земли производит работу, заставляя реки течь в более низко расположенное место — в море. Человек научился полезно использовать потенциальную энергию рек. В древние времена строили водяные мельницы, а с (20)-го века — гидроэлектростанции (ГЭС).
Гидроэлектростанция в Итайпу, находящаяся на границе между Бразилией и Парагваем на реке Паране, на сегодня является крупнейшим действующим сооружением такого рода в мире. У её плотины (через которую протекает вода) имеются шлюзы, состоящие из (14) ворот, через которые за секунду проходит (62200) кубометров воды.

Рис. (1). Шлюзовая система
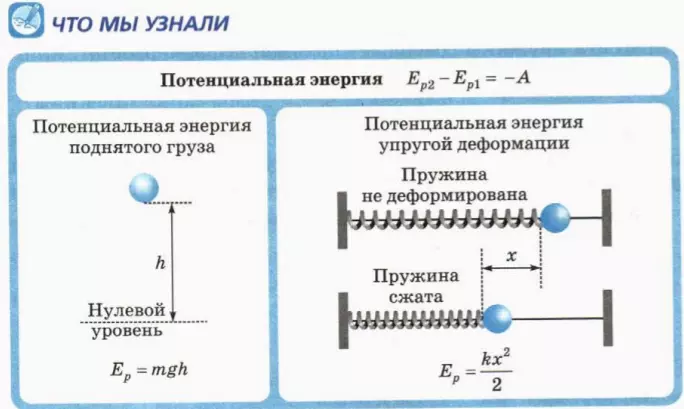
Потенциальную энергию тела, поднятого над опорой на высоту (h), рассчитывают по формуле:
, где
m
— масса тела, а
g
— ускорение свободного падения у поверхности Земли.
Потенциальную энергию тела измеряют относительно некоторого условного уровня отсчёта, чаще всего относительно поверхности Земли. В таком случае принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
Обрати внимание!
Тело одновременно может обладать и потенциальной, и кинетической энергией, и они могут переходить одна в другую.
Рис. (2). Мальчик на качелях
Человек, качающийся на качелях, обладает максимальной потенциальной энергией в наивысшей точке подъёма, в этой точке качели на мгновение замирают, и, значит, в этот момент кинетическая энергия человека равна нулю.
При движении из состояния (1) в состояние (2) потенциальная энергия уменьшается, а кинетическая растёт (так как высота тела над уровнем земли уменьшается, а скорость движения тела возрастает).
Когда человек находится в самой нижней точке траектории движения (2), кинетическая энергия является наибольшей, так как в этот его момент скорость самая высокая. При движении из состояния (2) в состояние (3) увеличивается потенциальная энергия (так как увеличивается высота подъёма тела), а кинетическая энергия уменьшается (так как скорость движения тела уменьшается).
В замкнутой системе сумма кинетической и потенциальной энергии в любой момент времени остаётся неизменной.
Сумма потенциальной и кинетической энергии тела называется полной механической энергией тела.
Привязанный отвес на высоте (h) обладает максимальной потенциальной энергией, а кинетическая энергия (энергия движения) в это время равна (0).

Рис. (3). Изменение энергии
Когда верёвку перерезают, отвес начинает свободно падать, высота уменьшается, а скорость увеличивается (с ускорением (g)), соответственно, потенциальная энергия уменьшается, а кинетическая энергия возрастает.
В каждый момент времени, до момента соударения, сумма потенциальной и кинетической энергии отвеса одинакова.
В момент соударения энергия отвеса не исчезает, она передаётся другому телу — гвоздю, который под воздействием этой энергии начинает движение, уходя глубже в брус. Некоторая часть энергии преобразуется во внутреннюю — тепловую энергию (так как отвес при соударении нагревается).
Любое тело обладает внутренней энергией, которая не связана с движением тела.
Внутреннюю энергию образует движение атомов и молекул тела.
Например, в результате удара частички начинают двигаться интенсивнее — это проявляется в виде нагрева тела. При сжатии пружины изменяется потенциальная энергия частиц.

Рис. (4). Натянутая резинка
Натянутая резинка обладает потенциальной энергией, причиной этого является взаимное притяжение молекул.
Закон сохранения энергии:
энергия не исчезает и не возникает снова, она только преобразуется из одного вида энергии в другой вид энергии или переходит от одного тела к другому.
Полная энергия тела — это сумма его механической и внутренней энергии.
Полная энергия тела
↗↖
Механическая энергия Внутренняя энергия
↗↖↗↖
Тела
Eпот
Тела
Eкин
Частиц
Eпот
Частиц
Eкин
Источники:
Рис. 2. Указание автора не требуется, 2021-07-22. Vecteezy License, https://www.vecteezy.com/vector-art/304022-boy-playing-hand-swing.
Рис. 3. Изменение энергии. © ЯКласс.

Энергия – важнейшее понятие в механике. Что такое энергия. Существует множество определений, и вот одно из них. Что такое энергия?

Энергия – это способность тела совершать работу.
Кинетическая энергия
Рассмотрим тело, которое двигалось под действием каких-то сил изменило свою скорость с
v
до
v
. В этом случае силы, действующие на тело, совершили определенную работу
A
. Работа всех сил, действующих на тело, равна работе равнодействующей силы. FрF1F2AF1scosα1F2scosα2Fрcosα.
Установим связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила
F
, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы
Fvas
совпадают по направлению и их можно рассматривать как алгебраические величины. Работа силы F равна AFs. Перемещение тела выражается формулой sv22v122a. Отсюда:
![[E=const]](https://fizikinfo.ru/wp-content/uploads/2019/07/Izmenenie-potentsialnoj-energii1.png)
AFsFvvamavva
Amv22mv222mv222mv222.
None Кинетическая энергия – энергия движения тела. При нулевой скорости она равна нулю.
Определение. Кинетическая энергия
[custom_ads_shortcode1]
Терема о кинетической энергии
Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела. Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы. AEK2EK1.
 Теорема о кинетической энергии
Теорема о кинетической энергии
Таким образом, кинетическая энергия тела массы
m
, движущегося со скоростью
v
, равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.
AmvEK
.
Чтобы остановить тело, нужно совершить работу Amv22EK
[custom_ads_shortcode2]
Потенциальная энергия
Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще потенциальная энергия, то есть энергия взаимодействия тел, которая зависит от их положения.
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.
Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными (или диссипативными).
 Важно!
Важно!
Примеры диссипативных сил: сила тяжести, сила упругости. Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу. Рассмотрим пример, когда шар переместился из точки с высотой h1 в точку с высотой h2. При этом сила тяжести совершила работу, равную Amgh2h1mgh2mgh1.
Эта работа равна изменению величины
mgh
, взятому с противоположным знаком. Величина ЕПmgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальная энергия тела равна нулю.
Определение. Потенциальная энергия
Потенциальная энергия – часть полной механической энергии системы, находящейся в поле диссипативных(консервативных) сил. Потенциальная энергия зависит от положения точек, составляющих систему. Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.

д. Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
AEПEП
.
Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.
EПGmMr
.
Здесь
G
– гравитационная постоянная,
M
– масса Земли.
[custom_ads_shortcode3]
Потенциальная энергия пружины
Представим, что в первом случае мы взяли пружину и удлинили ее на величину
x
. Во втором случае мы сначала удлинили пружину на
x
, а затем уменьшили на
x
. В обоих случаях пружина оказалась растянута на
x
, но это было сделано разными способами. При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равнаAупрAkx22.
Величина
Eупрkx
называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter.

Тела, находящиеся в потенциальном поле, обладают способностью в определённых условиях совершать работу. Например, тело, поднятое над Землёй, когда его отпускают, приходит в движение под действием гравитационной силы, совершая работу. Следовательно, тела в данном поле обладают энергией, которую называют потенциальной. Эта энергия зависит от расположения тел, создающих поле, и от положения тела в этом поле, т.е. она зависит от взаимного расположения взаимодействующих тел. Однако от взаимного расположения тел или частей одного и того же тела зависят силы взаимодействия между ними. Итак, энергия, обусловленная взаимодействием тел или частей одного и того же тела, называется потенциальной. Величина потенциальной энергии тела может быть определена лишь с точностью до произвольной постоянной, значение которой зависит от выбора так называемого нулевого уровня, т.е. положения тела, в котором потенциальную энергию условно принимают за ноль. Потенциальная энергия равна той работе, которую совершают силы поля, действующие на тело, при переносе его из данной точки на нулевой уровень. Однако выбор нулевого уровня не отражается на физических законах. Потенциальная энергия тела, находящегося в гравитационном поле, вычисляется по формуле: иWp = mgh, (10) если за нулевой уровень энергии выбрать в бесконечности или на поверхности Земли. Здесь — гравитационная постоянная, М — масса Земли, m — масса тела, h — расстояние от тела до нулевого уровня, g — ускорение свободного падения. Потенциальная энергия деформированной пружины находится по формуле: (11) где k и х — коэффициент жёсткости и величина деформации пружины.
[custom_ads_shortcode1]
Теорема о потенциальной энергии
Работа Ap, совершаемая силами потенциального поля при переносе тела из положенияв положение, может быть выражена через потенциальные энергииWp1иWp2в этих положениях. Она равна Ap= Wp1 Wp2(Wp2 Wp1) Wp, (12) т.е. работа сил потенциального поля равна уменьшению потенциальной энергии перемещаемого тела или изменению потенциальной энергии тела, взятому с обратным знаком. Соотношение (12) называют теоремой о кинетической энергии.
[custom_ads_shortcode2]
Закон сохранения механической энергии
Предположим, что тело движется в гравитационном поле Земли. На него действуют сила тяжести и сила сопротивления воздуха. Тогда работа Aпри переходе тела из одного положения в другое складывается из работыAнксилы сопротивления воздуха (неконсервативная сила) и работыAксилы тяжести (консервативная сила), т.е.A = Aнк + Aк. Согласно теореме о кинетической энергии, запишем:A = Wк2 –Wк1, гдеWк1иWк2—кинетическая энергия тела в начальном и конечном положениях. Левые части последних равенств равны.Поэтому приравняем и их правые части, т.е. Aнк + Aк = Wк2 – Wк1. Согласно теореме о потенциальной энергии, Aк = Wp – Wp,гдеWpиWp—потенциальная энергия тела в данном поле в начальном и конечном положениях. Учитывая это, из предыдущего равенства получаемAнк = (Wк2 + Wp)–(Wк1 +Wp). ВеличинуW, равную сумме кинетической и потенциальной энергии тела, т.е.W = Wк+ Wp, называютполной механической энергиейилимеханической энергией. ТогдаWк1 +Wp=WиWк2+Wp=W, гдеWиW—полная механическая энергия тела в начальном и конечном положении. Итак, (13) т.е. изменение полной механической энергии тела в силовом поле равно работе неконсервативных сил, действующих на него. Тело, находящееся в силовом поле, можно рассматривать как механическую систему, состоящую из тел, создающих поле, и самого тела. Поэтому возможна и другая формулировка выражения (13): изменение полной механической энергии системы равно работе неконсервативных сил, действующих на неё. Если на механическую систему и внутри неё действуют только консервативные силы, то Aнк= 0 иW2=W1, т.е.

(14) Следовательно, в механической системе, в которой действуют только консервативные силы, полная механическая энергия величина постоянная. В этом и состоит закон сохранения механической энергии.
Тела, находящиеся в потенциальном поле, обладают способностью в определённых условиях совершать работу. Например, тело, поднятое над Землёй, когда его отпускают, приходит в движение под действием гравитационной силы, совершая работу. Следовательно, тела в данном поле обладают энергией, которую называют потенциальной. Эта энергия зависит от расположения тел, создающих поле, и от положения тела в этом поле, т.е. она зависит от взаимного расположения взаимодействующих тел. Однако от взаимного расположения тел или частей одного и того же тела зависят силы взаимодействия между ними. Итак, энергия, обусловленная взаимодействием тел или частей одного и того же тела, называется потенциальной. Величина потенциальной энергии тела может быть определена лишь с точностью до произвольной постоянной, значение которой зависит от выбора так называемого нулевого уровня, т.е. положения тела, в котором потенциальную энергию условно принимают за ноль. Потенциальная энергия равна той работе, которую совершают силы поля, действующие на тело, при переносе его из данной точки на нулевой уровень. Однако выбор нулевого уровня не отражается на физических законах. Потенциальная энергия тела, находящегося в гравитационном поле, вычисляется по формуле: иWp = mgh, (10) если за нулевой уровень энергии выбрать в бесконечности или на поверхности Земли. Здесь — гравитационная постоянная, М — масса Земли, m — масса тела, h — расстояние от тела до нулевого уровня, g — ускорение свободного падения. Потенциальная энергия деформированной пружины находится по формуле: (11) где k и х — коэффициент жёсткости и величина деформации пружины.
[custom_ads_shortcode3]
Теорема о потенциальной энергии
Работа Ap, совершаемая силами потенциального поля при переносе тела из положенияв положение, может быть выражена через потенциальные энергииWp1иWp2в этих положениях. Она равна Ap= Wp1 Wp2(Wp2 Wp1) Wp, (12) т.е. работа сил потенциального поля равна уменьшению потенциальной энергии перемещаемого тела или изменению потенциальной энергии тела, взятому с обратным знаком. Соотношение (12) называют теоремой о кинетической энергии.
[custom_ads_shortcode1]
Закон сохранения механической энергии
Предположим, что тело движется в гравитационном поле Земли. На него действуют сила тяжести и сила сопротивления воздуха. Тогда работа Aпри переходе тела из одного положения в другое складывается из работыAнксилы сопротивления воздуха (неконсервативная сила) и работыAксилы тяжести (консервативная сила), т.е.A = Aнк + Aк. Согласно теореме о кинетической энергии, запишем:A = Wк2 –Wк1, гдеWк1иWк2—кинетическая энергия тела в начальном и конечном положениях. Левые части последних равенств равны.Поэтому приравняем и их правые части, т.е. Aнк + Aк = Wк2 – Wк1. Согласно теореме о потенциальной энергии, Aк = Wp – Wp,гдеWpиWp—потенциальная энергия тела в данном поле в начальном и конечном положениях. Учитывая это, из предыдущего равенства получаемAнк = (Wк2 + Wp)–(Wк1 +Wp). ВеличинуW, равную сумме кинетической и потенциальной энергии тела, т.е.W = Wк+ Wp, называютполной механической энергиейилимеханической энергией. ТогдаWк1 +Wp=WиWк2+Wp=W, гдеWиW—полная механическая энергия тела в начальном и конечном положении. Итак, (13) т.е. изменение полной механической энергии тела в силовом поле равно работе неконсервативных сил, действующих на него. Тело, находящееся в силовом поле, можно рассматривать как механическую систему, состоящую из тел, создающих поле, и самого тела. Поэтому возможна и другая формулировка выражения (13): изменение полной механической энергии системы равно работе неконсервативных сил, действующих на неё. Если на механическую систему и внутри неё действуют только консервативные силы, то Aнк= 0 иW2=W1, т.е.
(14) Следовательно, в механической системе, в которой действуют только консервативные силы, полная механическая энергия величина постоянная. В этом и состоит закон сохранения механической энергии.
«Физика – 10 класс»Вспомните, какая связь существует между работой силы тяжести и потенциальной энергией. Почему работа силы упругости определяется её средним значением?

Согласно теореме об изменении кинетической энергии работа силы, действующей на тело, равна изменению его кинетической энергии:
Если же силы взаимодействия между телами являются консервативными, то, используя явные выражения для сил, мы показали (см. § 43), что работу таких сил можно также представить в виде разности двух значений некоторой величины, зависящей от взаимного расположения тел (или частей одного тела):
Здесь высоты h и h определяют взаимное расположение тела и поверхности Земли, а удлинения х и х — взаимное расположение частей тела, например витков деформированной пружины. Из формул (5.18) и (5.19) следует, что

Величину, равную произведению массы m тела на ускорение свободного падения g и на высоту h тела над поверхностью Земли, называют потенциальной энергией тела в поле силы тяжести и обозначают Еп:
Еп = mgh. (5.20)
Величину, равную половине произведения коэффициента упругости k тела на квадрат удлинения или сжатия х, называют потенциальной энергией упруго деформированного тела:
![[Delta E=A]](https://fizikinfo.ru/wp-content/uploads/2019/07/Izmenenie-potentsialnoj-energii10.png)
Введя понятие потенциальной энергии, мы получаем возможность выразить работу любых консервативных сил через изменение потенциальной энергии.
Под изменением величины понимают разность между её конечным и начальным значениями, поэтому Еп = Еп2 – Еп1. Следовательно, оба уравнения (5.19) можно записать так:
А = Еп1 — Еп2 = -(Еп2 — Еп1) = -ΔЕп, (5.22)
откуда ΔЕп = -А. Изменение потенциальной энергии тела равно работе консервативной силы, взятой с обратным знаком.

Например, при падении камня на Землю его потенциальная энергия убывает (ΔЕп < 0), но сила тяжести совершает положительную работу (А > 0).
Следовательно, А и ΔЕп имеют противоположные знаки в соответствии с формулой (5.22).
Нулевой уровень потенциальной энергии.
Согласно уравнению (5.22) работа консервативных сил определяет не саму потенциальную энергию, а её изменение. Поскольку работа определяет лишь изменение потенциальной энергии, то только изменение энергии в механике имеет физический смысл. Поэтому можно произвольно выбрать состояние системы, в котором её потенциальная энергия считается равной нулю. Этому состоянию соответствует нулевой уровень отсчёта потенциальной энергии.

Ни одно явление в природе или технике не определяется значением самой потенциальной энергии.
Важна лишь разность значений потенциальной энергии в конечном и начальном состояниях системы тел. Выбор нулевого уровня производится по-разному и диктуется условиями данной задачи. Обычно в качестве состояния с нулевой потенциальной энергией выбирают состояние системы с минимальным значением энергии. Тогда потенциальная энергия всегда положительна или равна нулю. Итак потенциальная энергия системы «тело — Земля» — величина, зависящая от положения тела относительно Земли, равная работе консервативной силы при перемещении тела из точки, где оно находится, в точку, соответствующую нулевому уровню потенциальной энергии системы. У пружины потенциальная энергия минимальна в отсутствие деформации, а у системы «камень — Земля» — когда камень лежит на поверхности Земли. Поэтому в первом случае а во втором случае Еп = mgh. Но к данным выражениям можно добавить любую постоянную величину С. При этом изменение потенциальной энергии, определяемое работой консервативной силы, останется прежним.
Изолированная система тел стремится к состоянию, в котором её потенциапьная энергия минимальна. Если не удерживать тело, то оно падает на землю (h = 0); если отпустить растянутую или сжатую пружину, то она вернётся в недеформированное состояние (х = 0).
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский.

Следующая страница «Закон сохранения энергии в механике»
Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»
Законы сохранения в механике – Физика, учебник для 10 класса – Класс!ная физика Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»

Источники:
- zaochnik.com
- studfiles.net
- studfiles.net
- class-fizika.ru
1. Определение потенциальной энергии
В предыдущем параграфе мы говорили о работе, которую может совершить тело за счет уменьшения своей скорости, а теперь нас будет интересовать работа, которую может совершить тело или система тел вследствие изменения положения тел.
Рассмотрим примеры.
Работа поднятого груза. Когда подвешенный на тросе груз равномерно движется вниз, он действует на трос силой, направленной тоже вниз (рис. 30.1).
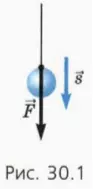
Эта сила обусловлена силой тяжести: она совершает работу, действуя на груз, а груз совершает работу, действуя на трос.
Итак, благодаря действию силы тяжести груз может совершить работу при движении вниз.
Работа пружины. Когда деформация пружины уменьшается, пружина действует на тело силой упругости, направленной так же, как перемещение тела (рис. 30.2). При этом пружина совершает положительную работу.
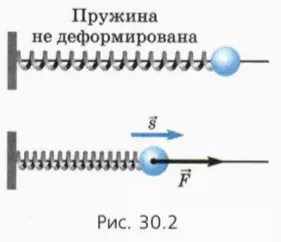
Итак, деформированная пружина может совершить работу при возвращении в недеформированное состояние.
В рассмотренных примерах работу совершают силы тяготения и силы упругости. Как мы уже знаем, общая важная особенность этих сил состоит в том, что при движении по замкнутой траектории (когда тело возвращается в начальное положение) работа этих сил равна нулю. (Такие силы называют консервативными. Если между телами замкнутой системы действуют только консервативные силы, то, как мы увидим далее, механическая энергия системы сохраняется («консервируется»).)
Благодаря этому для системы тел, взаимодействующих посредством сил тяготения и упругости, можно определить потенциальную энергию как величину, характеризующую способность системы тел совершать работу и зависящую только от взаимного положения тел.
Потенциальная энергия системы тел характеризует ее способность совершать работу вследствие изменения взаимного положения взаимодействующих тел.
Если система тел совершает положительную работу, потенциальная энергия системы уменьшается. А если система тел совершает отрицательную работу, ее потенциальная энергия увеличивается. При этом
изменение потенциальной энергии системы тел равно работе сил упругости и тяготения, действующих со стороны тел системы, взятой со знаком минус:
Ep2 – Ep1 = –A (1)
Здесь Ep1 и Ep2 обозначают начальную и конечную потенциальную энергию системы тел.
(Мы приводим определение потенциальной энергии, применимое к механическим явлениям. В дальнейшем мы расширим и уточним это определение.)
? 1. Как изменяется потенциальная энергия системы «камень + Земля», когда камень движется вверх? вниз? Объясните свои ответы.
? 2. Как изменяется потенциальная энергия пружины, когда деформация уменьшается? увеличивается? Объясните свои ответы.
Нулевой уровень потенциальной энергии. Из формулы (1) следует, что физический смысл имеет только изменение потенциальной энергии: оно измеряется работой, совершенной телами системы.
Поэтому нулевой уровень потенциальной энергии (состояние системы, которому сопоставляется нулевое значение потенциальной энергии) выбирают так, чтобы упростить расчеты.
2. Потенциальная энергия поднятого груза
Когда груз массой m равномерно перемещается вертикально вниз на расстояние h, он совершает положительную работу mgh, потому что он действует на опору или поднес направленной вниз силой (весом груза), равной силе тяжести.
Следовательно, при уменьшении высоты груза на h потенциальная энергия груза уменьшается на mgh. (Важно понимать, что это потенциальная энергия системы взаимодействующих тел – груза и Земли.) Если сопоставить нулевой уровень потенциальной энергии наинизшему положению груза, то
потенциальная энергия груза массой m, поднятого на высоту h, выражается формулой
Ep = mgh. (2)
? 3. Брусок массой 200 г поднят на высоту 1 м над поверхностью стола высотой 80 см (рис. 30.3).
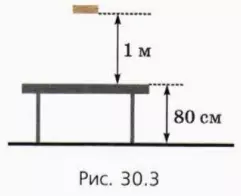
а) Чему равна потенциальная энергия бруска, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?
б) Чему равно изменение потенциальной энергии бруска при его падении на стол, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?
Эти примеры подтверждают, что имеет значение только изменение потенциальной энергии. Оно измеряется работой, совершенной телом или системой тел, и не зависит от выбора нулевого уровня потенциальной энергии.
3. Потенциальная энергия упругой деформации
При возвращении в недеформированное состояние сила упругости пружины совершает положительную работу
A = (kx2)/2.
При этом потенциальная энергия пружины уменьшается на такую же величину. Если нулевому уровню потенциальной энергии сопоставить состояние недеформированной пружины, то
потенциальная энергия деформированной пружины жесткостью k выражается формулой
Ep = (kx2)/2, (3)
где x – деформация пружины.
Потенциальную энергию, выражаемую формулой (3), называют также потенциальной энергией упругой деформации. Она зависит от квадрата деформации. Поэтому потенциальная энергия сжатой пружины равна потенциальной энергии растянутой пружины, если модуль деформации пружины в обоих случаях один и тот же.
? 4. В начальном состоянии пружина жесткостью 200 Н/м сжата на 1 см. Как изменилась потенциальная энергия пружины, если в конечном состоянии:
а) пружина не деформирована?
б) сжата на 2 см?
в) растянута на 1 см?
г) растянута на 2 см?
? 5. Шар массой 200 г подвешен к пружине жесткостью 100 Н/м и находится в равновесии, Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Как изменилась потенциальная энергия шара за время, в течение которого он возвращался в положение равновесия?
в) Как изменилась за то же время потенциальная энергия пружины?
г) Как изменилась за то же время потенциальная энергия системы «шар + Земля + пружина»?
Дополнительные вопросы и задания
6. С высоты 20 м над поверхностью земли свободно без начальной скорости падает камень массой 300 г. За нулевой уровень потенциальной энергии камня примите уровень земли.
а) Чему равна потенциальная энергия камня в начальный момент?
б) Чему равна потенциальная энергия камня через 1 с после начала движения?
в) Через какое время после начала движения потенциальная энергия камня уменьшилась в 2 раза по сравнению с ее начальным значением?
7. Шар массой 1 кг брошен с поверхности земли с начальной скоростью 20 м/с под углом 30º к горизонту. Считайте, что сопротивлением воздуха при движении шара можно пренебречь.
а) До какой максимальной высоты поднялся шар?
б) Как изменилась потенциальная энергия шара за время подъема?
8. По реке с постоянной скоростью плывет плот. Как изменяется со временем:
а) кинетическая энергия плота?
б) потенциальная энергия плота?
9. Когда сжатую пружину сжали еще на 2 см, ее потенциальная энергия увеличилась в 9 раз.
а) Во сколько раз модуль конечной деформации пружины больше, чем модуль начальной деформации?
б) Чему равен модуль начальной деформации пружины?
10. Две пружины жесткостью 100 Н/м и 400 Н/м соединены последовательно. Систему соединенных пружин растянули на 5 см.
а) Чему равна деформация более мягкой пружины?
б) Чему равна деформация более жесткой пружины?
в) Потенциальная энергия упругой деформации какой пружины больше, и во сколько раз?
Убыль – потенциальная энергия
Cтраница 1
Убыль потенциальной энергии равна приобретенной обручем кинетической энергии.
[1]
Таким образом, работа внутренних сил равна убыли потенциальной энергии взаимодействия частиц.
[2]
Работу Л1 – 2 нужно рассматривать как убыль потенциальной энергии заряженной частицы при перемещении ее между указанными точками.
[3]
Точка массы т под действием поля тяготения движется в сторону убыли потенциальной энергии. По закону сохранения энергии, совершаемая при этом работа равна уменьшению потенциальной энергии: Ai2 U – П2 – ДП.
[4]
Из сравнения двух последних уравнений видно, что за любой промежуток времени убыль потенциальной энергии свободно падающего тела равна приросту его кинетической энергии.
[5]
Как известно ( см. (12.2)), работа консервативных сил совершается за счет убыли потенциальной энергии.
[6]
Но работа внешних сил поля, в свою очередь, может быть представлена как убыль внешней потенциальной энергии, а именно А и – ДУвиеш.
[7]
Из сопоставления выражения (1.23) с выражением для работы сил потенциального поля ( которая равна убыли потенциальной энергии частицы в поле) можно сказать, что потенциал – это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля.
[8]
При сближении молекул до расстояний гга возрастание кинетической энергии перемещающейся молекулы происходит за счет убыли потенциальной энергии взаимодействия частиц. При прохождении второй молекулой точки гг0 притяжение сменяется отталкиванием и дальнейшее движение будет сопровождаться быстрой потерей ее скорости: кинетическая энергия переходит в потенциальную. В момент, когда потенциальная энергия ф ( гй) становится равной полной энергии системы Ег, скорость второй молекулы обращается в нуль.
[9]
Если в каком-либо процессе не происходит взаимопревращения механической энергии и других видов энергии, то убыль потенциальной энергии сопровождается приростом такого же в точности количества кинетической энергии, и обратно.
[10]
Из соотношений (3.8) следует, что работа консервативных сил, действующих на механическую систему, равна убыли потенциальной энергии этой системы.
[11]
Этот факт является следствием так называемой теоремы ви-риала, согласно которой в равновесной системе ровно половина общей убыли потенциальной энергии не уходит из системы и остается в ней в виде кинетической энергии частиц. Расстояния точек кривых 2 и 3 как раз и равны этой кинетической энергии электронов, частично компенсирующей ( так же как и взаимное отталкивание электронов) убыль потенциальной энергии от притяжения электронов к ядру.
[13]
Из сравнения выражений ( а) и ( б) видно, что за любой промежуток времени убыль потенциальной энергии свободно падающего тела равна приросту его кинетической энергии.
[14]
Страницы:
1
2
3
4
как изменяется потенциальная и кинетическая энергия падающего тела
Грегор ЭйзЭхорн
Ученик
(214),
закрыт
12 лет назад
ранис давлетшин
Ученик
(198)
12 лет назад
Потенциальная энергия=mgh, то есть зависит от высоты, на которой располагается тело. Кинетическая энергия=(mV^2)/2, то есть зависит от скорости. С уменьшением высоты уменьшается потенциальная энергия, но увеличивается кинетическая ( так как при падении V=V0+gt), причем по закону сохранения энергии их сумма будет постоянной.
