При разбавлении и концентрировании
растворов количество вещества (количества
вещества эквивалента) остается постоянным.
Пример 6. Какой объем раствора HCl,
С1(HCl) = 6 моль/л, необходимо
использовать для приготовления 250 мл
раствора этой кислоты с концентрацией
С2(HCl) = 2,5 моль/л.
Решение:
V(HCl) =
n(HCl) = const;
n(HCl) = C2(HCl)·V2 = 2,5·0,25 = 0,625 моль
V(HCl) =
= 0,104 л = 104 мл
Ответ: необходимо использовать 104
мл раствора.
Пример 7. До какого объема следует
упарить 3,5 л раствора серной кислоты,
С1(
H2SO4) = 0,04 моль/л,
чтобы получить раствор с концентрацией
кислоты 0,2 моль/л.
Решение:
Величина n(H2SO4) определяется
из данных условия:
n(H2SO4) = n(
H2SO4)·
= С1(
H2SO4)·
·V
= 0,04·
·3,5
= 0,07 моль
Отсюда V =
=
= 0,35 л = 350 мл
Ответ: исходный раствор следует
упарить до объема 350 мл.
2. 3. Расчеты, связанные со смешиванием растворов различной концентрации
При смешивании растворов количество
вещества n(X) (количества вещества
эквивалента) в полученном растворе
равно сумме количества вещества
(количества вещества эквивалента) в
смешиваемых растворах n 1(X), n
2(X) … n n(X):
n(X) = n 1(X) + n 2(X) + n 3(X) +…+
n n(X),
При смешивании растворов объем
полученного раствора не равен сумме
объемов смешиваемых растворов. Это
явление называют контракцией растворов.
Поэтому объем полученного раствора
следует рассчитывать.
При решении задач на смешивание растворов
часто приходится производить перерасчет
одной концентрации в другую.
Пример 8. Рассчитать массовую долю
1,25 н. раствора фосфорной кислоты, если
плотность раствора составляет 1,05 г/мл.
Решение:
ω(H3PO4) =
Объем раствора принимаем за 1 л (1000 мл).
Тогда масса раствора равна:
m(р-ра) = V·ρ = 1000·1,05 = 1050 г
Фактор эквивалентности H3PO4
=
Количество вещества: n(
H3PO4)
= C(
H3PO4)·V
= 1,25·1 = 1,25 моль
Масса H3PO4 в растворе:
m(H3PO4) = n(
H3PO4)·M(
H3PO4)
= n(
H3PO4)·
·M(H3PO4)
m(H3PO4) = 1,25·
·98
= 40,83 г
Массовая доля H3PO4 в растворе:
ω(H3PO4) =
= 0,039 или 3,9%
Ответ: ω(H3PO4) = 0,039 или
3,9%.
Пример 9. Смешали 3 литра раствора
H3PO4 (C(H3PO4) = 0,1 моль/л)
и 2 литра раствора H3PO4
(ω(H3PO4) = 90%, ρ = 1,05 г/мл). Вычислить
молярную концентрацию и молярную
концентрацию эквивалента полученного
раствора (контракцией можно пренебречь).
Решение:
Фактор эквивалентности H3PO4
=
С(H3PO4) =
С(
H3PO4)
=
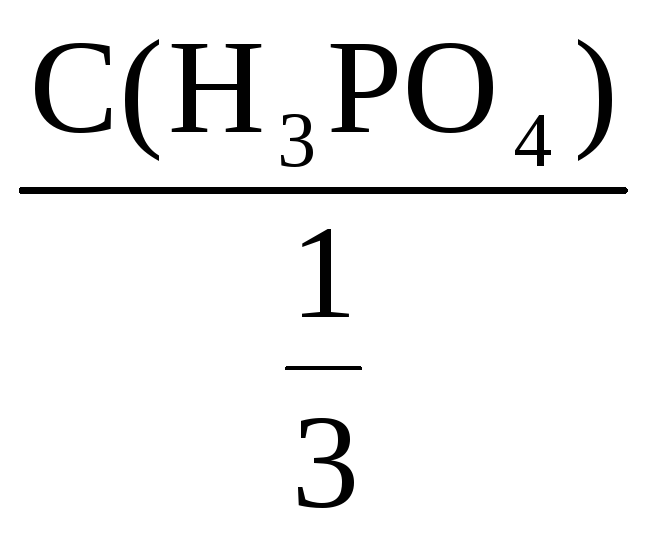
= 3·С(H3PO4)
Поскольку по условию задачи контракцией
пренебрегаем, то:
V = V1 +V2 = 3,0 + 2,0 = 5,0 л
Количества вещества в полученном
растворе определяется по формуле:
n(H3PO4) = n1(H3PO4)
+ n2(H3PO4)
Количества вещества в первом исходном
растворе:
n1(H3PO4) = C(H3PO4)·V1
= 0,1·3 = 0,3 моль
Количества вещества во втором исходном
растворе:
n2(H3PO4) =
=
=
= 1,928 моль
Отсюда n(H3PO4) = 0,3 + 1,928 = 2,228
моль
С(H3PO4) =
= 0,446 моль/л
С(
H3PO4)
= 3·0,446 = 1,337 моль/л
Ответ: молярная концентрация
полученного раствора H3PO4
равна 0,446 моль/л, молярная концентрация
эквивалента этого раствора равна 1,337
моль/л.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Разбавле́ние — уменьшение концентрации химического вещества в растворе добавлением растворителя или смешиванием с менее концентрированным раствором. При разбавлении сохраняется количество растворенного вещества.
Расчет растворов[править | править код]
Для приготовления растворов определенной концентрации следует тщательно рассчитывать массы и объемы смешиваемых растворов, исходя из сохранения количества растворенного вещества при разбавлении:
где 
Пример[править | править код]
Запись концентраций 
Друг над другом пишутся процентные концентрации (массовые или объемные) соответственно разбавляемого раствора и разбавителя (для чистого растворителя пишется 0 %). Справа посередине пишется желаемая концентрация (её значение должно быть между концентрациями разбавляемого раствора и разбавителя). Далее производится вычитание по диагоналям от большего значения меньшего и полученные разности записываются напротив исходных растворов. Полученные цифры являются массами (если были взяты массовые проценты) или объемами (если были взяты объемные проценты) соответствующих растворов, которые необходимо взять для приготовления раствора, с концентрацией записанной в середине. Затем полученные значения приводят к необходимым массам или объемам по условиям задания (для перевода массовых единиц в объемы может понадобится знать плотность растворов).
Действительно, чтобы из 50%-го раствора (по массовой концентрации) и воды (0 %) получить 18%-й раствор, следует взять 
Техника разбавления[править | править код]
При приготовлении растворов кислот требуется соблюдать правила техники безопасности: использовать очки, перчатки и фартуки. Во избежание резкой экзотермической реакции следует постепенно добавлять кислоту в воду.
Очень часто можно встретить задачу, в которой из одного раствора отбирают определенный объем и перемещают в другой объем растворителя, доводя его «до метки». Отобранный объем раствора называют аликвотой, а уровень, до которого доводят раствор – верхний или нижний мениск. Эти термины активно применяются в аналитической химии, при, так называемом, титриметрическом методе анализа. В данном случае мы говорим, что произошел процесс “разбавления“, то есть уменьшение концентрации вещества за счет добавления растворителя.
Как правило, в задачах, где имеются подобные формулировки, требуется найти либо количество вещества в исходном растворе, либо концентрацию исходного раствора, либо концентрацию вещества в разбавленном растворе.
Рассмотрим следующий пример разбавления:
40 г гидроксида натрия растворили в 500 мл колбе. Затем отобрали аликвоту пипеткой 50 мл и перенесли в колбу объемом 250 мл, добавив до уровня воду. Какая концентрация гидроксида натрия будет в разбавленном растворе?
Попробуем понять логику данной задачи. Вначале приготовили раствор с определенной концентрацией. Какой? Легко рассчитать, зная количество вещества гидроксида натрия (а его легко рассчитать, поделив массу гидроксида натрия на его молярную массу), и поделив это количество на объем раствора, выраженное в литрах.
Чему же равен объем полученного раствора? Объему сосуда, в котором он помещен, то есть 500 мл или 0,5 л. (Тогда концентрация гидроксида натрия составляет 2 моль/л. Проверь сам расчетами).
Что сделали дальше? Взяли часть вещества. Все вещество (1 моль) находится в объеме 500 мл, а взяли только 50 мл (аликвота показывает, сколько вещества взяли для дальнейшей работы). Тогда очевидно, количество вещества, которое окажется в аликвоте будет в 10 раз меньше того, что было в колбе (ведь взяли объем в 10 раз меньше – 50 мл от 500 мл).
И это количество составит всего 1/10, то есть 0,1 моль.
Что же дальше? А дальше это вещество поместили в 250 мл колбу и добавили воду до отметки, то есть довели объем раствора до данного значения (250 мл).
Опять не трудно рассчитать концентрацию полученного раствора: 0,1/0,250=0,4 моль/л.
Если мы теперь внимательно посмотрим на наши логические действия, то заметим, что все время умножали и делили одни объемы на другие.
При делении объема аликвоты на объем сосуда, в который помещается данная аликвота мы получаем “степень разбавления”. Умножая степень разбавления на исходную концентрацию раствора, мы получаем концентрацию разбавленного раствора. Вот и вся премудрость!
При нахождении концентрации исходного раствора поступаем с точностью до наоборот.
В ПОМОЩЬ МОЛОДОМУ
УЧИТЕЛЮ
Расчеты концентрации
растворенных веществ
в растворах
Решение задач на разбавление растворов особой
сложности не представляет, однако требует
внимательности и некоторого напряжения. Тем не
менее можно упростить решение этих задач,
используя закон разбавления, которым пользуются
в аналитической химии при титровании растворов.
Во всех задачниках по химии показаны решения
задач, представленных как образец решения, и во
всех решениях используется закон разбавления,
принцип которого состоит в том, что количество
растворенного вещества 
и масса m в исходном и разбавленном
растворах остаются неизменными. Когда мы решаем
задачу, то это условие держим в уме, а расчет
записываем по частям и постепенно, шаг за шагом,
приближаемся к конечному результату.
Рассмотрим проблему решения задач на
разбавление, исходя из следующих соображений.
• Количество растворенного вещества :
= c•V,
где c – молярная концентрация
растворенного вещества в моль/л, V – объем
раствора в л.
• Масса растворенного вещества m(р.в.):
m(р. в.) = m(р-ра)•
,
где m(р-ра) – масса раствора в г, – массовая доля
растворенного вещества.
Обозначим в исходном (или неразбавленном)
растворе величины c, V, m(р-ра), через с1, V1,
m1(р-ра), 1,
а в разбавленном растворе – через с2, V2,
m2(р-ра), 2.
Составим уравнения разбавления растворов. Левые
части уравнений отведем для исходных
(неразбавленных) растворов, а правые части – для
разбавленных растворов.
Неизменность количества растворенного вещества
при разбавлении будет иметь вид:
Сохранение массы m(р. в.):
Количество растворенного вещества связано с его массой m
(р. в.) cоотношением:
= m(р.
в.)/M(р. в.),
где M(р. в.) – молярная масса растворенного
вещества в г/моль.
Уравнения разбавления (1) и (2) связаны между собой
следующим образом:
с1•V1 = m2(р-ра)•2/M(р. в.),
m1(р-ра)•1 = с2•V2•M(р.
в.).
Если в задаче известен объем растворенного
газа V(газа), то его количество вещества связано с объемом
газа (н.у.) отношением:
= V(газа)/22,4.
Уравнения разбавления примут соответственно
вид:
V(газа)/22,4 = с2•V2,
V(газа)/22,4 = m2(р-ра)•2/M(газа).
Если в задаче известны масса вещества или
количество вещества, взятого для приготовления
раствора, то в левой части уравнения разбавления
ставится m(р. в.) или , в зависимости от условия задачи.
Если по условию задачи требуется объединить
растворы разной концентрации одного и того же
вещества, то в левой части уравнения массы
растворенных веществ суммируются.
Довольно часто в задачах используется плотность
раствора 
(г/мл). Но
поскольку молярная концентрация с
измеряется в моль/л, то и плотность следует
выражать в г/л, а объем V – в л.
Приведем примеры решения «образцовых» задач.
Задача 1. Какой
объем 1М раствора серной кислоты надо взять,
чтобы получить 0,5 л 0,1М H2SO4?
Дано:
с1 = 1 моль/л,
V2 = 0,5 л,
с2 = 0,1 моль/л.
Найти:
V1 = ?
Решение
V1•с1 = V2•с2,
V1•1 = 0,5•0,1; V1 = 0,05 л,
или 50 мл.
Ответ. V1 = 50 мл.
Задача 2 ([1],
№ 4.23). Определите массу раствора с массовой
долей (СuSО4)
10% и массу воды, которые потребуются для
приготовления раствора массой 500 г с массовой
долей
(СuSО4) 2%.
Дано:
1 = 0,1,
m2(р-ра) = 500 г,
2 = 0,02.
Найти:
m1(р-ра) = ?
m(H2O) = ?
Решение
m1(р-ра)•1 = m2(р-ра)•2,
m1(р-ра)•0,1 = 500•0,02.
Отсюда m1(р-ра) = 100 г.
Найдем массу добавляемой воды:
m(H2O) = m2(р-ра) – m1(р-ра),
m(H2O) = 500 – 100 = 400 г.
Ответ. m1(р-ра) = 100 г, m(H2O)
= 400 г.
Задача 3 ([1],
№ 4.37). Какой объем раствора с массовой долей
серной кислоты 9,3%
( = 1,05 г/мл)
потребуется для приготовления 0,35М раствора H2SO4
объемом 40 мл?
Дано:
1 = 0,093,
1 = 1050 г/л,
с2 = 0,35 моль/л,
V2 = 0,04 л,
М(H2SO4) = 98 г/моль.
Найти:
V1 = ?
Решение
m1(р-ра)•1 = V2•с2•М(H2SO4),
V1•1•1
= V2• с2•М(H2SO4).
Подставляем значения известных величин:
V1•1050•0,093 = 0,04•0,35•98.
Отсюда V1 = 0,01405 л, или 14,05 мл.
Ответ. V1 = 14,05 мл.
Задача 4 [2]. Какой
объем хлороводорода (н.у.) и воды потребуется,
чтобы приготовить 1 л раствора ( = 1,05 г/см3), в котором
содержание хлороводорода в массовых долях равно
0,1
(или 10%)?
Дано:
V(р-ра) = 1 л,
(р-ра) = 1050 г/л,
= 0,1,
М(HCl) = 36,5 г/моль.
Найти:
V(HCl) = ?
m(H2O) = ?
Решение
V(HCl)/22,4 = m(р-ра)•/М(HCl),
V(HCl)/22,4 = V(р-ра)•(р-ра)•/М(HCl),
V(HCl)/22,4 = 1•1050•0,1/36,5.
Отсюда V(HCl) = 64,44 л.
Найдем массу добавляемой воды:
m(H2O) = m(р-ра) – m(HСl),
m(H2O) = V(р-ра)•(р-ра) – V(HCl)/22,4• М(HCl),
m(H2O) = 1•1050 – 64,44/22,4•36,5 = 945 г.
Ответ. 64,44 л HCl и 945 г воды.
Задача 5 ([1],
№ 4.34). Определите молярную концентрацию
раствора с массовой долей гидроксида натрия 0,2 и
плотностью 1,22 г/мл.
Дано:
= 0,2,
= 1220 г/л,
М(NaOH) = 40 г/моль.
Найти:
c = ?
Решение
m(р-ра)• = с•V•М(NaOH),
m(р-ра)• = с•m(р-ра)•М(NaOH)/.
Разделим обе части уравнения на m(р-ра) и
подставим численные значения величин.
0,2 = c•40/1220.
Отсюда c = 6,1 моль/л.
Ответ. c = 6,1 моль/л.
Задача 6 ([1],
№ 4.30). Определите молярную концентрацию
раствора, полученного при растворении сульфата
натрия массой 42,6 г в воде массой 300 г, если
плотность полученного раствора равна 1,12 г/мл.
Дано:
m(Na2SO4) = 42,6 г,
m(H2O) = 300 г,
= 1120 г/л,
M(Na2SO4) = 142 г/моль.
Найти:
c = ?
Решение
m(Na2SO4) = с•V•М(Na2SO4).
Подставляя численные значения, получим:
42,6 = с•(42,6 + 300)/1120•142.
Отсюда с = 0,98 моль/л.
Ответ. с = 0,98 моль/л.
Задача 7 ([1],
№ 4.19). В лаборатории имеются растворы с
массовой долей хлорида натрия 10% и 20%. Какую массу
каждого раствора надо взять для получения
раствора с массовой долей соли 12% и массой 300 г?
Дано:
1 = 0,1,
2 = 0,2,
3 = 0,12,
m3(р-ра) = 300 г.
Найти:
m1(р-ра) = ?
m2(р-ра) = ?
Решение
m1(р-ра)•1 + m2(р-ра)•2 = m3(р-ра)•3,
m1(р-ра)•0,1 + m2(р-ра)•0,2
= 300•0,12.
Поскольку m1(р-ра) + m2(р-ра) = 300
г, то получаем систему из двух уравнений с двумя
неизвестными. Решая совместно два уравнения,
находим:
m1(р-ра) = 240 г, m2(р-ра) =
60 г.
Ответ. m1(р-ра) = 240 г, m2(р-ра)
= 60 г.
Задача 8 ([1],
№ 4.48). В воде массой 100 г при температуре 0 °С
растворяется фторид натрия массой 4,1 г, а при
температуре 40 °С – массой 4,5 г. Какая масса
фторида натрия выпадет в осадок при охлаждении
насыщенного при температуре 40 °С раствора NaF
массой 500 г до температуры 0 °С?
Дано:
m1(NaF) = 4,1 г,
m2(NaF) = 4,5 г,
m2(р-ра) = 500 г,
– массовая доля
NaF,
(1 – ) – массовая
доля воды.
Найти:
m(NaF) = ?
Решение
m(NaF) = m2(р-ра) – m1(р-ра).
Поскольку m2(Н2О) (40 °С) = m1(Н2О)
(0 °С), то можно записать:
m2(р-ра)•(1 – 2) = m1(р-ра)•(1 – 1).
Подставляем значения:
500•(1 – 4,5/(4,5 + 100)) = m1(р-ра)•(1 –
4,1/(4,1 + 100)).
Отсюда m1(р-ра) = 104,1/104,5•500 = 498,09 г,
m(NaF) = 500 – 498,09 = 1,91 г.
Ответ. m(NaF) = 1,91 г.
ЛИТЕРАТУРА
1. Хомченко Г.П., Хомченко И.Г. Задачи по химии
для поступающих в вузы. М.: Новая волна, 2002.
2. Фельдман Ф.Г., Рудзитис Г.Е. Химия-9. М.:
Просвещение, 1990, с. 166.
В.И.МАРТЫНОВ,
учитель химии
(пос. Архипо-Осиповка, Краснодарский край)
Вычисления при разбавлении и концентрировании растворов
По этой ссылке вы найдёте полный курс лекций по математике:
Процентная концентрация раствора выражает отношение массы растворенного вещества к массе раствора в целом. Если станем разбавлять раствор прибавлением к нему растворителя, масса растворенного вещества останется без изменения, а масса раствора увеличится. Отношение же этих масс (концентрация раствора) уменьшится и во столько раз, во сколько увеличится масса раствора.
Если же мы станем концентрировать раствор путем испарения растворителя, масса распора будет уменьшаться, а масса растворенного вещества останется без изменения. Отношение масс (концентрация раствора) увеличится и во столько раз, во сколько уменьшится масса раствора. Отсюда следует, что масса раствора и процентная концентрация обратно пропорциональны друг другу, что в математической форме можно выразить так: л. Эта закономерность лежит в основе вычислений при разбавлении и концентрировании растворов.
Возможно вам будут полезны данные страницы:
Пример 1. Имеется 90-процентный раствор. Какое количество его нужно взять, чтобы приготовить 500 кг 20-про-центного раствора? Решение. Согласно зависимости между массой и процентной концентрацией раствора Отсюда Следовательно, надо взять 111 кг 90-процентного раствора и прибавить к нему столько растворителя, чтобы масса раствора стала равной 500 кг. Пример 2. Имеется 15-процентный раствор. До какой массы надо упарить 8,50 т этого раствора, чтобы получить 60-процентный раствор? Решение.
Если количества растворов даны в объемных единицах, их нужно перечислить на массы.
В дальнейшем расчет вести по изложенной выше методике. Пример 3. Имеется 40-процентный раствор гидроокиси натрия плотностью 1,43 кг/л. Какой объем этого раствора нужно взять, чтобы приготовить 10 л 15-процентного раствора плотностью 1,16 кг/л? Ранение» Вычисляем массу 15-процентного раствора: кг п массу 40-процентного раствора: Определяем объем 40-процентного раствора: Пример 4. Имеется 1 л 50-процентного раствора серной кислоты плотностью 1,399 кг/л. До какого объема нужно разбавить этот раствор, чтобы получить 8-процентный раствор плотностью 1,055 кг/л ?
Решение. Находим массу 50-процентного раствора: кг и массу 8-процентного раствора: Рассчитываем объем 8-процентного раствора: V – – 8,288 -. = 8 л 288 мл Пример 5. 1 л 50-процентного раствора азотной кислоты, плотность которого 1,310 г/лм, разбавили 690 мл воды. Определить концентрацию полученного раствора *. Решение.
Находим массу 50-процентного раствора:
твоя = г и массу разбавленного раствора: Вычисляем концентрацию разбавленного раствора: 1 Примеры №5,6,7 взяты из книги Я Л. Голъдфарба, Ю. В. Хо-лакова «Сборник задач и упражнений по химии». М., «Просвещение», 1968ь Пример в. Имеется 93,6-процентный раствор кислоты плотностью 1,830 г/мл. Сколько требуется этого раствора, чтобы приготовить 1,000 л 20-процентного раствора плотностью 1,140 г/мл, и сколько требуется для этого воды?
Решение. Определяем массу 20-процен и массу 93,6-процентного раствора, требуемую для приготовления 20-процентного раствора: Высчитываем массу воды, требуемую для приготовления разбавленного раствора: Находим объем 93,6-процентного раствора: Пример 7. Сколько миллилитров серной кислоты плотностью 1,84 г/мл необходимо для приготовления 1,000 л аккумуляторной кислоты плотностью 1,18 г/мл} Процентная концентрация раствора и плотность его находятся в определенной зависимости, зафиксированной в специальных справочных таблицах. Пользуясь ими, можно установить концентрацию раствора по его плотности. Согласно этим таблицам серная кислота плотностью 1,84 г/мл является 98,72-процентной, а плотностью 1,18 г/мл — 24,76-
