Если сделать рисунок, то становится ясно следующее: пересечением квадратов будет восьмиугольник, имеющий как центр симметрии, так и несколько осей симметрии, проходящих через этот центр.
Если обозначить квадрат через $%ABCD$% (буквы идут против часовой стрелки) и повернуть его на 30 градусов против часовой стрелки, и повёрнутый квадрат обозначить через $%A_1B_1C_1D_1$%, то одной из осей симметрии будет прямая $%KL$%, где $%K$% — точка пересечения отрезков $%AB$% и $%A_1B_1$%, а $%L$% — симметричная её относительно центра точка пересечения отрезков $%CD$% и $%C_1D_1$%. Помимо восьмиугольника, площадь которого надо найти, на рисунке возникают ещё восемь треугольников, которые равны между собой. Их равенство легко усматривается из соображений симметрии. Все они — прямоугольные, с острым углом в 30 градусов. От квадрата $%ABCD$% отрезается четыре таких треугольника из восьми, поэтому задача сводится к нахождению площади одного из треугольников (любого).
Рассмотрим с этой целью треугольник $%KMA_1$%, где $%M$% — точка пересечения $%AB$% и $%A_1D_1$%. Пусть $%x$% — длина меньшего из катетов, лежащего против угла в 30 градусов, то есть $%x=A_1M$%. Тогда гипотенуза вдвое длиннее: $%MK=2x$%, а другой катет равен $%A_1K=xsqrt3$%. Сторона $%AB$% разбита на три отрезка: $%AM=A_1M=x$%, $%MK=2x$% и $%KB=A_1K=xsqrt3$% (равенства следуют из соображений симметрии), и в итоге мы получаем равенство $%a=AB=AM+MK+KB=x(3+sqrt3)$%. Из него выражаем $%x$%.
Площадь треугольника $%KMA_1$%, как и всех остальных равных ему, составляет $%x^2sqrt3/2$%. Как уже было сказано, надо из площади квадрата вычесть учетверённую площадь такого треугольника, получая $%a^2-2x^2sqrt3$%. После несложных преобразований приходим к ответу $$2left(1-frac{sqrt3}3right)a^2.$$
Это чуть больше $%84%$% от площади квадрата. Можно доказать, что если бы вместо угла в $%30$% градусов был дан острый угол $%alpha$%, то ответом было бы $%2a^2/(1+cosalpha+sinalpha)$%.

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону

S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ

S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности

S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности

S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр

S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Как рассчитать площадь квадрата
На данной странице калькулятор поможет рассчитать площадь квадрата онлайн. Для расчета задайте длину стороны или диагональ.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба.
Через сторону
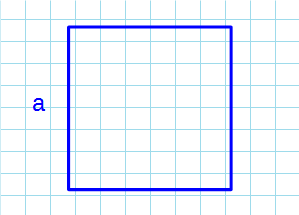
Формула для нахождения площади квадрата через сторону:
a – сторона квадрата.
Через диагональ
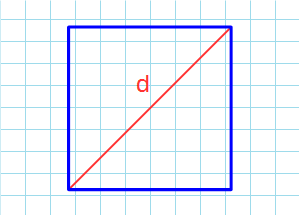
Формула для нахождения площади квадрата через диагональ:
d – диагональ квадрата.
Кроме стандартного произведения сторон в геометрии есть еще как минимум пять методов, о которых я хочу сейчас рассказать. Итак, поехали!
Формула 1. Площади квадрата через его диагональ
Выводится элементарно через один из прямоугольных треугольников.
Формула 2. Через периметр
Получается подстановкой в стандартную формулу площади значения а = p/4.
Формула 3. Через отрезок из вершины квадрата к середине противоположной стороны
Аналогично всё выводится из прямоугольного треугольника ABE.
Формула 4. Через радиус вписанной окружности
Очевидно, что радиус вписанной окружности равен половине стороны квадрата, исходя из чего, и выводится формула.
Формула 5. Через радиус описанной окружности
Вот такая тривиальная геометрия в это солнечное субботнее утро. Спасибо за внимание, уважаемые Читатели!
Читайте также:
Площадь квадрата можно найти с помощью двух основных формул:
1) Через сторону.
2) Через диагональ.
Как найти площадь квадрата, если известна его сторона.
Как известно, квадрат – это частный случай прямоугольника, у которого все стороны равны.
Площадь прямоугольника равна произведению 2 его сторон:
Sпр = a * b, a и b – стороны прямоугольника.
В случае с квадратом a = b.
Таким образом, площадь квадрата будет находиться по формуле:
Sкв = a².
Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².
Как найти площадь квадрата, если известна его диагональ.
Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата – катетами.
Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:
a*a + b*b = c*c.
a и b – катеты, c – гипотенуза.
В нашем случае a = b, а гипотенуза – это диагональ d.
Перепишем формулу в виде:
2a² = d².
a² = d² / 2.
Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.
Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².

