Угол падения
tyz144
Профи
(608),
закрыт
8 лет назад
Дополнен 15 лет назад
ПРЕЛОМЛЕННЫЙ УГОЛ, а не падения!!!!
Дополнен 15 лет назад
ПРЕЛОМЛЕННЫЙ УГОЛ, а не падения!!!!
Дополнен 15 лет назад
ПРЕЛОМЛЕННЫЙ УГОЛ, а не падения!!!!
Дополнен 15 лет назад
ПРЕЛОМЛЕННЫЙ УГОЛ, а не падения!!!!
Дополнен 15 лет назад
ПРЕЛОМЛЕННЫЙ УГОЛ, а не падения!!!!
Дополнен 15 лет назад
ПРЕЛОМЛЕННЫЙ УГОЛ, а не падения!!!!
Дополнен 15 лет назад
Луч проходит через стекло
Павел Митрофанов
Гуру
(3678)
15 лет назад

Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред и равна отношению показателей преломления этих сред, т. е. sin A / sin B = n2 / n1. Отсюда sin B = sin A*n1 / n2 и угол В = arcsin A*n1/n2
Enter the refractive indices of two different mediums and the angle of refraction into the calculator to determine the angle of incidence.
- Angle of Depression Calculator
- Index of Refraction Calculator
- Magnification Calculator
Angle of Incidence Formula
The following formula is used to calculate the angle of incidence.
θ1 = sin-1 ( n2 * sin (θ2) / n1 )
- Where θ1 is the angle of incidence
- θ2 is the refraction angle
- n2 is the refractive index of medium 2
- n1 is the refractive index of medium 1
To calculate the angle of incidence, multiply the refractive index of the 2nd medium by the sine of the refraction angle, then divide by the refractive index of the 1st medium. Finally, take this result and take the inverse sine of it to get the angle of incidence.
Angle of Incidence Definition
An angle of incidence is defined as the angle between the ray incident on a surface and the line perpendicular to the surface.
Angle of Incidence Example
How to calculate the angle of incidence?
- First, determine the refractive indices.
Calculate the refractive index of both mediums.
- Next, determine the angle of refraction.
Calculate or measure the refraction angle.
- Finally, calculate the angle of incidence.
Calculate the angle of incidence using the equation above.
FAQ
What is a refraction?
A refraction is defined as the change in the relative angle of reflected light based on the speed of light through two different mediums.
Как определить угол падения
При решении задач чаще всего приходится находить угол падения светового луча и предмета, брошенного горизонтально или под углом к горизонту. Угол падения луча находится с помощью построения или несложных расчетов, когда известен угол отражения или преломления. Угол падения тела находится в результате расчетов.
Вам понадобится
- – транспортир;
- – дальномер;
- – таблица абсолютных показателей преломления.
Инструкция
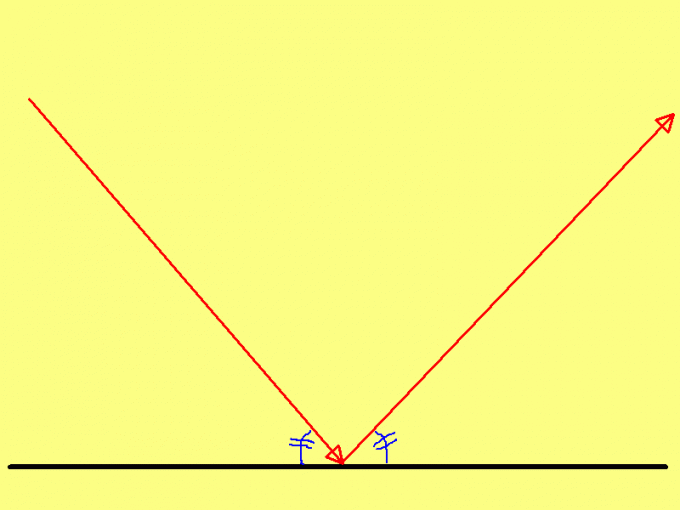
При падении светового луча на плоскую поверхность восстановите перпендикуляр к ней в точке падения с помощью транспортира, угольника или угломера. Угол между перпендикуляром и падающим лучом и будет углом падения. Если поверхность не является плоскостью, в точке падения луча постройте касательную, и опустите перпендикуляр к касательной в этой точке. Угол определите так же, как и в предыдущем случае. В обоих случаях для измерения угла пользуйтесь транспортиром или угломером.
Если известен угол отражения, то по первому закону отражения световых лучей он будет равен углу падения. Когда известен угол преломления на границе двух сред, найдите относительный показатель их преломления из таблицы или рассчитайте его, используя абсолютные показатели. Затем умножьте этот показатель на синус угла преломления. Результатом будет синус угла падения светового луча Sin(α)=n•Sin(β). С помощью инженерного калькулятора или специальных таблиц найдите значение угла падения, использовав функцию арксинуса.
Угол падения тела измерьте, восстановив перпендикуляр в точку падения, это угол между перпендикуляром и направлением конечной скорости тела. В том случае, когда тело брошено под углом к горизонту, который заранее известен, угол падения равен 90º минус угол, под которым брошено тело.
В случае, когда тело бросают горизонтально с некоторой высоты, померяйте расстояние, на котором тело упадет на землю и высоту, с которой оно было сброшено в метрах. Сделайте это при помощи рулетки или с дальномера. Чтобы найти угол падения, поделите расстояние, которое преодолело тело на удвоенную высоту, с которой оно падало. Это будет тангенс угла падения. Найдите угол при помощи калькулятора или таблицы.
В данных расчетах не учитывается сопротивление воздуха, которым можно пренебречь при небольших скоростях, с которыми движутся тела, например, брошенный камень. При большом сопротивлении среды при увеличении скорости результаты изменятся.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
| Показатель преломления | |
|---|---|
 |
|
| Размерность | безразмерная |
| Примечания | |
| скаляр или тензор |

Показа́тель преломле́ния (и́ндекс преломле́ния, и́ндекс рефра́кции) — безразмерная физическая величина, характеризующая различие фазовых скоростей света в двух средах. Для прозрачных изотропных сред, таких как газы[⇨], большинства жидкостей[⇨], аморфных веществ (например, стекло[⇨]), употребляют термин абсолютный показатель преломления, который обозначают латинской буквой 


Например, для воды показатель преломления составляет 1,333, что означает, что в ней свет движется в 1,333 раза медленнее, чем в вакууме (примерно 225 000 км/с). В случае двух прозрачных изотропных сред говорят об относительном показателе преломления одной среды по отношению к другой[⇨]. Если не указано иное, то обычно имеется в виду абсолютный показатель преломления. Абсолютный показатель преломления часто превышает единицу, поскольку скорость распространения света в любой среде меньше скорости света в вакууме. Однако фазовая скорость света при некоторых условиях может превышать скорость его распространения, и тогда показатель преломления может принимать значения меньше единицы[⇨].
Значение абсолютного показателя преломления зависит от состава и строения вещества, его агрегатного состояния, температуры, давления и так далее[⇨]. Для веществ показатель преломления изменяется под действием внешнего электрического поля (в жидкостях и газах[⇨], в кристаллах[⇨]) или магнитного поля[⇨]. Для измерения показателя преломления применяют гониометры, рефрактометры[⇨] или эллипсометры[⇨].
Показатель преломления изменяется в зависимости от длины волны, это приводит к расщеплению белого света на составляющие цвета при преломлении. Это называется дисперсией[⇨]. Её можно наблюдать в призмах и радугах, а также в виде хроматической аберрации в линзах. Распространение света в поглощающих материалах можно описать с помощью комплексного показателя преломления[2][3]:
,
где 

Основные понятия[править | править код]

Зависимость траектории луча света от угла падения при переходе из воды в воздух
Когда свет проходит границу раздела двух сред, то для вычисления угла преломления используют относительный показатель преломления, равный отношению абсолютных показателей преломления первой и второй сред. Относительный показатель преломления может быть больше единицы, если луч переходит в более оптически плотную среду, и меньше единицы — в противном случае[4][1].
Если луч света переходит из среды с меньшим показателем преломления в среду с бо́льшим показателем преломления (например, из воздуха в воду), то угол между лучом и нормалью к границе раздела уменьшается после преломления. И наоборот, в случае перехода в менее оптически плотную среду угол увеличивается. Во втором случае угол преломления может превышать 90°, так что преломления не происходит вообще и весь свет отражается; это явление называется полным внутренним отражением[5].
Частота света не меняется при преломлении. Поэтому длина волны света в среде уменьшается по сравнению с длиной волны в вакууме пропорционально уменьшению скорости света[6].
Типичные значения[править | править код]
Для видимого света большинство прозрачных сред имеют показатели преломления от 1 до 2. Несколько примеров приведены в таблице внизу[⇨]. Эти значения обычно измеряются на длине волны 589 нм, соответствующей дублетной D-линии натрия в жёлтой части спектра[7]. Газы при атмосферном давлении имеют показатель преломления, близкий к 1, из-за их низкой плотности. Почти все твёрдые тела и жидкости имеют показатель преломления выше 1,3, за исключением аэрогеля. Аэрогель — это твёрдое вещество очень низкой плотности, которое может демонстрировать показатель преломления в диапазоне от 1,002 до 1,265[8]. Муассанит находится на другом конце диапазона с показателем преломления до 2,65. Большинство пластиков имеют показатели преломления в диапазоне от 1,3 до 1,7, но некоторые полимеры с высоким показателем преломления могут иметь значения до 1,76[9].
Для инфракрасного света показатели преломления могут быть значительно выше. Германий прозрачен в диапазоне длин волн от 2 до 14 мкм и имеет показатель преломления около 4[10]. Во второй половине 2000-х годов был обнаружен тип новых материалов, получивших название топологических изоляторов, которые имеют очень высокий показатель преломления — до 6 в ближней и средней зонах инфракрасного диапазона частот. Более того, топологические изоляторы прозрачны при наноразмерных толщинах. Эти свойства потенциально важны для приложений в инфракрасной оптике[11].
Связь между скоростью и углом преломления света[править | править код]
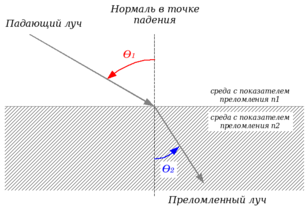
Падение и преломление лучей (волн) света
Свет, распространяющийся в неоднородной среде, проходит из одной точки в другую за минимальное время. Из этого принципа можно вывести закон преломления света на границе раздела между средами с разными показателями преломления, который называется законом Снеллиуса[12].
Он выражается в виде дроби[1]
-
(Ур. 1.1)
где θ1 и θ2 — углы падения и преломления луча света соответственно, которые отсчитываются от нормали к границе между средами, проведённой через точку падения луча, v1 и v2 — фазовые скорости в первой среде (из которой падает свет, на рисунке сверху) и второй среде (в которую свет проникает, на рисунке нижняя)[13].
Этот закон можно записать через показатели преломления двух сред, зная, что v1 = c/n1 и v2 = c/n2 (c — скорость света в вакууме)[12]:
-
(Ур. 1.2)
Закон Снеллиуса выполняется только для неподвижных сред. Для релятивистских скоростей поперечного движения прозрачной среды вследствие аберрации эффективный показатель преломления будет зависеть от скорости среды, что позволяет определять скорость движения среды[14].
Коэффициент отражения[править | править код]

Часть волны проходит через границу, а часть отражается
При падении на границу раздела двух сред только часть света проходит из среды с меньшим показателем преломления в среду с бо́льшим, а часть — отражается обратно. Чем сильнее отличаются показатели преломления сред, тем бо́льшая часть света отражается. В случае падения света по нормали к поверхности коэффициент отражения выражается как[15]:
-
(Ур. 1.3)
В этом случае при переходе луча света из воздуха в стекло (показатель преломления 1,5) отражается 4 % падающего света[16], а в случае алмаза (показатель преломления 2,42[17]) — более 17 %[18].
Рассчитать коэффициент отражения света для произвольных углов падения и поляризации можно с помощью формул Френеля[19].
Дисперсия[править | править код]

Свет разных цветов имеет немного разные показатели преломления в воде, что приводит к появлению радуги
Показатель преломления зависит от частоты света. Это явление называется дисперсией. В тех диапазонах частот, где вещество прозрачно, преломление увеличивается с частотой[20]. Например, вода и бесцветное стекло преломляют голубой свет сильнее, чем красный[1].
В природе этот эффект приводит к возникновению такого явления как радуга. Разложение света стеклянной призмой заложило основы спектрального анализа, который широко применяется в науке и технике. В то же время дисперсия приводит к трудностям в изготовлении оптических систем. Когда на стеклянную линзу падает пучок немонохроматического света, то лучи разных цветов фокусируются на разном расстоянии и вокруг контрастных деталей изображения образуется радужная кайма. Это явление получило название хроматической аберрации. Её компенсируют путём изготовления линз из разных сортов оптического стекла, имеющих разные показатели преломления[21].
Из-за зависимости показателя преломления от длины волны в таблицах указывают частоту, на которой производились измерения. Обычно применяется частота жёлтой линии натрия (точнее, поскольку эта спектральная линия является двойной, применяется среднее арифметическое от длин линий дублета, 5893 Å); в этом случае показатель преломления обозначается через 
Для оценки дисперсии в оптическом диапазоне применяют среднюю дисперсию или главную дисперсию (
- Дисперсия электромагнитных волн
-

Дисперсия в стеклянной призме
-
![Типичный вид графика зависимости показателя преломления от частоты в широком диапазоне. Резкие падения связаны с инфракрасной, ультрафиолетовой и рентгеновской зонами поглощения[24]](https://upload.wikimedia.org/wikipedia/commons/thumb/b/b5/Refractive_index_from_the_infrared_to_the_x-ray-ru.svg/599px-Refractive_index_from_the_infrared_to_the_x-ray-ru.svg.png)
Типичный вид графика зависимости показателя преломления от частоты в широком диапазоне. Резкие падения связаны с инфракрасной, ультрафиолетовой и рентгеновской зонами поглощения[24]
-

Зависимость показателя преломления (красный) и коэффициента поглощения (зелёный) кремния от длины волны при температуре 300 К
Другой характеристикой является число Аббе, равное:
-
(Ур. 1.4)
Большее число Аббе соответствует меньшей средней дисперсии[25].
В широком диапазоне длин волн электромагнитного излучения зависимость показателя преломления от частоты является нелинейной и состоит из участков, где показатель преломления возрастает с частотой — этот случай называется нормальной дисперсией (поскольку такая ситуация типична), — и небольших участков, где показатель преломления стремительно падает, что называется аномальной дисперсией. Участки аномальной дисперсии обычно расположены вблизи линий поглощения вещества[26].
Поляризация при преломлении[править | править код]
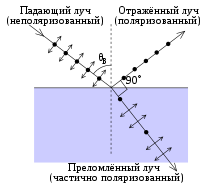
Отражение и преломление света, падающего под углом Брюстера на границу раздела двух сред
Интенсивности преломлённой и отражённой волн зависят от поляризации падающего света: s-поляризованный свет имеет более высокий коэффициент отражения, тогда как p-поляризованный лучше проникает в среду. Поэтому даже если на границу раздела сред падает неполяризованный свет, и преломлённый, и отражённый лучи становятся частично поляризованными (если угол падения не равен нулю). Если угол между отражённым и преломлённым лучами составляет 90°, отражённый свет становится полностью поляризованным. Угол падения, при котором это происходит, называется углом Брюстера. Его значение зависит от относительного показателя преломления сред[27]:
-
(Ур. 1.5)
В случае падения под таким углом преломлённый луч не становится полностью поляризованным, но степень его поляризации является максимальной[27].
Общее выражение[править | править код]
Существует другое определение показателя преломления, связывающее его с диэлектрической проницаемостью среды ε:
-
(Ур. 1.6)
где 




-
(Ур. 1.7)
Это определение приводит к действительным значениям для немагнитных сред[31] и описывает внутреннюю характеристику среды, которая позволяет установить, как падающая световая волна поляризует среду. И диэлектрическая проницаемость, и диэлектрическая восприимчивость являются действительными или комплексными величинами, поэтому показатель преломления также может иметь комплексные значения. Мнимая часть показателя преломления связана с поглощением среды, так что существует определённая зависимость между поляризацией материала и ослаблением световой волны в среде[28]. Фактически размерный коэффициент поглощения вычисляется из мнимой части безразмерного показателя преломления по следующей формуле
-
(Ур. 1.8)
где 


Механизм замедления света в среде[править | править код]
Причины замедления света в веществе могут быть (с упрощениями) объяснены с позиций классической электродинамики. Любая заряженная частица в поле электромагнитной волны испытывает действия периодических сил, которые вызывают её колебания. Обычно важнее действие периодического электрического поля, а не магнитного, поскольку скорости частиц в среде относительно невысокие. Под действием периодического электрического поля носители электрического заряда также начинают колебаться с определённой частотой, а следовательно сами становятся источниками электромагнитных волн[33]. Атомы всех веществ содержат электроны — лёгкие заряженные частицы, которые легко колеблются в электрическом поле волны. В случае волн оптического диапазона (частотой порядка 1015 Гц) поле, создаваемое электронами, обычно почти полностью описывает наведённое поле. Для волн меньшей частоты (инфракрасного или микроволнового излучения) заметными становятся и эффекты, вызванные перераспределением электронов между атомами в молекуле, колебания ионов в ионных кристаллах или вращение полярных молекул[34]. Волны, создаваемые каждым электроном, интерферируют между собой, создавая волну, которая распространяется в том же направлении, что и падающая волна (а также в обратном — что воспринимается как отражение от границы сред)[35]. Интерференция падающей и наведённой волн создаёт эффект замедления электромагнитной волны (хотя на самом деле обе волны движутся с одинаковой скоростью — скоростью света)[36]. В общем случае вычисление поля, создаваемого колебаниями электронов, является сложной задачей, поскольку каждый электрон испытывает действие не только падающей волны, но и волны, созданной колебаниями всех остальных электронов[35]. Простейшая модель выводится из предположения, что электроны друг на друга не действуют, что справедливо для очень разреженных сред с низким показателем преломления, таких как газы[35].
Пусть на тонкий слой вещества толщиной 


-
(Ур. 2.1)
Интенсивность лазерных источников света сравнительно невелика, так что напряжённость электрического поля световой волны значительно меньше напряжённости электрического поля в атоме. При таких условиях электрон в атоме можно рассматривать как гармонический осциллятор[4] (это допустимо с позиций квантовой механики) с резонансной частотой 

-
(Ур. 2.2)
где 

Решение такого уравнения имеет вид[38]:
-
(Ур. 2.3)
Если источник излучения находится достаточно далеко и фронт падающей волны плоский, то все электроны, которые находятся в этой плоскости, движутся одинаково. Поле, создаваемое такой заряженной плоскостью, равно:
-
(Ур. 2.4)
где 
С другой стороны, если в пластинке волна замедляется в 
-
(Ур. 2.5)
Это уравнение описывает волну, идентичную падающей, но с задержкой по фазе, которую выражает первая экспонента. В случае малой толщины пластинки можно разложить первую экспоненту в ряд Тейлора[39]:
-
(Ур. 2.6)
Таким образом, поле, создаваемое веществом, описывается формулой[39]:
-
(Ур. 2.7)
Сравнивая это выражение с выражением, полученным для поля ур. 2.4, созданного колебаниями электронов плоскости, можно получить[39]:
-
(Ур. 2.8)
Поскольку число зарядов на единицу площади равно концентрации электронов 
-
(Ур. 2.9)
где 
Эта формула также описывает зависимость показателя преломления от частоты падающей волны, то есть дисперсию[40]. В общем случае необходимо учитывать, что каждый атом содержит много электронов, имеющих различные резонансные частоты. Их вклады должны суммироваться в правой части уравнения[41]. В интенсивных световых потоках напряжённость электрического поля волны может быть соразмерна с внутриатомной. В таких условиях модель гармонического осциллятора становится неприменимой[4].
Эффект Поккельса[править | править код]
Модель ангармонического осциллятора с затуханием оказывается полезной для качественного рассмотрения зависимости показателя преломления в кристаллах без центра инверсии от постоянного электрического поля. Уравнение Ньютона для ангармонического осциллятора записывается в виде[42]
-
(Ур. 2.10)
где 






-
(Ур. 2.11)
При отсутствии ангармонического вклада гармонический осциллятор совершает колебания с резонансной частотой около нового положения равновесия из-за наличия электрического поля. В присутствии малого ангармонического вклада можно принять новое положение равновесия за начало координат, подставив в уравнение движения 
-
(Ур. 2.12)
Новое уравнение описывает колебания со сдвинутой резонансной частотой, то есть при наличии ангармонизма внешнее постоянное поле не только сдвигает положение равновесия осциллятора, но и изменяет квадрат резонансной частоты на величину 
-
(Ур. 2.13)
Электрическое поле — это выделенное направление в кристалле, поэтому в среде возникает зависимость дисперсии от направления распространения света — двулучепреломление. Это явление называется эффектом Поккельса. Как видно из качественной модели, это линейный по электрическому полю эффект[43]. Этот эффект находит применение в модуляторах света[44].
Связь с другими показателями[править | править код]
Диэлектрическая проницаемость[править | править код]
Из уравнений Максвелла можно получить формулу, связывающую скорость света в веществе с диэлектрической и магнитной проницаемостями вещества (обозначаются буквами 

-
(Ур. 3.1)
Таким образом, показатель преломления определяется характеристиками среды[46]:
-
(Ур. 3.2)
Магнитная проницаемость очень близка к единице в большинстве реальных прозрачных веществ, поэтому последнюю формулу иногда упрощают до 



-
(Ур. 3.3)
где
-
(Ур. 3.4)
или наоборот
-
(Ур. 3.5)
где 
Диэлектрическая проницаемость в этой формуле может значительно отличаться от табличных значений, поскольку в таблицах обычно приведены значения проницаемости в постоянном электрическом поле. В быстро меняющемся поле (именно такое поле создаёт электромагнитная волна) молекулы не успевают поляризоваться, что приводит к уменьшению диэлектрической проницаемости. Особенно это касается полярных молекул, таких как вода: диэлектрическая проницаемость воды в постоянном электрическом поле 
Для комплексного показателя преломления, зависящего от энергии 
-
(Ур. 3.6)
-
(Ур. 3.7)
где символ 
В случае кристаллов и других анизотропных сред диэлектрическая проницаемость зависит от кристаллографического направления и описывается тензором, поэтому показатель преломления является тензорной величиной[51].
Поляризуемость[править | править код]
Важным соотношением, связывающим показатель преломления с микроскопическими свойствами вещества, является формула Лоренца — Лоренца:
-
(Ур. 3.8)
где 

С другой стороны, молярная рефракция является мерой общей поляризуемости одного моля вещества и может быть рассчитана на основе показателя преломления как:
-
(Ур. 3.9)
где 


В простом случае газа при небольшом давлении показатель преломления выражается как[56]
-
(Ур. 3.10)
Формула Лоренца — Лоренца (ур. 3.8) выведена в предположении изотропности среды, поэтому справедлива для газов, жидкостей, аморфных тел. Однако и для многих других веществ она часто выполняется с хорошей точностью (погрешность не превышает нескольких процентов). Пригодность формулы для конкретного вещества определяется экспериментально. Для некоторых классов веществ, например, пористых материалов, погрешность может достигать десятков процентов[57]. Область применения формулы ограничивается видимым и ультрафиолетовым диапазонами спектра и исключает диапазоны поглощения в веществе. Для низших частот необходимо учитывать не только электронную поляризацию, но и атомную (поскольку ионы в ионных кристаллах и атомы в молекулах успевают сместиться в поле низкой частоты)[52].
Для полярных диэлектриков в случае волн большой длины также необходимо учитывать ориентационную поляризуемость, природа которой заключается в изменении ориентации дипольных молекул вдоль силовых линий поля. Для газов, состоящих из полярных молекул, или сильно разбавленных растворов полярных веществ в неполярных растворителях вместо формулы Лоренца — Лоренца необходимо использовать формулу Ланжевена — Дебая:
-
(Ур. 3.11)
где 



Плотность[править | править код]
Как правило, вещества с большей плотностью имеют более высокий показатель преломления. Для жидкостей показатель преломления обычно больше, чем для газов, а для твёрдых тел — больше, чем для жидкостей[59]. Однако количественная связь между показателем преломления и плотностью может быть разной для разных классов веществ. Существует несколько эмпирических формул, позволяющих оценить эту связь численно[60]. Наиболее известное соотношение следует из формулы Лоренца — Лоренца (ур. 3.9):
-
(Ур. 3.12)
которое хорошо описывает газы, а также удовлетворительно выполняется в случае изменения агрегатного состояния вещества[60]. Величину 
В случае газов при низком давлении это выражение сводится к ещё более простому, известному как формула Гладстона — Дейла[en][62]:
-
(Ур. 3.13)

Миражи образуются в неравномерно нагретом воздухе вследствие изменения показателя преломления в зависимости от плотности
Уменьшение плотности воздуха с высотой (соответственно, уменьшение показателя преломления) вызывает рефракцию света в атмосфере, что приводит к смещению видимого положения небесных светил. Вблизи горизонта такое смещение достигает 30 угловых минут (то есть размера диска Солнца или Луны)[63]. Неоднородный показатель преломления атмосферы может приводить к более раннему восходу Солнца, что наблюдается в северных широтах[64].
Для некоторых немагнитных сред точную оценку можно получить с помощью формулы, полученной Макдональдом:
-
(Ур. 3.14)
Она лучше описывает показатель преломления для воды, бензола и других жидкостей[60].
Также существует зависимость показателя преломления от других связанных с плотностью величин, в частности она уменьшается при увеличении температуры (из-за уменьшения концентрации частиц вследствие термического расширения)[59]. По тем же причинам при увеличении давления показатель преломления возрастает[65].

Как правило, показатель преломления стекла увеличивается с увеличением его плотности. Однако не существует общей линейной зависимости между показателем преломления и плотностью для всех силикатных и боросиликатных стёкол. Относительно высокий показатель преломления и низкая плотность могут быть получены для стёкол, содержащих оксиды лёгких металлов, таких как Li2O и MgO, тогда как противоположная тенденция наблюдается для стёкол, содержащих PbO и BaO, как показано на диаграмме справа[66].
Многие масла (например, оливковое масло) и этанол являются примерами жидкостей, которые обладают более высокими коэффициентами преломления, но менее плотны, чем вода, вопреки общей корреляции между плотностью и показателем преломления[67].
Для воздуха 
В неравномерно нагретом воздухе вследствие изменения показателя преломления траектория лучей света искривляется и наблюдаются миражи. Для «нижнего» миража приповерхностный слой нагрет, поэтому показатель преломления меньше, чем у более холодного воздуха выше. Траектория световых лучей будет искривляться так, что выпуклость траектории обращена вниз и часть голубого неба будет видеться наблюдателю ниже уровня горизонта, что похоже на воду. Для «верхних» миражей выпуклость траектории обращена вверх из-за более плотного и холодного приповерхностного слоя. В этом случае возможно заглянуть за горизонт и увидеть предметы, скрытые от прямого наблюдения[69].
Производные величины[править | править код]
В нефтехимии применяется производный от плотности показатель — рефрактометрическая разница или интерцепт рефракции:
-
(Ур. 3.15)
Эта величина одинакова для углеводородов одного гомологического ряда[70].
Оптическая длина пути[править | править код]

Оптическая длина пути (OPL) — это произведение геометрической длины 
-
(Ур. 3.16)
Это понятие определяет фазу света и управляет интерференцией и дифракцией света при его распространении. Согласно принципу Ферма, световые лучи можно охарактеризовать как кривые, оптимизирующие длину оптического пути[72].
Фокусное расстояние линзы определяется её показателем преломления 


-
(Ур. 3.17)
где 
Разрешение микроскопа[править | править код]
Разрешение хорошего оптического микроскопа в основном определяется числовой апертурой (NA) его объектива. Числовая апертура, в свою очередь, определяется показателем преломления 

-
(Ур. 3.18)
По этой причине для получения высокого разрешения в микроскопии часто используется масляная иммерсия. В этом методе для исследования образцов объектив погружается в каплю жидкости с высоким показателем преломления (иммерсионного масла, глицерина или воды)[75].
Волновое сопротивление[править | править код]
Волновое сопротивление плоской электромагнитной волны в непроводящей среде (без затухания) определяется выражением
-
(Ур. 3.19)
где 




Для немагнитных сред 
-
(Ур. 3.20)
-
(Ур. 3.21)
Таким образом, показатель преломления в немагнитной среде определяется как отношение волнового сопротивления вакуума к волновому сопротивлению среды. Отражательную способность 
-
(Ур. 3.22)
Это выражение совпадает с коэффициентом отражения света при нормальном падении (ур. 1.3)[77].
Волноводы[править | править код]
Электромагнитные волны могут распространяться внутри волноводов. Их дисперсионные соотношения устанавливаются из решения уравнений Максвелла с соответствующими граничными условиями. Если рассматривать волноводы с металлическими стенками, то электрическое поле не проникает в них и волна, распространяющаяся в них, может быть описана как плоская волна вдоль оси волновода, а поперечные колебания электромагнитного поля задаются свойствами такого резонатора. Если предполагать, что поперечное сечение не меняется, то существует ограничение снизу на частоту этих колебаний. Если обозначить соответствующие частоты мод, связанных с поперечными колебаниями, которые представляют собой поперечные стоячие волны, как 
-
(Ур. 3.23)
Она всегда больше, чем в неограниченном пространстве 
Групповой индекс[править | править код]
Иногда определяется «показатель преломления групповой скорости», обычно называемый групповым индексом (англ. group index):
-
(Ур. 3.24)
где vg — групповая скорость[79]. Это значение не следует путать с показателем преломления n, который всегда определяется относительно фазовой скорости — они совпадают только для сред без дисперсии. Когда дисперсия мала, групповая скорость может быть связана с фазовой скоростью соотношением
-
(Ур. 3.25)
где λ — длина волны в среде[80]. Таким образом, в этом случае групповой показатель может быть записан в терминах зависимости показателя преломления от длины волны как
-
(Ур. 3.26)
Когда показатель преломления среды известен как функция длины волны в вакууме, соответствующие выражения для групповой скорости и индекса имеют вид (для всех значений дисперсии)
-
(Ур. 3.27)
-
(Ур. 3.28)
где λ0 — длина волны в вакууме[81].
Воздух[править | править код]
Показатель преломления воздуха был предметом многочисленных исследований. Он имеет первостепенное значение для любого исследования и измерения, происходящего в атмосфере. Его значение зависит от многих параметров и было предметом измерений и теорий, точность которых очень варьируется. Первое грубое измерение было выполнено с помощью рефрактометра в начале XVIII века Исааком Ньютоном, который в 1700 году[82] замерил изменение видимых высот звёзд из-за преломления в атмосфере[83], что привело Эдмунда Галлея к публикации этих результатов в 1721 году для иллюстрации преломления в воздухе[84]. В 1806 году Франсуа Араго и Жан-Батист Био оценили значение индекса для воздуха[83].
Первая формула, устанавливающая показатель преломления воздуха, была составлена Х. Барреллом и Дж. Э. Сирсом в 1938 году. Названная формулой Баррелла — Сирса, она имеет вид формулы Коши с двумя членами, зависящими от длины волны света (в вакууме) как 

-
(Ур. 4.1)
где A, B, C — коэффициенты. Сейчас она устарела, но продолжает использоваться[83][85]. Для материалов с полосой поглощения в инфракрасном диапазоне и некоторых других материалов с полосой поглощения в ультрафиолетовом диапазоне (например, воды) используется формула Скотта — Бриота[86]
-
(Ур. 4.2)
и более точная формула Зельмейера
-
(Ур. 4.3)
Эти эмпирические законы, определяемые очень точными измерениями длины волны, применяются к прозрачным средам в видимом диапазоне электромагнитного спектра. В моделях учитывают, что, находясь далеко от полос поглощения (обычно расположенных в ультрафиолетовой и инфракрасных областях спектра), можно рассматривать индекс как вещественное число и определить зависимость показателя преломления от длины волны. Эти формулы, как правило, точны до пятого знака после запятой[86].
Две более свежие формулы, которые сейчас широко используются, дают лучшее приближение к показателю преломления воздуха: это формулы Филипа Э. Сиддора[87] и Эдлена[88]. Эти формулы учитывают большее или меньшее количество факторов, в частности наличие водяного пара и диоксида углерода, и действительны для того или иного диапазона длин волн.[83]
Показатель преломления воздуха можно очень точно измерить с помощью интерферометрических методов, вплоть до порядка 10−7 или меньше[89]. Он примерно равен 1,000 293 при температуре 0 °C и давлении 1 бар[90]. Эта величина очень близка к единице, поэтому в технической оптике используют другое определение для показателя преломления через отношение скорости света в воздухе к скорости света в среде[91].
Видимый и инфракрасный спектр[править | править код]
Значение показателя преломления воздуха, одобренное Joint Commission for Spectroscopy в Риме в сентябре 1952 года, записывается следующим образом:
-
(Ур. 4.4)
Эта формула справедлива для длин волн от 0,2 мкм до 1,35 мкм (видимого и инфракрасного диапазонов) и сухого воздуха, содержащего 0,03 % углекислого газа по объёму, при 15 °C и давлении 101,325 кПа[89].
Радарные исследования[править | править код]
Свойства воздуха в зависимости от высоты сильно меняются, что сказывается на точности действия систем глобального позиционирования. В частности, для микроволн и радиоволн очень важен состав воздуха, поскольку наличие водяного пара в тропосфере замедляет сигналы радаров из-за изменения показателя преломления воздуха, что приводит к ошибкам в позиционировании. На большой высоте в ионосфере дисперсию волн обуславливают свободные электроны. На показатель преломления воздуха также влияют температура и давление. В простейшем виде время задержки для сигнала радара определяется из уравнения 






В метеорологии и радарных исследованиях используют другое определение изменения индекса 



-
(Ур. 4.5)
где 






В ионосфере, однако, вклад электронной плазмы в коэффициент преломления существенен, а водяного пара — отсутствует, поэтому используют другую форму уравнения для показателя преломления:
-
(Ур. 4.6)
где 

Вклад холодной плазмы в ионосфере может изменить знак показателя преломления на больших высотах в микроволновом диапазоне. В общем случае ионосфера демонстрирует двулучепреломление[96].
Радарные технологии используются в метеорологии для определения количества капель и их распределения над территорией США и Западной Европы, поскольку эти территории практически полностью покрыты сетью радаров. Мощность отражённого сигнала пропорциональна радиолокационной отражаемости водяных капель и величине, зависящей от комплексного показателя преломления, 
Вода[править | править код]
Основная статья: Вода
Чистая вода прозрачна для света видимого, ультрафиолетового и инфракрасного диапазона спектра. В области длин волн от 0,2 мкм до 1,2 мкм и температур от −12 °C до 500 °C действительную часть показателя преломления воды можно получить из следующего эмпирического выражения:
-
(Ур. 5.1)

Показатель преломления воды (действительная и мнимая части) в зависимости от длины волны при 30 °C. Синие и голубые точки относятся к показателю преломления (ось слева), а красные и зелёные — к коэффициенту поглощения (ось справа)[98]
где безразмерные переменные параметры для температуры, плотности и длины волны заданы выражениями 













-
(Ур. 5.2)
где 
= 301,797 °C,
= 522 528,9 °C2,
= 69,34881 °C,
= 999,974 950 кг/м3[100].
В то же время коэффициент поглощения в воде для видимого спектра (в диапазоне от 300 нм до 700 нм) очень мал: в максимуме около 6⋅10−8, а в минимуме (418 нм) ещё на два порядка меньше[101].
Рефрактометрия растворов[править | править код]
На основе закона Снеллиуса строятся количественные методы рефрактометрии растворов. Среди растворителей наиболее часто используются вода с показателем преломления 1,3330, метанол — 1,3286, этанол — 1,3613, ацетон — 1,3591, хлороформ — 1,4456. Эти величины измерены на длине волны D-линии натрия (589,3 нм) при 20 °С и обозначаются 


-
(Ур. 5.3)
где 
Морская вода[править | править код]
Океанская вода представляет собой сложную смесь мутного раствора, солей и органических останков[104]. В диэлектрическую проницаемость дают вклад три источника, связанные с электронной, дипольно-релаксационной и ионной восприимчивостями. Магнитная проницаемость воды меньше единицы (диамагнетик)[105]. Солёность мирового океана зависит в основном от количества хлористого натрия[106]. Показатель преломления морской воды в видимой части спектра зависит в основном от трёх параметров: температуры, солёности и гидростатического давления. В простейшей модели для показателя преломления используют формулу Лоренца — Лоренца. Удельная рефракция уменьшается с ростом длины волны, солёности и температуры. При длине волны 480 нм, температуре 20 °C, атмосферном давлении и солёности 35 ‰ 

Оптическое стекло[править | править код]
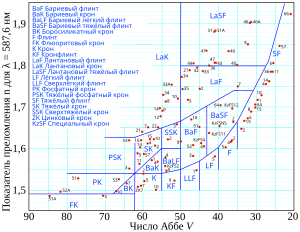
Зависимость показателя преломления от числа Аббе для ряда различных оптических стёкол (красные кружки). Стёкла классифицируются с использованием буквенно-цифрового кода, указывающего их состав и положение на диаграмме, низкодисперсные стёкла находятся в левой нижней части диаграммы. Данные взяты из каталога Schott Glass
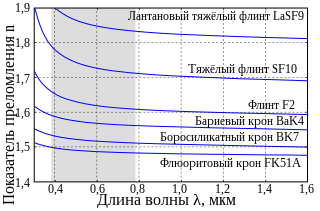
Изменение показателя преломления в зависимости от длины волны для различных стёкол. Заштрихованная зона указывает диапазон видимого света. Зависимости построены с использованием формулы Зельмейера для конкретного типа стекла
Широкое применение стёкол в оптике предполагает детальное знание показателя преломления конкретного типа материала. Наиболее свежие данные по свойствам различных стёкол можно найти в каталогах фирм-изготовителей, поскольку они составлены с использованием международных стандартов типа ISO 7944—84 (в России ГОСТ 23136—93 и ГОСТ 3514—94[109], в Германии DIN 58925 и DIN 58927)[110]. Главные характеристики стёкол показаны в коде стекла. Например, для N-SF6 код стекла несёт информацию о показателе преломлении nd, числе Аббе Vd и плотности ρ. Из кода 805254.337 следует, что nd = 1,805, Vd = 25,4 и ρ = 3,37 г/см3[7]. Индекс d обозначает длину волны жёлтой линии гелия при длине волны 587,5618 нм. Типы оптических стёкол можно разделить на группы, представленные на графике в координатах (nd, Vd). Часто используются и другие линии в зависимости от возможных применений. Например, индекс t используется для инфракрасной линии ртути (1013,98 нм), e — зелёной линии ртути (546,0740 нм), C — красной линии водорода (656,2725 нм), D — жёлтой линии натрия (589,2938 нм), i — ультрафиолетовой линии ртути (365,0146 нм), и так далее[7]. Типичными требованиями для оптических стёкол являются требования точности для показателя преломления ±2⋅10−5 и дисперсии ±1⋅10−5. В сертификатах указывают также температуру (22 °C) и давление (101,325 кПа). Высокие требования накладываются на однородность показателя преломления и коэффициент внутреннего пропускания. Стекло в высшей степени однородно, но допускает наличие дефектов макроструктуры, называемые свилями, пузырей и микровключений, если они не искажают фронт волны при учёте соотношения суммарной поперечной площади дефектов к объёму стекла. Для стандарта ISO3/IN010 площадь дефектов не превышает 0,03 мм2 в объёме 100 см3 и не более 10 включений[7]. Двойное лучепреломление — это нежелательное явление, которое также характеризуется по стандарту ISO 11455 методом Сенармона — Фриделя, который ограничивает разность хода 6 нм/см (на сантиметр толщины) для оптических стёкол. Для избавления от внутренних напряжений применяют отжиг стекла. Оптические стёкла также характеризуют климатической стойкостью, стойкостью к травлению, кислотостойкостью, щёлочестойкостью и стойкостью к фосфатам, поскольку все эти нежелательные внешние факторы приводят к дефектам и изменениям поверхности[7][111].
Для обозначения оптического стекла используют сокращения. Например для крона и флинта используют заглавные буквы: ЛК — лёгкий крон; ФК — фосфатный крон; ТФК — тяжёлый фосфатный крон; К — крон; БК — баритовый крон; ТК — тяжёлый крон; СТК — сверхтяжёлый крон; ОК — особый крон; КФ — крон-флинт; БФ — баритовый флинт; ТБФ — тяжёлый баритовый флинт; ЛФ — лёгкий флинт; Ф — флинт; ТФ — тяжёлый флинт; ОФ — особый флинт[112].
Нескалярная, нелинейная или неоднородная рефракция[править | править код]
До сих пор предполагалось, что преломление задаётся линейными уравнениями, включающими пространственно постоянный скалярный показатель преломления. Эти предположения могут нарушаться по-разному, что включает следующие возможности.
Анизотропия[править | править код]
Распространение света в кристалле зависит от направления оптических осей. Для кристаллов диэлектрическая проницаемость имеет вид тензора второго ранга, и при действии электрического поля световой волны смещение электрических зарядов в общем случае не совпадает с направлением электрического поля. Вектора электрической индукции D и электрического поля E не совпадают ни по направлению, ни по величине[113]. Есть, однако, возможность выбора прямоугольной системы координат, в которой оси координат направлены вдоль оптических осей. В этой системе координат записывается уравнение для характеристической поверхности, называемой эллипсоидом Френеля[114]
-
(Ур. 7.1)
Здесь индексы у коэффициента преломления отвечают за величину коэффициента преломления в определённом направлении в кристалле, то есть указывают на анизотропию скорости света. Если электрическое поле E направлено по одной из оптических осей, то индукция D имеет то же направление. Скорости распространения света в этих направлениях равны
-
(Ур. 7.2)
Эллипсоид Френеля имеет смысл поверхности постоянной фазы для излучения точечного источника[115]. Существуют как минимум два круговых сечения для эллипсоида Френеля, перпендикулярные направления к которым называются оптическими осями кристалла. Для одноосного кристалла 
Двулучепреломление[править | править код]
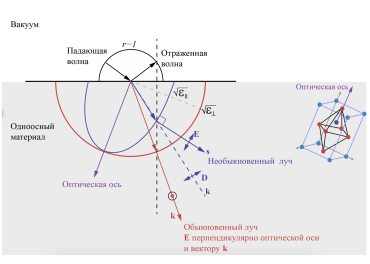
Иллюстрация нахождения направления распространения обыкновенной и необыкновенной волн в одноосном кристалле


Двулучепреломляющие материалы могут изменять цвет при помещении между скрещёнными поляризаторами. Это основа такого метода исследований как фотоупругость
В материалах, где показатель преломления зависит от поляризации и направления в кристалле, наблюдается явление двойного лучепреломления, которое также называют оптической анизотропией в общем случае[116].
В простейшем случае, одноосном двулучепреломлении, материал имеет только одно особое направление — оптическую ось материала[117]. Распространение света с линейной поляризацией, перпендикулярной этой оси, описывается с помощью показателя преломления для обыкновенной волны 



Многие кристаллы обладают естественным двойным лучепреломлением, но изотропные материалы, такие как пластмассы и стекло, также могут часто обладать двойным лучепреломлением вследствие возникновения предпочтительного направления, например, при действии внешней силы или электрического поля. Этот эффект называется фотоупругостью и может использоваться для выявления напряжений в конструкциях. Для этого двулучепреломляющий материал помещается между скрещёнными поляризаторами. Напряжения в кристалле приводят к возникновению эффекта двойного лучепреломления и свет, проходящий через кристалл, изменяет поляризацию и, следовательно, долю света, которая проходит через второй поляризатор[121]. Разность между показателями преломления для обыкновенной и необыкновенной волн пропорциональна давлению P
-
(Ур. 7.3)
где 
Некоторые данные для широко используемых одноосных кристаллов приведены в таблице[123].
| Кристалл | Химическая формула | Сингония | Знак  |
 |

|
|---|---|---|---|---|---|
| Лёд | H2O | Тригональная | + | 1,309 | 1,313 |
| Кварц | SiO2 | Тригональная | + | 1,544 | 1,553 |
| Берилл | Be3Al2(SiO3)6 | Гексагональная | – | 1,581 | 1,575 |
| Нитрат натрия | NaNO3 | Тригональная | – | 1,584 | 1,336 |
| Кальцит | CaCO3 | Тригональная | – | 1,658 | 1,486 |
| Турмалин | Сложный силикат | Тригональная | – | 1,669 | 1,638 |
| Сапфир | Al2O3 | Тригональная | – | 1,768 | 1,760 |
| Циркон | ZrSiO4 | Тетрагональная | + | 1,923 | 1,968 |
| Рутил | TiO2 | Тетрагональная | + | 2,616 | 2,903 |
Более общий случай трипреломляющих материалов описывается кристаллооптикой, а диэлектрическая проницаемость является тензором второго ранга (матрица 3 на 3). В этом случае распространение света невозможно просто описать показателями преломления, за исключением поляризаций вдоль главных осей. Кристаллы с орторомбической, моноклинной и триклинной сингонией принадлежат к этому классу материалов. Слюды являются типичными представителями трипреломляющих кристаллов[124].
Эффект Керра[править | править код]
Двулучепреломление возникает при приложении постоянного или переменного электрического поля к изотропной среде. Впервые этот эффект наблюдался Керром (в 1875 году) для диэлектрических жидкостей, но встречается в твёрдых телах и в гораздо более простых системах: он наблюдался в газах в 1930 году[125], что позволило объяснить происхождение эффекта[126]. При приложении сильного электрического поля к жидкости она становится аналогом одноосного кристалла с оптической осью, совпадающей с направлением электрического поля[125]. Разность между показателями преломления для необыкновенной и обыкновенной волн не зависит от ориентации электрического поля 
-
(Ур. 7.4)
где 



Эффект Коттона — Мутона[править | править код]
По аналогии с эффектом Керра можно наблюдать двулучепреломление в изотропных средах в сильном магнитном поле[129]. При распространении света перпендикулярно этому полю разность показателей преломления оказывается пропорциональной квадрату напряжённости магнитного поля H:
-
(Ур. 7.5)
где 



Неоднородность[править | править код]
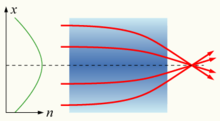
Линза с градиентным показателем преломления, который по параболическому закону зависит от радиального расстояния (
x). Объектив фокусирует свет так же, как и обычный объектив
Если показатель преломления среды не постоянен, а постепенно изменяется в пространстве, такой материал известен как среда с градиентным показателем, или GRIN-среда, и рассматривается в градиентной оптике[130]. Свет, проходящий через такую среду, преломляется или фокусируется, что можно использовать для создания линз, оптических волокон и других устройств. Внедрение GRIN-элементов в конструкцию оптической системы может значительно упростить систему, уменьшив количество элементов на треть при сохранении общей производительности[131]. Хрусталик человеческого глаза является примером GRIN-линзы с показателем преломления, изменяющимся от примерно 1,406 во внутреннем ядре до примерно 1,386 в менее плотной коре[132].
Вариации показателя преломления[править | править код]

Изображение дрожжевых клеток при дифференциальной интерференционной контрастной микроскопии
Неокрашенные биологические структуры в основном кажутся прозрачными при микроскопии в светлом поле[en], поскольку большинство клеточных структур не приводят к заметному ослаблению света[133]. Тем не менее изменение материалов, из которых состоят эти структуры, также сопровождается изменением показателя преломления. Следующие методы преобразуют такие вариации в измеримые разности амплитуд: фазово-контрастная микроскопия[134], фазово-контрастная рентгеновская визуализация, количественная фазово-контрастная микроскопия[135].
Для измерения пространственного изменения показателя преломления в образце используются методы фазово-контрастной визуализации. Эти методы позволяют детектировать изменения фазы световой волны, выходящей из образца. Фаза пропорциональна оптической длине пути, пройденной световым лучом, и, таким образом, даёт меру интеграла от показателя преломления вдоль пути луча[136]. Фазу нельзя измерить непосредственно на оптических или более высоких частотах, поэтому её необходимо преобразовать в интенсивность путём интерференции с опорным лучом. В видимом диапазоне спектра это делается с помощью фазово-контрастной микроскопии Цернике, дифференциальной интерференционно-контрастной микроскопии (ДИК) или интерферометрии[137].
Фазово-контрастная микроскопия Цернике добавляет фазовый сдвиг в низкочастотные пространственные компоненты изображения с помощью фазовращательного кольца в плоскости Фурье[en] образца, так что высокочастотные части пространственного изображения могут интерферировать с низкочастотными компонентами опорного луча[138]. В ДИК освещение разделяется на два луча, которые имеют разную поляризацию, по-разному сдвинуты по фазе и смещены в поперечном направлении относительно друг друга. После прохождения образца два пучка интерферируют, давая изображение производной оптической длины пути по разнице поперечного смещения[134]. В интерферометрии освещение разделяется на два луча частично отражающим зеркалом[en]. Один из лучей пропускается через образец, а затем они объединяются для интерференции и создания прямого изображения фазовых сдвигов. Если вариации оптической длины пути превышают длину волны, изображение будет содержать полосы[139][140][141].
Существует несколько методов фазово-контрастной рентгеновской визуализации[en] для определения двумерного или трёхмерного пространственного распределения показателя преломления образцов в рентгеновском спектре[142].
Эйконал[править | править код]
Электромагнитные волны являются решениями уравнений Максвелла, из которых можно получить волновое уравнение. Для пространства, заполненного веществом с неоднородным показателем преломления, решение во всём пространстве в виде плоских волн больше не существует, но, используя приближение геометрической оптики (коротковолновое приближение), можно получить приближённое решение уравнений Максвелла. Пусть электрическое поле представлено в виде плоской волны в малой области пространства как
-
(Ур. 7.6)
где E0(r) — медленно меняющаяся функция радиус-вектора r, S(r) — неизвестная функция координат[143]. Подставляя в уравнения Максвелла это выражение при условии, что волновое число k0 стремится к бесконечности, можно найти уравнение для неизвестной функции
-
(Ур. 7.7)
где 
-
(Ур. 7.8)
где Γ — траектория луча, v — фазовая скорость луча, L — оптическая длина пути[145].
Нелинейная оптика[править | править код]
Известно, что показатель преломления может изменяться в электрическом поле — это эффект Керра в жидкостях и газах или эффект Поккельса в кристаллах. Поскольку сама электромагнитная волна также несёт переменное электрическое поле, возникает зависимость показателя преломления от интенсивности света. Зависимость имеет вид 


Зависимость показателя преломления от напряжённости переменного электрического поля часто называют оптическим эффектом Керра по аналогии с электрооптическим эффектом Керра, где изменение показателя пропорционально напряжённости электростатического поля, приложенного к среде. Можно найти выражение для нелинейного показателя преломления, исходя из поляризуемости материала и соотношения 


-
(Ур. 7.9)
где 






-
(Ур. 7.10)
Для линейной части показателя преломления можно записать 

-
(Ур. 7.11)
так что[149]
-
.
(Ур. 7.12)
Явления, возникающие вследствие зависимости показателя преломления от интенсивности света, включают такие эффекты, как самофокусировка[150], фазовая самомодуляция[151], обращение волнового фронта[152] и генерация оптических солитонов[151]. Однако эти очень сложные проблемы нелинейной оптики возникают лишь в определённых условиях — при воздействии света очень высокой интенсивности и в средах, обладающих достаточно высокими коэффициентами нелинейности[153].
Особые случаи[править | править код]
Показатель преломления меньше единицы[править | править код]
Фазовая скорость света в веществе может быть больше скорости света в вакууме. Это не противоречит специальной теории относительности, так как передача энергии и информации связаны с групповой скоростью, не превышающей скорости света в вакууме. В таких случаях показатель преломления может быть меньше единицы. В оптическом диапазоне показатель преломления практически всегда больше единицы, однако в ультрафиолетовом и особенно в рентгеновском диапазонах показатели преломления меньше единицы являются типичными[154].
Высокая фазовая скорость рентгеновского излучения в веществе обусловлена взаимодействием электромагнитных волн с электронными оболочками атомов — в мягком рентгеновском диапазоне лежит много линий поглощения (K-серии). Показатель преломления для этого диапазона частот очень близок к единице и обычно записывается в виде 

Показатель преломления меньше единицы приводит к особым эффектам, например, вогнутые линзы для такого излучения работают как выпуклые и наоборот. Поскольку в данном случае вакуум является оптически более плотной средой, чем вещество, то при падении на вещество под малым углом рентгеновское излучение может испытывать полное внутреннее отражение[156]. Этот эффект используют в рентгеновских телескопах[157].
Комплексный показатель преломления[править | править код]
В отличие от идеальных сред, при прохождении электромагнитных волн через реальные среды необходимо учитывать их затухание. Это удобно сделать, вводя комплексный показатель преломления[56]:
-
(Ур. 8.1)
Здесь действительная часть 


То, что 





-
(Ур. 8.2)
экспонента распадётся на две, одна из которых имеет вещественное отрицательное значение показателя степени[159]. Таким образом, интенсивность света в веществе экспоненциально затухает с толщиной. Здесь 









Альтернативное соглашение использует нотацию 


![{displaystyle {rm {{Re}[exp(-iomega t)]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/556b7bae296d308b1b86c0f5e004beca7b08457e)
![{displaystyle {rm {{Re}[exp(+iomega t)]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2b37f0bcd1ebd521057a8705b8d3831a9822289)
Диэлектрические потери[en] и отличная от нуля проводимость по постоянному или переменному току в материалах вызывают поглощение[162]. Хорошие диэлектрические материалы, такие как стекло, имеют чрезвычайно низкую проводимость по постоянному току, а на низких частотах диэлектрические потери также незначительны, что приводит к почти полному отсутствию поглощения. Однако на более высоких частотах (например, в видимой области спектра) диэлектрические потери могут значительно увеличить поглощение, снижая прозрачность материала в области этих частот[163].
Действительная 



Для рентгеновского и экстремального ультрафиолетового[en] излучения комплексный показатель преломления незначительно отличается от единицы и обычно имеет действительную часть меньше единицы. Поэтому его записывают в виде 


-
(Ур. 8.3)
где 




-
(Ур. 8.4)
Следовательно, ур. 8.3 примет вид[2]
-
(Ур. 8.5)
-
(Ур. 8.6)
Величины 

Комплексные показатели преломления применяются:
- для описания взаимодействия света с непрозрачными веществами, такими как металлы (в этом случае показатель поглощения больше единицы, так что волна полностью поглощается на расстоянии в несколько микрометров)[166];
- для описания прохождения электромагнитной волны через среду, если её частота близка к частотам поглощения атомов этой среды (зоны аномальной дисперсии)[167];
- для описания преломления полярными жидкостями (например, водой), особенно в случае низкочастотного излучения[168];
- в других случаях, когда слой вещества достаточно толстый, чтобы необходимо было учитывать поглощение[32].
Металлы[править | править код]
| Металл |  |
 |

|
|---|---|---|---|
| Натрий | 2,61 | 0,05 | 99,8 |
| Серебро | 3,64 | 0,18 | 95,0 |
| Магний | 4,42 | 0,37 | 92,9 |
| Золото | 2,82 | 0,37 | 85,1 |
| Золото электролитическое | 2,83 | 0,47 | 81,5 |
| Ртуть | 4,41 | 1,62 | 73,3 |
| Медь цельная | 2,62 | 0,64 | 70,1 |
| Никель цельный | 3,32 | 1,79 | 62,0 |
| Никель электролитический | 3,48 | 2,01 | 62,1 |
| Никель распылённый | 1,97 | 1,30 | 43,3 |
| Железо распылённое | 1,63 | 1,51 | 32,6 |
Для диэлектрической проницаемости в модели Лоренца можно записать
-
(Ур. 8.7)
где 


-
(Ур. 8.8)
где 


-
(Ур. 8.9)
откуда можно определить мнимую часть комплексного показателя преломления. Некоторые значения показателя преломления для металлов представлены в таблице[169]. В пределе больших частот, когда 



Отрицательный показатель преломления[править | править код]

Уравнения Максвелла имеют физические решения для сред с отрицательным коэффициентом преломления, когда диэлектрическая и магнитная проницаемости имеют одновременно отрицательные значения. В этом случае закон Снеллиуса также выполним, но угол преломления становится отрицательным[172]. Материалы, которые демонстрируют отрицательную рефракцию, можно создать искусственно с помощью обычных материалов с положительным коэффициентом преломления, но определённым образом изменённой геометрией поверхности или объёма среды, например, в периодических фотонных кристаллах. Такие материалы называются метаматериалами и демонстрируют необычные свойства в том или ином диапазоне частот. Возникающая в результате изменения среды отрицательная рефракция в метаматериалах даёт возможность реализации новых явлений и применений (таких как суперлинзы). Основные физические принципы использования отрицательного коэффициента преломления появились в трёх работах:
- отрицательный показатель преломления среды Веселаго;
- суперлинза Пендри;
- неотражающие кристаллы Ефимова[173][174][175].
Метаматериалы с отрицательным показателем преломления обладают рядом интересных свойств:
- фазовая и групповая скорости волн имеют противоположные направления;
- возможно преодоление дифракционного предела при создании оптических систем («суперлинз»), повышение с их помощью разрешающей способности микроскопов, создание микросхем с наноразмерными структурами, повышение плотности записи на оптические носители информации[176][177][178].
Примеры[править | править код]
Показатели преломления nD (жёлтый дублет натрия, λD = 589,3 нм) некоторых сред приведены в таблице.
Показатели преломления для длины волны 589,3 нм
| Тип среды | Среда | Температура, °С | Значение |
|---|---|---|---|
| Кристаллы[67] | LiF | 20 | 1,3920 |
| NaCl | 20 | 1,5442 | |
| KCl | 20 | 1,4870 | |
| KBr | 20 | 1,5552 | |
| Оптические стёкла[179] | ЛК3 (Лёгкий крон) | 20 | 1,4874 |
| К8 (Крон) | 20 | 1,5163 | |
| ТК4 (Тяжёлый крон) | 20 | 1,6111 | |
| СТК9 (Сверхтяжёлый крон) | 20 | 1,7424 | |
| Ф1 (Флинт) | 20 | 1,6128 | |
| ТФ10 (Тяжёлый флинт) | 20 | 1,8060 | |
| СТФ3 (Сверхтяжёлый флинт) | 20 | 2,1862[180] | |
| Драгоценные камни[67] | Алмаз белый | – | 2,417 |
| Берилл | – | 1,571—1,599 | |
| Изумруд | – | 1,588—1,595 | |
| Сапфир белый | – | 1,768—1,771 | |
| Сапфир зелёный | – | 1,770—1,779 | |
| Жидкости[67] | Вода дистиллированная | 20 | 1,3330 |
| Бензол | 20—25 | 1,5014 | |
| Глицерин | 20—25 | 1,4730 | |
| Кислота серная | 20—25 | 1,4290 | |
| Кислота соляная | 20—25 | 1,2540 | |
| Масло анисовое | 20—25 | 1,560 | |
| Масло подсолнечное | 20—25 | 1,470 | |
| Масло оливковое | 20—25 | 1,467 | |
| Спирт этиловый | 20—25 | 1,3612 |
Полупроводники[править | править код]
| Кристалл | Окно прозрачности, мкм |  мкм мкм |

|
|---|---|---|---|
| Германий | 1,8—23 | 1,8 | 4,00 |
| Кремний | 1,2—15 | 1,1 | 3,42 |
| Арсенид галлия | 1,0—20 | 0,87 | 3,16 |
| Теллурид кадмия | 0,9—14 | 0,83 | 2,67 |
| Селенид кадмия | 0,75—24 | 0,71 | 2,50 |
| Селенид цинка | 0,45—20 | 0,44 | 2,41 |
| Сульфид цинка | 0,4—14 | 0,33 | 2,20 |
Оптические свойства полупроводников близки к свойствам диэлектриков[182]. Область длин волн, в которой наблюдается слабое поглощение, называется окном прозрачности; в этой области показатель преломления вещественен. Со стороны длинных волн окно прозрачности ограничено колебательным спектром поглощения в инфракрасной области спектра для полярных молекул[183], а также поглощением на свободных носителях для более узкозонных полупроводников при комнатной температуре[181]. Когда энергия фотонов достигает ширины запрещённой зоны, наблюдается другая граница окна прозрачности (край полосы поглощения), связанная с межзонными переходами[182]. В таблице приведены данные для окон прозрачности, длины волны 

Плазма[править | править код]
Плазма обладает коэффициентом преломления, который зависит от концентрации свободных электронов, причём квадрат индекса может оказаться меньше единицы:
-
(Ур. 10.1)
где 



Земля обладает магнитным полем, поэтому плазма ионосферы находится в однородном магнитном поле, что меняет её свойства. Траектории электронов плазмы в магнитном поле искривляются силой Лоренца, что приводит к изменению дисперсии волн в плазме. Для коэффициента преломления появляется выражение, зависящее от ларморовской частоты 
-
(Ур. 10.2)
где 
Другие волновые явления[править | править код]
Понятие показателя преломления применяется во всём электромагнитном спектре, от рентгеновских лучей до радиоволн. Его также можно применить к волновым явлениям, таким как звук. В этом случае вместо скорости света используется скорость звука, и необходимо выбрать среду сравнения, отличную от вакуума[189]. Для преломления звука на границе двух изотропных сред также выполняется закон Снеллиуса[190]
-
(Ур. 11.1)
где углы θ1 и θ2 соответствуют углам падения и преломления, а волновые вектора k1 и k2 относятся к падающей и преломлённой волнам. Это выражение получается из рассмотрения распространения плоских волн, падающих на плоскую границу раздела изотропных сред, где выполняются граничные условия: непрерывность давления и непрерывность нормальной компоненты скорости частиц среды. Соответствующий коэффициент преломления выражается в виде n = k2/k1[191].
Приближение геометрической оптики[править | править код]
Уравнение эйконала возникает в электродинамике при рассмотрении приближения геометрической оптики, когда свойства среды меняются медленно на расстояниях, сравнимых с длиной волны. Это приближение применяется в электродинамике, акустике, гидродинамике, квантовой механике и других науках[192]. Уравнение Гельмгольца для звука описывает амплитуду потенциала скоростей среды
-
(Ур. 11.2)
верно для неоднородной среды
-
(Ур. 11.3)
где k = ω/c0, показатель преломления n(r) = c0/c(r), c0 — характерная скорость звука, c(r) — скорость звука в точке r среды[193]. Для нерелятивистского уравнения Шрёдингера для искомой волновой функции также можно получить аналогичное уравнение
-
(Ур. 11.4)
где 

-
(Ур. 11.5)
где ψ(r) называется эйконалом, и подставить в уравнение Гельмгольца, то можно написать два уравнения для новых неизвестных величин[195]
-
(Ур. 11.6)
-
(Ур. 11.7)
Решение этих уравнений в квантовой механике эквивалентно использованию приближения ВКБ[196]. Эйконал описывает поверхность постоянной фазы в пространстве. Его градиент 
-
(Ур. 11.8)
где θ = 0° — угол луча по отношению к поверхности. В этом случае рефракция увеличивает расстояние прямой видимости, а при достаточно большом градиенте, когда радиус кривизны меньше радиуса Земли, возникает сверхрефракция[en], что увеличивает дальность радиосвязи[199]. Для звука эффект рефракции тоже наблюдается. Если коэффициент преломления звука с высотой уменьшается (из-за уменьшения температуры), то звуковые лучи отклоняются вверх в соответствии с законом Снеллиуса. В противном случае (холодный воздух у поверхности) при безветренной погоде вечером над поверхностью воды звуковой луч отклоняется вниз, что увеличивает расстояние слышимости[200].
Оптика для частиц[править | править код]
Другие частицы, как и свет, демонстрируют схожие свойства траекторий при движении в силовых полях. Наиболее тесная связь между ними раскрывается в соответствии между принципом Ферма для фотонов и принципом наименьшего действия для движения частиц[201]. Если использовать естественную параметризацию траектории частицы, то есть перейти к переменной длины её дуги (ds = vdt), то действие для свободной частицы при движении из точки A в точку B запишется в виде
-
(Ур. 11.9)
где v — скорость частицы, m — её масса[202]. Выражение для интеграла в принципе Ферма отличается наличием показателя преломления вместо скорости (ур. 7.8). Такая формальная аналогия нашла применение при рассмотрении движения заряженных частиц в неоднородных электрических и магнитных полях и получила название электронной оптики[202]. Более прозрачной аналогия становится при рассмотрении перехода электрона из области с одним потенциалом в область в другим потенциалом. Это естественным образом изменяет кинетическую энергию и скорость электрона, что аналогично изменению фазовой скорости света при переходе в среду с другим показателем преломления. Если потенциал принимает разные значения в двух полупространствах с плоской границей, то можно рассмотреть задачу о падении частицы на границу. Тангенциальная скорость электрона останется неизменной, а нормальная к границе — поменяется, что приведёт к возникновению преломлению
-
(Ур. 11.10)
где i и r — углы падения (отсчитанный от нормали) и преломления, v1 и v2 — начальная и конечная скорости электрона[203]. Для закона Снеллиуса (ур. 1.1) скорости входят в обратном соотношении. Здесь можно ввести коэффициент преломления, полученный из закона сохранения энергии в виде
-
(Ур. 11.11)
где φ1 и φ2 — потенциал в первой и второй областях полупространства, T — начальная кинетическая энергия, e — заряд электрона[203]. Неоднородное электрическое поле формирует эффект линзы для электронов, что применяется в электронных микроскопах[204].
Для других заряженных частиц формальная аналогия также работает. Релятивистское движение ионов и электронов в электромагнитном поле также подчиняется принципу наименьшего действия, а коэффициент преломления зависит от направления движения. Электронная и ионная оптика нашли применение в создании микроскопов, установок для ионного травления, фокусирующих систем для ускорителей заряженных частиц[205].
Для достаточно чистых материалов электроны в твёрдом теле ведут себя как баллистические[en], поэтому эффекты электронной отпики могут проявляться и в высокоподвижном электронном газе. В частности, для электронов в графене наблюдается аналог преломления с отрицательным показателем преломления на границе p—n-перехода, который демонстрирует свойства линзы Веселаго[206].
Аналогия Гамильтона между движение частиц в неоднородных полях и света в среде с неоднородным индексом послужила основанием для возникновения геометрической оптики для холодных нейтронов, которую рассмотрел Ферми в 1944 году, когда обнаружил, что из-за взаимодействия нейтронов с ядрами вещества можно рассмотреть нейтронную волну, распространяющуюся в среде с соответственным показателем преломления, близким в единице[207].
Измерение[править | править код]
Рефрактометрия[править | править код]


Принципиальная схема рефрактометра

Для измерения показателя преломления можно использовать несколько оптических метрологических приборов[fr]. Эти инструменты включают, среди прочего, рефрактометры, которые представляют собой тип интерферометра с оптическими путями, проходящими в разных средах, один — в вакууме, а другой — в измеряемом материале; гониометры для измерения углов, определённые призмы и так далее. Использование этих методов актуально для исследования прозрачных материалов. Точность измерений рефрактометров варьируется от 10−3 % для обычных до 10−6 % для интерферометрических типов приборов. Для анализа необходимо 0,05 — 0,5 г вещества, для высокоточных измерений можно снизить массу до долей миллиграмма. Время измерения зависит от типа рефрактометра и может занимать от секунды до десятков минут[208].
Показатель преломления можно измерить с помощью V-призмы, когда образец прозрачного материала помещается в V-образную выемку стеклянного блока, индекс которого точно известен. Отклонение светового луча позволяет определить показатель преломления образца[209].
Гониометр позволяет измерять показатель преломления прозрачного материала по нескольким спектральным линиям. Призма из этого материала используется для измерения минимального угла отклонения на нескольких длинах волн[209].
Недостатком интерферометрических методов является то, что их трудно использовать на объектах сложных форм и они могут оказаться разрушающими, поскольку необходимо измерять образец с чётко определённой геометрией, что исключает, например, такие образцы как художественная стеклянная посуда. В этих случаях используются измерения углов преломления, угла Брюстера или поиск жидкости с эквивалентным показателем преломления, но эти подходы обычно не позволяют достичь такой же высокой точности, как измерения с помощью гониометра или интерферометра[210].
Самым распространённым методом измерения показателя преломления является измерение угла полного внутреннего отражения. Преимуществами этого метода является малое количество вещества, необходимое для исследования, а также их компактность — например, в рефрактометре Аббе жидкость заливается в тонкую щель между гипотенузными гранями двух прямоугольных призм, имеющих высокий показатель преломления[211]. Этот метод позволяет достичь точности ±0,0002[212][213]. По схожему принципу работает рефрактометр Пульфриха, но в нём, наоборот, свет направляется параллельно границе раздела двух сред и измеряется угол, на который он отклонился[214].
Поскольку квантовая механика предсказывает, что частицы могут вести себя как волны, также возможно измерить показатель преломления волн материи. Такое измерение проводилось, в частности, на атомах лития и натрия с использованием интерферометрического метода[215].
Нелинейный показатель преломления можно измерить, наблюдая за фазовым сдвигом тестового светового луча путём перекрёстной фазовой модуляции[en], благодаря вращению эллиптической поляризации, анализу спектрального профиля волны или спектральному анализу при фазовой самомодуляции или возвращению к нелинейному показателю путём определения критической мощности самофокусировки. Также возможно измерение индекса с помощью спектральной интерферометрии суперконтинуумов[216].
Для мелких твёрдых частиц используют иммерсионный метод — частицы погружают в ряд жидкостей с известными показателями преломления и наблюдают за образующейся интерференционной картиной. Таким образом находится пара жидкостей, одна из которых будет иметь меньший показатель преломления, чем исследуемое вещество, а вторая — больший[217].
Рефлектометрия с низкой оптической когерентностью — распространённый интерферометрический метод для определения пространственного распределения показателя преломления по измерению амплитуды и фазового сдвига отражённого сигнала от различных неоднородностей. Низкая когерентность позволяет наблюдать интерференцию только из малой области образца порядка длины когерентности. Групповой индекс определяет задержку сигнала, в результате чего вычисляется расстояние до места отражения. Метод применяется в биологии и медицине[218]. Другой областью применения этого метода является дефектоскопия оптических волокон[219].
Эллипсометрия[править | править код]

Схема эллипсометрической установки
Показатели преломления и поглощения n и κ не могут быть измерены напрямую для тонких плёнок. Они должны определяться косвенно из измеряемых величин, которые зависят от них. Например, таких как отражательная способность, R, коэффициент пропускания, T, или эллипсометрические параметры, ψ и δ. Схема эллипсометра представлена на рисунке справа. Свет от источника проходит через монохроматический фильтр и коллиматор и поляризуется призмой, то есть падающий свет представляет собой линейно поляризованную волну, которую можно разделить на две поляризации относительно плоскости падения: s– (перпендикулярная плоскости падения и параллельная плоскости образца) и p-компоненты (лежащая в плоскости падения). После отражения от поверхности свет проходит через анализатор и регистрируется детектором. Компенсатор служит для изменения фазового сдвига между s– и p-компонентами. Изменяя ориентацию анализатора, можно получить информацию о коэффициенте отражения s- и p- волн[220]. Относительная разность фаз между s– и p-компонентами равна
-
(Ур. 12.1)
где δs и δp — фазовые постоянные для падающего света, соответствующие s– и p-компонентам, а штриховые величины относятся к отражённой волне[221]. Относительное изменение амплитуд описывается формулой
-
(Ур. 12.2)
где Es и Ep — амплитуды для падающего света, соответствующие s– и p-компонентам, а штриховые величины относятся к отражённой волне. Основное уравнение эллипсометрии запишется в виде
-
(Ур. 12.3)
где Rs и Rp — коэффициенты отражения, соответствующие s– и p-компонентам волны. Эти параметры устанавливаются из модели для отражающей поверхности с использованием формул Френеля[221]. Подгоняя теоретическую модель к измеренным значениям ψ и Δ, можно получить значения n и κ[222].
Применение[править | править код]

Показатель преломления — важнейший параметр элементов оптической системы. От него зависит устройство и функционирование оптических и оптоэлектронных приборов. Изучение оптических констант полупроводников даёт информацию о строении их зонной структуры[223]. Для оптических систем важна прозрачность и минимальные потери света, поэтому для этих целей используют бесцветное оптическое стекло. Для ультрафиолетовой и инфракрасной областей спектра используют кварцевое оптическое стекло, которое также обладает низким температурным коэффициентом расширения; также используют кристаллы фтористого лития и флюорита. Цветные стёкла применяют для производства светофильтров[224].
Различные типы призм с двулучепреломлением используются для контроля поляризации и направления лучей света в оптике. Призма Глана — Фуко преобразует неполяризованный свет в линейно поляризованный[225]. В оптических экспериментах используются волновые пластинки для изменения фазы между обыкновенным и необыкновенным лучами благодаря разнице в показателях преломления 
Коэффициент отражения материала определяется показателем преломления, но покрытие оптических элементов материалами с другими индексами допускает модификацию отражения света с использованием интерференции при многократном отражении от границ раздела, что используется в просветляющих покрытиях для оптических стёкол. Кроме того, многослойные покрытия используются для цветоделительных покрытий, интерференционных фильтров и так далее. Однослойное просветляющее покрытие помогает уменьшить отражение в пять раз в видимой области спектра[226]. В общем случае, чем большее число слоёв используется, тем для более широкой области частот можно добиться просветления, но практически применяют не более трёх слоёв[227]. Полупроводники обладают сильным отражением от границы раздела в воздухе, в результате чего теряется от 60 % до 70 % падающего на солнечную панель излучения. Для сохранения этой энергии используется просветляющее покрытие из менее оптически плотного материала (в основном оксидов титана или кремния, нитрида кремния)[228].
В офтальмологии отклонение показателя преломления от стандарта в хрусталике или стекловидном теле сказывается на зрении человека, в результате проводится рефрактометрия оптической системы глаза для выявления дефектов и способов лечения[229].
Количественная фазово-контрастная микроскопия[en] даёт возможность измерять трёхмерное распределение индекса в неоднородных жидкостях, таких как кровь, что позволяет использовать её для наблюдения за живыми клетками и тканями и определять, например, концентрацию гемоглобина в крови, зная распределение показателя преломления. Некоторые клетки рептилий достаточно велики для этого метода исследований[230].
Поскольку показатель преломления является одним из основных физических свойств вещества, он используется для идентификации вещества, определения его чистоты и измерения его концентрации с помощью рефрактометров. Таким образом исследуются твёрдые тела (стёкла, кристаллы и драгоценные камни), газы и жидкости. Часто на основе показателя преломления проверяется концентрация веществ в жидких растворах. Для растворённого сахара в воде доступны калибровочные таблицы[231]. Помимо сахара рефрактометрия растворов на основе воды или других жидкостей используется для количественного определения концентрации растворённых веществ, таких как кислот, солей, этилового спирта, глицерина, для определения содержания белка в крови и других[211]. Для определения чистоты и подлинности веществ в фармакологии используют рефрактометры, откалиброванные для D-линии натрия (nD), имеющие точность измерения показателя преломления лучше чем ±2⋅10−4[232].
Существование угла полного внутреннего отражения позволяет использовать этот эффект для построения световых волноводов или оптоволокна, состоящих из сердцевины и оболочки с более низким показателем преломления, для волоконно-оптической связи. Чаще всего используют материалы с индексами 1,62 и 1,52. Стеклянное оптоволокно представляет собой нить с диаметром от 5 до 200 микрометров[233]. Возможно использовать многомодовые волокна с градиентным изменение профиля показателя преломления в зависимости от диаметра оптоволокна[234].
Оптоволокно оказалось полезным для использования в оптоволоконных лазерах. В 1990-е годы был создан четырёхваттный Er:YAG лазер[235], а после 2000 года иттербиевые лазеры показали значительный рост мощности[236].
При добавлении серебра в оптическое стекло его свойства могут изменяться при облучении ультрафиолетом — происходит затемнение, которое может исчезать после прекращения облучения. Этот эффект используется при производстве стёкол для очков с затемняемыми стёклами[237]. Очки-хамелеоны просветляются в помещениях[238].

Иллюстрация направлений фазового синхронизма в одноосном кристалле
Процесс записи информации об амплитуде, фазе и направлении светового когерентного поля, называемый голографией, формирует на фотопластине дифракционную решётку, представляющею собой трёхмерную среду с модулированным комплексным показателем преломления. Голография используется в основном для получения трёхмерных изображений[239].
Помещая объектив микроскопа в среду с более высоким показателем преломления (масло), возможно увеличить числовую апертуру, что позволяет повысить разрешение микроскопа[240]. Это подход используется также в иммерсионной литографии[241].
Кристаллы, в которых наблюдается двулучепреломление, могут быть использованы для генерации второй гармоники, так как при некоторой ориентации распространения волны коэффициенты преломления для обыкновенного и необыкновенного лучей совпадают, что позволяет синхронизировать фазы первой и второй гармоники для максимального коэффициента преобразования. Это явление наблюдается в сегнетоэлектриках и называется естественным синхронизмом[242].
В искусстве[править | править код]
Американский художник Стефен Кнапп[en] работал в стиле светографики с использованием цветного стекла и призм, создавая призматические инсталляции на протяжении своей карьеры[243]. Известным изображением дисперсии в искусстве является обложка альбома The Dark Side of the Moon британской рок-группы Pink Floyd[244].
Трассировка лучей в 3D-графике при прохождении ими прозрачных сред и отражении от зеркальных поверхностей является важным примером использования показателя преломления, учёт которого необходим для достижения фотореализма[245][246][247].
При наличии одного слоя краски на картине существует возможность проявления его при написании новой картины поверх старой — этот эффект называется пентиме́нто[en]. При покрытии лаком поверхности картины он может нежелательно изменить цвет полотна со временем. Различные цвета природных и химических красителей (пигментов) могут быть прозрачными и непрозрачными, они имеют различающиеся индексы и влияют на цветопередачу при нанесении покрытия в несколько слоёв. Белые пигменты, такие как оксид титана и оксид цинка, имеют показатель преломления более 2 и способны хорошо отражать свет. Высокие показатели преломления и поглощения приводят к хорошей укрывистости краски. Чёрные краски поглощают больше света, поэтому превосходно скрывают более глубокие слои, а цветные пигменты более светлых тонов пропускают больше света, поэтому возможно появление отражения от более глубокого слоя и изменение цвета поверхностного слоя краски. Показатель преломления льняного масла меняется со временем с 1,479 до более чем 1,525 примерно за десять лет, поэтому такая краска может терять укрывистость. Эффект pentimento можно наблюдать на картинах старых мастеров, например, на картине Питера Пауля Рубенса «Чудеса святого Франциска из Паолы»[248].
Прозрачные художественные масляные краски состоят из пигмента и связующей основы. Они обладают схожими покателями преломления в диапазоне от 1,4 до 1,65. Такие краски при прохождении в них света окрашивают его благодаря поглощению пигментами и отражаются от хорошо отражающего грунта (нижнего слоя) полотна. Тип освещения также влияет на цвета красок[249].
История[править | править код]
Первым из европейцев, кто изучал преломление света, был Архимед. Исследуя преломление на границе воды с воздухом, он правильно описал несколько законов преломления и зрения (например, то, что падающий, преломлённый лучи и нормаль к поверхности в точке падения лежат в одной плоскости, а люди воспринимают изображение так, будто лучи света всегда распространяются прямолинейно). Также он установил, что угол преломления всегда меньше угла падения (когда луч падает из воздуха в воду)[250]. Атмосферную рефракцию описал Гиппарх, наблюдавший лунное затмение, при котором Солнце также находилось над горизонтом[250].
Через 100 лет после Архимеда вопрос рефракции изучал другой выдающийся античный учёный Птолемей. Его модель рефракции включала сферическую атмосферу постоянной плотности и конечной толщины. Он также измерял углы преломления при переходе света между воздухом и водой, воздухом и стеклом, водой и стеклом, пытаясь найти зависимость между ними, однако считал, что такая зависимость имеет вид квадратичной функции, поэтому выведенное им уравнение лишь приближённо описывало законы преломления[250]. Впрочем, это было первое математическое уравнение для этого явления. В формуле Птолемея присутствовал аналог показателя преломления — число, зависящее от свойств сред и определяющее зависимость угла падения от угла преломления. Птолемей связывал сильное преломление с разницей плотностей сред. Также он, анализируя видимое движение звёзд, сделал правильное предположение, что свет испытывает преломление при переходе в атмосферу из окружающего пространства, подобно преломлению при переходе из воздуха в воду, следовательно, показатель преломления воздуха отличается от такового для пустоты; однако он не смог описать это явление количественно[251].
Правильно сформулировать закон преломления впервые смог персидский учёный Ибн Сахл в 984 году. Этот закон не был востребован последующими арабскими учёными, а его работы не были известны в Европе, поэтому сейчас этот закон известен как закон Снеллиуса в честь Виллеброрда Снелла, который открыл его в 1621 году. Другим арабским учёным X—XI веков, чьи работы повлияли на европейскую оптическую науку, был Ибн аль-Хайсам, который так же, как и Ибн Сахл, занимался сферическими линзами, но также рассматривал модель атмосферы Птолемея для объяснения увеличения размера видимых небесных тел (иллюзия Луны), находящихся около горизонта. Он также смог оценить толщину атмосферы (86,3 км) по свету звёзд, скрывающихся за горизонтом[250]. Количественно измерить атмосферную рефракцию смог Тихо Браге в 1587 году[252].
В 1658 году Пьер Ферма сформулировал принцип наименьшего времени, который позволил связать преломление на границе сред со скоростью света в них[253].
В начале XVIII века показатели преломления многих веществ измерили Исаак Ньютон и Фрэнсис Хоксби[254]. Ньютон также заметил связь между плотностью среды и показателем преломления и смог сформулировать эмпирическое уравнение для связи между этими величинами (известное сейчас как правило Ньютона — Лапласа), согласно которому величина 
Развивая проведённые Ньютоном исследования дисперсии, в 1802 году Уильям Волластон и в 1814 году независимо от него Йозеф Фраунгофер создали спектроскоп и наблюдали тёмные линии в спектре Солнца и звёзд[257].

Томас Юнг ввёл термин «показатель преломления»
Томас Юнг предположительно был первым человеком, который ввёл и в 1807 году использовал название «показатель преломления» (англ. index of refraction)[258]. В то же время он записал это значение преломляющей силы в виде одного числа вместо традиционного отношения двух чисел. Использование отношения чисел имело тот недостаток, что его можно было представить разными способами. Так, Ньютон, называвший это отношение «пропорцией синусов падения и преломления», записывал его как отношение двух чисел, например «529 к 396» (или «почти 4 к 3» для воды). Хоксби, называвший эту величину «коэффициентом преломления», записывал его как отношение с фиксированным числителем, например «10000 к 7451,9» (для мочи)[259]. Хаттон[en] записал это как отношение с фиксированным знаменателем, например 1,3358 к 1 (вода)[260].
В 1807 году Юнг не использовал никакого символа для показателя преломления. В более поздние годы другие исследователи начали использовать различные символы: 


Волластон создал первые рефрактометр (1802) и гониометр (1809). В 1869 году Аббе создал модель рефрактометра (рефрактометр Аббе), схема которого является одной из самых популярных и в настоящее время[265]. Вероятно, около 1840 года Уильям Тальбот впервые наблюдал явление аномальной дисперсии, однако количественно проанализировал его Пьер Леру в 1862 году[266]. Максвелл использовал свои уравнения для выражения скорости света в среде через диэлектрическую и магнитную проницаемости, связанные с показателем преломления по формуле 
В период с 1869 по 1875 год датский физик Людвиг Лоренц сформулировал в нескольких работах теорию, которая связывала показатель преломления с микроскопическими свойствами веществ — электронной поляризуемостью. Такой же результат в 1878 году независимо получил голландский физик Хендрик Лоренц, который не был знаком с работами Людвига Лоренца, поскольку те были написаны на датском языке. Выведенное ими уравнение известно как формула Лоренца — Лоренца[255]. В 1875 году Джон Керр наблюдал двулучепреломление в изотропных веществах (жидкие диэлектрики), помещённых в электрическое поле, а годом позже обнаружил магнитооптический эффект в изотропной среде[125]. Оба эффекта являются примерами нелинейно-оптических явлений. В 1910 году Ланжевен построил теорию эффекта Керра[268].
Август Кундт измерил комплексный коэффициент преломления для металлов в 1888 году, а теорию отражения от поверхности металлов, основываясь на формулах Френеля, построил Пауль Друде годом позже[269].
В 1933 году Роберт Вуд открыл прозрачность щелочных металлов в ультрафиолетовой области частот[171]. Стекло может изменять показатель преломления при облучении ультрафиолетом, этот эффект был открыт и запатентован в 1937 году Дональдом Стуки[en][270].
В 1947 году Денеш Габор построил теорию получения информации о фазе волны с помощью фотографии, но не смог реализовать построение такого изображения из-за отсутствия когерентных источников излучения. После создания лазеров в 1964 году Эмметт Лейт и Юрис Упатниекс записали первую голограмму, изобразившую игрушечные поезд и птицу[271]. В СССР в 1962 году Юрий Денисюк предложил использовать голографию Габора и метод цветной фотографии Липпмана, где используется три монохроматических лазера основных цветов, чтобы получить цветную голограмму[272]. Габор получил Нобелевскую премию по физике в 1971 году[273].
В 1961 году Элиас Снитцер[de] и Уилл Хикс (англ. Will Hicks) продемонстрировали передачу лазерного излучения по оптоволокну[274]. В 1964 году Снитцер создал первый лазер, в качестве рабочей среды которого использовалось оптическое волокно, легированное неодимом[275]. Слабое затухание в оптических волокнах позволило использовать их как средство передачи сигналов на большие расстояния[276].
В 1967 году Виктор Веселаго высказал гипотезу о существовании материалов с отрицательным значением показателя преломления[172]. В 1999 году Джон Пендри предложил конструкции искусственных материалов, обладавших отрицательными эффективными значениями диэлектрической и магнитной проницаемостей[176][177].
В 2000 году Дэвид Смит[en] с коллегами, использовав комбинацию элементов конструкций Пендри и его рекомендации, экспериментально доказал возможность реализации искусственных материалов с отрицательным значением показателя преломления (метаматериалов)[176][177][277].
Примечания[править | править код]
- ↑ 1 2 3 4 Борисенко и др., 2014, с. 11.
- ↑ 1 2 3 4 Attwood D. Soft X-rays and extreme ultraviolet radiation: principles and applications. — 1999. — P. 60. — ISBN 978-0-521-02997-1.
- ↑ 1 2 3 Zajac & Hecht, 2003, p. 128.
- ↑ 1 2 3 Прохоров, 1994, Преломления показатель.
- ↑ Прохоров, 1994, Полное внутреннее отражение.
- ↑ Фейнман, Лейтон, 1967, p. 86.
- ↑ 1 2 3 4 5 Оптическое стекло 2020. www.schott.com. Schott AG (2020). Дата обращения: 16 мая 2021. Архивировано 16 мая 2021 года.
- ↑ Tabata M.; et al. (2005). “Development of Silica Aerogel with Any Density” (PDF). 2005 IEEE Nuclear Science Symposium Conference Record. 2: 816—818. DOI:10.1109/NSSMIC.2005.1596380. ISBN 978-0-7803-9221-2. Архивировано из оригинала (PDF) 2013-05-18.
- ↑ Sadayori, Naoki; Hotta, Yuji «Polycarbodiimide having high index of refraction and production method thereof» US patent 2004/0158021 A1 Архивная копия от 9 июля 2021 на Wayback Machine (2004)
- ↑ Tosi, Jeffrey L., article on Common Infrared Optical Materials Архивная копия от 21 мая 2021 на Wayback Machine in the Photonics Handbook, accessed on 2014-09-10
- ↑ Yue, Zengji; Cai, Boyuan; Wang, Lan; Wang, Xiaolin; Gu, Min (2016-03-01). “Intrinsically core-shell plasmonic dielectric nanostructures with ultrahigh refractive index”. Science Advances [англ.]. 2 (3): e1501536. Bibcode:2016SciA….2E1536Y. DOI:10.1126/sciadv.1501536. ISSN 2375-2548. PMC 4820380. PMID 27051869.
- ↑ 1 2 Ландсберг, 2003, с. 252.
- ↑ Прохоров, 1998, Снелля закон.
- ↑ Brown, 2020.
- ↑ Light at Interfaces. University of Delaware (2010). Дата обращения: 14 мая 2021. Архивировано 14 мая 2021 года.
- ↑ Ландсберг, 2003, с. 434.
- ↑ Optical constants of C (Carbon, diamond, graphite, graphene, carbon nanotubes). Refractive index database. Дата обращения: 14 мая 2021. Архивировано 28 апреля 2021 года.
- ↑ Harlow, George. The nature of diamonds. — Cambridge, U.K. New York, NY, USA : Cambridge University Press in association with the American Museum of Natural History, 1998. — P. 14. — ISBN 9780521629355.
- ↑ Ландсберг, 2003, с. 432.
- ↑ Кузнецов С. И. Нормальная и аномальная дисперсия. Архивная копия от 12 августа 2020 на Wayback Machine
- ↑ Вакуленко, 2008, c. 30 (Апохромат).
- ↑ 1 2 Барковский, Горелик, Городенцева, 1963, p. 105.
- ↑ Index of Refraction of Liquids (Refractometry). Universität Leipzig. Дата обращения: 14 мая 2021. Архивировано 17 июня 2021 года.
- ↑ Fox, 2010, p. 40.
- ↑ Paschotta, Rüdiger. Chromatic Dispersion. RP Photonics Encyclopedia. Дата обращения: 14 мая 2021. Архивировано 29 июня 2015 года.
- ↑ Прохоров, 1988, p. 211.
- ↑ 1 2 Савельев, 1988, p. 432.
- ↑ 1 2 Taillet, 2006, p. 216
- ↑ Chartier, 1997, p. 431
- ↑ Chartier, 1997, p. 429
- ↑ Born & Wolf, 2019, p. 14
- ↑ 1 2 3 Ефимов, 2008, с. 37, 63.
- ↑ Фейнман, Лейтон, 1967, p. 84.
- ↑ 1 2 Прохоров, 1983, p. 344.
- ↑ 1 2 3 Фейнман, Лейтон, 1967, p. 85.
- ↑ Фейнман, Лейтон, 1967, p. 83.
- ↑ Фейнман, Лейтон, 1977, p. 89.
- ↑ 1 2 3 4 Фейнман, Лейтон, 1967, p. 90.
- ↑ 1 2 3 Фейнман, Лейтон, 1967, p. 88.
- ↑ 1 2 Фейнман, Лейтон, 1967, p. 91.
- ↑ Фейнман, Лейтон, 1967, p. 94.
- ↑ 1 2 Сивухин, 1980, с. 562.
- ↑ 1 2 Сивухин, 1980, с. 563.
- ↑ Сивухин, 1980, с. 564.
- ↑ Сивухин, 1977, p. 358.
- ↑ Прохоров, 1994.
- ↑ Wooten, Frederick. Optical Properties of Solids. — New York City : Academic Press, 1972. — P. 49. — ISBN 978-0-12-763450-0.(online pdf) Архивировано 3 октября 2011 года.
- ↑ Optical constants of H2O, D2O (Water, heavy water, ice). Refractive index database. Дата обращения: 14 мая 2021. Архивировано 28 апреля 2021 года.
- ↑ The Handbook on Optical Constants of Metals, 2012, p. 12—13.
- ↑ Palik, 1991, p. 41—42.
- ↑ Шен, 1980, p. 67.
- ↑ 1 2 Прохоров, 1983, p. 352.
- ↑ Aparicio, Josep M. (2011-06-02). “An evaluation of the expression of the atmospheric refractivity for GPS signals”. Journal of Geophysical Research. 116 (D11): D11104. Bibcode:2011JGRD..11611104A. DOI:10.1029/2010JD015214.
- ↑ Born & Wolf, 2019, p. 93.
- ↑ Прохоров, 1992, p. 195.
- ↑ 1 2 Прохоров, 1994, p. 107.
- ↑ Schwarz, Daniel; Wormeester, Herbert; Poelsema, Bene (2011). “Validity of Lorentz–Lorenz equation in porosimetry studies”. Thin Solid Films. 519 (9): 2994—2997. DOI:10.1016/j.tsf.2010.12.053. (недоступная ссылка)
- ↑ Ланжевена-Дебая формула / Булыгин, В. С. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ 1 2 Иоффе, 1983, p. 23.
- ↑ 1 2 3 Burnett, D. (1927). “The Relation between Refractive Index and Density”. Mathematical Proceedings of the Cambridge Philosophical Society. 23 (8): 907—911. DOI:10.1017/S0305004100013773. Архивировано из оригинала 2021-05-14. Дата обращения 2021-05-14.
- ↑ Прохоров, 1998, p. 211.
- ↑ Куинн, 1985, p. 133.
- ↑ Рефракція світла в атмосфері. Український астрономічний портал. Дата обращения: 7 апреля 2021. Архивировано 14 мая 2021 года.
- ↑ Хотимский Д. Эффект Новой земли, или История одного миража // Наука и жизнь. — 2020. — Т. 6. — С. 28—39.
- ↑ Иоффе, 1983, p. 25.
- ↑ Calculation of the Refractive Index of Glasses. Statistical Calculation and Development of Glass Properties. Архивировано 15 октября 2007 года.
- ↑ 1 2 3 4 Физические величины : Справочник / Под ред. И. С. Григорьева, Е. З. Мейлихова. — М.: Энергоатомиздат, 1991. — 1232 с. — 50 000 экз. — ISBN 5-283-04013-5.
- ↑ Stone, Jack A. Index of refraction of air. Engineering metrology toolbox. National Institute of Standards and Technology (NIST) (28 декабря 2011). Дата обращения: 11 января 2014. Архивировано 11 января 2014 года.
- ↑ Тарасов Л. В. Физика в природе: книга для учащихся. — М.: Просвещение, 1988. — С. 40—41. — 351 с. — ISBN 5-09-001516-3.
- ↑ Проскуряков, Драбкин, 1981, p. 57.
- ↑ Paschotta R., article on optical thickness Архивировано 22 марта 2015 года. in the Encyclopedia of Laser Physics and Technology Архивировано 13 августа 2015 года., accessed on 2014-09-08
- ↑ Zajac & Hecht, 2003, p. 68–69.
- ↑ Nave, Carl R. page on the Lens-Maker’s Formula Архивировано 26 сентября 2014 года. in HyperPhysics Архивировано 28 октября 2007 года., Department of Physics and Astronomy, Georgia State University, accessed on 2014-09-08
- ↑ Carlsson, 2007, p. 6.
- ↑ Carlsson, 2007, p. 14.
- ↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — С. 226—227. — 336 с.
- ↑ Миллер М. А. Волновое сопротивление // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — 707 с. — 100 000 экз.
- ↑ Джексон, 1965, с. 273—274.
- ↑ Paschotta, Rüdiger. Group Index (англ.). https://www.rp-photonics.com//. Дата обращения: 19 мая 2021. Архивировано 19 мая 2021 года.
- ↑ Born & Wolf, 2019, p. 22.
- ↑ Bor, Z.; Osvay, K.; Rácz, B.; Szabó, G. (1990). “Group refractive index measurement by Michelson interferometer”. Optics Communications. 78 (2): 109—112. Bibcode:1990OptCo..78..109B. DOI:10.1016/0030-4018(90)90104-2.
- ↑ Gjertsen, 1986
- ↑ 1 2 3 4 Refractivity of air (англ.). Дата обращения: 18 февраля 2013. Архивировано 10 января 2015 года.
- ↑ Halley, 1720
- ↑ Barrell & Sears, 1939
- ↑ 1 2 Chartier, 1997, p. 437
- ↑ Ciddór, 1996, p. 1566—1573
- ↑ Edlén, 1966
- ↑ 1 2 Bach & Neuroth, 1998
- ↑ Zajac & Hecht, 2003.
- ↑ Шрёдер & Трайбер, 2006, с. 29.
- ↑ 1 2 3 Fabry, Frush & Kilambi, 1997
- ↑ Bevis et al., 1994
- ↑ 1 2 Hartmann & Leitinger, 1984, p. 114.
- ↑ 1 2 Fukao, 2013, p. 26.
- ↑ Hartmann & Leitinger, 1984.
- ↑ Fabry, 2015, p. 5, 32—33.
- ↑ Palik E. D. Handbook of Optical Constants of Solids. — Academic Press, 1991. — Т. 2. — С. 1059—1077. — 1096 с. — ISBN 978-0-12-544422-4.
- ↑ 1 2 The International Association for the Properties of Water and Steam. Release on the Refractive Index of Ordinary Water Substance as a Function of Wavelength, Temperature, and Pressure (IAPWS R9-97) (сентябрь 1997). Дата обращения: 8 октября 2008. Архивировано 23 ноября 2009 года.
- ↑ METROLOGY ATICLE N°18: Calculation of the density of water (англ.). https://metgen.pagesperso-orange.fr/. MetGen. Дата обращения: 17 мая 2021. Архивировано 17 мая 2021 года.
- ↑ Pope R. M.; Fry E. S. (1997). “Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements”. Applied Optics. 36 (33): 8710—8723. Bibcode:1997ApOpt..36.8710P. DOI:10.1364/AO.36.008710. PMID 18264420.
- ↑ Блинникова, 2004, с. 5.
- ↑ Блинникова, 2004, с. 7.
- ↑ Показеев, Чаплина и Чашечкин, 2010, с. 54.
- ↑ Показеев, Чаплина и Чашечкин, 2010, с. 19.
- ↑ Показеев, Чаплина и Чашечкин, 2010, с. 20.
- ↑ Показеев, Чаплина и Чашечкин, 2010, с. 49—50.
- ↑ Показеев, Чаплина и Чашечкин, 2010, с. 105.
- ↑ ГОСТ 3514—94 Стекло оптическое бесцветное. Технические условия.
- ↑ Шрёдер & Трайбер, 2006, с. 44.
- ↑ Шрёдер & Трайбер, 2006, с. 47.
- ↑ Шрёдер & Трайбер, 2006, с. 46.
- ↑ Бебчук и др., 1988, с. 21.
- ↑ 1 2 Бебчук и др., 1988, с. 22.
- ↑ Френеля эллипсоид // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Paschotta R., article on birefringence Архивировано 3 июля 2015 года. in the Encyclopedia of Laser Physics and Technology Архивировано 13 августа 2015 года., accessed on 2014-09-09
- ↑ Zajac & Hecht, 2003, p. 230.
- ↑ Zajac & Hecht, 2003, p. 236.
- ↑ 1 2 Zajac & Hecht, 2003, p. 237.
- ↑ Zajac & Hecht, 2003, p. 233.
- ↑ Ландсберг, 2003, с. 479—480.
- ↑ Ландсберг, 2003, с. 480.
- ↑ 1 2 3 Fox, 2010, p. 51.
- ↑ Fox, 2010, p. 49.
- ↑ 1 2 3 Ландсберг, 2003, с. 481.
- ↑ Ландсберг, 2003, с. 485.
- ↑ Ландсберг, 2003, с. 482.
- ↑ Таблицы физических величин / Под ред. акад. И. К. Кикоина. — М.: Атомиздат, 1976. — С. 775. — 1008 с.
- ↑ 1 2 Коттона — Мутона эффект // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Zajac & Hecht, 2003, p. 273.
- ↑ Zajac & Hecht, 2003, p. 276.
- ↑ Zajac & Hecht, 2003, p. 203.
- ↑ Alberts, Bruce. Molecular biology of the cell. — 4th ed. — New York : Garland Science, 2002. — ISBN 0-8153-3218-1.
- ↑ 1 2 Carlsson, 2007, p. 28.
- ↑ Fitzgerald, 2000.
- ↑ Принципы фазово-контрастной микроскопии (I). https://stormoff.ru. Stormoff (24 сентября 2020). Дата обращения: 12 июня 2021. Архивировано 13 декабря 2019 года.
- ↑ Lang, Walter (1968). “Nomarski differential interference-contrast microscopy” (PDF). ZEISS Information. 70: 114—120. Архивировано (PDF) из оригинала 2022-06-16. Дата обращения 31 August 2016.
- ↑ Принципы фазово-контрастной микроскопии (II). https://stormoff.ru. Stormoff (24 сентября 2020). Дата обращения: 12 июня 2021. Архивировано 17 сентября 2019 года.
- ↑ Zernike, Frits (1942). “Phase contrast, a new method for the microscopic observation of transparent objects part I”. Physica. 9 (7): 686—698. Bibcode:1942Phy…..9..686Z. DOI:10.1016/S0031-8914(42)80035-X.
- ↑ Zernike, Frits (1942). “Phase contrast, a new method for the microscopic observation of transparent objects part II”. Physica. 9 (10): 974—980. Bibcode:1942Phy…..9..974Z. DOI:10.1016/S0031-8914(42)80079-8.
- ↑ Richards, Oscar (1956). “Phase Microscopy 1954-56”. Science. 124 (3226): 810—814. Bibcode:1956Sci…124..810R. DOI:10.1126/science.124.3226.810.
- ↑ Fitzgerald, Richard (2000). “Phase-Sensitive X-Ray Imaging”. Physics Today. 53 (7). Bibcode:2000PhT….53g..23F. DOI:10.1063/1.1292471.
- ↑ Солимено, Крозиньяни & Порто, 1989, с. 61.
- ↑ Солимено, Крозиньяни & Порто, 1989, с. 62.
- ↑ Борисенко и др., 2014, с. 12.
- ↑ Paschotta, Rüdiger. Nonlinear Index. RP Photonics Encyclopedia (2008). Дата обращения: 14 мая 2021. Архивировано 7 марта 2021 года.
- ↑ Barton & Guillemet, 2005, p. 117
- ↑ 1 2 Boyd, 2008, p. 208
- ↑ Boyd, 2008, p. 207—208
- ↑ Boyd, 2008, p. 329
- ↑ 1 2 Boyd, 2008, p. 375
- ↑ Зельдович Б. Я. Обращение волнового фронта // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 389—391. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Boyd, 2008, p. 329—375
- ↑ Attwood, David. Reflection And Refraction. berkeley.edu (2009). Дата обращения: 14 мая 2021. Архивировано 26 января 2020 года.
- ↑ X-ray refraction. x-ray-optics.de. Дата обращения: 14 мая 2021. Архивировано 26 января 2020 года.
- ↑ Сторижко В. Е. и др. Способы фокусировки рентгеновского излучения // Успехи физики металлов. — 2010. — Т. 11. — С. 1—17.

- ↑ Андервуд, Х. Возрождение рентгеновской оптики : [арх. 11 июля 2019] = The Renaissance of X-ray Optics : Phys. Today. April 1984. V. 37, No. 4. P. 44–51. DOI:10.1063/1.2916193 : [пер. с англ.] / Х. Андервуд, Т. Аттвуд // Успехи физических наук : журн. — 1987. — Т. 151, вып. 1 (январь). — С. 105—117. — УДК 543.422.6(G). — doi:10.3367/UFNr.0151.198701d.0105.
- ↑ Dresselhaus, 1999, p. 3.
- ↑ Фейнман, Лейтон, 1977, p. 58.
- ↑ Годжаев Н. М. Оптика. Учебное пособие для вузов. — М.: Высшая школа, 1977. — С. 379. — 432 с.
- ↑ Bradley, Scott MIT OpenCourseWare 6.007 Supplemental Notes: Sign Conventions in Electromagnetic (EM) Waves Архивная копия от 18 августа 2021 на Wayback Machine — 2007
- ↑ Fox, 2010, p. 337.
- ↑ Fox, 2010, p. 24.
- ↑ Forouhi, A.R. (1986). “Optical Dispersion Relations for Amorphous Semiconductors and Amorphous Dielectrics”. Physical Review B. 34 (10): 7018—7026. Bibcode:1986PhRvB..34.7018F. DOI:10.1103/physrevb.34.7018. PMID 9939354.
- ↑ 1 2 Сторижко и др., 2010.
- ↑ 1 2 Архипкин & Патрин, 2006, с. 107.
- ↑ Фейнман, Лейтон, 1967, p. 96.
- ↑ Fatuzzo, E.; Mason, P.R. (1967). “A calculation of the complex dielectric constant of a polar liquid by the librating molecule method”. Proceedings of the Physical Society. 90 (3). DOI:10.1088/0370-1328/90/3/318. Архивировано из оригинала 2021-05-14. Дата обращения 2021-05-14.
- ↑ 1 2 Ландсберг, 2003, с. 449.
- ↑ Архипкин & Патрин, 2006, с. 110.
- ↑ 1 2 3 4 Архипкин & Патрин, 2006, с. 123.
- ↑ 1 2 Веселаго В. Г. Электродинамика веществ с одновременно отрицательными значениями ε и μ // УФН. — 1967. — Т. 92. — С. 517. — doi:10.3367/UFNr.0092.196707d.0517.
- ↑ Pendry, J. B; Schurig, D.; Smith D. R. «Electromagnetic compression apparatus, methods and systems», U.S. Patent 7 629 941, Date: Dec. 8, 2009
- ↑ Shalaev, V. M. (2007). “Optical negative-index metamaterials”. Nature Photonics. 1 (1): 41—48. Bibcode:2007NaPho…1…41S. DOI:10.1038/nphoton.2006.49.
- ↑ Efimov, Sergei P. (1978). “Compression of electromagnetic waves by anisotropic medium. (“Non-reflecting” crystal model)”. Radiophysics and Quantum Electronics. 21 (9): 916—920. DOI:10.1007/BF01031726. Архивировано из оригинала 2018-06-02. Дата обращения 2021-05-22.
- ↑ 1 2 3 Слюсар В. Метаматериалы в антенной технике: история и основные принципы // Электроника: наука, технология, бизнес. — 2009. — № 7. — С. 70—79.
- ↑ 1 2 3 Слюсар В. Метаматериалы в антенной технике: основные принципы и результаты // Первая миля. Last Mile (Приложение к журналу «Электроника: Наука, Технология, Бизнес»). — 2010. — № 3—4. — С. 44—60.
- ↑ Пендри Дж., Смит Д. В поисках суперлинзы. Elementy.ru. Дата обращения: 30 июля 2011. Архивировано 22 августа 2011 года.
- ↑ ГОСТ 13659-78. Стекло оптическое бесцветное. Физико-химические характеристики. Основные параметры. — М.: Издательство стандартов, 1999. — 27 с.
- ↑ Бесцветное оптическое стекло СССР. Каталог. Под ред. Петровского Г. Т. — М.: Дом оптики, 1990. — 131 с. — 3000 экз.
- ↑ 1 2 3 Fox, 2010, p. 12.
- ↑ 1 2 Fox, 2010, p. 11.
- ↑ Fox, 2010, p. 9—10.
- ↑ Fox, 2010, p. 11—13.
- ↑ 1 2 3 Постнов К. А. Другие методы диагностики космической плазмы. http://www.astronet.ru. Астронет. Дата обращения: 18 мая 2021. Архивировано 18 мая 2021 года.
- ↑ Джексон, 1965, с. 255.
- ↑ Джексон, 1965, с. 258.
- ↑ Кренкель Э. Т. RAEM — мои позывные. — М.: Советская Россия, 1973.
- ↑ Kinsler L. E. Fundamentals of Acoustics. — 2000. — P. 136. — ISBN 978-0-471-84789-2.
- ↑ Левин В. М. Отражение звука // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 504—505. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Бреховских, 1973, с. 9.
- ↑ Трубецков и Рожнёв, 2001, с. 407.
- ↑ 1 2 Трубецков и Рожнёв, 2001, с. 408.
- ↑ Трубецков и Рожнёв, 2001, с. 409.
- ↑ Трубецков и Рожнёв, 2001, с. 410.
- ↑ Трубецков и Рожнёв, 2001, с. 411.
- ↑ Трубецков и Рожнёв, 2001, с. 412.
- ↑ Трубецков и Рожнёв, 2001, с. 421.
- ↑ Трубецков и Рожнёв, 2001, с. 422.
- ↑ Трубецков и Рожнёв, 2001, с. 420.
- ↑ Путилов и Фабрикант, 1963, с. 66.
- ↑ 1 2 Путилов и Фабрикант, 1963, с. 67.
- ↑ 1 2 Путилов и Фабрикант, 1963, с. 68.
- ↑ Путилов и Фабрикант, 1963, с. 69.
- ↑ Стоянов П. А. Электронная и ионная оптика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- ↑ Katsnelson M. I. The Physics of Graphene. — 2nd ed.. — Cambridge University Press, 2020. — С. 97—98. — 426 с. — ISBN 978-1-108-47164-0. — doi:10.1017/9781108617567.
- ↑ Франк А. И. Оптика ультрахолодных нейтронов и проблема нейтронного микроскопа // УФН. — Т. 151. — С. 229—272. — doi:10.3367/UFNr.0151.198702b.0229.
- ↑ Стороженко, Тиманюк & Животова, 2012, с. 5—6.
- ↑ 1 2 Refractive index and dispersion. Schott AG. Дата обращения: 19 февраля 2013. Архивировано 20 января 2022 года.
- ↑ Dufrenne, Maës & Maës, 2005, p. 443
- ↑ 1 2 Костіна Т. А. Рефрактометрія. Фармацевтична енциклопедія. Дата обращения: 14 мая 2021. Архивировано 14 мая 2021 года.
- ↑ Aminot & Kérouel, 2004
- ↑ Briant, Denis & Hipeaux, 1997
- ↑ Барковский, Горелик, Городенцева, 1963, p. 119—121.
- ↑ Jacquey et al., 2007
- ↑ Wilkes, 2007, p. 7
- ↑ Вакуленко, 2008, с. 317—318 (Метод імерсійний).
- ↑ Masters B. R. Early development of optical low-coherence reflectometry and some recent biomedical applications // J. of Biomedical Optics. — 1999. — Т. 4. — С. 236—247. — doi:10.1117/1.429914. — PMID 23015210.
- ↑ Листвин А. В., Листвин В. Н. Рефлектометрия оптических волокон. — М.: ЛЕСАРарт, 2005. — 150 с. — ISBN 5-902367-03-4.
- ↑ Горшков, 1974, с. 48.
- ↑ 1 2 Горшков, 1974, с. 43.
- ↑ Горшков, 1974, с. 51.
- ↑ Adachi, 1999, p. xi.
- ↑ Бебчук и др., 1988, с. 147—148.
- ↑ Fox, 2010, p. 50.
- ↑ Шрёдер & Трайбер, 2006, с. 97.
- ↑ Бреховских, 1973, с. 91.
- ↑ Dittrich T. Materials concepts for solar cells. — Imperial College Press, 2014. — С. 51—53. — 552 с. — ISBN 978-1-78326-444-5.
- ↑ Рефрактометрия. https://lasik.ru/. Центр глазной хирургии. Дата обращения: 19 мая 2021. Архивировано 19 мая 2021 года.
- ↑ Kim G. et al. Measurements of three-dimensional refractive index tomography and membrane deformability of live erythrocytes from Pelophylax nigromaculatus // Sci. Rep.. — 2018. — Т. 8. — С. 9192. — doi:10.1038/s41598-018-25886-8.
- ↑ «ICUMSA Methods Book», op. cit.; Specification and Standard SPS-3 Refractometry and Tables — Official; Tables A-F
- ↑ ОФС.1.2.1.0017.15 Рефрактометрия. https://pharmacopoeia.ru//. Фармакопея.рф. Дата обращения: 19 мая 2021.
- ↑ Шрёдер & Трайбер, 2006, с. 152—153.
- ↑ Шрёдер & Трайбер, 2006, с. 155.
- ↑ Gan, 2006, p. 228.
- ↑ Agrawal, 2008, p. 179.
- ↑ Шрёдер & Трайбер, 2006, с. 169.
- ↑ Фотохромные очки — для чего они нужны? https://ochkarik.ru/. «Оптик-Вижн» (2021). Дата обращения: 6 июля 2021. Архивировано 9 июля 2021 года.
- ↑ Лейт Э., Упатниек Ю. Фотографирование с помощью лазера // «Наука и жизнь» : журнал. — 1965. — № 11. — С. 22—31. — ISSN 0028-1263.
- ↑ Иммерсионная система // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2. (CC BY-SA 3.0)
- ↑ Wei, Yayi. Advanced processes for 193-nm immersion lithography. — Bellingham, Wash : SPIE, 2009. — ISBN 0819475572.
- ↑ Бурсиан Э. В. Сегнетоэлектрики в нелинейной оптике // Соросовский образовательный журнал. — 2001. — Т. 8. — С. 98—102.
- ↑ Prismatic Paintings Produced From Refracted Light by Stephen Knapp (29 июля 2016). Дата обращения: 12 июня 2021. Архивировано 12 июня 2021 года.
- ↑ Harris, John (2006), The Dark Side of the Moon (third ed.), Harper Perennial, с. 143, ISBN 978-0-00-779090-6
- ↑ IOR LIST (англ.). Pixel and Poly, LLC (2017). Дата обращения: 12 июня 2021. Архивировано 12 июня 2021 года.
- ↑ Wood, Robin. Refraction Index for 3D Graphics Explained (англ.). Pixel and Poly, LLC (2017). Дата обращения: 12 июня 2021. Архивировано 12 июня 2021 года.
- ↑ Introduction to Ray Tracing: a Simple Method for Creating 3D Images (англ.). Scratchapixel 2.0. Дата обращения: 12 июня 2021. Архивировано 12 июня 2021 года.
- ↑ O’Hanlon G. Why Some Paints are Transparent and Others Opaque (англ.). https://www.naturalpigments.com/. Natural Pigments (12 июня 2013). Дата обращения: 12 июня 2021. Архивировано 12 июня 2021 года.
- ↑ Лентовский А. М. Оптические свойства красок. Светотени в живописи (7 июля 2016). Дата обращения: 12 июня 2021. Архивировано 12 июня 2021 года.
- ↑ 1 2 3 4 Lehn & van der Werf, 2005.
- ↑ Godet, Jean-Luc. A short recall about the history of the concept of refractive index. Université d’Angers. Дата обращения: 14 мая 2021. Архивировано 6 мая 2021 года.
- ↑ Mahan A. I. Astronomical Refraction–Some History and Theories // Appl Opt.. — 1962. — Т. 1. — С. 497—511. — doi:10.1364/AO.1.000497.
- ↑ Fermat’s principle. Britannica (1998). Дата обращения: 14 мая 2021. Архивировано 10 августа 2020 года.
- ↑ Hutton, 1815, p. 299.
- ↑ 1 2 Kragh, Helge (2018). “The Lorenz-Lorentz Formula: Origin and Early History”. Substantia. 2 (2): 7—18. DOI:10.13128/substantia-56. Архивировано из оригинала 2021-05-14. Дата обращения 2021-05-14.
- ↑ A spectrum of colours: the dispersion of light. Institute of Physics. Дата обращения: 14 мая 2021. Архивировано 14 апреля 2021 года.
- ↑ Bursey, Maurice M. (2017). “A brief history of spectroscopy”. AccessScience. DOI:10.1036/1097-8542.BR0213171. Архивировано из оригинала 2021-03-05. Дата обращения 2021-05-14.
- ↑ Wolfe, 2020, ch. 32.
- ↑ Hauksbee, Francis (1710). “A Description of the Apparatus for Making Experiments on the Refractions of Fluids”. Philosophical Transactions of the Royal Society of London. 27 (325—336). DOI:10.1098/rstl.1710.0015.
- ↑ Hutton, Charles. Philosophical and mathematical dictionary. — 1795. — P. 299. Архивная копия от 9 июля 2021 на Wayback Machine
- ↑ von Fraunhofer, Joseph (1817). “Bestimmung des Brechungs und Farbenzerstreuungs Vermogens verschiedener Glasarten”. Denkschriften der Königlichen Akademie der Wissenschaften zu München. 5. Архивировано из оригинала 2021-05-15. Дата обращения 2021-05-15. Exponent des Brechungsverhältnisses is index of refraction
- ↑ Brewster, David (1815). “On the structure of doubly refracting crystals”. Philosophical Magazine. 45 (202). DOI:10.1080/14786441508638398. Архивировано из оригинала 2021-05-15. Дата обращения 2021-05-15.
- ↑ Herschel, John F.W. On the Theory of Light. — 1828. — P. 368. Архивная копия от 15 мая 2021 на Wayback Machine
- ↑ Ландсберг, 2003, с. 479.
- ↑ History of refractometer. refractometer.pl. Дата обращения: 14 мая 2021. Архивировано 19 апреля 2021 года.
- ↑ Williams, S. R. (1908). “A Study of Dispersion in Highly Absorbing Media by Means of Channeled Spectra”. Physical Review. 27 (1): 27—32. DOI:10.1103/PhysRevSeriesI.27.27. Архивировано из оригинала 2021-05-14. Дата обращения 2021-05-14.
- ↑ Ландсберг, 2003, с. 21.
- ↑ Ландсберг, 2003, с. 486.
- ↑ Ландсберг, 2003, с. 448.
- ↑ Paul, 1990, p. 333.
- ↑ Лейт & Упатниек, 1965.
- ↑ Власенко В. И. Глава IV. Изобразительная голография // Техника объёмной фотографии / А. Б. Долецкая. — М.: «Искусство», 1978. — С. 67—95. — 102 с. — 50 000 экз.
- ↑ Ash, Eric A. (1979). “Dennis Gabor, 1900–1979”. Nature. 280 (5721): 431—433. Bibcode:1979Natur.280..431A. DOI:10.1038/280431a0. PMID 379651.
- ↑ Hayes, 2000, p. 8.
- ↑ Koester, Snitzer, 1964.
- ↑ Hayes, 2000, pp. 9—10.
- ↑ Pendry J. B., Smith D. R. Reversing Light with Negative Refraction (англ.) // Physics Today. — 2004. — Vol. 57, no. 6. — P. 37—43. — doi:10.1063/1.1784272.
Литература[править | править код]
- На русском языке
- Архипкин В. Г., Патрин Г. С. Лекции по оптике. — Красноярск: Институт физики им. Л. В. Керенского СО РАН, 2006. — 164 с.
- Барковский В. Ф., Горелик С. М., Городенцева Т. Б. Практикум по физико-химическим методам анализа. — М.: Высшая школа, 1963. — 349 с.
- Бебчук Л. Г., Богачев Ю. В., Заказнов Н. П., Комраков Б. М., Михайловская Л. В., Шапочкин Б. А. Прикладная оптика: Учебное пособие для приборостроительных специальностей вузов / Под общ. ред. Н. П. Заказнова. — М.: Машиностроение, 1988. — 312 с. — ISBN 5-217-00073-2.
- Блинникова А. А. Рефрактометрический метод в анализе лекарственных средств, концентратов, спиртоводных растворов. / Под ред. проф. Е. А. Краснова. — Томск: СибГМУ, 2004. — 37 с.
- Борисенко С. И., Ревинская О. Г., Кравченко Н. С., Чернов А. В. Показатель преломления света и методы его экспериментального определения. Учебно-методическое пособие. — Томск: Изд-во Томского политехнического университета, 2014. — 142 с.
- Бреховских Л. М. Волны в слоистых средах. — 2-е. — М.: Наука, 1973. — 343 с.
- Горшков М. М. Эллипсометрия. — М.: Сов. радио, 1974. — 200 с.
- Джексон Дж. Классическая электродинамика / Под ред. Э. Л. Бурштейна. — М.: Мир, 1965. — 703 с.
- Ефимов А. М. Оптические свойства материалов и механизмы их формирования. — СПб.: СПбГУИТМО, 2008. — 103 с.
- Иоффе Б. В. Рефрактометрические методы химии. — Ленинград: ГХИ, 1983. — 39 с.
- Куинн Т. Температура. — М.: Мир, 1985. — 448 с.
- Ландсберг Г. С. Оптика: учебное пособие для вузов. — 6-е изд. стереот. — М.: ФИЗМАТЛИТ, 2003. — 848 с. — ISBN 5-9221-0314-8.
- Показеев К. В., Чаплина Т. О., Чашечкин Ю. Д. Оптика океана: Учебное пособие.. — М.: МАКС Пресс, 2010. — 216 с. — ISBN 5-94052-028-6.
- Проскуряков В. А., Драбкин А. Е. Химия нефти и газа. — Ленинград: Химия, 1981. — 359 с.
- Прохоров О. М. Физический энциклопедический словарь. — М.: Советская энциклопедия, 1983. — 928 с.
- Прохоров О. М. Ааронова — Бома эффект — Длинные линии // Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 1. — 703 с.
- Прохоров О. М. Магнитоплазменный — Поинтинга теорема // Физическая энциклопедия. — М.: Научное издательство «Большая российская энциклопедия», 1992. — Т. 3. — 672 с. — ISBN 5-8527-0019-3.
- Прохоров О. М. Поинтинга — Робертсона эффект — Стриммеры // Физическая энциклопедия. — М.: Научное издательство «Большая российская энциклопедия», 1994. — Т. 4. — 704 с. — ISBN 5-8527-0087-8.
- Прохоров О. М. Стробоскопические приборы — Яркость // Физическая энциклопедия. — М.: Научное издательство «Большая российская энциклопедия», 1998. — Т. 5. — 691 с. — ISBN 5-85270-101-7.
- Путилов К. А., Фабрикант В. А. Оптика, атомная физика, ядерная физика // Курс физики. — 1963. — Т. III. — 634 с.
- Савельев И. В. Электричество и магнетизм. Волны. Оптика. // Курс общей физики: Учеб. пособие. — М.: «Наука», 1988. — Т. 2. — 496 с.
- Сивухин Д. В. Электричество // Общий курс физики. — М.: Наука, 1977. — Т. 3. — 704 с.
- Сивухин Д. В. Оптика // Общий курс физики. — М.: Наука, 1980. — Т. IV. — 752 с.
- Солимено С., Крозиньяни Б., Ди Порто П. Дифракция и волноводное распространение оптического излучения. — М.: Мир, 1989. — 664 с.
- Стороженко И. П., Тиманюк В. А., Животова Е. Н. Методы рефрактометрии и поляриметрии. — Харьков: Изд-во НФаУ, 2012. — 64 с.
- Трубецков Д. И., Рожнёв А. Г. Линейные колебания и волны. — М.: Физматлит, 2001. — 416 с. — ISBN 5-94052-028-6.
- Швец В. А., Спесивцев Е. В. Эллипсометрия. Учебно-методическое пособие к лабораторным работам. — Новосибирск, 2013. — 87 с.
- Фейнман Р. Ф., Лейтон Р. Излучение, волны, кванты // Фейнмановские лекции по физике. — М.: Мир, 1967. — Т. 3. — 235 с.
- Фейнман Р. Ф., Лейтон Р. Физика сплошных сред // Фейнмановские лекции по физике. — М.: Мир, 1977. — Т. 7. — 286 с.
- Шен И. Р. Принципы нелинейной оптики. — М.: «Наука», 1980. — 558 с.
- Шрёдер Г., Трайбер Х. Техническая оптика. — М.: Техносфера, 2006. — 424 с. — ISBN 5-94836-075-X.
- На английском языке
- Adachi S. The Handbook on Optical Constants of Metals: In Tables and Figures (англ.). — Singapore: World Scientific Publishing Company, 2012. — 684 p. — ISBN 9814405949.
- Adachi S. Optical Properties of Crystalline and Amorphous Semiconductors: Materials and Fundamental Principles (англ.). — World Scientific Publishing Company, 1999. — 271 p. — ISBN 978-1-4615-5241-3.
- Agrawal G. P. Applications of nonlinear fiber optics (англ.). — 2nd ed. — Academic Press, 2008. — Vol. 10. — 508 p. — (Optics and Photonis Series). — ISBN 9780123743022.
- Bach H., Neuroth N. The properties of optical glass (англ.). — 2. — Berlin: Springer, 1998. — 419 p. — ISBN 3-540-58357-2.
- Barrell H., Sears J. E. The Refraction and Dispersion of Air for the Visible Spectrum (англ.) // Philosophical transactions of the Royal Society A. — 1939. — Vol. 238.
- Bevis M. et al. GPS Meteorology: mapping zenith wet delay onto precipitable water (англ.) // Journal of Applied Meteorology and Climatology. — 1994. — Vol. 33. — P. 379–386. — doi:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2.
- Born M. Principles of optics : electromagnetic theory of propagation, interference, and diffraction of light (англ.). — Cambridge: Cambridge University Press, 2019. — ISBN 9781108477437.
- Boyd R. W. Nonlinear Optics (англ.). — 3rd ed.. — Burlington, MA: Academic Press, 2008. — 640 p. — ISBN 978-0-12-369470-6.
- Brown K. Refraction At A Plane Boundary Between Moving Media (англ.). https://www.mathpages.com (2020). Дата обращения: 18 мая 2021.
- Carlsson, Kjell Light microscopy (2007). Дата обращения: 2 января 2015. Архивировано 2 апреля 2015 года.
- Ciddór P. E. Refractive index of air: new equations for the visible and near infrared (англ.) // Applied optics. — Optical society of America, 1996. — Vol. 35, iss. 9. — P. 1566—1573. — doi:10.1364/AO.35.001566.
- Dresselhaus, M. S. Solid State Physics Part II Optical Properties of Solids. Course 6.732 Solid State Physics. MIT (1999). Дата обращения: 5 января 2015. Архивировано 24 июля 2015 года.
- Edlén B. The Refractive Index of Air (англ.) // Metrologia. — 1966. — Vol. 71, iss. 2. — doi:10.1088/0026-1394/2/2/002.
- Fabry F. Radar meteorology: principles and practice (англ.). — Cambridge, United Kingdom: Cambridge University Press, 2015. — ISBN 9781108460392.
- Fabry F., Frush C., Zawadzki I., Kilambi A. On the Extraction of Near-Surface Index of Refraction Using Radar Phase Measurements from Ground Targets (англ.) // Journal of Atmospheric and Oceanic Technology. — American Meteorological Society, 1997. — Vol. 4, iss. 14. — P. 2625—2628. — doi:10.1109/APS.1997.625552.
- Fox M. Optical properties of solids (англ.). — Oxford, New York: Oxford University Press, 2010. — ISBN 9780199573363.
- Fukao S. Radar for meteorological and atmospheric observations (англ.). — Tokyo: Springer, 2013. — ISBN 9784431543336.
- Gan F. Photonic glasses (англ.). — World Scientific, 2006. — 447 p. — ISBN 9789812568205.
- Gjertsen D. The Newton Handbook (англ.). — Taylor & Francis, 1986. — 665 p.
- Halley E. Some remarks on the allowances to be made in astronomical observations for the refraction of the air (англ.) // Philosophical transactions. — 1720. — Vol. 31. — P. 364—369. — doi:10.1098/rstl.1720.0042.
- Hartmann G. K., Leitinger R. Range errors due to ionospheric and tropospheric effects for signal frequencies above 100 MHz (англ.) // Bulletin géodésique volume. — 1984. — Vol. 58. — P. 109—136. — doi:10.1007/BF02520897.
- Hayes J. Fiber Optics Technician’s Manual (англ.). — 2th Ed. — Delmar Cengage Learning, 2000. — 242 p. — ISBN 978-0766818255.
- Hutton C. A Philosophical and Mathematical Dictionary (англ.). — London, 1815. — Vol. 2. — 628 p.
- Jacquey M., Büchner M., Trénec G., Vigué J. First measurements of the index of refraction of gases for lithium atomic waves (англ.) // Phys. Rev. Lett.. — 2007. — Vol. 98. — P. 240405. — doi:10.1103/PhysRevLett.98.240405.
- Koester C. J., Snitzer E. Amplification in a Fiber Laser (англ.) // Applied Optics — Optica, 1964. — Vol. 3, Iss. 10. — P. 1182—1186. — ISSN 1559-128X; 2155-3165; 0003-6935; 1539-4522 — doi:10.1364/AO.3.001182
- Lehn W. H., van der Werf S. Atmospheric refraction: a history (англ.) // Appl Opt.. — 2005. — Vol. 44. — P. 5624—5636. — doi:10.1364/ao.44.005624.
- Palik E. D. Handbook of Optical Constants of Solids (англ.). — Academic Press, 1991. — Vol. I. — ISBN 978-0-12-544422-4.
- Paul A. Chemistry of glasses (англ.). — London, New York: Chapman and Hall, 1990. — ISBN 0412278200.
- Wilkes Z. Investigation of the Nonlinear Index of Refraction of Water at 815 and 407 nanometers (англ.). — University of Maryland, 2007. — 97 p.
- Wolfe W. L. Rays, Waves and Photons. — IoP Publishing Ltd, 2020. — 350 с. — ISBN 978-0-7503-2612-4.
- Zajac A., Hecht E., Cummings E. Optics (англ.). — 4th ed. — Addison-Wesley, 2003. — ISBN 978-0-321-18878-6.
- На французском языке
- Aminot A., Kérouel R. Hydrologie des écosystèmes marins: paramètres et analyses (фр.). — La Rose de Clichy, 2004. — 336 с. — ISBN 2-9522492-0-2.
- Barton J. L., Guillemet C. Le verre, science et technologie (фр.). — Les Ulis: EDP Sciences, 2005. — 440 с. — ISBN 2-86883-789-1.
- Briant J., Denis J., Hipeaux J.-C. Physico-chimie des lubrifiants: Analyses et essais (фр.). — La Rose de Clichy, 1997. — 464 с. — ISBN 9782710807261.
- Chartier G. Manuel d’optique (фр.). — Paris: Hermès, 1997. — 683 с. — ISBN 2-86601-634-3.
- Dufrenne R., Maës J., Maës B. La Cristallerie de Clichy : Une prestigieuse manufacture du xixe siècle (фр.). — Clichy-la-Garenne: La Rose de Clichy, 2005. — 447 с. — ISBN 2-9522492-0-2.
- Itard J. Les lois de la réfraction de la lumière chez Kepler (фр.). — 1957. — Vol. 10, livr. 1. — P. 59—68.
- Taillet R. Optique physique : Propagation de la lumière (фр.). — Bruxelles/Paris: De Boeck, 2006. — 323 с. — ISBN 2-8041-5036-4.
- На украинском языке
- Вакуленко М. О., Вакуленко О. В. Тлумачний словник із фізики (укр.). — К.: Видавничо-поліграфічний центр «Київський університет», 2008. — 767 с. — ISBN 978-966-439-038-2.
- Романюк М. О., Крочук А. С., Пашук І. П. Оптика (укр.). — : ЛНУ ім. Івана Франка, 2012. — 564 с.
Ссылки[править | править код]
- Polyanskiy M. RefractiveIndex.INFO Refractive index database (англ.). https://refractiveindex.info/ (2008). Дата обращения: 18 мая 2021.
- Refractive Index Database (англ.). https://www.filmetrics.com. FilMetrics. Дата обращения: 18 мая 2021.
- Optical Data from Sopra SA (англ.). http://www.sspectra.com. Дата обращения: 18 мая 2021.
- n, k database (англ.). http://www.ioffe.ru/. Дата обращения: 18 мая 2021.
- Index of Refraction (англ.). https://henke.lbl.gov/. Дата обращения: 18 мая 2021.
Закон преломления света и полное внутреннее отражение
- Подробности
- Категория: Оптика
Закон преломления света
Наблюдение преломления света.
На границе двух сред свет меняет направление своего распространения. Часть световой энергии возвращается в первую среду, т. е. происходит отражение света. Если вторая среда прозрачна, то свет частично может пройти через границу сред, также меняя при этом, как правило, направление распространения. Это явление называется преломлением света.
Вследствие преломления наблюдается кажущееся изменение формы предметов, их расположения и размеров. В этом нас могут убедить простые наблюдения. Положим на дно пустого непрозрачного стакана монету или другой небольшой предмет. Подвинем стакан так, чтобы центр монеты, край стакана и глаз находились на одной прямой. Не меняя положения головы, будем наливать в стакан воду. По мере повышения уровня воды дно стакана с монетой как бы приподнимается. Монета, которая ранее была видна лишь частично, теперь будет видна полностью. Установим наклонно карандаш в сосуде с водой.
Если посмотреть на сосуд сбоку, то можно заметить, что часть карандаша, находящаяся в воде, кажется сдвинутой в сторону (рис. 96).
Эти явления объясняются изменением направления лучей на границе двух сред — преломлением света.
Закон преломления света определяет взаимное расположение падающего луча АВ (рис. 97), преломленного DB и перпендикуляра СЕ к поверхности раздела сред, восставленного в точке падения. Угол а называется углом падения, а угол β— углом преломления.
Падающий, отраженный и преломленный лучи нетрудно наблюдать, сделав узкий световой пучок видимым. Ход такого пучка в воздухе можно проследить, если пустить в воздух немного дыма или же поставить экран под небольшим углом к лучу. Преломленный пучок также виден в подкрашенной флюоресцеином воде аквариума (рис. 98).
Вывод закона преломления света. Закон преломления света был установлен опытным путем в XVII веке. Мы его выведем с помощью принципа Гюйгенса.
Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость волны в первой среде через v1, а во второй — через v2.
Пусть на плоскую границу раздела двух сред (например, из воздуха в воду) падает плоская световая волна (рис. 99). Волновая поверхность АС перпендикулярна лучам А1А и В1В. Поверхности MN сначала достигнет луч А1А. Луч В1В достигнет поверхности спустя время
Поэтому в момент, когда вторичная волна в точке В только начнет возбуждаться, волна от точки А уже имеет вид полусферы радиусом
Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную ко всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае это плоскость BD. Она является огибающей вторичных волн.
Угол падения α луча равен углу САВ в треугольнике АВС (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно,
Угол преломления β равен углу ABD треугольника ABD. Поэтому
Разделив почленно (5.2) на (5.3), получим
где n — постоянная величина, не зависящая от угла падения.
Из построения (рис. 99) видно, что падающий луч, луч преломленный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости. Данное утверждение совместно с уравнением (5.4), согласно которому отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред, представляет собой закон преломления света.
Убедиться в справедливости закона преломления можно экспериментально, измеряя углы падения и преломления и вычисляя отношение их синусов при различных углах падения. Это отношение остается неизменным.
Показатель преломления. Постоянная величина, входящая в закон преломления света, называется относительным показателем преломления или показателем преломления второй среды относительно первой.
Из принципа Гюйгенса не только следует закон преломления, но с помощью этого принципа раскрывается физический смысл показателя преломления. Он равен отношению скоростей света в средах, на границе между которыми происходит преломление:
Если угол преломления β меньше угла падения а, то согласно (5.4) скорость света во второй среде меньше, чем в первой.
Показатель преломления среды относительно вакуума называют абсолютным показателем преломления этой среды. Он равен отношению синуса угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.
Пользуясь формулой (5.5), можно выразить относительный показатель преломления через абсолютные показатели преломления n1 и n2 первой и второй сред.
Действительно, так как n1=c/v1 и n2=c/v2 , где с – скорость света в вакууме, то
Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой.
Абсолютный показатель преломления определяется скоростью распространения света в данной среде, которая зависит от физического состояния среды, т. е. от температуры вещества, его плотности, наличия в нем упругих напряжений. Показатель преломления зависит также и от характеристик самого света. Для красного света он меньше, чем для зеленого, а для зеленого — меньше, чем для фиолетового.
Поэтому в таблицах значений показателей преломления для разных веществ обычно указывается, для какого света приведено данное значение n и в каком состоянии находится среда. Если таких указаний нет, то это означает, что зависимостью от указанных факторов можно пренебречь.
В большинстве случаев приходится рассматривать переход света через границу воздух — твердое тело или воздух — жидкость, а не через границу вакуум — среда. Однако абсолютный показатель преломления n2 твердого или жидкого вещества отличается от показателя преломления того же вещества относительно воздуха незначительно. Так, абсолютный показатель преломления воздуха при нормальных условиях для желтого света равен приблизительно n1≈1,000292. Следовательно,
Значения показателей преломления для некоторых веществ относительно воздуха приведены в таблице 2 (данные относятся к желтому свету).
Ход лучей в треугольной призме.
Закон преломления света позволяет рассчитать ход лучей в различных оптических устройствах, например в треугольной призме, изготовленной из стекла или других прозрачных материалов.
На рисунке 100 изображено сечение стеклянной призмы плоскостью, перпендикулярной ее боковым ребрам. Луч в призме отклоняется к основанию, преломляясь на гранях ОА и ОВ. Угол φ между этими гранями называют преломляющим углом призмы. Угол 0 отклонения луча зависит от преломляющего угла призмы ф, показателя преломления n материала призмы и угла падения а. Он может быть вычислен с помощью закона преломления (5.4).
ПОЛНОЕ ОТРАЖЕНИЕ
При прохождении света из оптически менее плотной среды в более плотную, например из воздуха в стекло или воду, v1 и v2 согласно закону преломления (5.4) показатель преломления 1. Поэтому а>β (рис. 101, а):
преломленный луч приближается к перпендикуляру к границе раздела сред. Если направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль бывшего преломленного луча (рис. 101, б), то закон преломления запишется так:
Преломленный луч по выходе из оптически более плотной среды пойдет по линии бывшего падающего луча, поэтому а<β, т. е. преломленный луч отклоняется от перпендикуляра. По мере увеличения угла а угол преломления β растет, оставаясь все время больше угла а. Наконец, при некотором угле падения значение угла преломления приблизится к 90° и преломленный луч пойдет почти по границе раздела сред (рис. 102). Наибольшему возможному углу преломления β = 90° соответствует угол падения ао.
Попробуем сообразить, что произойдет при а>ао. При падении света на границу двух сред световой луч, как об этом уже упоминалось, частично преломляется, а частично отражается от нее. При а>a0 преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.
Для наблюдения полного отражения можно использовать стеклянный полуцилиндр с матовой задней поверхностью. Полуцилиндр закрепляют на диске так, чтобы середина плоской поверхности полуцилиндра совпадала с центром диска (рис. 103). Узкий пучок света от осветителя направляют снизу на боковую поверхность полуцилиндра перпендикулярно его поверхности. На этой поверхности луч не преломляется. На плоской поверхности луч частично преломляется и частично отражается. Отражение происходит в соответствии с законом отражения, а преломление — в соответствии с законом преломления (5.4).
Если увеличивать угол падения, то можно заметить, что яркость (и следовательно, энергия) отраженного пучка растет, в то время как яркость (энергия) преломленного пучка падает. Особенно быстро убывает энергия преломленного пучка, когда угол преломления приближается к 90°. Наконец, когда угол падения становится таким, что преломленный пучок идет вдоль границы раздела (см. рис. 102), доля отраженной энергии составляет почти 100%. Повернем осветитель, сделав угол падения а большим ао. Мы увидим, что преломленный пучок исчез и весь свет отражается от границы раздела, т. е. происходит полное отражение света.
На рисунке 104 изображен пучок лучей от источника, помещенного в воде недалеко от ее поверхности. Большая интенсивность света показана большей толщиной линии, изображающей соответствующий луч.
Угол падения ао, соответствующий углу преломления 90°, называют предельным углом полного отражения
При sin β= 1 формула (5.8) при нимает вид
Из этого равенства и может быть найдено значение предельного угла полного отражения ао. Для воды (n = 1,33) он оказывается равным 48°35′, для стекла (n =1,5) он принимает значение 41°51′, а для алмаза (n— 2,42) этот угол составляет 24°40′. Во всех случаях второй средой является воздух.
Явление полного отражения легко наблюдать на простом опыте. Нальем в стакан воду и поднимем его несколько выше уровня глаз. Поверхность воды при рассматривании ее снизу сквозь стенку кажется блестящей, словно посеребренной вследствие полного отражения света.
Полное отражение используют в так называемой волоконной оптике для передачи света и изображения по пучкам прозрачных гибких волокон — световодов. Световод представляет собой стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления. За счет многократного полного отражения свет может быть направлен по любому (прямому или изогнутому) пути (рис. 105). Волокна набираются в жгуты. При этом по каждому из волокон передается какой-нибудь элемент изображения (рис. 106). Жгуты из волокон используются, например, в медицине для исследования внутренних органов.
По мере улучшения технологии изготовления длинных пучков волокон— световодов все шире начинает применяться связь (в том числе и телевизионная) с помощью световых лучей.
Трехсантиметровые волны: закон отражения (металл)
Полное внутреннее отражение
Искривление луча в неоднородной среде
Модель световода
Куб и призма на пути трехсантиметровой волны
Трехсантиметровые волны: закон отражения (диэлектрик)
Трехсантиметровые волны: интерференция при отражении (просветление)
Трехсантиметровые волны: диэлектрическая линза
Трехсантиметровые волны: диэлектрическая призма
Решётка — зеркало для трёхсантиметровых волн
Дециметровые волны: «хорошее» и «плохое» зеркала







































































![{displaystyle mathbf {E} (z,t)=operatorname {Re} !left[mathbf {E} _{0}e^{i({underline {k}}z-omega t)}right]=operatorname {Re} !left[mathbf {E} _{0}e^{i(2pi (n+ikappa )z/lambda _{0}-omega t)}right]=e^{-2pi kappa z/lambda _{0}}operatorname {Re} !left[mathbf {E} _{0}e^{i(kz-omega t)}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2d46c6e63feb2740bc09706a3dbe4686510b3c)










![{displaystyle {textbf {v}}=nabla phi ({textbf {r}},t)=nabla operatorname {Re} [u({textbf {r}})e^{iomega t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/212c204c36dfd03be6f0df7d08846b0439c3bbc6)

![{displaystyle Delta Psi +{frac {2m}{hbar ^{2}}}left[E-U({textbf {r}})right]Psi =0,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db5a81777b09896823bf65e970abb0e18b917eae)










