
СРОЧНО. Электролампа помещена в матовый шар радиусом 20 см и подвешена на высоте 5 м над полом. Под лампой на высоте 1 м от пола висит непрозрачный шар радиуса 10
см. Найдите размеры тени и полутени на полу.

Светило науки – 1601 ответ – 21338 раз оказано помощи
L = 5 м – расстояние от центра плафона до экрана (пола)
l = 1 м – расстояние от предмета до экрана
R = 0.2 м – радиус плафона
r = 0.1 м – радиус предмета
h – радиус тени
H – радиус полутени
Из соотношения катетов подобных треугольников получаем для тени:
(r – h)/l = (R – r)/(L – l)
откуда радиус тени
h = r – l(R – r)/(L – l) = 0.1 – 1*(0.2 – 0.1)/(5 – 1) = 0.075 м
Из соотношения катетов подобных треугольников получаем для полутени:
(R + H)/L = (R + r)/(L – l)
откуда радиус полутени
H = L(R + r)/(L – l) – R = 5*(0.2 + 0.1)/(5 – 1) – 0.2 = 0.125 м
Из красных линий видно, что раз непрозрачный шар в 2 раза меньше (линейно) светящегося, то отсутствие полной тени можно добиться, когда нижний шар висит на половине расстояния, то есть 2 метра над полом.
Вопрос сформулирован некорректно. При всех его высотах ВЫШЕ двух метров будет только полутень.
Размер полутени тоже понятен из геометрии (см синюю линию), ее радиус х составляет 25/2 * 4 = 50 см, значит полный размер (диаметр) = 1 метру
Guten tag! ШиловаУченик (101)
2 года назад
Я, конечно, дико извиняюсь, но откуда в выражении взялась 4? Если бы всё было так просто, я бы и сама догадалась о причине и как решить. Но можно, пожалуйста, указать, откуда эта четверка взялась и разъяснить что к чему и как относится. Для таких особо тупых и желающих разобраться, как я
У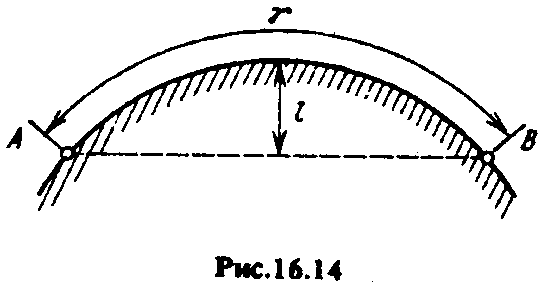
словия
распространения земной волны в этих
зонах определяются процессом дифракции
вдоль сферической полупроводящей
поверхности Земли. Расчет напряженности
поля ведется по общей дифракционной
формуле Фока
для
области как полутени, так и тени. Разница
лишь в том, что в зоне тени можно удерживать
меньшее число членов бесконечного ряда.
Ввиду сложности анализа формулы Фока
ограничимся качественными оценками
поведения поля.
Сферическую
поверхность Земли можно рассматривать
как расположенное между точками передачи
А
и
приема В
препятствие,
которое огибает волна (рис. 16.14). Процесс
огибания волной препятствия (процесс
дифракции) зависит от так называемого
электрического
размера препятствия,
т.е. от отношения l/,
где l
— высота шарового сегмента. Чем больше
l/,
тем большая часть существенного
эллипсоида перекрывается препятствием
и тем слабее дифракционная волна.
Поверхность
Земли является полупроводящей, что
приводит к оттоку энергии земной волны
из воздуха в почву. Выше отмечалось, что
с увеличением длины волны свойства
земной поверхности приближаются к
свойствам проводника, так как
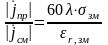
увеличивается. С учетом этих двух
обстоятельств и рассмотрим характер
изменения напряженности поля земной
волны в зонах полутени и тени в зависимости
от расстояния и длины волны.
При
увеличении расстояния напряженность
поля падает за счет прежде всего
естественной расходимости волны (как
и в свободном пространстве). Кроме того,
возрастает высота шарового сегмента l
и, следовательно, увеличиваются потери
на огибание волной данного препятствия.
И наконец, возрастают потери за счет
постепенного оттока энергии в почву. В
совокупности зависимость напряженности
поля от расстояния должна иметь убывающий
характер, причем степень убывания
зависит от длины волны. При уменьшении
длины волны, во-первых, возрастает
электрическая высота шарового сегмента
l/,
т.е.
увеличиваются дифракционные потери, а
во-вторых, свойства почвы становятся
ближе к свойствам диэлектрика, что
способствует утечке энергии волны в
почву, т.е. ослаблению поля в воздухе. В
сумме (при прочих равных условиях)
напряженность поля земной волны в зонах
полутени и тени в диапазоне УКВ должна
быть меньше, чем в диапазонах СВ и ДВ.
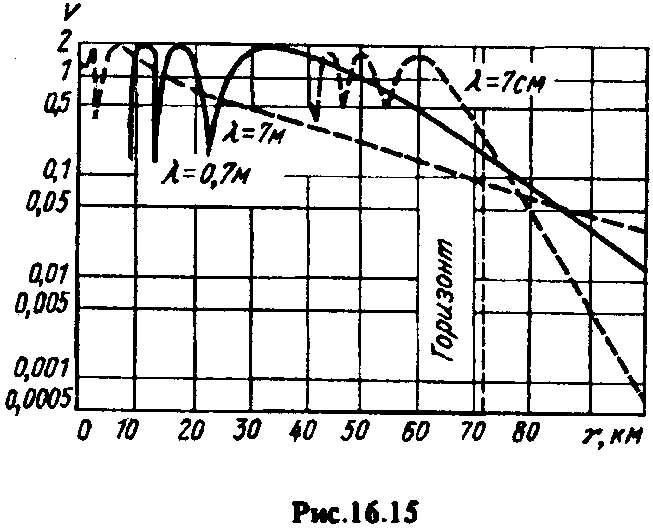
В
качестве иллюстрации на рис. 16.15 приведены
кривые зависимости модуля множителя
ослабления поля земной волны от
расстояния для трех длин волн диапазона
УКВ. Из рисунка видно, что за линией
горизонта поле быстро затухает в тысячи
и десятки тысяч раз, и тем быстрее, чем
короче волна. Напряженность поля земной
волны в диапазонах более длинных волн
(KB,
СВ, ДВ) обычно определяется по кривым
МККР, рассчитанным по дифракционной
формуле. Подводя итог, можно сказать,
что чем больше длина волны, тем на
большие расстояния за линию горизонта
проникает земная волна. Прием этой
волны на значительных удалениях от
передающей антенны практически возможен
только в диапазонах средних и длинных
волн.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

В элементах Бесселя являются геометрическими величинами , которые Фридрих Вильгельм Бессель ввел для описания местных условий во время солнечного затмения на месте наблюдения , на земле. В дополнение к солнечных затмений, принцип , связанный с этим также может быть использован для звезды или планеты покрытий со стороны Луны и транзитов от Венеры и Меркурия в передней части солнца. Вычисления, сделанные для лунных затмений , аналогичны вычислению элементов Бесселя, и в этом случае тень падает не на Землю, а на Луну.
В случае солнечных затмений, например, на основе элементов Бесселя, можно определить период покрытия в определенном месте или можно определить путь, по которому тень Луны проносится по поверхности Земли. Этот метод расчета был разработан Бесселем в 1829 году и позже усовершенствован Уильямом Шовене .
Основная идея процедуры состоит в том, что элементы Бесселя воспроизводят движение тени, вызванной покрывающими небесными телами – в солнечных затмениях это луна – на воображаемой фундаментальной плоскости. Это геоцентрическая нормальная плоскость теневой оси, в которой лежит центр Земли и которая перпендикулярна оси теневого конуса. Последняя представляет собой прямую линию, проходящую через центры закрытого и закрывающего небесного тела.
Чтобы описать движение тени в этой подходящим образом выбранной плоскости, достаточно указать сравнительно небольшое количество размеров – с достаточной точностью. Это не в последнюю очередь из-за того, что тень всегда круглая в этой плоскости на протяжении всего затмения и не подвержена никаким искажениям перспективы. На втором этапе значения для земной поверхности рассчитываются путем определения кривых пересечения теневых конусов с земной поверхностью, при этом только тогда необходимо учитывать приблизительно сферическую форму Земли, вращение Земли, а также положение и высоту места наблюдения.
сказка

Фридрих Вильгельм Бессель (1784–1846)

Уильям Шовене (1820-1870)
Этот метод описания затмений звезд и планет, а также солнечных затмений был разработан немецким ученым Фридрихом Вильгельмом Бесселем в 1820-х годах. Первую работу Бесселя по теме звездных покрытий можно найти в Astronomical News No. 50 за 1824 год, в которой он сделал некоторые вычисления на основе ранее наблюдавшихся звездных покрытий. В 1829 году он опубликовал обобщающую работу по прогнозированию звездных затмений в Astronomical News No. 145. В том же году он развил идею дальше, обобщив метод с целью применения его к планетным затмениям и солнечным затмениям.
До этого момента для расчета использовались два независимых метода с разными целями. Первый метод использовался для определения условий, как они представлялись наблюдателю в определенном месте. Используемый здесь метод восходит к Иоганнесу Кеплеру и позже был развит Жеромом Лаландом и Иоганном Готлибом Фридрихом фон Боненбергером . Второй метод, восходящий к Жозефу-Луи Лагранжу , использовался для вычисления времени соединения . Поскольку этот метод относился к центру Земли и не мог делать никаких заявлений о местных условиях на поверхности Земли, он использовался для расчета затмений реже, чем первый. Однако это упростило многие другие астрономические вычисления. Подход Бесселя теперь заключался в дальнейшем развитии метода Лагранжа таким образом, чтобы был также возможен расчет локальных условий, с помощью чего он добился комбинации обоих методов.
Во втором томе своих астрономических исследований в 1842 году Бессель опубликовал трактат из четырех разделов, озаглавленный « Анализ затмений» . В нем он резюмировал свои ранее опубликованные работы по этой теме и завершил ее некоторыми дополнениями. Эта публикация послужила основой для многих астрономов, которые позже занялись этой темой. В своей работе теории солнечных затмений и связанные с ними явлениями , опубликованной в 1858 году, Питер Андреас Хансен использовал в линии пересечения эклиптики с фундаментальной плоскостью в качестве оси, в отличии от Бесселя . Однако вариант Бесселя, использование экваториальной плоскости вместо эклиптики, имел некоторые преимущества, как указал в 1863 году американский астроном Уильям Човене . В своем Руководстве по сферической и практической астрономии он в основном следовал методу Бесселя, но разработал свои собственные подходы к решению некоторых подзадач. Презентация Chauvenet стала основой для многих дальнейших разработок в этой области.
Даже если расчеты затмений теперь производятся не вручную, а в электронном виде, элементы Бесселя не утратили своего значения. Напротив, они представляют собой связь между расчетами времени наступления затмения и расчетами местных условий.Многие компьютерные программы специализируются на одном из двух расчетов, при этом элементы Бесселя действуют как интерфейс , так сказать .
Солнечные затмения
Взаимное покрытие звезд, наблюдаемых в одном месте на земной поверхности, зависит от орбитальных данных более удаленного и более близкого. Эти даты ( эфемериды ) обычно даются как углы прямого восхождения и склонения . Эти углы относятся к центру Земли как геоцентрические координаты , так что небесный покров, который можно наблюдать в определенной точке земной поверхности, не может быть взят непосредственно из них.
Чтобы описать покрытие в точке на поверхности земли, данные об орбитах двух небесных тел, взятые из таблиц или известные иным образом, должны быть преобразованы. Элементы Бесселя используются для описания курса и размера тени и полутени на фундаментальном уровне. С одной стороны, описать ход тени в этой плоскости на основе орбитальных данных небесных тел несложно, с другой стороны, возможно очень простое преобразование в точку наблюдения. Для последнего преобразования элементы Бесселя также содержат информацию о том, как основная плоскость вращается относительно нулевого меридиана и экваториальной плоскости .
Покрытие солнца луной является наиболее сложным типом затмения с точки зрения описания условий на Земле , поскольку и закрытое тело – солнце – и покрывающее тело – луна – имеют весьма незначительные углы обзора . Кроме того, необходимо учитывать видимое движение солнца во время укрытия.
Определение элементов Бесселя

Фундаментальная плоскость с элементами Бесселя , , и
Во-первых, вводится прямоугольная система координат , которая называется фундаментальной или бесселевой системой координат . Отправной точкой является ось тени, прямая линия, соединяющая центр солнца и луны. Параллель теневой оси , которая проходит через центр Земли, представляет собой ось фундаментальной системы координат Бесселя и постоянно следует тени, так что система координат вращаются с направлением теневой оси. Основная плоскость перпендикулярна этой оси в центре Земли. В фундаментальном уровне, положение и размер тени и полутени описаны с помощью и координат. Оу является линия пересечения основной плоскости с экваториальной плоскости и указывает на восток, то ось указывает на север.
Первые две величины элементов Бесселя – это координаты и пересечение оси тени с фундаментальной плоскостью. Направление оси тени – которое соответствует направлению оси – определяется склонением и часовым углом эфемерид . Радиус конуса полутени в основной плоскости описывается, а радиус конуса тени – . отрицательна для полного затмения, положительна для кольцевого. Значения , , и , как правило , в единицах экваториального радиуса данного земли.


В дополнение к этим шести переменным, которые изменяются во время затмения, есть две другие переменные, которые можно рассматривать как постоянные: размеры и определяют угол полуоткрытия полутени или конуса тени .
Расчет элементов Бесселя
Элементы Бесселя, используемые для солнечных затмений, основаны на временном ходе геоцентрических положений Солнца и Луны, которые доступны через их эфемериды . Один из способов вычислить возникновение солнечных затмений – немедленно преобразовать положения солнца и луны в фундаментальную систему координат. Тогда можно довольно легко определить, проникает ли ось тени в фундаментальную плоскость в пределах земного шара, и когда это означает, что происходит центральное, то есть полное или кольцевое затмение.
Есть и другие способы рассчитать частоту солнечных затмений, например, используя предел затмений . Но также и в этом случае положения Солнца и Луны во время затмения должны быть преобразованы в фундаментальную систему координат, чтобы иметь возможность рассчитывать местные условия в каждом месте на Земле на основе элементов Бесселя.
На основе геоцентрических координат и расстояний от солнца и луны элементы Бесселя могут быть рассчитаны для определенного момента времени. Исходя из склонения и прямого восхождения, а также расстояния , векторы положения солнца и луны могут быть определены следующим образом:
Экваториальный радиус Земли обычно используется в качестве единицы для расстояний. В литературе расстояние часто выражается в терминах параллакса , который можно найти в таблицах эфемерид. Поскольку параллакс основан на радиусе Земли, расстояние можно вычислить в единицах сквозного экваториального радиуса .
Далее первыми из элементов Бесселя, которые должны быть вычислены, являются склонение и часовой угол эфемерид , то есть экваториальные координаты направления оси тени. Вместо того , чтобы угол часа, восхождение сначала вычисляется, из которого часовой угол может быть определен по формуле , в результате чего сидерическое время , связанные с Гринвич соответствует.


Для преобразования в основной системе координат, в единичных векторов , и , что точка в направлении осей координат этой системы координат, выражаются с помощью двух величин и :

Векторы положения солнца и луны, а также их вектор разности, соответствующий оси -ax
Поскольку направление оси -оси соответствует разнице между векторами положения от центра Земли до Солнца и Луны, единичный вектор в направлении оси -оси также можно выразить следующим образом:
Приравнивая эти два представления теперь может быть и таким образом определить все единичные векторы фундаментальной системы координат.
Используя эти единичные векторы, теперь можно определить координаты солнца и луны в этой системе координат. По определению фундаментальной плоскости, что и координаты Солнца и Луны совпадают. Они одновременно представляют собой пересечение оси тени с основной плоскостью и являются следующими определенными элементами Бесселя. Координата Луны также определяется, как это требуется для вычисления радиусов тени.

Определение углов конуса для полутени и тени ( а ); Для наглядности в каждом случае показана только одна касательная.
Углы между осью тени и касательными к солнцу и луне, которые образуют конусные оболочки полутени и тени, можно определить с помощью вспомогательного треугольника. Касательные сдвинуты параллельно, так что они проходят через центр луны (см. Рисунок справа). Гипотенуза обоих треугольников – это линия, соединяющая центр солнца и луны, противоположные катеты искомых углов образуют прямые, проходящие через центр солнца под прямым углом на параллельных смещенных касательных. В этих прямоугольных треугольниках длина двух сторон известна, с одной стороны, расстояние между Солнцем и Луной, с другой стороны, длина противоположного катета, которая соответствует сумме радиусов Солнца и Луны в случае полутени и разнице между этими двумя размерами в случае тени. Таким образом:
Для вычисления последних двух недостающих элементов Бесселя и радиусов полутени и тени в фундаментальной плоскости требуется расстояние между пересечением касательных и осью тени от фундаментальной плоскости. Для полутени эта точка, отмеченная значком, находится на оси тени между солнцем и луной и представляет собой вершину конуса полутени. Точка пересечения также находится на оси тени и является вершиной – то есть конечной точкой – тени. Применимо следующее:
Используя эти расстояния между точками и основной плоскостью, можно определить радиусы теневых конусов в этой плоскости следующим образом:
Если конус тени тени опускается за фундаментальную плоскость, если смотреть со стороны Луны, то есть если происходит полное солнечное затмение, оно отрицательное, в другом случае положительное, как в случае кольцевого солнечного затмения. В соответствии с соглашением знак радиуса тени выбирается таким образом, чтобы он был отрицательным в случае полной видимости и положительным в случае круговой видимости. Размеры а всегда положительны.
Радиус луны выбирается для расчета, который представляет собой усреднение неровностей края луны ( ). Однако, поскольку полное затмение не существует до тех пор, пока солнечные лучи, проходящие через самую глубокую лунную долину, все еще достигают места наблюдения, второе меньшее значение ( ) используется для вычисления общей зоны и продолжительности .
Публикация элементов Бесселя
Элементы Бесселя зависят от времени. Следовательно, чтобы описать затмение, они должны быть указаны для периода времени, который, например, включает несколько часов для полного описания солнечного затмения.
Существуют разные версии публикации бесселевых элементов солнечного затмения. В некоторых случаях значение не все (так, чтобы считать постоянными элементы , , , , и ) приведено в часовых интервалах в течение всего курса Darkness стола. Промежуточные значения можно интерполировать .
Другой вариант – указать элементы Бесселя для эталонного времени ( ), например, полный час, ближайший к максимуму земного времени (TT), а также почасовые изменения для всех элементов, которые не считаются постоянными. Это позволяет вычислять значения для других моментов времени в ходе затмения как линейную функцию времени.
Спецификация в полиномиальной форме позволяет получить несколько более точное приближение по сравнению с линейной интерполяцией. В дополнение к текущему значению для переменных величин указывается до трех полиномиальных коэффициентов. Расчет стоимости в определенный момент времени выполняется в следующей форме:
Одна из переменных величин соответствует разнице времени в часах.
На практике, часто в Goddard Space Flight Center из НАСА прибегли элементы , опубликованные в полиномиально Бесселе. Меры, принятые в опубликованном астрономическом альманахе, элементы Бесселя по практическим соображениям уже используют кандидатные тригонометрические функции ( синус и косинус указаны), а также размеры , которые можно рассматривать для всего курса затмения приблизительно как постоянные ежечасные изменения размеров и .
Пример применения элементов Бесселя
В следующем примере элементы Бесселя вычисляются для данного момента времени, так что положение и размер конуса тени и полутени в основной плоскости известны в этот момент времени. Затем для практических приложений необходимо исследовать, как точки на земной поверхности лежат относительно этих теневых конусов. Все необходимые для этого размеры задаются геометрией земли. В примере проверяется, находится ли данное местоположение в пределах конуса тени.
Определение элементов Бесселя на определенный момент времени
 |
 |
 |
 |
 |
 |

|
|---|---|---|---|---|---|---|
| 0 | 0,0700420 | 0,5028410 | 15,327340 | 0,5424690 | -0,0036500 | 343,687410 |
| 1 | 0,5443035 | -0,1184929 | −0,012035 | 0,0001168 | 0,0001163 | 15,002982 |
| 2 | −0,0000406 | −0,0001158 | -0,000003 | −0,0000117 | -0,0000116 | |
| 3 | −0,0000081 | 0,0000017 | ||||
 = 0,0046129; = 0,0045900 = 0,0046129; = 0,0045900 |
В соседней таблице приведены элементы Бесселя солнечного затмения 11 августа 1999 г. в полиномиальной форме. Теперь цель состоит в том, чтобы вычислить положение тени в основной плоскости для 12:34:03 CEST (соответствует 10:34:03 UT).
Прежде всего, необходимо определить разницу с эталонным временем (11: 00: 00: 00 DD ). Необходимо принять во внимание разницу между TT и всемирным временем (UT), которая на момент затмения составляла 63,7 секунды:
Координаты пересечения оси тени с основной плоскостью за желаемое время рассчитываются следующим образом:
Аналогичным образом рассчитываются склонение и часовой угол (значения , отсутствующие в таблице, должны быть установлены на 0):
Радиус тени в фундаментальной плоскости теперь также можно рассчитать для этого момента времени:
Радиус полутени можно рассчитать аналогичным образом, но для следующего расчета это не требуется.
Проверить, находится ли данная точка в зоне тотальности в это время
На первом этапе элементы Бесселя затмения 11 августа 1999 г. были рассчитаны для 12:34:03 CEST. Теперь следует проверить, была ли Штутгартская площадь Шлосплац ( 48 ° 46 ‘42,8 ” с.ш. , 9 ° 10′ 47,7″ в.д. ) в зоне тотальности в этот момент времени. Для этого координаты замковой площади переводятся в основную систему координат. Как только эти координаты определены, можно легко определить, находится ли эта точка внутри теневого конуса, поскольку ось тени по определению перпендикулярна фундаментальной плоскости.
Прежде всего, данные геодезические координаты замковой площади ( = 48,77855 ° и = 9,17991 °), включая высоту эллипса ( = 295 м), должны быть преобразованы в геоцентрические сферические координаты ( и ) при неизменной длине . Для этой цели численного эксцентриситета от Земли эллипсоида вращения и два других широт зависящих от вспомогательных переменных , полученного из него используется:

Связь между геодезической широтой и геоцентрической широтой
- Здесь экваториальный радиус и полярный радиус.
При радиусе экватора = 6378137 м геоцентрические координаты можно рассчитать следующим образом:
Он выражает расстояние от Шлосплац до центра Земли в единицах экваториального радиуса, представляет собой угол между экваториальной плоскостью и вектором положения, указывающим от центра Земли до Шлосплац .
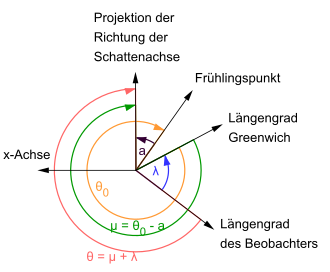
Часовой угол места наблюдения относительно оси основной системы координат теперь определяется как вспомогательная переменная . Следует отметить , что с элементами Бесселя, угол часа рассчитываются предполагая эфемерида день ( что соответствует земному времени, ранее: эфемериды времени). Однако, поскольку реальное вращение Земли не совсем регулярное, сначала необходимо скорректировать разницу во времени между земным временем и всемирным временем, что соответствует. Длина сидерического дня является решающей для расчета соответствующей угловой поправки ; разница с синодической продолжительностью дня ( солнечный день ) учитывается с коэффициентом 1.002738. Фактически, географическая долгота наблюдателя ( ) должна быть вычтена, но поскольку оба угла измеряются в противоположных направлениях, это добавление.
Итак, пусть декартовы координаты , и замок площади в основной системе координат, определенной после наклона основной плоскости по отношению к системе координат геодезических по склонению учитывается:
Радиус пересечения конуса тени в плоскости, проходящей через квадрат замка, параллельной основной плоскости, ближе к солнцу и луне и, следовательно, несколько больше, чем радиус тени в фундаментальной плоскости. Его можно рассчитать на основе угла конуса теневого конуса ( ), указанного в элементах Бесселя, и расстояния между замковым квадратом и фундаментальной плоскостью ( ). Следует отметить, что при полном затмении радиус тени по определению отрицательный.
Расстояние между замковым квадратом и осью тени в одной плоскости можно определить следующим образом:
Поскольку расстояние между квадратами замка на этом уровне меньше, чем радиус теневого конуса, квадрат замка в данный момент находился внутри тени ядра. Однако из-за того, что в то время в Штутгарте шел дождь, на Шлоссплац было невозможно наблюдать затемненное солнце.
Выполняя эти вычисления итеративно в течение определенного периода времени, в принципе можно определить время контакта в конкретном месте. Однако существуют и прямые методы расчета времени контакта.
Дальнейшие небесные покровы луной
Звездные затмения луной

Цилиндр тени со звездной окклюзией
В случае звездных затмений расчет элементов Бесселя может быть значительно упрощен по сравнению с солнечными затмениями, поскольку достаточно точно рассматривать закрытое небесное тело как бесконечно удаленное. Это предположение позволяет считать лучи света от удаленного объекта, достигающие системы Земля-Луна, параллельными. Это означает, что направление оси тени , то есть оси фундаментальной системы координат Бесселя, всегда указывает точно в направлении звезды в течение всего периода затмения и, следовательно, с самого начала задается экваториальными координатами звезды.
Другое упрощение по сравнению с солнечным затмением состоит в том, что не нужно описывать конус тени и полутени, но достаточно понимать «тень» как цилиндр , перпендикулярный фундаментальной плоскости . Радиус этого цилиндра равен радиусу Луны, который составляет 0,2725 экваториального радиуса Земли. Нет необходимости указывать переменные радиусы тени или углы раскрытия.
Фундаментальная плоскость выбирается аналогично солнечным затмениям, то есть нормальная плоскость этой теневой оси, проходящей через центр Земли. Линия пересечения фундаментальной плоскости с экваториальной плоскостью – это ось-ось, направленная на восток, перпендикулярная ей в центре Земли – ось-ось и указывает на север. Как и в случае с солнечными затмениями, вся информация в этой системе координат дается в единицах экваториального радиуса.
В отличие от солнечного затмения, отсчетным временем для элементов Бесселя часто является не полный час, а время соединения в прямом восхождении , то есть время, в которое звезда и луна имеют одинаковое прямое восхождение . В этот момент времени координата оси цилиндра имеет значение 0, поэтому в таблицах указывается только координата оси цилиндра в основной плоскости. Затем элементы Бесселя звездного затмения определяются следующим образом:
Для прогнозных расчетов этого достаточно, и он должен считаться постоянным в течение всего периода покрытия.
Планеты покрыты луной
Метод элементов Бесселя можно применить к любому небесному покрову, если оба небесных тела достаточно точно сферические. Вам нужно только заменить положение и размер солнца на рассматриваемую планету. В качестве исключения Бессель назвал планеты Юпитер и Сатурн только в 1842 году , поскольку их отклонение от сферической формы в то время было измеримо. Чтобы предсказать область видимости для покрытий планет Луной, можно использовать ту же упрощенную процедуру, что и для покрытий звезд (см. Выше ).
Однако для точного определения времени контакта необходимо учитывать любые отклонения планеты от сферической формы, а также то, какая часть планетарного диска освещается солнцем в момент ее покрытия. Этот метод был описан Шовене в 1865 году, потому что метод Бесселя уже не был достаточно точным для методов наблюдения, которые к тому времени стали более точными. Та часть планеты, которая освещена солнцем и видима с Земли, рассматривается напрямую, а не отображается на фундаментальной плоскости.
Транзит низших планет
Во время прохождения нижних планет Венеры и Меркурия перед Солнцем покровным небесным телом является планета. Это никогда не может полностью закрыть солнце, потому что тень слишком коротка, чтобы упасть на землю. Элементы Бесселя также используются для этих астрономических событий для расчета местных условий. Можно использовать тот же метод расчета, что и для солнечных затмений, когда планета играет роль луны.
Поскольку расстояние нижних планет от Земли намного больше, чем расстояние до Луны, существует возможность упрощенного расчета времен входа и выхода планетарного диска перед Солнцем во время транзитов. Этот метод работает без преобразования эфемерид в фундаментальную систему координат Бесселя. При этом используется используется тот факт , что квадрат или выше потенции поднятый параллакс планеты настолько мала , что ею можно пренебречь. На основе времени контакта, относящегося к центру Земли, соответствующие моменты времени могут быть рассчитаны таким образом в каждой точке Земли. Принцип этого упрощенного вычисления восходит к Лагранжу и был улучшен Уильямом Шовене , приняв во внимание уплощение земли.
Лунные затмения
Во время лунного затмения на небесном теле находится земной наблюдатель, отбрасывающий тень. Таким образом, виден один и тот же курс затмения из всех мест на Земле при условии, что видна Луна. При вычислении лунных затмений определяются соответствующие углы обзора ( полярные координаты ), что аналогично определению элементов Бесселя ( декартовых координат в фундаментальной плоскости Бесселя). Именно поэтому углы обзора, используемые для лунных затмений, иногда также называют элементами Бесселя. Однако фундаментальная плоскость не используется ни для Земли, ни для Луны, и описание лунных затмений обычно осуществляется исключительно в полярных координатах.
Как и в случае с солнечными затмениями, фундаментальная система координат относится к оси тени, которая в лунных затмениях всегда проходит через центр Земли. Расчет аналогичен расчету для солнечных затмений. В этом случае прямое восхождение и наклон оси тени являются прямым результатом соответствующих значений солнца, но ось -0 указывает от солнца. Таким образом:
Так же, как и с солнечными затмениями, вектор геоцентрического положения Луны можно преобразовать в фундаментальную систему. Положение центра Луны по отношению к теневой оси может быть определено с помощью его и компонентов. Поскольку все используемые углы имеют вершину в центре Земли, в отличие от солнечных затмений, для преобразования не требуется информация о длине. Координаты и относятся к единичной сфере . Углы, полученные из этого, даны в угловых секундах . За исключением пропущенного преобразования единиц, используемые формулы соответствуют тем, которые используются для солнечного затмения.
Отсюда можно рассчитать угловое расстояние между центром луны и осью тени:

Геометрия тени лунного затмения
Размеры радиусов полутени и тени также задаются как геоцентрические углы обзора. Размеры и описывают угол обзора радиусов тени на лунной орбите. На иллюстрации напротив пунктирная линия указывает орбиту Луны. Угол – это угол обзора радиуса Земли, если смотреть с Луны, и, следовательно, соответствует параллаксу Луны. Поскольку этот угол является внешним углом треугольника , применяется к углу обзора тени на лунной орбите.
-
,
где – половина угла раскрытия конуса тени. Аналогично, другое угловое соотношение может быть получено из треугольника : внешний угол соответствует углу обзора радиуса Солнца от Земли, углу к геоцентрическому параллаксу Солнца. Таким образом:
Теперь желаемый угол можно определить из обоих угловых соотношений, исключив угол конуса :
Аналогичным образом можно определить и геоцентрический угол обзора радиуса полутени на лунной орбите. Для этого получаются следующие отношения:

Элементы Бесселя для времени контакта при лунном затмении
Для определения времени контакта затмения три дополнительных вспомогательных переменных выводятся из размеров тени и полутени и радиуса Луны. Это углы обзора для расстояния центра луны от оси тени во время данного контакта, которые вычисляются из углов обзора радиусов тени и угла обзора радиуса луны:
-
Вход и выход Луны за полутень
-
Вход и выход луны для тени
-
Начало и конец полной темноты
Размеры , , , , , , и , и , и – часовые скорости изменения для соответствующих размеров – считаются бесселевы элементами лунного затмения. Они даны для отсчета времени, например, времени противостояния Луны . Однако, в отличие от солнечных затмений, не существует общепризнанного способа задания параметров.
В представленных до сих пор расчетах использовались только углы к оси тени и не определялась фундаментальная плоскость. Если вы хотите рассчитать, когда определенные лунные кратеры – то есть выступающие точки на лунной поверхности – входят или выходят из тени, это возможно, если вы выберете фундаментальную плоскость так, чтобы она проходила через центр Луны – аналогично точкам на поверхности Земли на Солнечные затмения.
При проверке расчетного времени контакта и, в частности, времени входа и выхода определенных лунных кратеров в тень и из нее, данные, рассчитанные таким образом, не показывают какого-либо полезного соответствия с реальностью. С одной стороны, это связано с тем, что Земля не отбрасывает достаточно круглую тень из-за ее уплощения . Во-вторых, это связано с земной атмосферой , которая увеличивает теневые конусы. Чтобы компенсировать эти эффекты, принято вводить два поправочных коэффициента в формулы для расчета размеров полутени и конуса тени, где коэффициент 1,02 – это увеличение земной тени под влиянием земной атмосферы на 1/50, а коэффициент 0, 998340 предназначен для компенсации выравнивания земли в среднем значении между экватором и диаметром полюса:
Андре Данжон указал в 1951 году, что для того, чтобы учесть влияние земной атмосферы, два теневых конуса не должны быть увеличены на одинаковую относительную величину 1/50, а скорее увеличение на ту же абсолютную величину соответствует фактическим геометрическим соотношениям. Данжон предполагает слой земной атмосферы высотой 75 километров, обладающий поглощающим эффектом, который соответствует увеличению радиуса Земли или параллакса Луны на 1/85. Коэффициент 1,01 объединяет это увеличение с коэффициентом выравнивания земли:
Размеры затмений для затмений тени, которые рассчитываются в соответствии с правилом 1/50, примерно на 0,005 больше по сравнению с расчетом по Данжону для полутеневых затмений около 0,026.
Но даже данные, рассчитанные таким образом, еще не показывают особенно точного соответствия действительности. В основном это связано с тем, что сглаживание земной атмосферы все еще значительно больше, чем сглаживание земной поверхности. Делается попытка разработать более точный метод коррекции на основе данных наблюдений различных лунных затмений.
Замечания
-
↑ Обычно за основу берутся эфемериды (DE200 / LE200), опубликованные Лабораторией реактивного движения . Эти эфемериды относятся к центрам масс небесных тел. Однако для затмений решающим является центр лунного, планетарного или солнечного диска. Это имеет разрушительный эффект в случае Луны, центр масс которой примерно на два километра ближе к Земле, чем ее геометрический центр. Величина вызванного этим отклонения указывает на связь с либрацией . Если такие поправки к координатам Луны производились при расчете элементов Бесселя, то это указывается ( и ).
- ↑ Эллипсоидальная высота Штутгарта примерно на 49 м выше, чем высота NHN или NN .
-
↑ Обратите внимание, что это исправление уже может быть включено в табличное представление элементов Бесселя, например, в Астрономический альманах .
- ↑ Данжон использует значение 1/297 для выравнивания земли; среднее значение между экватором и диаметром земли составляет 0,5 x 1/297 = 1/594, чтобы скорректировать размер тени. Это приводит к увеличению тени 1 + 1/85 – 1/594 ~ 1.01.
литература
- П. Кеннет Зайдельманн (ред.): Пояснительное приложение к астрономическому альманаху. Научные книги университета, Саусалито 2006, ISBN 1-891389-45-9
- Робин М. Грин: Сферическая астрономия. Издательство Кембриджского университета, Кембридж 1985, ISBN 0-521-23988-5
- Уильям Шовене: Руководство по сферической и практической астрономии. JB Lippincott & Co, Филадельфия, 1863 г., books.google.de
- Жан Миус : Элементы солнечных затмений 1951-2200 гг. Willmann-Bell, Richmond 1989, ISBN 0-943396-21-2 (с расчетным методом и элементами Бесселя всех солнечных плавников между 1951 и 2200 гг.)
- Жан Миус: Транзиты . Willmann-Bell, Richmond 1989, ISBN 0-943396-25-5 (с расчетным методом и элементами Бесселя всех транзитов Меркурия в период с 1600 по 2300 и всех транзитов Венеры от -2000 до 4000.)
- Жан Миус: Астрономические таблицы Солнца, Луны и планет, 3-е издание. Willmann-Bell, Richmond 20015, ISBN 978-1-942675-03-7 (с методом расчета и элементами Бесселя для покрытий ярких звезд в период с 2010 по 2040 год).
Индивидуальные доказательства
- ↑ a b c d e f Герман Мук , Жан Миус : Канон солнечных затмений: от -2003 до +2526. Astronomisches Büro, Вена, 1992, стр. XXXIII – LI.
- ↑ a b c d e Майкл Альтманн: Яркость во время солнечных затмений (II) (PDF; 71 kB)
- ↑ Фридрих Вильгельм Бессель: Расчет различных звездных покрытий господами Розенбергером, Штрелке и Клупсом. В: Astronomische Nachrichten , № 50, 3, февраль 1824 г., стр. 17–28, bibcode : 1824AN …… 3 … 17R (доступен полный текст)
- ↑ Фридрих Вильгельм Бессель: О предварительном расчете звездных покрытий. В: Astronomische Nachrichten , № 145, 7, сентябрь 1828 г., стр. 1–16, bibcode : 1828AN …… 7 …. 1B (доступен полный текст)
- ↑ a b Фридрих Вильгельм Бессель: Вклад в теорию затмений и методы их расчета. В: Astronomische Nachrichten , № 151, 7 января 1829 г., стр. 121–136, bibcode : 1829AN …… 7..119. (Доступен полный текст)
- ^ Фридрих Вильгельм Бессель: Вклад в теорию затмений и методы расчета того же (решение). В: Astronomische Nachrichten , № 152, 7 февраля 1829 г., стр. 137–144, bibcode : 1829AN …… 7..137B (доступен полный текст)
- ^ A b Фридрих Вильгельм Бессель: Астрономические исследования. Том 2, Кенигсберг 1842 г. ( books.google.de )
- ^ Робердо Бьюкенен: Математическая теория затмений в соответствии с преобразованием Шовене метода Бесселя. С. 17 ф., Филадельфия / Лондон 1904 г.
- ↑ Фред Эспеник: Бесселианские элементы солнечных затмений . НАСА
- ↑ а б в г Робин М. Грин: Сферическая астрономия. С. 459 и сл., См. Литературу
- ^ П. Кеннет Зайдельманн: пояснительное приложение к астрономическому альманаху. С. 424 е., См. Литературу
- ^ A b П. Кеннет Зайдельманн: Пояснительное приложение к астрономическому альманаху. С. 435-441, см. Литературу.
- ↑ б с д е е г Robin M. Green: сферическая астрономия. С. 450-453, см. Литературу.
- ↑ Отто Праксль солнечные и лунные затмения.
- ↑ Фред Эспенак, Джей Андерсон: Полное солнечное затмение 1 августа 2008 г. (PDF; 7,8 МБ) март 2007 г., стр. 6
- ^ Жан Meeus, Карл Грожан, Вилли Vanderleen: Канон солнечных затмений. Pergamon Press, Оксфорд, 1966 г.
- ^ Веб-сайт NASA Eclipse
- ↑ Astronomical Almanac 2005. S. A78ff., Stationery Office Books, 2003 ( books.google.de )
- ↑ Фред Эспеник (НАСА): Бесселианские элементы для полного солнечного затмения 11 августа 1999 г.
- ^ A b П. Кеннет Зайдельманн: Пояснительное приложение к астрономическому альманаху. Страницы 441–446, см. Литературу
- ↑ Шай Софи – солнечное затмение в Штутгарте . ( Memento из в оригинале от 3 июля 2010 года в Internet Archive ) Info: архив ссылка автоматически вставляется и еще не проверен. Проверьте исходную ссылку и ссылку на архив в соответствии с инструкциями, а затем удалите это уведомление. von-zeit-zu-zeit.de
- ^ A b c П. Кеннет Зайдельманн: Пояснительное приложение к астрономическому альманаху. Страницы 494–497, см. Литературу
- ^ Уильям Човене: Руководство по сферической и практической астрономии. С. 565, см. Литературу
- ^ Жан Миус: Транзиты . Willmann-Bell, 1989, ISBN 0-943396-26-3
- ^ A b Уильям Шовене: Руководство по сферической и практической астрономии. Стр. 593-598, см. Литературу.
- ^ П. Кеннет Зайдельманн: Пояснительное приложение к астрономическому альманаху. С. 471, см. Литературу
- ↑ б с д е е П. Кеннета Seidelmann: пояснительная Дополнение к астрономическому альманаху. Стр. 467-470.
- ^ A b Робин М. Грин: Сферическая астрономия. Страница 441f, см. Литературу
- ^ П. Кеннет Зайдельманн: Пояснительное приложение к астрономическому альманаху. Страницы 428–431, см. Литературу
- ↑ А. Данжон: Les Eclipses de Lune par la pénombre en 1951. В: L’Astronomie , 65, p. 51-53
- ^ J. Meeus, H. Mucke: Канон лунных затмений -2002 до +2526 , страница XXIV
- ^ Байрон В. Соулсби: Улучшенные эфемериды лунных затмений. В: Журнал Британской астрономической ассоциации. , 100, 1990, pp. 293–305 , bibcode : 1990JBAA..100..293S (доступен полный текст / PDF; 2,0 МБ)
Тип 30 № 2950 

i
Электролампа помещена в матовый шар радиусом 20 см и подвешена на высоте 5 м над полом. Под лампой на высоте 1 м от пола висит непрозрачный шар радиуса 10 см. Найти размеры тени и полутени на полу.
Спрятать решение
Решение.
Видеорешение: https://youtu.be/OoR42yq4Lx4?t=111
Ответ: Диаметр тени 15 см, внешний диаметр полутени 35 см.
Источник: Кирик Л. А. Самостоятельные и контрольные работы для 8 класса, Х.: «Гимназия», 2001 (№ 3 (высок.) стр. 93)


































































































