Решение: на шарик в верхней точке траектории действует две силы: mg – сила тяжести, направленная вертикально вниз и T – сила натяжения нити, направленная вдоль нити. Ускорение тела при движении по дуге окружности можно разложить на два слагаемых:
[ vec{a}={{vec{a}}_{tau }}+{{vec{a}}_{n}}. ]
Тангенциальное ускорение aτ — направлено по касательной к траектории и характеризует изменение скорости по модулю. Центростремительное или нормальное ускорение an — возникает всегда при движении точки по дуге окружности конечного радиуса, характеризует изменение скорости по направлению и направлено перпендикулярно вектору мгновенной скорости (к центру окружности).
В нижней точке траектории у тела только центростремительное ускорение, т.е.
[ a=frac{{{upsilon }^{2}}}{l},text{ }(1) ]
Где l – длина нити. В верхней точке траектории скорость тела равна нулю (υ = 0), тогда центростремительное ускорение тела тоже равно нулю.
[ {{a}_{n}}=frac{{{upsilon }^{2}}}{l}=0. ]
Тогда ускорение шарика в верхней точке равно тангенциальному:
a1 = aτ.
Ось z направим по касательной к траектории. Запишем второй закон Ньютона в векторном виде и спроецируем его на выбранную координатную ось.
[ vec{T}+mvec{g}=mcdot {{vec{a}}_{1}},text{ }mgcdot sin alpha =mcdot {{a}_{tau }},text{ }{{a}_{1}}={{a}_{tau }}=gcdot sin alpha . ]
Остаётся определить угол отклонения α нити от вертикали в верхнем положении. Для этого запишем закон сохранения энергии (за нулевой уровень потенциальной энергии примем нижнее положение шарика), тогда в нижней точке – только кинетическая энергия, в верхней точке – только потенциальная. Как видно из рисунка, высота подъёма шарика равна
[ h=l-lcdot cos alpha =lcdot left( 1-cos alpha right). ]
Тогда
[ begin{align}
& {{E}_{0}}={{E}_{1}},text{ }frac{mcdot {{upsilon }^{2}}}{2}=mcdot gcdot h,text{ } \
& text{ }frac{{{upsilon }^{2}}}{2}=gcdot lcdot left( 1-cos alpha right),text{ }frac{{{upsilon }^{2}}}{2cdot gcdot l}=1-cos alpha \
end{align} ]
Таким образом, с учётом (1), получим (используя основное тригонометрическое тождество)
[ 1-cos alpha =frac{1}{2cdot g}cdot frac{{{upsilon }^{2}}}{l},cos alpha =1-frac{a}{2cdot g},sin alpha =sqrt{1-{{cos }^{2}}alpha }=sqrt{1-{{left( 1-frac{a}{2cdot g} right)}^{2}}}. ]
Искомое ускорение
[ {{a}_{1}}=gcdot sin alpha =gcdot sqrt{1-{{left( 1-frac{a}{2cdot g} right)}^{2}}}. ]
[ {{a}_{1}}=9,8cdot sqrt{1-{{left( 1-frac{4}{2cdot 9,8} right)}^{2}}}=5,9. ]
Ответ: a = 5,9 м/с2
« Последнее редактирование: 06 Мая 2016, 06:18 от alsak »
Записан
Условие задачи:
Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения в крайнем и нижнем положениях равны по модулю друг другу, а сила натяжения в нижнем положении равна (T). Угол отклонения нити в крайнем положении равен (alpha). Чему равна масса шарика?
Задача №2.7.57 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(a_1=a_2), (T), (alpha), (m-?)
Решение задачи:
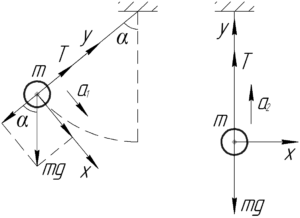Изобразим схему к задаче, на которой покажем крайнее и нижнее положении колеблющегося шарика.
Сначала рассмотрим крайнее положение (часть схемы слева). Чтобы найти ускорение шарика (a_1) в этом положении введем ось (y) по направлению нити, а ось (x) – перпендикулярно ей. Так как в этой точке у шарика нет скорости, значит отсутствует и центростремительное (нормальное) ускорение (a_ц). Тогда применив второй закон Ньютона в проекции на ось (x), найдем тангенциальную составляющую ускорения (или просто ускорение (a_1)):
[mg cdot sin alpha = m{a_1}]
[{a_1} = g cdot sin alpha ]
Для нижнего положения шарика введем оси как показано на правой части схемы. Вдоль оси (x) силы не действуют, значит нет тангенциального ускорения. Раз так, значит ускорение шарика (a_2) равно центростремительному (нормальному) ускорению в этой точке. Запишем второй закон Ньютона в проекции на ось (y):
[T – mg = m{a_2};;;;(1)]
[{a_2} = frac{T}{m} – g]
По условию (a_1=a_2), поэтому:
[g cdot sin alpha = frac{T}{m} – g]
[gleft( {1 + sin alpha } right) = frac{T}{m}]
[m = frac{T}{{gleft( {1 + sin alpha } right)}}]
Задача решена в общем виде.
Ответ: (m = frac{T}{{gleft( {1 + sin alpha } right)}}).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.56 Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную
2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с
2.8.2 Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули
Тип 5 № 282 
i
Как направлено ускорение качающегося на нити шарика (см. рисунок) в точках А, В, С? Точка А — крайняя точка траектории. Для точки В дайте качественный ответ.
Спрятать решение
Решение.
Видеорешение: https://youtu.be/CsM8hKs1P9A?t=83
Источник: Гельфгат И. М. Сборник задач по физике для 9 класса, Х.: «Гимназия», 2002 (9.17)
Маленький шарик, подвешенный на нити, движется по окружности так, что нить
Условие задачи:
Маленький шарик, подвешенный на нити, движется по окружности так, что нить составляет с вертикалью постоянный угол 30°. Другой такой же шарик, подвешенный на нити такой же длины, движется так, что его нить составляет с вертикалью постоянный угол 45°. Во сколько раз кинетическая энергия второго шарика больше, чем первого?
Задача №2.4.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
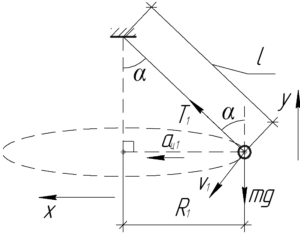Очевидно, что отношение кинетических энергий шариков будет равно отношению квадратов скоростей шариков, поскольку их массы одинаковы.
Смысла рассматривать оба шарика нет – достаточно рассмотреть только первый (для него и приведен рисунок). Запишем первый закон Ньютона в проекции на ось (y) и второй закон Ньютона в проекции на ось (x):
[left< begin
T_1 cdot cos alpha = mg hfill \
T_1 cdot sin alpha = m> hfill \
end right.]
Если первый шарик движется равномерно по окружности со скоростью (upsilon), то действующее на него центростремительное ускорение (a_ц) равно:
Система примет такой вид:
[left< begin
T_1 cdot cos alpha = mg hfill \
T_1 cdot sin alpha = mfrac<<upsilon _1^2>> hfill \
end right.]
Поделим нижнее равенство на верхнее, тогда:
На схеме видно, что радиус (R_1) равен:
[upsilon _1^2 = gl cdot sin alpha cdot tgalpha ;;;;(2)]
Для второго шарика, произведя аналогичные действия, вы получите:
[upsilon _2^2 = gl cdot sin beta cdot tgbeta ;;;;(3)]
Подставим полученные выражения (2) и (3) в (1), тогда:
Осталось посчитать ответ:
Ответ: в 2,45 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Равнодействующая сила, действующая на шарик, привязанный к нити и движущийся по окружности в горизонтальной плоскости с постоянной по модулю скоростью имеет направление : 1вертикально вниз?
Физика | 10 – 11 классы
Равнодействующая сила, действующая на шарик, привязанный к нити и движущийся по окружности в горизонтальной плоскости с постоянной по модулю скоростью имеет направление : 1вертикально вниз.
2 горизонтально по касательной к окружности.
3 горизонтально по радиусу к центру окружности.
4равнодействующая равна ноль.
Равнодействующая сила, действующая на шарик, привязанный к нити движущийся с постоянной по модулюскоростью поокружности в горизонтальной скоростью направлена горизонтально по радиусу к центру окружности (mV ^ 2 / R = T + mg – в векторной форме).
Если тело движется по окружности с постоянной по модулю скоростью то равнодействующая всех сил действующих на тело 1) равна 0 2)постоянна по модулю и направленна вдоль вектора оси 3) постоянна по моду?
Если тело движется по окружности с постоянной по модулю скоростью то равнодействующая всех сил действующих на тело 1) равна 0 2)постоянна по модулю и направленна вдоль вектора оси 3) постоянна по модулю и направленна по радиусу к центру окружности 4) постоянна по модулю и направлена от центра окружности.
, очень надо помогитеШар, подвешенный на нити, равномерно движется по окружности в горизонтальной плоскости?
, очень надо помогите
Шар, подвешенный на нити, равномерно движется по окружности в горизонтальной плоскости.
Какое направление имеет вектор равнодействующей всех сил, приложенных к нему ?
Варианты ответов : 2 Равнодействующая всех сил равна нулю.
Как направлена равнодействующая сил, приложенных к автомобилю, если он движется горизонтально вправо, равноускоренно прямолинейно с уменьшающейся по модулю скоростью?
Как направлена равнодействующая сил, приложенных к автомобилю, если он движется горизонтально вправо, равноускоренно прямолинейно с уменьшающейся по модулю скоростью?
А. Горизонтально влево
На тело, находящиееся на горизонтальной плоскости, действуют три горизонтальные силы(см?
На тело, находящиееся на горизонтальной плоскости, действуют три горизонтальные силы(см.
Каков модуль равнодействующей этих сил, если F1 = 1 H.
ОТВЕТ : корень из 10 Н.
Шарик массой 200 г, привязанный нитью к подвесу, движется с постоянной скоростью, описывая в горизонтальной плоскости окружность?
Шарик массой 200 г, привязанный нитью к подвесу, движется с постоянной скоростью, описывая в горизонтальной плоскости окружность.
Определите скорость шарика и период его вращения по окружности, если длина нити 1 м, а ее угол с вертикалью составляет 60 градусов.
С подробным решением, пожалуйста.
Вагонетка массой 5 т движется с постояннгой по модулю скоростью 5 м / с по горизонтальным рельсам, проложенным по дуге окружности радиусом 100 м?
Вагонетка массой 5 т движется с постояннгой по модулю скоростью 5 м / с по горизонтальным рельсам, проложенным по дуге окружности радиусом 100 м.
Чему равен модуль силы с которой рельсы действуют на вагонетку в направлении на центр окружности?
На движущийся автомобиль в горизонтальном направлении действует сила тяги 1200Н и сила сопротивления движения 1кН?
На движущийся автомобиль в горизонтальном направлении действует сила тяги 1200Н и сила сопротивления движения 1кН.
Чему равна равнодействующая этих сил?
Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью?
Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью.
Как направлен вектор ускорения самолета?
Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью?
Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью.
Как направлен вектор ускорения самолета?
Шар, подвешенный на нити, движется равномерно по окружности в горизонтальной плоскости?
Шар, подвешенный на нити, движется равномерно по окружности в горизонтальной плоскости.
Какое направление имеет вектор равнодействующей всех приложенных к нему сил.
На этой странице сайта размещен вопрос Равнодействующая сила, действующая на шарик, привязанный к нити и движущийся по окружности в горизонтальной плоскости с постоянной по модулю скоростью имеет направление : 1вертикально вниз? из категории Физика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 – 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.
Дано : s1 = 120 м s2 = 360 м t1 = 10 c t2 = 1, 5 мин = 90 с v(ср) – ? Решение : v(cp) = s / v s = s1 + s2 s = 120 + 360 = 480 (м) t = t1 + t2 = 10 + 90 = 100 (c) v(cp) = 480 / 100 = 4, 8 (м / с) Ответ : 4, 8 м / с.
F = mg = 24 * 10 = 240H Не забудь поблагодарить ; ).
Тут все относительно, а так : никак не меняется.
Решение на фото.
Q = cm / t Q = 920 * 2000 * 280 = 515200000.
Средняя скорость равна (4 + 3) / 2 = 3, 5 км / ч.
1) m * g = I * B * L I = m * g / B * L = 2 * 10 ^ – 3 * 10 / 0, 1 * 0, 2 = 1A 2) заряд нового ядра 91 – (5 * 2 – 2) = 83 массовое число А = 231 – (4 * 5) = 211 имеем 211 / 83 Bi 3 T = 2 * pi * sqrt(L * C) (1) C * Um ^ 2 / 2 = l * Im ^ 2 / 2 C = Im ^ ..
Нет, так как приложены к разным телам.
E = F / q E = 2 * 10 ^ – 8(H) / 10 ^ – 9(Кл) = 20(H / Кл) Ответ : г.
За первую секунду : v0 = 0 (скорость в начале секунды)t = 1 (время движения за первую секунду)Пройденный путь : S0 = v0 * t + (g * t ^ 2) / 2 = (g * t ^ 2) / 2 = 10 * 1 / 2 = 5 За последнюю секундуvp – скорость в начале последней секундыt = 1время дв..
Применение принципа Даламбера к решению задач на криволинейное движение точки
Условие задачи
Шарик А, масса которого 2 кг, подвешен на нити длиной 60 см, закрепленной в точке В. Он равномерно двигается по окружности в горизонтальной плоскости так, что нить описывает коническую поверхность и образует с вертикалью угол α=30°. Определить натяжение нити и скорость шарика.
Решение 1 (с применением метода проекций)
1. Если масса шарика m=2 кг, то его вес G=mg=2*9,81=19,62 н. Кроме веса, на шарик действует натяжение (реакция T) нити. Длина нити l=60 см=0,6 м.
Изобразим двигающийся шарик с приложенными к нему силами G и T (рис. 250, а). Так как шарик движется по окружности равномерно, то он имеет только нормальное ускорение an, направленное по радиусу АО=r окружности. Применяя принцип Даламбера, для уравновешивания сил T и G приложим к шарику нормальную (центробежную) силу инерции Pn и .
Изображая на рис. 250 силу инерции, необходимо учитывать, что она прикладывается к шарику условно. В действительности, сила инерции, как известно, приложена к двигающему телу или к связи. В данном случае нить служит для шарика и двигающим телом (через нить шарик приводится в движение), и связью (нить одновременно и ограничивает движение шарика). Поэтому сила инерции приложена к нити и отклоняет ее от вертикали.
2. Совместив оси координат с прямыми AO и BO и спроектировав силы на оси х и у, выведем уравнения равновесия:
Таким образом, натяжение нити составляет 22,7 н при скорости движения шарика 1,3 м/сек.
[spoiler title=”источники:”]
http://fizika.my-dict.ru/q/2334346_ravnodejstvuusaa-sila-dejstvuusaa-na-sarik-privazannyj/
http://exir.ru/termeh/princip_Dalambera_krivolineynoe_dvizhenie_216.htm
[/spoiler]
Задача о трех шариках и их ускорениях
Задача попалась в беседе учителей физики в ВК, и как-то неожиданно легко решилась.
Задача. Два небольших шарика с одинаковыми массами и зарядами
соединены нерастяжимым легким стержнем длины
. Эти шарики подвешены на двух нитях длиной
к третьему шарику с зарядом
, как показано на рисунке. Найти ускорения шариков
и
непосредственно после пережигания нити
.
Рисунок к задаче
Решение. Расставим все силы. При этом заметим, что нити и стержень образуют правильный треугольник. Поэтому все силы Кулона, действующие на шарики, равны. Я расставила силы на правый шарик, на левой стороне все симметрично.
Расставим силы на правый шарик
Направим оси традиционно и запишем уравнения по второму закону Ньютона:
Из второго уравнения
Из первого:
Подставим :
Теперь можем искать составляющие ускорения шарика слева, так как теперь нам известны все силы. Шарик был в равновесии и ускорение получит только из-за обрыва нити:
Сила натяжения нити исчезла с ее обрывом
Теперь можно определить полное ускорение шарика слева:
Для правого шарика ничего не изменилось – нить не рвалась и он по-прежнему в равновесии. Его ускорение равно нулю.
Ответ: .
