злато-серебро
Оракул
(87912)
11 лет назад
Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба находится по формуле , где d — диагональ, а — ребро куба.
, где d — диагональ, а — ребро куба.
Из этой формулы
а=d :√3
объем куба
а³=(d:√3)³
Подставляйте свое значение диагонали и получите ответ.
Шик Ени
Ученик
(102)
5 лет назад
Шли нафиг этих додиков, они дали тебе диагональ стороны куба, котоорая тебе не нужна, диагональ куба рассчитывается из грани и диагонали стороны, там все сложно, забей, подоййди к учителю чтобы тебе обьяснили
Объём куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём куба
Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Объём куба через ребро
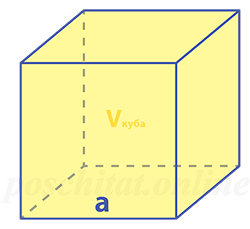
Чему равен объём куба, если:
ребро a =
Vкуба =
0
Округление ответа:
Объём куба через диагональ
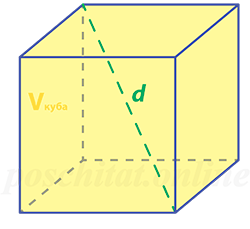
Чему равен объём куба, если:
диагональ d =
Vкуба =
0
Округление ответа:
Объём куба через площадь поверхности
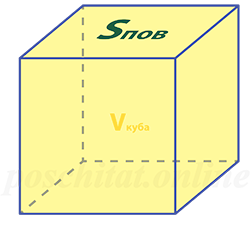
Чему равен объём куба, если:
Sпов =
Vкуба =
0
Округление ответа:
Теория
Как найти объём куба зная длину ребра
Чему равен объём куба Vкуба, если длина его рёбер a:
Формула
Vкуба = a³
Пример
Для примера, найдём объём куба, у которого рёбра a = 5 см:
Vкуба = 5³ = 125 см³
Как найти объём куба зная диагональ
Чему равен объём куба Vкуба, если его диагональ d:
Формула
Vкуба = d³ ⁄3√3
Пример
Для примера, найдём объём куба, длина диагонали которого d = 9 см:
Vкуба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³
Как найти объём куба зная площадь поверхности
Чему равен объём куба Vкуба, если площадь поверхности этого куба Sпов:
Формула
Vкуба = √Sпов³ ⁄6√6
Пример
Для примера, найдём объём куба, площадь поверхности которого Sпов = 24 см²:
Vкуба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³
См. также
Калькулятор объема куба
Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧊 Что считает калькулятор
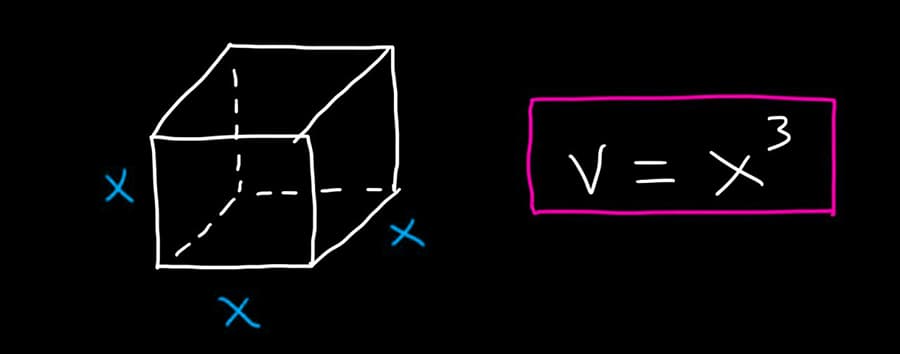
Калькулятор объема куба — это инструмент, который позволяет вычислять объем любого куба и выводить результат в разных единицах измерения.
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб является частным случаем параллелепипеда и призмы.
Как использовать калькулятор
Укажите значение стороны куба, после этого калькулятор произведет расчёт и выдаст его в указанных единицах измерения. Кроме того, можно указать диагональ куба или диагональ любой его стороны.
Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора объема куба зависит от нескольких факторов:
- Корректность ввода данных. Если вводимые значения длины, ширины и высоты куба некорректны, то расчет объема будет неправильным. Поэтому, важно убедиться в правильности вводимых значений перед выполнением расчета.
- Точность математических операций. Расчет объема куба требует выполнения математических операций, таких как умножение. Если калькулятор не выполняет математические операции точно, то результаты расчетов будут неточными.
- Точность округления. В некоторых случаях, результаты расчетов могут быть округлены. Если калькулятор округляет результаты до неправильного числа знаков, то результаты будут неточными.
- Алгоритм расчета. Различные калькуляторы могут использовать разные алгоритмы расчета. Если алгоритм расчета неправильный, то результаты могут быть неточными.
- Ошибки программирования. Если в программе калькулятора есть ошибки, то результаты расчетов могут быть неправильными. Поэтому, важно использовать калькуляторы, которые были разработаны и протестированы надежными разработчиками.
Где можно применить калькулятор
Калькулятор объема куба может быть использован во многих областях, где требуется расчет объема кубической формы. Некоторые из таких областей включают:
- 🧱 Строительство. Калькулятор объема куба может использоваться строителями при расчете объема кубических блоков, бетонных кубов, кирпичей и других материалов, используемых в строительстве.
- 🏭 Производство. Калькулятор объема куба может использоваться в производственных процессах для расчета объема материалов, таких как металл, пластик, стекло и другие, используемые в производстве кубических изделий.
- 📦 Логистика. Калькулятор объема куба может использоваться при планировании грузоперевозок, чтобы определить, сколько грузовых мест может вместить транспортное средство.
- 🎓 Образование. Калькулятор объема куба может использоваться учителями математики в школах и университетах для обучения геометрии и расчета объема кубических форм.
- 🎨 Интерьер и дизайн. Калькулятор объема куба может использоваться в дизайне интерьера для расчета объема кубических элементов, таких как шкафы, полки, столы и другие.
- 🛠️ Ремонт и обслуживание. Калькулятор объема куба может использоваться в ремонте и обслуживании, чтобы определить количество материалов, необходимых для замены кубических элементов, таких как плитка, обои и другие.
📐 Как посчитать объем куба
Объем куба можно вычислить самостоятельно, используя формулу
V = a³
где V – объем куба, a – длина ребра.
Для того, чтобы вычислить объем куба, нужно измерить длину одного из его ребер с помощью линейки или другого инструмента измерения длины. После этого возведите полученное значение в куб, используя калькулятор или ручной расчет.
Например, если длина ребра куба равна 5 см, то объем куба будет равен V = 5³ = 125 кубических сантиметров.
Важно помнить, что все единицы измерения должны быть одинаковыми – если длина ребра измеряется в сантиметрах, то и объем будет выражен в кубических сантиметрах.
🤔 Полезные советы
Несколько советов, которые могут помочь при вычислении объема куба:
- Определите длину одной из сторон куба. Обычно все стороны куба одинаковые, поэтому вы можете выбрать любую.
- Возведите длину стороны куба в квадрат. Это даст вам площадь одной грани куба.
- Умножьте площадь одной грани куба на 6. Это даст вам общую площадь поверхности куба.
- Определите длину любой из диагоналей куба. Вы можете использовать формулу теоремы Пифагора для нахождения длины диагонали, если известна длина стороны.
- Возвести длину диагонали куба в куб. Это даст вам объем куба.
- Если известна масса куба, можно использовать плотность материала для расчета его объема. Для этого нужно разделить массу на плотность.
- Убедитесь, что вы используете одни и те же единицы измерения при расчете. Например, если длина стороны куба измеряется в сантиметрах, то и объем должен быть выражен в кубических сантиметрах.
❓ Вопросы и ответы
Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.
Что такое объем куба и как его рассчитать?
Объем куба — это мера его вместимости, то есть объем пространства, которое он занимает. Он рассчитывается по формуле V = a³, где a – длина ребра куба.
Как найти длину ребра куба, если известен его объем?
Для этого нужно извлечь кубический корень из объема: a = V^(1/3). Это позволит определить длину ребра куба, зная его объем.
Что произойдет с объемом куба, если увеличить длину его ребра вдвое?
Объем куба увеличится в 8 раз. Это происходит потому, что объем куба пропорционален кубу его длины: V ~ a³. Если длина ребра увеличивается вдвое, то объем увеличивается в 222=8 раз.
Какие единицы измерения используются для объема куба?
Объем куба измеряется в кубических единицах длины, таких как кубические метры (м³), кубические сантиметры (см³), кубические дюймы (дюйм³) и т.д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
- Калькулятор площади трапеции. Рассчитайте онлайн площадь трапеции, не только зная длины ее оснований и высоту, но и по другим известным параметрам, например, диагоналям.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
|
Как найти объём куба зная диагональ?Вова маленький 10 месяцев назад
Как найти объём куба зная диагональ?
Nasos 10 месяцев назад Как известно из геометрии, объём куба (V), выраженный через длину диагонали (D) этого куба, будет рассчитываться по следующей формуле: V = D³ / (3 * √3), или V = D³ / 5.1961524227066318805823390245176. автор вопроса выбрал этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
Формула объёма куба через ребро
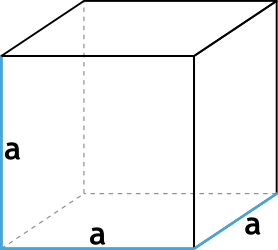
Формула объёма куба через диагональ грани
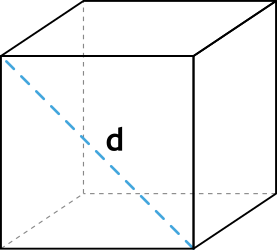
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
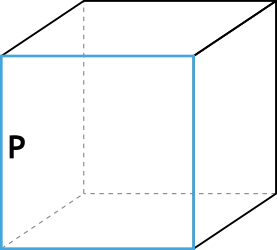
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
Формула объёма куба через диагональ куба
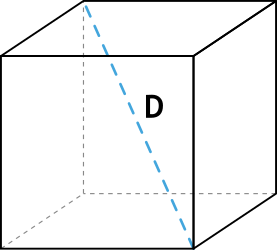
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
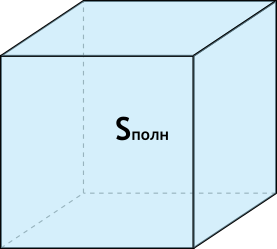
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
