Как найти сумму гармонического ряда

Гармони́ческий ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:

.

Ряд назван гармоническим, так как складывается из «гармоник»: -я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной от длины исходной струны^[1]. Кроме того, каждый член ряда, начиная со второго, представляет собой среднее гармоническое двух соседних членов.

Суммы первых n членов ряда (частичные суммы)[править | править код]

Отдельные члены ряда стремятся к нулю, но его сумма расходится.
Частичная сумма n первых членов гармонического ряда называется n-м гармоническим числом:

Разница между -м гармоническим числом и натуральным логарифмом сходится к постоянной Эйлера — Маскерони .

Разница между различными гармоническими числами никогда не равна целому числу и никакое гармоническое число, кроме , не является целым: ^[2].

Некоторые значения частичных сумм[править | править код]

Формула Эйлера[править | править код]

В 1740 году Эйлером было получено асимптотическое выражение для суммы первых членов ряда:

,

где  — постоянная Эйлера — Маскерони, а  — натуральный логарифм.

При значение следовательно, для больших

 — формула Эйлера для суммы первых членов гармонического ряда.

Пример использования формулы Эйлера

			, (%)
10	2,93	2,88	1,7
25	3,82	3,80	0,5

Более точная асимптотическая формула для частичной суммы гармонического ряда:

где  — числа Бернулли.

Данный ряд расходится, однако ошибка вычислений по нему никогда не превышает половины первого отброшенного члена^{[источник не указан 1715 дней]}.

Расходимость ряда[править | править код]

Гармонический ряд расходится: при однако очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 10⁴³ элементов ряда).

Расходимость гармонического ряда можно продемонстрировать, сравнив его со следующим телескопическим рядом, который получается из логарифмирования :

Частичная сумма этого ряда, очевидно, равна Последовательность таких частичных сумм расходится; следовательно, по определению телескопический ряд расходится, но тогда из признака сравнения рядов следует, что гармонический ряд тоже расходится.

Доказательство через предел последовательности частичных сумм^[3][править | править код]

Рассмотрим последовательность Покажем, что эта последовательность не является фундаментальной, то есть, что Оценим разность Пусть Тогда Следовательно, данная последовательность не является фундаментальной и по критерию Коши расходится. Тогда по определению ряд также расходится.

Доказательство Орема[править | править код]

Доказательство расходимости можно построить, если сравнить гармонический ряд с другим расходящимся рядом, в котором знаменатели дополнены до степени двойки. Этот ряд группируется, и получается третий ряд, который расходится:

(Группировка сходящихся рядов всегда дает сходящийся ряд, а значит если после группировки получился ряд расходящийся, то и исходный тоже расходится.)

Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).

Связанные ряды[править | править код]

Обобщённый гармонический ряд[править | править код]

Обобщённым гармоническим рядом (частный случай ряда Дирихле) называют ряд^[4]

.

Этот ряд расходится при и сходится при ^[4].

Сумма обобщённого гармонического ряда порядка равна значению дзета-функции Римана:

Для чётных это значение явно выражается через число пи — например, сумма ряда обратных квадратов . Но уже для α=3 его значение (константа Апери) аналитически неизвестно.

Другой иллюстрацией расходимости гармонического ряда может служить соотношение

Знакопеременный ряд[править | править код]

В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд

сходится по признаку Лейбница. Поэтому говорят, что такой ряд обладает условной сходимостью.
Его сумма равна натуральному логарифму 2:

Эта формула — частный случай ряда Меркатора, то есть ряда Тейлора для натурального логарифма.

Похожий ряд может быть получен из ряда Тейлора для арктангенса:

Это соотношение известно как ряд Лейбница.

Случайный гармонический ряд[править | править код]

В 2003 году изучены^[5][6] свойства случайного ряда

где  — независимые, одинаково распределённые случайные величины, которые принимают значения +1 и −1 с одинаковой вероятностью ½. Показано, что этот ряд сходится с вероятностью 1, и сумма ряда есть случайная величина с интересными свойствами. Например, функция плотности вероятности, вычисленная в точках +2 или −2, имеет значение:

0,124 999 999 999 999 999 999 999 999 999 999 999 999 999 7642…,

отличаясь от ⅛ на менее чем 10⁻⁴².

«Истончённый» гармонический ряд[править | править код]

См. Ряд Кемпнера^[en]

Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшийся ряд сходится, и его сумма меньше 80^[7]. Позже была найдена более точная оценка, ряд Кемпнера сходится к (последовательность A082838 в OEIS). Более того, доказано, что если оставить слагаемые, не содержащие любой заранее выбранной последовательности цифр, то полученный ряд будет сходиться. Из этого можно сделать ошибочное заключение о сходимости исходного гармонического ряда, что не верно, поскольку с ростом разрядов в числе всё меньше слагаемых берётся для суммы «истончённого» ряда. То есть, в конечном счёте отбрасывается подавляющее большинство членов, образующих сумму гармонического ряда, чтобы не превзойти ограничивающую сверху геометрическую прогрессию.

Примечания[править | править код]

Содержание:

Числовые ряды:

При решении ряда математических задач, в том числе и в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых решается в теории рядов.

Основные понятия. Сходимость ряда

Определение. Числовым рядом называется бесконечная последовательность чисел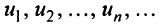

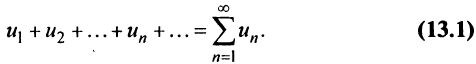
Числа 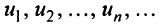называются членами ряда, а член 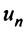— общим или 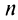-м членом ряда.

Ряд (13.1) считается заданным, если известен его общий член 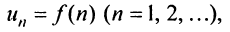т.е. задана функция 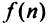натурального аргумента. Например, ряд с общим членом 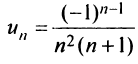имеет вид

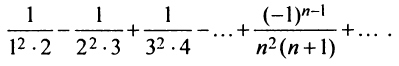
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение.

Пример:

Найти в простейшей форме общий член ряда:

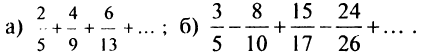
Решение:

Нетрудно убедиться, что для ряда а) общий член 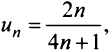а для ряда б)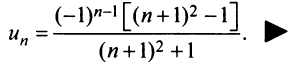

Рассмотрим суммы конечного числа членов ряда:

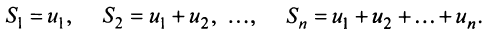
Сумма п первых членов ряда 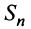называется 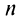-й частичной суммой ряда.

Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

Число 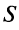называется суммой ряда. В этом смысле можно записать

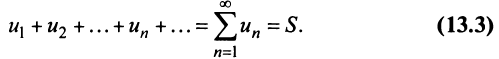
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Пример:

Исследовать сходимость геометрического ряда, т.е. ряда, составленного из членов геометрической профессии

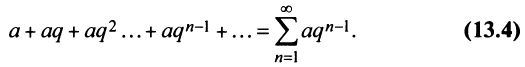
Решение:

Необходимо установить, при каких значениях знаменателя профессии 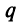ряд (13.4) сходится и при каких — расходится.

Из школьного курса алгебры известно, что сумма 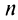первых членов геометрической профессии, т.е. 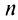-я частичная сумма ряда при 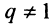равна

Возможно несколько случаев:

1) если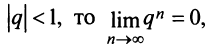

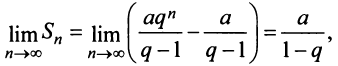т.е. ряд сходится и его сумма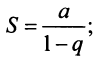

2) если 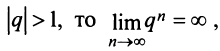следовательно, 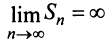и ряд расходится;

3) если 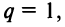то ряд (13.4) примет вид 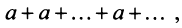его 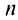-я частичная сумма 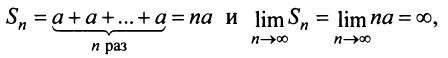т.е. ряд расходится;

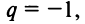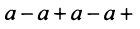
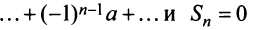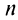4) если то ряд (13.4) примет вид при четном 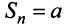и — при 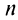нечетном, следовательно, 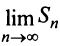не существует, и ряд расходится.

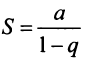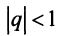Таким образом, геометрический ряд сходится к сумме при и расходится при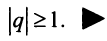

Пример:

Найти сумму ряда

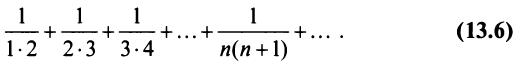
Решение:

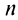-я частичная сумма ряда

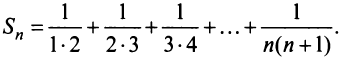Учитывая, что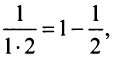

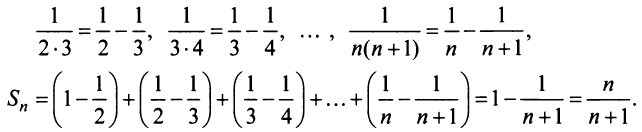Отсюда 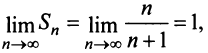т.е. сумма ряда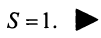

Свойства сходящихся рядов. 1. Если ряд сходится и имеет сумму 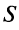, то и ряд 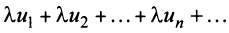(полученный умножением данного ряда на число 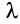) также сходится и имеет сумму .

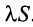2. Если ряды 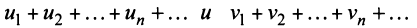сходятся и их суммы соответственно равны 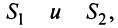то и ряд 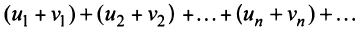(представляющий сумму данных рядов) также сходится, и его сумма равна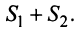

Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.

3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

Пусть в сходящемся ряде (13.1) отброшены 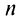членов (в принципе можно отбрасывать члены с любыми номерами, лишь бы их было конечное число). Покажем, что полученный ряд

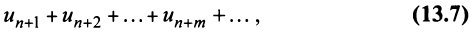
имеющий частичную сумму 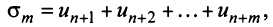также сходится.

Очевидно, что 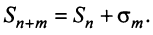Отсюда следует, что при фиксированном 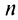конечный предел 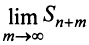существует тогда и только тогда, когда существует конечный предел 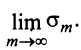. А это и означает, что ряд (13.7) сходится. ■

Ряд (13.7), полученный из данного отбрасыванием его первых 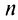членов, называется 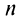-м остатком ряда.

Если сумму 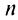-го остатка ряда обозначить через 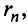т.е.

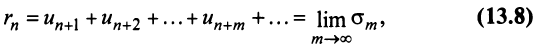
то сумму ряда (13.1) можно представить в виде

В результате мы подошли к свойству 4.

4. Для того чтобы ряд (13.1) сходился, необходимо и достаточно, чтобы при 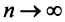остаток ряда стремился к нулю, т.е. чтобы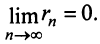

Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций (см. § 6.3).

Установить сходимость (расходимость) ряда путем определения 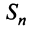и вычисления 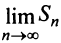(как это сделано в примерах 13.2, 13.3) возможно далеко не всегда из-за принципиальных трудностей при нахождении 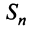(суммировании 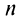членов ряда). Проще это можно сделать на основании признаков сходимости, к изучению которых мы переходим.

Необходимый признак сходимости. Гармонический ряд

Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 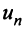при 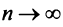равен нулю, т.е.

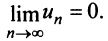
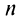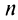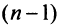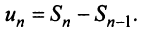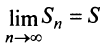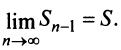Выразим -й член ряда через сумму его и членов, т.е. Так как ряд сходится, то и Поэтому

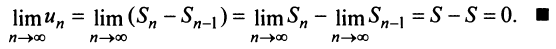
Пример №1

Проверить выполнение необходимого признака для ряда (13.6).

Решение:

Выше было доказано, что ряд (13.6) сходится, и действительно 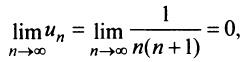т.е. необходимый признак сходимости выполняется. ►

Следствие. Если предел общего члена ряда (13.1) при 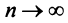не равен нулю, т.е. 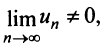то ряд расходится.

Предположим противное, т.е. ряд (13.1) сходится. Но в этом случае из приведенной выше теоремы следует 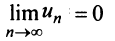, что противоречит условию, заданному в следствии, т.е. ряд (13.1) расходится. ■

Пример №2

Исследовать сходимость ряда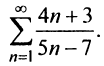

Решение:

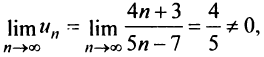т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится. ►

Замечание. Следует подчеркнуть, что рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если 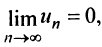то из этого еще не следует, что ряд сходится.

В качестве примера рассмотрим ряд

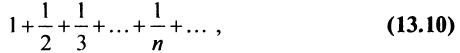
называемый гармоническим.

Необходимый признак сходимости выполнен: 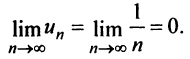Докажем, что, несмотря на это, гармонический ряд расходится.

Вначале получим вспомогательное неравенство. С этой целью запишем сумму первых 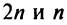членов ряда:

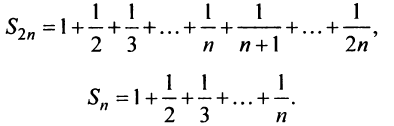
Найдем разность

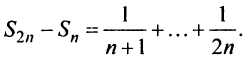
Заменяя в сумме каждое слагаемое наименьшим, равным 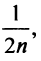придем к вспомогательному неравенству

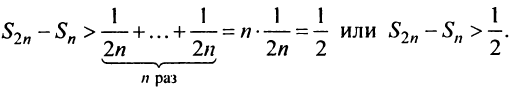
Предположим противное, т.е. что гармонический ряд сходится, тогда 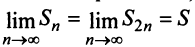и, переходя к пределу в неравенстве (см. § 6.5), получим, что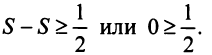

Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится. ■

В следующих двух параграфах рассмотрим достаточные признаки сходимости.

Ряды с положительными членами

Теорема (признак сравнения). Пусть даны два ряда с положительными членами: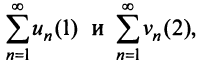 причем члены первого ряда не превосходят членов второго, т.е. при любом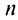

Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.

а) Пусть частичные суммы рядов 1 и 2 соответственно равны 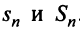. По условию ряд 2 сходится, следовательно, существует 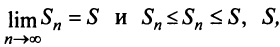так как члены ряда 2 положительны. Рассмотрим последовательность частичных сумм 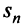ряда 1. Эта последовательность является: возрастающей (так как с ростом 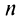увеличивается сумма 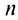положительных слагаемых) и ограниченной (так как 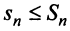в силу условия (13.11), т.е. ).

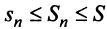Следовательно, на основании признака существования предела (см. § 6.5) последовательность 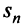имеет предел, т.е. ряд 1 сходится.

б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходится и ряд 1, что противоречит предположению; т.е. ряд 2 расходится. ■

Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие (13.11) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами 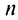. Достаточно, чтобы оно выполнялось, начиная с некоторого номера 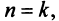или чтобы имело место неравенство 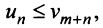где 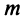— некоторое целое число.

Пример №3

Исследовать сходимость ряда

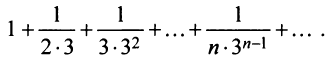
Решение:

Сравним данный ряд со сходящимся геометрическим рядом 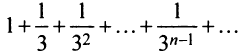(его знаменатель ).

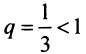Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 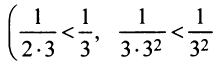и вообще 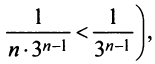то на основании признака сравнения ряд сходится. ►

Пример №4

Исследовать сходимость ряда

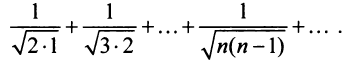
Решение:

Сравним данный ряд с гармоническим 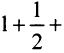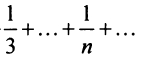, мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на расходимость ряда). Так как 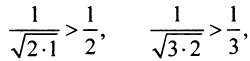и вообще 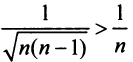(ибо 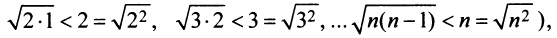т.е. члены данного ряда больше членов расходящегося гармонического ряда, то на основании признака сравнения ряд расходится. ►

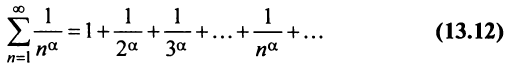
сходится при 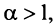расходится при 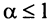здесь же отметим, что при 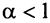расходимость ряда (13.12) следует из признака сравнения, так как в этом случае члены ряда 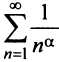больше соответствующих членов гармонического ряда 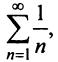а в частном случае при 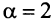сходимость ряда (13.12) может быть доказана сравнением этого ряда со сходящимся (13.6)).

Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (13.11), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п.). В ряде случаев более простым оказывается предельный признак сравнения.

Теорема (предельный признак сравнения)

Теорема (предельный признак сравнения). Если 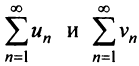— ряды с положительными членами и существует конечный предел отношения их общих членов 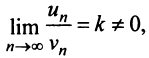то ряды одновременно сходятся либо расходятся.

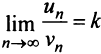Так как , то по определению предела числовой последовательности (см. § 6.1) для любого 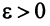существует такой номер 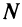, что для всех 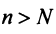выполняется неравенство

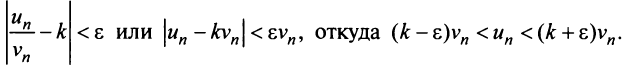
Если ряд 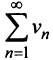сходится, то сходится ряд 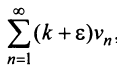и в силу признака сравнения будет сходиться ряд 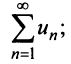аналогично, если сходится ряд 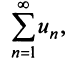сходится ряд 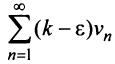и сходится 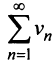. Таким образом, из сходимости одного ряда следует сходимость другого. Утверждение теоремы о расходимости рядов доказывается аналогично. 

Пример №5

Исследовать сходимость ряда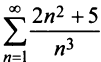

Решение:

Сравним данный ряд с расходящимся гармоническим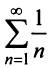 (выбор такого ряда для сравнения может подсказать то, что при больших 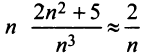). Так как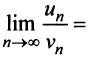 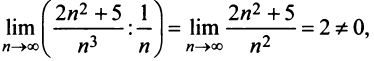то данный ряд, так же как и гармонический, расходится. ►

Весьма удобным на практике является признак Даламбера.

Теорема (признак Даламбера)

Теорема (признак Даламбера). Пусть для ряда 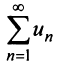с положительными членами существует предел отношения 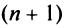-го члена к 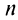-му члену 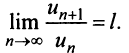Тогда, если 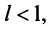то ряд сходится; если 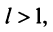то ряд расходится; если 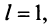то вопрос о сходимости ряда остается нерешенным.

 Из определения предела последовательности следует, что для любого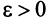 существует такой номер 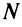, что для всех 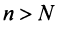выполняется неравенство 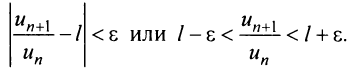1) Пусть 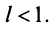Выберем 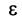настолько малым, что число

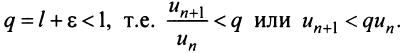
Последнее неравенство будет выполняться для всех 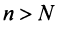, т.е. для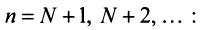

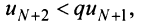
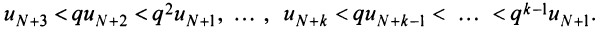
Получили, что члены ряда 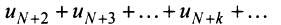меньше соответствующих членов геометрического ряда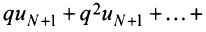 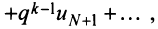сходящегося при 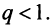Следовательно, на основании признака сравнения этот ряд сходится, а значит, сходится и рассматриваемый ряд 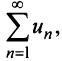отличающийся от полученного на первые 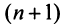членов.

2) Пусть 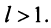Возьмем 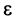настолько малым, что 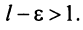Тогда из условия 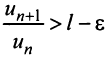следует, что 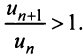Это означает, что члены ряда возрастают, начиная с номера 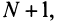поэтому предел общего члена ряда не равен нулю, т.е. не выполнен необходимый признак сходимости, и ряд расходится. ■

Пример №6

Исследовать сходимость рядов:

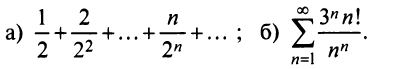
Решение:

а) Так как 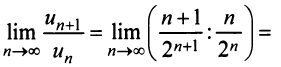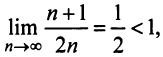то по признаку Даламбера ряд сходится.

б) Так как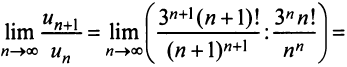

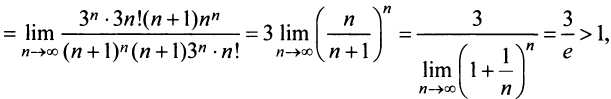то по признаку Даламбера ряд расходится. ►

Замечание 1. Если 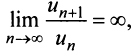то ряд расходится.

Замечание 2. Если 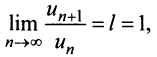то, как отмечалось выше, признак Даламбера ответа о сходимости ряда не дает, и рекомендуется перейти к другим признакам сходимости.

Теорема (интегральный признак сходимости)

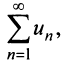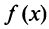Теорема (интегральный признак сходимости). Пусть дан ряд члены которого положительны и не возрастают, т.е.а функция , определенная при 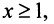непрерывная и невозрастающая и

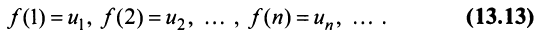
Тогда для сходимости ряда 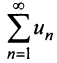необходимо и достаточно, чтобы сходился несобственный интеграл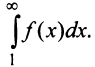

Рассмотрим ряд

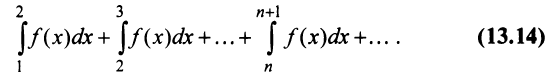
Его 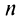-й частичной суммой будет

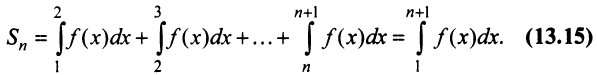
Сходимость ряда (13.14) означает существование предела последовательности его частичных сумм (13.15), т.е. сходимость несобственного интеграла 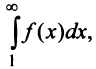поскольку 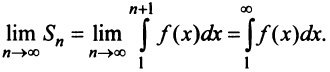В силу монотонности функции 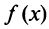на любом отрезке 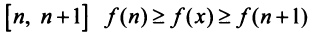или, учитывая (13.13),

Интегрируя (13.16) на отрезке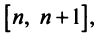 получим

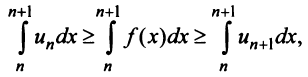
откуда

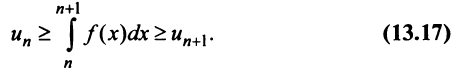
Если ряд 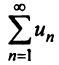сходится, то по признаку сравнения рядов в силу первого неравенства (13.17) должен сходиться ряд (13.14), а значит, и несобственный интеграл 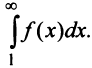Обратно, если сходится J/(jc)c&, т.е. ряд (13.14), то согласно тому же признаку сравнения на основании второго неравенства (13.17) будет сходиться ряд 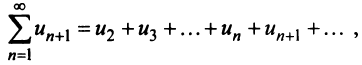а следовательно, и данный ряд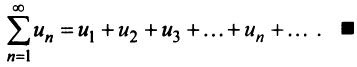

Пример №7

Исследовать сходимость обобщенного гармонического ряда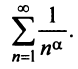

Решение:

Пусть 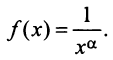Функция 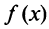при 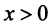(а значит, и при 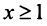) положительная и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла 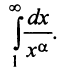Имеем 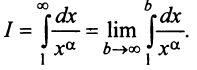Если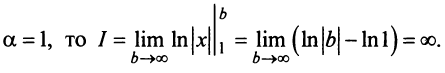

Если 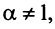то

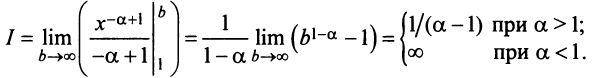Итак, данный ряд сходится при 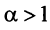и расходится при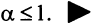

Ряды с членами произвольного знака

Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны

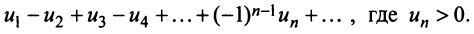
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 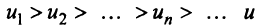и предел его общего члена при 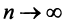равен нулю, т.е.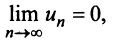то ряд сходится, а его сумма не превосходит первого члена: .

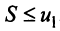 Рассмотрим последовательность частичных сумм четного числа членов при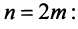

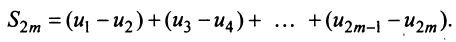
Эта последовательность возрастающая (так как с ростом 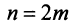увеличивается число положительных слагаемых в скобках) и ограниченная (это видно из того, что 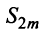можно представить в виде

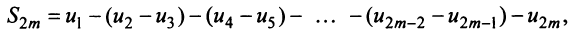
откуда следует, что 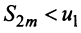). На основании признака существования предела (см. § 6.5) последовательность 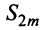имеет предел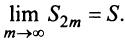

Попутно заметим, что, переходя к пределу в неравенстве 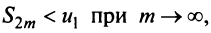получим, что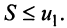

Теперь рассмотрим последовательность частичных сумм нечетного числа членов при 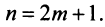Очевидно, что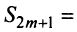 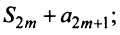поэтому, учитывая необходимый признак сходимости ряда,

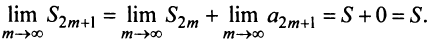
Итак, при любом 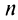(четном или нечетном) 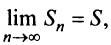т.е. ряд сходится. Рис. 13.1 иллюстрирует сходимость 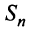к числу 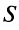слева при четном 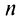и справа при нечетном . ■

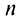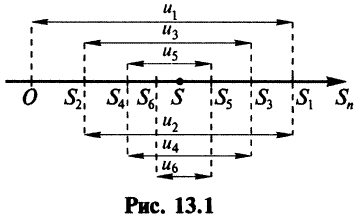
Из рис. 13.1 вытекает еще одна оценка для суммы 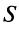сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница: при любом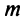

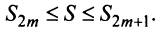
Пример №8

Исследовать сходимость ряда

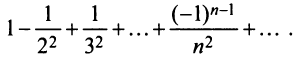
Решение:

Так как члены знакочередующегося ряда убывают по абсолютной величине 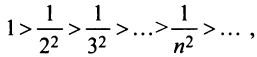и предел общего члена 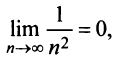то по признаку Лейбница ряд сходится. ►

Замечание. В теореме Лейбница существенно не только условие 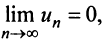но и условие 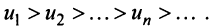Так, например, для ряда ,

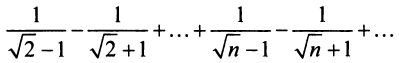второе условие нарушено и, хотя 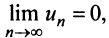ряд расходится. Это видно, если данный ряд представить (после попарного сложения его членов) в виде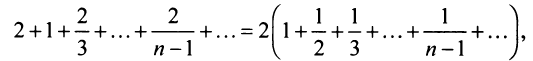

т.е. «удвоенного» гармонического ряда.

Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

По формуле (13.9) сумму сходящегося ряда можно представить как сумму 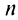членов ряда и суммы 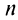-гo остатка ряда, т.е. 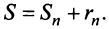Полагая приближенно 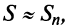мы допускаем погрешность, равную 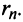Так как при четном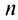 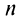-й остаток знакочередующегося ряда 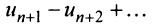представляет ряд, удовлетворяющий условиям теоремы Лейбница, то его сумма 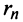не превосходит первого члена 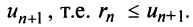Так как при нечетном 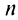для 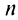-го остатка ряда 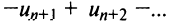его сумма 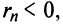то, очевидно, что при любом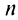

Пример №9

Какое число членов ряда 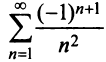надо взять, чтобы вычислить его сумму с точностью до 0,001?

Решение:

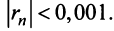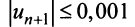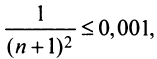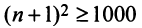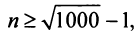По условию Учитывая следствие теоремы Лейбница (13.18), запишем более сильное неравенство или откуда и или 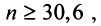т.е. необходимо взять не менее 31 члена ряда. ►

Знакопеременные ряды. Пусть знакопеременный ряд (13.1), в котором любой его член 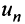может быть как положительным, так и отрицательным.

Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда (13.1)

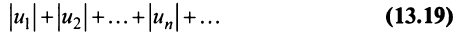
сходится, то сходится и данный ряд.

 Обозначим 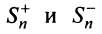суммы абсолютных величин членов данного ряда (13.1), входящих в него со знаком «плюс» и «минус».

Тогда частичная сумма данного ряда 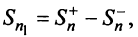а ряда, составленного из абсолютных величин его членов, 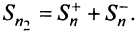По условию ряд (13.19) сходится, следовательно, существует конечный предел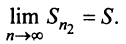

Последовательности 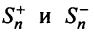являются возрастающими (так как с увеличением 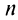увеличиваются 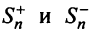) и ограниченными

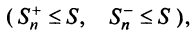значит, существуют пределы 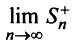и 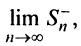и соответственно предел частичной суммы данного ряда

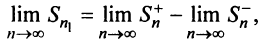т.е. ряд (13.1) сходится. ■

Следует отметить, что обратное утверждение неверно. Ряд (13.19) может расходиться, а ряд (13.1) сходиться. Например, ряд 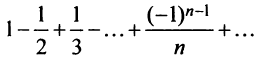сходится по признаку Лейбница, а ряд из абсолютных величин его членов 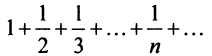(гармонический ряд) расходится.

Поэтому введем следующие определения.

Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Таким образом, рассмотренный выше ряд 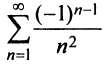— абсолютно сходящийся, а ряд 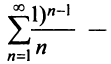условно сходящимся.

Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.

Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.

Условно сходящиеся ряды такими свойствами не обладают.

Возьмем, например, ряд 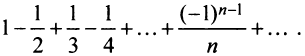Переставим члены местами и сгруппируем их следующим образом:

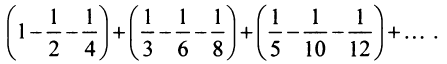
Перепишем ряд в виде:

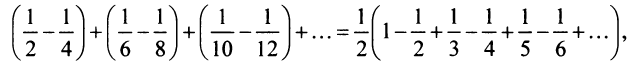
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.

Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.

Пример №10

Найти сумму ряда 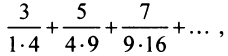доказав его сходимость.

Решение:

Очевидно, что общий член ряда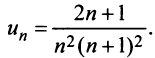

Представим сумму 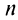членов ряда в виде 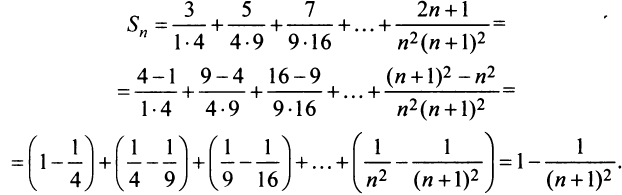Так как при 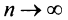последовательность 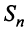имеет конечный предел, то ряд сходится, и его сумма

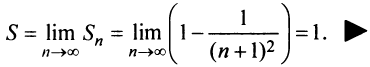
Пример №11

Исследовать сходимость ряда:

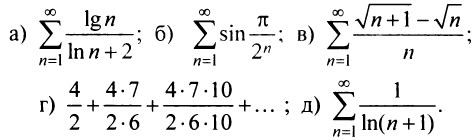
Решение:

а) Проверим выполнение необходимого признака сходимости, найдя предел общего члена:

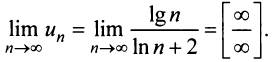
Для вычисления предела отношения двух бесконечно больших функций натурального аргумента правило Лопиталя непосредственно применять нельзя, ибо для таких функций не определено понятие производной. Поэтому применяя теорему о «погружении» дискретного аргумента 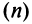в непрерывный 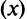, получим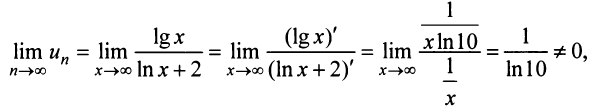

следовательно, ряд расходится.

б) Очевидно, что задан ряд с положительными членами, так как 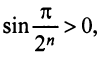ибо аргумент синуса 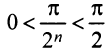при любом 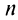. Так как члены данного ряда меньше членов сходящегося геометрического ряда со знаменателем

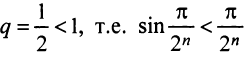(ибо при 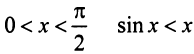), то данный ряд сходится.

в) Представим общий член ряда в виде

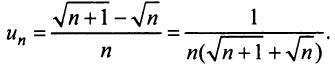Применим предельный признак сравнения, сравнив данный ряд со сходящимся «эталонным» рядом (13.12) при 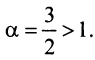Так как предел отношения общих членов двух рядов

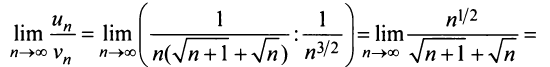
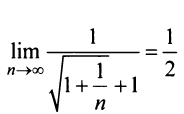
есть конечное число, не равное нулю, то данный ряд, так же как и «эталонный», сходится.

г) Применим признак Даламбера, заметив, что общий член ряда 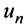имеет вид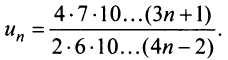

Тогда 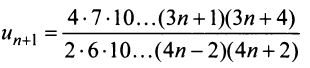и 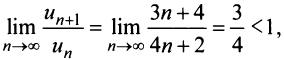т.е. данный ряд сходится.

д) Применим признак Даламбера:

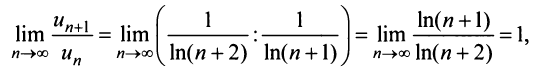
т.е. вопрос о сходимости ряда остается открытым. Проверим выполнение необходимого признака (с этого можно было начать исследование): 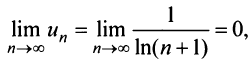т.е. необходимый признак выполнен, но вопрос о сходимости ряда по-прежнему не решен.

Применим признак сравнения в более простой предельной форме. Сравним данный ряд, например, с гармоническим.

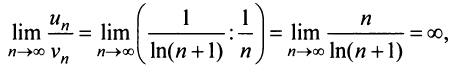т.е. ответа о сходимости ряда нет. Аналогичная картина ( 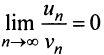или 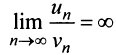) наблюдается и при использовании других «эталонных» рядов (см. § 13.3). Применим, наконец, признак сравнения в обычной форме. Сравним данный ряд с тем же гармоническим рядом, у которого отброшен первый член:

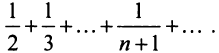Так как члены рассматриваемого ряда больше членов расходящегося гармонического ряда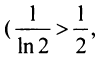 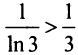и вообще

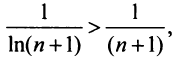что вытекает из очевидного неравенства 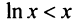), то данный ряд расходится. ►

Пример №12

Исследовать сходимость ряда:

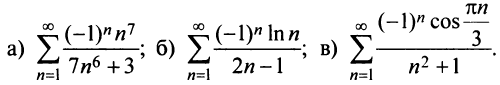
Решение:

а) Предел общего члена ряда 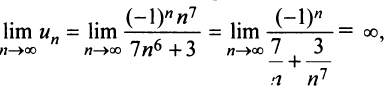так как знаменатель дроби стремится к нулю, а числитель колеблется, принимая значения 1 (при четном 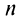) и —1 (при нечетном 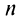). Следовательно, необходимый признак сходимости не выполнен, и ряд расходится.

б) Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине —

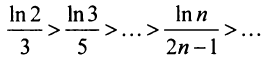
и предел общего члена 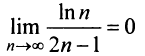(это можно установить, например, с помощью правила Лопиталя), то по признаку Лейбница ряд сходится. Ряд 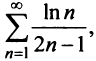составленный из абсолютных величин членов данного ряда, расходится, так как его члены больше членов расходящегося гармонического ряда, умноженного на 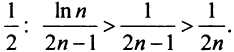Следовательно, данный ряд условно сходящийся.

в) Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося ряда (13.12) при 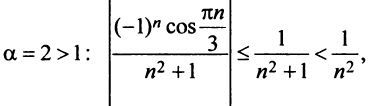следовательно, данный ряд сходится и притом абсолютно. ►

Определение ряда и его сходимость

Пусть

бесконечная последовательность чисел.

Определение 27.1.1. Выражение

называется числовым рядом, а элементы последовательности 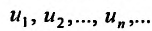членами ряда.

Поскольку выражение (27.1.2) рассматривается как единое целое, то для задания ряда необходимо задать каждый его член 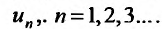Обычно член ряда задается как некоторая функция от своего номера. Аналитическое выражение этой функции называют общим членом ряда. Например, общим членом ряда геометрической прогрессии 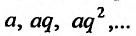является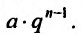

Припишем теперь определенный смысл выражению (27.1.2), т.е. введем определение.

Определение 27.1.2. Сумма n первых членов ряда (27.1.2) 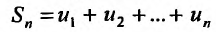называется n-ой частичной суммой этого ряда.

Ясно, что первая, вторая, третья и т.д. частичные суммы ряда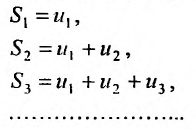

составляют бесконечную последовательность: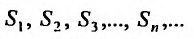

Определение 27.1.3. Ряд (27.1.2) называется сходящимся, если последовательность 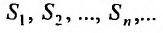его частичных сумм имеет конечный предел: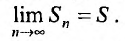

Значение S этого предела называется суммой ряда (27.1.2). Ряд (27.1.2) называется расходящимся, если последовательность его частичных сумм предела не имеет (например, если члены последовательности возрастают по модулю неограниченно).

Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов.

В принципе можно доказывать сходимость или расходимость каждого ряда, а также вычислять сумму сходящегося ряда, опираясь непосредственно на определения сходимости и суммы. Для этого в каждом случае составляется аналитическое выражение для n- ой частичной суммы ряда и находится предел этого выражения при возрастании n.

Пример:

Для ряда 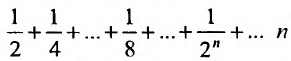-я частичная сумма 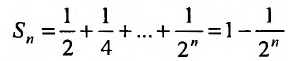, и предел ее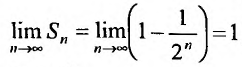, поэтому этот ряд сходится и его сумма равна 1.

Пример:

Последовательность вида

называется геометрической прогрессией, где а – первый член, а

q – её знаменатель; выражение 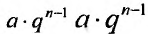называется общим членом геометрической прогрессии.

Числовой ряд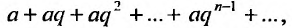 члены которого являются членами геометрической прогрессии, называется геометрическим рядом со знаменателем q .

Если в прогрессии (27.1.3) имеется только конечное число членов, то прогрессия называется конечной; в противном случае, если за каждым членом прогрессии следует ещё хотя бы один член, то прогрессия называется бесконечной.

В случае конечной прогрессии 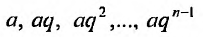можно говорить о сумме всех её членов 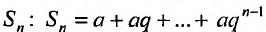, которую можно назвать n- ой частичной суммой геометрического ряда.

Известно, что при 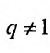, эта сумма равна 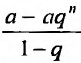. Из определения 27.1.3 следует, что суммой геометрического ряда

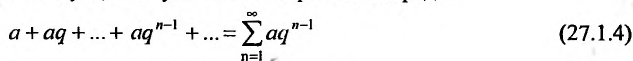
называется предел её частичных сумм 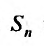при неограниченном возрастании n:

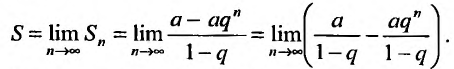
Так как а и q от n не зависят, то последнюю формулу представим в виде:

Если 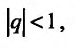то предел 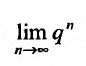равен нулю, и мы получаем

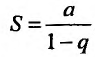, т.е. при 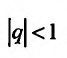прогрессия (27.1.5) сходится. Следователь-

но, сходится и ряд (27.1.4). Если же 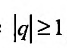, то предел справа в равенстве (27.1.5) не существует и, следовательно, ряд (27.1.4) расходится.

Итак, мы привели примеры, в которых исследование сходимости рядов проводили, применяя определение 27.1.3., т.е. вычисляли частичные суммы и находили предел их последовательностей. Ясно, что в общем случае, составление аналитического выражения для n- ой частичной суммы трудный вопрос. Кроме того, при исследовании рядов нередко значения сумм не представляют интереса, т.к. нужно определить только сходится ряд или нет. Поэтому представляют интерес методы анализа рядов, когда не требуется вычислять суммы рядов. Далее перейдем к изложению таких методов.

Свойства сходящихся рядов

Пусть дан ряд

Определение 27.2.1. Ряд 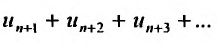называется n-м остатком ряда (27.2.1.)

Очевидно, m- я частичная суммаn -го остатка ряда равна разности 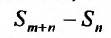частичных сумм самого ряда. Кроме того, 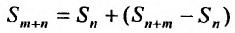, откуда, переходя к пределу по m при 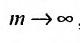, получим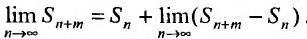

Предел слева есть сумма исходного ряда, а предел справа-сумма 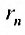его n – го остатка: 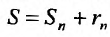. Ясно, что из существования предела в левой части равенства следует существование другого предела в правой части и наоборот. Поэтому если сходится один из остатков ряда, то сходится и сам ряд. Точно так же из сходимости ряда следует сходимость каждого его остатка. Кроме того, справедлива следующая теорема.

Теорема 27.2.1. Если ряд (27.2.1) сходится, то сумма его n-го остатка с ростом n стремится к нулю.

Доказательство. Выше показано, что 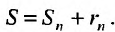. Так как это равенство справедливо для любого n, то мы можем перейти в нем по n к пределу: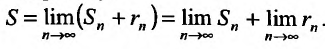

Но для сходящегося ряда 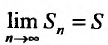, поэтому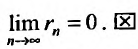

Рассмотрим теперь свойства сходящихся рядов, которые позволяют действовать с ними, как с конечными суммами.

Теорема 27.2.2. Если ряд

имеет сумму S, то ряд

полученный из предыдущего умножением всех членов на одно и тоже число a, имеет сумму aS.

Доказательство. Обозначим последовательность частичных сумм ряда (27.2.2) 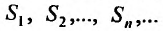Тогда последовательность частичных сумм ряда (27.2.3) очевидно будет иметь вид: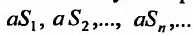. И поэтому 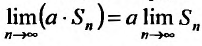. Так как ряд

(27.2.2) сходится, то 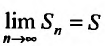существует и, следовательно, существует предел 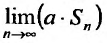ив силу этого же равенства он равен aS.

Теорема 27.2.3. Если ряды

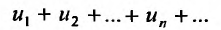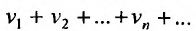и сходятся, а их суммы соответственно равны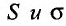, то и ряд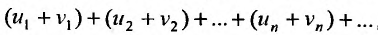называемый суммой данных рядов, также сходится и его сумма равна сумме сумм данных рядов 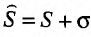, другими словами, сходящиеся ряды можно почленно складывать.

Доказательство. Пусть 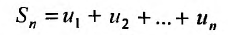и

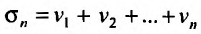. Тогда n -ая частичная сумм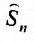а ряда

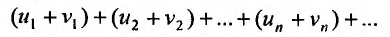будет равна 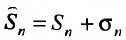и так как 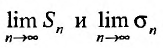существуют, то

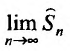существует и равен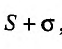, т.е.

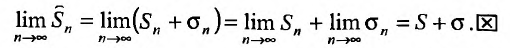
Следствие. Разность двух сходящихся рядов-ряд сходящийся.

Теорема 27.2.4. Свойства сходимости или расходимости ря-,ki не нарушается, если в ряде исключить или приписать к нему любое конечное число членов.

Доказательство. Пусть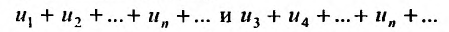 два ряда, причём второй получается из первого исключением первых двух членов. Тогда, если 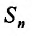– n-я частичная сумма первого ряда, а 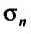– n-я частичная сумма второго ряда, то, очевидно, что

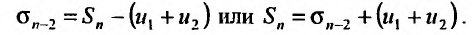
Из этого равенства следует, что, если 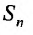имеет предел, то 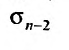также имеет предел. Ясно, что эти пределы будут различны, а, именно 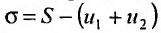Если же 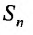не имеет предела, то 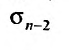также не имеет предела.

Теорема 27.2.5. (Необходимое условие сходимости ряда). Если ряд 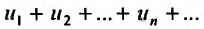сходится, то его общий член стремится к нулю, т.е.

Доказательство. Пусть ряд 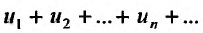сходится и его сумма равна S. Из определения n -ой частичной суммы следует, что общий член ряда можно представить в виде разности и-ой частичной суммы и (n-1)-ой частичной суммы: 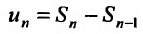. Переходя к пределу в этом равенстве, получим утверждение теоремы:

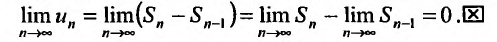
Отметим, что условие (27.2.4) не является достаточным, т.е. общий член может стремиться к нулю, но ряд все же может быть расходящимся. Но если общий член ряда не стремится к нулю, то ряд будет расходящийся.

• Заказать решение задач по высшей математике

Пример №13

Исследуем на сходимость гармонический ряд

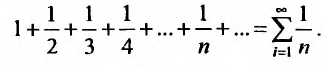
Решение:

Вначале находим предел общего члена: 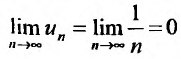. Нетрудно, однако, показать, что сумма n первых членов гармонического ряда беспредельно возрастает. Для этого сгруппируем слагаемые, начиная со второго, в группы из 1, 2, 4, 8,… членов: 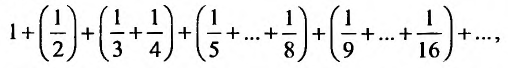так что в k – ой группе будет 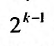членов. Fx л и в каждой групп заменим все члены последним, то получим ряд:

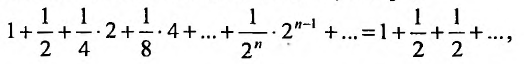сумма n первых членов которого, равна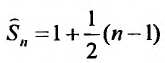, очевидно, стремится к :

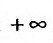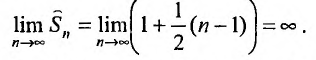Но сумма n первых членов заданного гармонического ряда больше суммы n первых членов преобразованного ряда, т.е. 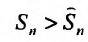. Тогда 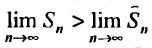, что означает, что 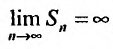следовательно, гармонический ряд расходится.

Пример №14

Найти формулу для общего члена ряда

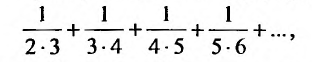
считая, что каждый его последующий член определяется по тому же закону, по которому образованы записанные члены, и найти ею сумму.

Решение:

Каждый член данного ряда представляет собой дробь, числитель которой равен 1, а знаменатель равен произведению двух последовательных натуральных чисел 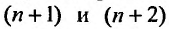. Следовательно, искомая формула общего члена ряда имеет вид:

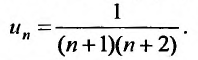
Для вычисления суммы ряда составим n -ую частичную сумму:

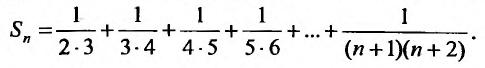
Представим выражение для общего члена в виде разности:

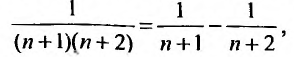
тогда

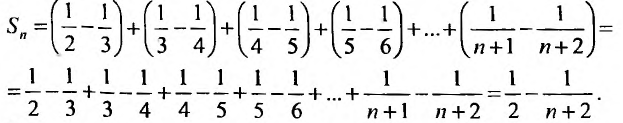
Переходя к пределу, получаем сумму ряда:

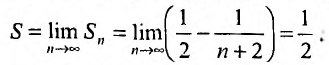
Пример №15

Исследовать сходимость ряда

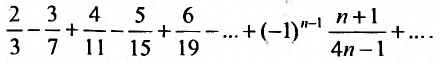
Решение:

Общий член ряда определяется формулой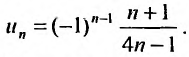

Вычислим предел модуля общего члена: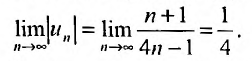

Так как предел общего члена не стремится к нулю, то ряд расходится.

Признаки сходимости числовых знакоположительных рядов

Рассмотрим числовые ряды с положительными членами. Существует много приёмов, называемых признаками сходимости, позволяющих установить сходимость или расходимость числовых рядов Так мы познакомились с методом исследования сходимости ряда на основании выяснения имеет ли предел последовательность частичных сумм. Стремление к нулю члена ряда по мерс роста его номера также является признаком сходимости, хотя только необходимым. Ниже мы приведём ряд достаточных признаков сходимости.

Признаки сравнения

Теорема 27.3.1. (I признак сравнения). Пусть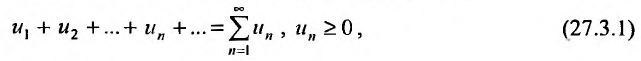

и

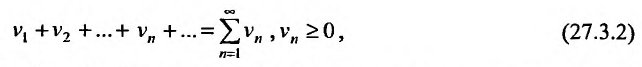
два ряда, причём члены первого ряда, начиная с некоторого номера k , не превосходят соответствующих членов второго

Тогда из сходимости ряда (27.3.2) следует сходимость ряда (27.3.1), а из расходимости ряда (27.3.1) следует расходимость ряда (27.3.2).

Доказательство. Так как исключение конечного числа членов ряда не влияет на его сходимость (теорема 27.2.4.), то достаточно доказать теорему для случая когда неравенства (27.3.3) выполняются для k = 1.

Пусть 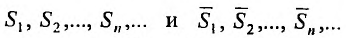последовательности частичных сумм рядов (27.3.1) и (27.3.2) соответственно. Это возрастающие последовательности, так как члены рядов неотрицательные числа. В силу неравенств (27.3.3), имеем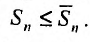

Пусть ряд (27.3.2) сходится. Тогда сходится соответствующая последовательность частичных сумм ряда (27.3.2), т.е.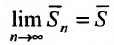

Поскольку выполняются неравенства (27.3.3), то члены последовательности частичных сумм ряда (27.3.1) удовлетворяют неравенству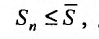 для всех т. Следовательно, последовательность 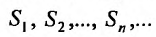возрастает и ограничена: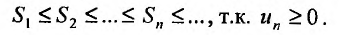

Поэтому, в силу признака Больцано-Всйсрштраса, последовательность частичных сумм ряда (27.3.1) сходится. По определению 27.1.3, сходится и ряд (27.3.1).

Пусть теперь ряд (27.3.1) расходится. Это значит, что его частичные суммы неограниченно возрастают. Но тогда, в силу неравенств (27.3.3), неограниченно возрастают и частичные суммы ряда (27.3.2), что означает, что этот ряд расходится. 

Пример №16

Пусть дан ряд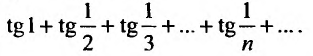

Исследуем его сходимость.

Решение:

Необходимый признак выполняется, т.е.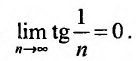

Для исследования сходимости заданного ряда применим 1 признак

сравнения (теорему 27.3.1). Сравним заданный ряд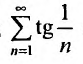с гармоничсским рядом 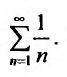. Так как выполняются неравенства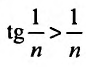то ряд 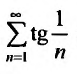расходится, потому что расходится гармонический ряд.

Пример №17

Исследовать сходимость ряда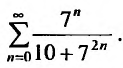

Решение:

Очевидно, что предел общего члена при возрастании т стремится к нулю.

Сравним данный ряд, общий член которого 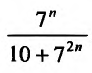с гармоническим рядом 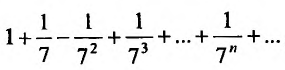который сходится, так как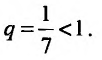

Поскольку 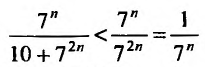для 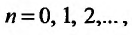т.е. выполняются неравенства (27.3.3), то на основании первого признака сравнения заключаем, что исследуемый ряд также сходится.

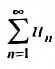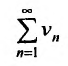Теорема 27.3.2. (II признак сравнения). Если для рядов и отношение общих членов 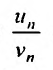стремится к некоторому положительному и конечному пределу:

то ряды 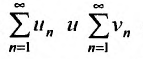сходятся или расходятся одновременно.

Доказательство. Предельное соотношение (27.3.4), в силу определения 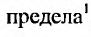означает, что, начиная с некоторою номера N ,

выполняется неравенство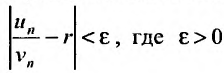. Это неравенство равносильно неравенству:

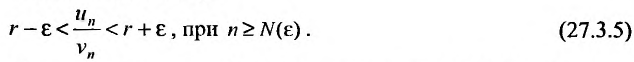
Обозначив 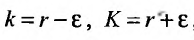, неравенство (27.3.5) запишется в виде:

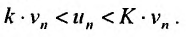
Предположим, что ряд 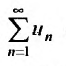сходится. Поскольку выполняется неравенство 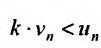то, из первого признака сравнения, следует сходимость ряда 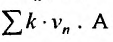в силу теоремы 27.2.2, и ряда 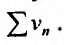. Если же ряд 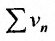расходится, то расходится и ряд 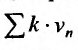по теореме 27.2.2. Тогда, поскольку выполняется неравенство 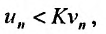, расходится и ряд 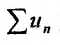в силу I признака сравнения. Аналогично рассуждая можно показать, что из сходимости ряда 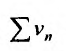следует сходимость ряда 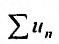по I признаку сравнения с использованием теоремы 27.2.2. 13

Последовательность 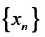называется сходящейся, если существует такое вещественное число а , что для любого положительного числа 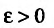найдется номер 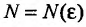такой, что для всех 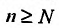выполняется неравенство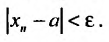

Пример №18

Исследовать сходимость ряда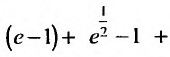

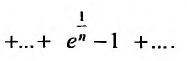
Решение:

Очевидно, что 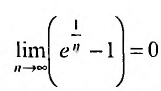. Поэтому, воспользуемся признаком сравнения, сравнив заданный ряд с гармоническим. Найдем предел отношения общих членов исследуемого ряда и гармонического:

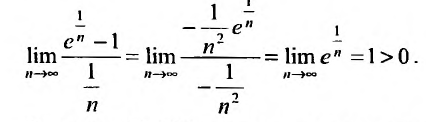
Теорема 27.3.2 выполняется, поэтому из расходимости гармонического ряда 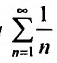следует расходимость исследуемого ряда.

Признаки Д’Аламбсра и Коши

Иногда вместо признаков сравнения оказываются полезными некоторые специальные признаки сходимости ряда. Отметим среди них признаки Д’Аламбсра и Коши, непосредственно получающиеся из признаков сравнения, если в качестве ряда сравнения взять соответствующим образом выбранную геометрическую прогрессию.

Теорема 27.3.3. (признак Д’Аламбера). Если для ряда

с положительными членами существует такой номер 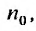, начиная с которого, т.е. при 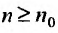, отношение последующего члена к предыдущему удовлетворяет неравенству: 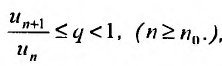, то ряд (27.3.6) сходится. Если же существует номер 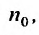, начиная с которого, т.е. при 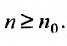отношение последующего члена к предыдущему больше единицы: 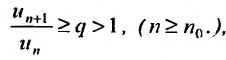то ряд (27.3.6) расходится.

Доказательство. Пусть 0 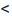q 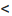1 и пусть существует такой номер 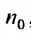, что при 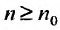. выполняется неравенство: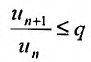Перепишем это неравенство в виде: 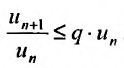. Тогда, начиная с номера 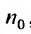буду последовательно выполнятся неравенства:

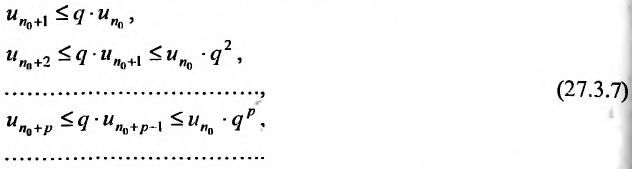
Ряд 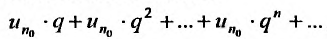, являясь суммой член геометрической прогрессии со знаменателем 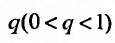, сходите Из неравенств (27.3.7) следует, что по I признаку сравнения, сходится и ряд 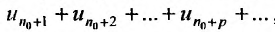значит и весь ряд (27.3.6

т.к. на сходимость ряда не влияет исключение конечного числа е^ членов.

Если же существует такое 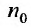, что выполняется неравенств 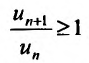для всех 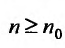, то, переписав его в виде 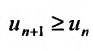, можно для всех 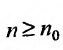, последовательно записать следующие неравенство

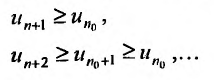
Так как по предположению 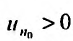, то n-ный член ряда будучи ограниченным снизу положительной постоянной не стремится к нулю. Следовательно, не выполняется необходимое условие сходимости ряда, и поэтому ряд (27.3.6) расходится.

Следствие 1. Пусть существует предел отношения последующего члена ряда (27.3.6) к предыдущему равный r :

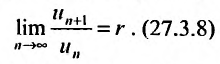
Тогда, если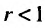 то ряд (27.3.6) сходится: если же 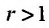то ряд (21.3.6) расходится.

Доказательство. Воспользовавшись определением предела, для фиксированного 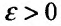, можно утверждать, что начиная с некоторого номера 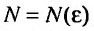, для всех 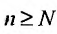, все отношения 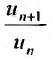будут отличатся от значения предела r на число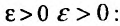

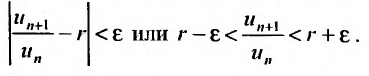
Рассмотрим правую часть двойного неравенства: 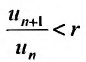. Тогда сославшись на доказанную теорему 27.3.3, в случае если r 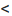1, получаем сходимость ряда. Рассматривая левую часть неравенства

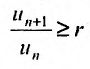, получаем расходимость ряда приr > 1. Следствие доказано.

Пример №19

Рассмотрим ряд 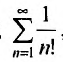, сходимость которого исследуем, используя признак Даламбера, т.е. следствие 1.

Решение:

Выпишем вначале значения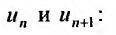

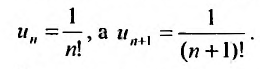
Затем вычислим предел отношения последующего члена ряда к предыдущему:

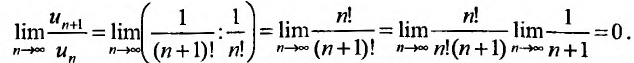
Так как этот предел меньше 1, то, в силу следствия 1, данный ряд сходится.

Заметим, что при исследовании сходимости ряда обычно (как правило, но не всегда) применяют следствие 1 из теоремы 27.3.3.

Теорема 27.3.4. (признак Kouiu). Если для ряда

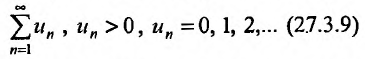
с положительными членами, начиная с некоторого номера 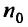. выполняется неравенство 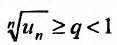для всех 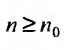, то ряд (27.3.6) сходится. Если же существует такой номер 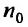, начиная с которого выполняется неравенство 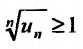для всех 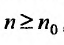, то данный ряд расходится.

Доказательство. Пусть существует такой номер 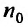, что при всех 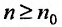выполняется неравенство 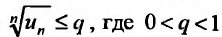Тогда, возводя обе части неравенства в степень n, получим 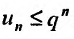. Так как сходится геометрический ряд 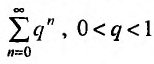, то на основании признака сравнения, получаем, что ряд 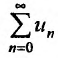сходится. Если же существует номер 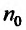, такой что 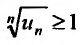для всех 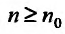, то ясно, что 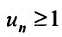, и значит 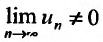(не выполняется необходимый признак сходимости), поэтому ряд 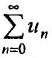расходится.

Следствие 2. Пусть существует предел корня n -ой степени из n-го члена ряда (27.3.9):

Тогда, если 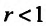, то ряд (27.3.9) сходится, если же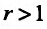, то ряд (27.3.9) расходится.

Доказательство. Из определения предела следует, что для фиксированного 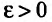существует номер 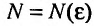, начиная с которого выполняется неравенство 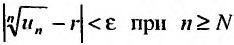Это неравенство равносильно неравенству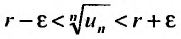. Из правой части неравенства следует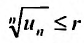, поскольку 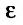сколь угодно малое число. Тогда из теоремы 27.3.4, получаем сходимость ряда (27.3.9). Рассматривая левую часть неравенства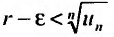, получим 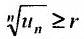и если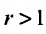, то из теоремы 27.3.4 следует расходимость ряда (27.3.9). Следствие доказано.

Пример №20

Рассмотрим ряд 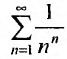, сходимость которого исследуем по признаку Коши, т.е. применим следствие 2.

Решение:

Выпишем значение n-го члена ряда 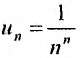н вычислим предел корня n -ой степени: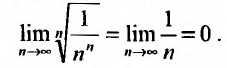

Так как этот предел меньше 1, то, согласно следствию 2, ряд сходится.

Замечание. Если пределы (27.3.8) и (27.3.10) равны 1, то для исследования сходимости ряда (27.3.9) нужно применять другие признаки, с которыми можно ознакомиться в [3].

Интегральный признак сходимости

Рассмотрим признак, достоинство которого состоит в исключительно высокой его чувствительности. Этим признаком проводится исследование сходимости там, где сформулированные признаки Д’Аламбсра и Коши «не работают».

Каждый член числового ряда 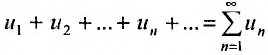можно рассматривать как значение функции f от его номера:

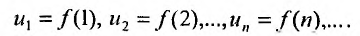
Эта функция определена пока только для целых положительных значений аргумента. Поэтому, доопределив значение функции f для всех нецелых значений аргумента, больших единицы, мы сможем, говорить о функции f(x), принимающей значения для любого 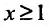и при х = n, равные членам числового ряда. Теорема 27.3.5. Пусть дан ряд

члены которого положительны и не возрастают 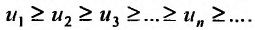Если функция f, определённая для всех 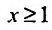, неотрицательна и монотонно убывает, то ряд (27.3.11) сходится или расходится тогда и только тогда, когда сходится или

расходится интеграл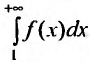

Доказательство. Пусть члены ряда (27.3.11) удовлетворяют условиям теоремы. Изобразим их графически, откладывая по оси Ох независимую переменную, а по оси Оу – соответствующие значения .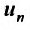

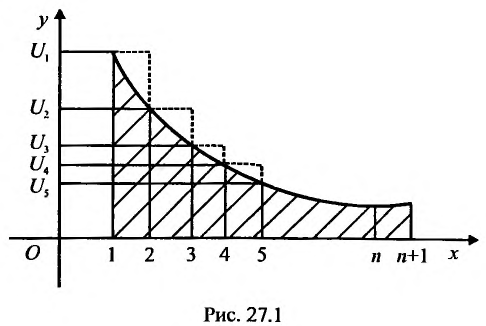
При таком графическом изображении сумма n первых членов ряда 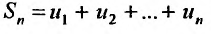представляет сумму площадей описанных прямоугольников, которая заключает внутри себя площадь, ограниченной кривой 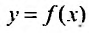, осью Ох и прямыми 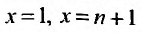и поэтому будет выполняться неравенство:

С другой стороны, криволинейная трапеция содержит сумму площадей вписанных прямоугольников, которая равна 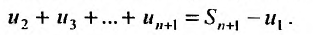Поэтому, выполняется неравенство:

Из (27.3.12) и (27.3.13) следует неравенство:

Предположим, что несобственный интеграл 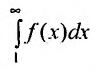сходится. Это означает, что 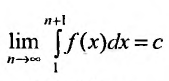является конечным числом. Тогда из неравенства (27.3.14) следует, что последовательность частичных сумм 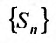возрастающая и ограничена при всех n. Тогда в силу теоремы: “возрастающая последовательность, ограниченная сверху, сходится”, числовой ряд (27.3.11) сходится. Если же несобствснный интеграл 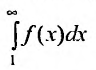расходится, т.е. 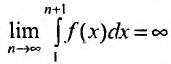, то из неравенства (27.3.12) следует, что последовательность частичных сумм 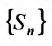не ограничена. Тогда в силу определения 27.1.3 ряд будет расходящимся.

Пример №21

Исследовать сходимость ряда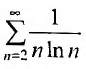

Решение:

Применим интегральный признак. Рассмотрим функцию 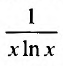которая положительна и убывает при х> 2, и исследуем сходимость несобственного интеграла:

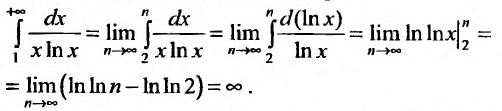
Так как несобственный интеграл расходится, то расходится и ряд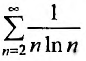 в силу инте1рального признака Коши.

Замечание. Исследовать сходимость данного ряда при помощи следствий 1 и 2 не представляется возможным, так как соответствующие пределы равны 1.

Пример №22

Исследовать сходимость ряда Дирихле

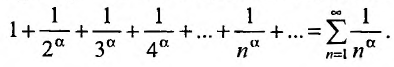
Решение:

Если 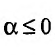, то общий член ряда 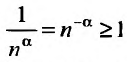не стремится к нулю. На основании следствия из необходимого признака сходимости, следует расходимость ряда Дирихле при .

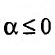Пусть а > 0, тогда необходимый признак, очевидно, выполняется. Применим интегральный признак Коши. Введем функцию

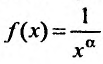, которая положительная и не возрастает при 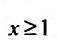и исследуем сходимость несобственного интеграла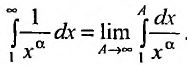

Вычислим определенный интеграл, записанный под знаком предела:

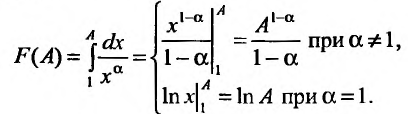
Если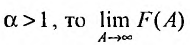 существует и равен 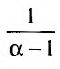а при 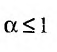указанный предел не существует.

Таким образом, при a>1 несобственный интеграл 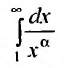сходится, следовательно, сходится и ряд Дирихле, а при 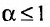несобственный интеграл расходится, следовательно, расходится и ряд Дирихле.

Гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных числам натурального ряда:

т.е. сумма всех чисел вида 1/n, где n – натуральное число, изменяющееся от нуля до бесконечности.

Ряд назван гармоническим так как каждый его член, начиная со второго, является гармоническим средним двух соседних.

Сумма первых n членов ряда

Отдельные члены ряда стремятся к нулю, нопредполагается чтосумма всех его членов расходится, т.е. что n-ное гармоническое число больше n-ного натурального.
n-ной частичной суммой s_n гармонического ряда называется n-ное гармоническое число, представляющее собой только сумму n первых членов гармонического ряда.:

Некоторые значения частичных сумм ( например для случая 1 слагаемого и 5-ти первых членов):

S1 = 1;

S5 = 137/60 = приблизительно 2,283

Теоретико-числовые свойства частичных сумм: для любых n > 1 сумма первых n членов рядаSn будет дробным числом.

Формула Эйлера

В 1740 году Л. Эйлером было получено асимптотическое выражение для суммы первых n членов ряда. Теоретико-числовые свойства частичных сумм
Для любых n>1

Сходимость ряда

Предполагалось до 7 августа 2010 года, что при стремлении n к бесконечностиSn также стремится к бесконечности, оставаясь меньше соответствующего натурального числа.

Предполагалось также Гармонический ряд расходится очень медленно: чтобы частичная сумма превысила 100, необходимо около 10⁴³ элементов ряда.

Сходимость гармонического ряда можно продемонстрировать, сравнив его с числами натурального ряда:
очевидно, что частичная сумма каждых n первых членов не может превышать такое же натуральное число n, которое равно числу членов гармонического ряда.

Рассмотрим известные доказательстване сходимости гармонического ряда

Доказательство Орема

Доказательство расходимости можно построить, группируя слагаемыетаким образом, чтобы сумма слагаемых в скобках была меньше 1/2. При этом получается ряд 1+1/2+1/2+…+1/2 +… :

Последний ряд, очевидно, расходится. Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).

В приведенном доказательстве проигнорирован очевидный факт: количество членов гармонического ряда строго равно количеству натуральных чисел (по определению). А при группировке членов ряда, для того чтобы получить 1/2 каждый раз в скобки объединялось все больше и большее количество членов гармонического ряда: 1, 2, 4, … т.е. 2^n соответственно.

Альтернативное доказательство расходимости

Предположим, что гармонический ряд сходится к сумме S:

Тогда, перегруппируя дроби так, что в первую группу объединяются только 1 и дроби с нечетными знаменателями, а во вторую группу – только с четными, и когда вынесем из второй скобки 1/2 а потом заменим вторую скобку на S и перенеся S/2 в левую часть, а также подставив обратно вместо S сумму ряда, получим что сумма дробей с четными знаменателями равна сумме дробей с нечетными знаменателями +1.

Это равенство, очевидно, неверно, так как единица больше одной второй, одна треть больше одной четвёртой, и так далее. Таким образом, наше предположение о сходимости ряда ошибочно, и ряд расходится.

Это равенство, также очевидно, может быть и верно, так как одна вторая больше одной третьей, одна четвёртая больше одной пятой, и так далее. Таким образом, необходимо также доказать, что сумма ряда: 1/2 – 1/3 + 1/4 – 1/5 + …

не равна 1.

В данном доказательстве также не учитывается тот факт, что каждому натуральному числу взаимооднозначно соответствует только один член гармонического ряда.

Частичные суммы

n-ая частичная сумма гармонического ряда, т.е. сумма только первых n членов ряда

называется n-ым гармоническим числом.

Разница между n-м гармоническим числом и натуральным логарифмом n сходится к постоянной Эйлера-Маскерони.

Разница между различными гармоническими числами никогда не равна целому число и никакое гармоническое число, кроме 1, не является целым числом.

Связанные ряды

Ряд Дирихле

Обобщенным гармоническим рядом (или рядом Дирихле) называют ряд, состоящий из членов гармонического ряда, возведенных в степень меньше или равную 1, или в степень большую 1. Считается, что Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1.

Сумма обобщённого гармонического ряда порядка α равна значению дзета-функции Римана от аргумента α.

Для чётных это значение явно выражается через число пи, например, дзета-функции Римана от аргумента α=2 равна числу пи в квадрате деленному на 6 , а уже для α=3 его значение аналитически неизвестно.

Знакопеременный ряд

В отличие от гармонического ряда, у которого все слагаемые берутся со знаком «+», ряд

сходится по признаку Лейбница. Поэтому говорят, что такой ряд обладает условной сходимостью.

Его сумма равна натуральному логарифму 2:

Эта формула — частный случай Ряд Меркатора (англ.), ряда Тейлора для натурального логарифма.

Похожий ряд может быть получен из ряда Тейлора для арктангенса, известного как ряд Лейбница.

Отметим, что если сходится гармонический ряд, то, естественно сходится и любой другой знакопеременный ряд, состоящий только из членов гармонического ряда.

Случайный гармонический ряд

Бирон Шмуланд из Университета Альберты рассмотрел свойства случайного ряда, в котором числителислагаемых рядаs_n независимые, одинаково распределённые случайные величины, которые принимают значения +1 и −1 с одинаковой вероятностью ½. Показано, что эта сумма с вероятностью 1, и сумма ряда есть случайная величина с интересными свойствами. Например, функция плотности вероятности, вычисленная в точках +2 или −2 имеет значение 0,124 999 999 999 999 999 999 999 999 999 999 999 999 999 7642 …, отличаясь от 1/8 на менее чем 10⁻⁴². Статья Шмуланда объясняет, почему эта величина близка, но не равна 1/8.

«Истончённый» гармонический ряд

Ряд Кемпнера (англ.)

Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшаяся сумма сходится к числу <80, точнее — к 22,92067 66192 64150 34816. Более того, доказано, что если оставить слагаемые, не содержащие любой заранее выбранной последовательности цифр, то полученный ряд будет сходиться.

Учитывая сходимость Ряда Кемпнера можно предположить что сходимость гармонического ряда хотя пока и не доказана, но имеет место быть! (см. обсужд.)

В пользу сходимости гармонического ряда свидетельствует и такой мысленный эксперимент: запишем три столбца,

№ п/п строки Частичная Сумма гармонического геометрическая прогрессияс коэффициентом,

(натуральное) ( ряда, до члена 1/n ) например ((256 в степени 256)-1)/(256 в степени 256)

1 1 ((256 в степени 256)-1)/(256 в степени 256)
2 1+1/2 +((256 в степени 256)-1)/(256 в степени 256)^2
3 1/3+1/2+1 +((256 в степени 256)-1)/(256 в степени 256)^3 . . … .
256 1+1/2+1/3 + …+ 1/256 +((256 в степени 256)-1)/(256 в степени 256)^256
…
(256 в степени 256) 1+1/2+…+1/(256^256) +((256^256)-1)^(256-1)^256)) ^((256^256)-1)^(256-1)^256))

(256 в степени 256) +1)) …. …

…

Очевидно, что для любого натурального, стермящегося к бесконечности, всегда найдется такое натуральное+1, которое будучи разделенным на то же самое натуральное +2 даст такой коэффициент, который будет меньше единицы и обеспечит сходимость суммы членов ряда геометрической прогрессии, каждый из которыхзаведомо меньше соответствующего (с таким же номером), члена гармонического ряда.

Примечания

См. http://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D1%80%D1%8F%D0%B4

Гармонический ряд

Доказательство группировкой слагаемых

Формула Эйлера

Среднее гармоническое

Сумма чисел, обратных простым

Depleted harmonic series

Знакопеременный ряд

В математике гармонический ряд – это расходящийся бесконечный ряд

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯. { displaystyle sum _ {n = 1} ^ { infty} { frac {1} {n}} = 1 + { frac {1} {2}} + { frac {1} {3}} + { frac {1} {4}} + { frac {1} {5}} + cdots.}

Его название происходит от концепции обертонов или гармоник в музыке : длины волн обертонов вибрирующей струны составляют 1/2, 1/3, 1/4 и т. д. от основной длины волны струны. Каждый член ряда после первого – это среднее гармоническое соседних членов; фраза «гармоническое среднее» также происходит от музыки.

Содержание

• 1 История
• 2 Дивергенция
  • 2.1 Сравнительный тест
  • 2.2 Интегральный тест
• 3 Скорость дивергенции
• 4 Частичные суммы
• 5 Связанные серии
  • 5.1 Чередование серия гармоник
  • 5.2 Общая серия гармоник
  • 5.3 Серия p
  • 5.4 Серия ln
  • 5.5 Серия φ
  • 5.6 Последовательность случайных гармоник
  • 5.7 Серия обедненных гармоник
• 6 Применения
• 7 См. Также
• 8 Ссылки
• 9 Внешние ссылки

История

Дивергенция гармонического ряда была впервые доказана в XIV веке Николь Орем, но это достижение ушло в безвестность. Доказательства были даны в 17 веке Пьетро Менголи и Иоганном Бернулли, последнее доказательство опубликовал и популяризировал его брат Якоб Бернулли.

Исторически гармонические последовательности имели определенная популярность у архитекторов. Это было особенно важно в период барокко, когда архитекторы использовали их для определения пропорций планов этажей, этажей и установить гармоничные отношения между внутренними и внешними архитектурными деталями церквей и дворцов.

Дивергенция

Есть несколько хорошо известных доказательств дивергенции гармонического ряда. Некоторые из них приведены ниже.

Сравнительный тест

Один из способов доказать дивергенцию – это сравнение гармонического ряда с другим расходящимся рядом, где каждый знаменатель заменяется следующей по величине степенью двойки :

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ { displaystyle { begin {alignat} {8} 1 + { frac {1} {2}} + { frac {1} {3}} + { frac {1} {4 }} + { frac {1} {5}} + { frac {1} {6}} + { frac {1} {7}} + { frac {1} {8}} + { frac {1} {9}} + cdots \ [5pt] {} geq 1 + { frac {1} {2}} + { frac {1} { color {красный } { mathbf {4}}}} + { frac {1} {4}} + { frac {1} { color {красный} { mathbf {8}}}} + { frac {1} { color {red} { mathbf {8}}}} + { frac {1} { color {red} { mathbf {8}}}} + { frac {1} { 8}} + { frac {1} { color {red} { mathbf {16}}}} + cdots end {alignat}}}

Каждый член гармонического ряда больше или равна соответствующему члену второго ряда, и поэтому сумма гармонического ряда должна быть больше или равна сумме второй серии. Однако сумма второй серии бесконечна:

1 + (1 2) + (1 4 + 1 4) + (1 8 + 1 8 + 1 8 + 1 8) + (1 16 + ⋯ + 1 16) + ⋯ знак равно 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞. { displaystyle { begin {align} 1 + left ({ frac {1} {2}} right) + left ({ frac {1} {4}} + { frac {1} {4} } right) + left ({ frac {1} {8}} + { frac {1} {8}} + { frac {1} {8}} + { frac {1} {8} } right) + left ({ frac {1} {16}} + cdots + { frac {1} {16}} right) + cdots \ [5pt] {} = {} 1+ { frac {1} {2}} + { frac {1} {2}} + { frac {1} {2}} + { frac {1} {2}} + cdots = infty. end {align}}}

Отсюда следует (из сравнительного теста ), что сумма гармонического ряда также должна быть бесконечной. Точнее, приведенное выше сравнение доказывает, что

∑ n = 1 2 k 1 n ≥ 1 + k 2 { displaystyle sum _ {n = 1} ^ {2 ^ {k}} { frac {1} { n}} geq 1 + { frac {k} {2}}}

для каждого положительного целого числа k.

Это доказательство, предложенное Николь Орем примерно в 1350 году, многие в математическом сообществе считают высшим достижением средневековой математики. Сегодня это стандартное доказательство, которому преподают на уроках математики. Тест конденсации Коши является обобщением этого аргумента.

Интегральный тест

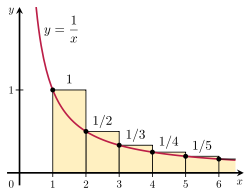Иллюстрация интегрального теста.

Можно доказать, что гармонический ряд расходится, сравнив его сумму с несобственным интегралом. В частности, рассмотрите расположение прямоугольников, показанных на рисунке справа. Каждый прямоугольник имеет ширину 1 единицу и высоту 1 / n, поэтому общая площадь бесконечного числа прямоугольников является суммой гармонического ряда:

площадь прямоугольников = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ { displaystyle { begin {array} {c} { text {area of}} \ { text {rectangles}} end {array}} = 1 + { frac {1} {2} } + { frac {1} {3}} + { frac {1} {4}} + { frac {1} {5}} + cdots}

Кроме того, общая площадь под кривой y = 1 / x от 1 до бесконечности задается расходящимся несобственным интегралом :

площадью под кривой = ∫ 1 ∞ 1 xdx = ∞. { displaystyle { begin {array} {c} { text {area under}} \ { text {curve}} end {array}} = int _ {1} ^ { infty} { frac {1} {x}} , dx = infty.}

Поскольку эта область полностью содержится внутри прямоугольников, общая площадь прямоугольников также должна быть бесконечной. Точнее, это доказывает, что

∑ n = 1 k 1 n>∫ 1 k + 1 1 x d x = ln ⁡ (k + 1). { displaystyle sum _ {n = 1} ^ {k} { frac {1} {n}}> int _ {1} ^ {k + 1} { frac {1} {x}} , dx = ln (k + 1).}

Обобщение этого аргумент известен как интегральный критерий.

Скорость расхождения

Гармонический ряд расходится очень медленно. Например, сумма первых 10 членов меньше 100. Это потому, что частичные суммы ряда имеют логарифмический рост. В частности,

∑ n = 1 k 1 n = ln ⁡ k + γ + ε k ≤ (ln ⁡ k) + 1 { displaystyle sum _ { n = 1} ^ {k} { frac {1} {n}} = ln k + gamma + varepsilon _ {k} leq ( ln k) +1}

, где γ – Постоянная Эйлера – Маскерони и ε k ~ 1 / 2k, которое стремится к 0, когда k стремится к бесконечности. Леонард Эйлер доказал и это, и более поразительный факт, что сумма который включает только , обратные простым числам, а также d iverges, то есть

∑ p простое 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞. { displaystyle sum _ {p { text {prime}}} { frac {1} {p}} = { frac {1} {2}} + { frac {1} {3}} + { frac {1} {5}} + { frac {1} {7}} + { frac {1} {11}} + { frac {1} {13}} + { frac {1} { 17}} + cdots = infty.}

Частичные суммы

Первые тридцать чисел гармоники

n	Частичная сумма гармонического ряда, H n
, выраженная в виде дроби	десятичной дроби	относительный размер
1	1	~ 1	1
2	3	/2	~ 1,5	1,5
3	11	/6	~ 1,83333	1,83333
4	25	/12	~ 2,08333	2,08333
5	137	/ 60	~ 2,28333	2,28333
6	49	/20	~ 2,45	2,45
7	363	/ 140	~ 2.59286	2,59286
8	761	/280	~ 2,71786	2.71786
9	7129	/2520	~ 2,82897	2,82897
10	7381	/ 2520	~ 2.92897	2.92897
11	83711	/27720	~ 3.01988	3.01988
12	86021	/ 27720	~ 3.10321	3.10321
13	1145993	/360360	~ 3,18013	3,18013
14	1171733	/ 360360	~ 3,25156	3,25156
15	1 195757	/ 360360	~ 3.31823	3.31823
16	2436559	/720720	~ 3.38073	3,38073
17	42142223	/ 12252240	~ 3.43955	3.43955
18	14274301	/4084080	~ 3,49511	3,49511
19	275295799	/ 77597520	~ 3,54774	3,54774
20	55835135	/15519504	~ 3.59774	3.59774
21	18858053	/5173168	~ 3.64536	3.64536
22	19093197	/ 5173168	~ 3.69081	3.69081
23	444316699	/118982864	~ 3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~ 3.81596	3.81596
26	34395742267	/ 8923714800	~ 3.85442	3.85442
27	312536252003	/80313433200	~ 3.89146	3.89146
28	315404588903	/ 80313433200	~ 3.92717	3.92717
29	9227046511387	/2329089562800	~ 3.96165	3,96165
30	9304682830 147	/ 2329089562800	~ 3.99499	3.99499

Конечные частные суммы расходящегося гармонического ряда,

H n = ∑ k = 1 n 1 k, { displaystyle H_ {n} = sum _ {k = 1} ^ {n} { frac {1} {k}},}

называются числами гармоник.

Разница между H n и ln n сходится к константе Эйлера – Маскерони. Разница между любыми двумя номерами гармоник никогда не бывает целой. Номера гармоник не являются целыми числами, за исключением H 1 = 1.

Родственные серии

Чередующиеся гармонические ряды

Первые четырнадцать частичных сумм чередующихся гармонических рядов ( черные отрезки), сходящиеся к натуральному логарифму 2 (красная линия).

Ряд

∑ n = 1 ∞ (- 1) n + 1 n = 1 – 1 2 + 1 3 – 1 4 + 1 5 – ⋯ { displaystyle sum _ {n = 1} ^ { infty} { frac {(-1) ^ {n + 1}} {n}} = 1 – { frac {1} {2 }} + { frac {1} {3}} – { frac {1} {4}} + { frac {1} {5}} – cdots}

известен как чередующийся гармонический ряд . Эта серия сходится с помощью теста чередующейся серии. В частности, сумма равна натуральному логарифму 2 :

1 – 1 2 + 1 3 – 1 4 + 1 5 – ⋯ = ln ⁡ 2. { displaystyle 1 – { frac {1} {2}} + { frac {1} {3}} – { frac {1} {4}} + { frac {1} {5}} – cdots = ln 2.}

чередующийся гармонический ряд, в то время как условно сходящийся, не является абсолютно сходящимся : если члены в ряду систематически переупорядочиваются, обычно сумма становится другой и, в зависимости от перестановки, возможно, даже бесконечно.

Формула переменного гармонического ряда является частным случаем ряда Меркатора, ряда Тейлора для натурального логарифма.

Родственный ряд может быть получен из ряда Тейлора для арктангенса :

∑ n = 0 ∞ (- 1) n 2 n + 1 = 1 – 1 3 + 1 5 – 1 7 + ⋯ = π 4. { displaystyle sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {2n + 1}} = 1 – { frac {1} {3}} + { frac {1} {5}} – { frac {1} {7}} + cdots = { frac { pi} {4}}.}

Это известно как серия Лейбница.

Общий гармонический ряд

Общий гармонический ряд имеет форму

∑ n = 0 ∞ 1 an + b, { displaystyle sum _ {n = 0} ^ { infty} { frac {1} {an + b}},}

где a ≠ 0 и b – действительные числа, а b / a не равно нулю или отрицательному целому числу.

При сравнении предельных значений с гармоническим рядом все общие гармонические ряды также расходятся.

p-ряд

Обобщением гармонического ряда является p-ряд (или гипергармонический ряд ), определяемый как

∑ n = 1 ∞ 1 np { displaystyle sum _ {n = 1} ^ { infty} { frac {1} {n ^ {p}}}}

для любого действительного числа p. Когда p = 1, p-ряд – это расходящийся гармонический ряд. Либо интегральный тест, либо тест конденсации Коши показывает, что p-ряд сходится для всех p>1 (в этом случае он называется сверхгармоническим рядом ) и расходится для всех p ≤ 1. Если p>1, то сумма p-ряда равна ζ (p), то есть дзета-функция Римана, вычисленная в p.

Задача нахождения суммы для p = 2 называется проблемой Базеля ; Леонард Эйлер показал, что это π / 6. Значение суммы для p = 3 называется константой Апери, поскольку Роджер Апери доказал, что это иррациональное число.

ln-ряд

С p-серией связан ln-series, определенный как

∑ n = 2 ∞ 1 n (ln ⁡ n) p { displaystyle sum _ { n = 2} ^ { infty} { frac {1} {n ( ln n) ^ {p}}}}

для любого положительного действительного числа p. Это можно показать с помощью интегрального теста, что он расходится при p ≤ 1, но сходится при всех p>1.

φ-ряд

Для любой выпуклой, действительной функции φ такой, что

lim sup u → 0 + φ (u 2) φ (u) < 1 2, {displaystyle limsup _{uto 0^{+}}{frac {varphi left({frac {u}{2}}right)}{varphi (u)}}<{frac {1}{2}},}

ряд

∑ N = 1 ∞ φ (1 n) { displaystyle sum _ {n = 1} ^ { infty} varphi left ({ frac {1} {n}} справа)}

сходится.

Случайный гармонический ряд

Случайный гармонический ряд

∑ n = 1 ∞ snn, { displaystyle sum _ {n = 1} ^ { infty} { frac {s_ {n}} {n}},}

где s n – независимые, одинаково распределенные случайные величины, принимающие значения +1 и -1 с равной вероятностью 1/2, является хорошо известным примером в теории вероятностей для ряда случайных величин, который сходится с вероятностью 1. Факт такой сходимости является простым следствием либо теоремы Колмогорова о трех рядах, либо тесно связанного с ним максимального неравенства Колмогорова. Байрон Шмуланд из Университета Альберты дополнительно исследовал свойства случайного гармонического ряда и показал, что сходящийся ряд – это случайная величина с некоторыми интересными свойствами. В частности, функция плотности вероятности этой случайной величины, оцененная как +2 или -2, принимает значение 0,12499999999999999999999999999999999999764…, отличающееся от 1/8 менее чем на 10. В статье Шмуланда объясняется, почему эта вероятность так близко, но не совсем к 1/8. Точное значение этой вероятности дается интегралом произведения бесконечного косинуса C 2, деленного на π.

Истощенный гармонический ряд

Истощенный гармонический ряд, в котором удалены все члены, в которых цифра 9 появляется в любом месте знаменателя, может быть показано, что они сходятся к значению 22.92067661926415034816…. Фактически, когда все члены, содержащие любую конкретную строку цифр (в любом основании ), удаляются, ряд сходится.

Приложения

Гармонический ряд может быть противоречит здравому смыслу для студентов, впервые столкнувшихся с ним, потому что это расходящийся ряд, хотя предел n-го члена при стремлении n к бесконечности равен нулю. Дивергенция гармонического ряда также является источником некоторых очевидных парадоксов. Одним из примеров этого является «червяк на резинке ». Предположим, что червяк ползет по бесконечно эластичной резиновой ленте длиной один метр, в то время как резинка равномерно растягивается. Если червь движется со скоростью 1 сантиметр в минуту, а полоса растягивается на 1 метр в минуту, дойдет ли червь до конца резинки? Ответом, как это ни парадоксально, будет «да», поскольку через n минут отношение расстояния, пройденного червем, к общей длине резиновой ленты составляет

1 100 ∑ k = 1 n 1 k. { displaystyle { frac {1} {100}} sum _ {k = 1} ^ {n} { frac {1} {k}}.}

(На самом деле фактическое соотношение немного меньше чем эта сумма при непрерывном расширении ленты.)

Поскольку ряд становится произвольно большим, когда n становится больше, в конечном итоге это отношение должно превышать 1, что означает, что червяк достигает конца резиновой ленты. Однако значение n, при котором это происходит, должно быть чрезвычайно большим: приблизительно e, т.е. число, превышающее 10 минут (10 лет). Хотя гармонический ряд действительно расходится, это происходит очень медленно.

Другой проблемой, связанной с гармоническим рядом, является проблема Jeep, которая (в одной форме) спрашивает, сколько всего топлива требуется для джипа с ограниченным расходом топлива. пропускная способность для пересечения пустыни, возможно, оставляя капли топлива по пути. Расстояние, которое можно преодолеть с заданным количеством топлива, связано с частичными суммами гармонического ряда, которые растут логарифмически. Таким образом, необходимое количество топлива увеличивается экспоненциально с желаемой дистанцией.

Проблема наложения блоков : блоки, выровненные в соответствии с гармонической последовательностью, перекрывают расщепления любой ширины.

Другим примером является проблема наложения блоков : учитывая набор одинаковые домино, очевидно, что их можно сложить на краю стола так, чтобы они свисали с края стола, не падая. Противоречивый результат состоит в том, что их можно сложить таким образом, чтобы свес был произвольно большим, при условии наличия достаточного количества костяшек домино.

Более простой пример, с другой стороны, – пловец, который продолжает прибавлять в скорости. при касании стенок бассейна. Пловец начинает пересекать 10-метровый бассейн со скоростью 2 м / с, и с каждым переходом к скорости прибавляется еще 2 м / с. Теоретически скорость пловца неограничена, но количество переходов через бассейн, необходимое для достижения этой скорости, становится очень большим; например, чтобы достичь скорости света (игнорируя специальную теорию относительности ), пловцу нужно пересечь бассейн 150 миллионов раз. В отличие от этого большого числа, время, необходимое для достижения заданной скорости, зависит от суммы ряда при любом заданном количестве переходов (итераций) пула:

10 2 ∑ k = 1 n 1 k. { displaystyle { frac {10} {2}} sum _ {k = 1} ^ {n} { frac {1} {k}}.}

Вычисление суммы (итеративно) показывает, что для получения до скорости света требуется всего 97 секунд. Продолжая движение дальше этой точки (превышая скорость света, снова игнорируя специальную теорию относительности ), время, необходимое для пересечения бассейна, фактически приближается к нулю, поскольку количество итераций становится очень большим, и хотя время, необходимое Чтобы пересечь пул, кажется, стремится к нулю (при бесконечном количестве итераций), сумма итераций (время, затрачиваемое на полное пересечение пула) все равно будет расходиться с очень низкой скоростью.

См. Также

На Викискладе есть материалы, связанные с Гармонический ряд .

• Эта функция Дирихле
• Гармоническая прогрессия
• Список сумм взаимных величин

Ссылки

Внешние ссылки

• , Энциклопедия математики, EMS Press, 2001 [1994]
• «Гармонические ряды расходятся снова и снова» (PDF). Обзор AMATYC. 27 : 31–43. 2006.
• Вайсштейн, Эрик У. «Гармонический ряд». MathWorld.
• Вайсштейн, Эрик У. «Задача наложения книг». MathWorld.
• Худельсон, Мэтт (1 октября 2010 г.). «Доказательство без слов: сумма переменного гармонического ряда равна ln 2» (PDF). Математический журнал. 83 (4): 294. doi :10.4169/002557010X521831.