Если (x) — неотрицательное число, то его модуль равен самому числу (x), то есть (|x|=x).
Если (x) — отрицательное число, то его модуль равен противоположному для (x) числу, то есть (|x|=-x).
Получаем:
x=x,если x≥0−x,если x<0
.
Например,
4=4;−4=−(−4)=4;−4.7=−(−4.7)=4.7;7−2=7−2(так как7−2>0).
Геометрический смысл модуля
Геометрическая модель множества действительных чисел
ℝ
— координатная прямая. Точки (a) и (b) на координатной прямой соответствуют действительным числам (a) и (b). Расстояние между точками (a) и (b) обозначим
ρ
((a, b)) (букву
ρ
греческого алфавита читаем «ро»). Это расстояние равно (b – a), если (b > a),

оно равно (a – b), если (a > b), и, наконец,

оно равно нулю, если (a = b).
Для всех трёх случаев справедлива формула:
ρa,b=a−b
.
Пример:
Уравнение задано в аналитическом виде
x−5=3
. С позиции геометрического смысла модуля на координатной прямой необходимо определить точки (x), для которых выполняется условие
ρ(x;5)=3
(точки (x) должны быть удалены от точки (5) на расстояние, равное (3)). Этому условию удовлетворяют точки (2) и (8).

Следовательно, уравнение имеет два корня: (2) и (8).
Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
![]()
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Вот смотри…
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Определение модуля:
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)
Свойства модуля:
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
![]()
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
![]()
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
![]()
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
![]()
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
![]()
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
( |mathbf{a}|,) (( a) — любое число).
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf{3} right|=mathbf{3})
( left| -mathbf{3} right|=mathbf{3}.)
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)
( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)
А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)
( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| text{ }le text{ } right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10}) | ( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Выражения также равны, если оба числа отрицательны:
| ( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10) | ( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4}) | ( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
или
| ( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4}) | ( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
( mathbf{4}<mathbf{10})
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
( {{left| x right|}^{2}}=?)
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
( {{left| x right|}^{2}}={{x}^{2}})
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
( {{left| 5 right|}^{2}}={{5}^{2}}=25)
( {{left| -5 right|}^{2}}=?)
Ну, и почему сомнения? Действуем смело!
( {{left| -5 right|}^{2}}={{5}^{2}}=25)
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
а) ( |3|text{ }+text{ }|-9|;)
б) ( |-5|text{ }-text{ }|6|;)
в) ( |15left| cdot right|-3|;)
г) ( displaystyle frac{|8|}{|-2|}).
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:
( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
![]()
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)
Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).
Решение:
( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)
( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)
( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb{R}):
- ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при text{ }c>0)
- ( {{left| x right|}^{2}}={{x}^{2}})
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Подготовка к ЕГЭ на 90+ в мини-группах
![]()
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Как решать уравнения с модулем: основные правила
30 декабря 2016
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
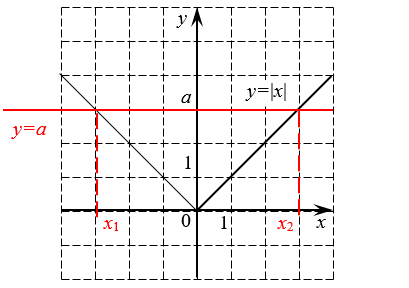
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
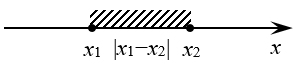
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft( x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft( x right) right|=a]
Ну и как такое решать? Напомню: $fleft( x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
или:
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left( 2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
[2x+1=5Rightarrow 2x=4Rightarrow x=2]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 \& 2x+1 lt 0 \end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
[2x+1=-5Rightarrow 2x=-6Rightarrow x=-3]
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft( x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft( x right) right|=aRightarrow fleft( x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; \& 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. \end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; \& 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. \end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft( x right)$ и $gleft( x right)$ :
[left| fleft( x right) right|=gleft( x right)Rightarrow left{ begin{align}& fleft( x right)=pm gleft( x right), \& gleft( x right)ge 0. \end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, \& 2xge 0. \end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2xRightarrow 3x-2x=2Rightarrow x=2; \& 3x-2=-2xRightarrow 5x=2Rightarrow x=frac{2}{5}. \end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5};$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft( x right) right|=gleft( x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left( x-{{x}^{3}} right), \& x-{{x}^{3}}ge 0. \end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; \& 2{{x}^{3}}-3{{x}^{2}}=0; \end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left( 2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 \& 2x-3=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left( x-{{x}^{3}} right); \& {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; \& -3{{x}^{2}}+2x=0; \& xleft( -3x+2 right)=0. \end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 \& -3x+2=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
[x-{{x}^{3}}ge 0]
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; \& x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; \& x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; \end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft( x right) right|=gleft( x right)$ или даже более простому $left| fleft( x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft( x right) right|=left| gleft( x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; \& 2x+3=-left( 2x-7 right)Rightarrow 2x+3=-2x+7. \end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft( x right) right|=left| gleft( x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left( x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
[x-1=pm left( {{x}^{2}}-3x+2 right)]
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; \& {{x}^{2}}-3x+2=-left( x-1 right)Rightarrow {{x}^{2}}-2x+1=0. \end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left( x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; \& left| x-1 right|=left| left( x-1 right)left( x-2 right) right|. \end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; \& left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; \& left| x-1 right|cdot left( 1-left| x-2 right| right)=0. \end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, \& left| x-2 right|=1. \end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; \& 0,004+0,0001=0,0041 gt 0; \& 5+0=5 gt 0. \end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, \& left| {{x}^{2}}+x-2 right|=0. \end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[x-{{x}^{3}}=0Rightarrow xleft( 1-{{x}^{2}} right)=0Rightarrow left[ begin{align}& x=0 \& x=pm 1 \end{align} right.]
[{{x}^{2}}+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin{align}& x=-2 \& x=1 \end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft( x right) right|=gleft( x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
[3x-5 gt 0Rightarrow left| 3x-5 right|=3x-5]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
[3x-5=5-3xRightarrow 6x=10Rightarrow x=frac{5}{3}]
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
[x=frac{5}{3}Rightarrow 3x-5=3cdot frac{5}{3}-5=5-5=0]
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
[3x-5 lt 0Rightarrow left| 3x-5 right|=5-3x]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
[5-3x=5-3x]
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
[3x-5 lt 0Rightarrow 3x lt 5Rightarrow x lt frac{5}{3}]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
[xin left( -infty ;frac{5}{3} right)]
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
[3x-5=0Rightarrow left| 3x-5 right|=0]
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
[0=3x-5Rightarrow 3x=5Rightarrow x=frac{5}{3}]
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
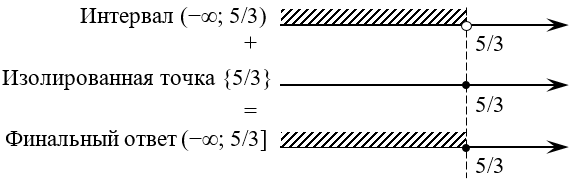
Итого окончательный ответ: $xin left( -infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:

Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
Смотрите также:
- Простейшие уравнения с модулем

- Уравнение с двумя модулями

- Сложные выражения с дробями. Порядок действий

- Сводный тест по задачам B15 (2 вариант)

- Как решать биквадратное уравнение

- B4: счетчики на электричество

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Модуль числа
Поддержать сайт![]()
Обозначим на
координатной прямой две точки, которые соответствуют числам
«−4» и 2.
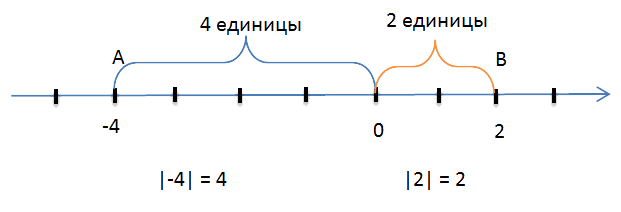
Точка «A», соответствующая числу «−4»,
находится на расстоянии
4 единичных отрезков от точки 0
(начала отсчёта), то есть длина отрезка «OA»
равна 4 единицам.
Число 4 (длина отрезка «OA») называют модулем
числа «−4».
Обозначают модуль числа так: |−4| = 4
Читают символы выше следующим образом: «модуль числа
минус четыре равен четырём».
Точка «B», соответствующая
числу «+2», находится на расстоянии двух единичных отрезков от начала отсчёта,
то есть длина отрезка «OB» равна двум единицам.
Число 2 называют модулем числа
«+2» и записывают:
|+2| = 2 или |2| = 2.
Если взять некоторое число «a» и изобразить его
точкой «A» на координатной прямой, то
расстояние от точки «A» до начала отсчёта
(другими словами длина отрезка «OA») и будет называться
модулем числа «a».
|a| = OA
Запомните!
![]()
Модулем рационального числа называют расстояние от
начала отсчёта до точки координатной прямой, соответствующей этому числу.
Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать,
что модуль числа не может быть отрицательным.
Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи.
- Модуль положительного числа равен самому числу.
|a| = a, если a > 0 - Модуль отрицательного числа равен противоположному числу.
|−a| = a, если a < 0 - Модуль нуля равен нулю.
|0| = 0, если a = 0 - Противоположные числа имеют равные модули.
|−a| = |a| = a
Примеры модулей рациональных чисел:
- |−4,8| = 4,8
- |5| = 5
- |0| = 0
- |− | =
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
18 января 2016 в 17:47
Евгения Плотникова

Профиль
Благодарили: 0
Сообщений: 1

Евгения Плотникова
Профиль
Благодарили: 0
Сообщений: 1
Модуль координаты точки равен 1)2;2)4;3)3.Вопрос.Какую координату может иметь точка.
0
Спасибо
Ответить
19 сентября 2016 в 10:45
Ответ для Евгения Плотникова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Знак моддуля, означает, что под ним может скрываться как отрицательное, так и положительное значение. Следовательно:
1) 2;2
-2;2
-2;-2
2;-2
2) 4;0
-4;0
0;4
0;-4
3) 3;0
-3;0
0;3
0;-3
подробнее здесь.
0
Спасибо
Ответить
17 января 2016 в 18:05
Заира Надырова

Профиль
Благодарили: 0
Сообщений: 1

Заира Надырова
Профиль
Благодарили: 0
Сообщений: 1
а) Что можно сказать о числе х, если известно, что модуль х=х?
б)модуль х=?х
0
Спасибо
Ответить
21 января 2016 в 16:18
Ответ для Заира Надырова
Сергей Фадеев

Профиль
Благодарили: 0
Сообщений: 6

Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
то что х=х больше х
0
Спасибо
Ответить
На этой странице вы узнаете
- Как перевернуть график модуля?
- Одной ногой тут, другой там: к какому промежутку относить граничные точки?
- Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0?
Модуль числа — это великая математическая мудрость, которая показывает дружбу и соперничество противоположных знаков: минуса и плюса. О том, что держит число в рамках, узнаем в статье.
Модуль
Мы легко можем найти расстояние от точки до точки, достаточно просто измерить его линейкой. Но можно ли найти расстояние от 0 до любого числа?
Представим, что наш дом находится посередине между школой и магазином. И до школы, и до магазина 500 метров, но они стоят по разные стороны от дома.
Расположим их на координатной прямой. Поскольку и школа, и магазин располагаются на одинаковом расстоянии, то от дома до них мы будем идти 500 метров. Но на координатной прямой до школы мы пройдем −500 метров, поскольку движемся против направления оси, а до магазина 500 метров.

Будет ли являться полученный результат противоречием? Нет, поскольку когда мы ищем расстояние, нам неважно направление движения и знак. В математике существует специальное определение — это модуль, или абсолютная величина.
Модуль — расстояние от любой точки на координатной прямой до начала координат.
Поскольку на координатной прямой мы можем отложить расстояние в две стороны, то такое расстояние можно найти и с отрицательными точками, и с положительными. Расстояние измеряет длину отрезка, то есть оно всегда будет положительно.
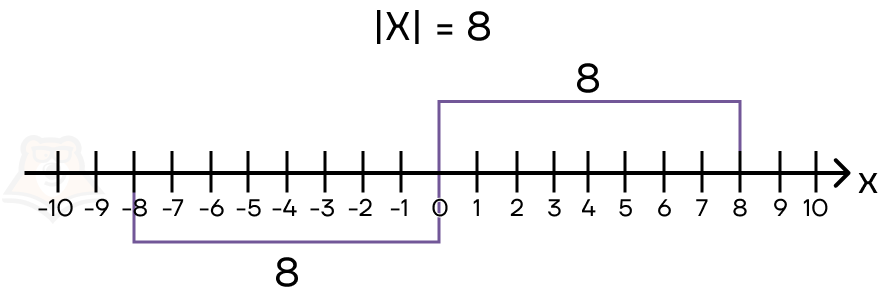
Можно сказать, что от любого числа модуль берет только цифры, а на знаки не обращает внимания. Например, |−8| = 8 и |8| = 8.
Может возникнуть вопрос: куда исчезает минус? Чтобы избавиться от минуса, достаточно умножить число на −1: (-8) * (-1) = 8. Значит, модуль просто умножает число на -1.
Отсюда получается, что модулем числа а называют выражение:

Возьмем два случая: a = 8 и a = -8. Для первого получаем |8| = 8, а для второго |-8| = -(-8) = 8, то есть определение выполняется.
Можно ли взять модуль функции? Да. Модулем произвольной функции называют выражение:
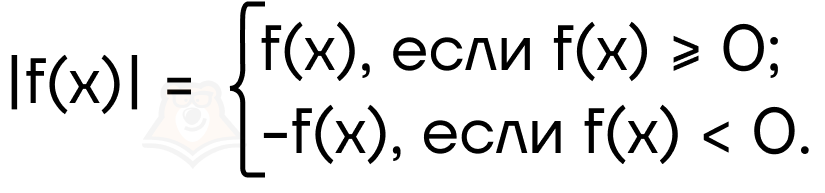
Свойства модуля
Модуль, как и все понятия в математике, обладает своими свойствами.
Свойство 1. |a| >= 0.
Как мы уже говорили, модуль всегда будет положительным числом, поскольку он не обращает внимания на знак числа.

Свойство 2. |a| = |-a|.
Это свойство также подтверждает рассуждения выше. Модули противоположных чисел, то есть чисел с разными знаками, равны.
Свойство 3. |a| >= a.
Если число а будет положительным, например, 5, то неравенство |5| >= 5 (rightarrow) 5 >= 5 выполняется, поскольку знак неравенства нестрогий.
Если число а будет отрицательным, например, -5, то неравенство |-5| >= -5 (rightarrow) 5 >= -5 выполняется, поскольку положительное число всегда больше отрицательного.
Свойство 4. |a * b| = |a| * |b|.
Пусть a = 5, b = -2, тогда |5 * (-2) | = |-10| = 10, и |5| * |-2| = 5 * 2 = 10, то есть выражения равны между собой.
Свойство 5. (|frac{a}{b}| = frac{|a|}{|b|}).
Рассуждения такие же, как и в предыдущем свойстве. Пусть a = 10, b = -5, тогда (|frac{10}{(-5)}| = |-2| = 2 и frac{|10|}{|-5|} = frac{10}{5} = 2).
Свойство 6. |a + b| <= |a| + |b|.
Почему появилось неравенство, а не уравнение, как в предыдущих двух свойствах? Разберем два примера.
Пусть a = 1, b = 2, тогда |1 + 2| = |3| = 3 и |1| + |2| = 1 + 2 = 3 — неравенство выполняется, поскольку знак нестрогий.
Но если a = -1, b = 2, тогда |-1 +2| = |1| = 1 и |-1| + |2| = 1 + 2 = 3, откуда получаем 1 < 3.
Свойство 7. (sqrt{a^2} = |a|).
Докажем это свойство. Пусть (sqrt{a^2} = x), тогда x0, поскольку квадратный «Корень» не может быть отрицательным. Возведем полученное уравнение в квадрат: a2 = x2
a2 — x2 = 0
(a — x)(a + x) = 0
Из уравнения x = a, из-за ограничений на x получаем a >= 0.
И x = -a, из-за ограничений на x получаем a < 0.
То есть получается выражение модуля.
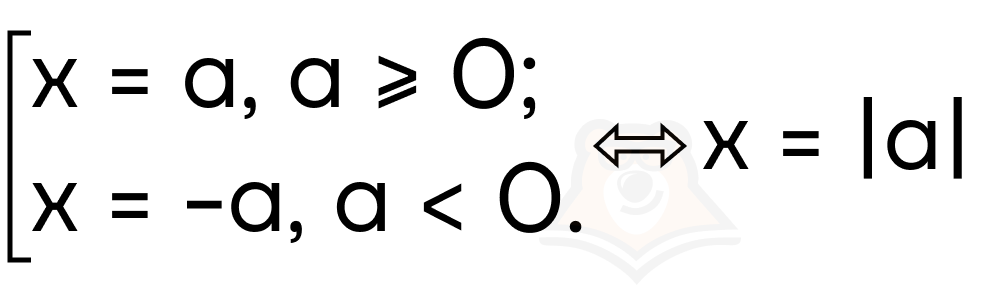
Свойство 8. |a|2 = a2.
Поскольку и модуль, и квадрат числа дают положительный результат, модуль в квадрате можно заменить просто квадратом числа.
График модуля
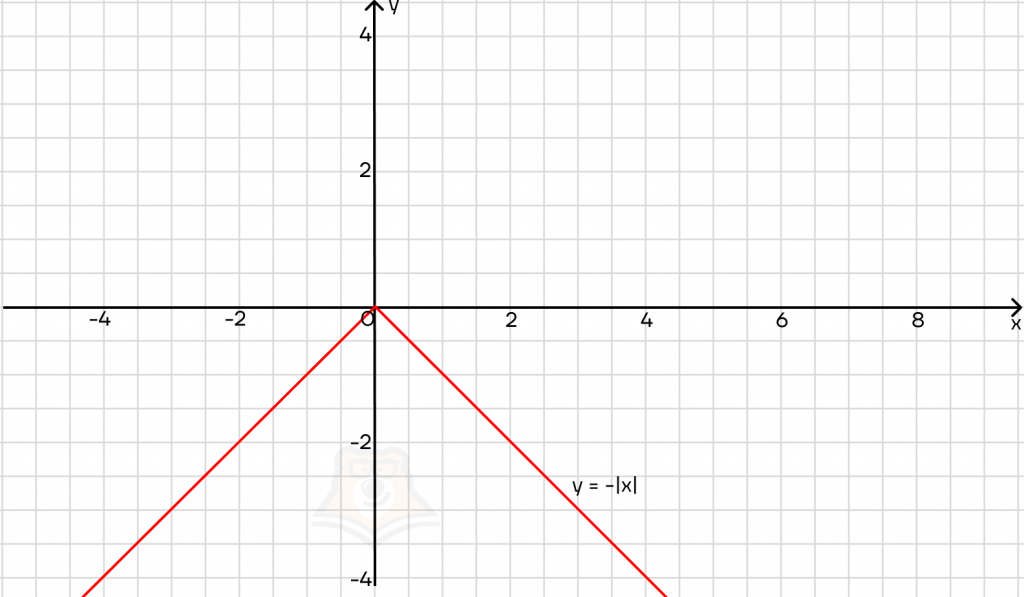
Как изобразить функцию с модулем? Для начала разберемся, что делает модуль с графиком функции.
Рассмотрим функцию y = x — это прямая. При этом у может быть и положительным, и отрицательным.
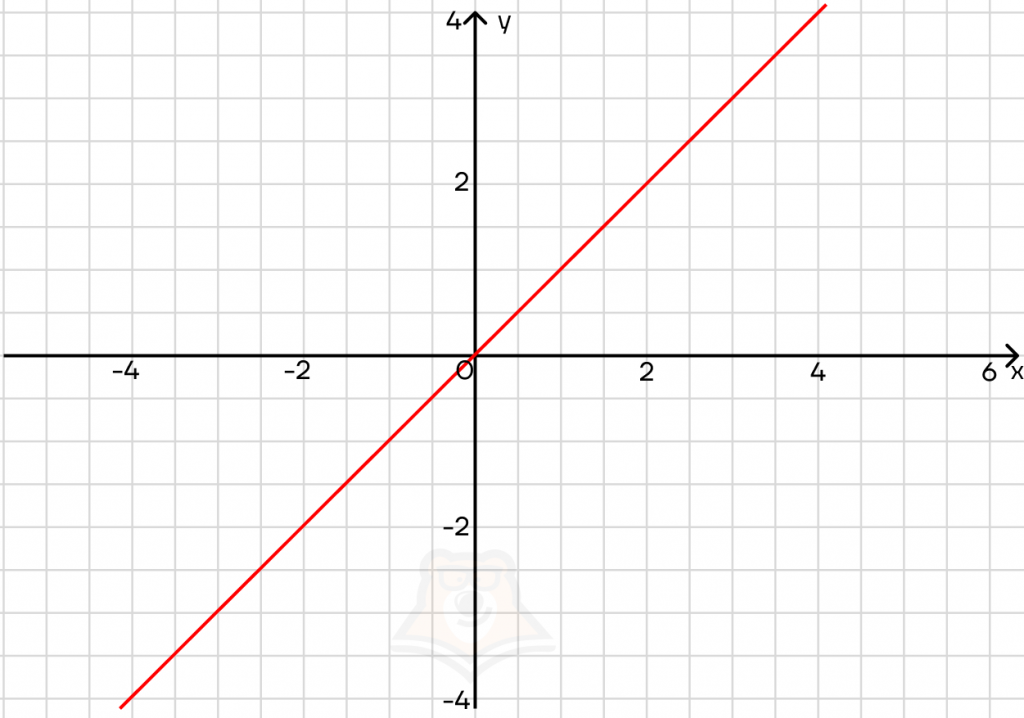
Занесем х под знак модуля: y = |x|. Теперь у может быть только положительным. Что происходит с частью графика, которая лежит ниже оси х? Она зеркально отражается. В итоге мы получаем галочку:
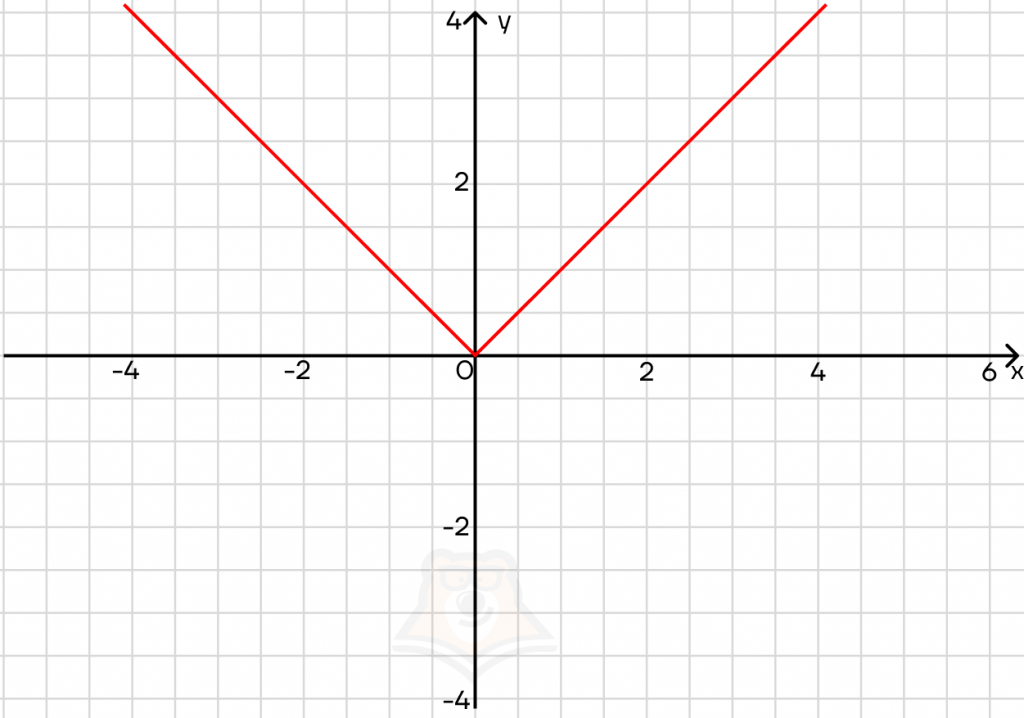
Модуль отражает любой график относительно оси х.
Что будет, если перед х будет стоять коэффициент? Построим графики:
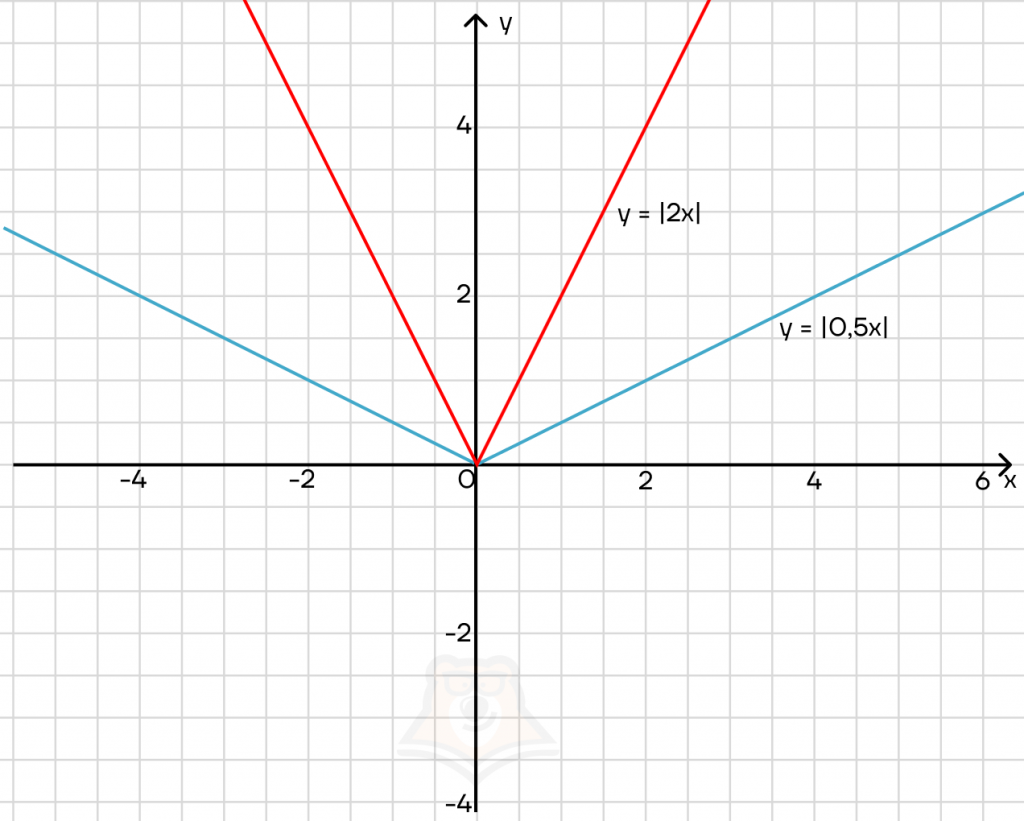
Галочка будет сужаться и расширяться. Причем чем больше коэффициент перед х, тем ýже будет галочка.
Попробуем добавить слагаемое к подмодульному выражению.
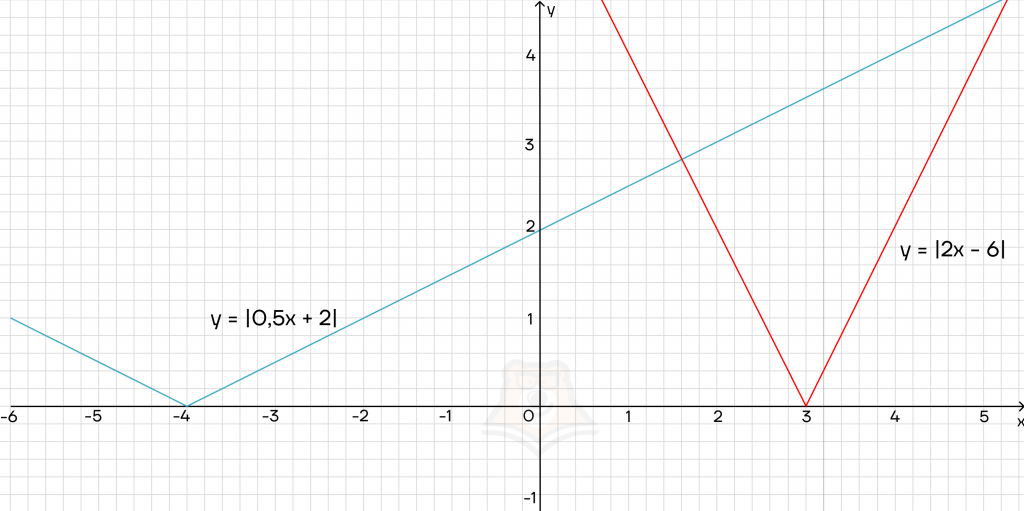
График модуля будет двигаться вдоль оси х. Причем:
- если мы прибавляем число, то график сдвигается влево;
- если мы вычитаем число, то график сдвигается вправо.
Добавим число к модулю, а не подмодульному выражению:
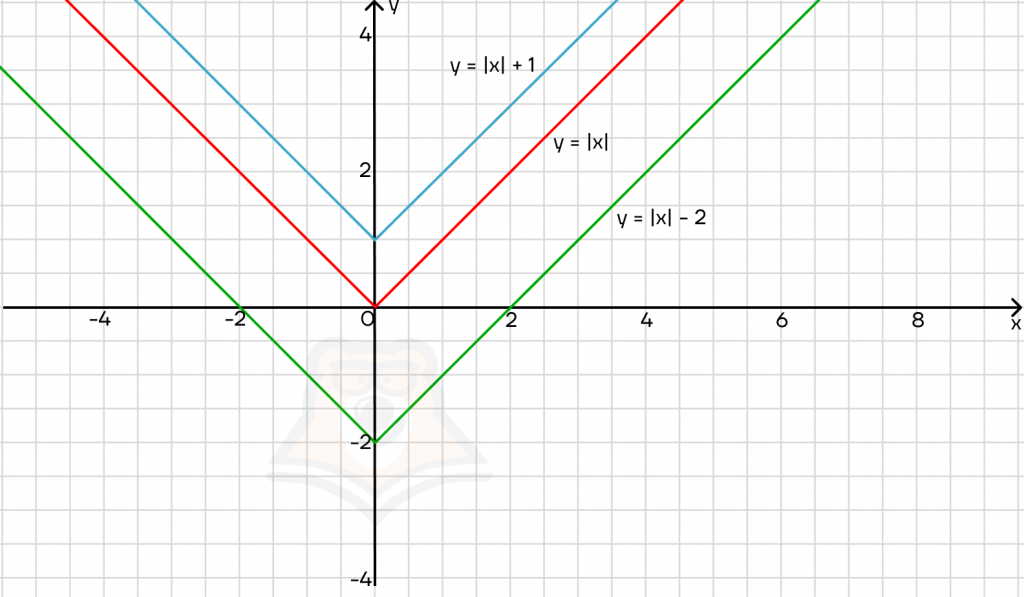
График будет двигаться вдоль оси у.
Для этого достаточно добавить перед модулем минус. Важно, чтобы минус стоял именно перед модулем, а не внутри него. Тогда график будет отзеркален относительно оси х и лежать только ниже нее.
Это легко проследить с помощью уравнений: если y = -|x|, то, при x = 3 получаем:
y = -|3| = -3
Уравнения с модулем
1. Возьмем уравнение вида |f(x)| = a. Поскольку модуль не может быть отрицательным, то и а не может быть отрицательным. Получаем следующий переход:
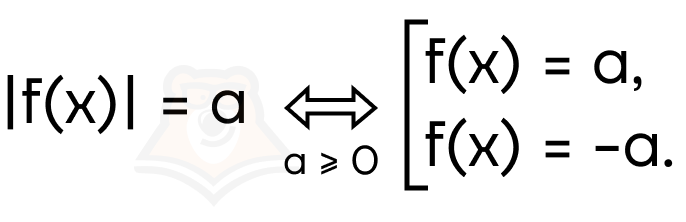
Пример 1. Решите уравнение |4x + 5| = 7.
Решение. В уравнении f(x) = 4x + 5, a = 7. Воспользуемся переходом:
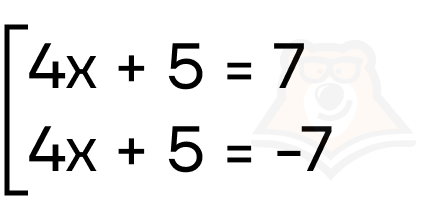
Из первого уравнения x = 0,5, а из второго уравнения x = -3.
Ответ: 0,5: -3.
2. В уравнениях и неравенствах можно встретить два разных модуля. Как быть в этом случае?
Шаг 1. Находим нули подмодульных выражений.
Шаг 2. Чертим числовую прямую и ищем знаки на промежутках для каждого модуля. Если подмодульное выражение отрицательно на промежутке, то ставится минус, если положительно — ставится плюс.
Шаг 3. Для каждого промежутка раскрываем модули. Если подмодульное выражение на промежутке отрицательно, то модуль раскрывается со знаком минус. Если положительно — модуль раскрывается со знаком плюс. Важно: полученные корни должны принадлежать промежуткам, на которых раскрывается модуль, иначе они не будут решениями уравнения.
Шаг 4. Записать все полученные корни в ответ.
Пример 2. Решите уравнение |x — 2| — |x + 2| = 4x — 5.
Решение. Найдем, в каких точках модули будут равны 0. Для этого подмодульное выражение также должно быть равно 0:
x — 2 = 0 (rightarrow) x = 2
x + 2 = 0 (rightarrow) x = -2
Нарисуем числовую прямую с этими точками:
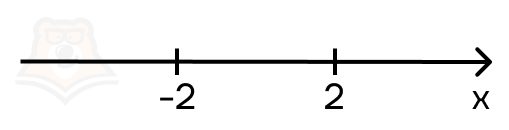
У нас получилось три промежутка:
- (-(infty);-2)
- [-2;2)
- [2;+(infty))
Обратим внимание, какие знаки имеет первый модуль на промежутках: x — 2 > 0 при x > 2. Следовательно, на первых двух промежутках модуль будет отрицательным, а на третьем положительным. Расставим его знаки красным цветом.
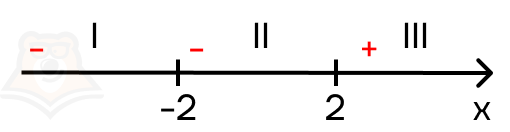
Проанализируем второй модуль: x + 2 > 0 (rightarrow) x>-2. Получается, подмодульное выражение будет положительно на втором и третьем промежутке, и отрицательным на первом промежутке. Расставим его знаки синим цветом.
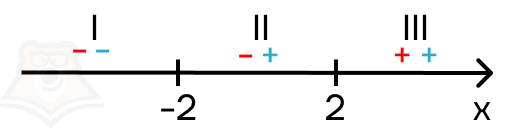
Теперь мы можем рассмотреть уравнение на всех трех промежутках. Однако для этого обязательно ввести ограничения: полученные точки должны принадлежать только этому промежутку, поскольку на следующем модули будут раскрываться уже по-другому.
2. Рассмотрим первый промежуток: x<-2. Оба модуля раскрываются с отрицательным знаком, и мы получаем следующее уравнение:
-(x — 2) — (-(x + 2)) = 4x — 5
-x + 2 + x + 2 = 4x — 5
4 = 4x — 5
4x = 9
x = 2,25
Точка не удовлетворяет ограничению, поскольку не лежит в промежутке (-(infty);-2):
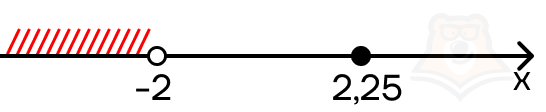
Рассмотрим второй промежуток: [-2;2). Первый модуль раскрывается с минусом, а второй с плюсом:
-(x — 2) — (x + 2) = 4x — 5
-x + 2 — x — 2 = 4x — 5
-2x = 4x — 5
6x = 5
(x = frac{5}{6})
Эта точка лежит в заданном промежутке и является решением уравнения.
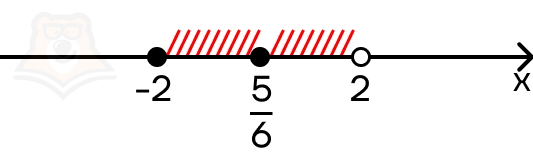
Рассмотрим третий промежуток [2;+(infty)). Оба модуля раскрываются со знаком плюс, мы получаем уравнение:
(x — 2) — (x + 2) = 4x — 5
x — 2 — x — 2 = 4x — 5
-4 = 4x — 5
4x = 1
x = 0,25 — эта точка не лежит в промежутке, то есть не является решением уравнения.
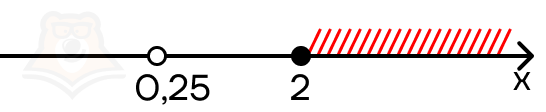
Решением уравнения будет только (x = frac{5}{6}).
Ответ: (frac{5}{6})
Разбивая прямую на промежутки, может возникнуть вопрос: а что делать с точками, в которых модуль равен 0? Их обязательно нужно проверять. Можно сделать это как отдельно, подставив точки в уравнение, так и сразу включить их в условие раскрытия модуля.
Если точки включаются в условие раскрытия модуля, то достаточно включить их только в один из двух промежутков. Включать их в два промежутка нецелесообразно: одна и та же точка будет проверяться дважды.

3. Уравнения вида |f(x)| = g(x)
Поскольку вместо функций могут стоять любые выражения, раскрыть модуль можно двумя способами. Выбор одного из них зависит от того, какая функция проще: f(x) или g(x).
Как можно раскрыть модуль?
- Можно раскрыть его в зависимости от знаков подмодульного выражения: если подмодульное выражение отрицательное, то модуль раскрывается с минусом, если положительное, то с плюсом.
- Можно возвести уравнение в квадрат. Но здесь необходимо ввести ограничения на g(x) — поскольку функция равна модулю, она не может быть отрицательной.
Для удобства можно пользоваться следующей схемой:
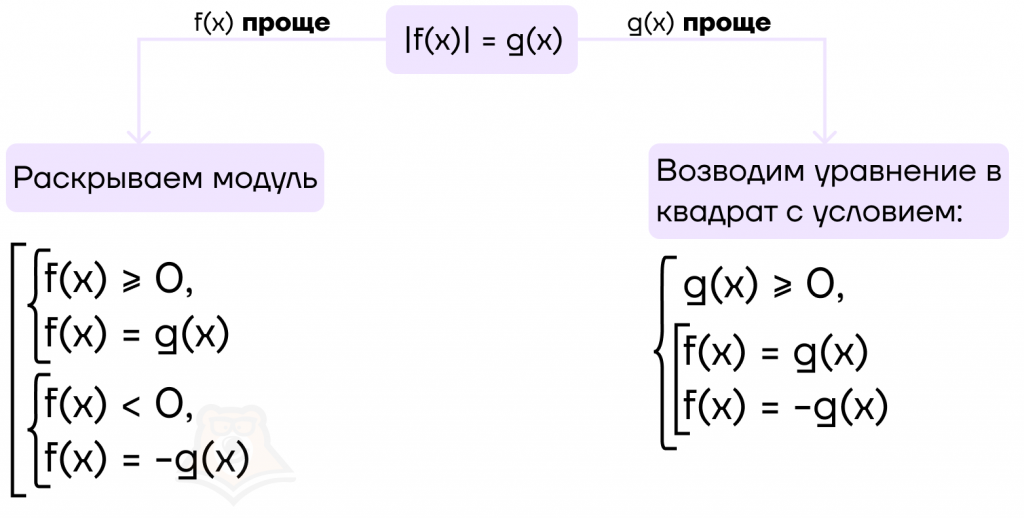
Пример 3. Решите уравнение |8 — x| = x2 — 5x + 11.
Решение. Заметим, что подмодульное выражение значительно проще функции справа, в этом случае удобнее будет раскрыть модуль. Получаем совокупность двух систем:
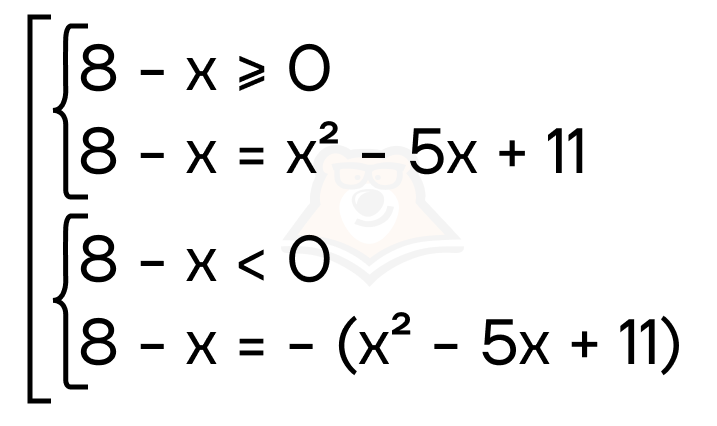
Рассмотрим первую систему.
8 — x >= 0 (rightarrow) x <= 8
Решим уравнение:
8 — x = x2 — 5x + 11
x2 — 4x + 3 = 0
D = 16 — 12 = 4
(x_1 = frac{4 + 2}{2} = 3)
(x_2 = frac{4 — 2}{2} = 1)
Оба корня уравнения удовлетворяют условию x <= 8, значит, решением системы будут 1 и 3.
Рассмотрим вторую систему.
8 — x < 0 (rightarrow) x > 8
Решим уравнение:
8 — x = -x2 + 5x — 11
x2 — 6x + 19 = 0
D = 36 — 76 = -40 — при отрицательном дискриминанте решения уравнений нет.
Решением всего уравнения будут x = 1 и x = 3.
Ответ: 1, 3
4. Разберем еще один тип уравнений, когда модуль равен модулю. Неужели придется рассматривать целых 4 случая раскрытия модуля? Нет, достаточно будет возвести в квадрат обе части уравнения. Таким образом, мы получаем следующий переход:
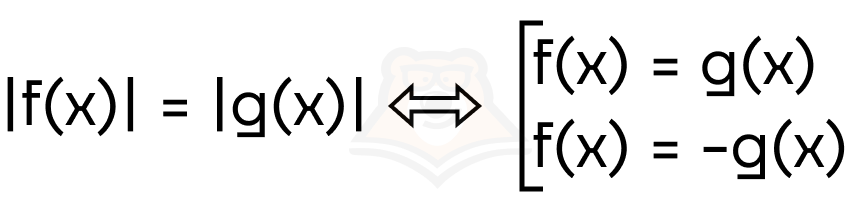
Пример 4. Решите уравнение |x — 2| = |2x + 8|.
Решение. Возведем обе части уравнения в квадрат. Для этого воспользуемся свойством 8.
(x — 2)2 = (2x + 8)2
(x — 2)2 — (2x + 8)2 = 0
Воспользуемся формулой сокращенного умножения:
((x — 2) — (2x + 8))((x — 2) + (2x + 8) = 0
Если произведение множителей равно 0, то каждый множитель равен 0. Тогда:
x — 2 — (2x + 8) = 0 (rightarrow) x — 2 = 2x + 8
x — 2 + (2x + 8) = 0 (rightarrow) x — 2 = -(2x + 8)
Получаем совокупность:
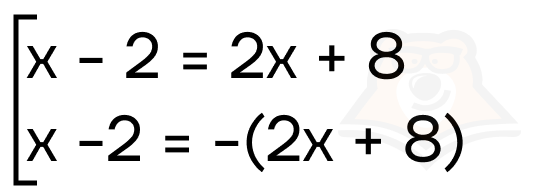
Решим первое уравнение совокупности:
x — 2 = 2x + 8
x = -10
Решим второе уравнение совокупности:
x — 2 = -2x — 8
3x = -6
x = -2
Решением уравнения будут x = -10 и x = -2
Ответ: -2, -10
Неравенства с модулем
Разобравшись, как решаются уравнения с модулем, можно приступать к неравенствам.
Пример 5. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Найдем, при каких значениях х модуль равен 0. Получаем 3x = 7 (rightarrow) (x = frac{7}{3}).
Определим, с какими знаками модуль будет раскрываться на каждом промежутке.
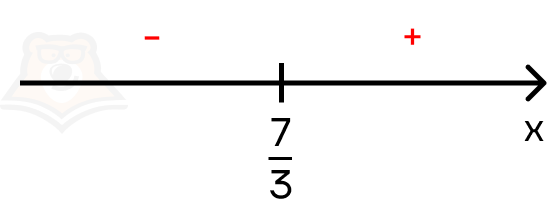
Осталось рассмотреть неравенство на двух промежутках.
1. (x leq frac{7}{3}), тогда
x2 — (-(3x — 7)) + 7 >= 0
x2 + 3x — 7 + 7 >= 0
x2 + 3x >= 0
x(x + 3) >= 0
Решим это неравенство «Методом интервалов». Сразу учтем ограничение (x leq frac{7}{3}).
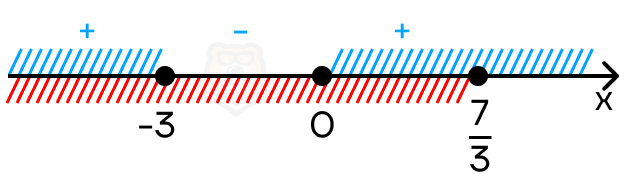
Получаем, что решением неравенства на заданном промежутке будет (x in (-infty; -3] U[0; frac{7}{3}]).
2. (x > frac{7}{3}), тогда
x2 — 3x + 7 + 7 >= 0
x2 — 3x + 14 >= 0
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней на заданном отрезке не будет.
Вспомним, что корни квадратного уравнения — это точки пересечения параболы и оси х. Если парабола не пересекает ось х, то неизбежно лежит выше или ниже ее. Поскольку в нашем случае ветви параболы направлены вверх, мы можем нарисовать ее примерный график.
Так как парабола задается функцией y = x2 — 3x + 14, то неравенство будет выполняться при всех y >= 0. Парабола целиком попадает в эту область, а решением неравенства будет любое х.
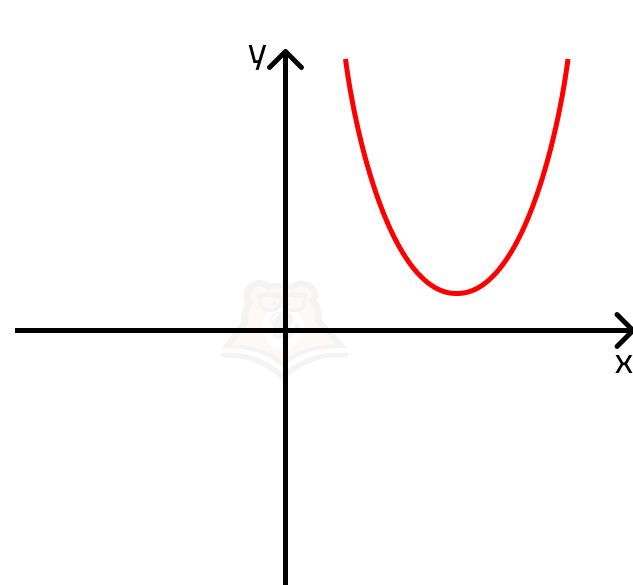
Однако не стоит забывать про ограничение (x > frac{7}{3}). Накладывая его, получаем решение ((frac{7}{3}; + infty)).
Осталось только объединить полученные на промежутках решения:
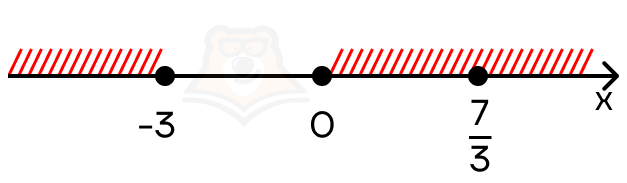
Получаем, что (x in (-infty;- 3] U [0; +infty)).
Ответ: (x in (-infty;- 3] U [0; +infty))
Рассмотрим неравенства вида |f(x)| > a и |f(x)| < a, где а — некоторое число и a >= 0. Модуль можно раскрыть двумя способами и получить два неравенства. Но будет это совокупность или система?
Это зависит от знака. Разберем случай |f(x)| > a. Заметим, что строгость знака может быть любой. Тогда модуль раскрывается как:
f(x) > a и -f(x) > a (rightarrow) f(x) < -a.
Отметим эти промежутки на числовой прямой:
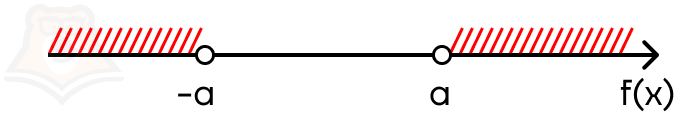
В ответе должны оказаться оба промежутка — их нужно объединить. В этом случае модуль раскрывается в совокупности.
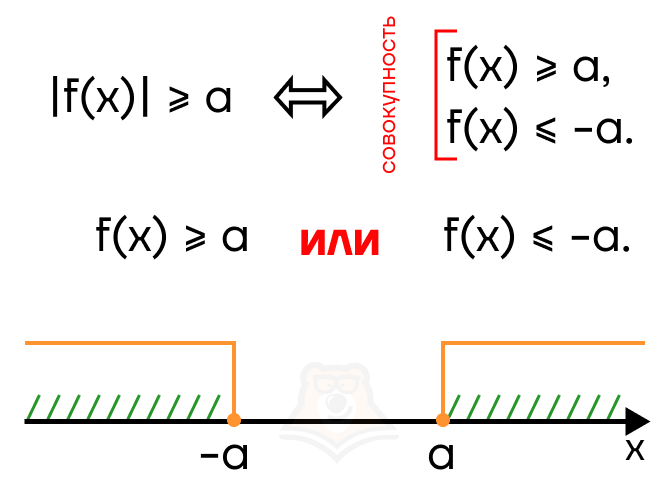
Рассмотрим случай |f(x)| < a, здесь строгость знака также может быть любой. Раскроем модуль: f(x) < 0 и -f(x) < a (rightarrow) f(x) > -a. На числовой прямой это будет выглядеть следующим образом:

В в ответе должен оказаться промежуток от —а до а. Следовательно, необходимо воспользоваться системой, чтобы “отсечь” лишние промежутки.
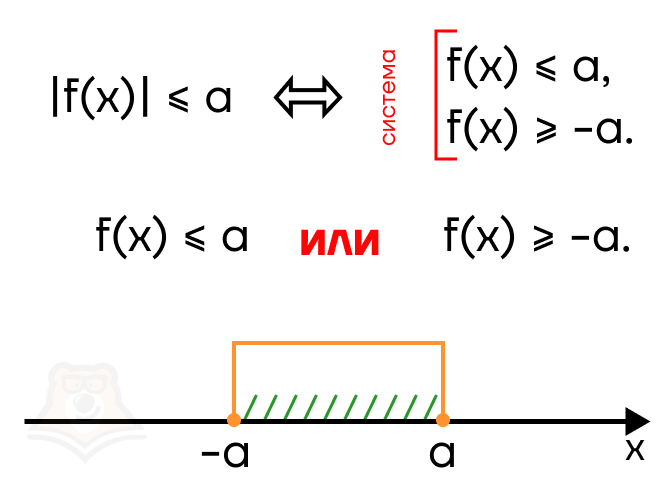
Можно ли обойтись в этом случае без раскрытия модуля? Да, но необходимо возвести неравенство в квадрат.
|f(x)| ⋁ a | (uparrow) 2 — вместо ⋁ может стоять любой знак неравенства.
f2(x) ⋁ a2
f2(x) — a2 ⋁ 0
Воспользуемся формулой сокращенного умножения:
(f(x) — a)(f(x) + a) ⋁ 0
Однако стоит помнить, что обе части неравенства можно возвести в квадрат только в том случае, если они неотрицательны. То есть обязательно должно выполняться условие a0.
Мы получили равносильный переход. Но существуют ли равносильные переходы, если вместо числа а стоит другая функция или даже модуль? Да. Они выводятся таким же способом, как и переход для неравенства с числом. Получаем еще два равносильных перехода:
- |f(x)| ⋁ g(x) (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
g(x) обязательно должно быть неотрицательным, чтобы можно было возвести неравенства в квадрат.
- |f(x)| ⋁ |g(x)| (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Разберем на примере, как можно использовать равносильный переход. Для этого возьмем то же неравенство, что и в примере 5, но решим его по-другому.
Пример 6. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Перенесем модуль в другую часть неравенства:
|3x — 7| <= x2 + 7. Модуль всегда неотрицателен. Правая часть неравенства неотрицательна, поскольку число в квадрате всегда положительно.
Повторим действия, чтобы прийти к равносильному переходу:
(3x — 7)2 <= (x2+7)2
(3x-7)2 — (x2 + 7)2 <= 0
(3x — 7 — (x2 + 7))(3x — 7 + x2 + 7) <= 0
(3x — 7 — x2 — 7)(3x + x2) <= 0
(-x2 + 3x — 14) * x(3 + x) <= 0
-(x2 — 3x + 14) * x(3 + x) <= 0
(x2 — 3x + 14) * x(3 + x) <= 0
Рассмотрим первую скобку:
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней нет. Выражение всегда будет положительно, то есть на него можно разделить все неравенство. Получаем:
x(3 + x) <= 0

Тогда (x in (-infty;- 3] U [0; +infty))
Ответ: (x in (-infty;- 3] U [0; +infty))
При решении можно сразу использовать равносильный переход, не расписывая его.
Итак, неравенства с модулем можно решить двумя способами: раскрывать модуль и воспользоваться равносильным переходом. Выбор способа зависит от личных предпочтений и удобства решения.
Фактчек
- Модуль — расстояние от любой точки на координатной прямой до начала координат. Модуль обозначается двумя вертикальными черточками: |a| = a и |-a| = a.
- Модулем числа называют выражение:

- График модуля представляет собой “галочку”, которая лежит выше оси х. Модуль отражает график любой функции зеркально оси х так, что значения у всегда больше 0.
- Модуль можно раскрыть двумя способами. Этим свойством можно пользоваться при решении уравнений с модулем.
- При решении неравенств с модулем можно раскрывать его, либо воспользоваться равносильным переходом, если в неравенстве выполняются все условия для него.
Проверь себя
Задание 1.
Чему равно выражение |-16 * 2|?
- 32
- −32
- −16
- 16
Задание 2.
Какой график имеет функция y = |x|?
- Парабола
- Гипербола
- Прямая
- Галочка
Задание 3.
Решите уравнение |x| = -3.
- 3
- −3
- Решений нет
- 3 и −3
Задание 4.
Решите уравнение |x + 2| = 15.
- −13
- 17
- 13 и -17
- Решений нет
Задание 5.
Какой равносильный переход можно использовать для неравенства вида |f(x) |⋁ |g(x)|?
- f(x) ⋁ g(x)
- f(x) ⋀ g(x)
- f2(x) — 2 * f(x) * g(x) + g2(x) ⋁ 0
- (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Ответы: 1. — 1 2. — 4 3. — 3 4. — 3 5. — 4
