С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:
Функция называется периодической, если существует такое число
, не равное нулю, что для любого
из ее области определения
Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число
называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.
Например, — периодические функции.
Для функций и
период
,
Для функций и
период
Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:
1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и
Найдите значение выражения
График функции может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках
будут также равны пяти. Здесь k — целое число.
Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.
Значения функции в точках -3 и 7 равны пяти. Мы получим:
2. График четной периодической функции совпадает с графиком функции
на отрезке от 0 до 1; период функции
равен 2. Постройте график функции
и найдите f(4 ).
Построим график функции при
Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при
симметричную части графика от 0 до 1.
Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем
3. Найдите наименьший положительный период функции
Наименьший положительный период функции равен
График функции получается из графика функции
сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).
Значит, у функции частота в 3 раза больше, чем у функции
, а наименьший положительный период в 3 раза меньше и равен
. Значит, на отрезке
укладывается ровно 3 полных волны функции
Рассуждая аналогично, получим, что для функции наименьший положительный период равен
На отрезке
укладывается ровно 5 полных волн функции
Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен
.

4. Период функции равен 12, а период функции
равен 8. Найдите наименьший положительный период функции
По условию, период функции равен 12. Это значит, что все значения
повторяются через 12, через
. Если мы выберем любую точку
на графике функции
то через
значение функции будет такое же, как и в точке
Аналогично, все значения функции повторяются через
. В этих точках значения
будут такие же, как и в точке
На каком же расстоянии от точки расположена точка, в которой значение функции
такое же, что и в точке
? Очевидно, на расстоянии
Это значит, что число
делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит,
.
Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Периодические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023
Цель: обобщить и систематизировать знания учащихся по теме “Периодичность
функций”; формировать навыки применения свойств периодической функции,
нахождения наименьшего положительного периода функции, построения графиков
периодических функций; содействовать повышению интереса к изучению математики;
воспитывать наблюдательность, аккуратность.
Оборудование: компьютер, мультимедийный проектор, карточки с заданиями,
слайды, часы, таблицы орнаментов, элементы народного промысла
Эпиграф:
“Математика – это то, посредством чего люди управляют природой и собой”
А.Н. Колмогоров
Ход урока
I. Организационный этап.
Проверка готовности учащихся к уроку. Сообщение темы и задач урока.
II. Проверка домашнего задания.
Домашнее задание проверяем по образцам, наиболее сложные моменты обсуждаем.
III. Обобщение и систематизация знаний.
1. Устная фронтальная работа.
Вопросы теории.
1) Сформируйте определение периода функции
2) Назовите наименьший положительный период функций y=sin(x), y=cos(x)
3). Назовите наименьший положительный период функций y=tg(x), y=ctg(x)
4) Докажите с помощью круга верность соотношений:
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+180º)
y=ctg(x) = ctg(x+180º)
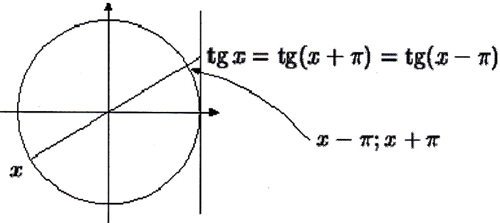
tg(x+πn)=tgx, n € Z
ctg(x+πn)=ctgx, n € Z
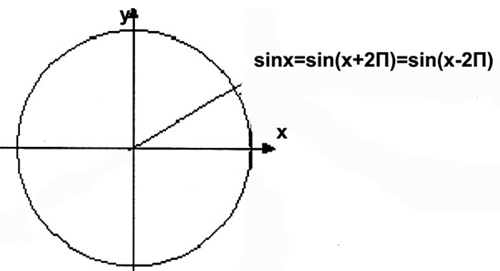
sin(x+2πn)=sinx, n € Z
cos(x+2πn)=cosx, n € Z
5) Как построить график периодической функции?
Устные упражнения.
1) Доказать следующие соотношения
a) sin(740º) = sin(20º)
b) cos(54º)
= cos(-1026º)
c) sin(-1000º) = sin(80º)
2. Доказать, что угол в 540º является одним из периодов функции y= cos(2x)
3. Доказать, что угол в 360º является одним из периодов функции y=tg(x)
4. Данные выражения преобразовать так, чтобы входящие в них углы по
абсолютной величине не превышали 90º .
a) tg375º
b) ctg530º
c) sin1268º
d) cos(-7363º)
5. Где вы встречались со словами ПЕРИОД, ПЕРИОДИЧНОСТЬ?
Ответы учащихся: Период в музыке – построение, в котором изложено более или
менее завершенная музыкальная мысль. Геологический период – часть эры и
разделяется на эпохи с периодом от 35 до 90 млн. лет.
Период полураспада радиоактивного вещества. Периодическая дробь.
Периодическая печать – печатные издания, появляющиеся в строго определенные
сроки. Периодическая система Менделеева.
6. На рисунках изображены части графиков периодических функций. Определите
период функции. Определить период функции.
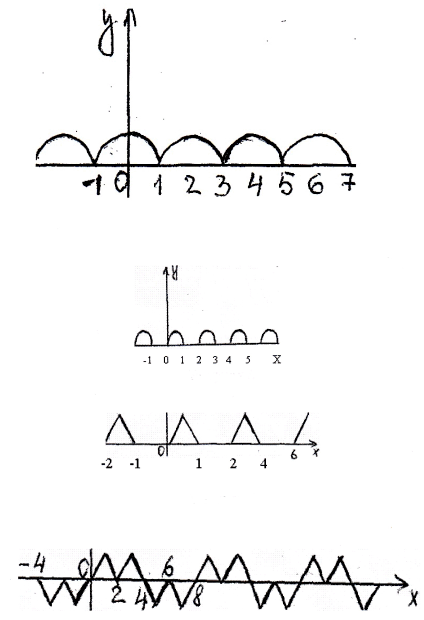
Ответ: Т=2; Т=2; Т=4; Т=8.
7. Где в жизни вы встречались с построением повторяющихся элементов?
Ответ учащихся: Элементы орнаментов, народное творчество.

IV. Коллективное решение
задач.
(Решение задач на слайдах.)
Рассмотрим один из способов исследования функции на периодичность.
При этом способе обходятся трудности, связанные с доказательством того, что
тот или иной период является наименьшим , а также отпадает необходимость
касаться вопросов об арифметических действиях над периодическими функциями и о
периодичности сложной функции. Рассуждение опирается лишь на определение
периодической функции и на такой факт: если Т – период функции, то и nT(n?0) – ее
период.
Задача 1. Найдите наименьший положительный период функции f(x)=1+3{x+q>5}
D(f)=R
Решение: Предположим, что Т-период данной функции. Тогда f(x+T)=f(x) для
всех x € D(f), т.е.
1+3{x+T+0,25}=1+3{x+0,25}
{x+T+0,25}={x+0.25}
Положим x=-0,25 получим
{T}={0}
{T}=0 <=> T=n, n € Z
Мы получили, что все периоды рассматриваемой функции (если они существуют)
находятся среди целых чисел. Выберем среди этих чисел наименьшее положительное
число. Это 1. Проверим, не будет ли оно и на самом деле периодом 1.
f(x+1) =3{x+1+0,25}+1
Так как {T+1}={T} при любом Т, то f(x+1)=3{(x+0.25)+1}+1=3{x+0,25}+1=f(x),
т.е. 1 – период f. Так как 1 – наименьшее из всех целых положительных чисел, то T=1.
Задача 2. Показать, что функция f(x)=cos2(x) периодическая и найти
её основной период.
Решение:
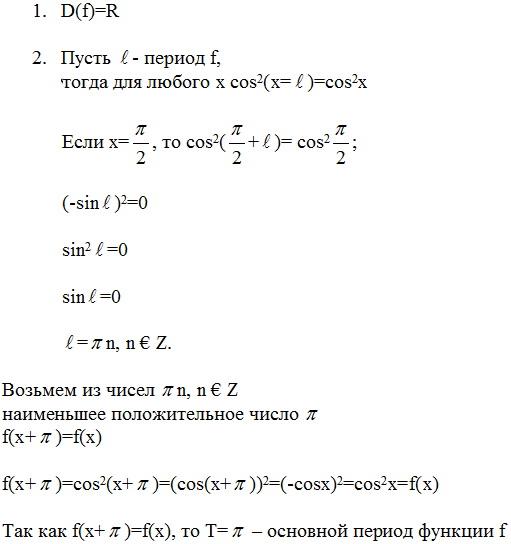
Задача 3. Найдите основной период функции
f(x)=sin(1,5x)+5cos(0,75x)
Решение:
1. D(f)=R
Допустим Т-период функции, тогда для любого х справедливо соотношение
sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)
Если х=0, то
sin(1,5T)+5cos(0,75T)=sin0+5cos0
sin(1,5T)+5cos(0,75T)=5
Если х=-Т, то
sin0+5cos0=sin(-1,5Т)+5cos0,75(-Т)
5= – sin(1,5Т)+5cos(0,75Т)
|
|
sin(1,5Т)+5cos(0,75Т)=5
– sin(1,5Т)+5cos(0,75Т)=5 |
Сложив, получим:
10cos(0,75Т)=10
cos![]() =1
=1
![]() =2πn,
=2πn,
n € Z
T=![]() ,
,
n € Z
Выберем из всех “подозрительных” на период чисел
![]()
наименьшее положительное и проверим, является ли оно периодом для f. Это число
![]()
Имеем:
f(x+![]() )=sin(1,5x+4π)+5cos(0,75x+2π)=
)=sin(1,5x+4π)+5cos(0,75x+2π)=
sin(1,5x)+5cos(0,75x)=f(x)
Значит
![]() –
–
основной период функции f.
Задача 4. Проверим является ли периодической функция f(x)=sin(x)
Решение:
Пусть Т – период функции f. Тогда для любого х
sin|x+Т|=sin|x|
Если х=0, то sin|Т|=sin0, sin|Т|=0 Т=πn,
n € Z.
Предположим. Что при некотором n число
πn является периодом
рассматриваемой функции πn>0.
Тогда sin|πn+x|=sin|x|
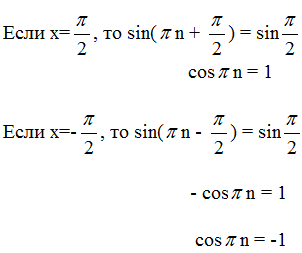
Отсюда вытекает, что n должно быть одновременно и четным и нечетным числом, а
это невозможно. Поэтому данная функция не является периодической.
Задача 5. Проверить, является ли периодической функция
f(x)=
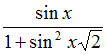
Решение:
D(f)=R
Пусть Т – период f, тогда
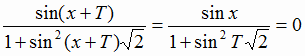 ,
,
отсюда sinT=0, Т=πn,
n € Z. Допустим, что при некотором n число
πn действительно является периодом
данной функции. Тогда и число 2πn
будет периодом
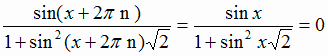
Так как числители равны, то равны и их знаменатели, поэтому
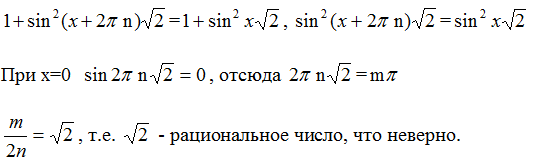
Значит, функция f не периодическая.
Работа в группах.
Задания для группы 1.
Проверьте является ли функция f периодической и найдите ее основной период
(если существует).
f(x)=|cosx|
Задания для группы 2.
Проверьте является ли функция f периодической и найдите ее основной период
(если существует).
f(x)=cos(2x)+2sin(2x)
Задания для группы 3.
f(x)=|sin|x||
По окончании работы группы презентуют свои решения.
VI. Подведение итогов урока.
Рефлексия.
Учитель выдаёт учащимся карточки с рисунками и предлагает закрасить часть
первого рисунка в соответствии с тем, в каком объёме, как им кажется, они
овладели способами исследования функции на периодичность, а в части второго
рисунка – в соответствии со своим вкладом в работу на уроке.
| Мои умения исследовать функции на периодичность |
Мой вклад в работу на уроке |
|
|
|
VII. Домашнее задание
1). Проверьте, является ли функция f периодической и найдите её основной
период (если он существует)
a). f(x)=√x
b). f(x)=x2-2x+4
c). f(x)=2tg(3x+5)
2). Функция y=f(x) имеет период Т=2 и f(x)=x2+2x при х € [-2; 0].
Найдите значение выражения -2f(-3)-4f(3,5)
Литература/
- Мордкович А.Г. Алгебра и начала анализа с углубленным изучением.
- Математика. Подготовка к ЕГЭ. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю.
- Шереметьева Т.Г. , Тарасова Е.А. Алгебра и начала анализа для
10-11 классов.
Изображение периодического оригинала.
Если
оригинал является периодической функцией
с периодом
![]() ,
,
то есть выполняется условие![]() ,
,
то изображение такой функции находится
по формуле:
![]()
и определено в
области:
![]()
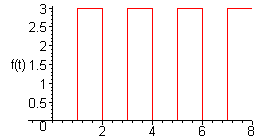
![]() Найти
Найти
изображение периодической функции с
периодом
![]() ,
,
график которой изображен на рисунке.
![]()
![]() Аналитическая
Аналитическая
запись функции на интервале периода
следующая:
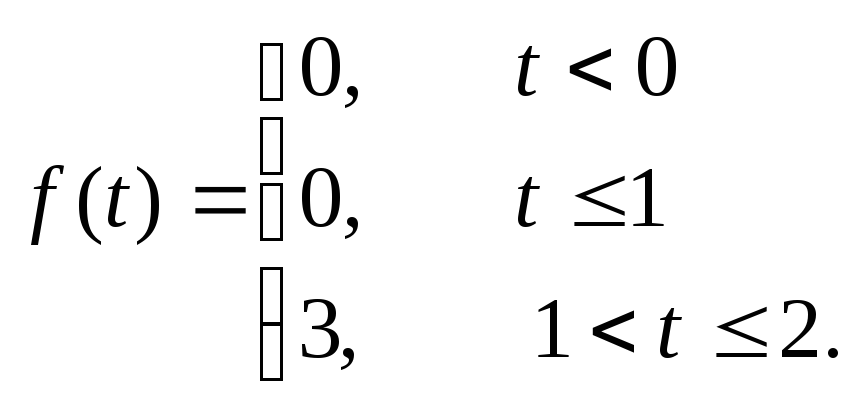
Период
функции
![]() .
.
Применив формулу для изображения
периодического оригинала и учитывая,
что![]() на интервале от0
на интервале от0
до 1
равна нулю, запишем:
![]()
![]()
![]()
![]() Найти
Найти
изображение периодической функции,
график которой изображен на рисунке.

![]()
![]() Период
Период
функции
![]() .
.
Аналитическая запись функции на интервале
периода следующая:
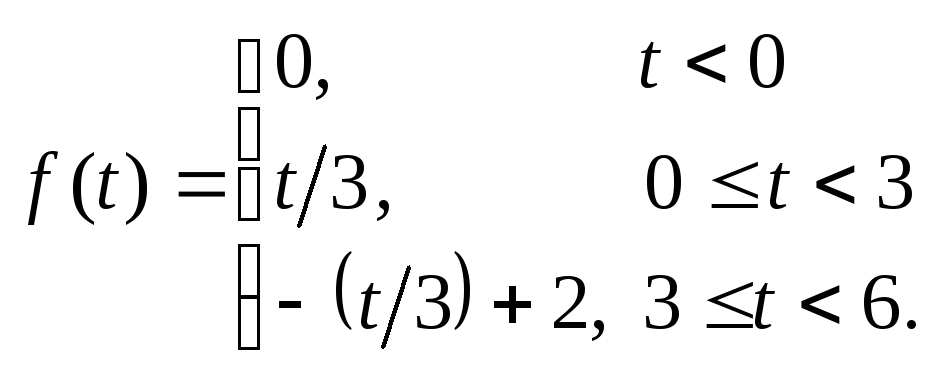
На
основании формул для периодически
определенного оригинала находим:
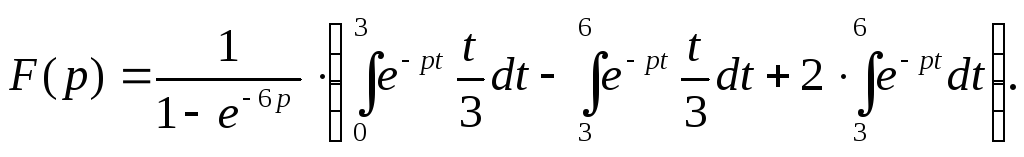
Интегрируя
по частям, получим:
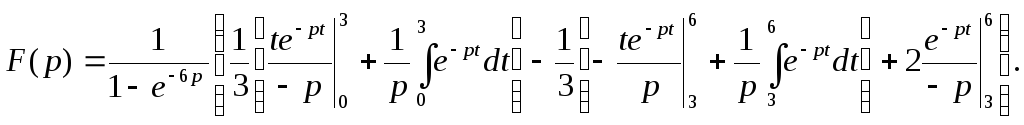
Произведя
все необходимые вычисления, окончательно
перейдем к следующему выражению:
![]()
Задачи на расчет электрических контуров.
В
электротехнике рассматривается модель
устройства и организация ее функционирования
на основе работы базовых электротехнических
устройств, используемых в быту и
промышленности. Как известно для того,
чтобы электротехническое устройство
работало, должна быть создана электрическая
цепь, задача которой передать электрическую
энергию данному устройству для обеспечения
требуемого ему режима работы.
Электрической
цепью называется совокупность устройств
и объектов, образующих путь для
электрического тока, электромагнитные
процессы в которых могут быть описаны
с помощью понятий об электрическом
токе, ЭДС (электродвижущая сила) и
электрическом напряжении.
Все
устройства и объекты, составляющие
электрическую цепь, могут быть разделены
на три группы:
-
Источники
электрической энергии (питания).
Общим свойством всех таких источников
питания является преобразование
какого-либо вида энергии в электрическую.
Источники, в которых происходит
преобразование неэлектрической энергии
в электрическую, называются первичными
источниками. Вторичные источники –
это такие источники, у которых и на
входе, и на выходе – электрическая
энергия (например, выпрямительные
устройства). -
Потребители
электрической энергии.
Общим
свойством всех потребителей является
преобразование электроэнергии в другие
виды энергии (например, нагревательный
прибор). Иногда потребители называют
нагрузкой. -
Вспомогательные
элементы цепи.
Соединительные
провода, коммутационная аппаратура,
аппаратура защиты, измерительные
приборы и т.д., без которых реальная
цепь не может
функционировать в требуемом режиме.
Все
элементы цепи участвуют
в
одном
электромагнитном
процессе.
Расчет и анализ электрических цепей
производится на основе: закона
Ома, первого
и второго законов Кирхгофа.
Эти законы позволяют устанавливать
взаимосвязь между значениями токов,
напряжений, ЭДС всей электрической цепи
и отдельных ее участков и параметрами
элементов, входящих в состав этой цепи.
В математических
приложениях, как правило, для вычисления
значения переходного тока используют
второй закон Кирхгофа. Приведем его
формулировку.
Формулировка
второго закона Кирхгофа.
В
любом замкнутом контуре электрической
цепи алгебраическая сумма ЭДС равна
алгебраической сумме падений напряжений
на всех его участках
![]() ,где
,где
n
– число источников ЭДС в контуре;
m
– число элементов с сопротивлением
![]()
в
контуре;
![]() – напряжение или падение напряжения
– напряжение или падение напряжения
на k-ом
элементе контура.
При
записи уравнений по второму закону
Кирхгофа необходимо:
1) задать
условные положительные направления
ЭДС, токов и напряжений;
2) выбрать
направление обхода контура, для которого
записывается уравнение;
3) записать
уравнение, пользуясь одной из формулировок
второго закона Кирхгофа, причем слагаемые,
входящие в уравнение, берут со знаком
«плюс», если их условные положительные
направления совпадают с обходом контура,
и со знаком «минус», если они противоположны.
Таким
образом, второй закон Кирхгофа позволяет
выписать интегро-дифференциальное
уравнение для силы тока
![]() :
:
![]() ,
,
здесь
![]() –
–
индуктивность катушки,![]() –
–
суммарное сопротивление,![]() –
–
ёмкость конденсатора,![]() – суммарное напряжение на конденсаторе
– суммарное напряжение на конденсаторе
в момент времени![]() (
(![]() ).
).
Для
того чтобы найти выражения переходных
токов, целесообразно перейти к изображению
интегро-дифференциального уравнения
Кирхгофа, то есть построить соответствующее
операторное уравнение. Для осуществления
данного перехода необходимо найти
начальные условия
![]() ,
,
учитывая условия конкретной задачи.
После чего, с помощью элементарных
алгебраических преобразований выразим
изображение переходного тока![]() .
.
Последний этап решения задач
рассматриваемого вида сводится к
отысканию оригинала для найденного
изображения переходного тока.
![]() Сила
Сила
тока удовлетворяет уравнению
![]() ,
,
найти![]() ,
,
если![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() Дифференциальное
Дифференциальное
уравнение Кирхгофа для этой задачи
имеет вид:
![]() .
.
Решим
это уравнение операторным методом.
Будем полагать, что
![]() .
.
Образом уравнения является следующее
равенство:
![]()
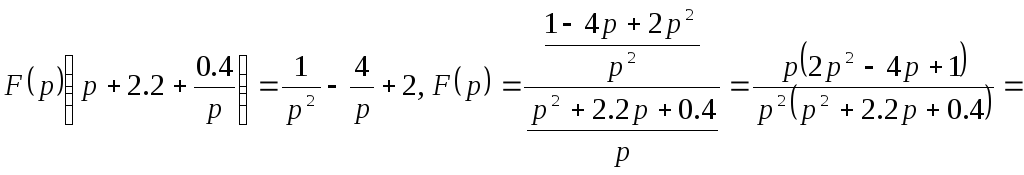
![]()
Найдем
оригинал получившегося изображения,
разложив дроби на простые слагаемые
методом неопределенных коэффициентов.
Представим наше изображение в виде
суммы трех изображений:
![]()
Приведем
данное выражение к общему знаменателю
и приравняв числители в двух представлениях
одного и того же изображения получим
равенство:
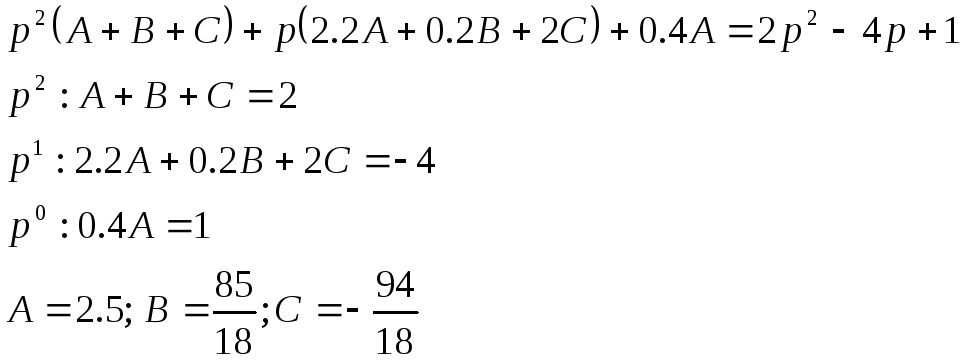
![]()
Таким
образом, мы отыскали изображение тока,
для того чтобы довести задачу до ответа
необходимо найти оригинал этого
изображения. Оригиналом получившейся
разности, в силу линейности преобразования
Лапласа, будет сумма трех оригиналов
слагаемых, следовательно,
![]() .
.
Заметим,
что часто встречающейся является ошибка
неверного определения изображений
функций, находящихся в правой части
уравнения Кирхгофа, так что на этот
момент решения следует обратить серьёзное
внимание.
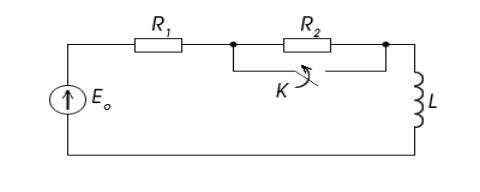
![]() Контур
Контур
подключен к постоянной э.д.с.
![]() (см.
(см.
рис.) При установившемся режиме включается
рубильник![]() и накоротко замыкает сопротивление
и накоротко замыкает сопротивление![]() .
.
Найти выражение переходного тока.![]() .
.
![]()
![]() Дифференциальное
Дифференциальное
уравнение Кирхгофа до включения
рубильника
![]() в данном случае имеет вид:
в данном случае имеет вид:
![]()
Согласно
постановке задачи
![]() .
.
Решим это уравнение операционным
методом, предполагая, что![]() .
.
![]()
![]() .
.
Найдем
оригинал получившегося изображения,
разложив дроби на простые слагаемые
методом неопределенных коэффициентов:
![]()
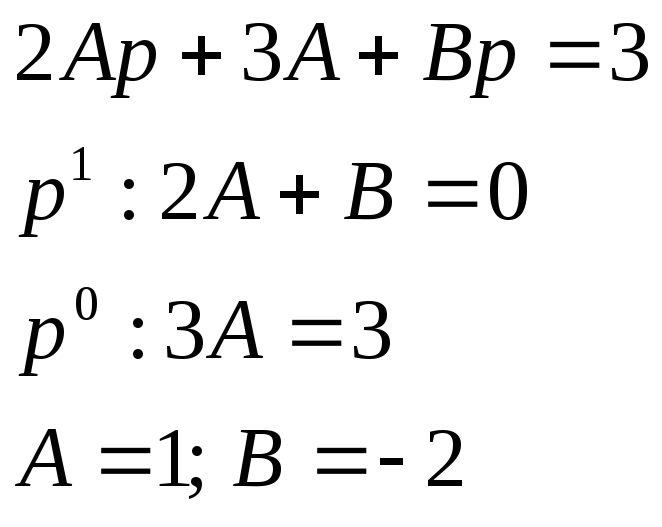
![]()
Таким
образом,
![]() .
.
Установившийся
ток в контуре до включения рубильника
![]() есть
есть![]() .
.
Дифференциальное уравнение Кирхгофа
после замыкания рубильника![]() имеет вид:
имеет вид:
![]() .
.
Решим это уравнение
операционным методом.
![]()
![]() .
.
Как
и в предыдущем случае воспользуемся
методом неопределенных коэффициентов
для разложения изображения на слагаемые.
![]()
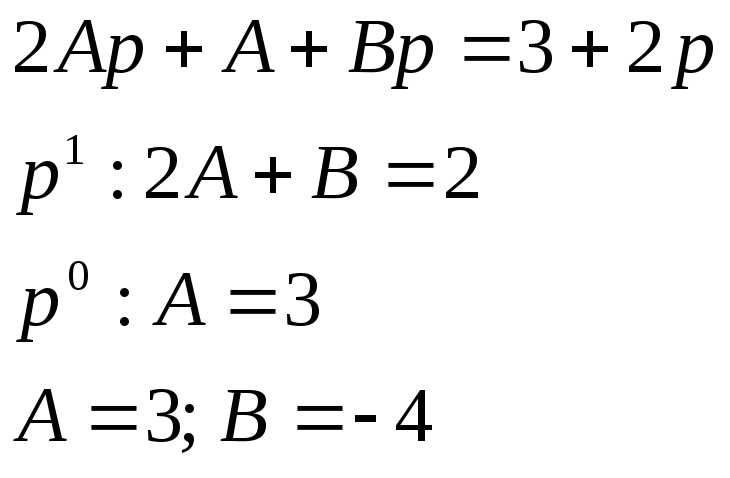
![]()
Оригиналом
получившейся разности, как нетрудно
заметить, будет
![]() .
.
Ниже приведены
варианты контрольной работы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ВИДЕО УРОК
Периодические функции.
Функцию у = f(х), х ∈ Х, называют периодической,
если существует такое отличное от нуля число
Т, что для любого х из области определения функции справедливо
равенство:
f(х + Т) = f(х) = f(х – Т).
Число Т называют периодом функции у = f(х).
Из этого
определения сразу следует, что если Т –
период функции
у = f(х), то
2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т
– также периоды
функций. Значит у периодической функции бесконечно много периодов.
Если Т – период функции, то число вида kТ,
где k – любое целое
число, также является периодом функции.
Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.
График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.

График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)
Графики
периодических функций обладают следующей особенностью. Если Т – основной период функции у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси х длиной
Т, а затем осуществить параллельный перенос этой ветви по
оси х на
± Т, ±
2Т, ± 3Т, …

Чаще всего в
качестве такого промежутка длиной Т выбирают промежуток с концами в точках
(–Т/2; 0) и (Т/2; 0) или
(0; 0) и (Т; 0).
ПРИМЕР:
Рассмотрим функцию
у = х – [х], где [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:
f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).
Следовательно, при любом
значении х
f(x + 1) = f(x).
А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.

График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.

Периодичность тригонометрических функций.
Возьмём произвольный угол α и построим
подвижной радиус ОМ единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.
Если мы к углу прибавим
2π или 360° (то есть полный
оборот), то углу α + 2π или α + 360° будет соответствовать то же положение
подвижного радиуса ОМ, что для угла α.

Так как синус и косинус угла,
составленного с осью Ох подвижным радиусом ОМ единичной
окружности, по сути соответственно ордината
у и
абсцисса х точки М, то
sin (α + 2π) = sin α или
sin (α + 360°) = sin α
и
cos (α + 2π)
= cos α или
cos (α + 360°) = cos α.
Таким образом, функции sin α и cos α от
прибавления к аргументу α одного
полного оборота (2π или 360°) не меняют своих значений.
Точно так же, прибавляя к
углу α любое целое
число полных оборотов, мы не изменим положения подвижного радиуса ОМ, а потому:
sin (α + 2kπ) = sin α или
sin (α + 360°k) = sin α
и
cos (α + 2kπ) = cos α или
cos (α + 360°k) = cos α,
где k – любое целое
число.
Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.
Периодом функции sin α и cos α
является 2π или 360°.
Функции tg α и сtg α также
периодические и их периодом является число
π или 180°.
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным
радиусом ОМ единичной окружности.
Построим точку М‘,

симметричную точке М относительно
начала координат. Один из углов, образованных с осью Ох подвижным
радиусом ОМ‘, будет равен α + π.
Если х и у – координаты точки
М, то точки М‘ будут –х и –у. Поэтому
sin α = у, cos α = х,
sin (α + π) = –у,
cos (α + π) = –х.
Отсюда

и, следовательно,
tg (α + π) = tg α,
сtg (α + π)
= сtg α.
отсюда следует, что значения tg α и сtg α не
изменяются, если к углу α прибавить любое число полуоборотов:
tg (α + kπ) = tg α,
сtg (α + kπ) = сtg α.
где k – любое целое
число.
Периоды функций
y = A sin (ωx + φ) и
y = A cos (ωx + φ)
вычисляются по формуле
T = 2π/ω,
а период функции
y = A tg (ωx + φ)
по формуле
T = π/ω.
Если период функции y = f(x) равен T1, а период функции y = g(x) равен T2, то период функций
y = f(x) + g(x) и
y = f(x) – g(x)
равен наименьшему числу, при делении которого
на T1 и T2 получаются целые числа.
ПРИМЕР:
Найти
период функции
y = 3 sin (x – 2) + 7 соs πx.
РЕШЕНИЕ:
Период
функции
y = 3 sin (x – 2)
равен
T1 = 2π/1 = 2π.
Период
функции
y = 7 соs πx
равен
T2 = 2π/π = 2.
Периода
у функции
y = 3 sin (x – 2) + 7 соs πx
не
существует, так как такого числа, при делении которого на 2π и
на 2 получались бы целые числа, нет.
ОТВЕТ:
Периода
не существует.
ПРИМЕР:
Доказать
следующее утверждение:
tg
3850° = tg 250°.
РЕШЕНИЕ:
Так как тангенс – периодическая функция с минимальным
периодом 20 ∙ 180°, то получим:
tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.
ПРИМЕР:
Доказать
следующее утверждение:
сos (–13π) = –1.
РЕШЕНИЕ:
Так как косинус – чётная и периодическая функция с
минимальным периодом 2π, то получим:
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
ПРИМЕР:
Доказать
следующее утверждение:
sin (–7210°) = – sin 10°.
РЕШЕНИЕ:
Так как синус – нечётная и периодическая функция с
минимальным периодом 20 ∙ 360°, то получим:
sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.
ПРИМЕР:
Найти основной период функции
sin 7х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
sin 7х = sin 7(х + t) = sin (7х + 7t)
так как 2πk период синуса, то получим:
sin (7х + 7t) = sin (7х + 2πk),

ОТВЕТ:

ПРИМЕР:
Найти основной период функции
соs 0,3х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)
так как 2πk период косинуса, то получим:
соs (0,3х + 0,3t) = соs (0,3х + 2πk),

ОТВЕТ:

ПРИМЕР:
Найти период функции:
y = 5sin 2x + 2ctg 3х.
РЕШЕНИЕ:
Период функции
y = 5sin 2x
равен Т1 = 2𝜋/2 = π,
а период функции
y = 2ctg 3х
равен Т2 = 𝜋/3.
Наименьшее число, при делении которого на
Т1 = π и Т2 = 𝜋/3
– получаются целые числа будет число π.
Следовательно, период заданной функции равен Т = π.
ПРИМЕР:
Найти период функции:
y = 9sin (5x + π/3) – 4cоs (7х + 2).
РЕШЕНИЕ:
Находим периоды слагаемых. Период функции
y = 9sin (5x + π/3)
равен Т1 = 2𝜋/5,
а период функции
y = 4cоs (7х + 2)
равен Т2 = 2𝜋/7.
Очевидно, что период заданной функции равен
Т = 2π.
ПРИМЕР:
Найти период функции:
y = 3sin πx + 8tg (х + 5).
РЕШЕНИЕ:
Период функции
y = 3sin πx
равен Т1 = 2π/π = 2,
а период функции
y = 8tg (х + 5)
равен Т2 = 𝜋/1 = π.
Периода у заданной функции не существует, так как нет
такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
ПРИМЕР:
Найти период функции:
y = sin 3x + соs 5х.
РЕШЕНИЕ:
Период функции
y = sin 3x
равен Т1 = 2π/3,
а период функции
y = соs 5х
равен Т2 = 2π/5.
Приведём к общему знаменателю периоды:
Т1 = 10π/15, Т2 = 6π/15.
Тогда наименьшее общее кратное (НОК) будет:
НОК (10π; 6π)
= 30π.
Теперь найдём период заданной функции:
Т = 30π/15 = 2π.
Задания к уроку 5
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
2. Доказать, что угол в 540º является одним из периодов функции y= cos(2x)
3. Доказать, что угол в 360º является одним из периодов функции y=tg(x)
4. Данные выражения преобразовать так, чтобы входящие в них углы по абсолютной величине не превышали 90º .
5. Где вы встречались со словами ПЕРИОД, ПЕРИОДИЧНОСТЬ?
Ответы учащихся: Период в музыке – построение, в котором изложено более или менее завершенная музыкальная мысль. Геологический период – часть эры и разделяется на эпохи с периодом от 35 до 90 млн. лет.
Период полураспада радиоактивного вещества. Периодическая дробь. Периодическая печать – печатные издания, появляющиеся в строго определенные сроки. Периодическая система Менделеева.
6. На рисунках изображены части графиков периодических функций. Определите период функции. Определить период функции.

7. Где в жизни вы встречались с построением повторяющихся элементов?
Ответ учащихся: Элементы орнаментов, народное творчество.

IV. Коллективное решение задач.
(Решение задач на слайдах.)
Рассмотрим один из способов исследования функции на периодичность.
При этом способе обходятся трудности, связанные с доказательством того, что тот или иной период является наименьшим , а также отпадает необходимость касаться вопросов об арифметических действиях над периодическими функциями и о периодичности сложной функции. Рассуждение опирается лишь на определение периодической функции и на такой факт: если Т – период функции, то и nT(n?0) – ее период.
Задача 1. Найдите наименьший положительный период функции f(x)=1+35>
Решение: Предположим, что Т-период данной функции. Тогда f(x+T)=f(x) для всех x € D(f), т.е.
Положим x=-0,25 получим
Мы получили, что все периоды рассматриваемой функции (если они существуют) находятся среди целых чисел. Выберем среди этих чисел наименьшее положительное число. Это 1. Проверим, не будет ли оно и на самом деле периодом 1.
Так как = при любом Т, то f(x+1)=3<(x+0.25)+1>+1=3+1=f(x), т.е. 1 – период f. Так как 1 – наименьшее из всех целых положительных чисел, то T=1.
Задача 2. Показать, что функция f(x)=cos 2 (x) периодическая и найти её основной период.

Задача 3. Найдите основной период функции
Допустим Т-период функции, тогда для любого х справедливо соотношение
 |
sin(1,5Т)+5cos(0,75Т)=5
– sin(1,5Т)+5cos(0,75Т)=5 |
cos =1
=1
 =2 π n, n € Z
=2 π n, n € Z
T= , n € Z
, n € Z
Выберем из всех “подозрительных” на период чисел  наименьшее положительное и проверим, является ли оно периодом для f. Это число
наименьшее положительное и проверим, является ли оно периодом для f. Это число 
f(x+ )=sin(1,5x+4 π )+5cos(0,75x+2 π )= sin(1,5x)+5cos(0,75x)=f(x)
)=sin(1,5x+4 π )+5cos(0,75x+2 π )= sin(1,5x)+5cos(0,75x)=f(x)
Значит  – основной период функции f.
– основной период функции f.
Задача 4. Проверим является ли периодической функция f(x)=sin(x)
Пусть Т – период функции f. Тогда для любого х
Если х=0, то sin|Т|=sin0, sin|Т|=0 Т= π n, n € Z.
Предположим. Что при некотором n число π n является периодом
рассматриваемой функции π n>0. Тогда sin| π n+x|=sin|x|

Отсюда вытекает, что n должно быть одновременно и четным и нечетным числом, а это невозможно. Поэтому данная функция не является периодической.
Задача 5. Проверить, является ли периодической функция
f(x)= 
Пусть Т – период f, тогда
 , отсюда sinT=0, Т= π n, n € Z. Допустим, что при некотором n число π n действительно является периодом данной функции. Тогда и число 2 π n будет периодом
, отсюда sinT=0, Т= π n, n € Z. Допустим, что при некотором n число π n действительно является периодом данной функции. Тогда и число 2 π n будет периодом

Так как числители равны, то равны и их знаменатели, поэтому

Значит, функция f не периодическая.
Работа в группах.
Задания для группы 1.
Проверьте является ли функция f периодической и найдите ее основной период (если существует).
Задания для группы 2.
Проверьте является ли функция f периодической и найдите ее основной период (если существует).
Задания для группы 3.
По окончании работы группы презентуют свои решения.
VI. Подведение итогов урока.
Учитель выдаёт учащимся карточки с рисунками и предлагает закрасить часть первого рисунка в соответствии с тем, в каком объёме, как им кажется, они овладели способами исследования функции на периодичность, а в части второго рисунка – в соответствии со своим вкладом в работу на уроке.


| Мои умения исследовать функции на периодичность |
Мой вклад в работу на уроке |
VII. Домашнее задание
1). Проверьте, является ли функция f периодической и найдите её основной период (если он существует)
2). Функция y=f(x) имеет период Т=2 и f(x)=x 2 +2x при х € [-2; 0]. Найдите значение выражения -2f(-3)-4f(3,5)
- Мордкович А.Г. Алгебра и начала анализа с углубленным изучением.
- Математика. Подготовка к ЕГЭ. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю.
- Шереметьева Т.Г. , Тарасова Е.А. Алгебра и начала анализа для 10-11 классов.
Построение графиков функций

О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
при х ≠ -1.
График функции — прямая y = x – 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x – a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x – a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/639853
http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij
[/spoiler]

