Все курсы > Анализ и обработка данных > Занятие 4 (часть 2)
Во второй части занятия рассмотрим нахождение различий в данных и выявление взаимосвязи.
Продолжим работать в том же ноутбуке⧉
Нахождение различий

Два категориальных признака
Вначале возьмем случай двух категориальных признаков. Например, мы хотим понять насколько выживаемость пассажира (целевая переменная) зависит от класса, которым он путешествовал.
countplot и barplot
В первую очередь стоит визуально оценить, есть ли такое различие или нет. Для этого подойдут столбчатые диаграммы, где мы либо располагаем два столбца целевого признака рядом друг с другом (grouped), либо делаем один столбец и разбиваем его на две части (stacked).
Библиотека Seaborn
Начнем с того, что построим несколько counplots/barplots в библиотеке Seaborn с помощью функции countplot() и параметра hue.
|
# создадим grouped countplot, где по оси x будет класс, а по оси y – количество пассажиров # в каждом классе данные разделены на погибших (0) и выживших (1) sns.countplot(x = ‘Pclass’, hue = ‘Survived’, data = titanic); |

|
# горизонтальный countplot получится, # если передать данные о классе пассажира в переменную y sns.countplot(y = ‘Pclass’, hue = ‘Survived’, data = titanic); |

Для создания таких графиков мы также можем использовать более универсальную функцию catplot(). Передадим ей все те же параметры, что и функции countplot(), а также параметр kind = ‘count’, который и сообщит, что мы хотим построить именно countplot.
|
sns.catplot(x = ‘Pclass’, hue = ‘Survived’, data = titanic, kind = ‘count’); |
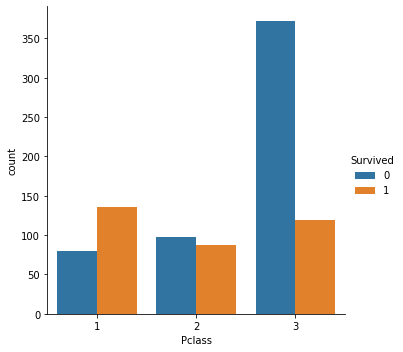
|
# добавим еще один признак (пол) через параметр col sns.catplot(x = ‘Pclass’, hue = ‘Survived’, col = ‘Sex’, kind = ‘count’, data = titanic); |

На основе графиков выше видно, что класс пассажира имеет большое значение для определения его виживаемости. При этом пол также оказал влияние. Например, в третьем классе большая часть мужчин погибла, в то время как среди женщин, количество выживших и не выживших примерно одинаковое.
Теперь посмотрим, как создать подобные графики в библиотеке Plotly.
Библиотека Plotly
Для построения графика countplot используем функцию px.histogram() (для barplot подойдет px.bar()). Начнем с варианта, когда разбитые по какому-либо признаку столбцы стоят рядом друг с другом (grouped).
|
px.histogram(titanic, # возьмем данные x = ‘Pclass’, # диаграмму будем строить по столбцу Pclass color = ‘Survived’, # с разбивкой на выживших и погибших barmode = ‘group’, # разделенные столбцы располагаются рядом друг с другом text_auto = True, # выведем количество наблюдений в каждом столбце title = ‘Survival by class’ # также добавим заголовок ) |

Теперь выведем вариант, когда каждый столбец диаграммы разделен на две части (stacked). Так как мы будем вручную корректировать подписи к графику и расстояние между столбцами, необходимо использовать объектно-ориентированный подход.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# создадим объект fig, в который поместим столбчатую диаграмму fig = px.histogram(titanic, x = ‘Pclass’, color = ‘Survived’, barmode = ‘stack’, # каждый столбец класса будет разделен по признаку Survived text_auto = True) # применим метод .update_layout к объекту fig fig.update_layout( title_text = ‘Survival by class’, # заголовок xaxis_title_text = ‘Pclass’, # подпись к оси x yaxis_title_text = ‘Count’, # подпись к оси y bargap = 0.2, # расстояние между столбцами # подписи классов пассажиров на оси x xaxis = dict( tickmode = ‘array’, tickvals = [1, 2, 3], ticktext = [‘Class 1’, ‘Class 2’, ‘Class 3’] ) ) fig.show() |

Теперь разобьем данные по трем категориальным переменным: полу, классу и выживаемости.
|
# для этого используем новый параметр facet_col = ‘Sex’ px.histogram(titanic, x = ‘Pclass’, color = ‘Survived’, facet_col = ‘Sex’, barmode = ‘group’, text_auto = True, title = ‘Survival by class and gender’) |
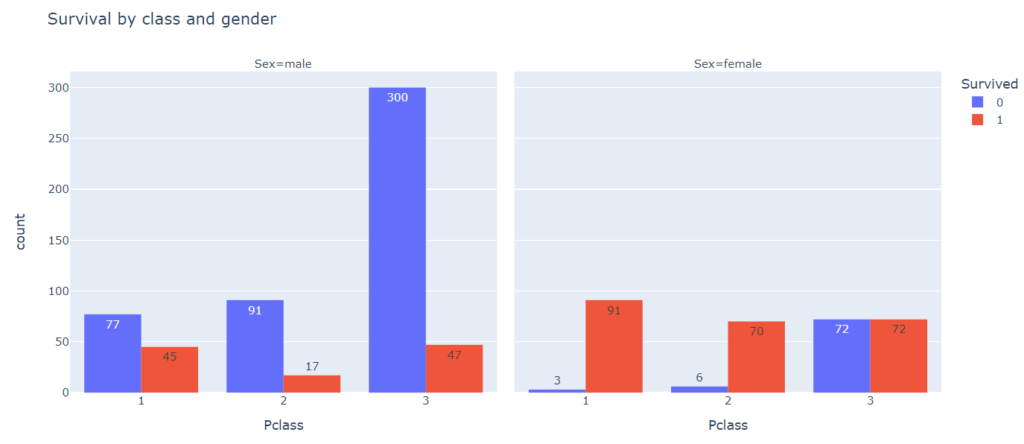
Более того, мы можем добавить еще один категориальный признак, порт посадки пассажира (Embarked).
|
# используем одновременно параметры facet_col и facet_row px.histogram(titanic, x = ‘Pclass’, color = ‘Survived’, facet_col = ‘Embarked’, facet_row = ‘Sex’, barmode = ‘group’, text_auto = True, title = ‘Survival by class, gender and port of embarkation’) |
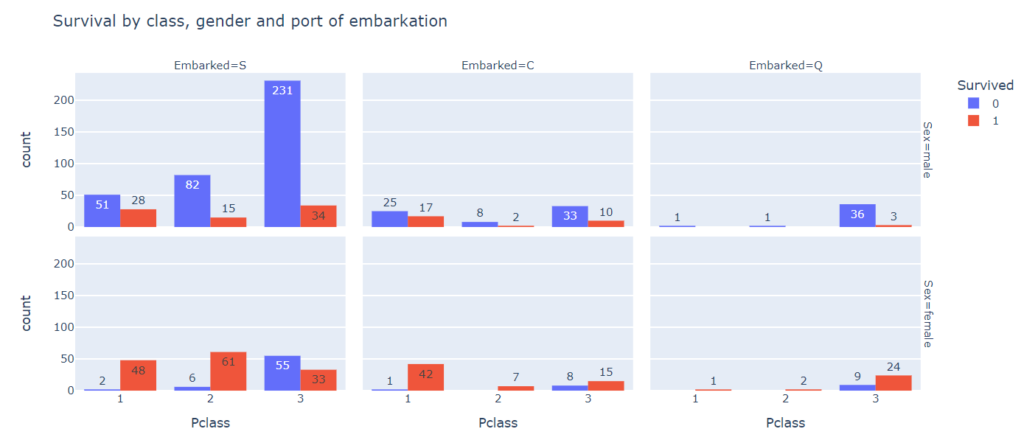
Здесь конечно, нужно следить за тем, чтобы объем предоставляемой информации не ухудшал информативности графиков.
Таблица сопряженности
Таблица сопряженности (contingency table) позволяет количественно измерить зависимость одной категориальной переменной от другой. Например, количественно оценим зависимость выживаемости от класса пассажира. Вначале оценим абсолютное количество наблюдений.
Абсолютное количество наблюдений
Для создания таблиц сопряженности в библиотеке Pandas используется функция pd.crosstab().
|
# создадим таблицу сопряженности # в параметр index мы передадим данные по классу, в columns – по выживаемости pclass_abs = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived) # создадим названия категорий класса и выживаемости pclass_abs.index = [‘Class 1’, ‘Class 2’, ‘Class 3’] pclass_abs.columns = [‘Not survived’, ‘Survived’] # выведем результат pclass_abs |

Теперь для каждого класса мы видим количество выживших и количество погибших. На основе таблицы сопряженности очень удобно строить столбчатую диаграмму (можно использовать график barplot, а не countplot, потому что количество значений в каждой категории уже посчитано).
Начнем с библиотеки Pandas.
|
# построим grouped barplot в библиотеке Pandas # rot = 0 делает подписи оси х вертикальными pclass_abs.plot.bar(rot = 0); |

|
# параметр stacked = True делит каждый столбец класса на выживших и погибших pclass_abs.plot.bar(rot = 0, stacked = True); |
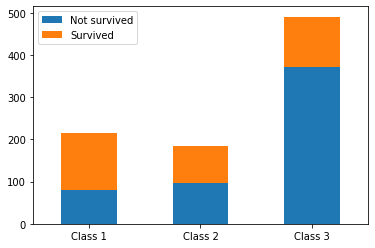
Теперь посмотрим, как построить stacked barplot в библиотеке Matplotlib.
|
# вначале создадим barplot для одной (нижней) категории plt.bar(pclass_abs.index, pclass_abs[‘Not survived’]) # затем еще один barplot для второй (верхней), указав нижнуюю в параметре bottom plt.bar(pclass_abs.index, pclass_abs[‘Survived’], bottom = pclass_abs[‘Not survived’]); |
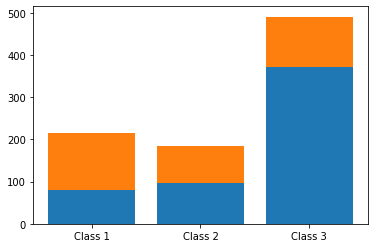
Таблица сопряженности вместе с суммой
С помощью параметра margins = True мы можем вывести сумму наблюдений по каждой строке и каждому столбцу (эти показатели еще называют маргинальными частотами, marginal frequencies).
|
# для подсчета суммы по строкам и столбцам используется параметр margins = True pclass_abs = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived, margins = True) # новой строке и новому столбцу с суммами необходимо дать название (например, Total) pclass_abs.index = [‘Class 1’, ‘Class 2’, ‘Class 3’, ‘Total’] pclass_abs.columns = [‘Not survived’, ‘Survived’, ‘Total’] pclass_abs |
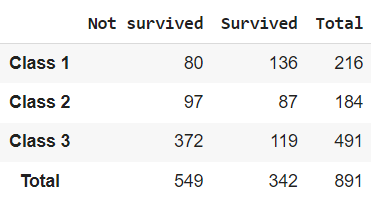
Относительное количество наблюдений
Для получения относительного количества наблюдений (относительных частот) следует использовать параметр normalize. Так как нам важно понимать долю выживших и долю погибших, укажем
normalize = ‘index’. В этом случае каждое значение будет разделено на общее количество наблюдений в строке.
|
# сумма по строкам в этом случае должна быть равна единице pclass_rel = pd.crosstab(index = titanic.Pclass, columns = titanic.Survived, normalize = ‘index’) pclass_rel.index = [‘Class 1’, ‘Class 2’, ‘Class 3’] pclass_rel.columns = [‘Not survived’, ‘Survived’] pclass_rel |

Если бы в индексе (в строках) была выживаемость, а в столбцах — классы, то логично было бы использовать параметр
normalize = ‘columns’ для деления на сумму по столбцам.
|
pclass_rel_T = pd.crosstab(index = titanic.Survived, columns = titanic.Pclass, normalize = ‘columns’) pclass_rel_T.index = [‘Not survived’, ‘Survived’] pclass_rel_T.columns = [‘Class 1’, ‘Class 2’, ‘Class 3’] pclass_rel_T |

Теперь на stacked barplot мы видим доли выживших в каждом из классов.
|
pclass_rel.plot.bar(rot = 0, stacked = True).legend(loc = ‘lower left’); |

Количественный и категориальный признаки
rcParams
Прежде чем продолжить, давайте посмотрим, как мы можем задать размер для всех (или почти всех) последующих графиков в ноутбуке. Так нам не придется вручную менять размер каждой визуализации.
В библиотеке Matplotlib и связанных с ней библиотеках (например, Seaborn) есть так называемые параметры конфигурации среды (runtime configuration parameters), то есть параметры, которые используются по умолчанию при создании графиков.
Эти параметры и их значения содержатся в словаре, к которому можно получить доступ через атрибут rcParams библиотеки Matplotlib.
|
# импортируем всю библиотеку Matplotlib import matplotlib # и посмотрим, какой размер графиков (ключ figure.figsize) установлен по умолчанию matplotlib.rcParams[‘figure.figsize’] |
Изменить эти параметры можно, обновив значение словаря rcParams по соответствующему ключу. Передадим новое значение размера по ключу figure.figuresize.
|
# обновим этот параметр через прямое внесение изменений в значение словаря matplotlib.rcParams[‘figure.figsize’] = (7, 5) matplotlib.rcParams[‘figure.figsize’] |
Также можно воспользоваться функцией sns.set() или, что то же самое, sns.set_theme().
|
# изменим размер обновив словарь в параметре rc функции sns.set() sns.set(rc = {‘figure.figsize’ : (8, 5)}) # посмотрим на результат matplotlib.rcParams[‘figure.figsize’] |
Теперь все последующие графики в библиотеках Matplotlib, Seaborn и Pandas будут иметь размеры восемь на пять дюймов. Вернемся к исследованию переменных.
Гистограммы
Когда у нас есть одна количественная и одна категориальная переменные, для их визуализации проще всего построить две наложенные друг на друга гистограммы. Мы уже строили такие графики в рамках вводного курса.
Посмотрим, различается ли распределение возраста выживших и погибших пассажиров Титаника.
|
# выведем две гистограммы на одном графике в библиотеке Matplotlib # отфильтруем данные по погибшим и выжившим и построим гистограммы по столбцу Age plt.hist(x = titanic[titanic[‘Survived’] == 0][‘Age’]) plt.hist(x = titanic[titanic[‘Survived’] == 1][‘Age’]); |
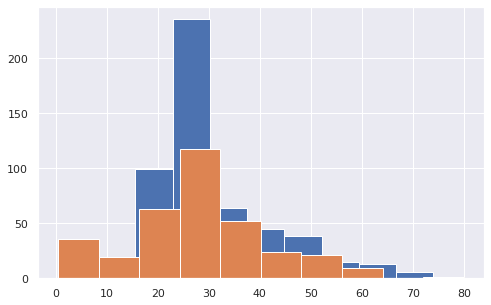
Теперь посмотрим, зависит ли распределение возраста от пола пассажира.
|
# в библиотеке Seaborn в x мы поместим количественный признак, в hue – категориальный sns.histplot(x = ‘Age’, hue = ‘Sex’, data = titanic, bins = 10); |

|
# в Plotly количественный признак помещается в x, категориальный – в color px.histogram(titanic, x = ‘Age’, color = ‘Sex’, nbins = 8, text_auto = True) |
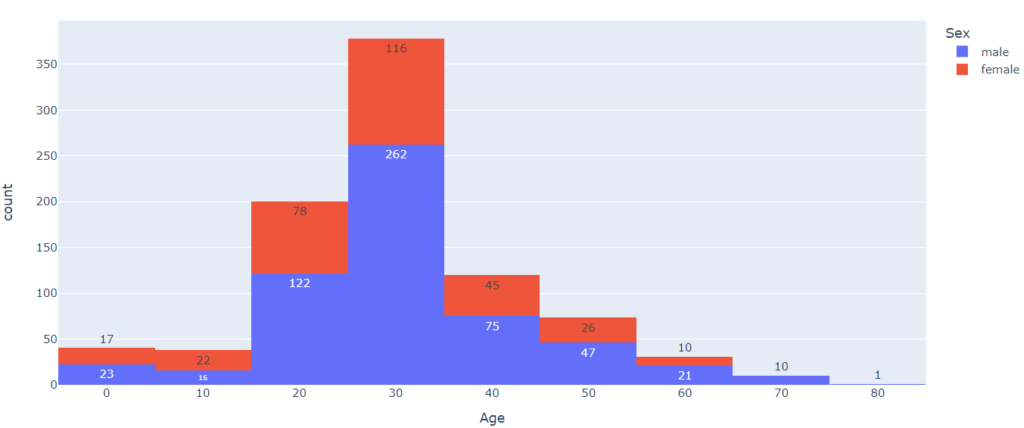
Сравнение двух распределений может быть не вполне корректным, если размер выборок существенно различается. Например, в нашем случае количество мужчин и женщин на борту далеко не одинаково.
|
# сравним количество мужчин и женщин на борту titanic.Sex.value_counts() |
|
male 577 female 314 Name: Sex, dtype: int64 |
Исправить ситуацию может параметр density = True.
|
# параметр alpha отвечает за прозрачность каждой из гистограмм plt.hist(x = titanic[titanic[‘Sex’] == ‘male’][‘Age’], density = True, alpha = 0.5) plt.hist(x = titanic[titanic[‘Sex’] == ‘female’][‘Age’], density = True, alpha = 0.5); |
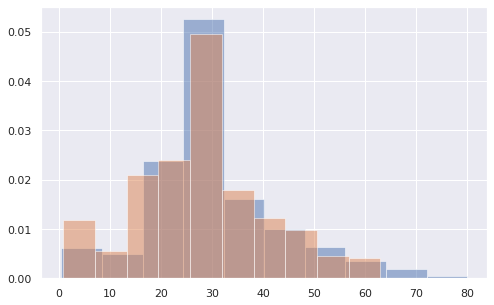
В этом случае гистограмма показывает плотность вероятности, а ее общая площадь всегда равна единице. Как следствие, мы можем адекватно сравнивать распределения между собой.
График плотности
С другой стороны, для плотности вероятности есть отдельный график, density plot. Площадь под кривой такого графика также всегда равна единице. Воспользуемся функцией .displot() с параметром kde = True.
|
# построим графики плотности распределений суммы чека в обеденное и вечернее время sns.displot(tips, x = ‘total_bill’, hue = ‘time’, kind = ‘kde’); |
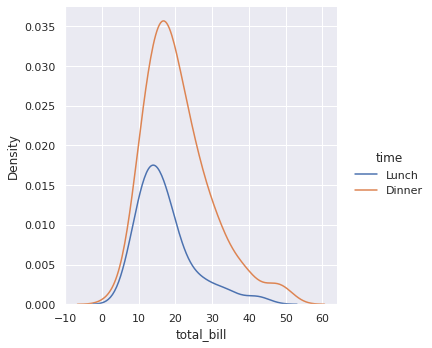
Из-за особенностей расчета графика kde мы можем получить «неестественные значения». Например, на диаграмме выше встречаются отрицательные значения чека. В реальности такого быть не может.
Избавиться от таких значений можно с помощью параметра clip, который задает диапазон значений.
|
# зададим границы диапазона от 0 до 70 долларов через clip = (0, 70) # дополнительно заполним цветом пространство под кривой с помощью fill = True sns.displot(tips, x = ‘total_bill’, hue = ‘time’, kind = ‘kde’, clip = (0, 70), fill = True); |

boxplots
Для сравнения распределений количественной переменной, разбитой по какому-либо категориальному признаку, также очень удобно использовать несколько графиков boxplot (side-by-side boxplots).
Построим такие графики в библиотеках Seaborn и Plotly. Вначале посмотрим, как различается сумма чека по дням недели.
|
sns.boxplot(x = ‘day’, y = ‘total_bill’, data = tips); |
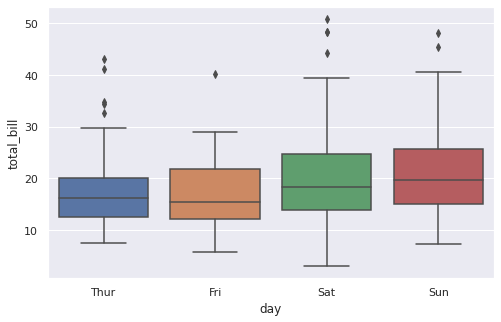
Что можно сказать про эти распределения?
- Медианный чек выше по воскресеньям
- Самый широкий диапазон суммы по чеку наблюдается в субботу, в пятницу же наоборот разброс наименьший
- Выбросы присутствуют только в верхних значениях распределения
Теперь посмотрим, как различается сумма чека в обеденное и вечернее время.
|
px.box(tips, x = ‘time’, y = ‘total_bill’, points = ‘all’) |
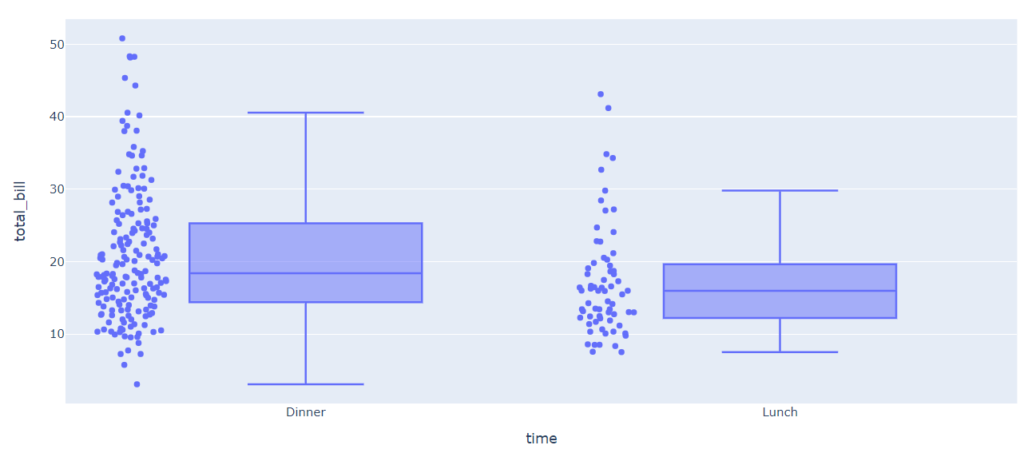
Ожидаемо, как разброс, так и медианное значение меньше в обеденное время.
Дополнительно замечу, что с помощью параметра points = ‘all’ в библиотеке Plotly для каждого распределения мы построили график, который называется stripplot. Он, в частности, показывает, что гостей за ужином бывает существенно больше. Об этом графике мы дополнительно поговорим чуть ниже.
Гистограммы и boxplots
Гистограммы и boxplots можно совместить. Сделать это проще всего в Plotly.
|
px.histogram(tips, x = ‘total_bill’, # количественный признак color = ‘sex’, # категориальный признак marginal = ‘box’) # дополнительный график: boxplot |
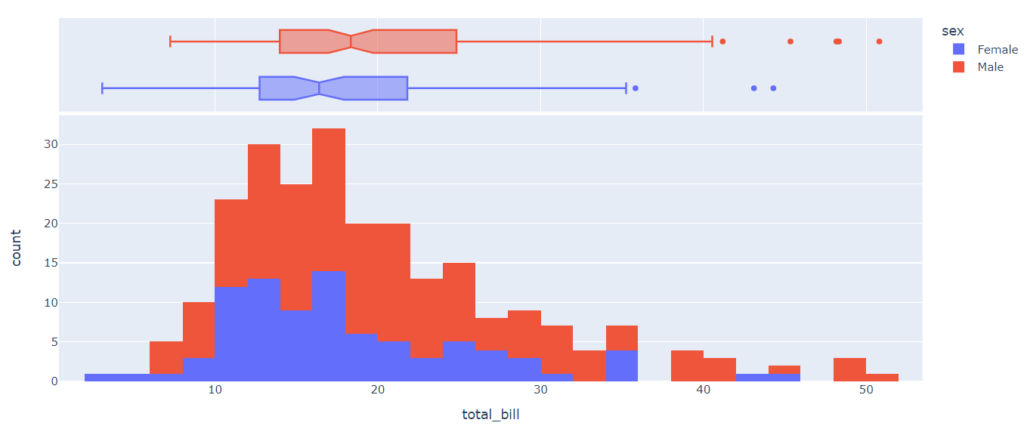
stripplot, violinplot
Более редкими типами графиков для визуализации количественных распределений являются stripplot и violinplot. Первый график, stripplot, как мы уже видели выше, визуализирует сами наблюдения.
|
# по сути, stripplot – это точечная диаграмма (scatterplot), # в которой одна из переменных категориальная sns.stripplot(x = ‘day’, y = ‘total_bill’, data = tips); |
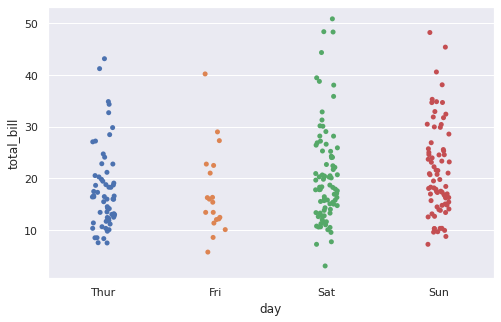
График stripplot можно построить как с помощью приведенной в примере выше функции sns.stripplot(), так и с помощью функции sns.catplot() с параметром kind = ‘strip’.
|
# с помощью sns.catplot() мы можем вывести распределение количественной переменной (total_bill) # в разрезе трех качественных: статуса курильщика, пола и времени приема пищи sns.catplot(x = ‘sex’, y = ‘total_bill’, hue = ‘smoker’, col = ‘time’, data = tips, kind = ‘strip’); |

Хотя stripplot достаточно информативен сам по себе, его очень удобно применять совместно с boxplot (как мы это делали выше).
График violinplot (от англ. violin, «скрипка») представляет собой комбинацию boxplot и графика плотности.
|
# построим violinplot для визуализации распределения суммы чека по дням недели sns.violinplot(x = ‘day’, y = ‘total_bill’, data = tips); |

Внутри каждого из violinplot находится миниатюрный boxplot, который помогает более точно оценить параметры распределения.
Преобразования данных
Иногда так бывает, что для повышения читаемости графика, данные сначала нужно преобразовать.
Логарифмическая шкала
Например, возьмем вот такие данные о продажах.
|
products = [‘Phone’, ‘TV’, ‘Laptop’, ‘Desktop’, ‘Tablet’] sales = [800, 4, 550, 500, 3] |
Предположим, что в этих данных нет ошибки и было действительно продано четыре телевизора и три планшета. На графике эти позиции из-за сильно различающегося масштаба будут нулевыми.
|
sns.barplot(x = products, y = sales) plt.title(‘Продажи в январе 2020 года’); |
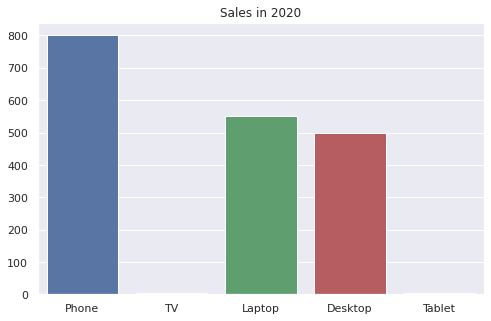
Для того чтобы эти продажи все-таки были видны, можно перевести ось y в логарифмическую шкалу.
|
sns.barplot(x = products, y = sales) plt.title(‘Продажи в январе 2020 года (log)’) plt.yscale(‘log’); |

Границы по оси y
В ноутбуке с моделью текучести кадров сотрудников⧉ (в разделе, посвященном практике), один из признаков — это баллы на последней аттестации. Для покинувших и продолжающих работать сотрудников различие не велико.
|
# код для получения этих значений вы найдете в ноутбуке по ссылке выше eval_left = [0.715473, 0.718113] # построим столбчатую диаграмму, # для оси x – выведем строковые категории, для y – доли покинувших компанию сотрудников sns.barplot(x = [‘0’, ‘1’], y = eval_left) plt.title(‘Last evaluation vs. left’); |

Иногда для наглядности бывает полезно ограничить диапазон значений по оси y.
|
sns.barplot(x = [‘0’, ‘1’], y = eval_left) plt.title(‘Last evaluation vs. left’) # для ограничения значений по оси y можно использовать функцию plt.ylim() plt.ylim(0.7, 0.73); |

Перейдем к выявлению взаимосвязи между переменными.
Выявление взаимосвязи

Выявление взаимосвязи предполагает анализ двух количественных переменных.
На сегодняшем занятии мы поговорим про графические способы ее выявления, а в следующем разделе разберем количественные показатели взаимосвязи переменных (то есть ковариацию и корреляцию).
Линейный график
Базовым способом визуализации двух количественных переменных является линейный график (linear plot). Построить его можно с помощью функции plt.plot() библиотеки Matplotlib.
|
# создадим последовательность от -2пи до 2пи # с интервалом 0,1 x = np.arange(–2*np.pi, 2*np.pi, 0.1) # сделаем эту последовательность значениями по оси x, # а по оси y выведем функцию косинуса plt.plot(x, np.cos(x)) plt.title(‘cos(x)’); |

Точечная диаграмма
Еще один базовый график — уже знакомая нам точечная диаграмма (scatter plot). Ее удобно использовать, когда одна переменная не имеет строгой зависимости от другой. Воспользуемся функцией plt.scatter() библиотеки Matplotlib.
|
plt.scatter(tips.total_bill, tips.tip) plt.xlabel(‘total_bill’) plt.ylabel(‘tip’) plt.title(‘total_bill vs. tip’); |

Такой же график можно построить в библиотеке Pandas.
|
# перед созданием этого графика в Pandas принудительно удалим # предупреждения и сообщения об ошибках # (в Colab появляется предупреждение, связанное с параметром c (color)) from matplotlib.axes._axes import _log as matplotlib_axes_logger matplotlib_axes_logger.setLevel(‘ERROR’) # воспользуемся методом .plot.scatter() tips.plot.scatter(‘total_bill’,‘tip’) plt.title(‘total_bill vs. tip’); |
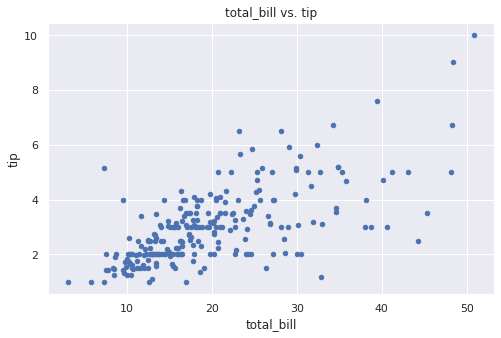
На графиках выше мы видим, что в среднем с ростом суммы чека растет и размер чаевых (другими словами, взаимосвязь прослеживается).
При этом мы видим гетероскедастичность (различную изменчивость) данных, когда при небольшом чеке диапазон чаевых меньше, чем когда сумма чека увеличивается.
Почему это влияет на качество модели и как с этим бороться, мы поговорим на следующем курсе.
В точечной диаграмме можно учесть и категориальный признак. Например, посмотрим, есть ли различие во взаимосвязи между суммой чека и размером чаевых в зависимости от времени дня.
|
# категориальный признак добавляется через параметр hue sns.scatterplot(data = tips, x = ‘total_bill’, y = ‘tip’, hue = ‘time’) plt.title(‘total_bill vs. tip by time’); |

Мы можем констатировать, что при сохранении взаимосвязи как в обеденное, так и в вечернее время, за ужином минимальная и максимальное сумма чека, а также разброс чаевых выше.
pairplot
График pairplot позволяет визуализировать взаимосвязи сразу нескольких количественных переменных. В библиотеке Pandas такой график строится с помощью функции pd.plotting.scatter_matrix().
|
# построим pairplot в библиотеке Pandas # в качестве данных возьмем столбцы total_bill и tip датасета tips pd.plotting.scatter_matrix(tips[[‘total_bill’, ‘tip’]]); |

Как вы видите, там, где перемекаются разные признаки, строится точечная диаграмма, на пересечении одного и того же признака по главной диагонали — его гистограмма.
Примерно такой же график можно построить с помощью функции sns.pairplot() библиотеки Pandas.
|
# параметр height функции pairplot() задает высоту каждого графика в дюймах sns.pairplot(titanic[[‘Age’, ‘Fare’]].sample(frac = 0.2, random_state = 42), height = 4); |

Обратите внимание на метод .sample() с параметром frac = 0,2, который мы применили к датафрейму titanic. Таким образом, мы сделали случайную выборку из 20% или $ 891 times 0,2 approx 178 $ наблюдений.
|
# параметр random_state обеспечивает воспроизводимость результата titanic[[‘Age’, ‘Fare’]].sample(frac = 0.2, random_state = 42) |

Метод .sample() в данном случае применяется для того, чтобы ускорить создание pairplot. Зачастую, при наличии большого числа наблюдений, график может строиться очень долго.
При добавлении параметра hue (разделение по категориальной переменной) гистограмма по умолчанию превращается в график плотности.
|
# обратите внимание, столбец Survived мы добавили и в параметр hue и в датафрейм с данными sns.pairplot(titanic[[‘Age’, ‘Fare’, ‘Survived’]].sample(frac = 0.2, random_state = 42), hue = ‘Survived’, height = 4); |

По большому счету с помощью такого графика мы пытаемся ответить на вопрос, есть ли взаимосвязь между возрастом пассажиров и стоимостью их билетов в разрезе выживаемости.
Функция sns.pairplot() является надстройкой (упрощенной версией) другой функции этой библиотеки, sns.PairGrid(). Ее стоит использовать, если требуются более продвинутые настройки графика pairplot.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим объект класса PairGrid, в качестве данных передадим ему # как количественные, так и категориальные переменные g = sns.PairGrid(tips[[‘total_bill’, ‘tip’, ‘time’, ‘smoker’]], # передадим в hue категориальный признак, который мы будем различать цветом hue = ‘time’, # зададим размер каждого графика height = 5) # метод .map_diag() с параметром sns.histplot выдаст гистограммы на диагонали g.map_diag(sns.histplot) # слева и снизу от диагонали мы выведем точечные диаграммы и зададим # дополнительный категориальный признак smoker с помощью размера точек графика g.map_lower(sns.scatterplot, size = tips[‘smoker’]) # справа и сверху будет график плотности сразу двух количественных признаков g.map_upper(sns.kdeplot) # добавим легенду, adjust_subtitles = True делает текст легенды более аккуратным g.add_legend(title = ”, adjust_subtitles = True); |
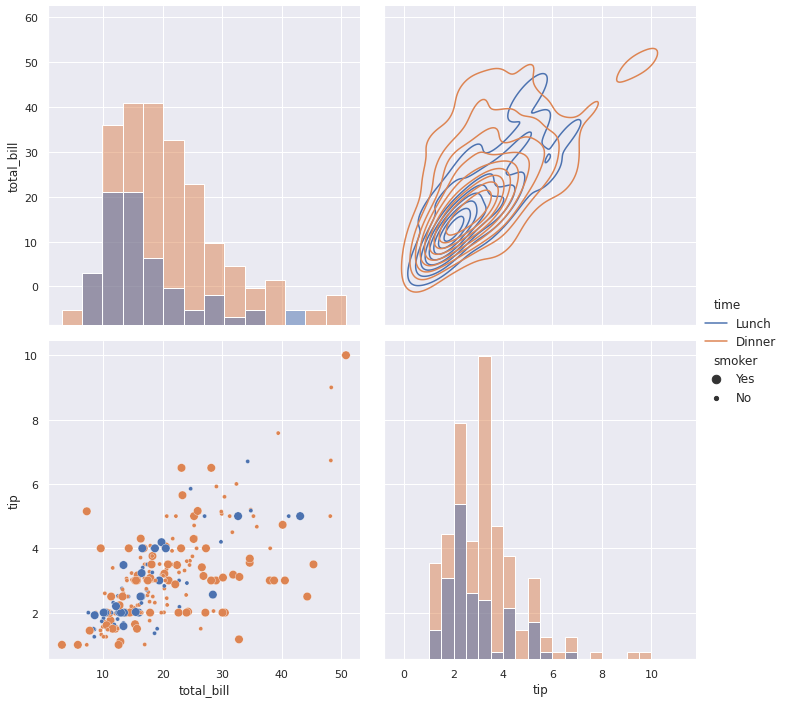
При построении таких сложных графиков важно помнить про их информативность. В примере выше некоторые графики (например, точечную диаграмму) уже достаточно сложно анализировать.
jointplot
Совместное распределение двух переменных
График плотности (kde plot) двух количественных признаков (верхний справа в примере выше) представляет собой визуализацию совместного распределения (joint distribution) двух количественных признаков (tip и total_bill) с разделением по категориальному признаку (time). Другими словами, мы смотрим на то, как изменяется распределение одного количественного признака под воздействием другого. И так для каждой из двух категорий.
В результате мы получаем графики изолиний (contour lines), которые показывают, что между суммой чека и чаевыми есть взаимосвязь (если бы ее не было, изолинии представляли бы собой круги). Теоретические основы совместных распределений мы рассмотрим на курсе по статистике вывода, а пока изучим инструмент их визуализации, который называется jointplot.
sns.jointplot()
Вначале построим точно такой же график плотности (kde plot) совместного распределения tip и total_bill с разделением по признаку time. Для этого функции sns.jointplot() передадим данные и укажем параметр kind = ‘kde’.
|
sns.jointplot(data = tips, # передадим данные x = ‘total_bill’, # пропишем количественные признаки, y = ‘tip’, hue = ‘time’, # категориальный признак, kind = ‘kde’, # тип графика height = 8); # и его размер |
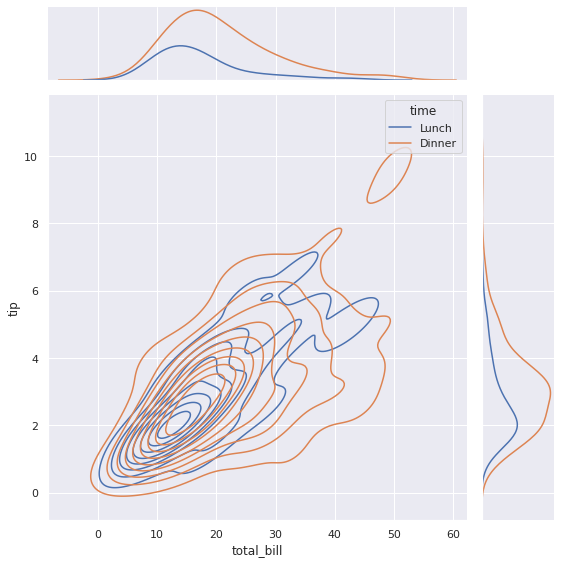
По краям мы видим графики плотности так называемого безусловного распределения (marginal distribution) каждого из признаков. Это одномерные распределения (univariate distribution). Основной график показывает совместное распределение (joint distribution) уже двух переменных. Это двумерное распределение (bivariate distribution).
Возможно более интуитивным покажется использование точечной диаграммы (kind = ‘scatter’) вместо графика плотности.
|
sns.jointplot(data = tips, x = ‘total_bill’, y = ‘tip’, hue = ‘time’, # построим точечную диаграмму kind = ‘scatter’, # дополнительно укажем размер точек s = 100, # и их прозрачность alpha = 0.7, height = 8); |
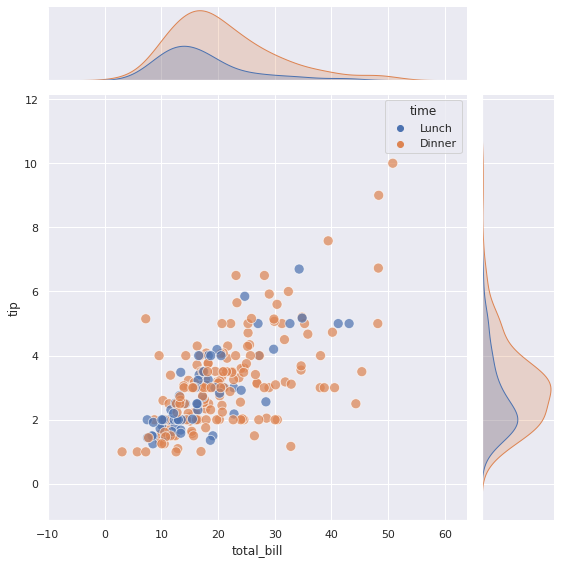
Кроме того, мы можем построить линию регрессии, проходящую через точки. Правда в этом случае придется отказаться от параметра hue, разделять данные на категории и одновременно строить линию регрессии sns.jointplot() не умеет.
|
# для построения линии регрессии на данных # используем параметр kind = ‘reg’ sns.jointplot(data = tips, x = ‘total_bill’, y = ‘tip’, kind = ‘reg’, height = 8); |

heatmap
Наконец, если мы хотим вывести какие-либо статистические показатели взаимосвязи двух количественных переменных (например, корреляцию), это можно сделать с помощью чисел. Выведем корреляционную матрицу между total_bill и tip с помощью метода .corr().
|
tips[[‘total_bill’, ‘tip’]].corr() |

В следующем разделе мы более подробно поговорим про взаимосвязь переменных в целом и корреляцию в частности.
Или с помощью цвета. Во втором случае мы будем строить то, что называется тепловой картой (heatmap). Поместим созданную выше корреляционную матрицу в функцию sns.heatmap().
|
sns.heatmap(tips[[‘total_bill’, ‘tip’]].corr(), # дополнительно пропишем цветовую гамму cmap= ‘coolwarm’, # и зададим диапазон от -1 до 1 vmin = –1, vmax = 1); |

Более насыщенный красный цвет (верхняя граница шкалы) демонстрирует корреляцию признака с самим собой, менее насыщенный — достаточно сильную положительную корреляцию признаков.
Сравнение датасетов
Рассмотрим еще одну библиотеку, которая позволяет не просто сравнивать количественные и качественные переменные в датасете, а сразу сравнивать два датасета. Зачастую, сравнение двух датасетов имеет смысл, когда перед нами обучающая и тестовая выборки.
Скачаем и подгрузим в сессионное хранилище тестовую часть датасета «Титаник».
Библиотека Sweetviz
Теперь установим и импортируем библиотеку sweetviz.
Импортируем обучающую и тестовую выборки.
|
train = pd.read_csv(‘/content/train.csv’) test = pd.read_csv(‘/content/test.csv’) |
Передадим оба датасета в функцию sv.compare(). Эта функция создаст объект DataframeReport, к которому мы сможем применить метод .show_notebook() для выведения результата.
|
comparison = sv.compare(train, test) |

|
# посмотрим на тип созданного объекта type(comparison) |
|
sweetviz.dataframe_report.DataframeReport |
|
# применим метод .show_notebook() comparison.show_notebook() |

Интерактивную версию этого отчета вы найдете в ноутбуке к занятию⧉.
Количественные переменные
По большому счету мы получаем информацию о каждой из переменных в разрезе двух датафреймов. Обратимся к столбцу Age.
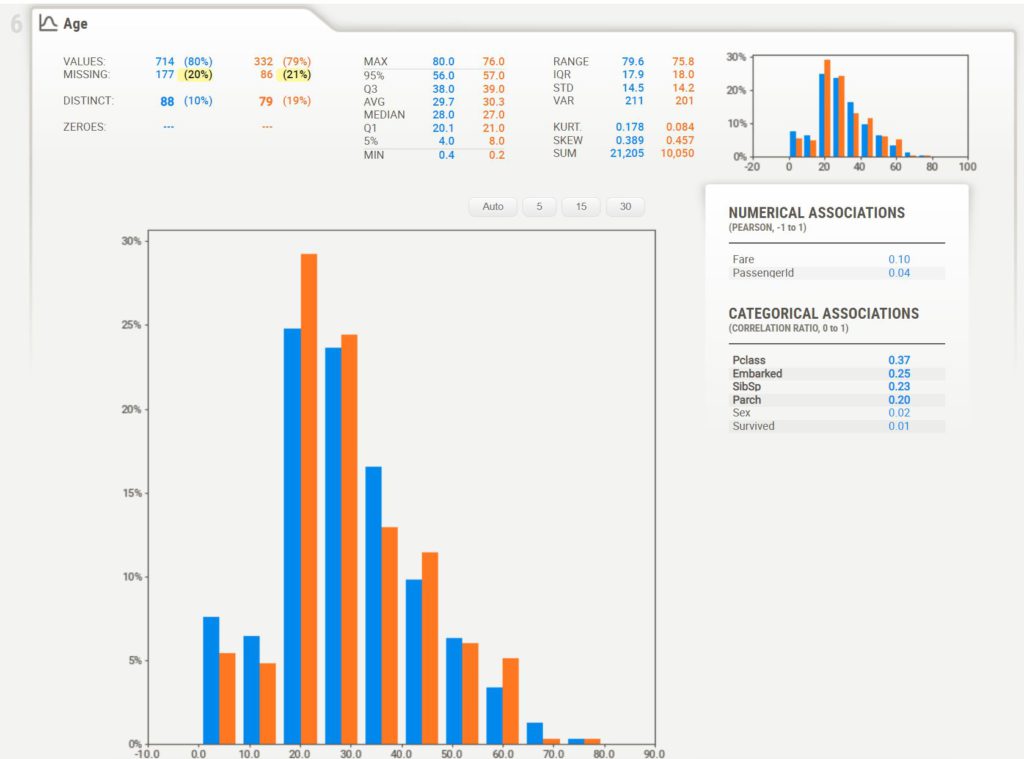
В отчете есть информация о присутствующих (values) и отсутствующих значениях (missing), количестве уникальных (distinct) и нулевых (zeroes) значений. Кроме того, мы видим базовые статистические показатели и гистограмму распределения переменной в каждом из датафреймов.
Отдельно стоит отметить выявление взаимосвязи:
- для двух количественных переменных используется коэффициент корреляции Пирсона (Pearson correlation coefficient); и здесь мы видим, что корреляция возраста со столбцами Fare и PassengerId ожидаемо близка к нулю
- для выявления взаимосвязи между количественной и качественной переменными используется корреляционное отношение (correlation ratio); например, мы видим, что возраст в некоторой степени связан с классом пассажира Pclass
Качественные переменные
Обратимся к столбцу Sex.

В первую очередь отметим, что программа самостоятельно определила, что речь идет именно о категориальном признаке. Для его визуализации была построена столбчатая диаграмма с разбивкой по обучающей и тестовой выборке. Кроме того, мы можем количественно оценить значения в каждой из категорий.
Для поиска же взаимосвязи между двумя категориальными переменными используется коэффициент неопределенности (uncertainty coefficient) или U Тиля, и мы видим некоторую связь с целевой переменной Survived. Для количественной и качественной переменных по-прежнему используется корреляционное отношение.
Более подробную информацию об этой библиотеке можно посмотреть на странице документации⧉.
Перейдем к третьей части занятия.
ВикиЧтение
Основы логистики
Левкин Григорий Григорьевич
Пример решения задачи
Пример решения задачи
Для проведения ABC-классификации следует использовать табличный процессор Excel. Исходные данные для расчета приведены в таблице.
Порядок расчетов следующий.
Этап 1. В столбец А внести порядковые номера позиций. В столбец В – показатели по выбранному критерию (к примеру, средний запас по позициям). Просуммировать значения по столбцу В.
Этап 2. Рассчитать долю отдельных позиций ассортимента в общем объеме запаса: в столбце С средний запас по первой позиции разделить на сумму запасов и умножить на 100 (или сразу разделить на полученную сумму). К примеру, при количестве позиций 14: В2/В$15*100. Обратить внимание на абсолютную ссылку (знак доллара). Формулу в ячейке С2 растянуть на весь столбец (рис. 10).
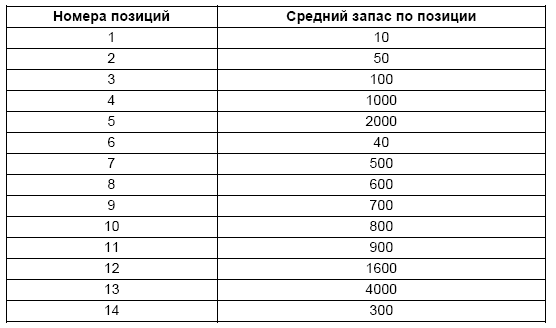
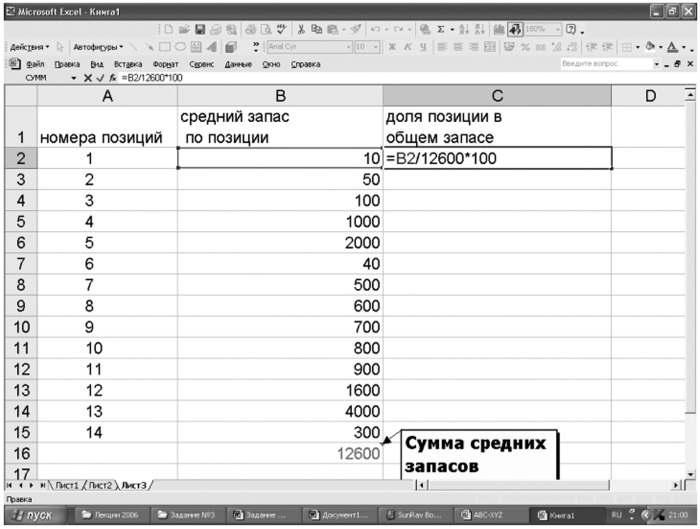
Рис. 10. Начальный этап АВС-классификации
Этап 3. Выстроить ассортиментные позиции в порядке убывания доли в общем запасе по столбцу С. Для сортировки таблицы использовать функцию <Данные> <Сортировка>.
Этап 4. Рассчитать нарастающий итог в столбце D. При этом первое число ряда остается без изменения. Второе число получаем суммированием первой и второй долей. Затем полученную сумму прибавляем к каждой последующей доле (рис. 11).
Этап 5. Построить кривую ABC. Для построения кривой выделяем столбец с нарастающим итогом – <Вставка> <Диаграмма>. В диаграмме выбираем <График> <Далее>. Для внесения подписей к оси X нажимаем <Ряд>. <Подписи к оси Х>, а затем выделяем столбец с номерами позиций (номера должны быть вразброс – упорядоченный список долей позиций по убыванию). Полученную диаграмму размещаем на отдельном листе.
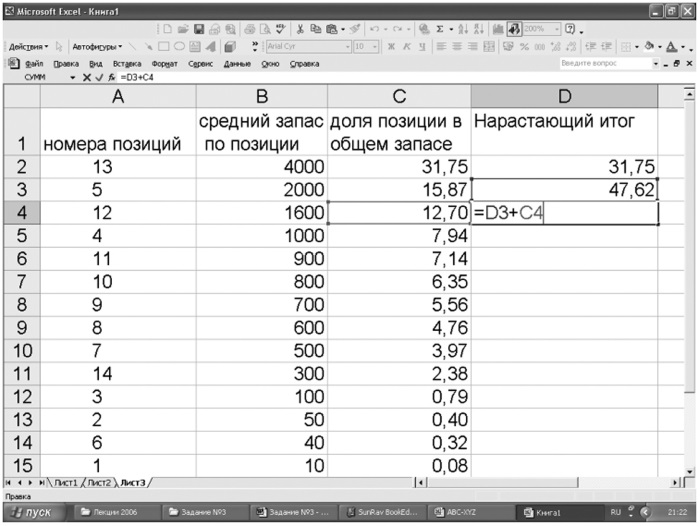
Рис. 11. Расчет нарастающего значения
Этап 6. При разделении анализируемого ассортимента на группы А, В и С можно воспользоваться следующим алгоритмом: в группу А включают 20 % позиций упорядоченного списка, начиная с наиболее значимой; в группу В включают следующие 30 % позиций; в группу С включают оставшиеся 50 % позиций (нижняя половина списка в таблице). В примере 20 % от 14 позиций составляет 3 позиции, 30 % около 5 позиций и все остальное – группа С (рис. 12).

Рис. 12. Разделение анализируемого ассортимента на группы
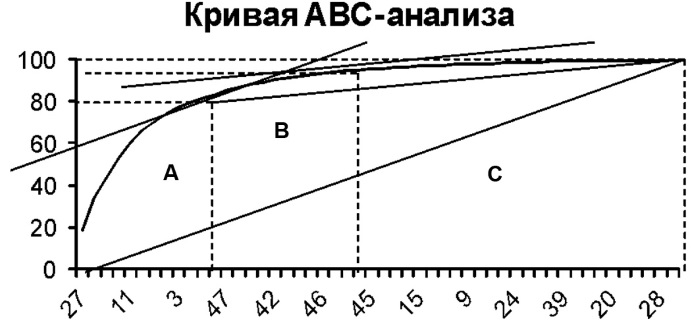
Рис. 13. Метод построения кумулятивной прямой
Кроме того, при разделении ассортимента на группы можно воспользоваться методом «кумулятивной прямой» (рис. 13).
Для разделения на группы используют построенную по результатам исследований кривую ABC-классификации.
На полученном графике соединяют прямой начало координат и конечную точку кривой. Полученную прямую копируют и затем помещают ее над кривой. Находим точку соприкосновения кривой ABC и кумулятивной прямой – это граница между группой А и группой В. Затем соединяют прямой оставшуюся часть кривой. Копируем кумулятивную прямую и перемещаем ее в область над кривой. Полученная точка соприкосновения является границей между группой В и С (рис. 13).
Данный текст является ознакомительным фрагментом.
Читайте также
Эмоции и решения
Эмоции и решения
Известный невролог Антонио Дамасио рассказывает, как еще в начале своей профессиональной деятельности осознал ошибочность традиционного взгляда на рациональное мышление. Он столкнулся с пациентом, у которого сохранились все способности к разумному
Находим решения
Находим решения
С помощью Кенни Сью закончила коллаж. Знаю о том, потому что они принесли готовый продукт ко мне на совместный прием. Это было подлинное произведение искусства.В процессе творчества Сью и Кенни разговорились. Сама Сью не стала бы смягчать настороженность
Решения и неопределенность
Решения и неопределенность
Оказывается, нежелание Боба принять потерю является частью намного большего набора когнитивных и эмоциональных предубеждений, влияющих на торговые решения. Растущее количество исследований в области поведенческих финансов помогает
Пример решения задачи
Пример решения задачи
Для проведения ABC-классификации следует использовать табличный процессор Excel. Исходные данные для расчета приведены в таблице.Порядок расчетов следующий.Этап 1. В столбец А внести порядковые номера позиций. В столбец В – показатели по выбранному
Пример решения задачи
Пример решения задачи
Рассмотрим условный пример. Допустим, нам необходимо сформировать развозочные маршруты для обслуживания пяти клиентов, вес партии товара каждого из них колеблется в диапазоне от 0,8 до 1,45 т, а общий вес всех товаров составляет 5,9 т. В нашем
56. Инвестиционные решения
56. Инвестиционные решения
Решения в сфере управления инвестициями можно разделить на три блока.I. Отбор и ранжирование. Инвестиционная деятельность осуществляется в различных условиях, и обычно перед инвестором имеется не одна, а по крайней мере несколько возможностей
2. Задачи маркетинга и некоторые пути их решения
2. Задачи маркетинга и некоторые пути их решения
Независимо от концепции, положенной в основу организации маркетинговой деятельности на предприятии, она должна решить четыре главные задачи:1) предложить разработку и производство продукта, необходимого потребителю, в
РЕШЕНИЯ
РЕШЕНИЯ
У этих проблем нет простых решений. Искоренить сексуальные преследования полностью крайне трудно. Однако усилия, чтобы справиться с ними, должны быть предприняты, и стоит рассмотреть следующие подходы:1. Издать недвусмысленное заявление генерального
Приложение Некоторые варианты решения задачи с девятью точками
Приложение
Некоторые варианты решения задачи с девятью
8. Если для решения задачи не хватает какой-то важной информации, продумайте различные возможные сценарии. Вы почти всегда обнаружите, что эта недостающая информация не нужна для решения проблемы
8. Если для решения задачи не хватает какой-то важной информации, продумайте различные возможные сценарии. Вы почти всегда обнаружите, что эта недостающая информация не нужна для решения проблемы
Почти всегда то, что мы называем логическими головоломками, использует
Подходит ли геймификация для решения моей бизнес-задачи?
Подходит ли геймификация для решения моей бизнес-задачи?
Геймификация не станет решением любой бизнес-задачи. Сейчас, когда вы уже примерили на себя роль разработчика игр, задайтесь вопросом, имеет ли смысл использовать геймификацию для тех задач, которые вы надеетесь
Идеи – это НЕ решения
Идеи – это НЕ решения
Самые лучшие в мире идеи никогда не реализуют свой потенциал, пока не будут применены. И самые прекрасные идеи терпят крах именно на стадии
Нестандартные решения
Нестандартные решения
ДРК помогает разобраться с причинами проблемы. Это методика разработки прорыва – оригинальных решений, которые опровергают традиционные подходы и ложные предположения – все то, что описывается словами «мы так всегда делаем».
Творческий подход
Нестандартные решения
Нестандартные решения
Своей гибкостью и потенциалом ДБР обязано именно этому компоненту – нестандартной идее (прорыву). По сути, это некое решение, событие, которого еще не существует в системе, но которое необходимо реализовать, чтобы изменить ситуацию к лучшему.
Решения
Решения
P: «Положите ваш материал мне на стол» – это не решение.A: Решение не обязательно должно иметь прецеденты.E: Побочные эффекты ваших решений могут быть опаснее проблемы, которую вы пытаетесь решить.I: Всеобщее одобрение не гарантирует действенности
Трудные решения
Трудные решения
Если в компании проводятся массовые увольнения, а ее высшее руководство получает за это бонусы, то, по словам Шлихтинг, «это подрывает доверие». Когда в трудные времена ее компания была вынуждена заморозить индексацию заработных плат, это коснулось и
Матрица Бостонской Консалтинговой Группы: подробный обзор
Начнем с определения. Матрица БКГ (также называется матрица «рост- доля рынка»») разработана Бостонской Консалтинговой Группой в конце 1960-х годах и является одной из первых моделей портфельного анализа.
Как построить матрицу БКГ? Что означают оси и элементы матрицы, как их рассчитать? Какая информация необходимая для проведения анализа? Как сделать правильные выводы и использовать матрицу максимально эффективно для бизнеса? Какие стратегии по матрице БКГ существуют? Ответы на все описанные вопросы содержатся в данной статье. Самое подробное, наглядное и простое описание модели БКГ с наглядным примером в Excel, а также с готовым шаблоном.
Оглавление:
- Сущность матрицы БКГ
- Основные показатели матрицы БКГ
- Интерпретация и анализ матрицы БКГ
- Идеальный портфель по модели БКГ
- Стратегические решения при анализе матрицы
- Ограничения в использовании матрицы
Что такое матрица БКГ?
В основе матрицы БКГ заложено две гипотезы:
- лидирующая компания в сегменте имеет конкурентное преимущество в издержках производства, а значит и самый высокий уровень рентабельности на рынке.
- для того, чтобы эффективно функционировать в быстрорастущих сегментах, компания должна инвестировать в развитие товара на высоком уровне; и наоборот, присутствие на рынке с низкими темпами роста позволяет сокращать расходы на развитие товара.
Основной смысл модели в 1 предложении: матрица БКГ предполагает, что компания для обеспечения продуктивного прибыльного долгосрочного роста должна генерировать и извлекать денежные средства из успешных бизнесов на зрелых рынках и инвестировать их в быстро растущие привлекательные новые сегменты, укрепляя в них положение своих товаров и услуг для получения в будущем устойчивого уровня дохода.
Рис.1 Пример таблицы БКГ
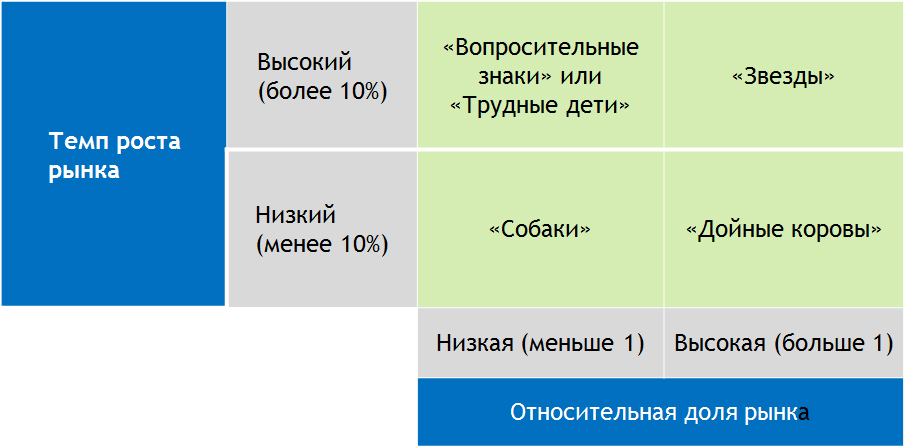
Таким образом, основной задачей модели БКГ является определение приоритетов в развитии ассортиментных единиц компании, определение ключевых направлений для будущих инвестиций. Метод помогает ответить на вопрос «Инвестиции в развитие каких товаров и услуг будут наиболее прибыльными?» и разработать долгосрочные стратегии развития каждой единицы ассортимента.
Какие товары можно анализировать в модели БКГ?
- Отдельные направления бизнеса компании, не связанные между собой. Например, страхование и производство газированных напитков
- Отдельные группы товаров, реализуемые предприятием на одном рынке. Например, страхование жизни, страхование автомобилей, страхование жилых помещений и т.п.
- Отдельные единицы товаров и услуг в рамках одной группы товаров. Например, страхование автомобилей может быть: ОСАГО, КАСКО, дополнительное страхование, и т.п.
Читайте также: другие модели, позволяющие оценить перспективы бизнеса:
- Матрица «привлекательность рынка-конкурентоспособность»
- Матрица Игоря Ансоффа: подробное описание стратегий роста
Основные показатели матрицы
Построение матрицы БКГ начинается с расчета трех показателей по каждой товарной группе, включенной в модель: относительная доля рынка товара компании, темп роста рынка и объем продаж/ прибыли анализируемых товарных групп.
Расчет относительной доли рынка
Рассчитывается делением абсолютной доли рынка товара компании на анализируемом сегменте на долю рынка ведущего конкурента в анализируемом сегменте. Относительная доля рынка откладывается по горизонтальной оси матрицы и является показателем конкурентоспособности товара компании в отрасли.
Если значение относительной доли рынка товара компании больше единицы, то товар компании занимает сильное положение на рынке и имеет высокую относительную долю рынка. Если значение относительной доли рынка меньше единицы, то товар компании имеет более слабые позиции на рынке в сравнении с ведущим конкурентом и его относительная доля считается низкой.
Пример расчета относительной доли рынка:
Компания оперирует в двух сегментах : завтраки и приправы. В сегменте » завтраки» доля компании 40%, а доля ключевого конкурента 20%. В сегменте «приправы» доля компании составляет 10%, а доля ключевого конкурента 30%.
Относительная доля рынка компании в сегменте «завтраки» будет составлять 40%/20% = 2, что больше 1, а значит показатель высокий.
Относительная доля рынка в сегменте » приправы» будет составлять 10%/30%=0,33, что меньше единицы, а значит показатель низкий.
Расчет темпов роста рынка
Откладывается по вертикальной оси матрицы БКГ и является показателем зрелости, насыщенности и привлекательности рынка, на котором компания реализует свои товары или услуги. Рассчитывается как средне взвешенное значение среди всех сегментов рынка, на которых действует компания.
Если показатель темпа роста рынка больше 10% — рынок быстрорастущий или рынок с высоким темпом роста. Если показатель роста рынка меньше 10% — рынок медленно растущий или рынок с низким темпом роста.
Пример расчета темпа роста рынка:
- Исходная информация: 3 рыночный сегмента А, В, С.
- Средневзвешенный темп роста рынка А = (годовой темп роста рынка А в % * годовая емкость рынка А, руб)/ (Сумму емкостей рынка А+В+С, в руб)
Объем продаж в модели БКГ
Объем продаж показывается в матрице через размер окружности. Чем больше размер, тем выше объем продаж. Информация собирается на основе имеющейся внутренней статистики компании и представляет наглядно, на каких рынках концентрируются основные денежные средства компании.
Рис.2 Пример заполненной матрицы БКГ предприятия:
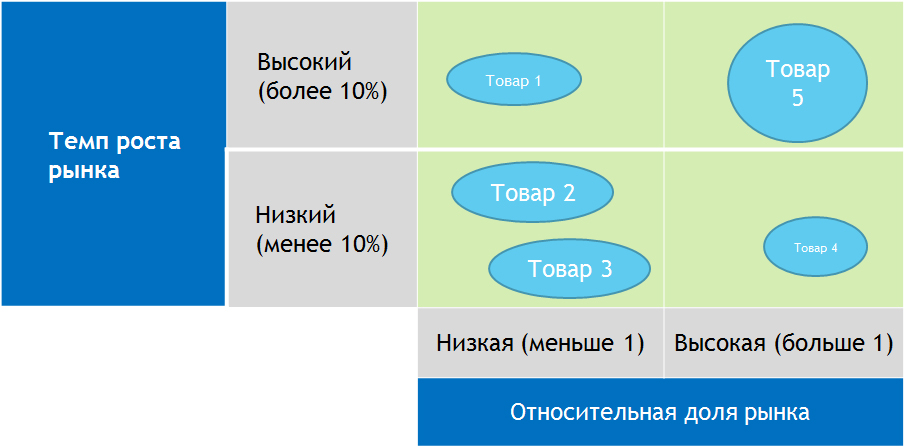
Вы знаете теорию и ва нужна только практика?
Читайте готовый пошаговый пример построения матрицы БКГ в отдельной статье «Матрица БКГ на примере предприятия». Пример содержит четкие и понятные инструкции о том, как правильно рассчитать показатели, используемые в модели, а также как сделать правильные выводы на основе составленной матрицы. Пример также включает шаблон построения и анализа матрицы БКГ в формате Excel.
Подробное описание четырех квадрантов матрицы
В результате построения матрицы БКГ все товарные группы или отдельные продукты компании разбиваются на 4 квадранта. Стратегия развития товарной группы зависит от того, в каком квадранте находится товар. Каждый квадрант имеет отдельные рекомендации.
Рис.3 Описание четырех квадрантов матрицы БКГ
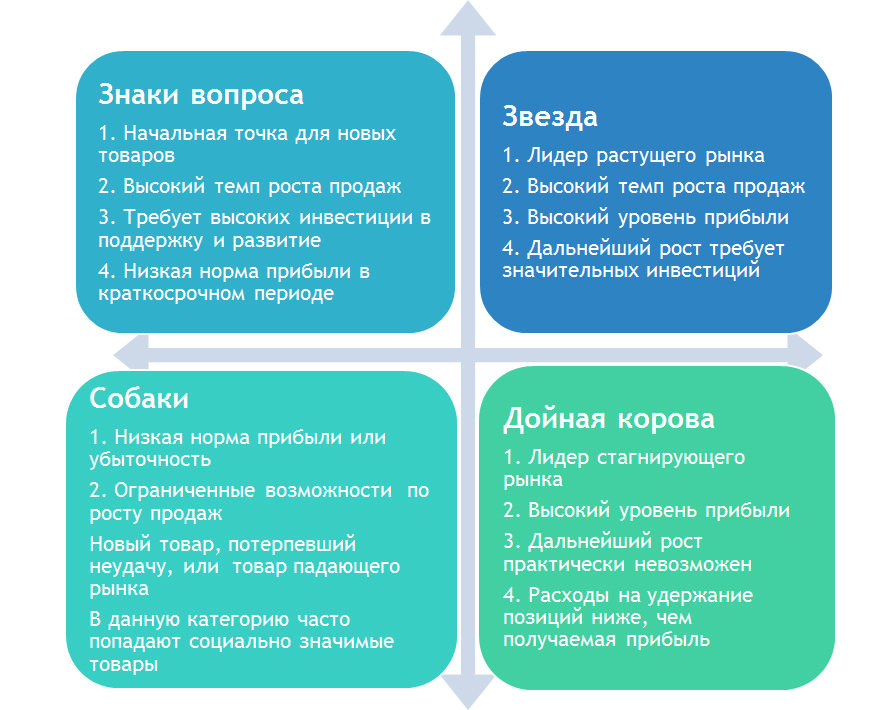
Первый квадрант: «вопросительные знаки» или «трудные дети»
В первом квадранте матрицы БКГ находятся такие направления бизнеса компании, которые представлены в быстрорастущих отраслях или сегментах, но имеют низкую долю рынка или, другими словами, занимают слабое положение на рынке. Такие виды деятельности требуют высокого уровня инвестиций для того, чтобы расти в соответствии с рынком и укреплять положение товара на рынке.
При попадании направления бизнеса в данный квадрант матрицы БКГ предприятие должно решить, есть ли сейчас достаточные ресурсы для развития товара на данном рынке (в таком случае: инвестиции направляются в развитие знания и ключевых преимуществ товара, в интенсивный прирост доли рынка). Если компания не обладает достаточными ресурсами для развития товара в данных рынках — товары не развиваются.
Второй квадрант: «звезды»
Во втором квадранте матрицы БКГ находятся направления бизнеса компании, которые являются лидерами в своей быстро растущей отрасли. Компания должна поддерживать и укреплять данный вид бизнеса, а значит не снижать, а, возможно, и увеличивать инвестиции.
На данные направления бизнеса должны быть выделены одни из лучших ресурсов компании( персонал, научные разработки, денежные средства) Данный вид бизнеса является будущим стабильным поставщиком денежных средств для компании.
Третий квадрант: «дойные коровы»
Представляет собой направления бизнеса с высокой относительной долей рынка на медленно растущих или даже стагнирующих рынках. Товары и услуги компании, представленные в данном квадранте матрицы БКГ являются основными генераторами прибылей и денежных средств.
Данные товары не требуют высоких инвестиций, только на поддержание текущего уровня продаж. Компания может использовать денежный поток от реализации таких товаров и услуг для развития своих более перспективных направлений бизнеса — «звезд» или » вопросительных знаков».
Четвертый квадрант: «собаки»
В данном квадранте матрицы БКГ сосредоточены направления бизнеса с низкой относительной долей рынка в медленно растущих или стагнирующих рынках. Данные направления бизнеса обычно приносят мало прибыли и являются неперспективными для компании. Стратегия работы с данными товарами: сокращение всех инвестиций, возможное закрытие бизнеса или его продажа.
Сбалансированный портфель по матрице БКГ
Идеальный портфель должен состоять из 2 групп товаров:
- Товаров, способных обеспечивать компанию свободными денежными ресурсами для возможности инвестирования в развитие бизнеса. (звезды и дойные коровы)
- Товаров, находящихся на стадии внедрения на рынок и на стадии роста, нуждающихся в инвестировании и способных обеспечить будущую стабильность и устойчивость компании (вопросительные знаки)
Другими словами, товары первой группы обеспечивают текущее существование компании, товары второй группы обеспечивают будущие доходы компании.
Какие формулировать выводы при анализе матрицы
Решения, которые должны быть приняты при анализе:
1. Для каждого товара в матрице БКГ должна быть принята стратегия развития. Верную стратегию помогает определить положение товаров внутри матрицы:
- Для «звезд» — сохранение лидерства
- Для «собак» — уход с рынка или снижение активности
- Для «знаков вопроса» — инвестирование или селективное развитие
- Для «дойных коров» — получение максимальной прибыли
2. Товары, попавшие в группу «собаки» должны быть исключены из портфеля в максимально быстрые сроки. Эта группа тянет компанию вниз, лишает свободных денежных средств, съедает ресурсы. Альтернативой исключения из портфеля может являться обновление и репозиционирование продукта.
3. При недостатке текущих свободных средств должны быть разработаны программы по увеличению количества «дойных коров» или «звезд» в долгосрочной перспективе, а в краткосрочной перспективе сокращен выпуск новых товаров (так как компания не в состоянии на необходимом уровне поддерживать развитие всех новинок)
4. При недостатке будущих средств необходимо вводить в портфель большее количество новых продуктов, способных стать «звездами» или «дойными коровами» в будущем
Ограничения и недостатки матрицы БКГ
- Темп роста рынка не может говорить о привлекательности отрасли в целом. Существует множество факторов влияющих на привлекательность сегмента — входные барьеры, макро и микро экономические факторы. Темп роста рынка не говорит, насколько тренд будет долгосрочным.
- Темп роста рынка не говорят о прибыльности отрасли, так как при высоких темпах роста и низких входных барьерах может возникнуть интенсивная конкуренция и ценовая конкуренция, что сделает отрасль не перспективной для компании.
- Относительная доля рынка не может говорить о конкурентоспособности товара. Относительная доя рынка — результат прошлых усилий и не гарантирует лидерство в продукте в будущем.
- Матрица БКГ предлагает правильные направления инвестирования, но не содержит тактических указаний и ограничений в реализации стратегии. Инвестирование в развитие товара без явных конкурентных преимуществ может пройти неэффективно.
Подробный видео-курс
Видео-курс «Матрица БКГ» включает 2 лекции. В результате просмотра вы получите исчерпывающую информацию о технологии построения матрицы БКГ и о правилах анализа получившихся результатов.
Часть 1: Основные элементы матрицы БКГ
Смотреть видео-курс полностью
Готовые решения
У нас есть готовый шаблон, с помощью которого вы с легкостью сможете применить теоретические знания данной статьи на практике. Скачать шаблон для построения матрицы БКГ в формате Excel можно в разделе «Полезные шаблоны по маркетингу».
comments powered by
Содержание:
- Динамика механической системы
- Геометрия масс
- Механическая система. Центр масс механической системы
- Порядок решения задач на определение центра масс механической системы
- Примеры решения задач на тему: Определение центра масс механической системы
- Моменты инерции твердого тела относительно оси
- Моменты инерции некоторых однородных тел
- Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
- Теорема о движении центра масс механической системы
- Закон сохранения движения центра масс
- Порядок решения задач на применение теоремы о движении центра масс
- Примеры решения задач на тему: Теорема о движении центра масс механической системы
- Теорема об изменении количества движения точки и механической системы
- Импульс силы
- Теорема об изменении количества движения точки и системы
- Закон сохранения количества движения системы
- Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
- Теорема об изменении момента количества движения точки и механической системы
- Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
- Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
- Теорема об изменении кинетической энергии механической системы
- Кинетическая энергия механической системы
- Определение кинетической энергии твердого тела в различных случаях его движения
- Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
- Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика механической системы
В предыдущей главе рассматривались задачи, связанные с движением материальной точки, которая находится под действием приложенных к ней сил. Однако часто приходится встречаться с такими случаями, когда движение одной точки невозможно рассматривать изолированно от движения других материальных точек. Это заставляет нас перейти к изучению движения совокупности материальных точек, или механических систем.
В механике под механической системой материальных точек или тел имеют в виду такую их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения или движения всех других.
Совокупность тел, между которыми отсутствуют силы взаимодействия и движение которых никаким образом не связано друг с другом, механическую систему не создают. Механические системы бывают свободными и несвободными.
Система материальных точек, движение которых не ограничено никакими связями, а определяется только действующими на эти точки силами, называется системой свободных точек.
Система материальных точек, движение которых ограничивается наложенными на точки связями, называется системой несвободных точек.
Решение задач динамики механической системы базируется на теоремах динамики и некоторых принципах, которые будут рассмотрены в данной главе.
Геометрия масс
Геометрия точки масс, в просторечии известная как точки масс , является проблемой геометрии – метод решения , который применяет физический принцип центра масс к геометрическим задачам, включающим треугольники и пересекающиеся чевианы . Все задачи, которые могут быть решены с использованием геометрии материальных точек, также могут быть решены с использованием аналогичных треугольников, векторов или соотношений площадей, но многие студенты предпочитают использовать массовые точки.
Механическая система. Центр масс механической системы
В механике под механической системой подразумевают совокупность взаимодействующих между собой материальных точек или тел.
Частным случаем механической системы является абсолютно твердое тело.
Массой механической системы называется сумма масс всех точек, входящих в систему:

где  – масса материальной точки с номером
– масса материальной точки с номером  ,
,
 – число всех точек системы.
– число всех точек системы.
Центром масс (центром инерции) механической системы называется точка  (рис.5.1), радиус-вектор
(рис.5.1), радиус-вектор  которой определяется по формуле:
которой определяется по формуле:

где  – масса системы материальных точек;
– масса системы материальных точек;
 – радиус-вектор точки с массой
– радиус-вектор точки с массой  .
.
Декартовы координаты центра масс системы материальных точек определяются по зависимостям:

Здесь  – координаты
– координаты  -ой материальной точки.
-ой материальной точки.

Для твердого тела центр масс совпадает с центром тяжести.
Порядок решения задач на определение центра масс механической системы
Решение задач, в которых необходимо определить положение центра масс и уравнение его траектории, рекомендуется проводить в следующей последовательности:
Выбрать систему координат.
Записать координаты центров тяжести каждой из масс системы, выразив их в виде функций времени:

Определить координаты центра масс системы по формулам (5.1), при этом  будут функциями времени, то есть, полученные выражения будут параметрическими уравнениями движения центра масс.
будут функциями времени, то есть, полученные выражения будут параметрическими уравнениями движения центра масс.
Для нахождения уравнений траектории центра масс надо с последних выражений (пункт 3) исключить время.
Примеры решения задач на тему: Определение центра масс механической системы
Задача № 1
Определить положение центра масс центробежного регулятора, изображенного на рис.5.2, если вес каждого из шаров  и
и  равен
равен  , вес муфты
, вес муфты  равен
равен  . Пули
. Пули  и
и  считать материальными точками. Массой стержней пренебречь.
считать материальными точками. Массой стержней пренебречь.
Решение. Система координат, относительно которой необходимо определить положение центра масс, изображена на рис.5.2.
Для определения положения центра масс системы надо определить его координаты по формулам (5.1):

где 
 – координаты центра масс пуль
– координаты центра масс пуль  ,
,  и муфты
и муфты  .
.
Следовательно,

Находим координаты центров масс:
пули  :
: 
пули  :
: 
муфты  :
: 
Тогда:

поскольку


Ответ: 
Задача № 2
Найти уравнение движения центра масс шарнирного параллелограмма  а также уравнение траектории его центра масс при вращении кривошипа
а также уравнение траектории его центра масс при вращении кривошипа  с постоянной угловой скоростью
с постоянной угловой скоростью  . Звенья параллелограмма – однородные стержни (рис.5.3), и
. Звенья параллелограмма – однородные стержни (рис.5.3), и 

Решение. Начало системы координат свяжем с шарниром  кривошипа
кривошипа  . Ось
. Ось  направим справа по линии
направим справа по линии  а ось
а ось  – перпендикулярно линии
– перпендикулярно линии  .
.
Поскольку звенья 1,2,3 параллелограмма однородны, то центры масс их лежат посередине звеньев (точки  ).
).
Из размеров звеньев вытекает: 
Определим координаты центров масс звеньев механизма как функции угла поворота  (рис.5.3):
(рис.5.3):

Для определения координат центра масс шарнирного параллелограмма  воспользуемся зависимостью (5.1):
воспользуемся зависимостью (5.1):


Для определения уравнения траектории центра масс (точки  ) исключим параметр
) исключим параметр  из уравнений (1) и (2). С этой целью выполним следующие преобразования:
из уравнений (1) и (2). С этой целью выполним следующие преобразования:

Сложим, соответственно, левые и правые части этих уравнений:

Таким образом, траекторией центра масс шарнирного параллелограмма является окружность:
с радиусом, равным  , с центром в точке
, с центром в точке  с координатами
с координатами 
Ответ: 

Задача № 3
Определить траекторию центра масс механизма эллипсографа (рис.5.4), который состоит из муфт  и
и  весом
весом  каждая, кривошипа
каждая, кривошипа  весом
весом  и линейки
и линейки  весом
весом  , если
, если 

Считать, что линейка и кривошип есть однородные стержни, а муфты – точечные массы.
Решение. Механизм состоит из 4 подвижных звеньев. Для удобства решения задачи пронумеруем звенья соответственно рис.5.4.
Система координат, относительно которой будет определяться траектория центра масс механизма показана на рисунке.
Сначала определим координаты центров масс всех звеньев механизма:

Для определения координат центра масс механизма эллипсографа воспользуемся формулой (5.1):

Следовательно, координаты центра масс эллипсографа имеют значения:

Для нахождения уравнения траектории центра масс в явном виде необходимо из этих уравнений исключить угол  . Решив оба уравнения относительно
. Решив оба уравнения относительно  и
и  , возводя их затем к квадрату и сложив, получим:
, возводя их затем к квадрату и сложив, получим:

Траекторией центра масс является окружность с центром в точке  и радиусом
и радиусом  , который равен:
, который равен:

Ответ: 
Задача № 4
Определить зависимость от угла поворота кривошипа  координат центра масс кривошипно-ползунного механизма, что изображено на рис.5.5. Длина кривошипа
координат центра масс кривошипно-ползунного механизма, что изображено на рис.5.5. Длина кривошипа  , его вес
, его вес  , длина шатуна
, длина шатуна  , его вес
, его вес  , вес ползуна
, вес ползуна  .
.
Решение. Выберем систему координат  как показано на рис.5.5. Рассмотрим механизм в произвольном положении, которое определяется углом
как показано на рис.5.5. Рассмотрим механизм в произвольном положении, которое определяется углом  (для любого положения
(для любого положения  , так как
, так как  ).
).
Применяя формулу (5.1), получим:

где  – координаты центров тяжести тел, составляющих систему,
– координаты центров тяжести тел, составляющих систему,
 – масса всей системы.
– масса всей системы.
С рис.5.5 находим:

Масса всей системы в данном случае равна:

Подставляя в выражения (1) и (2) значения координат центров масс тел механической системы и величину массы системы  , получим:
, получим:

Ответ: 
Задача № 5
Определить уравнение траектории центра масс кулисного механизма (рис.5.6), если вес кривошипа  равен
равен  , вес ползуна
, вес ползуна  равен
равен  , а вес кулисы и штанги
, а вес кулисы и штанги  равен
равен  . Кривошип, который вращается с постоянной угловой скоростью
. Кривошип, который вращается с постоянной угловой скоростью  , считать тонким однородным стержнем, а ползун
, считать тонким однородным стержнем, а ползун  – точечной массой. Центр тяжести кулисы и штанги расположен в точке
– точечной массой. Центр тяжести кулисы и штанги расположен в точке  , причем
, причем  . При расчетах принять:
. При расчетах принять:

Будем считать, что в начальный момент ползун  занимал крайнее правое положение.
занимал крайнее правое положение.
Решение. Выберем оси декартовых координат, как показано на рисунке, где положение кулисного механизма соответствует моменту времени  . Так как кривошип вращается равномерно, то его угол поворота равен
. Так как кривошип вращается равномерно, то его угол поворота равен 
Для определения положения центра масс системы  необходимо найти его координаты
необходимо найти его координаты  и
и  по формуле (5.1).
по формуле (5.1).
Поскольку механическая система состоит из трех тел – кривошипа  , ползуна
, ползуна  и кулисы со штангой
и кулисы со штангой  , то:
, то:

Индекс 1 соответствует кривошипу, индекс 2 – ползуну  , индекс 3 – кулисе со штангой.
, индекс 3 – кулисе со штангой.

Из рисунка видно:

Подставим значения  в формулы для определения
в формулы для определения  и
и  .
.

Исключим время  в уравнениях, которые определяют движение центра масс.
в уравнениях, которые определяют движение центра масс.
Для этого решим оба уравнения относительно  и
и  :
:

Возведем эти уравнения к квадрату и добавим:

Таким образом, траекторией центра масс кулисного механизма является эллипс с полуосями  и
и 
Центр эллипса лежит на оси  и отдален от начала координат
и отдален от начала координат  вправо на расстояние
вправо на расстояние 
Ответ: 
Моменты инерции твердого тела относительно оси
Влияние собственных свойств тела на вращательное движение значительно сложнее, чем в поступательном движении.
Также как масса тела является мерой инертности тела при его поступательном движении, так и момент инерции тела относительно данной оси является мерой инертности тела при его вращательном движении.
Как мера инертности тела момент инерции входит во все формулы вращательного движения. Не зная момента инерции тела, не умея его определить, нельзя решать задачи, которые связаны с вращательным или сложным движением тела, частью которого является вращательное движение.
Момент инерции тела (системы) относительно оси, например  , обозначим
, обозначим  (индекс указывает на ось, относительно которой определяется момент инерции).
(индекс указывает на ось, относительно которой определяется момент инерции).
Моментом инерции тела относительно оси, например  , называется скалярная величина, равная сумме произведений масс точек тела на квадраты их расстояний к оси:
, называется скалярная величина, равная сумме произведений масс точек тела на квадраты их расстояний к оси:

Если тело сплошное, то под  необходимо понимать массу элементарной частицы тела
необходимо понимать массу элементарной частицы тела  , тогда момент инерции будет выражаться интегралом:
, тогда момент инерции будет выражаться интегралом:

где  – расстояние доли
– расстояние доли  от оси.
от оси.
Этот интеграл берется по всей массе тела. Очевидно, что величина момента инерции зависит от размеров и формы тела , а также от закона распределения массы в теле.
Момент инерции измеряется в системе СИ – в  , в технической системе – в
, в технической системе – в  .
.
Для тел правильной геометрической формы определение моментов инерции делается с помощью интегрального вычисления. Если тело имеет неправильную форму, то момент инерции его определяется либо приблизительно, путем разбития тела на несколько тел, которые имеют правильную геометрическую форму, либо экспериментально.
Для однородного тела, при плотности  :
:

где интеграл берется по всему объему тела.
Для однородной материальной поверхности:

где  – масса единицы плоскости поверхности и интеграл берется по всей плоскости поверхности.
– масса единицы плоскости поверхности и интеграл берется по всей плоскости поверхности.
Для однородной материальной линии:

где  – масса единицы длины линии. Интеграл берется по длине
– масса единицы длины линии. Интеграл берется по длине  .
.
Для одной материальной точки, которая находится на расстоянии  от оси, момент инерции равен:
от оси, момент инерции равен:

Иногда при определении момента инерции тела пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси, например  , называется линейная величина
, называется линейная величина  , определяемая равенством:
, определяемая равенством:

где  – масса тела.
– масса тела.
Следовательно, радиус инерции определяет расстояние от оси  к точке, в которой необходимо сосредоточить всю массу
к точке, в которой необходимо сосредоточить всю массу  тела, чтобы момент инерции точки относительно этой оси равнялся моменту инерции тела.
тела, чтобы момент инерции точки относительно этой оси равнялся моменту инерции тела.
Момент инерции системы относительно начала координат равен

Моменты инерции относительно координатных осей (осевые моменты) выражаются зависимостями:

Существует простая зависимость между моментами инерции тела относительно параллельных осей, одна из которых проходит через его центр масс (теорема Гюйгенса-Штейнера).
Момент инерции тела относительно любой оси равен моменту инерции тела относительно оси, проходящей через центр масс тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями:

где  – момент инерции тела относительно оси, которая проходит через центр масс и параллельна данной;
– момент инерции тела относительно оси, которая проходит через центр масс и параллельна данной;
 – момент инерции тела относительно данной оси;
– момент инерции тела относительно данной оси;
 – расстояние между осями.
– расстояние между осями.
Из выражения (5.4) вытекает, что наименьшим момент инерции тела будет относительно той оси, которая проходит через центр его масс.
Моменты инерции некоторых однородных тел
| Форма тела. | Схема тела. | Момент инерции. |
| Тонкий прямолинейный стержень |  |
 |
| -„- |  |
 |
| Круглая пластинка малой толщины |  |
 |
| Кольцо (материальная окружность) |  |
 |
| Круглый цилиндр |  |
 |
| Прямоугольный параллелепипед |  |
 |
| Полый шар со стенками малой толщины |  |
 |
| Шар |  |
 |
Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
Задача №1
Маятник, изображенный на рис. 5.7, состоит из тонкого однородного стержня длиной  и массой
и массой  и круглого однородного диска с радиусом
и круглого однородного диска с радиусом  и массой
и массой 

Определить момент инерции  относительно оси его вращения
относительно оси его вращения  (ось
(ось  направлена перпендикулярно плоскости рисунка).
направлена перпендикулярно плоскости рисунка).
Решение. Маятник состоит из двух тел: стержня и диска, поэтому

где  и
и  моменты инерции относительно оси
моменты инерции относительно оси  стержня и диска, соответственно.
стержня и диска, соответственно.
Момент инерции стержня равен (см. 5.5):

Момент инерции диска найдем по формуле (5.4):

где  – момент инерции диска относительно оси, которая проходит параллельно оси
– момент инерции диска относительно оси, которая проходит параллельно оси  через его центр масс, точку
через его центр масс, точку  , а расстояние от центра масс к оси
, а расстояние от центра масс к оси  –
– 
Итак

Пользуясь выражениями для моментов инерции стержня (2) и диска (3), найдем момент инерции маятника относительно оси  :
:

После подстановки в выражение (4) числовых данных, получим:

Ответ: 
Задача №2.
Определить момент инерции  стального вала радиуса
стального вала радиуса  см и массой
см и массой  относительно его образующей. Вал считать однородным сплошным цилиндром (рис.5.8).
относительно его образующей. Вал считать однородным сплошным цилиндром (рис.5.8).

Решение. Для определения момента инерции стального вала относительно оси  , надо воспользоваться формой Гюйгенса-Штейнера
, надо воспользоваться формой Гюйгенса-Штейнера

где  – момент инерции относительно оси
– момент инерции относительно оси  , которая проходит через центр масс тела.,
, которая проходит через центр масс тела.,
 – масса вала,
– масса вала,
 – расстояние между осями, равное радиусу вала.
– расстояние между осями, равное радиусу вала.

Тогда

Ответ: 
Задача № 3
Определить осевые моменты инерции  и
и  изображенной на рис.5.9 однородной прямоугольной пластинки весом
изображенной на рис.5.9 однородной прямоугольной пластинки весом  .
.

Решение. Определим момент инерции пластинки относительно оси  . Для этого выделим на расстоянии
. Для этого выделим на расстоянии  полоску шириной
полоску шириной  .
.
Момент инерции этой тонкой полоски относительно оси  равен:
равен:

где  – масса полоски.
– масса полоски.
Масса полоски равна:

где  – площадь полоски;
– площадь полоски;
 – масса единицы площади поверхности пластинки.
– масса единицы площади поверхности пластинки.
Тогда:

а момент инерции всей пластинки будет равен сумме моментов инерции всех полосок, на которые можно разбить пластинку:

При предельном переходе, то есть, когда 

Итак,

Вычислим массу пластинки:

Таким образом

Момент инерции пластинки относительно оси  находим аналогичным путем и получим:
находим аналогичным путем и получим:

Ответ: 
Задача №4
Определить момент инерции относительно оси 
 однородного прямоугольного параллелепипеда весом
однородного прямоугольного параллелепипеда весом  (рис.5.10).
(рис.5.10).
Решение. Выделим элементарный параллелепипед со сторонами основания  и высотой
и высотой  Расстояние элементарного параллелепипеда от осей
Расстояние элементарного параллелепипеда от осей  и
и  равно
равно  и
и  соответственно.
соответственно.
Момент инерции элементарного параллелепипеда относительно оси  равен:
равен:

где:  – масса элементарного параллелепипеда, равна:
– масса элементарного параллелепипеда, равна:


Тогда, 
а момент инерции всего параллелепипеда

При предельном переходе, то есть при  то сумма, которая стоит справа, переходит в двойной интеграл:
то сумма, которая стоит справа, переходит в двойной интеграл:

Вычислим двойной интеграл:

Масса параллелепипеда:

Следовательно,

Ответ: 
Задача №5
Определить момент инерции относительно оси  тонкой однородной параболической пластинки (рис.5.11) массой
тонкой однородной параболической пластинки (рис.5.11) массой  . Предельная прямая пластинки параллельна оси
. Предельная прямая пластинки параллельна оси  и удалена от нее на расстояние
и удалена от нее на расстояние  . Уравнение параболы, которая ограничивает пластинку, имеет вид
. Уравнение параболы, которая ограничивает пластинку, имеет вид 

Решение. Проведем на пластинке (рис.5.11) две прямые, параллельные оси  и удаленные от нее на расстоянии
и удаленные от нее на расстоянии  и
и 
Вычислим момент инерции относительно оси  элементарной полоски, которая ограничена этими прямыми и параболическим контуром пластинки (заштрихована на рисунке):
элементарной полоски, которая ограничена этими прямыми и параболическим контуром пластинки (заштрихована на рисунке):

где  – элементарная масса плоскости, которая равна:
– элементарная масса плоскости, которая равна:

Здесь  – плотность пластинки,
– плотность пластинки,
 – площадь пластинки.
– площадь пластинки.
Итак,

Из уравнения  вытекает
вытекает 
Таким образом

Момент инерции пластинки относительно оси  равен:
равен:

Масса пластинки 
где площадь пластинки 
Тогда

Следовательно,

Ответ: 
Задача №6
Определить для тонкого равнобедренного треугольника  , основание которого равно
, основание которого равно  , высота
, высота  и масса
и масса  (рис.5.12), его моменты инерции относительно основания и относительно высоты.
(рис.5.12), его моменты инерции относительно основания и относительно высоты.

Решение. С серединой  основания равнобедренного треугольника свяжем начало системы координат
основания равнобедренного треугольника свяжем начало системы координат  ; ось
; ось  проведем по основанию
проведем по основанию  , а ось
, а ось  – перпендикулярно основанию.
– перпендикулярно основанию.
Для определения момента инерции треугольника относительно основания (относительно оси  ) выделим на расстоянии
) выделим на расстоянии  элементарную полоску шириной
элементарную полоску шириной  .
.
Момент инерции этой полоски относительно оси  составит:
составит:

где  , масса полоски длиной
, масса полоски длиной  , равна:
, равна:

Тогда момент инерции элементарной полоски относительно основания будет равен:

Найдем зависимость между координатой  и длиной полоски
и длиной полоски  . Из сходства треугольников
. Из сходства треугольников  и
и  (рис.5.12) следует:
(рис.5.12) следует:
 или
или 
откуда

Подставив (2) у (1’), получим:

а момент инерции треугольника  относительно основания определится как
относительно основания определится как

или

В интеграле (3) границы координаты  меняются от
меняются от  к
к  .
.
Высчитаем интеграл (3):

Выразим момент инерции  через массу
через массу  треугольника
треугольника  :
:

Преобразуем выражение (4):

или

Перейдем к определению момента инерции треугольника  относительно его высоты
относительно его высоты  .
.
Поскольку у треугольника  высота
высота  является осью симметрии, то достаточно определить момент инерции относительно этой оси для прямоугольного треугольника
является осью симметрии, то достаточно определить момент инерции относительно этой оси для прямоугольного треугольника  , тогда
, тогда

где  – момент инерции треугольника
– момент инерции треугольника  ;
;
 – момент инерции треугольника
– момент инерции треугольника  .
.
Расчетная схема для определения момента инерции  приведена на рис.5.13.
приведена на рис.5.13.

Выделим элементарную полоску на расстоянии  от оси
от оси  , ширина полоски –
, ширина полоски –  , длина –
, длина –  .
.
Определим момент инерции этой полоски относительно оси  :
:

где  – масса элементарной полоски.
– масса элементарной полоски.
Определим зависимость между длиной полоски  и координатой
и координатой  . Из сходства треугольников
. Из сходства треугольников  и
и  получается:
получается:
 или
или 
откуда

Подставив (6) у (5), получим:

Момент инерции треугольника  относительно оси
относительно оси  (относительно высоты
(относительно высоты  ), равен:
), равен:

или

Определим интеграл (7):

Окончательно,

Тогда, момент инерции треугольника  относительно высоты
относительно высоты  будет равен:
будет равен:

Ответ: 
Задачи, которые рекомендуются для самостоятельной работы: 34.9, 34.12, 34.16 [2].
Теорема о движении центра масс механической системы
Силы, действующие на механическую систему, можно условно поделить на внешние и внутренние.
Силы, которые действуют на точки данной механической системы со стороны точек или тел, не входящих в эту систему, называются внешними.
Силы, действующие на точки механической системы со стороны точек данной системы, называются внутренними.
Внешние силы обозначаются верхним индексом  , внутренние –
, внутренние –  :
:  -внешняя сила,
-внешняя сила,  – внутренняя сила.
– внутренняя сила.
Внутренние силы обладают следующими свойствами:
а) геометрическая сумма (главный вектор) внутренних сил равна нулю:

б) геометрическая сумма моментов (главный момент) всех внутренних сил относительно любого центра  или оси равна нулю:
или оси равна нулю:


Теорема о движении центра масс механической системы формулируется следующим образом:
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех внешних сил, действующих на систему.

где  – масса системы;
– масса системы;
 – ускорение центра масс;
– ускорение центра масс;
 – сумма внешних сил, которые действуют на систему.
– сумма внешних сил, которые действуют на систему.
Из сравнения приведенной выше формулы со вторым законом динамики, который, как известно, записан для материальной точки:

можно сделать следующий вывод:
Центр масс механической системы движется как материальная точка, в которой сосредоточено массу всей системы и к которой приложены те же внешние силы, действующие на систему.
Теорема о движении центра масс системы, если ее записать в проекциях на оси декартовой системы координат, имеет вид:

где  – координаты центра масс механической системы.
– координаты центра масс механической системы.
Из приведенных уравнений следует, что внутренние силы непосредственно не влияют на движение центра масс. Теорема позволяет исключить из рассмотрения все ранее неизвестные внутренние силы.
Задачи динамики поступательного движения твердого тела решаются с помощью теоремы о движении центра масс системы материальных точек.
Действительно, применив эту теорему, мы определим уравнение траектории, скорость и ускорение центра тяжести твердого тела. При поступательном движении твердого тела траектории всех его точек одинаковы, одинаковы и их скорости и ускорения.
Закон сохранения движения центра масс
Из теоремы о движении центра масс вытекает несколько следствий:
а) если геометрическая сумма всех внешних сил, действующих на систему, равна нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
Пусть  , тогда
, тогда
 или
или  , поэтому
, поэтому 
Если изначально центр масс был в покое, то он и останется в покое. Если же начальная скорость не равна нулю, то центр масс движется прямолинейно и равномерно с этой скоростью;
б) если геометрическая сумма внешних сил, действующих на систему, не равна нулю, но сумма их проекций на какую-нибудь ось (например, ось  ) равна нулю, то центр масс системы вдоль этой оси или не движется, или движется равномерно.
) равна нулю, то центр масс системы вдоль этой оси или не движется, или движется равномерно.
Если  , то:
, то:
 или
или  , поэтому
, поэтому 
Если при этом равна нулю начальная скорость, то есть  , то
, то  , то есть
, то есть 
Таким образом видим, что в этом случае координата центра масс  механической системы во время ее движения остается неизменной.
механической системы во время ее движения остается неизменной.
При  проекция центра масс на ось
проекция центра масс на ось  движется равномерно.
движется равномерно.
Все эти результаты выражают законы сохранения движения центра масс системы.
Порядок решения задач на применение теоремы о движении центра масс
Рекомендуется такая последовательность решения задач:
Изобразить на рисунке все внешние силы, действующие на систему;
Выбрать систему координат;
Записать теорему о движении центра масс в векторной форме;
Спроектировать это векторное уравнение на оси координат;
Высчитать суммы проекций всех внешних сил на оси координат и подставить их в проекции уравнения движения;
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема о движении центра масс механической системы
Задача № 1
Определить главный вектор внешних сил, действующих на колесо весом  , которое скатывается без скольжения с наклонной плоскости, если его центр масс
, которое скатывается без скольжения с наклонной плоскости, если его центр масс  движется по закону
движется по закону  (рис.6.1).
(рис.6.1).

Решение. Покажем внешние силы, которые действуют на колесо: силу тяжести  и реакцию поверхности
и реакцию поверхности  , которые проходят через центр масс колеса
, которые проходят через центр масс колеса  .
.
Запишем теорему о движении центра масс в векторной форме:

Выбираем систему координат  и спроектируем уравнение (1) на оси
и спроектируем уравнение (1) на оси  и
и  :
:

Поскольку  . то
. то  и
и  . То есть, главный вектор внешних сил является параллельным оси
. То есть, главный вектор внешних сил является параллельным оси  :
:

Найдем проекцию ускорения центра масс на ось  :
:

Итак,

Ответ: 
Задача №2
Колесо весом  и радиусом
и радиусом  катится со скольжением по прямолинейной горизонтальной рейке в результате действия постоянной силы
катится со скольжением по прямолинейной горизонтальной рейке в результате действия постоянной силы  , которая приложена к его центру тяжести
, которая приложена к его центру тяжести  (рис.6.2).
(рис.6.2).

Определить скорость центра масс колеса, если в начальный момент оно находилось в покое. Коэффициент трения скольжения равен  .
.
Решение. На колесо действуют внешние силы:  – сила тяжести колеса,
– сила тяжести колеса,  – движущая сила,
– движущая сила,  – нормальная реакция рейки,
– нормальная реакция рейки,  – сила трения скольжения, которая направлена вдоль рельса в сторону, противоположную силе
– сила трения скольжения, которая направлена вдоль рельса в сторону, противоположную силе  .
.
Запишем теорему о движении центра масс колеса в векторной форме:

где  – ускорение центра масс колеса.
– ускорение центра масс колеса.
Спроектируем это уравнение на оси координат  :
:

Во время движения колеса  Итак
Итак  из второго уравнения (1) получаем:
из второго уравнения (1) получаем:

Поскольку при качении колеса со скольжением сила трения достигает своего максимального значения, то

Подставим (3) в первое из уравнений (1) и получим:

Поскольку

то

Согласно начальным условиям при  с тех пор находим, что произвольная постоянная
с тех пор находим, что произвольная постоянная 
Итак, закон изменения скорости центра масс колеса  имеет вид:
имеет вид:

Ответ: 
Задача №3
На однородную призму  , которая лежит на горизонтальной плоскости, положили однородную призму
, которая лежит на горизонтальной плоскости, положили однородную призму  (рис.6.3,а), поперечные сечения призм – прямоугольные треугольники, вес призмы
(рис.6.3,а), поперечные сечения призм – прямоугольные треугольники, вес призмы  втрое больше веса призмы
втрое больше веса призмы  . Необходимые размеры показаны на рисунке.
. Необходимые размеры показаны на рисунке.
Определить длину  , на которую передвинется призма
, на которую передвинется призма  , когда призма
, когда призма  , спускаясь по поверхности призмы
, спускаясь по поверхности призмы  , дойдет к горизонтальной плоскости. Предположить, что все поверхности, которые соприкасаются, идеально гладкие.
, дойдет к горизонтальной плоскости. Предположить, что все поверхности, которые соприкасаются, идеально гладкие.
Решение. Рассмотрим движение механической системы, состоящей из 2-х призм  и
и  . Призма
. Призма  , спускаясь по призме
, спускаясь по призме  справа, как будто выжимает ее, отодвигает налево (рис.6.3, б).
справа, как будто выжимает ее, отодвигает налево (рис.6.3, б).
Для решения этой задачи применим теорему о движении центра масс.
На систему действуют внешние силы: тяжести  призмы
призмы  , тяжести
, тяжести  призмы
призмы  , нормальная реакция плоскости
, нормальная реакция плоскости  (рис.6.3). Внешняя сила трения призм по идеально гладкой поверхности равна нулю.
(рис.6.3). Внешняя сила трения призм по идеально гладкой поверхности равна нулю.
Таким образом, все внешние силы системы вертикальны. Внутренние силы системы (давление призмы  на призму
на призму  , реакция на это давление, а также силы трения между призмами
, реакция на это давление, а также силы трения между призмами  и
и  ), нас не интересуют.
), нас не интересуют.
Введем систему координат  , ось
, ось  направим по горизонтали справа и запишем теорему о движении центра масс системы в проекции на ось
направим по горизонтали справа и запишем теорему о движении центра масс системы в проекции на ось  :
:

Поскольку внешние силы перпендикулярны оси  , то
, то

Тогда

где  – постоянная интегрирования.
– постоянная интегрирования.
В начальный момент времени система находилась в состоянии покоя, то есть скорость центра масс  Итак,
Итак, 
Из этого следует, что  , то есть, абсцисса центра масс, независимо от перемещения призм, остается постоянной.
, то есть, абсцисса центра масс, независимо от перемещения призм, остается постоянной.

Запишем выражение для определения координаты центра масс в начале движения:

где  – абсцисса центра масс призмы
– абсцисса центра масс призмы  ,
,
 – абсцисса центра масс призмы
– абсцисса центра масс призмы  .
.
Выражение для определения координаты центра масс системы, когда призма  опускается по боковой грани призмы
опускается по боковой грани призмы  к горизонтальной плоскости:
к горизонтальной плоскости:

где  – новое значение абсциссы центра масс призмы
– новое значение абсциссы центра масс призмы  ,
,
 – новое значение абсциссы центра масс призмы
– новое значение абсциссы центра масс призмы  .
.
Поскольку  , то
, то

или

Перепишем это уравнение следующим образом:

Найдем перемещение центров масс призм  и
и  :
:

Присутствие слагаемого ( ) в последнем уравнении учитывает перемещение призмы
) в последнем уравнении учитывает перемещение призмы  вместе с призмой
вместе с призмой  слева на величину
слева на величину  .
.
Подставим значение перемещений в уравнение (1):
 .
.
Решим это уравнение относительно  , имея в виду, что
, имея в виду, что  :
:

Ответ: 
Задача №4
Три груза (рис.6.4), весом  соединенные невесомой нитью, которая не растягивается, и которая перекинута через неподвижные блоки
соединенные невесомой нитью, которая не растягивается, и которая перекинута через неподвижные блоки  и
и  . Во время опускания груза 1 вниз груз 2 перемещается по верхнему основанию четырехугольной усеченной пирамиды
. Во время опускания груза 1 вниз груз 2 перемещается по верхнему основанию четырехугольной усеченной пирамиды  весом
весом  справа, а груз 3 поднимается по боковой грани
справа, а груз 3 поднимается по боковой грани  вверх. Пренебрегая трением между срезанной пирамидой
вверх. Пренебрегая трением между срезанной пирамидой  и полом, определить перемещение
и полом, определить перемещение  усеченной пирамиды
усеченной пирамиды  относительно пола, если груз
относительно пола, если груз  опустится на
опустится на 
Решение. Изобразим все внешние силы, которые приложены к материальной системе, состоящей из пирамиды и трех грузов (рис.6.4). Внешними силами являются:  – сила тяжести пирамиды;
– сила тяжести пирамиды;  – силы тяжести грузов;
– силы тяжести грузов;  – нормальная реакций
– нормальная реакций

горизонтальной плоскости. Направим ось  по горизонтали справа и запишем теорему о движении центра масс системы материальных точек в проекции на эту ось:
по горизонтали справа и запишем теорему о движении центра масс системы материальных точек в проекции на эту ось:

Поскольку все внешние силы перпендикулярны оси  , то
, то 
Следовательно, 
тогда

В начальный момент времени система была в состоянии покоя, то есть  , поэтому
, поэтому 
Поскольку

то

Таким образом, абсцисса центра масс системы не зависит от перемещений грузов, входящих в систему, и остается неизменной относительно неподвижной системы координат  .
.
Запишем выражение для определения  для начального момента времени, когда грузы находились в состоянии покоя:
для начального момента времени, когда грузы находились в состоянии покоя:

где  – абсциссы центров масс пирамиды
– абсциссы центров масс пирамиды  и грузов 1,2 и 3.
и грузов 1,2 и 3.
Если груз 1 опустится на величину  при неподвижной пирамиде, то координата
при неподвижной пирамиде, то координата  при этом не изменится. Тогда груз 2 переместится вправо на величину
при этом не изменится. Тогда груз 2 переместится вправо на величину  и координата его центра масс будет равна
и координата его центра масс будет равна  . Груз 3 тоже подвинется по наклонной поверхности
. Груз 3 тоже подвинется по наклонной поверхности  на величину
на величину  , при этом по направлению оси
, при этом по направлению оси  его положение изменится на величину
его положение изменится на величину  и координата центра масс будет
и координата центра масс будет  . То есть, относительно пирамиды центр масс системы изменит свое положение, но не изменит его относительно неподвижной системы координат, поскольку должен выполняться закон сохранения движения центра масс. И тогда пирамида должна переместиться налево на некоторую величину
. То есть, относительно пирамиды центр масс системы изменит свое положение, но не изменит его относительно неподвижной системы координат, поскольку должен выполняться закон сохранения движения центра масс. И тогда пирамида должна переместиться налево на некоторую величину  .
.
Грузы 1,2 и 3 вместе с пирамидой также переместятся влево на расстояние  , и новые координаты всех центров масс будут равны:
, и новые координаты всех центров масс будут равны:

Запишем выражение для определения положения абсциссы центра масс для нового положения системы:

Поскольку  то
то

После приведения подобных получим:

или

Окончательно

После подстановки числовых величин, получим:

Ответ: 
Задача № 5
Электрический двигатель весом  с горизонтальным валом без всяких креплений установлен на гладком горизонтальном фундаменте.
с горизонтальным валом без всяких креплений установлен на гладком горизонтальном фундаменте.
На валу электродвигателя (рис.6.5) под прямым углом закреплен одним концом однородный стержень  длиной
длиной  и весом
и весом  , на второй конец стержня насажен точечный груз
, на второй конец стержня насажен точечный груз  весом
весом  ; угловая скорость вала равна
; угловая скорость вала равна  .
.
Определить:
Закон горизонтального движения электродвигателя;
Угловую скорость вала электродвигателя, при которой электродвигатель будет «подскакивать» над фундаментом;
Наибольшее горизонтальное усилие  , которое действует на болты, если ими закреплен корпус электродвигателя на фундаменте.
, которое действует на болты, если ими закреплен корпус электродвигателя на фундаменте.
Решение. Будем рассматривать электромотор, стержень и груз как одну механическую систему. Внешними силами, которые действуют на эту систему, являются: сила тяжести электродвигателя  , сила тяжести стержня
, сила тяжести стержня  , сила тяжести груза
, сила тяжести груза  , а также реакции фундамента
, а также реакции фундамента  и
и  . Все эти силы вертикальны.
. Все эти силы вертикальны.

Начало неподвижной системы координат возьмем в точке  , соответствующей положению центра вала электродвигателя, когда стержень направлен вертикально вверх (рис.6.5, а).
, соответствующей положению центра вала электродвигателя, когда стержень направлен вертикально вверх (рис.6.5, а).
Поскольку проекция на ось  главного вектора действующих на систему внешних сил равна нулю, то дифференциальное уравнение движения центра масс системы вдоль оси
главного вектора действующих на систему внешних сил равна нулю, то дифференциальное уравнение движения центра масс системы вдоль оси  имеет вид:
имеет вид:

где  – масса системы.
– масса системы.
В нашем случае  или
или

Тогда дифференциальное уравнение движения центра масс (1) приводится к виду:

откуда 
Предполагая, что в начальный момент скорость центра масс системы равна нулю, то есть, при пуске электродвигателя он был неподвижным, получим 
Следовательно,  , то есть, центр масс системы не перемещается вдоль оси
, то есть, центр масс системы не перемещается вдоль оси  .
.
Поскольку в начальный момент времени центр масс системы находится на оси  (то есть,
(то есть,  ), то и в любой момент времени
), то и в любой момент времени 
При вращении стержня координаты центров масс электрического двигателя, стержня и груза  будут варьироваться.
будут варьироваться.
Предположим, что в некоторый момент времени  координата центра масс мотора станет равной
координата центра масс мотора станет равной  , тогда координаты центров масс стержня и груза
, тогда координаты центров масс стержня и груза  будут равны
будут равны  и
и  (рис.6.5,b).
(рис.6.5,b).
Поскольку все время  , то
, то

где  На рисунке 6.5,b показан момент, когда координата
На рисунке 6.5,b показан момент, когда координата  отрицательна.
отрицательна.
Тогда

откуда

и, следовательно:

Таким образом, центр электродвигателя совершает гармонические колебания вдоль оси  с амплитудой, равной:
с амплитудой, равной:

и периодом

Определим угловую скорость вала, при которой электродвигатель будет «подскакивать» над фундаментом.
Для этого составим дифференциальное уравнение движения центра масс системы вдоль оси  :
:

или

где  – суммарная реакция фундамента.
– суммарная реакция фундамента.
Значение  найдем из выражения для координаты центра масс:
найдем из выражения для координаты центра масс:

поскольку

Последнее уравнение перепишем в виде:

Возьмем из обеих частей равенства вторую производную по времени

Из уравнений (2) и (3) вытекает, что

итак,

Минимальное значение реакции фундамента будет при  :
:

Если  , то это значит, что электромотор не прижимается к фундаменту. Итак, искомое значение угловой скорости, при которой электродвигатель начинает “подскакивать” над фундаментом, найдем из условия
, то это значит, что электромотор не прижимается к фундаменту. Итак, искомое значение угловой скорости, при которой электродвигатель начинает “подскакивать” над фундаментом, найдем из условия

откуда

В завершение определим наибольшее горизонтальное усилие  , которое действует на болты, если ими будет закреплен корпус электродвигателя на фундаменте.
, которое действует на болты, если ими будет закреплен корпус электродвигателя на фундаменте.
На рис.6.5 штрих-пунктирными линиями показаны оси болтов и горизонтальные реакции болтов  и
и  .
.
В этом случае дифференциальное уравнение движения центра масс системы вдоль оси  будет:
будет:

Значение  найдем по формуле:
найдем по формуле:

или

Тогда

При этом уравнение (4) принимает вид:

Из последнего уравнения выходит:

Таким образом, максимальное горизонтальное усилие, действующее на болты, будет при  :
:

Ответ:

Задачи, которые рекомендуются для самостоятельной работы: 35.1; 35.6; 35.10; 35.20 [2].
Теорема об изменении количества движения точки и механической системы
Теорема об изменении количества движения (импульса) системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает количество движения с импульсом внешних сил, действующих на тела, составляющие систему.
Импульс силы
Для характеристики действия силы за некоторый промежуток времени вводится понятие импульса силы.
Если сила  – постоянная, то импульс силы
– постоянная, то импульс силы  равен
равен

Направление импульса силы  совпадает с направлением
совпадает с направлением  .
.
Единица измерения импульса в системе СИ –  , в системе МкГс –
, в системе МкГс –  .
.
Если сила  переменная, то импульс силы за конечный промежуток времени
переменная, то импульс силы за конечный промежуток времени  определяется как интеграл:
определяется как интеграл:

Импульс силы – сложная физическая величина, которая одновременно учитывает влияние модуля, направления и времени действия силы на изменение состояния движения тела.
Модуль импульса силы можно определить через его проекции на оси координат:

где  – проекции силы;
– проекции силы;
 – проекции импульса на оси координат.
– проекции импульса на оси координат.
Углы между вектором  и осями координат определяются из следующих соотношений:
и осями координат определяются из следующих соотношений:

Теорема об изменении количества движения точки и системы
Одной из мер движения точки является количество ее движения.
Количеством движения точки называется вектор  , который равен произведению массы
, который равен произведению массы  точки на ее скорость
точки на ее скорость  и направлен по вектору скорости:
и направлен по вектору скорости:
 .
.
Понятие количества движения было введено в механику Декартом и положено в основу механики Ньютоном.
Единица измерения количества движения в системе СИ –  , в системе МкГс –
, в системе МкГс –  .
.
Если спроектировать вектор количества движения на оси координат, то ее проекции определяются следующим образом:

Теорема об изменении количества движения точки в дифференциальной форме имеет вид:

Производная по времени от количества движения материальной точки равна геометрической сумме всех сил, действующих на эту точку.
Теорема об изменении количества движения точки в интегральной форме:

Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех сил, которые приложены к точке.
Векторному уравнению (7.1) соответствуют три уравнения в проекциях на оси координат:

Большинство практических задач решается с использованием выражения (7.2).
Количеством движения механической системы называется векторная величина  , равная геометрической сумме (главному вектору) количеств движения всех точек этой системы.
, равная геометрической сумме (главному вектору) количеств движения всех точек этой системы.

Найти  можно путем построения многоугольника количеств движения всех точек системы (рис.7.1).
можно путем построения многоугольника количеств движения всех точек системы (рис.7.1).
Замыкающая сторона векторного многоугольника будет представлять собой вектор  .
.
Величина  может быть какой угодно, даже равняться нулю, когда многоугольник, построенный из векторов
может быть какой угодно, даже равняться нулю, когда многоугольник, построенный из векторов  , оказывается замкнутым.
, оказывается замкнутым.

Формулу (7.3) можно записать в виде:

где  – масса всей системы;
– масса всей системы;
 – скорость центра масс системы.
– скорость центра масс системы.
Из этой формулы следует, что количество движения системы равно нулю, когда скорость центра масс равна нулю. Например, если тело вращается вокруг неподвижной оси, которая проходит через его центр масс, то количество движения тела равно нулю.
В случае, когда колесо катится, вектор  характеризует только поступательную часть плоского движения колеса.
характеризует только поступательную часть плоского движения колеса.
Теорема об изменении количества движения системы в дифференциальной форме выразится формулой:

где  – главный вектор всех внешних сил, которые действуют на механическую систему.
– главный вектор всех внешних сил, которые действуют на механическую систему.
Производная по времени от количества движения механической системы равна геометрической сумме всех действующих на точки системы внешних сил.
В проекциях на оси координат уравнение (7.5) соответствует уравнениям:

В интегральной форме теорема об изменении количества движения системы имеет вид:

где  – количество движения системы в начальный момент времени.
– количество движения системы в начальный момент времени.
 – количество движения системы в конечный момент времени.
– количество движения системы в конечный момент времени.
Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, которые действуют на систему за тот же промежуток времени.
Векторному уравнению (7.7) соответствуют три уравнения в проекциях на оси координат:

Практическая ценность теоремы заключается в том, что она позволяет исключить из рассматривания неизвестные внутренние силы.
Закон сохранения количества движения системы
Выводы из теоремы об изменении количества движения системы, которые еще имеют название законов сохранения количества движения:
1. Если главный вектор внешних сил, действующих на систему, равен нулю, то вектор количества движения системы не меняется:
если 
то  и
и 
2. Если сумма проекций внешних сил на какую-либо ось, например  , равна нулю, то проекция количества движения системы на эту ось сохраняется постоянной:
, равна нулю, то проекция количества движения системы на эту ось сохраняется постоянной:
если 
то  и
и 
Эти результаты выражают законы сохранения количества движения системы. Из них вытекает, что внутренние силы не могут изменить количество движения системы.
Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
Для материальной точки:
Изобразить на рисунке все силы, приложенные к материальной точке, то есть активные силы и реакции связей.
Выбрать систему координат.
Записать теорему об изменении количества движения точки в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Для механической системы:
Изобразить на рисунке все внешние силы.
Выбрать систему координат.
Записать теорему об изменении количества движения системы в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
Задача № 1
Железнодорожный поезд движется по горизонтальному и прямолинейному участку пути (рис.7.2). Во время торможения до полной остановки развивается сила сопротивления, равная  веса поезда. В момент начала торможения скорость
веса поезда. В момент начала торможения скорость  поезда составляла 72 км/ч.
поезда составляла 72 км/ч.

Определить время  и путь
и путь  торможения.
торможения.
Решение. Изобразим силы, действующие на поезд во время торможения: сила тяжести поезда  , нормальная реакция пути
, нормальная реакция пути  , сила сопротивления
, сила сопротивления  , которая по величине равна
, которая по величине равна 
Выберем систему координат. Поскольку движение прямолинейное и горизонтальное, достаточно рассмотреть движение по направлению оси  .
.
Запишем теорему об изменении количества движения поезда (рассматривая его как материальную точку) в интегральной форме:

где  – масса поезда,
– масса поезда,
 – конечная и начальная скорость поезда,
– конечная и начальная скорость поезда,
 – сумма импульсов сил
– сумма импульсов сил  ,
,  ,
,  которые действуют на поезд во время торможения.
которые действуют на поезд во время торможения.
Спроектируем векторное уравнение (1) на ось  :
:

Проекции импульсов сил  и
и  на ось
на ось  равны нулю, поскольку векторы
равны нулю, поскольку векторы  и
и  перпендикулярны оси.
перпендикулярны оси.
Сила сопротивления  во время торможения по величине не изменяется, следовательно, ее импульс равен:
во время торможения по величине не изменяется, следовательно, ее импульс равен:

Скорость в конце участка торможения равна нулю, то есть 
Окончательно, уравнение импульсов (2) в проекции на ось  приобретет вид:
приобретет вид:

или

откуда

С учетом числовых значений величин  и
и  имеем:
имеем:

Путь торможения определим из формулы для равнопеременного движения:

В этом случае ускорение поезда определяется из формулы:

то есть,

Тогда

Ответ: 
Задача № 2
По шероховатой наклонной плоскости, которая составляет с горизонтом угол  , спускается тяжелое тело без начальной скорости.
, спускается тяжелое тело без начальной скорости.
Определить время  , за которое тело пройдет путь длиной
, за которое тело пройдет путь длиной  , если коэффициент трения
, если коэффициент трения  и
и  .
.
Решение. Во время движения на тело действуют сила тяжести тела  , нормальная реакция поверхности
, нормальная реакция поверхности  и сила трения
и сила трения  , которая направлена в сторону, противоположную движению(рис.7.3).
, которая направлена в сторону, противоположную движению(рис.7.3).

Направим ось  вдоль наклонной поверхности вниз и запишем теорему об изменении количества движения в векторной форме:
вдоль наклонной поверхности вниз и запишем теорему об изменении количества движения в векторной форме:

Спроектируем ровность (1) на ось  :
:

Проекция импульса нормальной реакции  на ось
на ось  равна нулю, поскольку сила
равна нулю, поскольку сила  перпендикулярна
перпендикулярна  .
.
Учитывая, что во время движения сила тяжести  и сила трения
и сила трения  не меняются , то
не меняются , то

Кроме того

Итак, уравнение импульса (2) примет вид:

Вычислим силу трения:

Тогда уравнение (3) примет вид:

или 
откуда

Поскольку

то

Используя полученную зависимость, сначала подсчитаем ускорение тела, а после этого – время движения.
Поскольку

то
 и
и 
Из формулы  , учитывая, что при
, учитывая, что при  получим
получим 
Из этой формулы находим время движения  :
:

Ответ: 
Задача № 3
На полигоне пушка, которая наклонена под углом  к горизонту, делает выстрел в мишень. Сила тяжести ствола пушки –
к горизонту, делает выстрел в мишень. Сила тяжести ствола пушки – 
 Сила тяжести снаряда равна
Сила тяжести снаряда равна  Скорость снаряда у дульного среза
Скорость снаряда у дульного среза 
Определить скорость  свободного отката ствола пушки в момент вылета снаряда.
свободного отката ствола пушки в момент вылета снаряда.
Решение. В задаче рассматривается движение материальной системы, состоящей из ствола и снаряда (рис.7.4).

На систему действуют внешние силы: тяжести ствола  и тяжести снаряда
и тяжести снаряда  . Внутренние силы определяются давлением пороховых газов
. Внутренние силы определяются давлением пороховых газов  . Эти силы необходимо исключить из рассмотрения, согласно теореме о количестве движения механической системы.
. Эти силы необходимо исключить из рассмотрения, согласно теореме о количестве движения механической системы.
Применим теорему об изменении количества движения системы:

где  – количество движения системы в конечный момент времени;
– количество движения системы в конечный момент времени;
 – количество движения системы в начальный момент времени;
– количество движения системы в начальный момент времени;
 – сумма импульсов всех внешних сил (
– сумма импульсов всех внешних сил ( ,
,  ).
).
Ось  направим перпендикулярно векторам внешних сил
направим перпендикулярно векторам внешних сил  и
и  .
.
Спроектируем уравнение (1) на ось  :
:

Поскольку проекции сил  и
и  на ось
на ось  равны нулю, то и проекции импульсов
равны нулю, то и проекции импульсов  и
и  также равны нулю. Итак:
также равны нулю. Итак:
 или
или 
Таким образом, проекция количества движения системы на ось  в конечный момент времени равна проекции количества движения системы в начальный момент времени.
в конечный момент времени равна проекции количества движения системы в начальный момент времени.
В начальный момент времени (до выстрела) снаряд и ствол были неподвижны, следовательно, их количества движения равнялись нулю и

В момент вылета снаряда проекция количества движения системы на ось равна:

или

Поскольку

то

откуда
 и
и 
С учетом числовых значений:

Знак минус показывает, что скорость ствола направлена в сторону, противоположную скорости снаряда.
Ответ: 
Задача № 4
Буксирный пароход весом  набрал скорость
набрал скорость  , после чего натянулся буксирный канат, и баржа весом
, после чего натянулся буксирный канат, и баржа весом  двинулась вслед за пароходом.
двинулась вслед за пароходом.
Определить общую скорость парохода и баржи  , считая, что движущая сила и сила сопротивления воды уравновешиваются, то есть, (
, считая, что движущая сила и сила сопротивления воды уравновешиваются, то есть, ( )
)  дв =
дв =  соп (
соп ( ).
).
Решение. Для определения скорости  применим теорему об изменении количества движения системы.
применим теорему об изменении количества движения системы.
На систему, которая состоит из парохода и баржи, действуют внешние силы: силы тяжести  и
и  , силы выталкивания
, силы выталкивания  и
и  , которые приложены к баржи и буксиру, а также движущая сила
, которые приложены к баржи и буксиру, а также движущая сила  дв и сила сопротивления воды
дв и сила сопротивления воды  соп (рис.7.5).
соп (рис.7.5).

Внутренняя сила – натяжение буксирного каната  – неизвестна.
– неизвестна.
Ось  направим горизонтально, вправо.
направим горизонтально, вправо.
Запишем теорему об изменении количества движения данной системы в интегральной форме:

где  – количество движения системы баржа-буксир в тот момент времени, когда они начинают двигаться с одинаковой скоростью;
– количество движения системы баржа-буксир в тот момент времени, когда они начинают двигаться с одинаковой скоростью;
 – количество движения этой системы в начальный момент времени;
– количество движения этой системы в начальный момент времени;
 – сумма импульсов всех внешних сил.
– сумма импульсов всех внешних сил.
Спроектируем уравнение (1) на ось  :
:

Поскольку по условиям  дв =
дв =  соп, а направлены они в разные стороны, то
соп, а направлены они в разные стороны, то

Кроме того, проекции на ось  сил тяжести парохода и баржи, а также выталкивающих сил
сил тяжести парохода и баржи, а также выталкивающих сил  и
и  , равны нулю. Следовательно, проекции импульсов этих сил на ось
, равны нулю. Следовательно, проекции импульсов этих сил на ось  тоже равны нулю. Таким образом уравнение проекций принимает вид:
тоже равны нулю. Таким образом уравнение проекций принимает вид:
 или
или 
Подсчитаем количество движения парохода и баржи в начальный момент времени, когда скорость парохода равна  , а скорость баржи
, а скорость баржи  .
.

Совместимое движение парохода и баржи происходит с одинаковой скоростью  , поэтому количество движения системы в это время
, поэтому количество движения системы в это время

Поскольку

то 
Отсюда имеем

Ответ: 
Задача № 5
Механическая система состоит из грузов 1 и 2 массами  и
и  соответственно, а также прямоугольной вертикальной плиты 3 массой
соответственно, а также прямоугольной вертикальной плиты 3 массой  которая движется вдоль горизонтальных направляющих( рис.7.6). В момент времени
которая движется вдоль горизонтальных направляющих( рис.7.6). В момент времени  , когда скорость плиты
, когда скорость плиты  груз под действием внутренних сил начинают двигаться по желобам плиты. Груз 1 движется по дуге окружности с радиусом
груз под действием внутренних сил начинают двигаться по желобам плиты. Груз 1 движется по дуге окружности с радиусом  по закону
по закону  , где
, где  выражено в радианах,
выражено в радианах,  – в секундах (ось, от которой ведется положительное направление отсчета угла
– в секундах (ось, от которой ведется положительное направление отсчета угла  показано на рисунке). Груз 2 движется от точки
показано на рисунке). Груз 2 движется от точки  прямолинейно по закону
прямолинейно по закону  , где
, где  выражено в метрах,
выражено в метрах,  – в секундах (на рисунке груз 2 изображен в положении положительного отсчета координаты
– в секундах (на рисунке груз 2 изображен в положении положительного отсчета координаты  ), угол
), угол  .
.
Определить зависимость  , то есть, скорость движения плиты как функцию времени, считая грузы материальными точками и пренебрегая всеми силами сопротивления движения.
, то есть, скорость движения плиты как функцию времени, считая грузы материальными точками и пренебрегая всеми силами сопротивления движения.
Решение. Рассмотрим механическую систему в произвольном положении (рис.7.6).
Изобразим все внешние силы, действующие на систему: силы тяжести  ,
,  ,
,  и реакцию направляющей
и реакцию направляющей  .
.
Проведем координатные оси  так, чтобы ось
так, чтобы ось  проходила через точку
проходила через точку  , где находится центр масс плиты
, где находится центр масс плиты  в начальный момент времени
в начальный момент времени 
Определим  с помощью теоремы об изменении количества движения
с помощью теоремы об изменении количества движения  механической системы в проекции на ось
механической системы в проекции на ось  .
.
Поскольку все внешние силы, действующие на систему, вертикальны, то  и, согласно (7.10), имеем:
и, согласно (7.10), имеем:
 или
или  , (1)
, (1)
где  – проекция количества движения системы в момент времени
– проекция количества движения системы в момент времени 
 – проекция количества движения системы в произвольный момент времени
– проекция количества движения системы в произвольный момент времени  .
.
Определим количества движения  и
и  :
:

где 
Выразим координаты  и
и  через координату
через координату  .
.
С рис.7.6 видно, что в произвольный момент времени абсцисса первого груза

а абсцисса второго груза

Тогда


Подставляя полученные выражения для  и
и  в (3), получим:
в (3), получим:

Поскольку  то
то

В соответствии с (1), выражения (2) и (4) равны, то есть:

Отсюда окончательно получим:

Ответ: 
Задачи, которые рекомендуются для самостоятельной работы: 28.3; 28.7; 36.9; 36.11; 36.16 [2].
Теорема об изменении момента количества движения точки и механической системы
Наряду с количеством движения, как векторной меры поступательного движения, для вращательного движения можно ввести момент количества движения.
Для материальной точки массой  , которая имеет скорость
, которая имеет скорость  , момент количества движения
, момент количества движения  относительно любого центра
относительно любого центра  определяется из выражения (рис.8.1):
определяется из выражения (рис.8.1):


Вектор момента количества движения прикладывается в точке  , относительно которой он вычисляется. Если спроектировать обе части уравнения (8.1) на оси декартовой системы координат, получим моменты количества движения точки относительно осей координат:
, относительно которой он вычисляется. Если спроектировать обе части уравнения (8.1) на оси декартовой системы координат, получим моменты количества движения точки относительно осей координат:

Кинетическим моментом  или главным моментом количества движения механической системы относительно данного центра называется вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого же центра:
или главным моментом количества движения механической системы относительно данного центра называется вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого же центра:

Подобно тому, как количество движения системы является характеристикой поступательного движения, кинетический момент является характеристикой вращательного движения системы.
Кинетический момент твердого тела, которое вращается относительно оси  с угловой скоростью
с угловой скоростью  , равной произведению угловой скорости тела на его момент инерции относительно оси вращения:
, равной произведению угловой скорости тела на его момент инерции относительно оси вращения:

Производная по времени от момента количества движения точки, взятого относительно любого неподвижного центра  равна моменту силы, действующей на эту точку, относительно того же центра:
равна моменту силы, действующей на эту точку, относительно того же центра:

Спроектировав это уравнение на оси координат, получим:

Если рассматривать движение системы, на которую действуют внешние  и внутренние силы
и внутренние силы  , то производная по времени от кинетического момента механической системы относительно некоторого центра равна геометрической сумме моментов всех внешних сил относительно того же центра:
, то производная по времени от кинетического момента механической системы относительно некоторого центра равна геометрической сумме моментов всех внешних сил относительно того же центра:

Проектируя обе части уравнения на неподвижные оси  и учитывая, что проекция вектора, который изображает момент силы относительно точки на ось, равна моменту силы относительно этой оси, получим:
и учитывая, что проекция вектора, который изображает момент силы относительно точки на ось, равна моменту силы относительно этой оси, получим:

Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки, или вращательную часть движения тела в общем случае движения свободного твердого тела.
Практическая ценность теоремы заключается еще и в том, что она позволяет при изучении движения системы исключить из рассмотрения неизвестные внутренние силы.
Из теорем об изменении кинетического момента системы (8.7)-(8.8) вытекают важные выводы:
Если сумма моментов относительно центра  всех внешних сил, действующих на систему, равна нулю, то кинетический момент системы
всех внешних сил, действующих на систему, равна нулю, то кинетический момент системы  относительно той же точки является постоянным по величине и направлению, то есть,
относительно той же точки является постоянным по величине и направлению, то есть,
если  , то
, то  и
и 
Если сумма моментов всех внешних сил, действующих на систему, относительно некоторой оси, например  , равна нулю, то проекция кинетического момента на эту же ось является постоянной по величине, то есть,
, равна нулю, то проекция кинетического момента на эту же ось является постоянной по величине, то есть,
если  . то
. то  и
и 
Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
Кинетический момент тела относительно оси вращения по уравнению (8.4) , если ось  является осью вращения тела, равен:
является осью вращения тела, равен:

Следовательно,

Сумма моментов внешних сил  относительно оси вращения называется вращательным моментом и обозначается
относительно оси вращения называется вращательным моментом и обозначается

Таким образом, дифференциальное уравнение вращательного движения тела имеет вид:

Из (8.9) следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение тела равно вращательному моменту

Это уравнение позволяет решать следующие задачи:
– если заданы уравнения вращения тела  и его момент инерции
и его момент инерции  , то можно определить вращательный момент:
, то можно определить вращательный момент:

– если заданы внешние силы, приложенные к телу, начальные условия вращения  и
и  , момент инерции
, момент инерции  тела, то можно найти уравнение вращения тела
тела, то можно найти уравнение вращения тела  :
:

– определить момент инерции тела  относительно оси вращения, если известны величины
относительно оси вращения, если известны величины  и
и  :
:

Из уравнения  вытекают отдельные случаи:
вытекают отдельные случаи:
1. Если  , то
, то  , а если
, а если  , то и
, то и  . В этом случае тело вращается равномерно.
. В этом случае тело вращается равномерно.
2. Если  , то
, то  , а если
, а если  то и
то и  . Итак, твердое тело вращается равнопеременно.
. Итак, твердое тело вращается равнопеременно.
Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
Задачи, которые относятся к этой теме, можно разделить на следующие четыре основных типа:
Вычисление кинетического момента.
Изучение движения конкретной точки механической системы, если эта точка участвует во вращательном движении системы.
Изучение вращательного движения твердого тела.
Изучение движения механической системы, в которую входят тела, совершающие как поступательные, так и вращательные движения.
Задачи первого типа могут быть решены с помощью общих формул (8.4), (8.5).
Порядок решения задач второго типа может быть следующим:
- Выбрать систему координат.
- Изобразить все внешние силы, приложенные к материальной точке; в случае произвольной точки к этим силам добавить реакции внешних связей.
- Записать в скалярной форме выражение теоремы об изменении момента количества движения точки.
- Высчитать сумму моментов сил, которые приложены к материальной точке.
- Определить количество движения материальной точки и его момент относительно осей.
- Подставить данные пунктов 4 и 5 в уравнения (8.6) теоремы об изменении момента количества движения материальной точки.
- Решить, в соответствии с условием, прямую или обратную задачу динамики точки.
При решении задач третьего типа сохранять рекомендации первых двух пунктов, а далее делать следующим образом:
- Записать дифференциальное уравнение вращательного движения тела вокруг неподвижной оси (8.9).

- Определить момент инерции твердого тела относительно неподвижной оси.
- Подсчитать сумму моментов всех внешних сил относительно оси вращения.
- Величины, полученные в п. п. 4 и 5, подставить в уравнение (8.9).
- Записать начальные условия.
- Решить уравнение п. 6 в зависимости от условия, как прямую или обратную задачу.
При решении задач четвертого типа необходимо предварительно расчленить заданную систему на отдельные твердые тела, и к каждому из них, в зависимости от характера движения, применить одну из теорем: об изменении количества движения – в случае поступательного движения тел расчлененной системы; об изменении кинетического момента – при наличии тел, которые совершают вращательные движения.
Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
Задача №1
Однородный круглый диск весом  и с радиусом
и с радиусом  катится без скольжения по горизонтальной плоскости, делая вокруг собственной оси 60 об/мин (рис.8.2).
катится без скольжения по горизонтальной плоскости, делая вокруг собственной оси 60 об/мин (рис.8.2).

Определить главный момент количеств движения диска  относительно оси
относительно оси  , которая проходит через центр диска перпендикулярно плоскости движения.
, которая проходит через центр диска перпендикулярно плоскости движения.
Решение. Главный момент количеств движения системы (кинетический момент) относительно оси вращения равен (8.6):

где  – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения,
 – угловая скорость вращения.
– угловая скорость вращения.
В данном случае кинетический момент относительно оси, проходящей через центр диска  , равен:
, равен:


Ответ: 
Задача №2
Во время вращения барабана 1 весом  и радиусом
и радиусом  вокруг неподвижной оси
вокруг неподвижной оси  на его боковую поверхность наматывается невесомая и нерастяжимая нить, что вызывает движение груза 2 весом
на его боковую поверхность наматывается невесомая и нерастяжимая нить, что вызывает движение груза 2 весом  , который скользит по неподвижной гладкой горизонтальной плоскости (рис.8.3).
, который скользит по неподвижной гладкой горизонтальной плоскости (рис.8.3).

Определить главный момент количества движения (кинетический момент) системы относительно оси  и выразить его как зависимость от угловой скорости. Барабан считать однородным круглым цилиндром. Ось
и выразить его как зависимость от угловой скорости. Барабан считать однородным круглым цилиндром. Ось  направлена перпендикулярно рисунку.
направлена перпендикулярно рисунку.
Решение. В состав механической системы входят два твердых тела: барабан 1 и груз 2.
Следовательно, кинетический момент системы равен:

где  – кинетический момент барабана;
– кинетический момент барабана;
 – кинетический момент груза относительно неподвижной оси
– кинетический момент груза относительно неподвижной оси  .
.
Кинетический момент барабана равен (8.5):

где

тогда

Главный момент количества движения груза, который движется поступательно, определяется как момент количества движения материальной точки, то есть:

поскольку

то

Окончательно

Ответ: 
Задача №3
Шарик  , который находится в сосуде с жидкостью и прикреплен к концу стержня
, который находится в сосуде с жидкостью и прикреплен к концу стержня  длиной
длиной  , приводится в вращение вокруг вертикальной оси
, приводится в вращение вокруг вертикальной оси  с начальной угловой скоростью
с начальной угловой скоростью  (рис.8.4, а). Сила сопротивления жидкости пропорциональна угловой скорости вращения
(рис.8.4, а). Сила сопротивления жидкости пропорциональна угловой скорости вращения  :
:  , где
, где  – масса шарика,
– масса шарика,  – коэффициент пропорциональности.
– коэффициент пропорциональности.

Определить, через какой промежуток времени  угловая скорость вращения станет вдвое меньше начальной, а также число оборотов
угловая скорость вращения станет вдвое меньше начальной, а также число оборотов  , которое сделает стержень с шариком за этот промежуток времени. Массу шарика считать сосредоточенной в ее центре, массой стержня пренебречь.
, которое сделает стержень с шариком за этот промежуток времени. Массу шарика считать сосредоточенной в ее центре, массой стержня пренебречь.
Решение. Ось  направим вдоль оси вращения
направим вдоль оси вращения  и покажем силы, действующие на вал с шариком: силу сопротивления
и покажем силы, действующие на вал с шариком: силу сопротивления  , которая направлена в сторону, противоположную вращению (рис.8.4, б), силу тяжести шарика
, которая направлена в сторону, противоположную вращению (рис.8.4, б), силу тяжести шарика  , реакции
, реакции  подшипника
подшипника  и
и  подпятника
подпятника  .
.
Все силы указаны на рисунках, направления сил  и
и  изображены произвольно.
изображены произвольно.
Запишем дифференциальное уравнение вращательного движения шарика относительно оси  :
:

где момент инерции шарика

Поскольку момент силы тяжести  относительно оси
относительно оси  равен нулю (
равен нулю (  параллельна оси
параллельна оси  ), то вращательный момент
), то вращательный момент  равен моменту силы сопротивления
равен моменту силы сопротивления  относительно оси
относительно оси  (как известно, момент силы сопротивления всегда отрицательный):
(как известно, момент силы сопротивления всегда отрицательный):

Следовательно, дифференциальное уравнение вращательного движения имеет вид:

или

Разделим переменные и проинтегрируем:

Произвольную постоянную  определим по начальным условиям: при
определим по начальным условиям: при  .
.

Следовательно,

Высчитаем, через какой промежуток времени  угловая скорость вращения станет вдвое меньше начальной, то есть,
угловая скорость вращения станет вдвое меньше начальной, то есть,  .
.

Откуда:

Для определения числа оборотов, которые сделает стержень с шариком за промежуток времени  , необходимо найти зависимость угла поворота
, необходимо найти зависимость угла поворота  от времени
от времени  :
:

Следовательно,

Разделим переменные и проинтегрируем это дифференциальное уравнение:

Произвольную постоянную  определим по начальным условиям: при
определим по начальным условиям: при  .
.

Итак закон изменения угла поворота  по времени имеет вид:
по времени имеет вид:

или

При  , угол поворота
, угол поворота  равен
равен

Поскольку за 1 оборот шарик обернется на  , то количество оборотов
, то количество оборотов  составит
составит

Ответ: 
Задача №4
Для определения момента трения в цапфах, на вал насажен маховик весом  , радиус инерции маховика
, радиус инерции маховика  Маховику придана угловая скорость, соответствующая
Маховику придана угловая скорость, соответствующая  об/мин. Без внешнего воздействия на него, он остановился через
об/мин. Без внешнего воздействия на него, он остановился через  мин.
мин.
Определить момент трения  , считая его постоянным.
, считая его постоянным.
Решение. Направим ось  вдоль неподвижной оси вращения. Изобразим на рис.8.5 внешние нагрузки, действующие на вал и маховик: силу тяжести маховика
вдоль неподвижной оси вращения. Изобразим на рис.8.5 внешние нагрузки, действующие на вал и маховик: силу тяжести маховика  , реакции опор
, реакции опор  и
и  и момент сил трения
и момент сил трения  .
.
Запишем теорему об изменении кинетического момента относительно оси вращения:

Поскольку мы рассматриваем вращение твердого тела, то

Найдем вращательный момент внешних сил относительно оси вращения  , если учтем, что момент сил
, если учтем, что момент сил  ,
,  и
и  относительно оси
относительно оси  равны нулю, поскольку эти силы пересекают ось. Следовательно, вращательный момент равен моменту сил трения и направлен в сторону, противоположную вращению маховика.
равны нулю, поскольку эти силы пересекают ось. Следовательно, вращательный момент равен моменту сил трения и направлен в сторону, противоположную вращению маховика.
Таким образом

Высчитаем величины, которые входят в это уравнение:

где  – угловая скорость маховика в момент остановки,
– угловая скорость маховика в момент остановки,  ,
,
 – угловая скорость в начальный момент времени.
– угловая скорость в начальный момент времени.
Поскольку  то
то 
С учетом значений  и
и  получим:
получим:

Ответ: 
Задача №5
Однородный цилиндр (рис.8.6) радиусом  вращается вокруг своей геометрической оси
вращается вокруг своей геометрической оси  угловой скоростью
угловой скоростью  .
.

Определить, как изменится угловая скорость  цилиндра, если ось вращения перейдет в положение
цилиндра, если ось вращения перейдет в положение  , которое совпадает с образующей цилиндра?
, которое совпадает с образующей цилиндра?
Решение. На цилиндр действует сила тяжести  , которая направлена вертикально вниз.
, которая направлена вертикально вниз.
Запишем теорему об изменении кинетического момента цилиндра:

где  – момент инерции цилиндра,
– момент инерции цилиндра,
 – сумма моментов внешних сил относительно оси вращения.
– сумма моментов внешних сил относительно оси вращения.
Поскольку сила  параллельна оси вращения, то
параллельна оси вращения, то
 и
и 
Итак,  , тогда
, тогда

где  – момент инерции цилиндра относительно оси
– момент инерции цилиндра относительно оси  ,
,
 – момент инерции цилиндра относительно оси
– момент инерции цилиндра относительно оси  ,
,
По теореме Гюйгенса-Штейнера

где  – масса цилиндра.
– масса цилиндра.
Из формулы (1) получим:

Вычислим  и
и  :
:

Следовательно,

Угловая скорость уменьшилась в три раза, поскольку в три раза увеличился момент инерции.
Ответ: 
Задача №6
Молотильный барабан начинает вращаться из состояния покоя ( ) под действием постоянного момента
) под действием постоянного момента 
Определить, пренебрегая трением, частоту вращения барабана после того, как он начнет вращаться и сделает  оборотов (рис.8.7), зная, что момент инерции барабана относительно оси вращения
оборотов (рис.8.7), зная, что момент инерции барабана относительно оси вращения 

Решение. Для определения угловой скорости барабана воспользуемся формулой:

где  – начальная угловая скорость вращения,
– начальная угловая скорость вращения,
 – конечная угловая скорость вращения,
– конечная угловая скорость вращения,
 – угол, на который поворачивается барабан.
– угол, на который поворачивается барабан.
Из (1) вытекает:
 где
где 
Следовательно,

Таким образом, для определения угловой скорости необходимо знать угловое ускорение  .
.
Для определения  воспользуемся теоремой об изменении кинетического момента:
воспользуемся теоремой об изменении кинетического момента:

где  – сумма моментов всех внешних сил относительно оси вращения.
– сумма моментов всех внешних сил относительно оси вращения.
На барабан действуют следующие внешние нагрузки:  – сила тяжести барабана;
– сила тяжести барабана;  ,
,
 – реакции подшипников
– реакции подшипников  и
и  ;
;  – вращательный момент.
– вращательный момент.
С учетом действующих сил уравнение (2) будет иметь вид:

При этом  , поскольку силы
, поскольку силы  ,
,  и
и
 пересекают ось
пересекают ось  и моментов не образуют. Итак,
и моментов не образуют. Итак,

Тогда,

Ответ: 
Задача №7
Груз весом  подвешен на канате, который навитый на цилиндрический барабан, ось вращения которого горизонтальна (рис.8.8).
подвешен на канате, который навитый на цилиндрический барабан, ось вращения которого горизонтальна (рис.8.8).

Определить угловое ускорение барабана  во время опускания груза
во время опускания груза  , пренебрегая весом каната, сопротивлением воздуха, трением в подшипниках. Барабан считать однородным цилиндром весом
, пренебрегая весом каната, сопротивлением воздуха, трением в подшипниках. Барабан считать однородным цилиндром весом  и радиусом
и радиусом 
Решение. Для определения углового ускорения  барабана будем рассматривать движение системы, в которую включим следующие тела: барабан весом
барабана будем рассматривать движение системы, в которую включим следующие тела: барабан весом  , груз весом
, груз весом  и канат, натяжение которого заранее неизвестно.
и канат, натяжение которого заранее неизвестно.
Если применить теорему об изменении кинетического момента системы относительно оси, то натяжение каната, являющегося внутренней силой, в уравнение не войдет.
Относительно оси, которая проходит через точку  , эта теорема имеет вид:
, эта теорема имеет вид:

На систему действуют следующие внешние силы:  – вес груза,
– вес груза,  – вес барабана,
– вес барабана,  – реакция опоры
– реакция опоры  .
.
Силы  и
и  не создают моментов относительно оси
не создают моментов относительно оси  , потому что они ее пересекают. Только сила
, потому что они ее пересекают. Только сила  создает момент относительно оси
создает момент относительно оси  , который равен:
, который равен:

Итак,

Определим кинетический момент системы относительно оси вращения  :
:

где  – кинетический момент барабана,
– кинетический момент барабана,
 – кинетический момент груза.
– кинетический момент груза.

где  – момент инерции барабана относительно оси вращения
– момент инерции барабана относительно оси вращения  ;
;

поскольку 
Тогда кинетический момент системы равен:

Подставим полученные результаты в уравнение (1):

Знак момента силы  взят положительным, поскольку направление вращения барабана совпадает с направлением момента силы
взят положительным, поскольку направление вращения барабана совпадает с направлением момента силы  .
.
Решаем уравнение (2) и определяем угловое ускорение  .
.
Выносим из под знака дифференциала в левой части уравнения (2) постоянные величины:

или

С учетом числовых значений угловое ускорение  равно:
равно:

Ответ: 
Теорема об изменении кинетической энергии механической системы
Теорема о кинетической энергии системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему.
Кинетическая энергия механической системы
Кинетической энергией  материальной точки называется скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости:
материальной точки называется скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости:

Кинетической энергией  механической системы называется арифметическая сумма кинетических энергий всех точек механической системы:
механической системы называется арифметическая сумма кинетических энергий всех точек механической системы:

Кинетическая энергия системы не зависит от направлений скоростей точек.
Кинетическая энергия может равняться нулю, если скорости всех точек системы равны нулю.
Кинетическая энергия системы характеризует и поступательное, и вращательное движения системы. Поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Единицей кинетической энергии в системе СИ является Джоуль (Дж).
Определение кинетической энергии твердого тела в различных случаях его движения
Поступательное движение твердого тела:
При поступательном движении твердого тела скорости всех его точек (в том числе скорость  центра масс тела) в каждый момент времени равны между собой; то есть, для любой точки
центра масс тела) в каждый момент времени равны между собой; то есть, для любой точки  . Итак
. Итак

Кинетическая энергия твердого тела при поступательном движении равна половине произведения массы тела  на квадрат скорости его центра масс.
на квадрат скорости его центра масс.
Вращательное движение твердого тела:
Скорость любой точки твердого тела, которое вращается с угловой скоростью  , равна
, равна

где  – расстояние от точки к оси вращения.
– расстояние от точки к оси вращения.
Тогда кинетическая энергия тела определяется согласно зависимости:

Поскольку

то

Следовательно кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Плоскопараллельное движение твердого тела:
При плоскопараллельном движении скорости всех точек тела в каждый момент времени распределены так, будто тело вращается вокруг оси, которая перпендикулярна плоскости движения и которая проходит через мгновенный центр скоростей  .
.
В этом случае кинетическую энергию тела можно определить по формуле:

где  – момент инерции тела относительно оси, которая проходит через мгновенный центр скоростей.
– момент инерции тела относительно оси, которая проходит через мгновенный центр скоростей.
Поскольку (согласно теореме Штейнера-Гюйгенса)

где  – момент инерции относительно оси, которая проходит через центр масс тела и параллельна мгновенной оси вращения, то
– момент инерции относительно оси, которая проходит через центр масс тела и параллельна мгновенной оси вращения, то

Поскольку  , то окончательно
, то окончательно

Таким образом,
в случае плоскопараллельного движения тела кинетическая энергия состоит из кинетических энергий поступательного движения вместе со скоростью центра масс и вращательного движения вокруг оси, которая проходит через центр масс перпендикулярно плоскости движения.
Теорема об изменении кинетической энергии механической системы:
Дифференциальная форма:
Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему:

Производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних и внутренних сил, действующих на систему:

Интегральная форма:
Изменение кинетической энергии механической системы при конечном перемещении ее из положения (1) в положение (2) равно сумме работ на этом перемещении всех внешних и внутренних сил, действующих на эту систему

Если механическая система неизменна, то сумма работ внутренних сил равна нулю и теорема запишется так:

Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в следующей последовательности:
а) изобразить на рисунке все внешние силы системы;
б) высчитать сумму работ всех внешних сил на перемещении точек системы;
в) вычислить кинетическую энергию системы материальных точек в начальном и конечном ее состояниях;
г ) пользуясь результатами подсчетов по пунктам б) и в) записать теорему об изменении кинетической энергии механической системы и определить искомую величину.
Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Задача № 1
Механизм эллипсографа (рис.10.1) состоит из ползунов  и
и  весом
весом  каждый, кривошипа
каждый, кривошипа  весом
весом  , и линейки
, и линейки  весом
весом  . Кривошип
. Кривошип  вращается вокруг неподвижной оси
вращается вокруг неподвижной оси  , которая перпендикулярна плоскости чертежа с угловой скоростью
, которая перпендикулярна плоскости чертежа с угловой скоростью  .
.
Определить кинетическую энергию механизма эллипсографа, полагая, что линейка  и кривошип
и кривошип  – однородные тонкие стержни, а ползуны
– однородные тонкие стержни, а ползуны  и
и  – материальные точки, а также, что
– материальные точки, а также, что 

Решение. Заданная механическая система состоит из четырех тел: кривошипа 1 и линейки 2, ползунов 3 и 4.
Кинетическая энергия всей системы равна:

где  – кинетическая энергия кривошипа 1,
– кинетическая энергия кривошипа 1,
 – кинетическая энергия линейки 2,
– кинетическая энергия линейки 2,
 – кинетическая энергия ползунов 3 и 4.
– кинетическая энергия ползунов 3 и 4.
Кривошип  совершает вращательное движение вокруг неподвижной оси
совершает вращательное движение вокруг неподвижной оси  , которая перпендикулярна оси рисунка. В этом случае кинетическая энергия тела равна
, которая перпендикулярна оси рисунка. В этом случае кинетическая энергия тела равна

Тогда

Линейка 2 движется плоскопараллельно. Ее кинетическая энергия равна

где  – скорость точки С, которая является центром масс линейки 2,
– скорость точки С, которая является центром масс линейки 2,
 – угловая скорость линейки 2,
– угловая скорость линейки 2,
 – момент инерции линейки относительно оси
– момент инерции линейки относительно оси  , которая проходит через центр масс линейки
, которая проходит через центр масс линейки  .
.
Для определения угловой скорости  линейки 2 используем понятие мгновенного центра скоростей. Как известно, мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям двух точек тела, движущихся плоскопараллельно. Тогда в нашем случае он будет расположен в точке
линейки 2 используем понятие мгновенного центра скоростей. Как известно, мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям двух точек тела, движущихся плоскопараллельно. Тогда в нашем случае он будет расположен в точке  , и скорость точки
, и скорость точки  определится:
определится:

С другой стороны, точка  принадлежит звену 1, и ее скорость равна
принадлежит звену 1, и ее скорость равна

Тогда, учитывая, что  получим:
получим:

Момент инерции линейки относительно оси  равен:
равен:

С учетом полученных значений  кинетическая энергия линейки 2 равна:
кинетическая энергия линейки 2 равна:

Подсчитаем кинетическую энергию ползунов 3 и 4, которые двигаются поступательно:
 .
.
Скорости точек  можно определить, учитывая положение мгновенного центра скоростей линейки 2:
можно определить, учитывая положение мгновенного центра скоростей линейки 2:

Тогда

Подставляя найденные выражения (2), (4), (5) в (1), получим:

Ответ: 
Задача № 2
На рисунке 10.2 изображен подъемный механизм лебедки. Груз  весом
весом  поднимается с помощью невесомого и нерастяжимого троса, который переброшен через блок
поднимается с помощью невесомого и нерастяжимого троса, который переброшен через блок  и намотан на барабан
и намотан на барабан  радиусом
радиусом  и весом
и весом  . К барабану приложен вращательный момент, который пропорционален квадрату угла поворота
. К барабану приложен вращательный момент, который пропорционален квадрату угла поворота  барабану:
барабану:

где  – постоянный коэффициент.
– постоянный коэффициент.

Определить скорость груза  в момент, когда он поднимется на высоту
в момент, когда он поднимется на высоту  . Массу барабана
. Массу барабана  считать равномерно распределенной вдоль его обода. Блок
считать равномерно распределенной вдоль его обода. Блок  – сплошной диск весом
– сплошной диск весом  . В начальный момент система находилась в покое.
. В начальный момент система находилась в покое.
Решение. Изобразим на рисунке все внешние силы, действующие на барабан  , блок
, блок  и груз
и груз  : силы тяжести
: силы тяжести  ,
,  ,
,  ; вращательный момент, а также реакции шарниров
; вращательный момент, а также реакции шарниров  и
и  . Внутренней силой является натяжение троса
. Внутренней силой является натяжение троса  .
.
Запишем теорему об изменении кинетической энергии системы:

где  – кинетическая энергия системы в конечном положении;
– кинетическая энергия системы в конечном положении;
 – кинетическая энергия системы в исходном положении;
– кинетическая энергия системы в исходном положении;
 – сумма работ всех внешних сил на перемещении
– сумма работ всех внешних сил на перемещении  ;
;
 – сумма работ всех внутренних сил на перемещении
– сумма работ всех внутренних сил на перемещении  .
.
Поскольку в начальный момент времени система находилась в состоянии покоя, то

В связи с тем, что трос не растягивается и при движении системы находится в натянутом состоянии, сумма работ внутренних сил системы равна нулю, следовательно

При поднятии груза  на высоту
на высоту  сумма работ равна:
сумма работ равна:

Поскольку точки приложения сил  и
и  – неподвижны, то
– неподвижны, то

Работа силы  равна:
равна:

Работа вращательного момента в случае, когда он не меняется

где  – угол поворота тела под действием момента.
– угол поворота тела под действием момента.
Поскольку в нашем случае вращательный момент меняется, то его работа определится следующим образом:

Определим угол  , на который вернулся барабан
, на который вернулся барабан  при подъеме груза
при подъеме груза  на высоту
на высоту  :
:

Следовательно,

Таким образом,

Перейдем к подсчету кинетической энергии системы в конечном положении:

где  – кинетическая энергия груза
– кинетическая энергия груза  ;
;
 – кинетическая энергия диска
– кинетическая энергия диска  ;
;
 – кинетическая энергия барабана
– кинетическая энергия барабана  .
.
Груз  движется поступательно и его кинетическая энергия равна:
движется поступательно и его кинетическая энергия равна:

Диск  совершает вращательное движение, его кинетическая энергия определяется из выражения:
совершает вращательное движение, его кинетическая энергия определяется из выражения:
где  – момент инерции диска относительно оси вращения;
– момент инерции диска относительно оси вращения;
 – угловая скорость диска.
– угловая скорость диска.
Поскольку диск  – сплошной, то
– сплошной, то  равен:
равен:

где  – радиус диска.
– радиус диска.
Поскольку линейная скорость обода диска равна скорости груза, угловая скорость вращения  :
:

Итак,

Кинетическая энергия барабана  , поскольку он совершает вращательное движение, равна:
, поскольку он совершает вращательное движение, равна:

Поскольку масса барабана  распределена по ободу, то:
распределена по ободу, то:

Угловую скорость барабана высчитаем из условия равенства линейных скоростей на ободах диска и барабана:

Откуда

Таким образом

Кинетическая энергия системы в конечном положении равна

Итак, теорема об изменении кинетической энергии системы имеет вид:

Решая это уравнение относительно  , находим скорость груза
, находим скорость груза  после того, как он пройдет путь
после того, как он пройдет путь  :
:

Ответ: 
Задача № 3
Груз  (рис.10.3) весом
(рис.10.3) весом  , опускаясь вниз с помощью перекинутого через неподвижный блок
, опускаясь вниз с помощью перекинутого через неподвижный блок  невесомого и нерастяжимого троса, поднимает вверх груз
невесомого и нерастяжимого троса, поднимает вверх груз  весом
весом  , который закреплен к оси подвижного блока
, который закреплен к оси подвижного блока  . Блоки
. Блоки  и
и  считать однородными сплошными дисками весом
считать однородными сплошными дисками весом  каждый.
каждый.

Определить скорость груза  в момент, когда он опустится на высоту
в момент, когда он опустится на высоту  . Скольжением на ободах блоков и силами сопротивления пренебречь.
. Скольжением на ободах блоков и силами сопротивления пренебречь.
В начальный момент система находилась в состоянии покоя.
Решение. Изобразим внешние силы, которые действуют на систему: силы тяжести  ; реакцию шарнира
; реакцию шарнира  и реакцию в точке
и реакцию в точке  –
–  . Внутренней силой является натяжение троса
. Внутренней силой является натяжение троса  .
.
Запишем теорему об изменении кинетической энергии системы:

В начальный момент времени система находилась в покое, следовательно,  . Работа внутренней силы натяжения троса, равна нулю. Итак,
. Работа внутренней силы натяжения троса, равна нулю. Итак,

Сумма работ внешних сил при перемещении системы в конечное положение составляет:

Работа сил  равна нулю, поскольку точки приложения сил 3
равна нулю, поскольку точки приложения сил 3  неподвижны.
неподвижны.
Итак,

Работа силы  при опускании груза
при опускании груза  на высоту
на высоту  равна:
равна:

Работу силы тяжести  блока
блока  определим следующим образом. При опускании груза
определим следующим образом. При опускании груза  на высоту
на высоту  точка
точка  блока
блока  поднимается вверх на расстояние
поднимается вверх на расстояние  , которая равна
, которая равна  , а центр блока
, а центр блока  на величину
на величину  , так как точка
, так как точка  – мгновенный центр скоростей блока
– мгновенный центр скоростей блока  .
.
Таким образом,

Груз  поднимается вверх так же на величину
поднимается вверх так же на величину  . Тогда работа силы тяжести груза
. Тогда работа силы тяжести груза  будет равна:
будет равна:

Итак,

Вычислим кинетическую энергию системы в конечном положении:

Груз  перемещается поступательно и его кинетическая энергия равна
перемещается поступательно и его кинетическая энергия равна

где  – скорость груза
– скорость груза  в конце перемещения.
в конце перемещения.
Блок  осуществляет плоскопараллельное движение. В этом случае:
осуществляет плоскопараллельное движение. В этом случае:

Кинетическая энергия поступательного движения блока  равна:
равна:

Поскольку точка  – мгновенный центр скоростей блока
– мгновенный центр скоростей блока  , а скорость точки
, а скорость точки  равна скорости груза
равна скорости груза  , то скорость вращения блока
, то скорость вращения блока  :
:

Тогда

Таким образом,

Кинетическая энергия вращательного движения блока  определяется из равенства:
определяется из равенства:

где  – момент инерции блока
– момент инерции блока  относительно оси, которая проходит через центр масс
относительно оси, которая проходит через центр масс  . Блок
. Блок  – сплошной однородный диск, поэтому
– сплошной однородный диск, поэтому

Тогда

Таким образом, кинетическая энергия блока  равна:
равна:

Блок  совершает вращательное движение и его кинетическая энергия:
совершает вращательное движение и его кинетическая энергия:

то есть

Груз  совершает поступательное движение со скоростью точки
совершает поступательное движение со скоростью точки  то есть со скоростью
то есть со скоростью  . Поэтому
. Поэтому

Следовательно, кинетическая энергия системы  в конечном положении:
в конечном положении:

Таким образом, теорема об изменении кинетической энергии системы имеет вид:

Находим скорость груза  , решая это уравнение относительно
, решая это уравнение относительно  :
:

Ответ: 
Задача № 4
Прямоугольная пластинка  (рис.10.4) со сторонами
(рис.10.4) со сторонами  и
и  , и весом
, и весом  вращается вокруг вертикальной оси
вращается вокруг вертикальной оси  с начальной угловой скоростью
с начальной угловой скоростью  . Каждый элемент пластинки несет при этом сопротивление воздуха, направление которого перпендикулярно плоскости пластинки, а величина пропорциональна площади элемента и квадрату его скорости. Коэффициент пропорциональности равен
. Каждый элемент пластинки несет при этом сопротивление воздуха, направление которого перпендикулярно плоскости пластинки, а величина пропорциональна площади элемента и квадрату его скорости. Коэффициент пропорциональности равен  .
.

Определить, сколько оборотов сделает пластинка к тому мгновению, когда ее угловая скорость станет вдвое меньше начальной?
Решение. Поскольку силы сопротивления, приложенные к пластинке, не постоянные, а зависят от скорости, то для решения задачи воспользуемся теоремой об изменении кинетической энергии системы в дифференциальной форме:

Высчитаем дифференциал кинетической энергии пластинки. Поскольку пластинка вращается вокруг неподвижной оси, то ее кинетическая энергия равна:

откуда:

где  – момент инерции пластинки относительно оси
– момент инерции пластинки относительно оси  .
.
Перейдем к определению суммы элементарных работ внешних сил, которые действуют на пластинку. Это такие силы (рис.10.4):
– сила тяжести пластинки  ;
;
– реакции в опорах  и
и  :
:  и
и  ;
;
– сила сопротивления воздуха  .
.
Итак,

где  – элементарная работа силы тяжести пластинки;
– элементарная работа силы тяжести пластинки;
 – элементарные работы реакций подшипников;
– элементарные работы реакций подшипников;
 – элементарная работа силы сопротивления
– элементарная работа силы сопротивления  .
.
Работы реакций  и
и  равны нулю, ибо точки их приложения неподвижны. Работа силы тяжести
равны нулю, ибо точки их приложения неподвижны. Работа силы тяжести  тоже равна нулю в связи с тем, что высота центра тяжести пластинки не меняется.
тоже равна нулю в связи с тем, что высота центра тяжести пластинки не меняется.
Таким образом,

Для вычета работы сил сопротивления воспользуемся формулой для работы сил, которые приложены к вращающемуся твердому телу:

где  – сумма моментов всех приложенных к телу сил относительно оси вращения;
– сумма моментов всех приложенных к телу сил относительно оси вращения;
 – элементарный угол поворота.
– элементарный угол поворота.
Чтобы определить  , разобьем пластинку на элементарные прямоугольники со сторонами
, разобьем пластинку на элементарные прямоугольники со сторонами  и
и  . Тогда сила сопротивления, приложенная к элементарному прямоугольнику, будет равняться:
. Тогда сила сопротивления, приложенная к элементарному прямоугольнику, будет равняться:

и

Следовательно,

или

и
 .
.
Таким образом, уравнение (1) принимает вид:

Разделим переменные и проинтегрируем:

Момент инерции пластинки составляет:

Тогда

Откуда находим:

Число оборотов  составляет:
составляет:

Ответ: 
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac{π}{2}, frac{π}{3}, frac{7π}{4}, 10π, -frac{29π}{6})) разбирается в этой статье.
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам, расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки – положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.


Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» – точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности – каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π): ( frac{π}{2}),(-frac{π}{2}),(frac{3π}{2}),(2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье).

Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
(t_0+2πn), (n∈Z),
где (t_0) – любое значение это точки.
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео.
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь.
Что надо запомнить про числовую окружность:

Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
