Контакты
admin@mama-pomogi.ru
- Подробности
- Категория: Мышление
 Важная сторона развития у школьника логической культуры (способности логически мыслить) – это умение устанавливать смысловые связи в тексте. Для части учеников это довольно сложно.
Важная сторона развития у школьника логической культуры (способности логически мыслить) – это умение устанавливать смысловые связи в тексте. Для части учеников это довольно сложно.
Им полезно прежде научиться устанавливать смысловые связи между предметами и явлениями. Этот навык облегчит им более сложную работу с текстом.
Смысловые связи между предметами
Пример.
Даны два предмета КОРОВА – ТЕЛЁНОК. Какая между ними связь?
Варианты детских ответов (подготовительная группа)
- Корова гуляет с телёнком.
- Корова кормит телёнка молоком.
- Телёнок – это сынок коровы.
К первым двум утверждениям можно задать вопросы:
- Почему корова гуляет с телёнком?
- Почему она кормит его молочком?
Исчерпывающий – третий вариант, включающий и первый, и второй ответы.
Начинать тренировку установления смысловых связей полезно в подготовительной группе детского сада. Подойдут эти задания и для учеников начальной школы с затруднениями в обучении из-за недостатков логического мышления.
Задание на установление связей между предметами
Инструкция. Берём два предмета и ищем между ними максимально исчерпывающую смысловую связь.
Лодка/вода;
Птица/небо;
Лыжи/зима;
Зубы/жевать;
Звонок/урок;
Ручка/буква;
Лошадь/жеребёнок;
Мыло/руки;
Человек/дом;
Дерево/листья;
Мороз/шуба;
Роза/лето;
Ухо/слышать.
Задания на установление смысловых связей по аналогии
Взрослым может показаться задание очень примитивным. Давайте усложним для легко справляющихся ребят.
Слева написаны два слова с определённой смысловой связью. К примеру, между словами ПТИЦА/ГНЕЗДО есть смысловая связь: птица живёт в гнезде. Справа тоже слово и ряд слов на выбор: ЧЕЛОВЕК/девочка, ПТЕНЕЦ, РАБОЧИЙ, хлев, ДОМ. Из этого ряда слов выбираем одно, у которого смысловая связь как у птицы и гнезда.
Рассуждаем. Какая же связь между птицей и гнездом? Правильно, жилище птицы – гнездо. Значит надо найти жилище человека. Выбираем ДОМ.
|
Птица/гнездо |
Человек/девочка, птенец, рабочий, хлев, дом |
|
Школа/учитель |
Больница/больной, лечение, ученик, доктор, учреждение |
|
Хлеб/пекарь |
Дом/город, жилище, вагон, строитель, окно |
|
Ложка/борщ |
Вилка/ масло, тарелка, нож, мясо, посуда |
|
Песня/певец |
Картина/учитель, рисунок, рамка, художник, стена |
|
Овца/ягнёнок |
Корова/молоко, кефир, пастух, телёнок, рога |
|
Глаз/видеть |
Зубы/ слышать, рот, лечить, зубная паста, жевать |
|
Коньки/зима |
Лодка/ весло, каток, река, пароход, лето |
|
Нож/сталь |
Стол/ложка, скатерть, стул, дерево, еда |
|
Самолёт/лётчик |
Трактор/пахать, железо, транспорт, тракторист, рабочий |
|
Шапка/зима |
Панама/ осень, головной убор, одежда, сапоги, лето |
|
Автомобиль/шоссе |
Трамвай/вагоновожатый, транспорт, пассажиры, рельсы, кондуктор |
|
Торт/кондитер |
Суп/кастрюля, повар, плита, обед, стол |
|
Дерево/сосна |
Цветок/ваза, подарок, роза, куст, красота |
|
Лодка/вода |
Сани/зима, лошадь, снег, ямщик, шуба |
|
Дерево/ветки |
Рука/варежка, пальцы, кожа, мальчик |
|
Птица/воробей |
Металл/нож, плуг, железо, коньки, каток |
|
Дождь/зонтик |
Мороз/сани, шуба, зима, Новый год, подарки |
|
Снег/вода |
Лёд/река, мороз, шапка, вода, валенки |
|
Зима/лыжи |
Лето/коньки, поход, лагерь, велосипед. |
|
Шапка/вязать |
Платье/лето, сарафан, шить, надевать, гулять |
Кажется всё так просто. На деле многим детям требуется не один раз разъяснить суть задания и помочь сделать выбор и обосновать его. Но благодаря этой работе есть шанс научиться быстро устанавливать простые смысловые связи.
Добавить комментарий
Е.А. Иванов
Раздел второй. Суждение
Более сложной по сравнению с понятием формой мышления выступает суждение. Оно включает в себя понятие, но не сводится к нему, а представляет собой качественно особую форму, выполняющую свои, иные функции в мышлении.
Чтобы дать логический анализ этой формы, необходимо вначале выяснить, что такое всякое суждение вообще, независимо от форм его проявления; затем произвести классификацию суждений; далее установить, какие существуют отношения между суждениями, и наконец, показать, какие возможны логические операции с суждениями.
Необходимость такого анализа обусловлена тем, что наше мышление, будучи понятийным, слагается все же не из отдельных, изолированных понятий, а из суждений – от самых простых, обиходных, повседневных до наиболее сложных, научных или философских. Буквально обо всем на свете, что в той или иной мере затрагивает наши материальные и духовные потребности, интересы, мотивы деятельности, мы так или иначе судим: рассуждаем, высказываем мнение, всему даем свои оценки. Поэтому вся наша речь, по существу, либо выражает суждения, либо основывается на них, либо предполагает их получение. Отсюда – важность и значение исследования суждения как формы мышления. Термин «суждение» широко используется в юридической науке и практике.
Глава I. Общая характеристика суждения
Как и понятие, суждение в известном смысле находится между действительностью и языком. Поэтому его следует рассматривать тоже в двух важнейших аспектах: во-первых, по отношению к действительности, формой отражения которой оно является; а во-вторых, по отношению к языку, средствами которого оно выражается.
Происхождение и сущность суждения. Будучи продуктом человеческого мышления, суждение подобно понятию своими корнями уходит глубоко в действительность.
Каково же происхождение суждения? Почему помимо понятия возможна и необходима именно такая форма мышления? Ее возможность обусловлена характером самой действительности. Как подчеркивалось выше, объективную основу понятия составляет предметный характер действительности, т. е. наличие в нем предметов, обладающих качественной определенностью. Объективной же основой суждения служит ее связный характер, т. е. связи и отношения между ними.
Но что возникает раньше – понятие или суждение? Здесь налицо аналогия со знаменитой проблемой «курицы и яйца». Как известно, она неразрешима, если рассматривать курицу и яйцо в «готовом» виде. Если же подходить к ней с точки зрения теории развития, то обнаружится, что то и другое возникает одновременно: лишь в процессе эволюции органического мира курица становится курицей, кладущей яйца. Точно так же нельзя однозначно ответить на вопрос: «Что раньше – понятие или суждение?» Ни то ни другое в отдельности. Они складываются вместе, в процессе становления мышления. .Образование простейших понятий есть одновременно процесс возникновения суждений, и наоборот: «Это дом», «Дом большой», «Дом сделан из камня» и т. д. В конечном счете такова сама действительность, лежащая в основе понятий и суждений. Нельзя сказать, что» в ней возникло раньше: предметы или связи и отношения между ними. То и другое появляется одновременно в процессе развития окружающего мира.
Связи и отношения между предметами мысли носят самый разнообразный характер. Они могут быть между двумя отдельными предметами, между предметом и группой предметов, между группами предметов и т.п. Многообразие таких реальных связей и отношений находит свое отражение в многообразии суждений.
Для правильного понимания суждения важно учитывать, что одна из фундаментальных особенностей действительности заключается в ее своеобразной «раздвоенности»: предметы могут существовать или не существовать; обладать теми или иными свойствами или не обладать; находиться в тех или иных связях и отношениях с другими предметами или не находиться. В суждениях и раскрывается наличие или отсутствие чего-либо у чего-то. Например, железо обладает ковкостью. Наличие этой связи между предметом и отдельным свойством делает возможным суждение: «Железо ковко». Графически такую связь можно представить следующим образом:

где А – железо, а В – класс предметов, обладающих свойством ковкости.
В то же время железо не обладает пластичностью. Отсутствие связи предмета с этим свойством обусловливает возможность суждения: «Железо не пластично». Графически подобное соотношение выглядит так:

где А – железо, а С – класс предметов, обладающих свойством пластичности.
Другие примеры: «Россия – федерация», «Россия – не унитарное государство» или «Мораль древнее права», «Право связано с политикой».
Необходимость же суждений, как и понятий, коренится в практической деятельности людей. Взаимодействуя с природой в процессе труда, человек должен не только выделять те или иные предметы среди других, но и постигать их соотношения, чтобы успешно воздействовать на них.
Отсюда сущность суждения. Это форма мышления, посредством которой раскрывается наличие или отсутствие каких-либо связей и отношений между предметами. (Подобно тому как предмет в логике трактуется весьма широко – как все, на что может быть направлена мысль, так связи и отношения здесь понимаются в самом широком смысле – как всякие соотношения между предметами мысли.)
Важнейший отличительный признак суждения – утверждение или отрицание чего-либо о чем-либо. В понятии лишь выделяется сам предмет мысли. Например, «День», «Ночь», «Солнечный день» или «Несолнечный день». В суждении же акцентируется внимание на самом соотношении между какими-либо предметами мысли: «День солнечный» или «День не солнечный», «День прошел», «Ночь настала». Причем делается это в форме утверждения или отрицания. Другие, юридические примеры: «Закон» – понятие, а «Закон опубликован» – суждение; «Опубликованный закон» – понятие, а «Опубликованный закон вступил в силу» – суждение.
По своему содержанию суждение может быть истинным или ложным. Суждение истинно, если оно соответствует действительности (т.е. связывает то, что связано в самой действительности, и разъединяет то, что фактически разъединено). Вспомним наши примеры: «Железо ковко», «Железо не пластично» или «Россия – федерация», «Россия – не унитарное государство». Но суждение будет ложным, если оно не соответствует действительности: «Железо не ковко», «Железо пластично» или «Россия – не федерация», «Россия – унитарное государство».
Истинность и ложность – важнейшие характеристики суждения, отличающие его от понятия. Ведь понятие само по себе не может быть ни истинным ни ложным. Вспомним снова понятие «вечный двигатель»: оно пустое, но не ложное и не истинное. А суждение «Вечный двигатель невозможен» – истинно, суждение: «Вечный двигатель существует» – ложно. Истинность и ложность суждений не зависит от нашего отношения к ним, от того, считаем ли мы их истинными или ложными, а определяется отношением к самой действительности, носит объективный характер.
В то же время разграничение истинных и ложных суждений относительно. «День солнечный» – истинно, если вовсю сияет Солнце, и ложно, если льет дождь. Не учитывать этого – значит оказываться в положении Иванушки, который применил пожелание: «Таскать вам не перетаскать», доброе в одной житейской ситуации, к прямо противоположной.
Установление истинности или ложности суждения не представляет труда лишь в простейших случаях типа: «День солнечный», «Ночь лунная». Достаточно взглянуть в окно, чтобы убедиться в истинности или ложности подобных суждений. В научном же познании истинность или ложность суждения устанавливается в итоге более или менее длительного исследования. Например, в течение тысячелетий считалось истинным суждение «Вселенная стационарна». Но только в начале XX в. была обнаружена его ложность и установлена истинность суждения «Вселенная нестационарна». Это означает, что, как и все на свете, она подвержена эволюции, развивается от одного, первоначального состояния к какому-то другому («разбегание галактик»).
В юридической практике установление истинности или ложности чего-либо – тоже нередко сложный, мучительный процесс. Вспомним, сколько времени понадобилось для расследования деятельности ГКЧП, чтобы установить виновность или невиновность каждого из его членов. И лишь амнистия в связи с принятием Конституции Российской Федерации 1993 г. разом разрубила этот «гордиев узел». Но тут есть и своя специфика. Во-первых, юридическое выяснение объективной истины по делу предполагает в качестве непременного условия точное соблюдение норм уголовного или гражданского права. А во-вторых, помимо общезначимых понятий «истинность» и «ложность» и равнозначных им «правдивость» и «неправдивость» особо выделяются еще понятия специфически юридические: «заведомая ложность» и «добросовестное заблуждение». Могут быть заведомо ложные показания свидетеля или потерпевшего, заведомо ложное заключение эксперта, заведомо неправильный перевод с одного языка на другой. Так, по российскому уголовному праву заведомо ложное показание свидетеля квалифицируется как преступление, состоящее в умышленном сокрытии им фактов или сознательном извращении истины. Опасность такого преступления кроется в том, что в результате преступник может быть оправдан, а невиновный осужден. Поэтому за дачу ложных показаний предусмотрена ответственность.
Добросовестное заблуждение – это искажение истины не по умыслу, не сознательно, а по ошибке, из-за незнания, недостаточной компетентности и т.д. В этом случае оснований для привлечения к ответственности нет.
Роль и функции суждений, их структура. Суждения играют поистине огромную – не менее, чем понятия, – роль в мышлении, выполняя тоже важные функции в познании и общении. Но конкретное содержание роли и функций суждений по сравнению с понятиями качественно иное. Если назначение понятия сводится к выделению предмета мысли, то суждение – универсальная форма раскрытия реальных связей и отношений между предметами в природе и обществе, между любыми предметами мысли.
В форме суждения происходит процесс образования понятия, хотя понятие, как отмечалось, есть предпосылка суждения. Недаром Гегель, характеризуя диалектику понятия и суждения, остроумно заметил, что понятие – свернутая форма суждения, а суждение – развернутая форма понятия.
Форму суждения обретает также процесс оперирования уже сложившимися, готовыми понятиями. Чтобы подвести тот или иной предмет под существующее понятие, необходимо, во-первых, знать содержание этого понятия; во-вторых, выявить характерные признаки исследуемого предмета и, в-третьих, установить соответствие между тем и другим. Например: «Холст есть товар», «Мошенничество – преступление», «Свидетель неправдив». В форму суждения облекаются определения, а также приемы, сходные с ними (сравнение, характеристика, описание и др.). Форма суждения используется в операциях деления и расчленения, классификации и типологии.
В виде суждений формулируются, по существу, все научные положения, ими выражаются достигнутые научные истины. Особое значение суждений определяется тем, что они служат мыслительной формой, в которую, как правило, облекаются объективные закономерности окружающего мира, открываемые естественными и общественными науками, например: закон всемирного тяготения, закон сохранения и превращения энергии, закон единства организма и среды, закон соответствия производственных отношений характеру и уровню развития производительных сил. Суждения служат также универсальной формой духовного общения между людьми, взаимообмена информацией о самых различных сторонах действительности.
Специально подчеркнем, что в законодательстве любая норма есть суждение, т. е. утверждение или отрицание какого-либо права или обязанности. Так, Конституция Российской Федерации состоит из множества статей, каждая из которых представляет собой либо отдельное суждение, либо совокупность суждений. Например: «Носителем суверенитета и единственньм источником власти в Российской Федерации является ее многонациональный народ» (ст. 3). Или: «Человек, его права и свободы являются высшей ценностью. Признание, соблюдение и защита прав и свобод человека и гражданина – обязанность государства» (ст. 2).
Однако норма – это особая, весьма сложная разновидность суждений. Правовые суждения-нормы возникают лишь на определенном этапе развития общества – с появлением частной собственности и представляют собой отражение и закрепление соответствующих общественных отношений между людьми, в первую очередь экономических. Их назначение состоит в том, что они регулируют эти отношения, способствуя их совершенствованию и развитию. В них запечатлеваются установленные или санкционированные государством разрешения и запрещения, права и обязанности. Естественно поэтому, что такие суждения имеют и особую структуру. Они содержат указание, когда и при каких условиях применяется норма, как должен в соответствии с ней поступать человек, и какие санкции последуют, если эта норма не выполняется. Специфика таких суждений-норм во всей их сложности исследуется в особом разделе современной логики – модальной логике, где есть специальный подраздел «логика норм».
Естественно также, что не только законодательство, но и все судопроизводство – уголовное, гражданское – неразрывно связано с использованием суждений. Любопытно отметить, что в Уголовно-процессуальном кодексе Российской Федерации прямо указывается на это обстоятельство: «Присяжные заседатели не могут разглашать суждения, имевшие место во время совещания» (ст. 341). И это понятно: ведь само слово «суд» имеет общий корень со словами «судить», «обсуждать», «рассуждать», «суждение».
Будучи сложной формой мышления, суждение обладает особой структурой. Она обусловлена тем, что всякое суждение предполагает наличие, по крайней мере, двух мыслимых предметов, так или иначе соотносящихся друг с другом. Поэтому суждение состоит из двух основных компонентов – субъекта и предиката, определенным образом связанных между собой.
Субъект суждения (от лат. subjectum – лежащий в основе) – это мысль о предмете, о котором утверждается или отрицается что-либо. Сокращенно он обозначается в логике буквой «S».
Предикат суждения (от лат. praedicatum – сказанное) – мысль о том, что именно утверждается или отрицается о предмете. Сокращенно он обозначается буквой «Р».
Субъект и предикат называются терминами суждения. Поскольку они выражаются понятиями, то очевидно, что применительно к суждениям понятия выполняют роль их терминов. В этом состоит одна из логических функций понятий.
Термины суждения носят соотносительный характер. Один не существует без другого (нет субъекта без предиката, как и наоборот). Обусловлено это тем, что сами связи и отношения не существуют отдельно от вещей и обратно. Есть лишь вещи, обладающие свойствами (и притом многими свойствами), а следовательно, находящиеся в различных связях и отношениях.
Однако роль терминов в суждении далеко не одинакова. Субъект содержит уже известное знание, а предикат несет о нем новое знание. Благодаря этому обеспечивается не только связность знаний, но и их накопление и развитие, их прогресс.
Правда, различение терминов не абсолютно. То, что в одном суждении выступает как субъект, в другом может быть предикатом и соответственно наоборот. Например: «Это (S) береза (Р)»; «Береза (S) – дерево (Р)»; «Дерево (S) – живой организм (Р)».
Связь (отношение) между субъектом и предикатом, отражая объективное отношение между мыслимыми предметами, раскрывается посредством логической связки. В русском языке она выражается словами «есть» («не есть»), «является» («не является»), «представляет собой» («не представляет собой») и другими, синонимичными им. Двоякий характер связки («есть – не есть») и отражает реальную раздвоенность мира – наличие или отсутствие чего-либо у чего-то. В ряде случаев связка выражается с помощью тире. Например: «Не пойман – не вор». (Предполагается: «Не пойманный не есть вор».) Нередко она попросту отсутствует, а логическое соотношение между субъектом и предикатом раскрывается посредством грамматического согласования слов: «Конституция принята», «Закон не действует» (ср.: «Конституция есть то, что принято», «Закон не есть то, что действует»).
Связка играет в суждении особую роль. Именно благодаря ей суждение становится суждением. В ней выражается глубочайшая сущность суждения: ведь только она раскрывает наличие или отсутствие чего-либо у предмета мысли и заключает в себе утверждение или отрицание.
Раскрываемая в суждении связь между предметами мысли предстает обычно как связь понятий. Ее только не следует ни отрывать от действительности, ни отождествлять с ней. В форме суждения раскрываются по существу все многообразные отношения между понятиями по их содержанию и объему – сравнимости и несравнимости («Роза – растение», «Роза – не верблюд»); совместимости и несовместимости: равнозначности («А. Пушкин – автор романа «Евгений Онегин»), подчинения («Все адвокаты – юристы»), пересечения («Некоторые юристы – таможенники») и т. д.
Поскольку субъект и предикат, будучи понятиями, могут рассматриваться с точки зрения их содержания и объема, то связка тоже может быть истолкована в двух планах – содержательном и объемном.
В содержательном плане она выражает принадлежность или непринадлежность признака или совокупности признаков предмету. С объемной точки зрения она раскрывает включение подкласса (подмножества) в класс (множество) предметов или принадлежность элемента классу (множеству).
В самом общем виде суждение можно наглядно выразить следующей формулой: «S есть (не есть) Р». В современной логике «S» и «Р» называются логическими переменными, так как они могут вмещать в себя самое различное содержание. А связка – это логическая постоянная. В ней заключено одно и то же, неизменное содержание: она всякий раз служит показателем наличия или отсутствия чего-либо у предмета мысли.
Единство элементов мысли в суждении, обеспечиваемое связкой, есть лишь отражение реального единства мира: самих вещей, их свойств, связей и отношений.
2. Суждение и предложение
Суждение и назначение предложений. Подобно понятию, суждение выражается посредством языка. Но, как более сложная форма мышления, она облекается и в более сложную языковую форму. Если материальной оболочкой понятия служит слово (или словосочетание), то материальной формой существования, носителем суждения выступает предложение (или сочетание предложений). Образно говоря, суждение есть «душа» предложения (в которой отражается какой-то фрагмент действительности), а предложение – «плоть и кровь» суждения.
Однако связь между ними неоднозначна. Всякое суждение выражается в предложении, но не всякое предложение выражает суждение.
Как известно, предложения по своему назначению (или цели высказывания) делятся на повествовательные, вопросительные и побудительные.
Повествовательные предложения и выражают собой суждения. Например: «Я потерял книгу». Здесь сообщается что-то о чем-то – следовательно, содержится утверждение (или отрицание), которое может быть истинным или ложным. Другие примеры: «Криминалистика – наука», «Подсудимый невиновен»; «Пенсия будет повышаться».
Но связь здесь подвижна. Одно и то же суждение может выражаться в разных повествовательных предложениях. Например: «Аристотель является основателем науки логики»; «Воспитатель Александра Македонского – основоположник логики как науки»; «Великий Стагирит (Аристотель был родом из Стагиры. – Е. И.) положил начало логической науки».
В свою очередь, одно и то же предложение может заключать в себе разные суждения. Например, высказывание «Аристотель – основатель логики» может быть использовано для выражения, по крайней мере, трех мыслей: «Аристотель (а не кто-то другой) является основателем логики»; «Аристотель – основатель (а не просто один из представителей) логики»; «Аристотель – основатель логики (а не какой-то другой науки)». Аналогичные примеры: «Москва – столица России»; «Высшая цель – благо народа».
Повествовательные предложения, в свою очередь, могут быть не только двусоставными, но и односоставными (назывными, безличными, неопределенно-личными и т.п.). Последние тоже выражают собой суждения. Возьмем, например, назывное предложение: «Весна». Достаточно поставить вопрос: «Что это за время года?» Ответ: «Весна» (или: «Это весна»). Здесь налицо суждение. Отсюда становится ясным логический смысл различных наименований – вывесок на зданиях, названий книг, кинофильмов, живописных полотен. Так, слово «суд», взятое безотносительно к чему-либо, заключает в себе понятие и только. Но это же слово в качестве вывески на здании выражает уже суждение: «Это суд». И оно может быть как истинным, так и ложным – в зависимости от того, висит ли вывеска на здании суда или театра. В этой связи вспоминается случай. Как-то под Ленинградом мы с женой осматривали галерею скульптурных портретов великих людей, расположенную под открытым небом. На одном из постаментов находился бюст худощавого с умным лицом человека, а подпись гласила: «Сенека». Я не поверил своим глазам. На противоположной стороне галереи стоял бюст другого человека – круглолицего и бородатого. Подпись, однако, гласила: «Цицерон». Я обратил на это внимание экскурсовода: «Вот этот Сенека – не Сенека, а этот Цицерон – не Цицерон». Внимательно присмотревшись, она согласилась. Оказывается, после уборки бюсты были расставлены неправильно. Поэтому надписи-суждения под ними стали ложными.
Еще примеры. «Преступление» и «наказание» – слова, выражающие лишь понятия из юридической области. Эти же слова, взятые Достоевским в качестве названия своего известного произведения, – уже суждение: «Это роман “Преступление и наказание”». Интересно отметить, что до наших дней дошел замечательный литературный памятник Древней Руси, который назывался именно так: «Се (это) повести временных лет…»
Безличные предложения тоже выражают суждения, например: «Морозит», «Грустно», хотя предмет мысли здесь лишь подразумевается (внешняя среда; человек, испытывающий определенное душевное состояние).
Суждение, взятое в единстве с его языковой формой – повествовательным предложением, именуется в символической логике «высказыванием» (отсюда – «логика высказываний»).
Вопросительные предложения, наоборот, не выражают суждений. Их логическая природа иная, и она специально исследуется в такой отрасли логики, как «логика вопросов». Эта отрасль ныне интенсивно развивается, что обусловлено рядом обстоятельств, и прежде всего – потребностями развития компьютерной техники, где все большую роль играют диалоговые и другие системы. Однако логика вопросов имеет не только сугубо техническое, а и более широкое, общенаучное и практическое значение.
Если, как сказано, вопросительные предложения не выражают суждений, то что же они тогда представляют собой? Рассмотрим пример: «Найдена ли книга?» Здесь непосредственно нет ни утверждения, ни отрицания. Иначе мы сказали бы просто: «Книга найдена» (или «Книга не найдена»). В вопросительных предложениях суждения содержатся лишь в скрытом виде, имплицитно: «Книга существует», «Книга потеряна», «Книгу ищут». Однако логическая сущность вопроса к такого рода суждениям отнюдь не сводится. Он представляет собой посредствующее звено между одними, известными суждениями и другими, новыми. Вот почему вопрос всегда предполагает ответ («Книга найдена» или «Книга не найдена»). Это и есть новое суждение.
Не будучи ни утверждением, ни отрицанием, вопрос не может быть также истинным или ложным. Он бывает лишь правильным и неправильным. Это всецело зависит от того, какие суждения лежат в его основе – истинные или ложные. Например: «Закончил ли Аристотель чтение лекций в нашей Академии?» Здесь предполагаются ложные суждения о том, что «Аристотель жив», что зачем-то «Он приехал в нашу Академию» и в настоящее время «Он читает здесь лекции». Следовательно, и самый вопрос, основанный на них, сформулирован неправильно.
Вопрос как особая логическая операция, тесно связанная с суждением и в то же время отличная от него, также возникает в процессе практической деятельности людей. Воздействуя на предметы и явления действительности, человек отражает ее не пассивно, а активно. Это воздействие требует все новых знаний. И тогда человек запрашивает их у действительности, у других людей. Возникая из недостатка информации о том или ином предмете мысли, вопрос служит средством ее восполнения. Если сказать кратко, это логическая форма перехода от известного к неизвестному. В вопросе особенно рельефно проявляется диалектический характер процесса познания. Правда, именно поэтому ответ на него возможен далеко не всегда. Вспомним знаменитое, актуальное и поныне, обращение Н. Гоголя: «Русь, куда несешься ты? Дай ответ. Не дает ответа». Впрочем, ответа на этот жгучий вопрос о путях общественного развития страны нет и сегодня.
Познавательная роль вопросов очень велика. Наряду с суждениями они позволяют осуществлять процесс научного познания, двигаться от незнания к знанию, от менее полного знания к более полному, более точному и глубокому. Форму вопроса нередко принимают цели и задачи исследования, научные проблемы, гипотезы и т.д., без которых не может быть развития науки.
Вопросы весьма часто используются в практике общения – как средство получения новой информации, расширения кругозора, выяснения отношений. При знакомстве мы спрашиваем: «Как Вас зовут?»; «Учитесь или работаете?»; «Сколько Вам лет?». При встрече со знакомыми или друзьями: «Как живы-здоровы?»; «Что нового?». Даже последний пьяница-забулдыга желает знать от своего собутыльника об отношении к себе: «Ты меня уважаешь?»
Вопросно-ответная форма – эффективное средство осуществления учебного процесса. Эта форма широко применяется врачами во время беседы с больными. Ее широко используют в интервью с известными людьми – в печати, по радио, телевидению.
Она особенно важна также в юридической практике – например, когда ведется расследование какого-либо дела, а также в ходе самого суда. «Вопросы здесь задаю я» – эта фраза следователей и судей стала крылатым выражением.
Вопросно-ответные ситуации предполагают выполнение ряда требований. Прежде всего, это требования к вопросам. Главное из них – предпосылки вопроса должны быть истинными. Все значение этого видно из лукавого вопроса, который дошел до нас из глубины веков: «Перестал ли ты бить своего отца?» Здесь в качестве предпосылки используется суждение, которое во многих случаях окажется ложным: «Ты бил своего отца». Но если оно ложно, то правильный ответ по формуле «да-нет» невозможен: если перестал бить, значит, бил; если не перестал, значит, продолжаешь бить. Недаром говорят: «На глупый вопрос может быть глупый ответ».
Другое требование: сам вопрос должен быть сформулирован точно и определенно – так, чтобы был возможен правильный ответ. Если я во время экзамена спрошу студента: «Что Вы думаете о логике?» – то это вопрос неопределенный, так как думать о логике, вообще говоря, можно что угодно. Поэтому он в состоянии поставить в тупик даже самого умного студента.
Иногда вопрос лишь кажется неясным или неопределенным, но только потому, что ответ на него неясен или неизвестен. Во время экзамена бывает так, что студент говорит: «Я не понимаю вопроса». Это зачастую означает, что он не знает ответа.
Особые требования предъявляются и к самим ответам. Поскольку ответ принимает форму суждения, то он прежде всего должен быть истинным. Это не всегда удается на практике, но стремиться к этому необходимо.
Надо также учитывать, что всякое суждение принимает форму утверждения или отрицания. Поэтому, если на поставленный вопрос ответ дается утвердительный, то тем самым признается все, что стоит за самим вопросом. Но если что-то не признается, то это должно быть специально оговорено. Вспомним поучительный анекдот. «Верно ли, что Петров выиграл в лотерею «Волгу»?» – «Верно, но не Петров, а Сидоров, и не «Волгу», а сто рублей, и не в лотерею, а в преферанс, и не выиграл, а проиграл».
Ответ, далее, должен быть не только истинным по содержанию, но и правильным по форме: он должен соответствовать вопросу. Если на точно сформулированный вопрос дается неполный или избыточный ответ, то это, строго говоря, логическая ошибка.
На определенный вопрос требуется давать определенный ответ. Но вот что получается, если это требование не соблюдается. В одном интервью на вопрос корреспондента известному артисту: «Алкоголь мешает или способствует сближению?» был дан ответ: «Навряд ли. Не очень уверен. Вообще даже не уверен. И вообще даже против».
Ответа не получилось. Вот почему заметка об этом была характерно названа: «Так мешает или способствует?» (МК в воскресенье. 4 февраля 2001 г.).
Наиболее важные аспекты юридических вопросно-ответных ситуаций специально оговорены в законодательстве. Так, в Уголовно-процессуальном кодексе Российской Федерации, в гл. 26. «Допрос» (который как раз и состоит из вопросов и ответов), в частности, подчеркнуто, что «задавать наводящие вопросы запрещается»; «адвокат присутствует при допросе, но при этом не вправе задавать вопросы свидетелю и комментировать его ответы»; «после дачи показаний следователь может задавать вопросы каждому из допрашиваемых лиц. Лица, между которыми проводится очная ставка, могут с разрешения следователя задавать вопросы друг другу».
Во время суда при допросе подсудимого «председательствующий отклоняет наводящие вопросы и вопросы, не имеющие отношения к уголовному делу»; «Суд задает вопросы подсудимому после его допроса сторонами» (ст. 275); «никакие вопросы к подсудимому во время его последнего слова не допускаются» (ст. 293). В ст. 299 «Вопросы, разрешаемые судом при постановлении приговора», дается их подробный перечень.
Особенно тщательно в УПК РФ разработаны вопросно-ответные ситуации в суде с участием присяжных заседателей. Так, согласно ст. 328: «Председательствующий разъясняет кандидатам в присяжные заседатели их обязанность правдиво отвечать на заданные им вопросы …». В ст. 338 предусмотрена «постановка вопросов, подлежащих разрешению присяжными заседателями». В ст. 339 раскрыто содержание вопросов присяжным заседателям. Здесь выделены 3 основных вопроса: доказано ли деяние; доказано ли, что его совершил подсудимый; виновен ли он.
Выдвигаются особые требования к вопросам, задаваемым во время судебного заседания: «Формулировки вопросов не должны допускать при каком-либо ответе на них признания подсудимого виновным в совершении деяния, по которому государственный обвинитель не предъявлял ему обвинения либо не поддерживал обвинения к моменту постановки вопросов» (ст. 339). После основного вопроса о виновности подсудимого могут ставиться частные вопросы о таких обстоятельствах, которые увеличивают или уменьшают степень виновности, либо изменяют ее характер, влекут за собой освобождение подсудимого от ответственности (причем сами эти вопросы специально указываются – см. ст. 339).
Перед совещанием присяжных заседателей председательствующий обращается к ним с напутственным словом. И снова в нем речь идет о вопросно-ответной ситуации. Председательствующий разъясняет порядок совещания, в частности, – «подготовки ответов на поставленные вопросы, голосование по ответам и вынесение вердикта» (ст. 340).
Наконец, вынесение самого вердикта предполагает голосование «за утвердительный ответ» и «за отрицательный ответ». При этом формулируется специальное требование к ответам:
«Ответы на поставленные перед присяжными заседателями вопросы должны предусматривать собой утверждение или отрицание с обязательным пояснительным словом или словосочетанием, раскрывающим или уточняющим смысл ответа» («Да, виновен»; «Нет, не виновен»).
Особой тщательности формулировок требуют вопросы, имеющие большое общественное значение, – например, выносимые на всенародный референдум. Так, в марте 1991 г., еще в условиях существования СССР, состоялся первый Всесоюзный референдум по вопросу: «Считаете ли Вы необходимым сохранение Союза Советских Социалистических Республик как обновленной Федерации равноправных суверенных республик, в которой будут в полной мере гарантированы права и свободы человека любой национальности?» Столь сложный вопрос был сформулирован не вполне корректно. Он задавался еще в условиях старого Союза, и не было ясно, в какой мере этот Союз будет обновлен. Тот, кто хотел быть против сохранения Союза, выходит, выступал бы против его обновления. А тот, кто желал обновления Союза, вовсе не обязан был голосовать за его сохранение.
От вопросительных предложений в собственном смысле отличаются так называемые риторические вопросы. Как и повествовательные предложения, они по существу тоже выражают собой суждения, но в особой, специфической форме. Например: «Как тебе не стыдно?» Здесь лишь усиливается категоричность, безусловность суждения: «Ты должен этого стыдиться». Еще пример. «Кто не любит хорошо поесть?» Или цицероновское: «Quousque tandem?» («До каких пор, наконец?»), которым лишь подчеркивалось его гневное нетерпение: «Пора этому положить конец». У Н. Гоголя: «И какой же русский не любит быстрой езды?»
Отсюда ясно, что риторический вопрос не требует ответа. «Куда, куда вы удалились, весны моей златые дни?» – вопрошает Ленский в романе Пушкина «Евгений Онегин». Разве здесь требуется конкретный ответ – куда именно они удалились? Нет, этим лишь подчеркивается печальная мысль, что «весны… златые дни» ушли безвозвратно. У того же Пушкина: «Что же и составляет величие человека, как не мысль?» взятое нами в качестве эпиграфа ко всей книге. Разве Пушкина интересуют здесь помимо мысли еще какие-либо составляющие величия человека? Любопытно отметить, что, говоря о риторических вопросах, мы сами невольно использовали их: «Разве здесь…»
Множество примеров использования риторических вопросов можно найти и в современной художественной литературе. Так, у известного поэта и прозаика В. Сысоева находим: «Что знали бы мы о горьком, не будь сладкого?» Это эквивалентно суждению-утверждению: «Все познается в сравнении». Или: «Где кончается раздражительность и начинается гнев?» Здесь на конкретном примере демонстрируется великая философская диалектическая мысль: как и в природе, в общественной жизни нет жестких разграничительных линий между явлениями; одно переходит в другое постепенно, незаметно, так что грань указать невозможно. И еще почти шутливое: «Надо ли помогать друзьям садиться в лужу?» Ответ ясен сам собой.
Своеобразие риторических вопросов позволяет воспользоваться ими как средством создания остроты. В этой связи юристам полезно поразмышлять над мудрым высказыванием Козьмы Пруткова о единстве и многообразии законов: «Если бы вся Вселенная обратилась в одно государство, то как не установить повсюду одинаковых законов?»
Побудительные предложения подобно вопросительным тоже основаны на каких-либо суждениях. Например: «Найдите книгу!» Здесь предполагается, что «Книга существовала», «Книга потеряна», «Книга необходима». Однако логический смысл и назначение таких предложений состоят не в констатации этих фактов, а в побуждении кого-то к совершению действия, требовании, пожелании, просьбе. Аналогичный пример: «Встать, Суд идет!»
Побуждения – тоже продукт деятельности людей. В ходе их совместных действий возникает потребность в том или ином волеизъявлении, проявлении чувств и т. п. Она и находит свое конкретное выражение в побудительных предложениях.
Познавательное значение побуждений также велико. В них так или иначе закрепляется человеческая мудрость, основанная на опыте и знаниях. Вот почему многие побудительные предложения стали своего рода афоризмами, превратились в пословицы и поговорки. «Не судите, да не судимы будете», – сказано в Священном Писании. «Познай самого себя!» – изречение, высеченное на колонне при входе в храм Аполлона в Дельфах (Греция). «…Старайся быть точен, как свидетель при показаниях», – советовал Цицерон.
А как актуально ныне звучат такие высказывания: «Голосуй за человека, который обещает меньше всех, будешь меньше всех разочарован»; «Если хочешь узнать, что представляет собой человек, дай ему власть», «Надейся на лучшее, а приготовься к худшему».
Побудительные предложения широко используются в художественной литературе – и нередко тоже для выражения глубокой философской мысли, назидания, остроты или шутки. Так, у того же В. Сысоева: «На пороге вечности не ноги вытирай, а душу отмывай»; «Забудь о неизбежности, помни о выборе»; «Не надо помогать всему человечеству, помоги хотя бы одному».
Итак, каждому из типов предложений соответствует своя логическая форма: повествовательному предложению – суждение; вопросительному – вопрос как форма перехода от одного суждения к другому; побудительному – побуждение кого-то к чему-то. Вопросительные и побудительные предложения, хотя и заключают в себе суждения, но отнюдь не сводятся к ним. Вот почему мы сказали, что всякое суждение есть предложение, но не всякое предложение есть суждение.
Суждение и структура предложения. Неоднозначны отношения также между структурой суждения и структурой предложения. В наиболее общем виде различие между ними сводится к тому, что в мышлении людей, говорящих на самых разных языках, суждение имеет одну и ту же структуру, а предложения в этих языках строятся по-разному.
Но и в рамках одного и того же языка – например, русского – структуры суждений и предложений различны. Так, в суждении лишь два взаимосвязанных члена: субъект и предикат. А в предложении могут быть как главные члены – подлежащее и сказуемое, составляющие его грамматическую основу, так и второстепенные – определение, дополнение, обстоятельство.
Нет однозначного соответствия даже между субъектом и предикатом суждения, с одной стороны, подлежащим и сказуемым предложения – с другой. Такое соответствие может иметь место лишь в простых нераспространенных предложениях типа: «Роза красна», «Люди смертны», «Суд идет». В распространенных же предложениях дело обстоит сложнее. Так, в предложении «Любой, кто получил выгоду от преступления, виновен в его совершении» подлежащее – «любой», а сказуемое – «виновен». Субъект же заключенного здесь суждения выражен группой подлежащего: «любой, кто получил выгоду от преступления», а предикат – группой сказуемого: «виновен в его совершении». Причем может быть и обратная ситуация, когда субъект суждения выражен в предложении сказуемым (или его группой). Например: «Выдающимся русским писателем является М. Шолохов». Здесь субъект суждения – «выдающийся русский писатель» выражен группой сказуемого, а предикат – «М. Шолохов» – подлежащим. Более сложный, юридический пример: «Разрешено все, что не запрещено законом». Субъект суждения здесь выражен сказуемым («то, что разрешено»), а предикат – группой подлежащего («все, что не запрещено законом»).
Наконец, субъект и предикат суждения подвижны, тогда как подлежащее и сказуемое предложения неподвижны.
Примеры. «Суд состоится». Субъект суждения выражен здесь подлежащим предложения – «суд», а предикат – сказуемым «состоится» (ср.: «Суд есть то, что состоится»). «Суд состоится завтра». Предикат здесь выражен уже другим словом – «завтра» (ср.: «День, когда состоится суд, – это завтра»). «Суд состоится завтра в Москве». Предикат выражен третьим словом – «Москва» (ср.: «Город, где состоится завтра суд, – Москва»).
Причина подвижности предиката – в его характере как носителя новизны.
Чтобы выявить логический смысл предложения, надо найти в нем субъект и предикат суждения. А это, как очевидно, не простая задача. Ведь они подвижны и могут выражаться в предложении разными способами. Знание таких способов имеет огромное практическое значение для точного выражения наших мыслей. О каких же конкретно способах идет речь?
Прежде всего это соответствующая грамматическая форма предложения. Оно может быть построено так, чтобы субъект суждения был выражен непременно подлежащим (или его группой), а предикат – сказуемым (или его группой). Если, например, мы хотим высказать мысль, что именно Петров, а не какой-то другой адвокат, будет выступать в суде, то ей можно придать следующую грамматическую форму: «Адвокат, который будет выступать в суде, – это Петров». Но если мы хотим выразить другую мысль, что Петров будет выступать именно в суде, а не на коллегии адвокатов, то можем грамматически оформить ее так: «Место, где будет выступать адвокат Петров, – это суд». Правда, при таком способе выражения мысли сама конструкция предложения может оказаться искусственной или громоздкой. Поэтому ограничиваться им нельзя.
Другой способ – порядок слов в предложении. Его суть в том, что все известное в суждении сдвигается в сторону субъекта, в начало предложения, а предикат как носитель новизны ставится в конце. Представим себе, что психолог читает лекцию о корыстолюбии как одной из психологических черт личности и, в частности, раскрывает роль корысти в совершении преступлений. Как же в этом случае можно построить фразу? «Корысть – основной мотив преступлений». Здесь «корысть» – субъект, а «основной мотив преступлений» – предикат. А если лекцию читает юрист и она посвящена другой теме – преступлениям, в частности их мотивам? Тогда правильнее построить фразу иначе: «Основной мотив преступлений – корысть». Почему? Потому что субъектом здесь является «основной мотив преступлений», а предикатом – «корысть».
Порядок слов используется в практике мышления нередко. Так, в Священном Писании сказано: «В начале было Слово, и Слово было у Бога, и Слово было Бог». Здесь «Слово» стоит то в конце предложения, то в его начале. Почему? Потому что в разных предложениях оно несет совершенно различную смысловую нагрузку. В первом оно выражает новое знание, следовательно, выступает предикатом (ср.: «То, что было в начале, – это Слово»). Во втором и третьем оно выражает уже известное, т.е. является субъектом, а новое знание воплощено в словах: «у Бога» и «Бог».
С этих позиций понятен также порядок слов в «Фаусте» Гете: «В начале было дело». Здесь содержится совершенно иной ответ на тот же вопрос: «Что было в начале?» «То, что было в начале, – это дело». Но если мы по поводу какой-то иной ситуации скажем: «Дело было вначале» («а отдых был потом»), то слово «дело» будет выражать уже субъект, а «вначале» – предикат (ср.: «Делу – время, потехе – час»). Еще примеры: «Мы – не рабы», «Рабы – не мы»; «Люди – не боги», «Боги – не люди». Субъект и предикат здесь меняются потому, что в этих предложениях заключены совершенно разные мысли.
Еще одним из способов выражения предиката служит логическое ударение. В устной речи оно достигается усилением голоса, а на письме – подчеркиванием. Так, в предложении «Преступление произошло вчера» при одном и том же порядке слов, но с помощью логического ударения могут быть выражены три разные мысли: «Преступление (а не какое-то другое событие) произошло вчера»; «Преступление произошло (а могло не произойти) вчера»; «Преступление произошло вчера (а не позавчера и не сегодня)».
Наконец, к способам выражения субъекта и предиката относится контекст. Например, трудно сразу определить логический смысл, т.е. найти субъект и предикат в известном высказывании акад. И. Павлова: «Большого напряжения и великой страсти требует наука от человека». Здесь помогает контекст. О чем идет речь в предыдущей фразе? О науке. «Наука требует от человека всей его жизни». Значит, в последующей фразе субъектом будет уже не «наука», а «то, что требует наука от человека», предикатом же – «большого напряжения и великой страсти».
Знание способов выражения субъекта и предиката в предложении позволяет правильно устанавливать логическую структуру суждения. А это, в свою очередь, необходимо для правильного преобразования суждений и построения умозаключений.
Глава II. Классификация суждений
Обладая определенной структурой, суждения различаются в первую очередь по степени сложности. В зависимости от этого все их бесконечное многообразие можно разделить на две обширные группы (два типа) – простые и сложные.
Простые суждения характеризуются тем, что в них нельзя выделить правильную часть, которая, в свою очередь, была бы самостоятельным суждением. Например: «Я человек» или «Ничто человеческое мне не чуждо».
Сложные суждения состоят из двух и более простых суждений, тем или иным способом связанных между собой. Примером может служить соединение двух предыдущих простых суждений, которые вместе образуют известный афоризм: «Я человек, и ничто человеческое мне не чуждо».
Рассмотрим каждый из этих типов суждений в отдельности.
1. Простые суждения
Природа простых суждений. Простые суждения, поскольку в них раскрывается безусловная связь между предметами мысли, называются еще иначе категорическими. С точки зрения функций они служат отражением той или иной относительно самостоятельной связи объективного мира – независимо от того, какая это связь по своему содержанию. С точки зрения структуры простые категорические суждения, будучи далее неделимыми на еще более простые суждения, включают в себя в качестве составных частей лишь понятия, образующие субъект и предикат.
Однако простые суждения весьма многообразны по своим проявлениям. Они делятся на виды по следующим основным логическим признакам: характеру связки, субъекта, предиката, а также по отношению между субъектом и предикатом. Особое значение в логике придается делению простых суждений на виды по характеру связки (ее качеству) и субъекта (по его количеству).
Виды суждений по качеству и количеству. Качество суждения – одна из важнейших его логических характеристик. Под ним разумеется не фактическое содержание суждения, а его самая общая логическая форма – утвердительная или отрицательная. В этом проявляется наиболее глубокая сущность всякого суждения вообще – его способность раскрывать наличие или отсутствие тех или иных связей и отношений между мыслимыми предметами. А определяется это качество характером связки – «есть» или «не есть». В зависимости от этого простые суждения делятся по характеру связки (или ее качеству) на утвердительные и отрицательные.
В утвердительных суждениях раскрывается наличие какой-либо связи между субъектом и предикатом. Выражается это посредством утвердительной связки «есть» или соответствующими ей словами, тире, согласованием слов. Общая формула утвердительного суждения – «S есть Р». Например: «Киты – млекопитающие».
В отрицательных суждениях, наоборот, раскрывается отсутствие той или иной связи между субъектом и предикатом. И достигается это с помощью отрицательной связки «не есть» или соответствующими ей словами, а также просто частицей «не». Общая формула – «S не есть Р». Например: «Киты не рыбы». Важно при этом подчеркнуть, что частица «не» в отрицательных суждениях стоит непременно перед связкой или подразумевается. Если же она находится после связки и входит в состав самого предиката (или субъекта), то такое суждение все равно будет утвердительным. Например: «Мои стихи живит не ложная свобода», «Не всякий плод сладок».
В связи с этим выделяются две основные разновидности утвердительных суждений: а) суждения с предикатом, который выражен положительным понятием. Формула «S есть Р». Пример: «Судьи самостоятельны»; б) суждения с предикатом, представляющим собой отрицательное понятие. Формула «S есть не-Р». Пример: «Судьи независимы». Другие примеры: «Многие законы действуют», «Некоторые законы бездействуют».
Отрицательные суждения тоже имеют две разновидности: •а) суждения с положительным предикатом. Формула: «S не есть Р». Пример: «Петров не есть патриот»; б) суждения с отрицательным предикатом: «Петров не есть непатриот». Еще примеры: «Органы местного самоуправления не входят в систему органов государственной власти» и «Федеральное Собрание не является негосударственным органом».
Деление суждений на утвердительные и отрицательные в известной степени относительно. Любое утверждение содержит в себе в скрытом виде отрицание. Вспомним афоризм: «Determinatio est negatio». И наоборот. Так, если «Это слон», то, значит, «это» не какое-то другое животное – лев, жираф и т. д. А если «Это не слон», то, значит, «это» другое животное – лев, жираф и т. п. Вот почему утвердительное суждение можно выразить в форме отрицательного и наоборот. Например: «Петров – патриот» – «Петров не есть непатриот». Здесь как в математике: двойное отрицание равно утверждению.
Познавательное значение утвердительных и отрицательных суждений определяется их особенностями, которые носят объективный характер. Утвердительные суждения (если они истинные) дают знания о том, что именно представляет собой предмет мысли, какова его качественная определенность, выделяющая его среди других предметов. А так как в природе и обществе все взаимосвязано, то из любого утверждения вытекают соответствующие, и притом многообразные, последствия. Так, говоря, что «Это человек», мы в то же время утверждаем, что «Это животное, способное к труду, одаренное разумом и речью» и т. д.
Отрицательные (истинные) суждения, вопреки мнению некоторых логиков, тоже имеют рациональный смысл, если не иметь в виду суждений типа «Роза не верблюд». Они важны прежде всего сами по себе, так как отражают объективное отсутствие чего-либо у чего-то. Недаром говорят: «Отрицательный результат тоже результат». Но они не менее важны в их отношении к утвердительным суждениям. Установление того, чем не является предмет мысли, – ступень к раскрытию его действительной сущности. Так, суждение: «Киты – не рыбы» диалектически связано с суждением: «Киты – млекопитающие», служит его предпосылкой.
И все же утвердительные суждения информационно более насыщенны, а следовательно, обладают большей познавательной силой. Из отрицательного суждения далеко не всегда определенно следует, чем непосредственно является предмет. А из утвердительного вполне определенно следует не только то, чем он является, но и то, чем не является.
Знание особенностей утвердительных и отрицательных суждений имеет не только теоретическую, но и практическую значимость. Взять для примера известный юридический принцип презумпции невиновности. Как правильнее, сильнее, категоричнее, а следовательно, гуманнее и демократичнее его сформулировать: «Обвиняемый считается невиновным» или «Обвиняемый не считается виновным»? В законодательстве нашей страны была принята первая его формулировка – утвердительная. В процессе обсуждения проекта новой Конституции Российской Федерации некоторые авторы предлагали дать ему иную, отрицательную. При этом делалась ссылка на конституции некоторых государств, в частности Италии, Польши, Югославии. И все же в принятом ныне тексте Конституции России принцип презумпции невиновности дан в утвердительной форме: «Каждый обвиняемый в совершении преступления считается невиновным, пока его виновность не будет доказана в предусмотренном федеральным законом порядке и установлена вступившим в законную силу приговором суда» (ст. 49). Сделано это, разумеется, правильно, так как утвердительная форма суждения так или иначе «сильнее» отрицательной.
Помимо исходного, фундаментального деления простых категорических суждений по качеству существует еще их деление по количеству.
Количество суждения – это его другая важнейшая логическая характеристика. Под количеством здесь разумеется отнюдь не какое-нибудь конкретное число мыслимых в нем объектов (например, число дней недели, месяцев или времен года, планет Солнечной системы и т.д.), а характер субъекта, т.е. его логический объем. В зависимости от этого выделяются общие, частные и единичные суждения.
Общими называются суждения, в которых что-либо утверждается обо всей группе предметов, и притом в разделительном смысле. В русском языке такие суждения выражаются словами «все», «всякий», «каждый», «любой» (если суждения утвердительные) или «ни один», «никто», «никакой» и др. (в отрицательных суждениях). В символической логике такие слова называются кванторами (от лат. quantum – сколько). В данном случае это квантор общности. Для его обозначения используется символ ∀ (от англ, all – все). Формула «∀ хР(х) интерпретируется так: «для всех х имеет место Р(х)». В традиционной логике общие суждения выражаются формулой «Все S есть Р» («Ни одно S не есть Р»).
Примеры: «Все люди смертны», «Ни один человек не бессмертен».
Юридические примеры: «Все адвокаты – юристы»; «Никто не может нести ответственность за деяние, которое в момент его совершения не признавалось правонарушением». Кванторное слово нередко опускается, его можно подставить лишь мысленно. Так, в суждении: «Кто ясно мыслит, тот ясно излагает» имеется в виду «всякий», «любой». У Пушкина в суждении «Острая шутка не есть окончательный приговор» подразумевается «никакая». Общими суждениями этого же типа являются афоризмы: «Сравнение – не доказательство», «Невежество – не аргумент» и др.
Юридические документы часто содержат подобные суждения: «Граждане Российской Федерации…» (имеются в виду «все») или «Судьи неприкосновенны» (тоже относится к «каждому»).
Общие суждения имеют свои разновидности. Прежде всего они могут быть выделяющими и невыделяющими.
В выделяющих нечто говорится лишь о данной группе. В русском языке они выражаются словами «только», «лишь», «лишь только» и т. д. Примеры: «Только люди – разумные существа на Земле» (это означает, что других разумных существ на Земле нет); «Только суд осуществляет в Российской Федерации правосудие»; «Лишь лицо, совершившее общественно опасное деяние, может быть признано виновным в преступлении».
В невыделяющих то, что сказано о данной группе, может быть отнесено и к другим группам: «Все люди смертны» (это означает, что смертны не только люди, но и животные, и растения). «Все адвокаты – юристы» (означает, что юристами могут быть прокуроры, судьи, следователи и т. д.).
Частные суждения – те, в которых что-либо высказывается о части какой-то группы предметов. В русском языке они выражаются такими словами, как «некоторые», «не все», «большинство», «часть», «отдельные» и др. В символической логике такие слова носят наименование «квантор существования» и обозначаются символом «Ǝ» (от англ, exist – существовать). Формула Ǝ х Р(х) читается так: «Существует х такой, что имеет место Р(х)» или «Для некоторых х имеет место Р(х)». В традиционной логике принята следующая формула частных суждений: «Некоторые S есть (не есть) Р».
Примеры: «Некоторые войны справедливы», «Некоторые войны несправедливы» или «Некоторые свидетели правдивы», «Некоторые свидетели не правдивы», «Некоторые таможенники – юристы», «Некоторые таможенники – не юристы». Кванторное слово здесь тоже может опускаться. Поэтому, чтобы определить, имеется ли налицо частное или общее суждение, надо мысленно подставить соответствующее слово. Например, латинская пословица: «Errare humanum est» («Людям свойственно ошибаться») не означает, что это относится к каждому человеку. Здесь понятие «люди» взято в собирательном смысле. В другой латинской пословице: «Quod licet Jovi, non licet bovi» («Что дозволено Юпитеру, то не дозволено быку») предполагается не «всё», лишь «кое-что».
Нетрудно понять, что кванторные слова частных суждений, логически тождественные, фактически по-разному характеризуют объем субъекта. Поэтому на практике они далеко не взаимозаменяемы. Так, суждения: «Большинство населения проголосовало за Конституцию» и «Меньшинство населения проголосовало за Конституцию» в логическом отношении оба – частные, но их конкретный смысл принципиально различен. Поэтому их политические и юридические последствия прямо противоположны: «Конституция принята» или «Конституция не принята».
Подобную разницу тонко уловила одна из моих слушательниц Вера Аксенова. Она рассказала, как однажды проводилась проверка работы отдела предпринимательской деятельности Комитета по управлению госимуществом г. Истра. В результате выявилось, что «Некоторые предприятия зарегистрированы без представления необходимых документов» (из 30 предприятий таких оказалось 5). Однако в акте проверки записано, что «Большинство предприятий было зарегистрировано без представления необходимых документов». Разумеется, и то и другое суждение – частные. Но если первое суждение, основанное на фактах, истинно, то второе – ложно.
Частные суждения тоже имеют свои разновидности. Они делятся на определенные и неопределенные.
В определенных частных суждениях что-либо говорится лишь о части какой-то группы предметов и не может быть распространено на всю группу предметов в целом. Слово «некоторые» здесь понимается в смысле «только некоторые». Примеры: «Некоторые люди красивы»; «Некоторые книги не интересны»; «Некоторые юристы – депутаты Государственной Думы».
В неопределенных частных суждениях что-либо высказывается о части предметов так, что может быть отнесено ко всей их группе вообще. Слово «некоторые» используется здесь в другом смысле: «По крайней мере некоторые, а может быть, и все». Например, увидев на первых столах студенческой аудитории новый учебник логики, я уже могу высказать суждение: «Некоторые студенты имеют учебник логики». Опросив остальных, я могу убедиться в том, что «Все студенты имеют учебник логики». Значит, предыдущее суждение было неопределенно-частным.
Разумеется, в живой практике мышления не всегда так просто можно решить, в каком смысле высказывается частное суждение. Возьмем для примера пословицу: «Не все то золото, что блестит». Ясно, что это частное суждение. Но какое? Найдем вначале субъект и предикат суждения, а для этого выразим его в соответствующей грамматической форме: «Не все то, что блестит, есть золото», т. е. «Лишь некоторые блестящие вещи есть золото». Теперь ясно, что это определенное частное суждение.
Единичные суждения – такие, в которых нечто высказывается об отдельном предмете мысли. В русском языке они выражаются словами «это», именами собственными и т.д. Формула «Это S есть (не есть) Р». Примеры: «Это кремль»; «Московский Кремль – самый красивый в мире»; «Санкт-Петербург не является столицей России». Юридические примеры: «Уголовный кодекс Российской Федерации пересмотрен», «Пенсионный фонд России работает успешно».
Единичные суждения, так же как общие и частные, имеют свои разновидности. Одна из них – суждения об индивидуальном предмете: «Это Солнце», «Солнце – источник жизни на Земле», «Луна – не планета». Другую составляют суждения о совокупности предметов, рассматриваемых как единое целое и выражаемых собирательными понятиями. Например: «Солнечная система – не единственная планетная система в нашей Галактике»; «Большая Медведица – созвездие». Поскольку в том и другом случае нечто говорится о предмете мысли в целом, единичные суждения в логике приравниваются к общим и отдельному логическому анализу не подлежат.
Между частными и общими суждениями тоже нет абсолютной грани. Например: «Все студенты, не считая двоих, пришли на семинар по логике». Какое это суждение? С одной стороны, здесь кванторное слово «все». Значит, это по форме общее суждение. А с другой – слова «не считая двоих». Значит, не «все», а «некоторые». Следовательно, по существу это частное суждение. Подобные суждения, носящие промежуточный характер, называются в логике исключающими. Они выражаются в русском языке словами: «исключая», «кроме», «помимо» и т.п. В юридической практике такие суждения нередки. Например: «Как правило, закон обратной силы не имеет» (т.е. бывают исключения); «Разбирательство дел во всех судах открытое, за исключением случаев, когда это противоречит интересам охраны государственной тайны»; «Потерпевший, как правило, допрашивается ранее свидетелей».
Наконец, относительна грань между частными и единичными суждениями. Так, словесное выражение частного суждения «по крайней мере некоторые» означает «хотя бы один». Например, достаточно кому-либо в научной или философской литературе, средствах массовой информации и т.д. высказать какое-либо мнение, чтобы можно было сказать: «Некоторые авторы выдвигают такое мнение…» Или если хотя бы в одной из конституций стран мира записана какая-либо статья, то можно сказать: «В некоторых конституциях…»
Познавательная ценность общих, частных и единичных суждений различна, но по-своему велика. Так, в единичных суждениях содержатся знания об отдельных предметах и явлениях: исторических событиях, великих личностях, фактах современной общественной жизни. Юридическая практика, по существу, вся основывается на единичных суждениях: например, гражданские и уголовные дела – на отдельных фактах, лицах, вещах. Единичные суждения дают также знания и о целых Совокупностях, «ансамблях» предметов, а следовательно, могут выражать определенные общие закономерности, приобретать огромное мировоззренческое значение. Например: «Земля – рядовое небесное тело» (а не центр мироздания, как полагали до Коперника); «Солнечная система не вечна» (а возникла из первоначальной гигантской туманности, как предполагал И. Кант); «Вселенная нестационарна» (как доказывал на основе теории относительности А. Эйнштейна А. Фридман).
Частные суждения содержат знания о типах, формах, видах, разновидностях и т.д. той или иной группы предметов. Например: «Некоторые металлы легче воды», «Некоторые млекопитающие живут в воде», «Некоторые люди гениальны». При определенных условиях частные суждения могут превращаться в общие. Например: «Некоторые металлы электропроводны» – «Все металлы электропроводны».
В общих суждениях выражаются общие свойства (или целые совокупности свойств) мыслимых предметов, общие связи и отношения между предметами, включая и объективные закономерности. Форму общих суждений принимают юридические законы, указы, другие нормативные акты. Так, в форме общих суждений выражены конституционные права и обязанности граждан Российской Федерации, статьи Трудового кодекса, Уголовного кодекса, Таможенного кодекса и т. п.
В процессе познания и общения единичные, частные и общие суждения взаимодействуют между собой. На основе единичных суждений возникают обобщения в виде частных и общих суждений. Так, кропотливое исследование фактов преступности в стране позволяет сделать общие выводы о ее причинах, характере, тенденциях развития, возможных последствиях. В свою очередь, наличие общих суждений становится основой для подведения отдельных случаев под общее правило.
Рассмотренные в методических целях порознь, качество и количество суждения тесно связаны. Поэтому в логике большое значение придается объединенной классификации суждений по их количеству и качеству. Возможны четыре вида таких суждений: общеутвердительные, частноутвердительные, общеотрицательные и частноотрицательные.
Общеутвердительными называются суждения, по количеству, т. е. по характеру субъекта, общие, а по качеству, т. е. характеру связки, утвердительные. Например: «Все адвокаты – юристы».
Частноутвердительные суждения – частные по количеству, утвердительные по качеству. Например: «Некоторые свидетели дают достоверные показания».
Общеотрицательные суждения – общие по количеству, отрицательные по качеству. Пример: «Ни один обвиняемый не оправдан».
Наконец, частноотрицательные суждения – частные по количеству, отрицательные по качеству. Пример: «Некоторые свидетели не дают верных показаний».
Для формульной записи этих видов суждений в логике используются гласные буквы двух латинских слов «affirmo» («утверждаю») и «nego» («отрицаю»). Конкретно они означают суждения:
А – общеутвердительные,
I – частноутвердительные,
Е – общеотрицательные,
О – частноотрицательные.
Чтобы правильно понимать смысл суждений и правильно оперировать ими, необходимо знать распределенность терминов в них – субъекта и предиката.
Распределенным считается термин, мыслимый во всем объеме; нераспределенным – если он мыслится не во всем объеме, а частично.
В общеутвердительных суждениях (А): «Все S есть Р» – субъект распределен, а предикат не распределен. Это видно на графической схеме (штриховкой отмечена степень их распределенности).

Исключение составляют лишь случаи, когда суждение – общевыделяющее. Например: «Только люди – разумные существа на Земле». Здесь распределены и субъект, и предикат.

В частноутвердительных суждениях (I): «Некоторые S есть Р» – субъект и предикат не распределены.

Исключение составляют лишь случаи, когда субъект по объему шире предиката. Например: «Некоторые смертные существа – люди», «Некоторые юристы – адвокаты». В них субъект не распределен, а предикат распределен.

В общеотрицательных суждениях (Е): «Ни одно S не есть Р» – субъект и предикат распределены.

Наконец, в частноотрицательных суждениях (О): «Некоторые S не есть Р» – субъект не распределен, предикат распределен.

Обобщая сказанное, можно вывести следующие закономерности, характеризующие распределенность терминов в суждениях:
а) субъект распределен в общих и не распределен в частных суждениях)
б) предикат распределен в отрицательных и не распределен в утвердительных суждениях.
Знание распределенности терминов в суждениях имеет большое значение в практике мышления. Оно необходимо, во-первых, для правильного преобразования суждений и, во-вторых, для проверки правильности умозаключений (см. об этом ниже).
Виды суждений по характеру предиката. Предикат суждения, будучи носителем новизны, может иметь самый различный характер. С этой точки зрения во всем многообразии суждений выделяются три наиболее распространенные группы: атрибутивные, реляционные и экзистенциальные.
Атрибутивные суждения (от лат. attributum – свойство, признак), или суждения о свойствах чего-либо, раскрывают наличие или отсутствие у предмета мысли тех или иных свойств (или признаков). Например: «Все республики бывшего СССР объявили о своей независимости»; «Содружество Независимых Государств (СНГ) непрочно». Поскольку понятие, выражающее предикат, имеет содержание и объем, атрибутивное суждение может рассматриваться в двух планах: содержательном и объемном.
В содержательном плане это суждение о том, обладает или не обладает предмет мысли совокупностью свойств или отдельным свойством. В зависимости от этого различаются две разновидности атрибутивных суждений. В одной из них предикат выражен конкретным понятием, т. е. понятием о самих предметах и явлениях в строгом смысле этого слова. Например: «Ртуть – металл» (т. е. она обладает всеми свойствами металлов).
В другой разновидности предикат – абстрактное понятие. Например: «Ртуть электропроводна» (т.е. она обладает отдельным свойством – электропроводности). Нетрудно, однако, заметить относительность различий между этими разновидностями. Достаточно сравнить следующие пары суждений: «Человек – мыслящее существо» и «Человеку свойственно мыслить»; «Всякое преступление – общественно опасное деяние» и «Всякое преступление обладает общественной опасностью».
В объемном плане атрибутивные суждения – это суждения о том, входит или не входит предмет мысли в тот или иной класс предметов. Они именуются тогда «суждениями включения (или невключения) в класс предметов». В зависимости от объемных отношений различаются тоже две их разновидности. Для одной характерно включение (или невключение) подкласса в класс. Например: «Все металлы электропроводны» (здесь подкласс металлов включается в класс электропроводных веществ). В другой устанавливается принадлежность (или непринадлежность) элемента классу. «Данное вещество – металл». В символической логике те и другие суждения выражаются формулами: S ⊂ Р (читается: объем S входит в объем Р) и S ∈ Р (читается: S принадлежит Р).
Правда, грань между этими двумя разновидностями суждений включения (невключения) в класс также относительна. Например, «Все металлы электропроводны» означает, что любой предмет, являющийся элементом класса металлов, является также элементом класса электропроводных веществ.
Реляционные суждения (от лат. relatio – отношение), или суждения об отношениях чего-либо к чему-то, раскрывают наличие или отсутствие у предмета мысли того или иного отношения к другому предмету (или нескольким предметам). Поэтому они обычно выражаются специальной формулой: х R у, где х и у – предметы мысли, a R (от relatio) – отношение между ними. Например: «СНГ не равно СССР», «Москва больше Санкт-Петербурга», «Дураку закон не писан».
У реляционных суждений тоже есть свои разновидности. Одну из них составляют суждения об отношениях между двумя предметами. Например: «Рязань меньше Москвы», «Знания подобны деньгам» (чем больше их имеешь, тем больше хочется иметь); «Даже самые незначительные проступки порождают великие преступления». Или, как подметил Козьма Прутков, «легче держать вожжи, чем бразды правления». В отличие от «одноместного» предиката атрибутивных суждений предикат в них называется «двухместным». Другая разновидность реляционных суждений – суждения об отношениях между тремя и более предметами. Например: «Рязань находится между Москвой и Тамбовом». Предикат здесь – «многоместный».
Относительность различий между атрибутивными и реляционными суждениями проявляется в их способности превращаться друг в друга. Так, атрибутивные суждения можно представить как частный случай реляционных, поскольку в них связка «есть» («не есть») раскрывает отношение тождества (принадлежности, включения и т.д.) между мыслимыми в S и Р предметами. А реляционное суждение, в свою очередь, можно представить как частный случай атрибутивного.
Примеры. Суждение «Все металлы электропроводны» можно превратить в суждение «Все металлы подобны электропроводным телам». В свою очередь, суждение «Рязань меньше Москвы» можно превратить в суждение «Рязань принадлежит к городам, которые меньше Москвы». Или: «Знания есть то, что подобно деньгам». В современной логике имеется тенденция свести реляционные суждения к атрибутивным.
Экзистенциальные суждения (от лат. existentia – существование), или суждения о существовании чего-либо, – это такие, в которых раскрывается наличие или отсутствие самого предмета мысли. Предикат здесь выражается словами «существует» («не существует»), «есть» («нет»), «был» («не был»), «будет» («не будет») и др. Например: «Дыма без огня не бывает», «СНГ существует», «Советского Союза нет». В процессе судопроизводства решается прежде всего вопрос: имело ли место событие: «Преступление есть» («Доказательств нет»).
Несомненно, экзистенциальные суждения обладают определенной спецификой. Однако их целесообразнее рассматривать как частный случай атрибутивных суждений. Так, суждение «СНГ существует» означает, что «СНГ обладает свойством существовать», или в объемной трактовке: «СНГ принадлежит к классу существующих межгосударственных объединений». Вот почему в последующем логическом анализе экзистенциальные суждения самостоятельно не рассматриваются.
Познавательное значение рассмотренных видов суждений по характеру предиката трудно переоценить. В атрибутивные суждения облекаются знания о все новых открываемых свойствах бесконечно разнообразных предметов мысли. Например, Пьер и Мария Кюри установили, что полоний, как и уран, обладает свойством радиоактивности, и тем самым значительно расширили горизонт наших знаний. Выявление тех или иных свойств исследуемых предметов или особенностей тех или иных лиц важно, например, в криминалистике.
В реляционных суждениях отражается бесконечное богатство отношений между предметами мысли: пространственные и временные, природные и социальные, а среди социальных – производственные и непроизводственные (политические, нравственные, религиозные, семейные и т. д.). С их помощью выражается вся гамма правовых отношений между людьми: отношения кредитора и должника, продавца и покупателя, начальника и подчиненного, родителей и детей, участников судебного процесса и др. Например: «Иван взял взаймы у Петра», «Петров заключил договор с Сидоровым», «Судья задал вопрос свидетелю».
Особое значение имеют экзистенциальные суждения. Первое, с чем сталкивается человек в своей практической деятельности, – это существование (или отсутствие) тех или иных предметов и явлений. И в настоящее время нас волнуют вопросы: есть ли жизнь на других планетах, есть ли другие разумные существа во Вселенной, существуют ли «снежный человек», «биополе», «телепатия», «полтергейст» и многое другое. В судебной практике установление факта преступления, трудового или гражданского спора – начало всего последующего разбирательства.
Знание особенностей атрибутивных, реляционных и экзистенциальных суждений имеет, таким образом, важное значение для всякого человека вообще и юриста в частности.
Виды суждений по модальности. В заключение – еще одно деление простых суждений на виды – по модальности (от лат. modus – образ, способ). Юристам хорошо известен основанный на этом слове юридический термин «modus vivendi». Под ним имеется в виду определенный образ жизни или способ существования. Это такая совокупность условий, при которой возможны пусть временные, но более или менее нормальные, мирные взаимоотношения сторон (если при сложившейся ситуации нельзя добиться постоянного или исчерпывающего их соглашения между собой).
Логический же термин «модальность суждений», тоже производный от слова «modus», означает, что помимо основного конкретного содержания всякое суждение так или иначе несет с собой дополнительную смысловую нагрузку. Это информация об объективном характере (или способе) связи между субъектом и предикатом, раскрываемой в суждении, о субъективном отношении к ней человека, характере и степени вероятности заключенного в суждении знания и т. д. В русском языке модальность суждения выражается посредством огромного множества слов, таких как «возможно», «разрешено», «ценно» и им подобных, а также их отрицаний: «невозможно», «не разрешено» и др. Они называются в логике «модальными операторами». Нередко их заменяет контекст.
Наиболее важными и распространенными выступают такие виды модальности, как алетическая, деонтическая, аксиологическая и эпистемическая.
Алетическая, или истинная, модальность (от греч. aleteja – истина) выражает характер связи между мыслимыми предметами, а следовательно, между субъектом и предикатом суждения. Модальными словами в русском языке служат «возможно», «необходимо», «случайно» и их синонимы.
С точки зрения алетической модальности различают следующие разновидности суждений:
а) ассерторические суждения, или суждения о факте, действительности чего-либо. Например: «Россия переходит к рыночной экономике». В таких суждениях модальность не выражена, а констатируется лишь самый факт чего-либо;
б) проблематические суждения, или суждения о возможности чего-либо. Например: «Россия может перейти к рыночной экономике»;
в) аподиктические суждения, или суждения о необходимости чего-либо. Например: «Россия по необходимости перейдет к рыночной экономике».
Разумеется, различия между этими разновидностями относительны. Возможное способно стать необходимым, необходимое –случайным и т. д.
Во взаимоотношениях модальных суждений можно подметить определенные закономерности – например, несбалансированность (несимметричность). Так, что действительно, то и возможно, но не наоборот; то, что необходимо, то и действительно, но не наоборот.
Деонтическая, или нормативная, модальность (от греч. deon – нужное, должное) относится непосредственно к деятельности людей, нормам их поведения в обществе, как нравственным, так и правовым. Она выражается в русском языке с помощью таких слов, как «разрешается», «запрещается», «обязательно» и их аналогов.
В зависимости от характера социальных норм деонтическая модальность имеет разновидности. Так, любое правоотношение, как «двуликий Янус», предполагает, с одной стороны, какое-либо право, а с другой – соответствующую обязанность. Поэтому недаром говорят: «Нет прав без обязанностей, и нет обязанностей без прав». С учетом этого принципа вся совокупность правовых норм может быть разбита на две важнейшие группы: уполномочивающие, т. е. правопредоставляющие (или запрещающие) и обязывающие нормы. Отсюда по крайней мере две основных разновидности деонтической модальности:
а) суждения о наличии (или отсутствии) какого-либо права. Они формулируются с помощью слов «разрешено», «запрещено», «вправе» и др. Например: «Каждый имеет право на жизнь»; «В Российской Федерации признается идеологическое многообразие» (правопредоставляющие нормы). Или: «Принудительный труд запрещен»; «Никто не может быть повторно осужден за одно и то же преступление»; «Никакая идеология не может устанавливаться в качестве государственной…» (правозапрещающие нормы). Модальное слово может и отсутствовать: «Труд свободен». Диалектика наличия-отсутствия прав отражена в известной формуле: «Разрешено все, что не запрещено законом». Правда, она предполагает наличие правового государства, обладающего развитой системой законодательства, которое охватывало бы все сферы общественной жизни и, следовательно, четко очерчивало бы «запретную зону». Распространяясь лишь на отдельных граждан и их объединения, она дополняется формулой: «Запрещено все, что не разрешено законом» для должностных лиц и государственных органов;
б) суждения о наличии (или отсутствии) какой-либо обязанности. Они формулируются посредством слов «обязан», «должен», «необходимо» и др. Например: «Государственные органы… обязаны всемерно содействовать профессиональным союзам в их деятельности»; «Основное общее образование обязательно» (правообязывающие нормы). Без модального слова: «Право частной собственности охраняется законом».
Между правами и обязанностями должна быть так называемая «деонтическая сбалансированность». Под ней разумеется соответствие каждому праву какой-либо обязанности, а каждой обязанности – какого-либо права. В противном случае правовая система может быть неэффективной.
Эпистемическая, или познавательная, модальность (от греч. episteme – знание) означает характер и степень вероятности знания. Она выражается при помощи слов: «знаю», «верю» («считаю», «полагаю») и им подобных. В связи с этим можно выделить, по крайней мере, тоже две основные разновидности суждений эпистемической модальности в соответствии с двумя видами знаний – объективными (научными) и субъективными (мнениями):
а) суждения, основанные на вере. При этом не имеет значения, религиозная она или нерелигиозная. Например: «Верю, что Бог существует», «Считаю, что есть загробная жизнь», «Христос воскрес» или «Верю в наступление лучшей жизни», «Полагаю, что я счастливый человек»;
б) суждения, основанные на знании, независимо от того, проблематичные они или достоверные. Например: «Знаю, что существует закон всемирного тяготения»; «Во Вселенной, по-видимому, есть другие разумные существа», «Телепатия, вероятно, существует»; «На Марсе достоверно отсутствие жизни».
Аксиологическая, или ценностная, модальность (от греч. axios – ценный) выражает отношение человека к ценностям – материальным и духовным. Она фиксируется такими словами, как «хорошо», «плохо», «безразлично» (в ценностном отношении), «лучше», «хуже» и др. Например: «Хорошо смеется тот, кто смеется последним»; «Хорошо учиться осторожности на ошибках других»; «Плохо жить без друзей», «К сожалению, демократия – несовершенная форма правления, но она лучше других».
Разумеется, сказанным не исчерпаны все формы проявления модальности суждений. Они подробно исследуются так называемой «модальной логикой»: это обширная, относительно самостоятельная и быстро развивающаяся отрасль современной логики, имеющая большое теоретическое и практическое значение, в том числе, как отмечено выше, и для юристов.
2. Сложные суждения
Образование и особенности сложных суждений. Напомним, что сложные суждения образуются из простых путем того или иного их соединения (а также, добавим здесь для полноты анализа, путем соединения простых со сложными и сложных между собой).
Подобно простым сложные суждения могут быть истинными и ложными. Но если истинность или ложность простого суждения непосредственно определяется его соответствием или несоответствием действительности, то истинность или ложность сложного суждения зависит прежде всего от истинности или ложности составляющих его простых (и иных) суждений.
Сложные суждения отличаются от простых также по своим функциям и структуре. Их функции носят более сложный характер, так как в них раскрывается не одна, а одновременно несколько – две или более – связей между предметами мысли. Их структура тоже характеризуется большей сложностью, обретая новое качество. Основными структурообразующими элементами здесь выступают уже не понятия-термины (субъект и предикат), а самостоятельные суждения (причем их внутренняя субъектно-предикатная структура уже не учитывается). И связь между ними осуществляется не с помощью связки «есть» («не есть»), а в качественно иной форме – посредством логических союзов (они называются также «логическими связками»). Это такие союзы, как «и», «или», «если… то» и др. Они близки по смыслу к соответствующим грамматическим союзам, но, как будет показано ниже, полностью с ними не совпадают. Главное их отличие сводится к тому, что они однозначны, тогда как грамматические союзы могут иметь множество смыслов и оттенков.
Каждый из логических союзов является бинарным, т.е. соединяет между собой только два суждения независимо от того, простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.
Если в простых суждениях переменными были субъект и предикат (S и Р), а постоянными – логические связки «есть» и «не есть», то в сложных суждениях переменными выступают уже отдельные, далее нерасчленяемые суждения (назовем их «А» и «В»), а постоянными – логические союзы: «и», «или» и др.
В русском языке сложные суждения имеют весьма многообразные формы выражения. Они могут выражаться прежде всего сложносочиненными предложениями. Например: «Ни один виновный не должен уйти от ответственности, и ни один невиновный не должен пострадать». Они могут быть выражены также сложноподчиненными предложениями. Таково, например, высказывание Цицерона: «Ведь если бы даже ознакомление с правом представляло огромную трудность, то и тогда сознание его великой пользы должно было бы побуждать людей к преодолению этой трудности». Наконец, они могут облекаться и в особую форму простых распространенных предложений. Этого нетрудно добиться, например, в результате своеобразного «свертывания» сложных предложений. Так, сложносочиненное предложение «Аристотель был великим логиком, и Гегель тоже был великим логиком» можно превратить в простое распространенное: «Аристотель и Гегель были великими логиками». Благодаря подобному «свертыванию» достигается большая лаконичность речи, а следовательно, ее экономность и динамичность.
Таким образом, не всякое сложное суждение выражается непременно сложным предложением, но всякое сложное предложение выражает сложное суждение.
Виды сложных суждений по характеру логического союза. В сложных суждениях, как и в простых, есть свои виды. Они определяются прежде всего характером логического союза. В зависимости от смысла и назначения логического союза различаются следующие основные группы сложных суждений.
1. Конъюнктивные (или соединительные) суждения (от лат. conjunctio – связь, соединение). Они образуются из исходных посредством логического союза конъюнкции «и» (символически: «д»). Их наиболее общая схема: А∧В (читается: «А и В»), где А и В – исходные суждения, а знак ∧ – символ их конъюнкции. Например: «Никто не забыт, и ничто не забыто».
В русском языке логический союз конъюнкции выражается многими грамматическими союзами: «и», «а», «но», «да», «хотя», «а также», «несмотря на то, что…» Вот примеры. Современное изречение: «Трудолюбие – душа бизнеса и ключ к процветанию». Философское положение одного из древнекитайских мыслителей: «Самое большое не имеет внешней границы, а самое маленькое не имеет предела внутри себя». Слова Аристотеля: «Платон друг, но истина еще больший друг». Из народной мудрости: «Русские долго запрягают, да быстро ездят». Среди юристов распространен афоризм: «Pereat mundus et fiat justitia» («Правосудие должно совершиться, хотя бы погиб мир»). Нередко грамматические союзы заменяются запятой, двоеточием, точкой с запятой и даже точкой. Например, как полагал один из семи древнегреческих мудрецов: «Наслаждения смертны, добродетели бессмертны». Или: «Тысячелетие по кирпичику создает государство – один час может превратить его в пыль».
Если конъюнкция выражена простым распространенным предложением, то она может иметь три исходных структуры:
а) один субъект и два предиката – «S есть (не есть) Р1 и Р2». Например: «Все равны перед законом и судом». Здесь можно вычленить два исходных суждения с общим субъектом и разными предикатами: «Все равны перед законом» и «Все равны перед судом»;
б) два субъекта и один предикат – «S1 и S2 есть (не есть) Р». Например: «Государственные пенсии и социальные пособия устанавливаются законом». Здесь также налицо два простых суждения;
в) два субъекта и два предиката – «S1 и S2 есть (не есть) Р1 и Р2». Например: «Основные права и свободы человека неотчуждаемы и принадлежат каждому от рождения». Здесь уже четыре простых суждения.
Понятно, что на этой основе могут быть еще более сложные мыслительные конструкции.
Пример: «Осуществление прав и свобод человека и гражданина не должно нарушать права и свободы других лиц».
Возможны четыре способа сочетания двух исходных суждений «А» и «В» в зависимости от их истинности («и») и ложности («л»). Какая здесь действует закономерность? Конъюнкция таких суждений истинна в одном случае: если истинно каждое из них в отдельности. В остальных случаях она ложна. Вот таблица (матрица) конъюнкции:

В принципе логический союз «и» в отличие от грамматического может объединять даже такие суждения, которые по смыслу очень далеки друг от друга. Классический пример: «2 × 2 = 4, и снег бел». Правда, и здесь можно найти что-то общее, например: «Это верно, что 2 × 2 = 4 и что снег бел». Другой пример. Что общего между такими простыми суждениями: «Существует звездное небо над головой» и «Есть нравственный закон в душе человека»? Однако их конъюнкция возможна: они могут быть сближены, если учесть, что именно то и другое больше всего поразило И. Канта. В практике мышления такие суждения бывают довольно редко, но они лишь подчеркивают универсальный характер закономерности конъюнкции: она не зависит от конкретного содержания исходных суждений, а ее истинность или ложность всецело определяется истинностью или ложностью каждого из них. Важно лишь, чтобы исходные суждения обладали свойством коммутативности (перестановочности), т.е. их истинность или ложность не менялась от перестановки.
Впрочем, иногда признают некоммутативную конъюнкцию: «Наступила зима, и мы катаемся на лыжах» (а не наоборот).
Логический союз «и» может соединять и более двух исходных суждений – по формуле: А∧В∧С… Вспомним в этой связи стихи Пушкина:
: Теперь у нас дороги плохи,
: Мосты забытые гниют,
: На станциях клопы да блохи
: Заснуть минуты не дают.
В подобных случаях важно другое – чтобы исходные суждения обладали свойством ассоциативности (сочетаемости), т.е. их истинность или ложность не менялась от способа сочетания: (А∧В)∧С или А∧(В∧С) и т. д. Общая закономерность конъюнкции остается здесь в силе: она истинна лишь при истинности всех ее составляющих.
Знание особенностей конъюнкции имеет немалое значение в практике мышления. Строя более или менее сложное рассуждение, следует тщательно проверять истинность исходных суждений. Ведь от этого напрямую зависит его собственная истинность или ложность. Так, достаточно одного ложного суждения, чтобы придать всей, даже весьма сложной, конъюнкции ложность. Недаром еще древние утверждали: «Дырявая пола халата делает всю одежду дырявой». Эта же мысль заложена в русских пословицах – о том, что» делает ложка дегтя в бочке меда или одна паршивая овца в стаде.
Все это важно учитывать в юридической практике, когда нередко выстраивается более или менее сложная цепь рассуждений. А из-за одного ложного звена она может распасться. В то же время достаточно обнаружить хотя бы одно ложное суждение в доводах оппонента, чтобы опровергнуть все рассуждение в целом.
2. Дизъюнктивные (разделительные) суждения (от лат. disjunctio – разобщение, обособление). Бывает две их разновидности: слабая и сильная (или нестрогая и строгая).
Слабая (нестрогая) дизъюнкция образуется логическим союзом «или» (знак «∨»), Он характеризуется тем, что объединяемые им суждения не исключают друг друга. Общая формула: A∨B (читается: «А или В»). Языковые средства выражения слабой дизъюнкции – грамматические союзы «или», «либо» и другие в их разделительно-соединительном значении. Например, как сказано в древнем поучении: «Мудрая книга, оставленная человеком после его смерти, более полезна, чем дворец или часовня на кладбище» (или чем то и другое вместе). Еще пример: «Право может способствовать экономическому развитию либо препятствовать ему» (но оно может одновременно способствовать в одном отношении и препятствовать в другом). Из Трудового кодекса РФ: «Комиссии по трудовым спорам образуются по инициативе работников и (или) работодателя из равного числа представителей работников и работодателя» (ст. 384).
Слабая дизъюнкция истинна в тех случаях, когда истинно, по крайней мере, одно из составляющих ее суждений (или оба вместе), и ложна, когда оба суждения ложны.
Вот таблица слабой дизъюнкции:

Как и в конъюнкции, логический союз «или» обладает свойством коммутативности. Дизъюнкция может состоять из трех и более исходных суждений – по формуле: A∨B∨C… Примером может служить рассуждение ходжи Насреддина, который взялся за десять лет научить падишахова ишака грамоте: «Через десять лет либо ишак сдохнет, либо падишах умрет, либо меня аллах приберет» (а может, и все вместе). Великолепный образец многочленной дизъюнкции, полезной для юристов, мы находим у Цицерона: «Люди ведь гораздо чаще руководствуются в своих решениях ненавистью, или любовью, или пристрастием, или гневом, или горем, или радостью, или надеждой, или боязнью, или заблуждением, или другим каким-либо душевным движением (а может быть, одновременно тем или иным их сочетанием. – Е. И.), чем справедливостью, или предписанием, или каким-нибудь правовым установлением, или судебным решением, или законами». В подобных случаях, как и в конъюнкции, логический союз «или» обладает свойством ассоциативности.
Дизъюнктивное суждение может не исчерпывать всех возможных случаев. Тогда в русском языке ставятся выражения типа: «и так далее», «и тому подобное», «и прочее». Они применимы даже в юридических текстах (к которым предъявляются особо строгие требования), если нет возможности перечислить все варианты чего-либо.
Сильная (строгая) дизъюнкция образуется логическим союзом «либо… либо» (символ ṿ). Она отличается от слабой тем, что ее составляющие исключают друг друга. Общая формула: А ṿ В (читается: «А либо В»). И она выражается, по существу, теми же грамматическими средствами, что и слабая: «или», «либо» и др., но уже в ином, разделительно-исключающем значении.
Примеры. «Гражданин Российской Федерации не может быть лишен своего гражданства или права изменить его» (Конституция РФ, ст. 6); «Закон, устанавливающий или отягчающий ответственность, обратной силы не имеет» (там же, ст. 54); «Виновным в преступлении признается лицо, совершившее деяние умышленно или по неосторожности» (УК РФ, ст. 24).
Для того чтобы подчеркнуть строго разделительный характер грамматических союзов, используется их усиленная, двойная форма: «или… или», «либо… либо», «то… то», «ли… ли» и др.
Примеры. Как считали древние: «De mortuus aut bene, aut nihil» («О мертвых либо хорошо, либо ничего»); у Брэгга подчеркнуто: «Человек к 40 годам либо сам себе доктор, либо он дурак»; или: «Либо я найду путь, либо проложу его».
Строгая дизъюнкция истинна лишь тогда, когда одно из составляющих ее суждений истинно, а другое ложно.

Дизъюнктивное суждение может включать в себя три и более исходных суждения. Формула: A ṿ B ṿ C… Примеры: «Вечно он был занят либо судебной речью, либо домашними упражнениями, либо обдумывал, либо писал»; «Всякое заинтересованное лицо вправе в порядке, установленном законом, обратиться в суд за защитой нарушенного или оспариваемого права или охраняемого законом интереса». Еще более сложный случай: «При хищении, недостаче, умышленном уничтожении или умышленной порче материальных ценностей ущерб определяется по ценам, действующим в данной местности на день причинения ущерба». Строгая дизъюнкция тоже обладает свойствами коммутативности и ассоциативности.
Дизъюнкция – слабая и сильная – широко распространена в практике мышления. В ней выражаются логические операции деления, расчленения, перечисления чего-то. Юридическая практика особенно богата такого рода суждениями. Ведь здесь особое значение имеет детальное указание видов права, видов преступления и наказания, перечисление юридически важных случаев, форм осуществления того или иного права или обязанности и пр.
3. Импликативные (или условные) суждения (от лат. implicatio – сплетение, тесная связь). В них объединяются суждения на основе логического союза «если…, то» (обозначается «→»). Формула А → В (читается: «Если А, то В»). Для выражения импликации русский язык имеет следующие грамматические союзы: «если…, то», «когда…, тогда», «в случае, если…, то» и др.
Примеры. Афоризм древних: «Cum tacent – clamant» («Когда молчат – кричат»); «Если мы хотим добиться уважения к закону, мы сначала должны создать закон, достойный уважения»; «Если правительство нарушает закон, оно порождает неуважение к нему». Грамматический союз «если» может стоять и не перед первым суждением.
Примеры. Известное крылатое выражение Достоевского, часто цитируемое, «Красота спасет мир» на самом деле есть сложное, условное суждение: «Красота спасет мир, если она добра». У Шекспира:
: И добродетель стать пороком может,
: Когда ее неправильно приложат.
Юридический пример. «Заседание комиссии по трудовым спорам считается правомочным, если на нем присутствует не менее половины членов, представляющих работников, и не менее половины членов, представляющих работодателя» (Трудовой кодекс РФ, ст. 387).
В условных суждениях отражаются прежде всего многообразные реальные зависимости между предметами и явлениями – причинно-следственные, пространственно-временные, функциональные и т. д. Но они могут, как и предыдущие, представлять собой соединение разнородных по конкретному содержанию суждений типа: «Если 2 × 2 = 4, то снег бел». Именно в таком обобщенном смысле импликация используется в классической логике. Суждение, стоящее после слов «если», «когда», называется «антецедентом» (предшествующим) или «основанием», а после «то» – «консеквентом» (последующим) или «следствием».
Импликация истинна во всех случаях, кроме одного: когда предшествующее (основание) есть, а последующего (следствия) нет. Таблица истинности импликации:

Импликация может включать в себя три и более суждений. Например: «Участие прокурора в разбирательстве гражданского дела обязательно в случаях, когда это предусмотрено законом или когда необходимость участия прокурора в данном деле признана судом».
Законодательство и юридическая практика его применения свидетельствуют, что в форме импликации выражаются не только объективные зависимости одних предметов и явлений от других, но и также права и обязанности людей, связанные с теми или иными условиями. Например: «Каждый вправе в соответствии с международными договорами Российской Федерации обращаться в межгосударственные органы по защите прав и свобод человека, если исчерпаны все имеющиеся внутригосударственные средства правовой защиты» (Конституция РФ, ст. 46).
4. Эквивалентные (равнозначные) суждения (от лат. aequivalens – равноценный, равнозначный). В них объединяются суждения с взаимной (прямой и обратной) условной зависимостью. Они называются еще «двойной импликацией». Их образует логический союз «если и только если…, то» (символ «↔»). Формула эквивалентности: А ↔ В (читается: «Если и только если А, то В»), Грамматически эквивалентность выражается союзами: «тогда и только тогда…, когда», «лишь в том случае, если…, то», «только при условии, если…, то» и др. Примеры: «Если число делится на два, то оно четное»; «Если и только если человек достиг пенсионного возраста, то он имеет право на получение пенсии по возрасту».
Эквивалентное суждение истинно в двух случаях: когда оба составляющие его суждения истинны и когда они оба ложны. Таблица истинности эквивалентности:

5. Отрицание суждений. При характеристике сложных суждений широко используется еще один логический союз: «неверно, что» или просто «не» (знак отрицания «˥» ). В отличие от бинарных союзов он относится к одному суждению. Прибавление его к какому-либо суждению означает образование нового суждения, которое находится в определенной зависимости от исходного. Например, исходное суждение: «Все судьи неподкупны». Его отрицание: «Неверно, что все судьи неподкупны» или «Не все судьи неподкупны», «Некоторые судьи не неподкупны».
Отрицание истинно, если исходное суждение ложно, и наоборот. Таблица отрицания суждений:

Логические союзы, рассмотренные из методических соображений порознь, в реальной практике мышления нередко переплетаются друг с другом, образуя порой весьма сложные мыслительные конструкции. Например: «Суд не принимает отказа истца от иска, признания иска ответчиком и не утверждает мирового соглашения сторон, если эти действия противоречат закону или нарушают чьи-либо права и охраняемые законом интересы». Здесь налицо сочетание нескольких конъюнкций с дизъюнкцией и импликацией. Или: «Судья, народный заседатель, прокурор, секретарь судебного заседания, эксперт и переводчик не могут участвовать в рассмотрении дела и подлежат отводу, если они лично, прямо или косвенно, заинтересованы в исходе дела или имеются иные обстоятельства, вызывающие сомнения в их беспристрастности».
Различия между логическими союзами относительны. Подобно тому как один и тот же логический союз может соединять самые разные по конкретному содержанию суждения, так одно и то же конкретное суждение может быть выражено разными логическими союзами. Например: «День прошел, и настала ночь»; «Если день прошел, то настала ночь»; «Или день не прошел, или настала ночь»; «День не прошел, ночь не настала»; «Если ночь не настала, то день не прошел». Взаимосвязь и взаимозаменяемость логических союзов имеет большое значение для преобразования символических формул в процессе исчисления высказываний.
Глава III. Отношения между суждениями
Так же как и между понятиями, между суждениями существуют определенные логические отношения. Они тоже могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми. Но есть и принципиальное различие. Понятия, поскольку они ни истинны, ни ложны, не могут соотноситься друг с другом с точки зрения истинности или ложности. Между суждениями же складываются многообразные отношения прежде всего по истинности и ложности. Причем это касается как простых, так и сложных суждений.
Анализ отношений среди тех и других имеет важное теоретическое и практическое значение.
1. Отношения между простыми суждениями
Отношения между простыми суждениями определяются, с одной стороны, их конкретным содержанием, а с другой – логической формой: характером субъекта, предиката, логической связки.
Поскольку по характеру предиката простые суждения делятся прежде всего на атрибутивные и реляционные, рассмотрим каждый из этих видов в отдельности.
Отношения между атрибутивными суждениями. По своему содержанию атрибутивные суждения могут находиться в двух важнейших отношениях – сравнимости и несравнимости.
Несравнимые суждения. У них разные субъекты или предикаты или то и другое вместе. Таковы, например, суждения: «Космос необъятен» и «Закон суров». В подобных случаях истинность или ложность одного из суждений непосредственно не зависит от истинности или ложности другого. Она прямо определяется отношением к действительности – соответствием или несоответствием ей. Правда, в условиях универсальной связи и взаимодействия предметов и явлений действительности суждения о них не могут быть абсолютно независимыми друг от друга. Очевидна лишь их относительная самостоятельность, независимость с точки зрения истинности или ложности. Так, если истинно суждение «Энергия сохраняется» (а не исчезает и не возникает из ничего, как гласит закон сохранения и превращения энергии), то будет ложным суждение «Вечный двигатель возможен», хотя по конкретному содержанию они не имеют ничего общего – ни субъекта, ни предиката, а следовательно, являются несравнимыми.
К несравнимым относятся также суждения, у которых может быть одинаковым субъект или предикат. Например: «Закон суров» и «Закон вступил в силу» или «Закон вступил в силу» и «Указ вступил в силу». И хотя смысловое различие здесь меньше, чем в предыдущем случае, они тоже не могут соотноситься между собой по истинности или ложности. Поэтому в дальнейшем их анализ не производится.
Сравнимые суждения. Они, наоборот, имеют одинаковые термины – и субъект, и предикат, но могут различаться по количеству и качеству. Это суждения, как говорят, «одинаковой материи», а следовательно, сопоставимы по истинности и ложности.
По своей логической форме – прежде всего по количеству и качеству – сравнимые суждения подразделяются на совместимые и несовместимые.
Совместимые суждения содержат одну и ту же мысль – полностью или частично. Между ними возникают следующие логические отношения: эквивалентности, подчинения, частичной совместимости.
Эквивалентность (равнозначность) – это отношение между суждениями, у которых субъект и предикат выражены одними и теми же или равнозначными понятиями (хотя и разными словами), причем и количество и качество одни и те же. Таковы, например, общеутвердительные суждения: «Все адвокаты – юристы» и «Все защитники в суде имеют специальное, юридическое образование». Аналогично может обстоять дело с общеотрицательными, частноутвердительными и частноотрицательными суждениями. Отношения между такого рода суждениями по их истинности или ложности характеризуются взаимно-однозначным соответствием: они или одновременно истинны, или одновременно ложны. Поэтому если истинно одно, то истинно и другое, а если одно ложно, то и другое ложно.
Последующие отношения между простыми атрибутивными суждениями – А, Е, I, О – для наглядности изображаются графически в виде «логического квадрата».
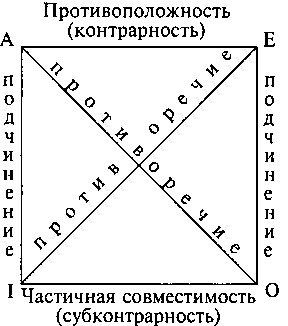
Подчинение – это отношение между такими суждениями, у которых количество различно, а качество одно и то же. В таком отношении находятся общеутвердительное (А) и частноутвердительное (I), общеотрицательное (Е) и частноотрицательное (О) суждения. При подчинении действуют следующие закономерности:
а) Если истинно подчиняющее суждение (А, Е) , то тем более истинно подчиненное (соответственно I, О), но если истинно подчиненное (I, О), то подчиняющее (А, Е) неопределенно: оно может быть как истинным, так и ложным.
Примеры. Если истинно А, что «Все адвокаты – юристы», то тем более истинно I, что «По крайней мере некоторые адвокаты – юристы». Но если истинно I, что «Некоторые свидетели правдивы», то отсюда еще не следует, что истинно А: «Все свидетели правдивы».
В данном случае это ложное суждение. В других случаях А может быть истинным. Например: если истинно I, что «Некоторые адвокаты – юристы», то истинно А, что «Все адвокаты – юристы».
б) Если ложно подчиненное суждение (I, О), то тем более ложно подчиняющее (А, Е), но если ложно подчиняющее (А, Е), то подчиненное (I, О) неопределенно: оно может быть как истинным, так и ложным.
Примеры. Если ложно I, что «Некоторые граждане вправе нарушать законы», то тем более ложно А, что «Все граждане вправе нарушать законы». Но если ложно А, что «Все свидетели правдивы», то отсюда еще не следует, что ложно I: «Некоторые свидетели правдивы». В данном случае это истинное суждение. В других случаях I может быть ложным. Например: если ложно А, что «Все граждане вправе нарушать законы», то ложно и I, что «Некоторые граждане вправе нарушать законы».
Частичная совместимость (субконтрарность) – это отношение между суждениями одинакового количества, но разного качества: между частноутвердительными (I) и частноотрицательными (О) суждениями. Для нее характерна следующая закономерность: оба суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Например, при истинности I, что «Некоторые свидетели правдивы», может быть истинно и О, что «Некоторые свидетели не правдивы». Но О может быть и ложным. Например: если истинно I, что «Некоторые адвокаты – юристы», то это не значит, что истинно О: «Некоторые адвокаты – не юристы». Оно ложно. Однако если ложно I, что «Некоторые граждане вправе нарушать законы», то не может быть ложным О, что «По крайней мере некоторые граждане не вправе нарушать законы». Оно будет непременно истинным.
Несовместимые суждения. Они имеют следующие логические отношения: противоположности и противоречия.
Противоположность – это отношение между общеутвердительными (А) и общеотрицательными (Е) суждениями. Оба таких суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Тут, следовательно, закономерность, обратная той, что характеризовала отношения частичной совместимости. Так, если истинно А, что «Все адвокаты – юристы», то ложно Е, что «Ни один адвокат – не юрист». И если истинно Е, что «Ни один гражданин не вправе нарушать законы», то ложно А, что «Все граждане вправе нарушать законы». Но если ложно А, что «Все свидетели правдивы», то отсюда еще не следует истинность Е; что «Ни один свидетель не правдив». В данном случае оно тоже ложное.
Истинно здесь I, что «Некоторые свидетели правдивы», и О, что «Некоторые свидетели не правдивы». В других случаях Е может быть истинным. Так, если ложно А, что «Все граждане вправе нарушать законы», то истинно Е, что «Ни один гражданин не вправе нарушать законы».
Противоречие (контрадикторность) – отношение между такими суждениями, как общеутвердительное (А) и частноотрицательное (О), общеотрицательное (Е) и частноутвердительное (I). Им присущи следующие закономерности: они не могут быть одновременно истинными и не могут быть одновременно ложными. Это «самые несовместимые» из всех суждений: между ними, образно говоря, отношения «кошки и собаки», поскольку те не могут ужиться друг с другом.
Примеры. Если истинно А, что «Все адвокаты – юристы», то ложно О, что «Некоторые адвокаты – не юристы». Если ложно А, что «Все свидетели правдивы», то истинно О, что «Некоторые свидетели не правдивы».
Вот таблица истинности (и) и ложности (л), а также неопределенности (н) простых, категорических суждений А, Е, I, О.

Знание отношений между простыми атрибутивными суждениями по их истинности и ложности важно в познавательном и практическом отношениях. Оно помогает прежде всего избегать возможных логических ошибок в собственных рассуждениях. Так, из истинности частного суждения (I или О) нельзя выводить истинность общего (А или Е). Например, из того, что «Некоторые судьи неподкупны», еще не следует, что «Все судьи неподкупны». Подобная ошибка называется в логике поспешным обобщением и допускается часто.
В дискуссии, споре, в частности по юридическим вопросам, чтобы опровергнуть общее ложное суждение, вовсе не обязательно прибегать к противоположному ему общему суждению, так как легко попасть впросак: оно может оказаться тоже ложным. Вспомним пример: если ложно А, что «Все свидетели правдивы», то это еще не значит, что истинно Е: «Ни один свидетель не правдив». Оно тоже ложно, хотя в других случаях Е может оказаться истинным. В логическом отношении достаточно привести противоречащее суждение О: «Некоторые свидетели не правдивы». Если А ложно, то О всегда истинно. Это самый безопасный и неуязвимый, наиболее надежный способ опровержения.
Отношения между реляционными суждениями. Реляционные суждения (или суждения об отношениях между предметами мысли), как уже отмечалось, имеют нечто общее с атрибутивными суждениями: трехчленность строения х R у, наличие количества и качества. Поэтому они могут находиться тоже в отношениях подчинения, частичной совместимости, противоположности, противоречия. Так, если истинно I, что «Некоторые металлы легче воды», то это еще не значит, что истинно А: «Все металлы легче воды», но означает, что ложно Е: «Ни один металл не легче воды» и что неопределенно О: «Некоторые металлы не легче воды» (в данном случае оно истинно).
В то же время реляционные суждения отличаются от атрибутивных тем, что раскрывают не свойства предметов, а отношения между предметами и, следовательно, имеют не одночленный (одноместный) предикат, а многочленный (n-местный: от двух и более). Поэтому в зависимости от характера отношения R между предметами х и у внутри суждения устанавливаются свои, особые отношения.
Отношения между х и у могут быть прежде всего симметричными и несимметричными.
Симметричные (от греч. symmetria – соразмерность) – это такие отношения между х и у, для которых не имеет значения, какой из этих членов предшествующий, а какой последующий. Иначе говоря, их можно менять местами, при этом их истинность или ложность не изменится. Это раскрываемые в суждениях отношения равенства, сходства, подобия, одновременности и др. Например: «Иван – брат Петра», следовательно, «Петр – брат Ивана». Такие два реляционных суждения могут быть одновременно истинными либо одновременно ложными. Если истинно одно из них, то истинно другое, и наоборот, если ложно одно из них, то ложно и другое.
Несимметричными являются такие отношения между х и у, при которых важен порядок их расположения. Поэтому менять их местами нельзя без изменения смысла суждения, а следовательно, его истинности или ложности. Например, «Иван – отец Степана». Но это не значит, что «Степан – отец Ивана». Если истинно одно из этих суждений, то ложно другое. Истинным здесь будет «Степан – сын Ивана». Несимметричными оказываются и такие отношения: «Иван любит Марью». Отсюда вовсе не следует, что «Марья любит Ивана». Она может любить его, а может и не любить. Если истинно одно из таких суждений, то другое – неопределенно.
Важно также учитывать относительный характер различий между симметричностью и несимметричностью. Симметричное в одном отношении может быть несимметричным в другом и наоборот. Например: если «Иван – брат Петра», то «Петр – брат Ивана». Но если «Иван – брат Елены», то это не значит, что «Елена – брат Ивана» (она ему сестра).
Отношения между хну могут быть транзитивными и нетранзитивными.
Транзитивные, или переходные, отношения (от лат. transitus – переход). Если, например, x эквивалентен y, а у эквивалентен z, то и x эквивалентен z. Это могут быть также отношения величины (больше – меньше), пространственные (дальше – ближе), временные (раньше – позже) и др. Например: «Иван – брат Петра», «Петр – брат Елены», значит, «Иван – брат Елены». Такие суждения могут быть либо одновременно истинными, либо одновременно ложными.
Нетранзитивные (непереходные) отношения обладают обратной зависимостью по сравнению с предыдущей. Так, если «Иван – отец Степана», а «Степан – отец Николая», то это вовсе не значит, что «Иван – отец Николая». Он ему дед. Следовательно, такие суждения не могут быть одновременно истинными: если истинно одно, то ложно другое.
Есть еще отношения рефлексивности и нерефлексивности.
Рефлексивные отношения (от лат. reflexio – обращение назад, отражение) характеризуются тем, что каждый из членов отношения R – х и у – находится в таком же отношении к самому себе. Если два события произошли одновременно, то они одновременны с собой. Оба суждения могут быть либо истинными, либо ложными.
Нерефлексивные отношения таковы, что если 2 меньше 3, то это не значит, что 2 меньше 2 и 3 меньше 3. Из истинности одного следует ложность другого.
Знание особенностей подобных отношений между реляционными суждениями по их истинности или ложности важно всюду, где есть такого рода отношения. Особое значение это имеет в сфере правовых отношений. Так, в судебной практике учитываются одновременность или разновременность событий, отношения родства, знакомства между людьми и т. д. Например, если Иванов знает Петрова, а Петров – Сидорова, то это еще не значит, что Иванов знает Сидорова. Тут отношения нетранзитивные со всеми вытекающими отсюда последствиями по истинности и ложности между раскрывающими их реляционными суждениями.
2. Отношения между сложными суждениями
Сложные суждения аналогично простым находятся в определенных отношениях между собой. Общим здесь является то, что они тоже могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми, причем и для них характерны отношения именно по их истинности или ложности. Однако отношения между сложными суждениями в известной мере специфичны. Обусловлено это их особой, более сложной и качественно иной структурой, отличной от структуры простых суждений.
Сравнимые сложные суждения характеризуются тем, что они включают в себя одинаковые исходные суждения и различаются логическими союзами – конъюнкцией, дизъюнкцией и т.д. (включая отрицание). Возьмем для примера два сложных суждения (обозначим их буквами Р и Q): «Прокуроры и судьи имеют юридическое образование» (Р) и «Неверно, что прокуроры и судьи имеют юридическое образование» (Q). Исходные составляющие здесь – А и В – одинаковые: «Прокуроры имеют юридическое образование» (А) и «Судьи имеют юридическое образование» (В). Но логическая форма обоих сложных суждений разная: первое (Р) – конъюнкция (А∧В), а второе – отрицание конъюнкции (
А∧В). Одинаковость составляющих и дает возможность соотносить их по смыслу и выяснять отношения между ними по истинности и ложности.
Несравнимые сложные суждения отличаются тем, что их составляющие полностью или частично разные. Например: «Прокуроры и судьи имеют юридическое образование» (Р) и «Прокуроры и судьи стоят на страже законности» (Q). Здесь общие субъекты, но разные предикаты. Может быть наоборот: разные субъекты, но общие предикаты. Например: «Прокуроры и судьи имеют юридическое образование» (Р) и «Следователи и адвокаты имеют юридическое образование» (Q). Наконец, разными могут быть и субъекты, и предикаты одновременно. Например: «Кража и мошенничество – преступления» (Р) и «Грабеж и разбой строго караются по закону» (Q). Поэтому такие суждения невозможно сопоставить по смыслу и анализировать их отношения по истинности и ложности.
Сравнимые тоже бывают совместимыми и несовместимыми. Поэтому здесь имеют место все основные отношения, что и между простыми.
Среди совместимых это эквивалентность, подчинение и частичная совместимость.
Эквивалентность. В таком отношении находятся те сложные суждения, которые при одних и тех же значениях истинности составляющих имеют одинаковые значения. Если истинно Р, то истинно Q, и если ложно Р, то ложно и Q. Но не может быть так, что Р истинно, a Q ложно, и так, что Р ложно, a Q истинно.
Подчинение. Это отношение между сложными суждениями характеризуется тем, что при истинности подчиняющего подчиненное ему всегда истинно. Если Р истинно, то и Q истинно; если Р ложно, то Q может быть как истинным, так и ложным. Но не может быть так, что Р истинно, a Q ложно.
Частичная совместимость. Она выражается в том, что оба сложных суждения одновременно могут быть истинными, но не могут быть одновременно ложными.
Среди несовместимых сложных суждений – отношения противоположности и противоречия.
Противоположность. Она проявляется в том, что оба сложных суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Если Р истинно, то Q ложно; если Р ложно, то Q может быть истинным и ложным. Но Р и Q не могут быть вместе истинными (ср.: отношения частичной совместимости).
И наконец, противоречие. Характерным для этого отношения между сложными суждениями является то, что их значения могут лишь исключать друг друга: они не могут быть одновременно истинными и не могут быть одновременно ложными. Если Р истинно, то Q – ложно; если Р – ложно, то Q – истинно и т. д.
Вот сводная таблица отношений между сложными суждениями по истинности и ложности (зачеркнутые строки означают, что оба суждения не могут принимать данные значения одновременно):

Знание отношений между сложными суждениями, как и между простыми, помогает правильно сочетать их в рассуждениях, избегать собственных ошибок и находить ошибки у оппонентов.
Глава IV. Логические операции с суждениями
Суждения, как и понятия, тоже могут подвергаться различным логическим операциям. Но если применительно к понятиям речь шла лишь об операциях с их содержанием и объемом (вспомним определение и деление, обобщение и ограничение понятий), то в отношении суждений дело обстоит гораздо сложнее. Логические операции с ними затрагивают и их типы и виды, и их субъектно-предикатную структуру и т. д. Среди таких операций выделяются две наиболее общие группы: преобразование простых и сложных суждений; отрицание тех и других суждений.
Поскольку эти операции часто производятся в практике мышления, их логический анализ необходим в теоретическом отношении и важен в практическом.
1. Преобразование суждений
Преобразование простых атрибутивных суждений. Простые атрибутивные суждения, заключая в себе определенный смысл, сами по себе не раскрывают полностью всей гаммы содержащихся в них взаимоотношений между их субъектом и предикатом, количеством и качеством. Например, известно, что «Все поэты – впечатлительные люди». Но «Все ли впечатлительные люди непременно поэты»? Перефразируя известную шутку: «Чтобы сделать рагу из зайца, надобно иметь, как минимум, кошку», спросим себя: «Чтобы числиться по разряду поэтов, достаточно ли слыть впечатлительным человеком?»
Для выяснения точного логического смысла суждения нередко требуется преобразование его формы. Это достигается прежде всего посредством таких логических операций, как обращение, превращение, противопоставление субъекту и противопоставление предикату.
Обращение. Это преобразование суждения путем перестановки его субъекта и предиката местами. При этом количество суждения (кванторное слово) может изменяться, а качество не меняется.
Какие здесь действуют закономерности? Их три:
а) общеутвердительное суждение (А) преобразуется в частноутвердительное (I). Обусловлено это тем, что субъект в нем распределен, а предикат, как правило, не распределен. Формула обращения: «Все S есть Р» – «Некоторые Р есть S». Так, в суждении «Все адвокаты – юристы» поставим субъект на место предиката, а предикат на место субъекта. В результате получим: «Некоторые юристы – адвокаты» (ибо юристами, как отмечалось, являются не только адвокаты, но и прокуроры, судьи, следователи и др.). Это графически можно представить так:
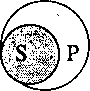
где S – адвокаты, Р – юристы.
Такое преобразование называется «обращение с ограничением». Исключение составляет обращение общеутвердительных выделяющих суждений, в которых и субъект и предикат распределены. Они обращаются в общеутвердительные же. Это «чистое обращение». Формула: «Все S (и только S) есть Р» – «Все Р есть S». Например: «Все люди – разумные существа» – «Все разумные существа – люди». Это видно на круговой схеме:

Все правильные определения, поскольку в них объем определяющего равен объему определяемого (правило соразмерности), тоже допускают лишь чистое обращение;
б) частноутвердительное суждение (I) обращается в частноутвердительное (I). Субъект и предикат в них, как правило, не распределены. Формула обращения: «Некоторые S есть Р» – «Некоторые Р есть S». Пример: «Некоторые юристы – депутаты Государственной Думы» – «Некоторые депутаты Государственной Думы – юристы». На круговой схеме:

Исключение составляют суждения, в которых субъект не распределен, а предикат распределен. В этих случаях частноутвердительное суждение преобразуется в общеутвердительное. Формула: «Некоторые S (и только S) есть Р». – «Все Р есть S». Пример: «Некоторые преступники – убийцы» – «Все убийцы – преступники». Это «обращение с приращением». Графически:

в) общеотрицательное суждение (Е) обращается в общеотрицательное (Е), так как субъект и предикат здесь распределены. Формула: «Ни одно S не есть Р» – «Ни одно Р не есть S». Например: «Ни один свидетель не явился в суд» – «Ни один явившийся в суд не свидетель».

Частноотрицательные суждения не обращаются. Субъект в них не распределен, следовательно, он не может стать предикатом нового, тоже отрицательного суждения, где предикат всегда распределен. Попробуем для примера выяснить, что произойдет с суждением «Некоторые мужчины – не женатые». Означает ли оно, что «Ни один женатый – не мужчина»? Или только «некоторые»? И тот и другой вывод бессмысленны. А иного сделать нельзя. Это видно на схеме:

Какое значение имеет такая логическая операция, как обращение, в практике мышления? Благодаря ей полнее раскрываются взаимоотношения между субъектом и предикатом суждения, а следовательно, связи и отношения между предметами мысли, отражаемыми в суждении. С субъекта, четко выраженного кванторным словом, наш взор переносится на предикат, который становится субъектом, а следовательно, обретает свое кванторное слово. Вспомним наши утверждения: «Всякое понятие выражается в слове, но не всякое слово выражает понятие» или «Всякое суждение есть предложение, но не всякое предложение есть суждение». Обращение может принимать и не столь развернутую, полную форму. Примером сокращенного обращения может служить пословица: «Не все то золото, что блестит». Очевидно, это результат обращения суждения: «Все то, что золото, блестит» (но «Не все то, что блестит, – золото»). С помощью обращения проверяется правильность определений. Если после перестановки определяемого и определяющего смысл определения не меняется, значит, оно правильное. Нетрудно понять, что эту операцию можно производить и в юридической практике, когда требуется более точно выявить соотношения между теми или иными понятиями. Например: «Всякий закон есть нормативный правовой акт», но «Не всякий нормативный правовой акт есть закон» (есть еще указы, инструкции, правила и т. п.). Обращение играет незаменимую роль в проверке правильности юридических определений, от которых требуется особая точность.
Превращение. Это преобразование суждения путем перемены его качества на противоположное. Количество суждения, его субъект и предикат при этом не меняются.
В превращении проявляются следующие закономерности:
а) общеутвердительное суждение (А) преобразуется в общеотрицательное (Е). Формула превращения: «Все S есть Р» – «Ни одно S не есть не-Р». Так, суждение: «Все адвокаты – юристы» по качеству утвердительное. Превращаем его в отрицательное, но так при этом, чтобы его смысл не изменился: «Ни один адвокат не является неюристом». Вот графическое изображение:

б) общеотрицательное суждение (Е), наоборот, превращается в общеутвердительное (А). Формула: «Ни одно S не есть не-Р» – «Все S есть Р». Пример: «Ни одно преступление не осталось нераскрытым» – «Все преступления раскрыты». Графически:

в) частноутвердительное суждение (I) превращается в частноотрицательное (О). Формула: «Некоторые S есть Р» – «Некоторые S не есть не-Р». Пример: «Некоторые свидетели дали верные показания» – «Некоторые свидетели не дали неверных показаний». Графически:

г) частноотрицательное суждение (О) превращается в частноутвердительное (I). Формула: «Некоторые S не есть Р» – «Некоторые S есть не-Р». Например: «Некоторые книги не есть интересные» – «Некоторые книги есть неинтересные». Графически:
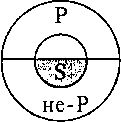
Значение превращения как логической операции состоит в том, что благодаря ему в суждении раскрывается новый, более богатый смысл: утверждение принимает форму отрицания и наоборот. Представим себе спор нескольких людей. Один говорит: «Петров – патриот». Другой возражает: «Петров – не патриот». Находится третий, который возражает второму: «Петров не является непатриотом». Высказанное им суждение и есть пример превращения. С одной стороны, оно равнозначно первому: двойное отрицание равно утверждению: «Петров – патриот», а с другой – противоположно суждению: «Петров – не патриот».
В юридических дискуссиях, спорах и т.д. подобный прием используется нередко. О нем свидетельствуют, в частности, выражения типа: «не есть не …», «не является не …» и др.
Обращение и превращение выступают основными, исходными логическими операциями с суждениями. Их различное сочетание порождает еще две операции: противопоставление субъекту и противопоставление предикату, которые считаются производными или смешанными.
Противопоставление субъекту. Так называется преобразование суждения путем обращения и последующего превращения. Приведем для краткости лишь один пример. Если суждение: «Все адвокаты – юристы» сначала обратим в суждение: «Некоторые юристы – адвокаты», а это последнее, в свою очередь, превратим в суждение: «Некоторые юристы не есть неадвокаты» (хотя есть и прокуроры, и судьи, и др.), то получим противопоставление субъекту. Предикат заключительного суждения – «неадвокаты» противопоставляется субъекту исходного суждения – «адвокаты». Отсюда название самой операции.
Противопоставление предикату. Это преобразование суждения путем превращения и последующего обращения. Пример. Суждение: «Все адвокаты – юристы» сначала превратим в суждение: «Ни один адвокат не является неюристом», а это последнее обратим в суждение: «Ни один неюрист не является адвокатом» (попросту говоря, среди неюристов адвокатов искать не следует). Получается, что предикату исходного суждения «юристы» мы противопоставили понятие «неюристы» и сделали его субъектом нового суждения. Этим объясняется название операции.
Значение двух последних операций, поскольку они носят производный, смешанный характер, слагается из значения исходных, основных, т.е. они позволяют извлечь дополнительную информацию, заложенную в преобразуемом суждении, раскрыть новые его грани и оттенки.
Преобразование простых реляционных суждений. Как и суждения о свойствах чего-либо, реляционные суждения (или суждения об отношениях между предметами) могут подвергаться тем же основным преобразованиям – обращению или превращению и с той же целью уточнения их логического смысла. Однако здесь неизбежны некоторые особенности, обусловленные особенностями самих суждений об отношениях. Для преобразования такого рода суждения прежде всего необходимо знать свойства выражаемого им отношения – является ли оно симметричным или несимметричным, рефлексивным или нерефлексивным, транзитивным или нетранзитивным.
Обращение. Если отношение симметрично, обращение реляционного суждения будет сводиться к простой перестановке местами членов отношения х и у. Причем само отношение R остается тем же. Например: «В. Маяковский – современник М. Горького» – «М. Горький – современник В. Маяковского». Другие примеры: «СНГ не равно СССР» – «СССР не равен СНГ»; «Нормы права подобны нормам морали» – «Нормы морали подобны нормам права». Если же отношение несимметрично, то обращение предполагает не только перестановку местами х и у, но и замену самого отношения R на обратное. Примеры: «М. Горький родился раньше Л. Леонова» – «Л. Леонов родился позже М. Горького»; «Рязань восточнее Москвы» – «Москва западнее Рязани»; «Земля больше Луны» – «Луна меньше Земли». Важно при этом обращать внимание на то, чтобы смысл суждения оставался одним и тем же: меняться должна лишь его логическая форма. Естественно, что в таком случае суждения оказываются синонимичными, поэтому в процессе рассуждения их можно заменять одно на другое. Так, если «Мораль возникла раньше права», то равнозначным ему будет суждение «Право возникло позже морали».
Если отношение транзитивно или нетранзитивно, то обращение принимает соответственно несколько иной вид. В случае транзитивности обращение суждения предполагает замену отношения на обратное. Так, если «Солнце больше Земли, а Земля больше Луны», то «Солнце больше Луны». Отсюда «Луна меньше Солнца». В случае же нетранзитивности обращение требует не только замены отношения на обратное, но и предварительного подбора соответствующего отношения. Так, если «Отец моего отца мне не отец, а дед», то «Я не сын ему, а внук».
Превращение. Применительно к реляционным суждениям оно тоже обладает своеобразием. Так, в случае симметричности отношения утвердительное суждение превращается в отрицательное (разумеется, с двойным отрицанием, иначе смысл суждения изменится на прямо противоположный, и, следовательно, это будет уже другое суждение). Например: «В. Маяковский – современник М. Горького» – «В. Маяковский не может быть не современником М. Горького». В случае же несимметричности отношения утвердительное суждение непросто становится отрицательным, а предполагает замену отношения на обратное. Например: «М. Горький родился раньше Л. Леонова» – «М. Горький родился (во всяком случае) не позже Л. Леонова». Естественно, что такие суждения тоже синонимичны, а следовательно, в практике мышления могут меняться одно на другое.
Следует лишь учитывать относительный характер этой синонимичности. Так, в результате превращения может меняться модальность суждения, оно может приобретать дополнительный смысл, не заложенный в исходном суждении и т. д.
Нетрудно понять, что если возможны обращение и превращение реляционных суждений, то на этой основе возможны и другие, производные и смешанные формы преобразования подобных суждений.
Преобразование сложных суждений. Сложные суждения, образованные из простых или других сложных суждений с помощью логических союзов, могут тоже подвергаться преобразованиям. Выше отмечалось, что одно и то же по смыслу сложное суждение может быть выражено в различной логической форме – конъюнкции, дизъюнкции, импликации и т. д. Это означает, что эквивалентность (равносильность, равнозначность) подобных суждений делает возможным производить над ними различные логические операции – преобразовывать их друг в друга, выражать одно через другое. Вот лишь некоторые из таких преобразований:
а) конъюнкция может быть выражена через дизъюнкцию, а именно: отрицание конъюнкции эквивалентно дизъюнкции отрицаний. Формула такого преобразования: ˥(A∧B)≡˥A∨˥B. Например: «Неверно, что Петров адвокат и в то же время судья». Это равнозначно суждению: «Петров не адвокат или он не судья». Обратим внимание, что дизъюнкция здесь не исчерпывающая. Поэтому может быть так, что Петров и не адвокат, и не судья, а например, прокурор;
б) дизъюнкция может быть выражена через конъюнкцию: отрицание дизъюнкции эквивалентно конъюнкции отрицаний. Формула ˥(A∨B)≡˥A∧˥B. Например: «Неверно, что Петров изучал логику в вузе или что он изучал ее самостоятельно». Это равносильно суждению: «Петров не изучал логики в вузе, и он не изучал ее самостоятельно»;
в) импликация может быть выражена через конъюнкцию: импликация эквивалентна отрицанию конъюнкции антецедента (основания) и ложного консеквента (следствия). Формула: А → В ≡ ˥(А∧˥В). Пример: «Если Петров юрист, то он знает логику». Это равноценно суждению: «Неверно, что Петров юрист и он не знает логики»;
г) импликация может быть выражена через дизъюнкцию: импликация эквивалентна дизъюнкции ложного антецедента и консеквента. Формула: А → В ≡ ˥А∧В). Пример: «Если Петров адвокат, то он имеет специальное, юридическое образование» – «Или Петров не адвокат, или он имеет специальное, юридическое образование».
Конъюнкция и дизъюнкция, в свою очередь, могут быть выражены через импликацию. Возможны и иные, самые разнообразные преобразования сложных суждений в другие. Важно при этом учитывать, что в процессе преобразования может меняться лишь логическая форма сложного суждения, его логический союз. Что же касается смысла самого суждения, то он должен оставаться тем же самым. В противном случае это будет уже новое суждение с иным смыслом.
Как же устанавливается эквивалентность суждений? Это достигается с помощью таблиц истинности. Так, если мы сравним таблицы истинности конъюнкции и (слабой) дизъюнкции (см. выше), то заметим, что сложное суждение конъюнкции А∧В истинно только тогда, когда истинны оба исходных суждения А и В; а суждение дизъюнкции A∨B ложно только в том случае, когда ложны как А, так и В. Следовательно, логические союзы конъюнкции ∧ и дизъюнкции ∨ находятся, можно сказать, в обратной зависимости. Учитывая это, конъюнкцию можно выразить через дизъюнкцию, а дизъюнкцию через конъюнкцию. При этом получаются именно эквивалентные формы, т. е. такие, которые истинны и ложны при тех же значениях составляющих их суждений.
Установление подобных эквивалентностей с помощью таблиц истинности открывает возможность, уже не обращаясь всякий раз непосредственно к сопоставлению самих таблиц, преобразовывать одни суждения в другие.
Для чего это нужно? Благодаря замене одних суждений другими, эквивалентными им, можно упрощать сложные рассуждения, используя одни логические союзы вместо других. Так, в любом, самом сложном суждении можно, пользуясь правилом замены одних логических союзов другими, устранить все знаки, кроме только знаков конъюнкции и отрицания, или лишь дизъюнкции и отрицания, или же импликации и отрицания. Этим обстоятельством широко пользуются в символической логике – прежде всего в логике высказываний.
2. Отрицание суждений
Кроме преобразования суждений другую важнейшую логическую операцию с ними представляет собой отрицание суждений. Естественно, что как логическая операция оно и сходно с преобразованием суждений, и отлично от него. В чем состоит сходство? В том, что результатом отрицания выступает тоже новое суждение. А в чем отличие? В процессе преобразования суждения, как мы видели, так или иначе меняется лишь его логическая форма, тогда как смысл остается тем же самым. В процессе же отрицания меняется не только форма суждения, но и самый его смысл: оно становится противоречащим исходному, исключающим его. Таким образом, если в основе преобразования суждений лежит их эквивалентность по смыслу, то в основе отрицания – их несовместимость.
Отрицание простых суждений. Рассмотрим вначале отрицание простых атрибутивных суждений. Сущность этой логической операции здесь составляет замена одного исходного суждения другим, не только несовместимым с ним, но и противоречащим ему. Языковыми средствами выражения такой операции служат обороты речи типа «неверно, что…» или частица «не» и ей подобные.
Если формула простого атрибутивного утвердительного суждения – «S есть Р», то формулой отрицания его будет: «Неверно, что S есть Р» или «S не есть Р». В символической записи: ˥А (читается: «неверно, что А» или: «не-А»). Например: «Все судьи справедливы» – «Неверно, что все судьи справедливы» или «Не все судьи справедливы» (это равносильно признанию, что «Некоторые судьи несправедливы»). Отрицанию могут подвергаться и отрицательные суждения. Если формула отрицательного суждения – «S не есть Р», то его отрицание будет выражено формулой: «Неверно, что S не есть Р» (что равносильно утверждению: «S есть Р»), Символически: ˥(˥А).
Уже отсюда явствует, что отрицание нельзя отождествлять с отрицательными суждениями. Когда мы говорим об отрицательном суждении, то имеем в виду один из видов суждений по характеру связки, т. е. по качеству. Причем в этом случае речь идет о качестве самого суждения безотносительно к утвердительному, а именно: о непринадлежности какого-либо свойства предмету мысли, о невключении мыслимого предмета в класс предметов и т. д. А когда говорится об отрицании, то разумеется особая логическая операция с суждениями. Она предполагает наличие определенного исходного суждения и определенное отношение к нему – именно отношение отрицания. В этом случае исходное суждение называется отрицаемым, а новое суждение – отрицающим. При этом безразлично, какое именно по качеству суждение отрицается: утвердительное или отрицательное. Может отрицаться и то и другое. Пример отрицания утвердительного суждения: «Россия – демократическое государство» – «Неверно, что Россия – демократическое государство» или: «Россия – не демократическое государство». Примеры отрицания отрицательного суждения: «Демократия – не политическое явление» – «Неверно, что демократия – не политическое явление» или «Демократия не есть неполитическое явление» (и здесь двойное отрицание равносильно утверждению: «Демократия – политическое явление»).
Подобно тому как утвердительное и отрицательное суждения могут быть истинными и ложными, отрицание одного суждения другим может быть истинным или ложным. Но если истинность или ложность утвердительного или отрицательного суждений определяется лишь их отношением к действительности, соответствием или несоответствием ей, то с отрицанием дело обстоит иначе. Его истинность или ложность определяется отношением к другому, исходному суждению, зависит всецело от того, истинно оно или ложно. Закономерностью здесь становится взаимная обратная зависимость: если исходное суждение истинно, то его отрицание ложно, и наоборот, если исходное суждение ложно, то его отрицание истинно. Вот таблица (матрица) их истинности:

Исходя из этой закономерности, нетрудно определить, какие из простых атрибутивных суждений могут считаться отрицаниями, а какие нет. Так, в отношении взаимного отрицания находятся противоречащие суждения: общеутвердительные (А) и частноотрицательные (О), общеотрицательные (Е) и частноутвердительные (I). Ведь, как отмечалось выше, если истинно одно из них, то ложно другое, и наоборот. Таким образом, несложно сделать вывод, что в процессе отрицания меняется и количество, и качество исходного суждения.
Что же касается противоположных суждений – общеутвердительных (А) и общеотрицательных (Е), то они не находятся в отношении взаимного отрицания: хотя они не могут быть вместе истинными, но могут быть вместе ложными.
Точно так же нет отношений взаимного отрицания между субконтрарными суждениями. Хотя они могут быть вместе истинными, но не могут быть вместе ложными. Их отношения, вспомним, это как бы «зеркальное» отражение отношений противоположных суждений.
Аналогично атрибутивным отрицаются реляционные суждения, но тут есть некоторые особенности. Так же как и отрицание атрибутивных суждений, их отрицание означает изменение и количества и качества на обратное. Но само отрицание касается уже не свойства какого-либо предмета, а отношения между предметами. Если формула исходного суждения имеет здесь вид х R у, то его отрицание будет ˥ (х R у) (читается: «Неверно, что х и у находятся в отношении R»).
Каков здесь механизм отрицания? Учитывая, что реляционные суждения, как и атрибутивные, различаются не только качеством, но и количеством, а следовательно, имеют кванторные слова, логическая операция отрицания будет сводиться к следующему:
а) квантор общности (∀) заменяется на квантор существования ($), а квантор существования соответственно на квантор общности;
б) перед исходным суждением ставится знак отрицания (˥). Если формула исходного суждения имеет, например, вид: ∀xRy, то его отрицанием будет ˥$(xRy).
Например, будем отрицать общеутвердительное ложное суждение (А): «Все металлы тяжелее воды». Получим истинное суждение: «Неверно, что все металлы тяжелее воды» (что равнозначно истинному частноотрицательному суждению: «Некоторые металлы не тяжелее воды»). Или будем отрицать истинное частноутвердительное суждение: «Некоторые металлы легче воды». Результат – ложное суждение: «Ни один металл не легче воды».
Другой пример: «Мужчина и женщина равны перед законом». Это истинное суждение. Его отрицанием будет ложное суждение: «Неверно, что мужчина и женщина равны перед законом» (или: «Мужчина и женщина не равны перед законом»).
Отрицание сложных суждений. Отрицание здесь имеет тот же характер замены несовместимым по смыслу суждением, то же соотношение по истинности и ложности, те же языковые средства выражения: «неверно, что…», которое ставится перед всем суждением, или «не», которое используется внутри сложного суждения перед тем или иным из составляющих его суждений. Но с учетом специфики сложных суждений их отрицание обладает и определенными отличиями.
Как уже подчеркивалось, в результате отрицания исходного простого суждения образуется хотя и новое, но тоже простое суждение. Что же касается выражения «неверно, что…», то отдельно взятое оно не составляет самостоятельного суждения. В итоге же отрицания исходного сложного суждения получается тоже сложное суждение.
Отрицание конъюнкции. Если формула конъюнкции А∧В, то отрицание конъюнкции может быть записано так: ˥(А∧В). Например, отрицание суждения: «Все юристы знают логику, и все юристы знают латинский язык» будет означать: «Неверно, что все юристы знают логику и все юристы знают латинский язык». Но отрицание может быть выражено и в эквивалентной положительной форме. Вспомним, что конъюнкция ложна, если ложно хотя бы одно из составляющих ее суждений. Следовательно, достаточно отрицать одно из них, чтобы стало возможным отрицание всей конъюнкции. Вот почему отрицание конъюнкции может принять форму дизъюнкции отрицаний (нестрогой). Так, если мы будем отрицать суждение «Все юристы знают логику, и все юристы знают латинский язык», то мы можем получить суждение: «Некоторые юристы не знают логики, или некоторые юристы не знают латыни» (а может быть и то и другое вместе). Символически: ˥(А∧В)≡(˥A∨˥В). Отрицание конъюнкции возможно и в форме импликации.
Отрицание дизъюнкции. Если использовать в качестве примера нестрогую дизъюнкцию (A∨B), то ее отрицанием будет ˥(A∨B). Например, отрицая суждение: «Применяются нормы морали, или применяются нормы права», будем иметь: «Неверно, что применяются нормы морали или применяются нормы права». Но поскольку отрицание дизъюнкции означает отрицание каждого из исходных суждений одновременно, то этим можно объяснить, почему оно может облечься в эквивалентную форму конъюнкции отрицаний. Например: отрицание суждения: «Применяются нормы морали, или применяются нормы права» означает то же самое, что «Не применяются нормы морали, и не применяются нормы права». Записывается: ˥A∨B≡(˥A∧˥B).
Отрицание импликации. В результате отрицания импликации можно получить конъюнктивное суждение. Например: «Если закон вступил в силу, то он должен исполняться» – «Закон вступил в силу, но он не исполняется». Запись: (А→В)≡(А∧˥B).
Знание смысла отрицания как простого, так и сложного суждения имеет принципиальное значение для понимания сущности формально-логических законов противоречия и исключенного третьего, а также логических основ косвенного доказательства (см. об этом разделы IV и VI).
Отрицание как логическая операция тоже часто применяется в практике мышления. Оно незаменимо, например, в полемике, когда в противовес одним суждениям высказываются другие, противоречащие им, когда сталкиваются взаимоисключающие мнения.
Чтобы правильно пользоваться этой логической операцией, необходимо знать не только условия и пределы ее приложимости, но и логический смысл отрицаемого суждения. Как, например, опровергнуть высказывание: «Суд состоится завтра»? Ведь уже подчеркивалось, что в зависимости от логического ударения в нем могут содержаться три суждения. А это означает, что и отрицание его может принять три различные формы: «Не суд (а совещание судей) состоится завтра»; «Суд не состоится (а будет отложен) завтра»; «Суд состоится не завтра (а послезавтра)». Аналогично обстоит дело и с отрицанием сложных суждений.
В заключении главы отметим, что между основными логическими операциями – преобразованием суждений и отрицанием их – нет жесткой грани: они могут взаимодействовать между собой, взаимно проникать друг в друга. Так, в процессе преобразования суждений используется их отрицание (например, при превращении). А в процессе отрицания применяется преобразование (например, превращение) – отрицательная форма суждения нередко преобразуется в эквивалентную положительную. Пример с простым суждением: «Прокурор не может не знать законов» – «Прокурор знает (должен знать) законы». Преобразование суждения в процессе его отрицания широко используется и в отношении сложных суждений. Без этого немыслимо исчисление высказываний, особенно более или менее сложных.
Обозревая теперь всю проблематику раздела о суждении в целом (сюда, как мы видели, входят сущность суждений, их классификация, отношения между ними, логические операции с ними), можно сделать общий вывод, что в рамках формальной логики анализируются в основном «готовые», уже существующие, сложившиеся суждения. Это необходимая и важная задача, в ней много еще нерешенного и интересного, но ею формальная логика, по существу, и ограничивается.
Диалектическая логика значительно раздвигает горизонт логического знания. Она исследует процесс становления и развития суждения как формы мышления в истории человечества, его взаимодействия с другими формами. В ней раскрывается внутренняя диалектика всякого суждения – от самого простого до самого сложного – как отражение объективной диалектики вещей (диалектика отдельного и общего, явления и сущности, случайного и необходимого и т.д.). Не ограничиваясь анализом отдельных – пусть и многообразных – видов суждений, их координацией – пусть даже важной, она выявляет их субординацию, выводит одни формы суждений из других, показывает диалектику перехода в мысли от единичного к особенному и общему (включая и всеобщие, универсальные связи и отношения действительности).
В этом смысле диалектическая логика представляет собой качественно новую и в известном отношении более высокую теорию суждения, особую ступень в его всестороннем исследовании.
Источник: Логика: учебник для студентов юридических вузов и факультетов / Е. А. Иванов. – Изд. 3-е, перераб. и доп. – Москва: Волтерс Клувер, 2007. – 405 с. – (Библиотека студентв).; ISBN 5-466-00105-8
Комментарии для сайта Cackle
Игры на развитие логического
мышления младших школьников.
Выявление логических связей между
предметами.
Подобрать из каждой картинки из
первого ряда соответствующую картинку из второго ряда. По каждой получившейся
паре составить предложение.
В каждом ряду по пять картинок:
1. ряд.
Удочка, цветок, ключ, отвёртка.
2. ряд
.Ваза, дрова, замок, шуруп, рыба.
К указанному предмету подобрать
слово, которое логически с ним связано (как в предыдущей паре). И подробно
объяснить свой выбор.
Пример: стрелка- часы; колесо-…
Стрелка – это часть часов, значит,
к слову «колесо» можно подобрать слово «машина», потому что колесо- часть
машины.
Колесо-круг, ковёр-…?
Белка – дупло, медведь-…?
Магазин – продавец, больница…
День- ночь, вечер-…
Охотник ружьё. рыбак -…
Лес- деревья, поле-…
Палец- кольцо, ухо-…
Подобрать слово противоположного
значения.
Покупать – .помнить -, встречать-,
толстый -, полный -, открывать-.
Упражнение «Отвечай быстро»
Цель: продолжать
учить детей сравнивать. анализировать, обобщать, согласовывать числительное с
прилагательным и прилагательные с существительными.
1. Как
можно назвать всех, кто нарисован в первом ряду?
2. Сколько
всего птиц в таблице? Назовите их.
3. Кого
больше: зверей или насекомых?
4. На
сколько групп можно разделить всех, кто нарисован в таблице?
5. Посмотрите
на рисунок в третьем столбике. Что общего у всех, кто там нарисован?
6. Сравните
животных первого и второго столбика. Что вы заметили общего?
Словесная игра «Что
лишнее?» – – Света. Марина, Коля, Кристина. Вера.
·
«Назови соседей» – числа 5, вторника, осени.
·
«Найди закономерность» – детям предлагается найти закономерность и
продолжить ряд.
·
«Что перепутал художник»
·
«Найди 10 отличий» – у детей развивается не только мышление. Но и
зрительное восприятие, внимание.
·
«Шуточные логические задачи» – «Какого цвета волосы у колобка»
·
Выложи рисунок из палочек (спичек)»
3 часть. Итог мастер – класса
Именно в процессе развития
логического мышления у ребёнка формируется умение рассуждать, делать
умозаключения, выстраивать причинно – следственные связи. Умение детей
последовательно и доказательно мыслить, догадываться, проявлять умственное
напряжения. Мыслить логически – просто необходимо для успешного освоения
школьной программы.
2. Логические концовки
Дидактическая цель: развивать
логическое мышление.
Содержание: вооружись
логическим мышлением, учащиеся должны закончить и фразы:
Если стол выше стула, то стул… (ниже стола).
Если 2 больше одного, то один… (меньше двух).
Если сестра старше брата, то брат… (младше сестры).
Если правая рука справа, то левая… (слева).
Если река глубже ручейка, то ручеек… (мельче реки).
Если из ведра льется вода, то ведро… (дырявое).
3. Математический футбол
Дидактическая цель: формировать
навыки сложения и вычитания в пределах 20, 100, 1000 или умножения и
деления.
Оборудование: картинки
ворот, мячей с примерами.
Содержание: на
доске ворота, дети разделились на 2 команды. Выбегают по очереди, берут мяч, с
обратной стороны написан пример, если решил правильно – то забил гол. Побеждает
тот, кто считает без ошибок и больше забил мячей.
Дидактическая цель: развивать
логическое мышление.
Оборудование: шоколад,
камни, шахматная доска.
Содержание: учитель
озвучивает задачи:
Задача 1. Двое
по очереди ломают шоколадку 6 х 8. За ход разрешается сделать прямолинейный
разлом любого из кусков вдоль углубления. Проигрывает тот, кто не сможет
сделать ход.
Решение. Основное
соображение: после каждого хода количество кусков увеличивается ровно на 1.
Сначала был один кусок. В конце игры, когда нельзя сделать ни одного хода,
шоколадка разломана на маленькие дольки. А их 48! Таким образом, игра будет
продолжаться ровно 47 ходов. Последний, 47-й ход (так же, как и все другие
ходы с нечетными номерами) сделает первый игрок. Поэтому он в этой игре
побеждает, причем независимо от того, как будет играть.
Задача 2. Имеется
три кучки камней: в первой — 10, во второй — 15, в третьей — 20. За ход
разрешается разбить любую кучку на две меньшие; проигрывает тот, кто. не
сможет сделать ход.
Решение. После
каждого хода количество кучек увеличивается на 1. Сначала их было 3, в конце —
45. Таким образом, всего будет сделано 42 хода. Последний выигрывающий 42-й
ход сделает второй игрок.
Задача 3.
Числа от 1 до 20 выписаны в строчку. Игроки по очереди расставляют между ними
плюсы и минусы. После того как все места заполнены, подсчитывается результат.
Если он четен, то выигрывает первый игрок, если нечетен, то второй.
Решение. Четность
результата не зависит от расстановки плюсов и минусов, а зависит только от
количества нечетных чисел в первоначальном наборе. Так как в данном случае их
10 (т.е. четное число), то выигрывает первый игрок.
Задача 4. Двое
по очереди ставят ладей на шахматную доску так, чтобы ладьи не били друг друга.
Проигрывает тот, кто не может сделать ход.
Решение.
После каждого хода и количество вертикалей, и количество горизонталей, на
которые можно поставить ладей, уменьшается на 1. Поэтому игра будет
продолжаться ровно 8 ходов. Последний, выигрышный ход будет сделан вторым
игроком.
14. Поиграем в задачу
Дидактическая цель: проверить
усвоение понятия задача.
Оборудование: карточки
«задача», «условие», «вопрос», «решение», «ответ».
Содержание: получает
карточку ребенок и должен найти свое место.
Современная начальная школа идет по пути усложнения
содержания по целому ряду традиционных предметов. Математика не является
исключением. Интеллект человека в первую очередь определяется не суммой
накопленных им знаний, а высоким уровнем логического мышления. Поэтому уже в
начальной школе необходимо научить детей анализировать, сравнивать и обобщать
информацию, полученную в результате взаимодействия с объектами не только
действительности, но и абстрактного мира.
Ничто так, как математика, не способствует развитию мышления,
особенно логического, так как предметом ее изучения являются отвлеченные
понятия и закономерности, которыми в свою очередь занимается математическая
логика.
В методологии УДЕ делается акцент на развитие мышления детей, а
это положительно складывается на всем последующем умственном развитии учащихся.
Большую роль в деле развития мышления учащихся на уроках математики могут
сыграть содержательно- логические задания, направленные на развитие
различных характеристик внимания: его объема, устойчивости, умения переключать
внимание с одного предмета на другой, распределять его на различные предметы и
виды деятельности.
От того, какие задания подберёт учитель, в какой
последовательности будет их выстраивать, существенно зависит достижение целей
урока и степень активности учащихся в процессе познания.
Чтобы ребенок учился в полную силу своих способностей, стараюсь
вызвать у него желание к учебе, к знаниям, помочь ребенку поверить в себя, в
свои способности.
В первом и во втором классах рассматриваются:
– задачи логического характера с целью совершенствования
мыслительных операций младших школьников;
– умения делать заключение из двух суждений, в которых указывается
соотношение между первым и вторым объектами, вторым и третьим;
– умения сравнивать числа, выражения, текстовые задачи, глубоко осознавая
смысл операции сравнения;
– умения делать обобщения.
Дети упражняются в поиске закономерностей, выполняя задания
следующего вида:
- Сравнение предметов с указанием сходства и
различия, дробление недостающих элементов.

- Обобщение, где требуется или продолжить
или найти и дорисовать недостающий предмет.

3. ”Логические цепочки” (продолжить вправо и влево).
……, 5, 7, 9, …… (1, 3, 5, 7, 9, 11, 13, 15)
6, 12, 18, …. (6, 12, 18, 24, 30, 36)
……, 6, 12, 24, …. (3, 6, 12, 24, 48, 96)
4. “Лишнее число”
Из чисел 1, 10, 6 найди лишнее. (1 – нечетное, 10 – двузначное, 6
– не используется 1)
Из чисел 6, 18, 81 найди лишнее.
5. Что общего? 3 + 4 и 1 + 6
-Составь аналогичную пару примеров на вычитании
Во втором классе логические упражнения постепенно усложняются:
- Прочитай числа: 22, 35, 48, 51, 31, 45,
27, 24, 36, 20.
– Распредели на 2 группы – четные и нечетные.
– Найди верное решение:
31, 35, 27, 45, 51, 22 48, 24, 20, 36
31, 35, 27, 45, 51 27, 20, 24, 36, 22, 48
27, 31, 35, 45, 51 20, 22, 24, 36, 48
26, 31, 36, 35, 45, 51 20, 22, 24, 48
- Раздели на 2 группы числа: 1, 2, 3, 4, 5,
6, 7, 8, 9, 10
Четные –
Нечетные –
К какой группе отнесешь числа 16, 31, 42, 18, 57?
- Раздели на 2 группы числа: 2, 13, 3, 43,
6, 55, 18, 7, 9, 31
однозначные –
двузначные –
- Назови группы чисел одним словом:
2, 4, 6, 8 – это …
1, 3, 5, 7, 9 – это …
- Поиск недостающей фигуры.
Как правило, они наглядно предоставлены тремя горизонтальными и
вертикальными рядами: это могут быть изображения предметов, сюжетные картинки,
геометрические фигуры, числа. Путем зрительного и мысленного анализа рядов
фигур по горизонтали и по вертикали или на основе подсчёта количества фигур
рисуют недостающую.

![]()
![]()
В привитии детям интереса к урокам математики задачи занимательного
характера играют большую роль. Такие задачи вносят в урок оживление, повышают
интерес к знаниям, развивают воображение и память детей.
Обучение начальной математики проходит в тесной неразрывной связи
с воспитанием и развитием учащихся. Занятия математикой способствуют
формированию у детей основ научного мировоззрения, развивают познавательные
способности, воспитывают добросовестное отношение к учебе.
Усвоение математических понятий на конкретном жизненном материале
дает возможность показать детям, что все понятия и правила, с которыми они
знакомятся на уроках, служат практике, родились из потребностей жизни. Это
кладет начало правильному пониманию связи между наукой и практикой.
Первоначальное ознакомление детей с разного рада зависимостями
является важной основой для обучения в последующем умении раскрывать причинные
связи между явлениями окружающей действительности. На основе собственных
практических действий учащиеся знакомятся с некоторыми закономерностями, учатся
применять приобретенные знания при решении практических вопросов.
Решение деформированных примеров основано на многократном
сравнении промежуточных результатов с конечным. Его решение более содержательно
в психологическом отношении, т.к. при его решении возникает ситуация
затруднения, являющаяся исходным пунктом активного мышления.
![]()


![]()


Реши магический квадрат
сумма чисел – 15

![]()
Решение магического квадрата, умение составлять тройку простых
задач являются ключевым алгоритмом общего знания. Такой алгоритм является
базисным психологическим умением, необходимым для рационального обучения любых
вопросов математики и в старших классах.
Ребенок 7–8 лет обычно мыслит конкретными категориями. Развитию
теоретического мышления предшествует развитие способности к абстрагированию и
обобщению.
К моменту перехода в среднюю школу дети должны научиться
самостоятельно рассуждать, делать выводы, сопоставлять, сравнивать,
анализировать, находить частное и общее, устанавливать закономерности.
Поэтому в отдельную группу выделяются элементарные комбинаторные
задачи. Их особенность заключается в том, что они имеют не одно, а несколько
решений и при их решении детям необходимо осуществлять выбор решений в
рациональной последовательности с тем, чтобы быть уверенным, что рассмотрены
все возможные случаи и не пропущен ни один из них. Важно, чтобы дети увидели и
осознали возможность составления нескольких комбинаций и нашли рациональный
способ их выбора. Например:

Такие опережающие упражнения создают обстановку активности и
повышенному интересу к изучаемому предмету.
Все эти задания вызывают активизацию мыслительных процессов и в
тоже время вполне доступны учащимся.
В школьной практике мы постоянно сталкиваемся с тем, что ребенок
использует привычные, во многом навязанные ему способы решения. Так, например,
некоторые дети, после того как изучены приемы письменных вычислений, начинают
применять эти  способы
способы
и при устном решении примеров.

![]()

![]()
Прививая любовь к устным упражнениям, учитель будет помогать
ученикам активно действовать с учебным материалом, пробуждать у них
стремление совершенствовать способы вычислений и решения задач, менее
рациональные заменять более совершенными, более экономичными. А это — важнейшее
условие сознательного усвоения материала.
Направленность мыслительной деятельности ученика на поиск
рациональных путей решения проблемы свидетельствует о вариативности
мышления.
Важно показать учащимся красоту и изящество устных вычислений,
используя разнообразные вычислительные приемы, помогающие значительно облегчить
процесс вычисления.
Работа над приемами устных вычислений должна вестись с I класса.
Например, при рассмотрении примеров вида: 5+3+1=9 с постановкой вопроса: ”
Сколько всего прибавили к числу 5?” (5+4 =9) и далее — примеров
вида 12+5=10+(2+5)
Перестановка, вытекающая из переместительного и
сочетательного свойств суммы, видна на следующих примерах:
6+7+4+3 =(6+4)+(7+3) =20
2) 33+28+27+12= (3 +27)+(28+12) =60+40 =100
При выполнении устных вычислений иногда полезно округлять числа,
прибавляя к ним несколько единиц или убавляя их, имея в виду, что, например:
83-80+3 или 48-50-2.
Учащиеся знакомятся с округлением компонентов арифметических
действий.
При выполнении таких заданий внимание обращается на выявление
закономерности и нахождение более рационального приема вычислений.
Округление компонентов действия можно проследить на следующих
примерах:
1. Округление одного из слагаемых: 27+59 =27+60-1-86.
2. Округление двух слагаемых: 27+59=30+60-3-1=86
3. Округление при нахождении суммы нескольких
слагаемых:
19+23+49=20+23+50-1-1= 91.
4. Округление вычитаемого: 53-28=53-30+2=25.
Большое значение в программе УДЕ придается усвоению правил работы
с матрицей. Матрицы в обучении выполняют развивающую функцию, являются способом
пространственной организаций знаний. Преимущество использования матриц в
наглядности, лаконизме знаний, в использовании минимума исходной информации.

Вводятся нестандартные задачи. Одни из них требуют повышенного
внимания к анализу условия и построения цепочки взаимосвязанных логических
рассуждений
Марина, Катя, Таня и Света нарисовали по одной кукле. Куклы Марины
и Кати с цветами,
а куклы Светы и Кати с шарами. Кто нарисовал какую куклу?
Лучше для решения составить таблицу:
|
цветы |
шары |
|
|
М |
+ |
|
|
К |
+ |
+ |
|
Т |
||
|
С |
+ |
Особый интерес представляют головоломки. Цифры, соединившись в
числа и участвуя по нашей воле в математических действиях, образуют иной раз
весьма причудливые и по своему красивые числовые комбинации. Например:
«Числовой треугольник». «Нарисуй такие кружки и заполни их различными нужными
цифрами от 1 до 9 так, чтобы сумма чисел по каждой стороне «треугольника» была
равна 20, 17 и др.»
В третьем – четвертом классах мы
продолжаем и углубляем направления, заложенные в первом и втором классах, но
имеются и свои особенности.
1) Смещение акцента на усиление роли содержательно-логических
заданий для развития мышления учащихся. Задания становятся более разнообразными
как по содержанию, так и по форме их представления.
2) Увеличение объема самостоятельной умственной деятельности,
развитие навыков контроля и самоконтроля, развитие познавательной активности
детей.
Умение сравнивать отрабатывается при проведении сравнения двух
чисел, примеров, задач, уравнений, двух фигур, а затем и группы чисел, группы
примеров, группы задач и т. д.:
1)Напишите два числа: 100 и 1000. Сравни эти числа. Чем похожи,
чем отличаются?
2)Вычисли значение выражений:
28 : 4 24 : 4
Подчеркни подмеченные различия.
3) Найди сумму длин сторон квадратов:
![]()
4)Реши задачи. Отметь сходство и различие в задачах и их решениях.
Сделай вывод.
-Витя сделал из дерева лодку длиной 36см, а Миша – в 4 раза
короче. Какой длины лодка у Миши?
– Масса бульдога 14 кг, а щенка в 7 раз меньше. Какова масса
щенка?
- В
приведённых группах числа записаны по определённому правилу. Установи для
каждого столбца своё правило и впиши вместо точек нужные числа:
40 20 60 20 70 40 80 10 70
10 80 90 30 20 0 30 20 10
70 30 … 50 90 … 60 20 …
При выполнении этого задания необходимо сказать детям, что правило
следует искать не только путем сравнения чисел по строкам, но и сравнивая их по
столбцам.
- Раздели
числа на 2 группы: 15, 24, 25, 28, 30, 32, 35, 36, 40
При выполнении этого задания очень важно обратить внимание детей
на то, что признак разделения заданных чисел на группы не задан и им предстоит
определить его самим. Числа могут быть разделены на 2 группы по разным
признакам:
- четные,
нечетные - двузначные,
которые делятся на 5, и которые не делятся на 5.
При этом важно сказать, что необходимо следить за тем, чтобы все
числа были распределены по группам и не случилось так, чтобы одно и то же число
попало в обе группы.
Большое место отводится задачам на построение цепочки логических
рассуждений с последующими выводами, на логический перебор возможных вариантов.
Несколько усложняются задачи комбинаторного характера за счет
увеличения количества предметов, из которых образуются соединения,
Содержательно-логические задания развивающего характера включаются
в каждый урок математики в течение всего учебного года,
органично увязываются с программным математическим материалом.
Творческий проект
числа 9.
Логико- математические игры для старших
дошкольников. Эффективное развитие интеллектуальных способностей детей
дошкольного возраста — одна из актуальных задач современности. Дети с развитым
интеллектом быстрее запоминают материал, более уверены в своих силах, легче
адаптируются в новой обстановке, лучше подготовлены к школе. В интеллектуальном
развитии ребенка большую роль играет математика. Она оттачивает ум, развивает
гибкость мышления, учит логике. Свой первый математический опыт ребенок
приобретает в разнообразных видах повседневной деятельности.
Логико-математическое мышление формируется на основе образного и является
высшей стадией развития мышления. Достижение этой стадии – длительный и сложный
процесс. Не следует ждать, когда ребенку исполнится 14 лет, и он достигнет
стадии формально математических операций, когда его мышление приобретает черты,
характерные для мыслительной деятельности взрослых. Начинать развитие
логического мышления следует в дошкольном детстве. Но зачем логика маленькому
ребенку, дошкольнику? Дело в том, что на каждом возрастном этапе создается как
бы определенный «этаж», на котором формируются психические функции, важные для
перехода следующему этапу. Таким образом, навыки, умения, приобретенные в
дошкольный период, будут служить фундаментом для получения знаний и развития
способностей в более старшем возрасте – в школе. И важнейшим среди этих навыков
является навык логикоматематического мышления, способность «действовать в уме».
Ребенку, не овладевшему приемами логико-математического мышления, труднее будет
даваться учеба – решение задач, выполнение упражнений потребуют больших затрат
времени и сил. В результате может пострадать здоровье ребенка, ослабнет, а то и
вовсе угаснет интерес к учению. В целях развития логико-математического
мышления нужно предлагать старшему дошкольнику самостоятельно производить
анализ, синтез, сравнение, классификацию, обобщение, строить индуктивные и
дедуктивные умозаключения. Овладев логическими операциями, старший дошкольник
станет более внимательным, научится мыслить ясно и четко, сумеет в нужный
момент сконцентрироваться на сути проблемы, убедить других в своей правоте.
Учиться станет легче, а значит, и процесс учебы, и сама школьная жизнь будут
приносить радость и удовлетворение. Для более качественного и быстрого процесса
обучения старшего дошкольника логическим операциям и нужны дидактические игры.
Главной целью системы образования является подготовка подрастающего поколения к
активной жизни в условиях постоянно меняющегося социума. И, поскольку развитие
современного общества носит перманентный и динамический характер, постольку
ключевой задачей образовательного процесса является передача детям таких знаний
и воспитание таких качеств, которые позволили бы им успешно адаптироваться к
подобным изменениям. Поиск эффективных дидактических средств развития
логико-математического мышления дошкольников является неотъемлемой частью
данной задачи. Мышление является высшим познавательным процессом.. В процессе
мышления производится целенаправленное и целесообразное преобразование
действительности. Мышление – это особого рода умственная и практическая
деятельность, предполагающая систему включённых в неё действий и операций
преобразовательного и познавательного (ориентировочно – исследовательского)
характера». Человек включается в процесс интеллектуальной работы всякий раз,
когда приступает к решению вставшей перед ним задачи. Можно сказать, что
развитие логического мышления ребёнка – это процесс перехода мышления с эмпирического
уровня познания (наглядно-действенное мышление) на научно-теоретический уровень
(логическое мышление), с последующим оформлением структуры взаимосвязанных
компонентов, где компонентами выступают приёмы логического мышления (логические
умения), которые обеспечивают целостное функционирование логического мышления
Роль дидактической игра в сложном процессе мышления, состоит в том, чтобы через
систему специальных заданий и упражнений организовать ситуацию, позволяющую
формировать и развивать у ребенка компоненты математического мышления:
гибкость, системность, пространственную подвижность, логические приемы
умственных действий и т.п. При этом суть процесса сводится не к целевому
обучению элементам математики, а к всестороннему стимулированию развития
логической сферы мыслительных процессов ребенка. Рассмотрим возможности
активного включения в процесс математического развития ребенка старшего
дошкольного возраста различных приемов умственных действий на математическом
материале. Сериация – построение упорядоченных возрастающих или убывающих
рядов. Классический пример сериации: матрешки, пирамидки, вкладные мисочки и т.
д. Сериации можно организовать по размеру: по длине, по высоте, по ширине –
если предметы одного типа (куклы, палочки, ленты, камешки и т. д.) и просто «по
величине» (с указанием того, что считать «величиной») – если предметы разного
типа (рассадить игрушки по росту).Сериации могут быть организованы по цвету: по
степени интенсивности окраски. Анализ – выделение свойств объекта, выделение объекта
из группы или выделение группы объектов по определенному признаку. Например,
задан признак: кислый. Сначала у каждого объекта множества проверяется наличие
или отсутствие этого признака, а затем они выделяются и объединяются в группу
по признаку «кислые». Синтез – соединение различных элементов (признаков,
свойств) в единое целое. В психологии анализ и синтез рассматриваются как
взаимодополняющие друг друга процессы (анализ осуществляется через синтез, а
синтез – через анализ). Задания на формирование умения выделить элементы того
или иного объекта (признаки), а также на соединение их в единое целое можно
предлагать с первых же шагов математического развития ребенка. Для развития
продуктивной аналитико-синтетической мыслительной деятельности у ребенка
старшего дошкольного возраста в методике рекомендуют задания, в которых ребенку
необходимо рассматривать один и то т же объект с разных точек зрения. Способом
организации такого всестороннего (или по крайней мере многоаспектного)
рассмотрения является прием постановки различных заданий к одному и тому же
математическому объекту. Сравнение – логический прием, требующий выявления
сходства и различия между признаками объекта (предмета, явления, группы
предметов). Сравнение требует умения выделять одни признаки объекта и
абстрагироваться от других. Для выделения различных признаков объекта можно
использовать игру «Найди это»: • Какие из этих предметов большие желтые? (Мяч и
медведь.) • Что большое, желтое, круглое? (Мяч.) и т.д. Старший дошкольник
должен использовать роль ведущего так же часто, как и отвечающего, это
подготовит его к следующему этапу – умению отвечать на вопрос: • Что ты можешь
рассказать об этом предмете? (Арбуз большой, круглый, зеленый.Солнце круглое,
желтое, горячее.) Вариант. Кто больше расскажет об этом? (Лента длинная, синяя,
блестящая, шелковая.) Вариант. «Что это: белое, холодное, рассыпчатое?» и т. д.
Методически рекомендуется сначала учить старшего дошкольника сравнивать два
объекта, затем группы объектов. Дошкольнику легче сначала найти признаки
различия объектов, затем – признаки их сходства. Задания на разделение объектов
на группы по какому-то признаку (большие и маленькие, красны
Сравнение – логический прием, требующий
выявления сходства и различия между признаками объекта (предмета, явления,
группы предметов). Сравнение требует умения выделять одни признаки объекта и
абстрагироваться от других. Для выделения различных признаков объекта можно
использовать игру «Найди это»: • Какие из этих предметов большие желтые? (Мяч и
медведь.) • Что большое, желтое, круглое? (Мяч.) и т.д. Старший дошкольник
должен использовать роль ведущего так же часто, как и отвечающего, это
подготовит его к следующему этапу – умению отвечать на вопрос: • Что ты можешь
рассказать об этом предмете? (Арбуз большой, круглый, зеленый.Солнце круглое,
желтое, горячее.) Вариант. Кто больше расскажет об этом? (Лента длинная, синяя,
блестящая, шелковая.) Вариант. «Что это: белое, холодное, рассыпчатое?» и т. д.
Методически рекомендуется сначала учить старшего дошкольника сравнивать два
объекта, затем группы объектов. Дошкольнику легче сначала найти признаки
различия объектов, затем – признаки их сходства. Задания на разделение объектов
на группы по какому-то признаку (большие и маленькие, красные и синие и т. п.)
требуют сравнения. Все игры вида «Найди такой же» направлены на формирование
умения сравнивать. Для детей старшего дошкольного возраста количество и
характер признаков сходства могут широко варьироваться. Классификация –
разделение множества на группы по какому-либо признаку, который называют
основанием классификации. Основание для классификации может быть задано, но
может и не указываться (этот вариант чаще используется со старшими детьми, так
как требует умения анализировать, сравнивать и обобщать). Следует учитывать,
что при классификационном разделении множества полученные подмножества не
должны попарно пересекаться и объединение всех подмножеств должно составлять
данное множество. Иными словами, каждый объект должен входить в одно и только в
одно подмножество. Классификацию с детьми старшего дошкольного возраста можно
проводить: • по наименованию предметов (чашки и тарелки, ракушки и камешки,
кегли и мячики и т. д.); • по размеру (в одну группу большие мячи, в другую –
маленькие мячики; в одну коробку длинные карандаши, в другую – короткие и т.
д.); • по цвету (в эту коробку красные пуговицы, в эту – зеленые); • по форме
(в эту коробку квадраты, а в эту – кружки; в эту коробку – кубики, в эту –
кирпичики и т. д.); • по другим признакам (съедобное и несъедобное, плавающие и
летающие животные, лесные и огородные растения, дикие и домашние звери и т.
д.). Все перечисленные выше примеры – это классификации по заданному основанию:
педагог сам сообщает его детям. В другом случае старшие дошкольники определяют
основание самостоятельно. Педагог задает только количество групп, на которые
следует разделить множество предметов (объектов). При этом основание может быть
определено не единственным образом. При подборе материала для задания педагог
должен следить за тем, чтобы не получился набор, ориентирующий детей на
несущественные признаки объектов, что будет подталкивать к неверным обобщениям.
Следует помнить, что при эмпирических обобщениях дети опираются на внешние,
видимые признаки объектов, что не всегда помогает правильно раскрыть их
сущность и определить понятие. Формирование у старших дошкольников способности
самостоятельно делать обобщения является
крайне важным с общеразвивающей точки зрения.
В связи с изменениями в содержании и методике обучения математике в начальной
школе, которые ставят своей целью развивать у учащихся способности к
эмпирическому, а в перспективе и теоретическому обобщению, важно уже в детском
саду обучать детей различным приемам моделирующей деятельности с помощью
вещественной, схематической и символической наглядности (В.В. Давыдов), учить
ребенка сравнивать, классифицировать, анализировать и обобщать результаты своей
деятельности. Использование игровых приемов, дидактических игр делает обучение
в этом возрасте сообразным природе ребенка. Игра создает «зону ближайшего
развития ребенка» (Л.С.Выготский) «В игре ребенок всегда выше своего среднего
возраста, выше своего обычного повседневного поведения; он в игре как бы на
голову выше самого себя. Игра в конденсированном виде содержит в себе, как в фокусе
увеличительного стекла, все тенденции развития; ребенок в игре как бы пытается
сделать прыжок над уровнем своего обычного поведения». Таким образом,
дошкольник развивается в разных видах деятельности. Особо важное значение в
подготовке его перехода на следующую возрастную ступень имеет игра. Она
является ведущей деятельностью в дошкольный период, поскольку, как никакая
другая деятельность, отвечает особенностям психики дошкольника, наиболее
свойственна и характерна для него. По характеру используемого материала
дидактические игры условно делятся на игры с предметами, настольно-печатные
игры и словесные игры. Так как важным средством формирования мыслительной
деятельности ребёнка, его интеллекта является игра, то в дошкольной педагогике
существует множество разнообразных методических материалов: методик,
технологий, которые обеспечивают интеллектуальное развитие детей это:
логические блоки Дьенеша, палочки Кюизенера, игры В. Воскобовича и
игры-головоломки. Благодаря этим играм у ребенка развиваются все психические
процессы, мыслительные операции, развиваются способности к моделированию и
конструированию, формируются представления о математических понятиях. В первую
очередь, на мой взгляд, это означает отказ от авторитарного способа обучения и
воспитания детей. Обучение должно быть развивающим, обогащать ребенка знаниями
и способами умственной деятельности, формировать познавательные интересы и
способности. В связи с этим особое значение приобретают новые игровые формы
обучения и воспитания детей, в частности новые развивающие дидактические игры.
Сущность игры как ведущего вида деятельности заключается в том, что дети
отражают в ней различные стороны жизни, особенности взаимоотношений взрослых,
уточняют свои знания об окружающей действительности. Игра есть средство
познания ребенком действительности и одно из самых привлекательных для детей
занятий. Наиболее эффективными средствами развития мыслительной активности
являются палочки Кюизенера, логические блоки Дьенеша, игры Воскобовича, игры
головоломки. Применение в работе нестандартных дидактических игр, требует
разработки некоторых этапов при ознакомлении детей с новой игрой. Каждый этап
несёт в себе определенные цели и задачи. Этапы знакомства детей с новой игрой 1
Этап: Внесение новой игры в группу. Цель: знакомство детей с новой игрой, с ее
особенностями и правилами. 2 Этап: Собственно игра. Цель: Развивать: логическое
мышление, представление о множестве, умение выявлять свойства в объектах,
называть их, обобщать объекты по их свойствам, объяснять сходства и различия
объектов. Познакомить с формой, цветом, размером, толщиной объектов Развивать
пространственные отношения Развивать познавательные процессы, мыслительные
операции. 3 Этап: Самостоятельная игра детей с развивающим материалом.
Развивать творческие способности, воображение, фантазию, способности к
конструированию и моделированию. Перспективное планирование занятий с
нетрадиционными дидактическими играми с детьми 6-7 лет математическое развитие
СЕНТЯБРЬ : Свойства 1. Геометрические фигуры «2-х цветный квадрат» – игровое
задание: найди и сложи разные пятиугольники «Чудо-крестики – 2,3» – игровое
задание: найти все не треугольники, не красные, и т.д. (конструирование по
схемам) Блоки Дьенеша 2.Преобразование «4-х цветный квадрат» – игровое задание:
помочь шутам Двану и Трину вернуть цвет (схемы 11,13,16) 3. Многоугольники
«Геоконт» – игровое задание: с помощью резинок разного цвета выложить разные по
величине многоугольники. «Прозрачные льдинки» – игровое задание: найди все
многоугольники. Окттябрь: Отношения Целого и части «Геоконт» – игровое задание
разделить прямоугольник на четыре равные а затем не равные части
«Чудо-крестики – 2,3» – игровое задание:
собрать крестики не цветной стороной (конструирование по схемам)
Пространственные отношения «Прозрачный квадрат» – игра «Волшебный мешочек» –
игровое задание: назвать невидимые льдинки и описать их. Количественные
отношения «Прозрачная цифра» – игровое задание: из каких пластинок можно
сложить цифры (4,5,7,8), описание пластинок. «Двухцветный квадрат» – превращение
квадрата в домик – игровое задание: сколько в этом домике квадратов красного,
зеленого цвета; сколько разноцветных. Палочки Кьюзенера Интегрированные
занятия. Ноябрь: Числа и цифры Состав числа. «Кораблик «Брызг – брызг» –
игровые задания: название мачт, насколько больше на каждой мачте флажков,
размещение флажков по словесному заданию. «Счетовозик» – знакомство с игрой –
игровое задание: в каких окнах больше всего фонариков, где меньше, где нет и
почему? «Волшебная восьмерка» – игровое задание: сколько предметов? (выложить
цифры) Палочки Кьюзенера Декабрь: Пространственные отношения «Геоконт», «2-х
цветный, 4-х цветный квадрат» – игровое задание: работа со схемами,
преобразование фигур. «Чудо-соты», «Чудо –крестики» 1,2,3 – выкладывание по
схемам. «Змейка» – знакомство с игрой (из методики) «Игровизор» – «Катя, Рыжик,
Рыбка» (листы 1,2,3) «Кораблик «Брызг-Брызг» – игровые задания: раскладывание
флажков на мачтах по схеме «Лесенка», «Радуга», «Тельняшка».
Логико-математическое занятие. Январь: Состав чисел второго десятка
«Счетовозик» – игровые задания: на сколько больше окошек зажглось в каждом
ряду, отметь шнурком из каких чисел состоит 11, 13,15 и т.д. «Игровизор» –
игровые задания: посели жильцов в домики, расставь знаки (,= ) Преобразование
«Геоконт» – знакомство с понятиями «луч», «отрезок», «прямая», «кривая» с
помощью сказки (главы 3,7, 9, 10,11) «Логоформочки – 3,5» – знакомство с игрой
название формочки, верх, низ. Конструирование из
частей, в ячейках линейки, на столе и по
образцу. Палочки Кьюзенера Логико-математическое занятие. Февраль: Сложение и
вычитание чисел «Счетовозик» – игровое занятие соединить с помощью шнурка два
числа «Лабиринты цифр»- решение арифметических действий с помощью «игровизора»
Сохранение количества «Прозрачный квадрат» – неизменность величины, задание на
поиск закономерностей игра «Кто быстрее сложит девять квадратов» – игровое
задание «Чудо-крестики» игра «Волшебный мешочек», «Змейка» – игровое задание:
перекрути, вспомни как собирали фигуру. Связь изменения и неизменности в
зависимости от расположения предмета «Прозрачная цифра» – игровое задание: что
нужно сделать, чтобы превратить 6 в 9? Как тройку превратить в девятку,
перевернув только одну пластинку? Палочки Кьюзенера Март: Алгоритмы (чтение
схем, способов и пути при выполнении действий) «Геоконт»– конструирование фигур
по сказке; на чудесной Поляне появляется паутина любой формы, перенести ее на
«геовизор» «2-х цветный квадрат» – игровое задание сложить предметные формы,
назвать, сочинить описательные рассказы или сюжетные рассказы. «4-цветный
квадрат» – Шуты сочиняют новые забавы для короля, игровое задание: придумать
новые фигуры, сложить и назвать их. «Чудо-соты» – игровое задание: обводят
детали головоломки, раскрашивают и сочиняют рассказ. «Змейка» – складывание по
схемам плоскос тных и объемных фигур. «Чудо-крестики» – вспомнить приключения,
сложить одну сюжетную картинку и придумать рассказ. «Прозрачный квадрат»- показ
предметов; игровое задание: выложить точно такой же из «льдинок» «Прозрачная
цифра» – складывание предметов, не пользуясь картинкой – схемой «Кораблик Брызг
– Брызг» Игра «Да – нет» Игра «Посмотри и вспомни» «Волшебная восьмерка» –
игровые задания: зашифруй цифру с помощью, считалки «кохлеохле…» Нетрадиционные
игры на развитие логического мышления. Название игры Описание, назначение
Цветные счетные палочки Кюизенера Каждая палочка – это число, выраженное цветом
и величиной. С математической точки зрения палочки это множество, на котором
легко обнаруживаются отношения эквивалентности и порядка. В этом множестве
скрыты многочисленные математические ситуации. Цвет и величина, моделируя
число, подводят детей к пониманию различных абстрактных понятий, возникающих в
мышлении ребенка естественно как результат его самостоятельной практической
деятельности. Использование «чисел в цвете» позволяет одновременно развить у
детей представление о числе на основе счета и измерения. К выводу, что число
появляется на основе счета и измерения, дети приходят на базе практической
деятельности, в результате разнообразных упражнений. С помощью цветных палочек
детей также легко подвести к осознанию отношений больше – меньше, больше –
меньше на…, научить делить целое на части и измерять объекты условными мерками,
поупражнять в запоминании состава чисел из единиц и меньших чисел, подойти
вплотную к сложению, умножению, вычитанию и делению чисел. Кроме этого, играя с
палочками, дети осваивают такие понятия как «левое», «длинное», «между»,
«каждый», «одна из…», «какой-нибудь», «быть одного и того же цвета», «быть не
голубого цвета», «иметь одинаковую длину» и др. Комплект состоит из 116
пластмассовых призм 10-ти различных цветов и форм. Наименьшая призма имеет
длину 10 мм и является кубом. Выбор цвета преследует цель облегчить
использование комплекта. Палочки 2,4,8 образуют «красную семью», 3,6,9 – «синюю
семью». «Семейство желтых» составляют 5 и 10. Подбор палочек в одно семейство
(класс) происходит не случайно, а связан с определенным соотношением их по
величине. Например, в семейство красных входят числа кратные двум и т.д. В
каждом из наборов действует правило: чем больше длина палочки, тем больше
значение того числа, которое она выражает. Логические блоки Дьенеша Набор
логических блоков состоит из 48 объемных геометрических фигур, различающихся по
цвету, форме, размеру и толщине. Таким образом, каждая фигура характеризуется
четырьмя свойствами. В наборе нет даже двух фигур, одинаковых по всем
свойствам. Основная цель – научить ребенка решать логические задачи на
разбиение по свойствам Геоконт • Поле (480х500 мм, фанера, цветная пленка) с
нанесенной координатной сеткой. В тридцати трех точках координатной сетки
установлены разноцветные пластмассовые гвоздики (цвета радуги, черный и белый).
• Резинка трех цветов. • Альбом схем. • Набор резинок «Радуга». Что развивает –
различение цветов радуги; – освоение названий и структуры геометрических фигур,
их размера; – умение строить симметричные, несимметричные фигуры, узоры,
ориентироваться в пространстве; – умение конструировать фигуры по схеме,
картинке, словесному алгоритму и собственному замыслу; – внимание, память,
элементы логического мышления; Чудо- крестики • Рамка (210х297 мм, фанера,
цветная пленка). • 7 фигур-вкладыше
• Рамка (210х297 мм, фанера, цветная пленка).
• 7 фигур-вкладышей в форме крестиков (фанера, пленка розового, малинового,
салатного, бирюзового, светло-голубого, лимонного, лилового цветов): 1 целая и
6 составных (из четырех, пяти, шести, семи частей). Части – это геометрические
фигуры: прямоугольники, треугольники, параллелограмм, другие многоугольники и
круг, составленный их двух половинок. • Альбом фигурок (50 фигур). Что
развивает – сенсорные способности (различение цветов радуги, геометрических
фигур, их размера); – умение «читать» схемы, сравнивать и составлять целое из
частей; – внимание, память; – воображение, творческие способности; – мелкую
моторику рук. Счетовозик • Игровое поле (280х200 мм, фанера, шелкография) в
форме паровозика. На поле закреплены кнопки тремя рядами (1-й – цифры первого
десятка, 2-й – цифра 0 и арифметические знаки, 3-й – цифры второго десятка). •
Шнурок. Что развивает – освоение порядкового и количественного счета; –
соотнесение цифры и количества; – сравнение чисел первого и второго десятка,
состав чисел второго десятка; – сложение чисел, решение простейших
арифметических задач; – внимание, память, элементы логического мышления; –
мелкую моторику рук. Математические • Два игровых поля (210х297 мм, фанера,
цветная пленка, шелкография) с вкладышами – 11 «корзинок» и 34 «грибка»
(фанера, цветная пленка, шелкография); Что развивает – умения составлять числа
первого и второго десятка, складывать и вычитать в пределах 10, различать
полное, неполное множество; – внимание, память, элементы логического мышления;
– мелкую моторику рук. корзинки Логоформочки • Игровое поле (237х318 мм,
фанера, белая пленка, шелкография). • Фигуры-вкладыши (фанера, белая пленка,
шелкография): 5 эталонных (круг, треугольник, квадрат, прямоугольник, овал) и
20 составных фигур; подвижная линейка, части эталонных фигур. Что развивает –
освоение названий и структуры геометрических фигур, пространственных отношений
(верх, низ, лево, право); – составление предметных силуэтов из частей; –
внимание, память, воображение; – умение сравнивать, анализировать,
синтезировать; – мелкую моторику рук. Кораблик «Брызг – брызг» • Игровое поле
из ковролина в виде корабля с прикрепленным корпусом (фанера, шелкография). На
корпусе нанесены цифры – номера мачт. • 28 флажков (фанера, цветная пленка): 1
красный, 2 оранжевых, 3 желтых, 4 зеленых, 5 голубых, 6 синих, 7 фиолетовых.
Флажки снабжены держателями и липучкой. • Подложка (280х380 мм, ковролин). Что
развивает – внимание, память, мышление, речь; – мелкую моторику рук; –
математические представления о цвете, высоте, пространственном расположении
предметов, условной мерке, количестве предметов и их порядковом номере,
цифровом ряде; – умение решать логико-математические задачи. Волшебная
восьмёрка • Игровое поле для конструирования одной цифры (164х300 мм, фанера,
белая пленка, шелкография). На поле закреплена круглая резинка, нанесен рисунок
восьмерки и написаны слова считалки «Кохле-Охле…». • 7 двусторонних
элементов-палочек (фанера, цветная пленка). С одной стороны они окрашены в
цвета радуги, с другой – в любой другой цвет. • Инструкция, включающая схемы
сложения цифр от 0 до 9. Что развивает -освоение количественного счета,
моторного образа цифр, пространственных отношений; – умение сравнивать,
анализировать, синтезировать, проводить тактильный и оптический анализ цифр; –
внимание, память; – координацию «глаз-рука»; – мелкую моторику рук. Игровизор •
Блокнот (210х297 мм) из двух листов. Один лист – светлый картон с названием и
изображением персонажа и сетки (цветная печать), второй лист – прозрачная
пленка ПВХ. Листы сброшюрованы. • Маркер для белой доски. Что развивает –
математическое, речевое развитие, экологическое образование, знакомство с
предметным миром и многое другое. – внимание, память, пространственное и
логическое мышление; – сообразительность, воображение, творческие способности;
– мелкую моторику рук. Квадрат Воскоб овича • На квадратную основу из ткани
(140х140 мм) на некотором расстоянии друг от друга наклеены треугольники из
плотного картона. Одна сторона «Квадрата» – зеленого и желтого цвета, другая –
синего
• На квадратную основу из ткани (140х140 мм)
на некотором расстоянии друг от друга наклеены треугольники из плотного
картона. Одна сторона «Квадрата» – зеленого и желтого цвета, другая – синего и
красного. • Цветные рисунки 18 сложенных фигур в книжечке «Квадратные забавы»
(100х95 мм, цветная печать). Что развивает – умение ориентироваться в форме и
размере геометрических фигур, пространственных отношениях; – умение
конструировать плоскостные и объемные фигуры; – внимание, память,
пространственное и логическое мышление; – воображ
1. Суждение и связь (отношение) предметов
Происхождение и сущность суждения. Будучи продуктом человеческого мышления, суждение подобно понятию своими корнями уходит глубоко в действительность.
Каково же происхождение суждения? Почему помимо понятия возможна и необходима именно такая форма мышления? Ее возможность обусловлена характером самой действительности. Как подчеркивалось выше, объективную основу понятия составляет предметный характер действительности, т. е. наличие в нем предметов, обладающих качественной определенностью. Объективной же основой суждения служит ее связный характер, т. е. связи и отношения между ними.
Но что возникает раньше — понятие или суждение? Здесь налицо аналогия со знаменитой проблемой «курицы и яйца». Как известно, она неразрешима, если рассматривать курицу и яйцо в «готовом» виде. Если же подходить к ней с точки зрения теории развития, то обнаружится, что то и другое возникает одновременно: лишь в процессе эволюции органического мира курица становится курицей, кладущей яйца. Точно так же нельзя однозначно ответить на вопрос: «Что раньше — понятие или суждение?» Ни то ни другое в отдельности. Они складываются вместе, в процессе становления мышления. .Образование простейших понятий есть одновременно процесс возникновения суждений, и наоборот: «Это дом», «Дом большой», «Дом сделан из камня» и т. д. В конечном счете такова сама действительность, лежащая в основе понятий и суждений. Нельзя сказать, что” в ней возникло раньше: предметы или связи и отношения между ними. То и другое появляется одновременно в процессе развития окружающего мира.
Связи и отношения между предметами мысли носят самый разнообразный характер. Они могут быть между двумя отдельными предметами, между предметом и группой предметов, между группами предметов и т.п. Многообразие таких реальных связей и отношений находит свое отражение в многообразии суждений.
Для правильного понимания суждения важно учитывать, что одна из фундаментальных особенностей действительности заключается в ее своеобразной «раздвоенности»: предметы могут существовать или не существовать; обладать теми или иными свойствами или не обладать; находиться в тех или иных связях и отношениях с другими предметами или не находиться. В суждениях и раскрывается наличие или отсутствие чего-либо у чего-то. Например, железо обладает ковкостью. Наличие этой связи между предметом и отдельным свойством делает возможным суждение: «Железо ковко». Графически такую связь можно представить следующим образом:
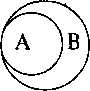
где А — железо, а В — класс предметов, обладающих свойством ковкости.
В то же время железо не обладает пластичностью. Отсутствие связи предмета с этим свойством обусловливает возможность суждения: «Железо не пластично». Графически подобное соотношение выглядит так:
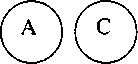
где А — железо, а С — класс предметов, обладающих свойством пластичности.
Другие примеры: «Россия — федерация», «Россия — не унитарное государство» или «Мораль древнее права», «Право связано с политикой».
Необходимость же суждений, как и понятий, коренится в практической деятельности людей. Взаимодействуя с природой в процессе труда, человек должен не только выделять те или иные предметы среди других, но и постигать их соотношения, чтобы успешно воздействовать на них.
Отсюда сущность суждения. Это форма мышления, посредством которой раскрывается наличие или отсутствие каких-либо связей и отношений между предметами. (Подобно тому как предмет в логике трактуется весьма широко — как все, на что может быть направлена мысль, так связи и отношения здесь понимаются в самом широком смысле — как всякие соотношения между предметами мысли.)
Важнейший отличительный признак суждения — утверждение или отрицание чего-либо о чем-либо. В понятии лишь выделяется сам предмет мысли. Например, «День», «Ночь», «Солнечный день» или «Несолнечный день». В суждении же акцентируется внимание на самом соотношении между какими-либо предметами мысли: «День солнечный» или «День не солнечный», «День прошел», «Ночь настала». Причем делается это в форме утверждения или отрицания. Другие, юридические примеры: «Закон» — понятие, а «Закон опубликован» — суждение; «Опубликованный закон» — понятие, а «Опубликованный закон вступил в силу» — суждение.
По своему содержанию суждение может быть истинным или ложным. Суждение истинно, если оно соответствует действительности (т.е. связывает то, что связано в самой действительности, и разъединяет то, что фактически разъединено). Вспомним наши примеры: «Железо ковко», «Железо не пластично» или «Россия — федерация», «Россия — не унитарное государство». Но суждение будет ложным, если оно не соответствует действительности: «Железо не ковко», «Железо пластично» или «Россия — не федерация», «Россия — унитарное государство».
Истинность и ложность — важнейшие характеристики суждения, отличающие его от понятия. Ведь понятие само по себе не может быть ни истинным ни ложным. Вспомним снова понятие «вечный двигатель»: оно пустое, но не ложное и не истинное. А суждение «Вечный двигатель невозможен» — истинно, суждение: «Вечный двигатель существует» — ложно. Истинность и ложность суждений не зависит от нашего отношения к ним, от того, считаем ли мы их истинными или ложными, а определяется отношением к самой действительности, носит объективный характер.
В то же время разграничение истинных и ложных суждений относительно. «День солнечный» — истинно, если вовсю сияет Солнце, и ложно, если льет дождь. Не учитывать этого — значит оказываться в положении Иванушки, который применил пожелание: «Таскать вам не перетаскать», доброе в одной житейской ситуации, к прямо противоположной.
Установление истинности или ложности суждения не представляет труда лишь в простейших случаях типа: «День солнечный», «Ночь лунная». Достаточно взглянуть в окно, чтобы убедиться в истинности или ложности подобных суждений. В научном же познании истинность или ложность суждения устанавливается в итоге более или менее длительного исследования. Например, в течение тысячелетий считалось истинным суждение «Вселенная стационарна». Но только в начале XX в. была обнаружена его ложность и установлена истинность суждения «Вселенная нестационарна». Это означает, что, как и все на свете, она подвержена эволюции, развивается от одного, первоначального состояния к какому-то другому («разбегание галактик»).
В юридической практике установление истинности или ложности чего-либо — тоже нередко сложный, мучительный процесс. Вспомним, сколько времени понадобилось для расследования деятельности ГКЧП, чтобы установить виновность или невиновность каждого из его членов. И лишь амнистия в связи с принятием Конституции Российской Федерации 1993 г. разом разрубила этот «гордиев узел». Но тут есть и своя специфика. Во-первых, юридическое выяснение объективной истины по делу предполагает в качестве непременного условия точное соблюдение норм уголовного или гражданского права. А во-вторых, помимо общезначимых понятий «истинность» и «ложность» и равнозначных им «правдивость» и «неправдивость» особо выделяются еще понятия специфически юридические: «заведомая ложность» и «добросовестное заблуждение». Могут быть заведомо ложные показания свидетеля или потерпевшего, заведомо ложное заключение эксперта, заведомо неправильный перевод с одного языка на другой. Так, по российскому уголовному праву заведомо ложное показание свидетеля квалифицируется как преступление, состоящее в умышленном сокрытии им фактов или сознательном извращении истины. Опасность такого преступления кроется в том, что в результате преступник может быть оправдан, а невиновный осужден. Поэтому за дачу ложных показаний предусмотрена ответственность.
Добросовестное заблуждение — это искажение истины не по умыслу, не сознательно, а по ошибке, из-за незнания, недостаточной компетентности и т.д. В этом случае оснований для привлечения к ответственности нет.
Роль и функции суждений, их структура. Суждения играют поистине огромную — не менее, чем понятия, — роль в мышлении, выполняя тоже важные функции в познании и общении. Но конкретное содержание роли и функций суждений по сравнению с понятиями качественно иное. Если назначение понятия сводится к выделению предмета мысли, то суждение — универсальная форма раскрытия реальных связей и отношений между предметами в природе и обществе, между любыми предметами мысли.
В форме суждения происходит процесс образования понятия, хотя понятие, как отмечалось, есть предпосылка суждения. Недаром Гегель, характеризуя диалектику понятия и суждения, остроумно заметил, что понятие — свернутая форма суждения, а суждение — развернутая форма понятия.
Форму суждения обретает также процесс оперирования уже сложившимися, готовыми понятиями. Чтобы подвести тот или иной предмет под существующее понятие, необходимо, во-первых, знать содержание этого понятия; во-вторых, выявить характерные признаки исследуемого предмета и, в-третьих, установить соответствие между тем и другим. Например: «Холст есть товар», «Мошенничество — преступление», «Свидетель неправдив». В форму суждения облекаются определения, а также приемы, сходные с ними (сравнение, характеристика, описание и др.). Форма суждения используется в операциях деления и расчленения, классификации и типологии.
В виде суждений формулируются, по существу, все научные положения, ими выражаются достигнутые научные истины. Особое значение суждений определяется тем, что они служат мыслительной формой, в которую, как правило, облекаются объективные закономерности окружающего мира, открываемые естественными и общественными науками, например: закон всемирного тяготения, закон сохранения и превращения энергии, закон единства организма и среды, закон соответствия производственных отношений характеру и уровню развития производительных сил. Суждения служат также универсальной формой духовного общения между людьми, взаимообмена информацией о самых различных сторонах действительности.
Специально подчеркнем, что в законодательстве любая норма есть суждение, т. е. утверждение или отрицание какого-либо права или обязанности. Так, Конституция Российской Федерации состоит из множества статей, каждая из которых представляет собой либо отдельное суждение, либо совокупность суждений. Например: «Носителем суверенитета и единственньм источником власти в Российской Федерации является ее многонациональный народ» (ст. 3). Или: «Человек, его права и свободы являются высшей ценностью. Признание, соблюдение и защита прав и свобод человека и гражданина — обязанность государства» (ст. 2).
Однако норма — это особая, весьма сложная разновидность суждений. Правовые суждения-нормы возникают лишь на определенном этапе развития общества — с появлением частной собственности и представляют собой отражение и закрепление соответствующих общественных отношений между людьми, в первую очередь экономических. Их назначение состоит в том, что они регулируют эти отношения, способствуя их совершенствованию и развитию. В них запечатлеваются установленные или санкционированные государством разрешения и запрещения, права и обязанности. Естественно поэтому, что такие суждения имеют и особую структуру. Они содержат указание, когда и при каких условиях применяется норма, как должен в соответствии с ней поступать человек, и какие санкции последуют, если эта норма не выполняется. Специфика таких суждений-норм во всей их сложности исследуется в особом разделе современной логики — модальной логике, где есть специальный подраздел «логика норм».
Естественно также, что не только законодательство, но и все судопроизводство — уголовное, гражданское — неразрывно связано с использованием суждений. Любопытно отметить, что в Уголовно-процессуальном кодексе Российской Федерации прямо указывается на это обстоятельство: «Присяжные заседатели не могут разглашать суждения, имевшие место во время совещания» (ст. 341). И это понятно: ведь само слово «суд» имеет общий корень со словами «судить», «обсуждать», «рассуждать», «суждение».
Будучи сложной формой мышления, суждение обладает особой структурой. Она обусловлена тем, что всякое суждение предполагает наличие, по крайней мере, двух мыслимых предметов, так или иначе соотносящихся друг с другом. Поэтому суждение состоит из двух основных компонентов — субъекта и предиката, определенным образом связанных между собой.
Субъект суждения (от лат. subjectum — лежащий в основе) — это мысль о предмете, о котором утверждается или отрицается что-либо. Сокращенно он обозначается в логике буквой «S».
Предикат суждения (от лат. praedicatum — сказанное) — мысль о том, что именно утверждается или отрицается о предмете. Сокращенно он обозначается буквой «Р».
Субъект и предикат называются терминами суждения. Поскольку они выражаются понятиями, то очевидно, что применительно к суждениям понятия выполняют роль их терминов. В этом состоит одна из логических функций понятий.
Термины суждения носят соотносительный характер. Один не существует без другого (нет субъекта без предиката, как и наоборот). Обусловлено это тем, что сами связи и отношения не существуют отдельно от вещей и обратно. Есть лишь вещи, обладающие свойствами (и притом многими свойствами), а следовательно, находящиеся в различных связях и отношениях.
Однако роль терминов в суждении далеко не одинакова. Субъект содержит уже известное знание, а предикат несет о нем новое знание. Благодаря этому обеспечивается не только связность знаний, но и их накопление и развитие, их прогресс.
Правда, различение терминов не абсолютно. То, что в одном суждении выступает как субъект, в другом может быть предикатом и соответственно наоборот. Например: «Это (S) береза (Р)»; «Береза (S) — дерево (Р)»; «Дерево (S) — живой организм (Р)».
Связь (отношение) между субъектом и предикатом, отражая объективное отношение между мыслимыми предметами, раскрывается посредством логической связки. В русском языке она выражается словами «есть» («не есть»), «является» («не является»), «представляет собой» («не представляет собой») и другими, синонимичными им. Двоякий характер связки («есть — не есть») и отражает реальную раздвоенность мира — наличие или отсутствие чего-либо у чего-то. В ряде случаев связка выражается с помощью тире. Например: «Не пойман — не вор». (Предполагается: «Не пойманный не есть вор».) Нередко она попросту отсутствует, а логическое соотношение между субъектом и предикатом раскрывается посредством грамматического согласования слов: «Конституция принята», «Закон не действует» (ср.: «Конституция есть то, что принято», «Закон не есть то, что действует»).
Связка играет в суждении особую роль. Именно благодаря ей суждение становится суждением. В ней выражается глубочайшая сущность суждения: ведь только она раскрывает наличие или отсутствие чего-либо у предмета мысли и заключает в себе утверждение или отрицание.
Раскрываемая в суждении связь между предметами мысли предстает обычно как связь понятий. Ее только не следует ни отрывать от действительности, ни отождествлять с ней. В форме суждения раскрываются по существу все многообразные отношения между понятиями по их содержанию и объему — сравнимости и несравнимости («Роза — растение», «Роза — не верблюд»); совместимости и несовместимости: равнозначности («А. Пушкин — автор романа «Евгений Онегин»), подчинения («Все адвокаты — юристы»), пересечения («Некоторые юристы — таможенники») и т. д.
Поскольку субъект и предикат, будучи понятиями, могут рассматриваться с точки зрения их содержания и объема, то связка тоже может быть истолкована в двух планах — содержательном и объемном.
В содержательном плане она выражает принадлежность или непринадлежность признака или совокупности признаков предмету. С объемной точки зрения она раскрывает включение подкласса (подмножества) в класс (множество) предметов или принадлежность элемента классу (множеству).
В самом общем виде суждение можно наглядно выразить следующей формулой: «S есть (не есть) Р». В современной логике «S» и «Р» называются логическими переменными, так как они могут вмещать в себя самое различное содержание. А связка — это логическая постоянная. В ней заключено одно и то же, неизменное содержание: она всякий раз служит показателем наличия или отсутствия чего-либо у предмета мысли.
Единство элементов мысли в суждении, обеспечиваемое связкой, есть лишь отражение реального единства мира: самих вещей, их свойств, связей и отношений.
Читайте также
§ 2. ПРИЗНАКИ ПРЕДМЕТОВ И ИХ ВИДЫ
§ 2. ПРИЗНАКИ ПРЕДМЕТОВ И ИХ ВИДЫ
Поскольку в понятиях предметы обобщаются и выделяются на основе систем признаков, целесообразно познакомиться с основными видами признаков.Признак — это наличие или отсутствие свойства у предмета, а также наличие или отсутствие
1. Область предметов и суждений
1. Область предметов и суждений
Суждение необходимо относится к предметам. Нет такой категории и такого вида предметов, к которым суждение не могло бы относиться. Предметами суждений могут становиться не только вещи, вещества, лица, но и состояния, особенности, процессы,
Различные виды восприятия, соответствующие разнообразию предметов
Различные виды восприятия, соответствующие разнообразию предметов
Перед тем, как подробнее заняться отдельными типичными формами этой субъективации ценностей вообще и эстетических ценностей в частности, мы хотели бы вкратце остановиться на различении ценностей и
§ 1. СУЖДЕНИЕ КАК ФОРМА МЫШЛЕНИЯ. СУЖДЕНИЕ И ПРЕДЛОЖЕНИЕ
§ 1. СУЖДЕНИЕ КАК ФОРМА МЫШЛЕНИЯ. СУЖДЕНИЕ И ПРЕДЛОЖЕНИЕ
Суждение как форма мышленияПознавая окружающий мир, человек раскрывает связи между предметами и их признаками, устанавливает отношения между предметами, утверждает или отрицает факт существования предмета. Эти
§ 2. ПРИЗНАКИ ПРЕДМЕТОВ И ИХ ВИДЫ
§ 2. ПРИЗНАКИ ПРЕДМЕТОВ И ИХ ВИДЫ
Поскольку в понятиях предметы обобщаются и выделяются на основе систем признаков, целесообразно познакомиться с основными видами признаков.Признак — это наличие или отсутствие свойства у предмета, а также наличие или отсутствие
1. Суждение и связь (отношение) предметов
1. Суждение и связь (отношение) предметов
Происхождение и сущность суждения. Будучи продуктом человеческого мышления, суждение подобно понятию своими корнями уходит глубоко в действительность.Каково же происхождение суждения? Почему помимо понятия возможна и
1. Умозаключение и взаимосвязь (взаимоотношение) предметов
1. Умозаключение и взаимосвязь (взаимоотношение) предметов
Происхождение и сущность умозаключения. Чтобы уяснить происхождение и сущность умозаключения, необходимо сопоставить два рода знаний, которыми мы располагаем и пользуемся в процессе своей жизнедеятельности, —
1. Доказательство и всеобщая обусловленность предметов
1. Доказательство и всеобщая обусловленность предметов
Возникновение и природа доказательства. Объективная возможность доказательства неразрывно связана с всеобщей обусловленностью предметов и явлений действительности, прежде всего с их причинной зависимостью.
1. Умозаключение и взаимосвязь (взаимоотношение) предметов
1. Умозаключение и взаимосвязь (взаимоотношение) предметов
1. Из приведенных примеров выделите умозаключения:
«Таможня». «Правоохранительный орган». «Петров». «Таможня — правоохранительный орган». «Петров работает в таможне». «Все таможни — правоохранительные органы.
1. Доказательство и всеобщая обусловленность предметов
1. Доказательство и всеобщая обусловленность предметов
Какова объективная основа следующего доказательства:
«Поскольку римляне кремировали усопших, в распоряжении ученых было очень мало скелетов римской эпохи. Однако уже существовала известная гипотеза, что именно
II. Об основании различения всех предметов вообще на phaenomena и noumena
II. Об основании различения всех предметов вообще на phaenomena и noumena
Явления, поскольку они мыслятся как предметы на основе единства категорий, называются phaenomena. Но если я допускаю вещи лишь как предметы рассудка, которые тем не менее как таковые могут быть даны в качестве
§ 64. Первые черты феномена мира: раскрытость сущего как сущего и «как»; отношение к сущему как давание и не-давание бытия (отношение-к…, себя-удержание, самость)
§ 64. Первые черты феномена мира: раскрытость сущего как сущего и «как»; отношение к сущему как давание и не-давание бытия (отношение-к…, себя-удержание, самость)
Когда, переходя от обсуждения тезиса о том, что животное скудомирно, к рассмотрению тезиса «человек
2. ПРАКТИЧЕСКОЕ РАСЧЛЕНЕНИЕ И СОЕДИНЕНИЕ ПРЕДМЕТОВ И ЛОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ
2. ПРАКТИЧЕСКОЕ РАСЧЛЕНЕНИЕ И СОЕДИНЕНИЕ ПРЕДМЕТОВ И ЛОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ
Собственно анализ и синтез есть мысленное расчленение и соединение предметов в указанном выше смысле. Однако необходимо при этом учесть, что исторически содержание этого процесса логической
III. Различающая практика предметов
III. Различающая практика предметов
В силу всех вышеперечисленных причин — раз уж социальная стратификация, мобильность и стремления являются ключами к социологическому исследованию «мира» предметов — именно конфигурация предметов в поднимающихся, подвижных или

Юлия КОМИССАРОВА,
учитель иностранных языков
ГУО «Средняя школа № 22 имени И.П.Бохана г. Гродно»
Как и обещали, публикуем облако слов с ответами тех, кто протестировал сервис Мentimeter, приняв участие в опросе читателей «Мне важно ваше мнение о публикации».

Развитие и образование ни одному человеку не могут быть даны или сообщены.
Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью,
собственными силами, собственным напряжением.
А.Дистервег
Ключевая идея нашего веб-проекта: «Играя обучать и обучаться!» То есть принцип игрового момента на уроке играет первостепенную роль. Только в такой форме учащимся будет значительно проще усваивать материал, а их учителям – преподавать его. И наша задача – создать такой «момент».
При составлении ребусов намеренно не соблюдаются строгие правила, а значит, методика их отгадывания по шаблону здесь не всегда сработает – придется рассчитывать на свою сообразительность.
Как начать урок? Как повторить изученный материал? Чем его завершить? Как заинтересовать учащихся и удержать их внимание? Этим вопросом задаются многие наши коллеги. Современные учащиеся воспринимают визуальную информацию лучше, чем представители любого другого поколения. Об этом следует помнить и учитывать этот факт при подготовке и проведении занятий.
Одним из самых интересных приёмов мгновенной активизации познавательной деятельности и раскрытия творческого потенциала является ребус. Помните, что ребусы – это не тест, где проверяются ваши знания. Разгадывание ребусов – это способ научиться мыслить образно, строить ассоциативные цепочки, уметь находить связи между предметами. Здесь главным является сам процесс, а не его результат.
Автоматически создать ребус? Зашифровать слово и целую фразу? Генератор ребусов Квестодел (http://kvestodel.ru/generator-rebusov) к вашим услугам!
Дети, которые уже умеют читать и писать, оценят увлекательную игру – ребусы. Это интересные головоломки, в которых слова и фразы зашифровываются при помощи картинок и символов.
Расшифровка ребусов – это настолько увлекательное занятие, что оторваться от них тяжело не только юному эрудиту, но и взрослому.
Что потребуется, чтобы разгадать ребус? Конечно, нужно знать правила разгадывания. С правилами можно ознакомиться, перейдя по ссылке http://kvestodel.ru/kak-razgadyvat-rebusy, а также здесь: Правила разгадывания ребусов
Умение определить и правильно назвать изображенный на рисунке предмет представляет одну из главных трудностей при расшифровке ребусов. Кроме знания правил вам понадобятся смекалка и логика.

Метод ребусов можно использовать с любой целевой аудиторией.
Когда можно использовать ребусы в преподавании?
1 На этапе закрепления материала. При этом обучающиеся не просто воспроизводят знания в том виде, в каком они были усвоены, а трансформируют, преобразовывают их, учатся оперировать ими в зависимости от игровой ситуации.
2 На этапе самостоятельной работы обучающихся. Организация активного самостоятельного поиска, нахождения и использования научной информации.
3 На этапе переключения и активизации внимания (введения, объяснения, закрепления, упражнения, контроля).
Представлю подборку из нескольких сайтов, которые упростят вам работу.
1 Квестодел

Плюсы:
– можно генерировать не только одним словом, но и фразой. По умолчанию ребус составляется без учёта пробелов, то есть, фраза шифруется как единое целое. Вы можете это изменить и шифровать слова по отдельности. В этом случае каждое новое слово в ребусе будет начинаться с новой строки;
– можно регулировать уровень сложности ребуса;
– можно указать ширину изображения (что особенно удобно для составления карточек и подбора размера кармашка при создании лэпбука);
– на изображениях нет водяного знака;
– если ребус вам не подходит, его можно создать заново;
– после создания ребуса вы можете скачать его как картинку;
– на этом сайте можно составить довольно интересный квест.
Минусы:
– доступен только русский язык.
2 RebusKids

Генератор ребусов позволяет зашифровать слово по правилам составления ребусов. Для создания ребуса выберите язык и введите слово, для которого вы хотите получить зашифрованное изображение.
Плюсы:
– слово можно зашифровать на трех языках: русском, английском и французском, что удобно при составлении заданий для урока иностранного языка;
– ребусы составляются из простых рисованных изображений;
– составленный ребус можно скачать в виде картинки и распечатать;
– если ребус вам не подходит, его можно создать заново;
– есть телеграм-бот для составления ребусов.
Минусы:
– можно генерировать только одно слово.
– сложность ребусов больше подходит детям, чем взрослым.
– водяной знак на изображениях; для чего его применяют, мы все знаем, но не все любят такие изображения.
3 Яндекс Переводчик
При переводе с русского языка на язык эмодзи слова превращаются в эмодзи (смайлики). Подходит для составления простых предложений. Может использоваться при создании загадок, своеобразных ребусов, например, при угадывании песни по эмодзи.
Онлайн-сервисы, обзор которых мы сегодня сделали, русскоязычные, ребусы составляются автоматически. Каждое новое слово в вашем ребусе будет начинаться с новой строки. Еще одним преимуществом является управление уровнем сложности ребуса: от самого элементарного уровня до уровня повышенной сложности. Если есть необходимость, то сам ребус можно уменьшить или увеличить в размере, а затем скачать его как картинку в формате PNG.
Опять же универсального решения здесь нет и быть не может. Выбирайте приложение, в котором вам удобно работать и которое максимально отвечает вашим потребностям.
