Дорогие сметчики!
Подскажите пожалуйста как правильно посчитать среднюю высоту при подъеме и опуске (вертикаль). На примере: Есть колонное оборудование, которое осмечивается по расценкам РН-61 и РН-62. в них подъем и опуск учтен на 5м и 35м соответственно.
Нам нужно опустить и поднять на высоту 47м.
и тут возник спор, как правильно посчитать среднее (47-5)/2 , т.к. 5 м учтено в расценке или же (47+5)/2 или же просто (47-5)
Так же аналогично работы по монтажу
технологического трубопровода
по ТЕРм12, т.к. там тоже учтен подъем на 5 м и дается формула Кв=1+0,04*М, где М – это количество метров сверх 5. Нужно ли в этой формуле вычитать еще раз 5 метров, учтенных в сборнике
Очень нужна помощь
Вход
Быстрая регистрация
Если вы у нас впервые:
О проекте
FAQ
ГЛАВНАЯ
ВОПРОСЫ
ТЭГИ
СООБЩЕСТВО
НАГРАДЫ
ЗАДАТЬ ВОПРОС
|
1
Можно ли узнать среднюю высоту над уровнем моря страны?Agni 8 лет назад
тэги: высота, география, уровень моря категория: образование ответить комментировать
в избранное
бонус 1 ответ: старые выше новые выше по рейтингу 0
Alou 8 лет назад теоретически да, но тут нужно вычислять не просто среднее. Нужно разбить всю площадь на более-мелкие равномерные участки и вычислить их высоты над уровнем моря, а потом взять не среднее, а в статистике есть другое понятие – средне-взвешенное значение по площади. комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Смотрите также: Что значит выражение “высота над уровнем моря”? Какие составить предложения со словосочетанием “уровень моря”? Что будет с ГЭС, если уровень моря будет повышаться? Как изменяется уровень моря в течение одного года? Что будет, если растают все ледники на Земле? Уровень моря ускоряется, а не сокращается, вопреки прогнозам учёных? Как определяют уровень моря? От какого уровня моря меряют высоту в Украине? Как определить свою высоту над уровнем моря? Какой город находится ниже всех других городов на Земле (ниже уровня моря)? |
|
Есть интересный вопрос? Задайте его нашему сообществу, у нас наверняка найдется ответ! |
Делитесь опытом и знаниями, зарабатывайте награды и репутацию, заводите новых интересных друзей! |
Задавайте интересные вопросы, давайте качественные ответы и зарабатывайте деньги. Подробнее.. |
Статистика проекта за месяц
Новых пользователей: 4366
Создано вопросов: 16389
Написано ответов: 37978
Начислено баллов репутации: 904034
ВОПРОСЫ
Свежие
С бонусами
Без ответов
Задать вопрос
Пульс проекта
СООБЩЕСТВО
Авторы
Награды
Тэги
Наши модераторы
Сейчас online
НАШ ПРОЕКТ
О проекте
Правила
Как заработать?
Партнерская программа
РЕСУРСЫ
Наш блог
Обратная связь
FAQ
Помогите нам стать лучше
Telegram-канал
Средняя высота насаждений
Высота деревьев
в любом насаждении не одинакова. В
пределах насаждения различия в высоте
наблюдаются не только у деревьев разной
толщины, но они имеют место и у деревьев
равных диаметров.
В
процессе таксации леса учесть
индивидуальную высоту каждого дерева
не представляется возможным. В связи с
этим принято устанавливать среднюю
высоту для всей совокупности деревьев,
образующих насаждение.
Средняя
высота насаждений зависит от древесной
породы, условий местопроизрастания,
возраста и осуществляемых в лесу
хозяйственных мероприятий. В пределах
насаждения различия в высоте обусловливаются
разным положением деревьев в отношении
света, смежных деревьев, микроповышений
и почвенных разностей. Влияние
перечисленных факторов на высоту
деревьев не имеет количественно
выраженных зависимостей, и их установление
представляет трудную задачу. При одном
и том же диаметре деревьев в пределах
насаждения высоты оказываются разными.
Из-за конкуренции за свет распределение
деревьев по высоте показывает положительную
асимметрию.
Однако
стохастические связи между h
и d
позволяют строить кривые высот на основе
небольшого количества измерений, но
дающих достаточно точные оценки высот
для практических и научных целей
Профессором Лореем
более 100 лет назад предложена следующая
формула для определгния средней высоты
насаждения:
hL
=
![]() ,
,
где
hL
– средняя высота;
h1
. . . hn
– высота для отдельных ступеней
толщины;
g1
. . . gn
– площади сечения деревьев каждой
ступени толщины.
Большинство
современных учёных считают среднею
высоту, вычисленную по формуле Лорея,
абстракцией, ничего в насаждении не
выражающей. Средние таксационные
показатели нам нужны чаще всего для
нахождения запаса. Средняя высота,
найденная по формуле Лорея, не всегда
будет соответствовать среднему дереву
по диаметру. Если же мы в качестве средней
высоты возьмём высоту среднего дерева
по диаметру, то в результате получим
среднее дерево по объёму, учитывая
высокую корреляционную зависимость
высоты и видового числа. Поэтому наиболее
корректно определять среднюю высоту
по уравнениям связи между диаметрами
и высотами.
В
этом случае среднюю высоту можно найти
графически, путем построения кривой
высот (рисунок 9.1). С этой целью обмеряют
диаметры и высотs
у ряда деревьев, отобранных тем или иным
способом Результаты этих обмеров
наносят на график, который строится в
прямоугольных координатах.
Если
на графике взять длину перпендикуляра,
восстановленного из точки, соответствующей
среднему диаметру насаждения, то эта
длина будет определять среднюю высоту
всего насаждения. При построении кривых
высот рекомендуется вычислять на основе
обмеренных высот средние высоты по
ступеням толщины и проводить плавную
кривую через средние значения.
.
Пользуясь кривой высот, можно найти
высоту деревьев любого диаметра. Для
этого из точки на оси абсцисс,
соответствующей диаметру данного
дерева, надо восставить перпендикуляр
до пересечения с кривой высот. Длина
этого перпендикуляра (ординаты) является
искомой высотой дерева.
В
более или менее однородных насаждениях
наблюдается стохастическая (вероятностная)
зависимость высоты деревьев от их
диаметров. С увеличением последних у
большинства деревьев соответственно
растет и высота. Гогенадль, Кренн и
другие исследователи связь между
d1,3
и h в насаждении характеризуют
уравнением параболы второго порядка.
В настоящее время исследованием многих
отечественных и зарубежных ученых
установлено, что парабола 2-го порядка
плохо описывает зависимость H-D.
Она занижает значение высот в начале
ряда и завышает их в конце.
Для
характеристики связи высоты и диаметра
применяются более сложные кривые.
Исследованиями К.Е.Никитина Ф.Корсуня,
А.Г.Мошкалёва, Ф.П.Моисеенко установлено,
что уравнения
связи Н = f
(Д) описываются разными уравнениями:
полиномы от 3 до 4 степени, логарифмические
кривые (простые и сложные), степенные и
показательные функции.
Среднюю
высоту можно найти и как среднеарифметическую
величину. Но это будет чисто статистическая
величина. Она не характеризует среднее
дерево по диаметру и запасу.
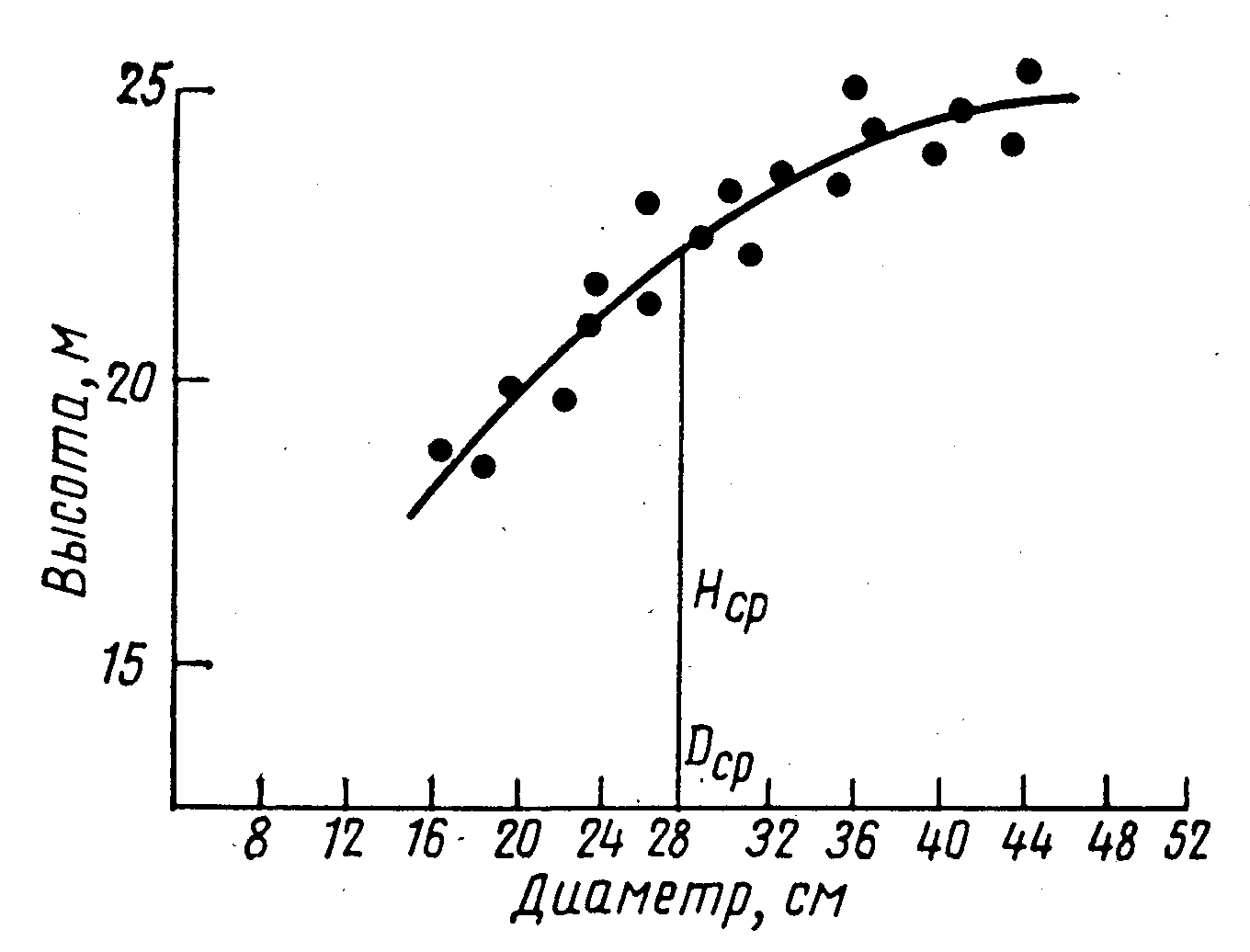
Рисунок 9.1.
Определение средней высоты насаждения
по кривой высот
Аналогично
среднему диаметру можем найти высоту
срединного дерева (hw),
высоту средних ступеней толщины (hg
m)
и т.д. В этом ряду наименьшее значение
будет иметь средняя арифметическая
высота, а наибольшей будет высота,
вычисленная по формуле Лорея.
При
отводе и таксации лесосек с использованием
разрядных таблиц среднюю высоту для
нахождения разряда высот определяют,
измеряя 9 деревьев: 3 из центральной
ступени толщины и по 3 из соседних.
Варьирование высот в приспевающих и
спелых древостоях составляет 6-8%.
Следовательно, измеряя 12-15 деревьев мы
определим Hср
с точностью около 2%, а при 9 замерах
2-3%.
В
разновозрастных, многоярусных древостоях
Hср
находят
для каждого яруса. В смешанном древостое
измерения делают для каждой породы.
Опытный таксатор после ежегодно
проводимых тренировок среднюю высоту
определяет глазомерно..
Средняя
высота, определяемая как по формуле
Лорея так и по графику высот, как
таксационный показатель имеет недостаток,
заключающийся в том, что на ее величину
оказывает влияние вырубка части деревьев
при уходе за лесом.
Если
этот уход ведется низовым способом,
заключающимся в
изъятии
из насаждения отставших в росте более
мелких деревьев, то средняя высота
насаждения после ухода за ним увеличивается.
При проведении верхового способа ухода
за лесом вырубаются более крупные
деревья. Соответственно этому
обстоятельству после проведения таких
рубок средняя высота насаждения
уменьшается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
#1 24 февраля 2011г. 10:31:46

- Ivachenkov
- Участник
- Откуда: Иркутская область / Иркутск
- На форуме с 22 декабря 2008г.
- Сообщений: 46
- Спасибо: 0
Тема: Посчитать среднюю отметку по точкам?
Как посчитать в куче точек среднюю отметку высоты Z? 😀 Не используя сторонних приложений, наверняка такое должно быть? Я использую цивил 3D.
#2 Ответ от vdim 24 февраля 2011г. 13:00:21

- vdim
- Участник
- На форуме с 8 мая 2009г.
- Сообщений: 49
- Спасибо: 5
Re: Посчитать среднюю отметку по точкам?
[S]А чего же тогда в ветке AutoCad пишите?[/S]
Постройте поверхность по этим точкам.В Свойствах Поверхности увидите ее max,min и среднюю высоты.
(закладка Статистика).В закладке Анализ можете построить контур по желаемой высоте…
#3 Ответ от Ivachenkov 25 февраля 2011г. 03:17:18

- Ivachenkov
- Участник
- Откуда: Иркутская область / Иркутск
- На форуме с 22 декабря 2008г.
- Сообщений: 46
- Спасибо: 0
Re: Посчитать среднюю отметку по точкам?
Да че то тут посетителей просто больше ))), понятно спасибо!
#4 Ответ от Boltrushko 15 марта 2011г. 14:35:35

- Boltrushko
- Участник
- На форуме с 15 марта 2011г.
- Сообщений: 1
- Спасибо: 0
Re: Посчитать среднюю отметку по точкам?
Может попробуешь так???
;;================================>TXT-SUM<====================================
;; Команда вычисления суммы и суммы произведений групп чисел
;; TXTSUM.lsp Version 2.01
;; Автор: Протасов Георгий
;;Программа вычисляет сумму групп чисел, заданных в виде простого текста.
;;При выборе парных групп чисел с одинаковым количеством элементов вычисляется
;;сумма произведений /Удобно для подсчета спецификаций/. Группы чисел для
;;определения суммы произведений могут быть организованы вертикально и
;;горизонтально. Десятичный разделитель может быть запятой и точкой.
;;Результат копируется в буфер обмена.
;;============================================================================
(DEFUN TXT-SUM ( / l1 l2 sum1 sum0 msg TXTIPNT MAXY MAXX REMBER SORT STRREPL
GETNUMBERS CPCBD cmdecho-save error-save)
(SETQ error-save *error*
cmdecho-save (GETVAR “CMDECHO”)
);SETQ
(DEFUN *error* (msg)
(IF error-save (SETQ *error* error-save))
(IF msg (PRINC “nВыполнение функции прервано “))
;; Восстановление значений системных переменных
(SETVAR “CMDECHO” cmdecho-save)
(PRINC)
);DEFUN
;Функция копирования числа в буфер обмена
(DEFUN CPCBD (num / convn)
(IF (AND (SETQ convn (FINDFILE “G_StrToCbd.exe”)) num)
(STARTAPP convn (RTOS num))
);
);DEFUN
;Функция поиска левой нижней точки текста
(DEFUN TXTIPNT (en / ed ins p p1 p2 wdth hght hght0 ang)
(SETQ ed (ENTGET en));Описание текста
(IF (AND
(AND (NOT (NULL (CDR (ASSOC 72 ed)))) (NOT (NULL (CDR (ASSOC 73 ed)))))
(OR (/= (CDR (ASSOC 72 ed)) 0) (/= (CDR (ASSOC 73 ed)) 0))
);AND
(SETQ ins (CDR (ASSOC 11 ed)))
(SETQ ins (CDR (ASSOC 10 ed)))
);IF
(SETQ ins (TRANS ins en 2) ;Точка вставки
p1 (CAR (TEXTBOX ed))
p2 (CADR (TEXTBOX ed))
wdth (- (CAR p2) (CAR p1)) ;Ширина
hght (- (CADR p2) (CADR p1)) ;Высота
hght0 (CADR p2);Высота
ang (IF (NULL (ASSOC 50 ed)) 0 (CDR (ASSOC 50 ed))) ;Угол наклона
);SETQ
(COND
((AND (= (CDR (ASSOC 72 ed)) 0) (= (CDR (ASSOC 73 ed)) 0))
(SETQ p1 ins)
);Влево
((AND (= (CDR (ASSOC 72 ed)) 1) (= (CDR (ASSOC 73 ed)) 0))
(SETQ p1 (POLAR ins (+ ang PI) (/ wdth 2)))
);По центру
((AND (= (CDR (ASSOC 72 ed)) 2) (= (CDR (ASSOC 73 ed)) 0))
(SETQ p1 (POLAR ins (+ ang PI) wdth))
);Вправо
((AND (= (CDR (ASSOC 72 ed)) 3) (= (CDR (ASSOC 73 ed)) 0))
(SETQ p1 (POLAR ins (+ ang PI) wdth))
);Вписанный
((AND (= (CDR (ASSOC 72 ed)) 4) (= (CDR (ASSOC 73 ed)) 0))
(SETQ p (POLAR ins (- ang PI) (/ wdth 2))
p (POLAR p (+ ang (* PI 0.5)) (/ hght0 2))
p1 (POLAR p (- ang (* PI 0.5)) hght0)
);SETQ
);По середине
((AND (= (CDR (ASSOC 72 ed)) 5) (= (CDR (ASSOC 73 ed)) 0))
(SETQ p1 (POLAR ins (+ ang PI) wdth))
);По ширине
((AND (= (CDR (ASSOC 72 ed)) 0) (= (CDR (ASSOC 73 ed)) 1))
(SETQ p1 ins)
);Низ и Влево
((AND (= (CDR (ASSOC 72 ed)) 1) (= (CDR (ASSOC 73 ed)) 1))
(SETQ p1 (POLAR ins (+ ang PI) (/ wdth 2)))
);Низ и По центру
((AND (= (CDR (ASSOC 72 ed)) 2) (= (CDR (ASSOC 73 ed)) 1))
(SETQ p1 (POLAR ins (+ ang PI) wdth))
);Низ и Вправо
((AND (= (CDR (ASSOC 72 ed)) 0) (= (CDR (ASSOC 73 ed)) 2))
(SETQ p (POLAR ins (+ ang (* PI 0.5)) (/ hght 2))
p1 (POLAR p (- ang (* PI 0.5)) hght)
);SETQ
);Середина и Влево
((AND (= (CDR (ASSOC 72 ed)) 1) (= (CDR (ASSOC 73 ed)) 2))
(SETQ p (POLAR ins (- ang PI) (/ wdth 2))
p (POLAR p (+ ang (* PI 0.5)) (/ hght 2))
p1 (POLAR p (- ang (* PI 0.5)) hght)
);SETQ
);Середина и Центр
((AND (= (CDR (ASSOC 72 ed)) 2) (= (CDR (ASSOC 73 ed)) 2))
(SETQ p2 (POLAR ins (+ ang (* PI 0.5)) (/ hght 2))
p (POLAR p2 (+ ang PI) wdth)
p1 (POLAR p (- ang (* PI 0.5)) hght)
);SETQ
);Середина и Вправо
((AND (= (CDR (ASSOC 72 ed)) 0) (= (CDR (ASSOC 73 ed)) 3))
(SETQ p1 (POLAR ins (- ang (* PI 0.5)) hght))
);Верх и Влево
((AND (= (CDR (ASSOC 72 ed)) 1) (= (CDR (ASSOC 73 ed)) 3))
(SETQ p (POLAR ins (+ ang PI) (/ wdth 2))
p1 (POLAR p (- ang (* PI 0.5)) hght)
);SETQ
);Верх и По центру
((AND (= (CDR (ASSOC 72 ed)) 2) (= (CDR (ASSOC 73 ed)) 3))
(SETQ p (POLAR ins (+ ang PI) wdth)
p1 (POLAR p (- ang (* PI 0.5)) hght)
);SETQ
);Верх и Вправо
(t
(SETQ p1 ins)
);Влево по умолчанию
);COND
);DEFUN
;;;Поиск самого верхнего элемента списка
(DEFUN MAXY (l / m i)
(SETQ i 1
m (CAR l));
(WHILE (<= i (1- (LENGTH l)))
(IF (<= (CADR (TXTIPNT m)) (CADR (TXTIPNT (NTH i l))))
(SETQ m (NTH i l))
);IF
(SETQ i (1+ i))
);WHILE
m
);DEFUN
;;;Поиск самого левого элемента списка
(DEFUN MAXX (l / m i)
(SETQ i 1
m (CAR l));
(WHILE (<= i (1- (LENGTH l)))
(IF (<= (CAR (TXTIPNT m)) (CAR (TXTIPNT (NTH i l))))
(SETQ m (NTH i l))
);IF
(SETQ i (1+ i))
);WHILE
m
);DEFUN
;;;Удаление первого вхождения элемента a в список l
(DEFUN REMBER (a l)
(COND ((NULL l) nil)
((EQUAL (CAR l) a) (CDR l))
(t (CONS (CAR l) (REMBER a (CDR l))))
);COND
);DEFUN
;;;Сортировка списка в соответствии с заданным критерием
(DEFUN SORT (crit l / m)
(COND
((NULL (CDR l))
(CONS (CAR l) nil)
)
(t
(SETQ m (EVAL (LIST crit ‘l)))
(CONS m (SORT crit (REMBER m l)))
);t
);COND
);DEFUN
;;Функция замены в строке base подстроки srch на repl
(DEFUN STRREPL (base srch repl / basel i)
(SETQ i 1)
(IF (AND (/= srch “”)
(<= (STRLEN srch) (STRLEN base))
);AND
(PROGN
(SETQ basel (STRLEN base))
(WHILE
(< i (+ (- basel (STRLEN srch)) 2))
(IF (= (SUBSTR base i (STRLEN srch)) srch)
(PROGN
(SETQ base
(IF (= i 1)
(STRCAT repl
(SUBSTR base (+ i (STRLEN srch)))
);STRCAT
(STRCAT
(SUBSTR base 1 (- i 1))
repl
(SUBSTR base
(+ i (STRLEN srch))
);SUBSTR
);STRCAT
);IF
);SETQ
(SETQ i (+ i (strlen repl))
basel (STRLEN base)
);SETQ
);PROGN
(SETQ i (1+ i))
);IF
);WHILE
);PROGN
);IF
base
);DEFUN
;;;Выбор группы чисел
(DEFUN GETNUMBERS ( / en ss n i l sum)
(PRINC “nВыберите группу чисел:”)
(SETQ ss (SSGET ‘((0 . “TEXT”))))
(COND ((NULL ss) nil)
(t
(SETQ
n (SSLENGTH ss)
i 0
l nil
);SETQ
(WHILE (<= i (1- n))
(SETQ l (CONS (SSNAME ss i) l)
i (1+ i)
);SETQ
);WHILE
(SETQ ss nil
l (MAPCAR
‘(LAMBDA (en) (ATOF (STRREPL (CDR (ASSOC 1 (ENTGET en))) “,” “.”))
);LAMBDA
(SORT ‘MAXY (SORT ‘MAXX l)));MAPCAR
sum (APPLY ‘+ l)
);SETQ
(TERPRI)
(PRINC (MAPCAR ‘RTOS l))
(PRINC “nКоличество: “)
(PRINC (ITOA n))
(PRINC “nCумма: “)
(PRINC (RTOS sum))
; Добавить среднее значение
(CPCBD sum)
l
);t
);COND
);DEFUN
;;; Основной текст программы
(SETVAR “CMDECHO” 0)
(SETQ l1 (GETNUMBERS)
sum1 0
sum0 0
);SETQ
(IF l1 (SETQ l2 (GETNUMBERS)))
(WHILE (AND l1 l2)
(IF (= (LENGTH l1) (LENGTH l2))
(PROGN
(SETQ sum0 (+ sum0 (APPLY ‘+ l1) (APPLY ‘+ l2))
sum1 (+ sum1 (APPLY ‘+ (MAPCAR ‘* l1 l2)))
);SETQ
(PRINC “nОбщая сумма: “)
(PRINC (RTOS sum0))
(PRINC “nСумма произведений: “)
(PRINC (RTOS sum1))
(CPCBD sum1)
);PROGN
(PROGN
(PRINC “nРазное количество чисел в группах!”)
(SETQ sum0 (+ sum0 (APPLY ‘+ l1) (APPLY ‘+ l2)))
(PRINC “nОбщая сумма: “)
(PRINC (RTOS sum0))
(CPCBD sum0)
);PROGN
);IF
(SETQ l1 (GETNUMBERS))
(IF l1 (SETQ l2 (GETNUMBERS)))
);WHILE
(SETVAR “CMDECHO” cmdecho-save)
(SETQ *error* error-save)
(PRINC)
);DEFUN
(IF (OR (NULL C:TXT-SUM)
(NOT (LISTP C:TXT-SUM))
);OR
(DEFUN C:TXT-SUM () (TXT-SUM))
);IF
(PRINC “nДобавлена команда TXT-SUM…”)
(PRIN1)
;;; Это нужно еще поправить!!!
Страницы 1
Чтобы отправить ответ, вы должны войти или зарегистрироваться
Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.

После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.
Алгоритм решения задач на расчет средней величины
А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.
Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.
В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).
Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.
В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.
В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.
Рассмотрим на примерах использование данного алгоритма.
Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.
А. Так как данные представлены в строчку то используем простой способ расчета.
Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.

Средний размер пенсии пенсионера составляет 9208,3 рубля.
Задача 2. Рассчитать средний размер детских выплат по следующим данным

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти средний размер выплаты на одного ребенка, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.

Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.

В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.

Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.
Задача 3. Рассчитать среднюю себестоимость единицы изделия

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.
Средняя себестоимость единицы изделия составила 314,4 рубля.
Задача 4. Рассчитать среднюю число пропусков одного студента

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (общее число пропусков) задана неявным количеством (это произведение двух показателей числа пропусков и числа студентов, имеющих такое количество пропусков), значит, для расчета используется средняя гармоническая взвешенная. Будем использовать пункт алгоритма В2.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.
Составляем логическую формулу расчета среднего числа пропусков одного студента.

Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.
Среднее число пропусков одного студента 13,8 дня.
