Как найти косинус угла между диагоналями четырехугольника
Сразу скажу, что я не математик, я бы решала так:
Дано:
Четырёхугольник ‘ABCD’, имеющий две диагонали ‘AC’ и ‘BD’, пересекающиеся в точке ‘О’.
Известны все углы у его вершин `ABC`, `BCD`, `CDA`, `DAB` и ещё углы `OAD`, `OAB`, `OCB` и `OCD`.
Нужно найти:
Углы между диагоналями четырёхугольника: т.е., углы ‘АОВ’, ‘АОD’, ‘DOC’, ‘COB’.
Я думаю, что решение данных задач станет возможно, если добавить условие, что в данном четырехугольнике одна пара связанных углов равна между собой.
В таком случае, мой вариант части решения:
Подсказка:
читать дальше Т.к. все диагонали в данном четырехугольнике пересекаются, то мы имеем дело с выпуклым четырехугольником (в противном случае, все диагонали не смогли бы пересечься).
Согласно свойству связанных углов выпуклого четырёхугольника https://mathvox.ru/geometria/mnogougolniki/glava-2-chetirehugolniki-i-ih-svoistva/ugli-vipuklogo-chetirehugolnika-svoistvo-3/ “Если в выпуклом четырёхугольнике одна пара связанных углов равна,
(Например, угол ‘BCA’ = углу ‘BDA’),
то вторая пара связанных углов (‘ABD’ и ‘АСD’) также будут равны между собой.
Если посмотреть на задачу шире, то, углы между диагоналями четырёхугольника (АОВ’, ‘АОD’, ‘DOC’, ‘COB’) ОДНОВРЕМЕННО являются также углами треугольников (‘АОB’, ‘BOC’, ‘COD’, ‘DOA’).
Что мы знаем о треугольниках?
“Сумма ВСЕХ УГЛОВ любого вида треугольников равна 180 градусам”.
Поиск угла ‘АОD’
Далее вычислим один из углов диагоналей четырехугольника (он же угол, входящий в состав одного из треугольников) на примере треугольника ‘АOD’:
Сумма всех углов треугольника ‘OAD’ =
угол ‘OAD’ + угол ‘ADO’ + угол ‘AOD’=180 градусов.
По условию задачи мы знаем:
1. Чему равен угол ‘OAD’ (согласно условию задачи).
Неизвестны углы ‘ADO’ и ‘AOD’.
2. Вычисляем угол ‘ADO’:
Снова расширяем своё видение.
Мы знаем:
1. Чему равен угол ‘CDA’ (согласно условию задачи), составной частью которого является угол ‘ADO’.
T. е., угол ‘CDA’ = угол ‘AOD’ + угол ‘ADO’.
2. Вычисляем значение угла ‘АDO’:
Угол ‘АDO’ = углу ‘BDA’.
Согласно свойству связанных углов выпуклого четырёхугольника:
угол ‘BDA’ = углу ‘BCA’, а угол ‘ВСА’ = углу “OCB’.
Т.о., угол ‘ADO’ = углу ‘OCB’ (значение угла ‘OCB’ мы знаем по условию задачи).
3. Угол ‘AOD’ = (угол ‘ОAD’ +угол ‘АDO’) – 180 градусов.
Поздравляем, первый угол ‘АОD’ – найден! .
Поиск угла ‘DOC’
Треугольник ‘DOC’ имеет углы: ‘ОСD’, ‘СDO’ и ‘DOC’.
Мы знаем:
1. Чему равен угол ‘ОСD’ (по условию задачи).
2. Вычислим чему равен угол ‘СDO’:
Угол ‘СDO’ входит в состав угла ‘CDA’, вместе с углом ‘АDO’.
Т.о., угол ‘СDO’ = угол ‘СDA’ – угол ‘АDO’.
3. Вычислим чему равен угол ‘DOC’:
Угол ‘DOC’ = (угол ‘OCD’ + угол ‘CDO’) – 180 градусов.
и т.д.
Творческая работа учащегося “Теорема косинусов для четырёхугольника”
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику

Муниципальное автономное общеобразовательное учреждение
«Гимназия №1 Октябрьского района г. Саратова»
Научно-практическая конференция школьников.
Теорема косинусов для четырехугольника
Творческая работа ученицы 10 «А» класса
Всем известна теорема косинусов для треугольника
Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними .
Но не все знают, что существуют аналогичные теоремы и для других фигур.
Целью данной работы явилось:
Установить, существует ли теорема косинусов для фигур, отличных от треугольника
Доказать утверждение теоремы косинусов для четырехугольника
Применить теорему при решении задач
Получить полезные следствия из теоремы косинусов для четырехугольника
Теоретическая часть 
Первая теорема косинусов
Рассмотрим четырехугольник (рис.1).
Возведем обе части равенства в квадрат
Так как скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними, то для вычисления скалярного произведения векторов будем откладывать векторы от одной точки.
Учитывая также, что скалярный квадрат вектора равен квадрату его длины, получаем:
Заметим, что , где угол, образованный продолжениями сторон . 
Введем обозначения сторон четырехугольника (рис.2).
Полученное соотношение между сторонами четырехугольника называют первой теоремой косинусов для четырехугольника. Ее формулируют так:
Квадрат стороны четырехугольника равен сумме квадратов трех других его сторон без удвоенных произведений этих сторон, взятых попарно, и косинусов углов между ними. 
Рассмотрим еще раз рис.2. Понятно, что
Тогда равенство теоремы косинусов может быть записано в виде
Теорему косинусов, так как она доказывалась с использованием векторов, можно считать верной и для невыпуклого четырехугольника, и для четырехугольника с самопересечением сторон.
Вторая теорема косинусов 
Можно получить еще один аналог теоремы косинусов, который назовем второй теоремой косинусов для четырехугольника.
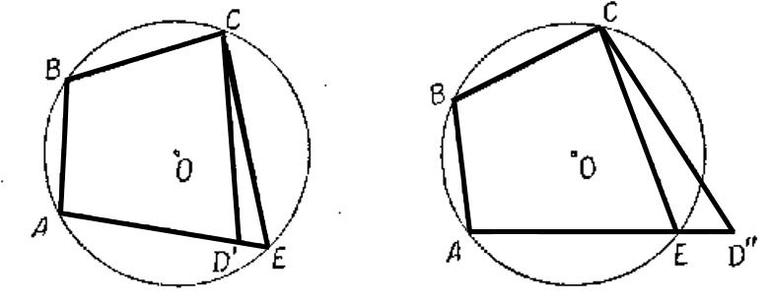
Рассмотрим четырехугольник с проведенными в нем диагоналями, длины которых обозначим e и f (рис.3А).
Построим вне этого четырехугольника

Ясно, что по двум углам
Составим отношения сходственных сторон
Построим вне этого четырехугольника 
Тогда по двум углам.
Составим отношения сходственных сторон:
откуда 
Заметим, что имеют равные длины.
Совместим рисунки 3Б и 3В на одном рисунке 4.
Рассмотрим четырехугольник и треугольник .
В четырехугольнике BDEF сумма равна сумме углов треугольника.
В треугольнике сумма всех углов равна 180, поэтому сумма четырехугольника равна 180.
– это односторонние углы при прямых и секущей , а значит, . Кроме того, . Значит, четырехугольник – параллелограмм. И , т.е. равен диагонали f .
Рассмотрим треугольник . Заметим, что равен сумме углов и четырехугольника .
Применим традиционную теорему косинусов к этому треугольнику:
Используя введенные обозначения, получим:
Так как сумма углов выпуклого четырехугольника равна 360,
Значит, в равенстве в качестве множителя + может участвовать и . Тогда вывод из равенства можно сформулировать так:
Квадрат произведения диагоналей четырехугольника равен сумме квадратов произведений противоположных сторон минус удвоенное произведение всех сторон четырехугольника на косинус суммы противоположных углов.
Это соотношение назовем второй теоремой косинусов для четырехугольников. Автором этого соотношения считают немецкого математика 19 века Карла Антона Бретшнайдера .
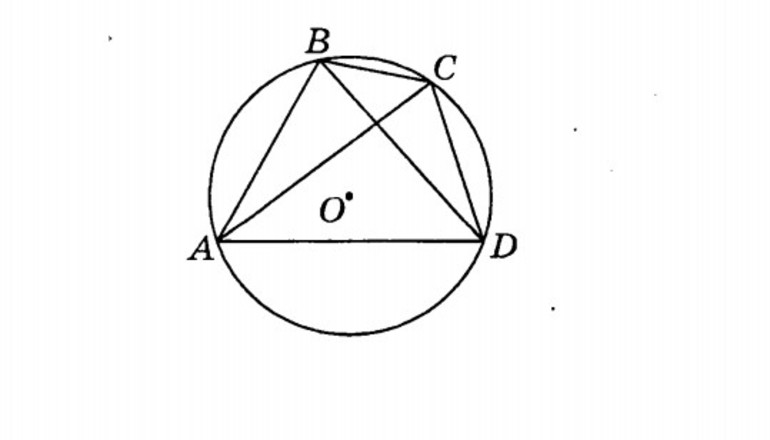
Получить из второй теоремы косинусов для четырехугольника теорему Птолемея.
Рассмотрим четырехугольник (рис.5), который может быть вписан в окружность. В таком четырехугольнике суммы противоположных углов равны 180. Тогда в равенстве
. И соотношения для диагоналей и сторон четырехугольника принимает вид 
Это равенство известно под названием теорема Птолемея :
Для четырехугольника, вписанного в окружность, произведение диагоналей равно сумме произведений противоположных сторон.
Доказать, что в параллелограмме с углом в 45 градусов квадрат произведения диагоналей равен сумме четвертых степеней двух его смежных сторон (рис.6).
c = a , d = b 
Задача №3. 
Получить из второй теоремы косинусов для четырехугольника теорему Стюарта.
Рассмотрим четырехугольник со сторонами и диагоналями (рис.7).
По теореме косинусов для этого четырехугольника справедливо равенство
Представим себе, что четырехугольник будет таким, что сумма сторон равна диагонали , то есть четырехугольник вырождается в треугольник (рис.8), то есть 
Вычисляем по теореме косинусов для треугольника, получаем,
Тогда для этого вырожденного четырехугольника имеем
Полученное соотношение называется теоремой М. Стюарта.
Получить из теоремы Стюарта формулу длины медианы треугольника.
Решение. 
Квадрат медианы равен четверти суммы удвоенных квадратов сторон треугольника, заключающих медиану, минус квадрат третьей стороны треугольника.
Получить из теоремы Стюарта формулу длины биссектрисы треугольника.
Если – биссектриса, то по свойству биссектрис в треугольнике

Квадрат биссектрисы треугольника равен разности произведений сторон треугольника, заключающих биссектрису, и отрезков противоположной стороны, на которые она разделена биссектрисой.
В данной работе получены следующие результаты:
сформулированы и доказаны две теоремы косинусов для четырехугольника;
с использованием доказанной теоремы доказана теорема Птолемея;
доказана теорема Стюарта;
получены два следствия из теоремы Стюарта: формула длины медианы и формула длины биссектрисы;
приведен пример использования теоремы косинусов для четырехугольника при решении задач.
Атанасян Л.С. ГЕОМЕТРИЯ. 7-9 кл. Москва, Издательство «Просвещение», 2006г.
Атанасян Л.С. ГЕОМЕТРИЯ. 10-11 кл. Москва, Издательство «Просвещение», 2006г.
Понарин Я.П. Элементарная геометрия в 3-х томах. Том 1. Планиметрия, преобразования плоскости. Москва, Издательство МЦНМО, 2004г.
Единая коллекция цифровых образовательных ресурсов https://school-collection.edu.ru
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 967 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 340 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 691 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Гришина Ирина ВладимировнаНаписать 1671 15.07.2017
Номер материала: ДБ-603154
-
15.07.2017 2165
-
15.07.2017 648
-
15.07.2017 386
-
15.07.2017 827
-
15.07.2017 571
-
15.07.2017 177
-
15.07.2017 770
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
Названы главные риски для детей на зимних каникулах
Время чтения: 3 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Число участников РДШ за 2021 год выросло в три раза
Время чтения: 2 минуты
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
[spoiler title=”источники:”]
http://infourok.ru/tvorcheskaya-rabota-uchaschegosya-teorema-kosinusov-dlya-chetiryohugolnika-2025162.html
[/spoiler]
Как найти угол между диагоналям
Диагональ многоугольника – отрезок, который соединяет две не граничащие между собой вершины фигуры (т.е. несмежные вершины или не принадлежащие одной стороне многоугольника). В параллелограмме, зная длину диагоналей и длину сторон, можно рассчитать углы между диагоналями.

Инструкция
Для удобства восприятия информации начертите на листе бумаги произвольный параллелограмм АВСD (параллелограмм – это четырехугольник, противоположные стороны которого попарно равны и параллельны). Соедините противоположные вершины отрезками. Полученные АС и ВD – диагонали. Обозначьте точку пересечения диагоналей буквой О. Необходимо найти углы ВОС (АОD) и СOD (АОВ).
Параллелограмм обладает целым рядом математических свойств:- диагонали точкой пересечения делятся пополам; – диагональ параллелограмма делит его на два равных треугольника;- сумма всех углов в параллелограмме равна 360 градусов;- сумма углов, прилежащих к одной стороне параллелограмма, равна 180 градусам;- сумма квадратов диагоналей равна двойной сумме квадратов его смежных сторон.
Чтобы найти углы между диагоналями, воспользуйтесь теоремой косинусов из теории элементарной геометрии (Евклидовой). Согласно теореме косинусов, квадрат стороны треугольника (A) можно получить, сложив квадраты двух его других сторон (B и C), и из полученной суммы вычесть двойное произведение этих сторон (B и C) на косинус угла между ними.
Применительно к треугольнику ВОС параллелограмма АВСD теорема косинусов будет выглядеть следующим образом:Квадрат ВС = квадрат ВО + квадрат ОС – 2*ВО*ОС*cos угла ВOCОтсюда соs угла BOC = (квадрат ВС –квадрат ВО – квадрат ОС) / (2*ВО*ОС)
Найдя значение угла ВОС (АОD) легко вычислить значение другого угла, заключенного между диагоналями – СОD (АОВ). Для этого из 180 градусов вычтите значение угла ВОС (АОD) – т.к. сумма смежных углов равна 180 градусам, а углы ВОС и СОD и углы АОD и АОВ – смежные.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
Для произвольного четырёхугольника даже данность 2-х диагоналей будет недостаточно для однозначности этого четырёхугольника.Пусть в 4-нике АВСД диагонали пересекаются в т.О.Пусть АО=d1,BO=d2,CO=d3,DO=d4.И даже тогда 4-ник не будет определен однозначно.Нужен или угол между диагоналями,или еще какая-нибудь сторона.Пусть известна АВ.Тогда в тр-ке АВО по теореме синусов и косинусов можно определить внутренние углы тр-ка АВО,в том числе и между диагоналями.Задачу желательно конкретизировать. модератор выбрал этот ответ лучшим Смотря что известно. Если известны длина сторон четырехугольника, то с помощью тригонометрических функций можно вычислить углы, сначала между сторонами четырехугольника, потом между сторонами и диагоналями, а затем между диагоналями. Знаете ответ? |
Светило науки – 5 ответов – 0 раз оказано помощи
1)Докажем,что данный четырёхугольник является прямоугольником.
1)ST=(0+1;-2-0)=(1;-2)
2)RP=(-4+5;-4+2)=(1;-2)
3)PS=(-1+5;0+2)=(4;2)
4)PT=(0+4;-2+4)=(4;2)
Координаты векторов равны,следовательно будут равны и их длины.
Теперь докажем,что углы данного четырёхугольника равны по 90 градусов.Ведь прямоугольник это такой четырехугольник,у которого все углы по 90 градусов.
1)PS*ST=(4*1)+(2*(-2))=4-4=0
2)PT*ST=(4*1)+(2*(-2))=4-4=0 =>
Углы STP u TSP= 90 градусов.
Значит и противоположные углы равно по 90 градусов.Данный четырёхугольник — прямоугольник.
2)RT=PS как диагонали прямоугольника.Найдем их длины:
|RT|= V(0+5)^2 + (-2+2)^2
|RT| =V25
|RT|= 5
|PS|= 5
Вычислим и координаты:
PS= (-1+4;0+4)=(3;4)
TR=(-5-0;-2+2)=(-5;0)
Вычислим косинус по формуле:
сos a = (a(вектор) * b(вектор))/ |а| * |b| = cos a = PS*TR / |PS|*|TR| = 3*(-5)+4*0 / 5*5 = — 3/5 = —0,6.
3)S= |PR|* |PT|
|PR| = V(-5+4)^2 + (-2+4)^2 = V5
|PT| = V(0+4)^2 + (-2+4)^2 = V20
S= V5*V20= V100 = 10
Для справки:
Не забудьте поставить векторы(стрелки) над буквенными выражениями.
V — это обозначение корня.
^2 — это обозначение степени 2.
/ — это палочка,обозначающая дробное выражение.
геометрия — Найти угол между диагоналями четырехугольника
В четырехугольнике суммы квадратов противоположных сторон равны. Найти угол между диагоналями этого четырехугольника.
задан 20 Май ’14 23:02
@Vipz3, Если вы получили исчерпывающий ответ, отметьте его как принятый.
1 ответ
Диагонали четырёхугольника перпендикулярны, это его свойство в данном случае. Для доказательства распишите квадраты сторон через теорему косинусов. В итоге придете к тому, что косинус умножить на положительную сумму равно нулю. Понятно, что косинус равен нулю и угол 90.
Геометрия. Урок 4. Четырехугольники
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение четырехугольника
- Выпуклые четырехугольники
- Параллелограмм
- Робм
- Прямоугольник
- Квадрат
- Трапеция
- Примеры решений заданий из ОГЭ
Определение четырехугольника
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .
Выпуклые четырехугольники
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S = 1 2 d 1 d 2 ⋅ sin φ
где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 ° .
- Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )
Площадь параллелограмма можно найти по трём формулам.
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
Как произведение двух смежных (соседних) сторон на синус угла между ними.
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
Как произведение стороны ромба на высоту ромба.
Как квадрат стороны ромба на синус угла между двумя сторонами.
Как полупроизведение диагоналей ромба.
Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
Как произведение двух смежных (соседних) сторон прямоугольника.
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
Как квадрат стороны.
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
Трапеция
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .
B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180 ° .
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2
Площадь трапеции можно найти по двум формулам:
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Четырехугольник, вписанный в окружность — основные свойства, признаки и формулы
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.
Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.
Основные правила
Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:
- Сумма углов, которые являются противоположными, соответствует 180 градусам.
- Соблюдается равенство смежного и противоположного углов.
- Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
- Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
- Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
- Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).
Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.
Свойства и утверждения
При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
- Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
- Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
- При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.
Данные утверждения применяются не всегда. В некоторых случаях можно ограничиться формулами и основными соотношениями — они позволяют легко и быстро искать нужные величины.
Формулы и соотношения
Очень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами.
Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника.
Периметр и полупериметр
Периметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д.
Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой.
Понятие площади
Площадь двумерных фигур — понятие геометрии, которое показывает ее численную характеристику или размер. Очень часто она обозначается литерой S. Измеряется величина в квадратных единицах (см 2 , м 2 и т. д. ). Фигура, имеющая характеристику S, называется квадратируемой.
Для нахождения S применяется интегральный метод, но существуют частные случаи, при которых интегрировать необязательно. Очень часто возникает необходимость перевода одной единицы в другую. Для этого существует простой алгоритм, позволяющий корректно выполнить данную операцию. Например, нужно перевести м 2 в см 2 . Необязательно заучивать единицы площади и их эквивалентность другим. Достаточно выполнить следующие действия:
- Определить базовую единицу: м и см.
- Выполнить перевод одной метрической величины в другую: 1 м = 100 см.
- Возвести обе части выражения во втором пункте в квадрат: 1 м 2 = 100 2 см 2 = 10000 см 2 .
Однако бывают и другие единицы, которые применяются для измерения размерности земельных участков: 1 ар (сокращенно а) = 1 сотке = 100 м 2 и 1 гектар (га) = 10000 м 2 .

Когда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты.
Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2.
Площадь можно выразить и другим соотношением, когда известны все стороны и угол А, который не является прямым: S = [(a 2 — b 2 — c 2 + d 2 ) * tg (A)] / 4. При известном радиусе описанной окружности и углах (A, B и Y) можно воспользоваться такой формулой: S = 2 * R^(2) * sin (A) * sin (B) * sin (Y). Следствием из последнего соотношения является S <= 2 * R 2 . Если четырехугольник является квадратом, то неравенство преобразуется в равенство, т. е. S = 2 * R 2 .
Диагонали и углы
Для вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d.
При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2).
Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD).
Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом:
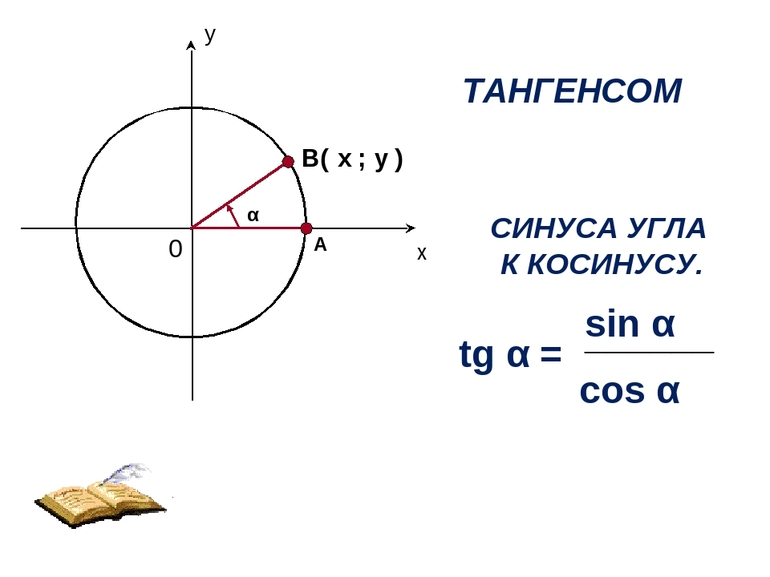
- cos (A) = (a 2 + d 2 — b 2 — c 2 ) / (2 * (a * d + b + c)).
- sin (A) = [(p — a) * (p — b) * (p — c) * (p — d)]^(½) / (a * d + b + c).
- tg (A/2) = [((p — a) * (p — d)) / ((p — b) * (p — c))]^(½).
В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½).
В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры:
- Стороны: a, b, c и d.
- Диагонали: s и t.
- Площадь: S.
- Радиус описанной окружности: R.
В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения:
- a = [k * (l + m) + (1 — (l * m))] * [l + m — k * (1 — (l * m))].
- b = (1 — l 2 ) * (m — k) * (1 + k * m).
- c = k * (1 + l 2 ) * (1 + m 2 ).
- d = (1 + m 2 ) * (l — k) * (1 + k * l).
- s = l * (1 + k 2 ) * (1 + m 2 ).
- t = m * (1 + k 2 ) * (1 + l 2 ).
- S = l * m * [2 * k * (1 — l * m) — (l + m) * (1 — k 2 )] * [2 * k (l + m) + (1 — l * m) * (1 — k 2 )].
- 4 * R = (1 + l 2 ) * (1 + m 2 ) * (1 + k 2 ).
Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается.
Параметры для окружности
Радиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
При комбинации данной формулы с соотношением Брахмагупты можно получить следующее соотношение: 4 * S * R = [(a * b + c * d) * (a * c + b * d) * (a * d + b *c)]^(½). Следует отметить, что величина S является площадью вписанного четырехугольника. Для ортогонального четырехугольника с перпендикулярными диагоналями, которые делятся на отрезки s1, s2, t1 и t2, существует некоторое соотношение, позволяющее найти диаметр окружности (D): D 2 = (s1)^2 + (s2)^2 + (t1)^2 + (t2)^2 = a 2 + c 2 = b 2 + d 2 .
Радиус в этом случае находится таким образом: R = D / 2 = [(s1)^2 + (s2)^2 + (t1)^2 + (t2)^2] / 2 = [a 2 + c 2 ] / 2 = [b 2 + d 2 ] / 2. Если выполнить сложение квадратов сторон, то получится такое равенство: 8 * R = a 2 + b 2 + c 2 + d 2 . По формуле Эйлера R можно также выразить через диагонали (s и t) и расстояние v между их серединами: R = [(s 2 + t 2 + 4 * v 2 ) / 8]^(½).
Таким образом, специалисты рекомендуют на начальных этапах обучения использовать уже готовые формулы для вычисления основных параметров выпуклого четырехугольника, вписанного в окружность.
