All electromagnetic radiation is light, and it occurs over an extremely wide range of wavelengths, from high-energy gamma waves with shorter wavelengths to low-energy radio waves with longer wavelengths. But the human eye can detect only a small portion of the radiation, and that portion is referred to as visible light. In an electromagnetic spectrum, the visible spectrum lies in between the infrared spectrum and the UV spectrum. Visible light ranges between a wavelength of 400 nm and 700 nm. The human eye cannot detect other electromagnetic radiation as the radiation has either large or small wavelengths and is out of biological limitations.
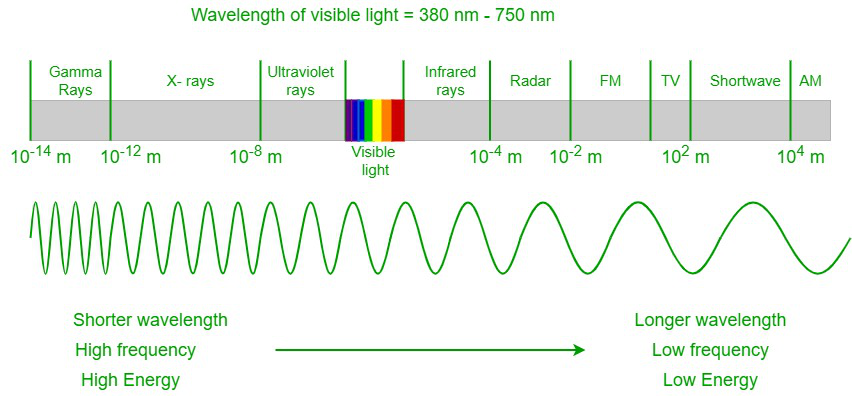
Electromagnetic spectrum
When a visible spectrum travels through a prism, the light gets separated into a spectrum of colors of different wavelengths. The violet color has the shortest wavelength of around 380 nm, and the red color has the longest wavelength of around 700 nm. Our eyes can detect the outer-most layer of the sun, the corona, in visible light.
Wavelength
A wavelength is one of the properties of a wave and is defined as the distance between the two successive crests or troughs of a wave, where a crest is the highest point of the wave, and a trough is the lowest point of the wave. Since wavelength is a distance or length between two points, it is measured in meters, centimeters, millimeters, micrometers, etc. It is denoted by the symbol Lambda ‘λ’.

Wave
Frequency
Frequency (f) is defined as the total number of wave cycles or oscillations produced per unit of time. Frequency is measured in terms of Hertz (Hz) or s-1.
The formula for the frequency:
Frequency (f) = 1/period(T)
f = 1/T
- A period is defined as the time taken to complete an oscillation.
- From the equation of frequency, we can conclude that the frequency of a wave is inversely proportional to its period.
- 1 Hertz = 1 oscillation/second
Wave velocity
The velocity of a wave or wave velocity is defined as the distance traveled by the wave in a unit of time. The S.I. unit of wave velocity is ms-1.
- Light travels with a speed in the vacuum of 29,97,92,458 m/s, i.e., approximately 3 × 108 m/s, and it is represented by the symbol c.
Wavelength of the light
We know that light possesses the characteristics of both a wave and a particle. So, the wavelength of a light wave is given as;
λ =
Where λ is the wavelength of light
c is the velocity of light and
f is the frequency of the light
The energy of a photon is given as,
E = h × f =
Where E is the energy of a photon
h is the Planck’s constant i.e., h = 6.64 × 10-34 joule-second
Wavelength, Frequency, and Energy of the visible light spectrum
| Colour | Wavelength | Frequency | The energy of a photon |
| Violet | 380 – 450 nm | 668-789 THz |
2.75 – 3.26 eV |
| Blue | 450-495 nm | 606-668 THz |
2.50 – 2.75 eV |
| Green | 495-570 nm | 526-606 THz |
2.17 – 2.50 eV |
|
Yellow |
570-590 nm | 508-526 THz |
2.10 – 2.17 eV |
|
Orange |
590-620 nm | 484-508 THz |
2.00 – 2.10 eV |
|
Red |
620-750 nm | 400-484 THz |
1.65 – 2.00 eV |
Sample Problems
Problem 1: Calculate the wavelength of the visible light with a frequency of 5.36 × 1014 Hz.
Solution:
Given the frequency of light = 5.36 × 1014 Hz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) =
⇒ λ =
⇒ λ = 5.60 × 10-7 m
Hence, the wavelength is 5.60 × 10-7 m
Problem 2: If a microwave oven emits microwave energy of 1.64 × 10-24 J, then calculate the wavelength of the microwave emitted.
Solution:
Given data,
The energy of microwave emitted = 1.64 × 10-24 J
We know, that the energy of a photon =
h = 6.64 × 10-34 joule-second
⇒ 1.64 × 10-24 =
⇒ λ =
⇒ λ = 12.146 × 10-2 m = 12.15 cm
Hence, the wavelength of the microwave emitted is 12.15 cm.
Problem 3: If a radio station broadcasts at a frequency of 555 kHz, then calculate the wavelength of radio waves emitted.
Solution:
Given,
Frequency of radio waves = 555 KHz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) =
⇒ λ =
⇒ λ = 540 m
Hence the wavelength of radio waves emitted is 540 m.
Problem 4: Calculate the wavelength of yellow light emitted from a sodium lamp at a frequency of 5.15 × 1014 Hz.
Solution:
Given,
The frequency of yellow light = 5.15 × 1014 Hz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) =
⇒ λ =
⇒ λ = 582.5 × 10-9 m = 582.5 nm
Hence, the wavelength of the yellow light is 582.5 nm.
Problem 5: Calculate the wavelength of a photon with an energy of 3.35 × 10-19 Joules.
Solution:
Given,
The energy of a photon = 3.35 × 10-19 Joules.
We know, that the energy of a photon =
h = 6.64 × 10-34 joule-second
⇒ 3.35 × 10-19 =
⇒ λ =
⇒ λ= 5.94 × 10-7 m = 594 nm
Hence, the wavelength of the photon is 594 nm.
Problem 6: The broadcasting frequency of a radio station is 101 MHz. What will be the wavelength of the wave if the broadcast wave is an electromagnetic wave?
Solution:
Given data, Frequency of the wave = 101 MHz = 101 × 106 Hz
Speed of light = 3 × 108 m/s
Now, the wavelength of light (λ) = c/f
⇒ λ = (3 × 108)/(101 × 106)
⇒ λ = 2.97 m
Hence, the wavelength of the broadcast wave is 2.97m
Last Updated :
15 May, 2022
Like Article
Save Article
Загрузить PDF
Загрузить PDF
Длина волны – это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие “длина волны” ассоциируется с электромагнитным спектром.[1]
Метод вычисления длины волны зависит от данной информации. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой.
-

1
Воспользуйтесь формулой для вычисления длины волны. Чтобы найти длину волны, разделите скорость волны на частоту. Формула:
[2]
-

2
Используйте соответствующие единицы измерения. Скорость измеряется в единицах метрической системы, например, в километрах в час (км/ч), метрах в секунду (м/с) и так далее (в некоторых странах скорость измеряется в британской системе, например, в милях в час). Длина волны измеряется в нанометрах, метрах, миллиметрах и так далее. Частота, как правило, измеряется в герцах (Гц).[3]
- Единицы измерения конечного результата должны соответствовать единицам измерения исходных данных.
- Если частота дана килогерцах (кГц), или скорость волны в километрах в секунду (км/с), преобразуйте данные значения в герцы (10 кГц = 10000 Гц) и в метры в секунду (м/с).
-

3
Известные значения подставьте в формулу и найдите длину волны. В приведенную формулу подставьте значения скорости и частоты волны. Разделив скорость на частоту, вы получите длину волны.[4]
- Например. Найдите длину волны, распространяющейся со скоростью 20 м/с при частоте колебаний 5 Гц.
-

4
Реклама
-

1
-

2
Перепишите представленную формулу, чтобы найти длину волны. Для этого проделайте ряд математических операций. Обе стороны формулы умножьте на длину волны, а затем обе стороны разделите на энергию; вы получите формулу:
. Если энергия фотона известна, можно вычислить длину световой волны.[7]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
-

3
В полученную формулу подставьте известные значения и вычислите длину волны. В формулу подставьте только значение энергии, потому что две константы являются постоянными величинами, то есть не меняются. Чтобы найти длину волны, перемножьте константы, а затем результат разделите на энергию.[9]
- Например. Найдите длину световой волны, если энергия фотона равна 2,88 x 10-19 Дж.
Реклама
-

1
Проверьте ответ. Для этого умножьте длину волны на частоту. Если вы получите данное значение скорости, решение правильное; в противном случае проверьте вычисления. Если вы пользуетесь калькулятором, правильно вводите числа.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
- Решите эту задачу как описано выше и получите значение 4,9 м.
- Проверьте ответ: 4,9 м х 70 Гц = 343 м/сек. Это данная в условии задачи скорость, поэтому решение верное.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
-

2
Используйте экспоненциальную запись чисел, чтобы избежать ошибок при округлении чисел (в калькуляторе). Порой в вычислении длины волны участвуют очень большие числа, особенно когда присутствует скорость света. Это может привести к ошибкам округления чисел. Поэтому используйте экспоненциальную запись чисел.[10]
- Например. Свет проходит сквозь воду со скоростью 225000000 м/с. Найдите длину световой волны, если ее частота равна 4 x 1014 Гц.
-

3
Помните, что частота волны не меняется при изменении среды ее распространения. Во многих задачах волна распространяется в двух средах, и некоторые учащиеся пытаются вычислить две длины волны. Это ошибка, потому что в отличие от скорости распространения и длины волны частота волны не меняется при изменении среды ее распространения.[11]
- Например, световая волна длиной λ, распространяющаяся со скоростью v при частоте f, переходит из воздушного пространства в некоторую среду, показатель преломления которой равен 1,5. Как изменятся указанные три величины?
Реклама
Об этой статье
Эту страницу просматривали 158 119 раз.
Была ли эта статья полезной?

График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе[1][2].
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π[3].
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на
;
- как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву 
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
Длина волны — пространственный период волнового процесса[править | править код]
Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний 





Связь с частотой[править | править код]
Получить соотношение, связывающее длину волны с фазовой скоростью 


Для электромагнитных волн в вакууме скорость 



Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.
Длина волны в среде[править | править код]
В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.
Длина электромагнитной волны в среде короче, чем в вакууме:
- где
— показатель преломления среды;
— относительная диэлектрическая проницаемость среды;
— относительная магнитная проницаемость среды.
Величины 









Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением 

Волны де Бройля[править | править код]
Волнам де Бройля также соответствует определённая длина волны. Частице с энергией 

- частота:
- длина волны:
- где
— постоянная Планка.
Примеры[править | править код]
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару 

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм[4].
Примечания[править | править код]
- ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в
, и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine
Литература[править | править код]
- Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:
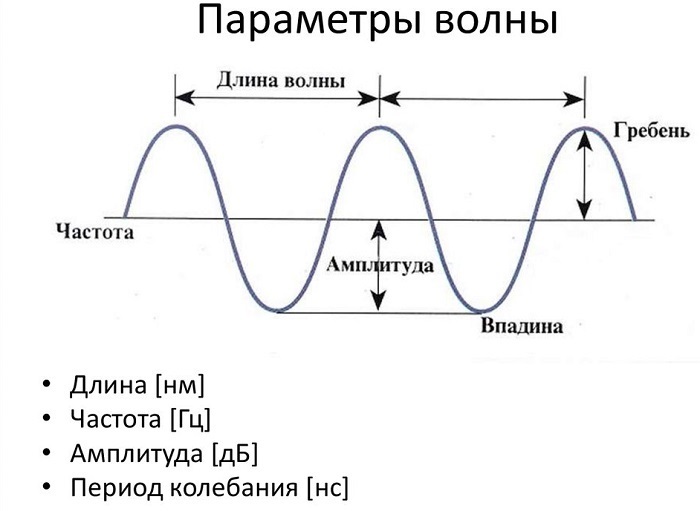
Определение и формула длины волн
Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
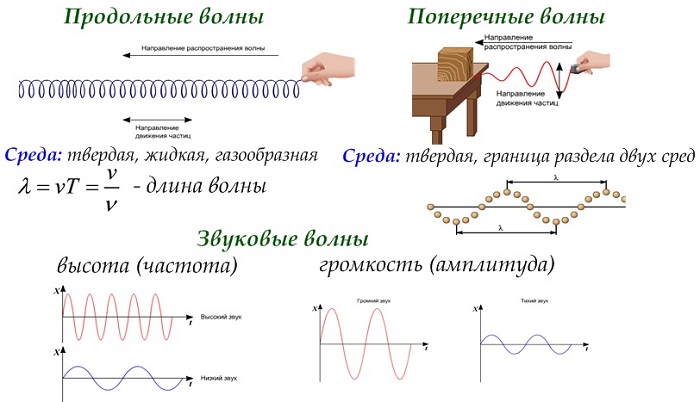
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
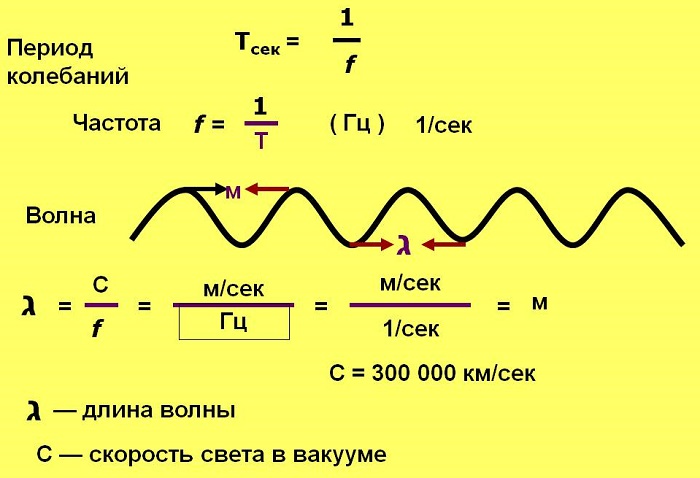
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
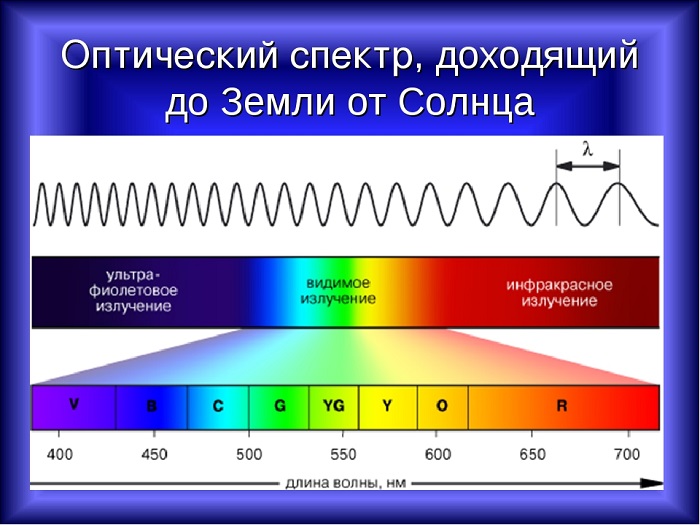
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
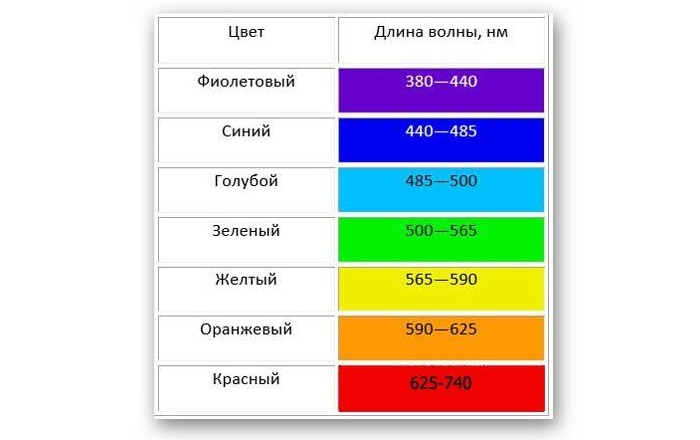
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
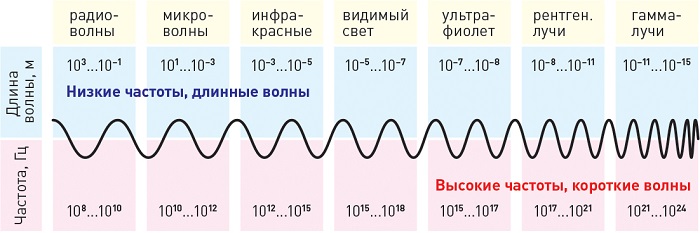
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Тема: Определение длины волны светового излучения с помощью дифракционной решётки
Цель: Познакомиться на опыте с явлением многолучевой интерференции световых волн. Используя решётку с известным расстоянием между штрихами измерить длину волны светового излучения.
Оборудование:
- Штатив.
- Дифракционная решётка 100 штрихов на мм.
- Измерительная лента.
Теория
Дифракция волн – огибание волнами различных препятствий (неоднородностей).
Препятствия нарушают прямолинейность распространения фронта волны.
Дифракция волн свойственна всякому волновому движению; проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней, однако проявляется всегда. Для увеличения яркости дифракционной картины нужно пропускать свет через несколько параллельных щелей. В этом случае кроме явления дифракции будет происходить ещё и явление интерференции, т.к. лучи, идущие от всех лучей, оказываются когерентными.
Когерентными называются волны, имеющие одинаковую частоту и постоянную разность фаз.
Дифракционная решетка – оптический прибор, представляющий собой большое число параллельных и очень близко расположенных узких щелей, которые пропускают или отражают свет.
Дифракционные решетки с различным числом щелей на 1 мм:

Параллельный пучок света с длиной волны λ, проходя через дифракционную решётку, вследствие дифракции за решёткой, распространяется по всевозможным направлениям и интерферирует. На экране, установленном на пути интерферирующего света, можно наблюдать интерференционную картину:

Максимумы света наблюдаются в точках экрана, для которых выполняется условие максимума:
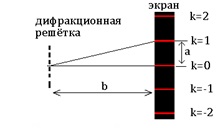
Условие максимума: на разности хода волн укладывается четное число полуволн (целое число длин волн): Δ=k·λ, (1)
где Δ=АС – разность хода волн; λ – длина световой волны; k – номер максимума.
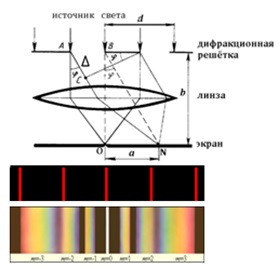
Центральный максимум (в точке О) называют нулевым; для него Δ=0. Слева и справа от него располагаются максимумы высших порядков.
Условие возникновения максимума можно записать иначе:
d·sinφ=k·λ
где k=0; ± 1; ± 2; ± 3…
Здесь d – период дифракционной решётки в мм, φ – угол, под которым виден световой максимум k-го порядка в точке N на расстоянии а от нулевого максимума, а λ – длина волны.
Так как углы дифракции малы, то для них можно принять: sinφ ≈ tgφ, а tgφ=a/b.
Поэтому: 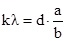 , и искомая длина световой волны равна
, и искомая длина световой волны равна 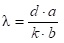 (2)
(2)
В данной работе формулу (2) используют для вычисления длины световой волны.
Из условия максимума следует sinφ=(k·λ)/d .
Пусть k=1, тогда sinφкр=λкр/d и sinφф=λф/d.
Известно, что λкр>λф , следовательно sinφкр>sinφф. Т.к. y= sinφф – функция возрастающая, то φкр>φф
Поэтому фиолетовый цвет в дифракционном спектре располагается ближе к центру.
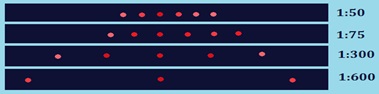
Между максимумами расположены минимумы освещенности. Чем больше общее число щелей и чем ближе друг к другу они расположены, тем более широкими промежутками разделены максимумы.
Картина дифракции лазерного излучения красно цвета на решётках с различным числом щелей на 1 мм:
Ход работы
- Перенести рисунок в тетрадь.

- Подготовить таблицу для записи результатов измерений:
|
Порядок спектра, цвет k |
Постоянная d мм |
Расстояние от решётки до экрана, b мм |
Расстояние от нулевого максимума до максимума k-порядка а мм |
Длина волны, нм |
Средняя длина волны нм |
Относительная погрешность δ % |
|
1-ый, красный |
1:100=0,001 |
|||||
|
2-ой, красный |
1:100=0,001 |
|||||
|
1-ый, фиолетовый |
1:100=0,001 |
|||||
|
2-ой, фиолетовый |
1:100=0,001 |
- Укрепить в штативе линейку с экраном и закрепить на направляющей линейки дифракционную решётку.
- Установить расстояние от решётки до экрана 40 см (b).Результат записать в таблицу.
- Смотря через дифракционную решётку, направить прибор на источник света. Пронаблюдать спектр:
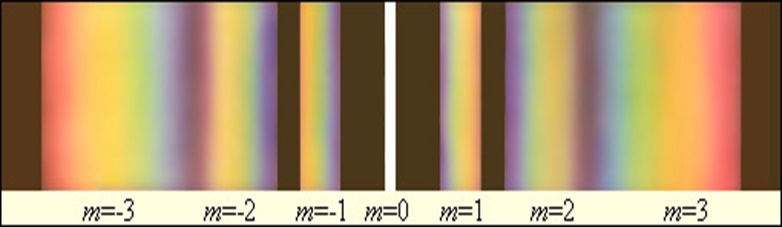
Измерить на экране расстояние а между нулевым максимумом и максимумом 1-го порядка для красного света. Результат записать в таблицу.
- Измерить на экране расстояние а между нулевым максимумом и максимумом 2-го порядка для красного света. Результат записать в таблицу.
- Повторить опыт, измерив на экране расстояние а между нулевым максимумом и максимумом 1-го и 2-го порядка для фиолетового света. Результат записать в таблицу.
- По формуле
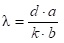 рассчитать длину волны излучения.
рассчитать длину волны излучения. - Найти среднее значение длины волны светового излучения для красного λкр ср=( λкр1+λкр2)/2
и фиолетового света .λф ср=( λф1+λф2)/2
- Зная истинное значение длины волны лазерного излучения , рассчитать относительную погрешность измерений:
δ=( λкр ср – λкр табл)/λкр табл *100% и δ=( λф ср – λф табл)/λф табл *100%
Диапазон длин волн, нм
Красный 625—740 нм (λкр табл= 680 нм)
Фиолетовый 380—440 нм (λф табл = 410 нм)
- Записать вывод по результатам выполненной работы.
- Ответить письменно на контрольные вопросы.
Контрольные вопросы
- Какие волны называются когерентными?
- В чём заключается явление дифракции?
- Какие свойства света подтверждает дифракция света?
- При каких условиях наблюдается дифракция света?
- Как образуется дифракционный спектр?
- Почему максимумы располагаются как слева, так и справа от нулевого максимума?
- В чём разница в дифракционных картинах решёток с 50 и 300 штрихами на одном миллиметре?





