Алгоритм вычисления комплексного корня полинома произвольной степени
Время на прочтение
10 мин
Количество просмотров 9.4K
Это завершение моей первой статьи: “Алгоритм расчёта вещественных корней полиномов”.
Спасибо комментаторам, сделавшим более ясным мое слишком уж конспективное изложение метода Лобачевского. В самом деле, мне следовало явно написать, что квадрированный полином надо рассматривать как полином от аргумента x^2, где x — аргумент исходного полинома.
Главное же, там был описан простой алгоритм вычисления всех вещественных корней полинома произвольной степени.
Теперь на этом фундаменте будет построен вполне элементарный алгоритм вычисления комплексного корня полинома, не имеющего вещественных корней.
Сначала нормируем полином так, чтобы его свободный член стал равным единице. Тогда при значении аргумента x=0 значение полинома будет вещественным и равным единице. Это широко известная математикам отправная точка рассуждений.
Представим аргумент x полинома в виде:
x=r*exp(i*fi)
Здесь i — это мнимая единица.
При изменении fi от нуля до 2*pi (=6.28318…) значение полинома p опишет некоторую замкнутую кривую. Назовём эту кривую эпициклоидой.
При исчезающе малом r эпициклоида будет похожа на маленькое колечко вокруг точки p=1. Не будем отвлекаться на ситуации, когда линейный член нашего полинома равен нулю.
При бесконечно большом значении r эпициклоида опишет несколько петель вокруг точки p=1. Количество петель равно степени полинома, форма близка к окружности большого радиуса.
Было бы полезно научиться вычислять все значения fi, при которых мнимая часть полинома обращается в нуль. Это позволит каждому значению r конструктивно поставить в соответствие минимальное значение координаты x, при которой эпициклоида пересекает ось абсцисс.
Это значение положительно при малых r и отрицательно при больших r.
Методом деления отрезка пополам можно найти такое r, при котором это значение будет в точности равно нулю. Соответствующие значения r и fi определят искомый комплексный корень полинома.
Перейдём к реализации намеченного плана.
Мнимая часть полинома с коэффициентами kf0, kf1, kf2,…, kfn представится в виде:
Im=kf1*r*sin(fi)+kf2*r^2*sin(2*fi)+...+kfn*r^n*sin(n*fi)
Хотелось бы представить её в виде какого-нибудь полинома, поскольку вещественные корни полиномов мы умеем вычислять. И действительно, эту мнимую часть можно представить как произведение синуса fi, на некоторый полином от косинуса fi. При небольшой степени полинома это можно непосредственно проверить.
Используем метод математической индукции для доказательства этого утверждения в общем виде.
Пусть
cos(n*x)=polynomC(cos(x))
sin(n*x)=sin(x)*polynomS(cos(x))
Тогда
cos(n*x+x)=cos(n*x)*cos(x)-sin(n*x)*sin(x)=
=polynomC(cos(x))*cos(x)-sin^2(x)*polynomS(cos(x))
Поскольку sin^2(x)=1-cos^2(x), ясно, что последнее выражение является некоторым полиномом от cos(x).
Аналогично:
sin(n*x+x)=sin(n*x)*cos(x)+cos(n*x)*sin(x)=
=sin(x)*(polynomS(cos(x)*cos(x)+polynomC(cos(x))))
И здесь очевидно, что сомножитель при sin(x) в последнем выражении является полиномом от cos(x).
Понятно, что тщательное выписывание приведенных соотношений позволяет получить рекуррентные формулы для коэффициентов нужных нам полиномов.
Дальнейшие подробности реализации намеченного плана удобнее проследить по приведенным ниже комментированным текстам соответствующей программы.
Полный комплект этой демонстрационной программы состоит из приведенных ниже трех файлов и двух файлов, описанных в предыдущей публикации.
Текст файла polynomComplexRoot.h
Содержимое
//*************************************************************************
class polinomComplexRoot
{
public:
//тело класса определяется степенью исследуемого полинома и набором его коэффициентов
polinomComplexRoot(int _degree,double* _kf);
~polinomComplexRoot();
//основная процедура внешнего интерфейса класса
//возвращает код ошибки
//при успешном завершении код ошибки равен нулю,
//а значения параметров rootRe и rootIm станут равны соответственно
//вещественной и мнимой части комплексного корня исследуемого полинома
int run(double& rootRe,double& rootIm);
private:
int degree,errorCode;
double *kf;
double *ki;
double *cosRootsArray;
double *rpw;
int **ck;
int **sk;
//основная рабочая процедура
//при заданном r находит минимальное значение вещественной части
//исследуемого полинома от аргумента r*exp(i*fi)
//при том значении fi, которое обеспечивает равенство нулю
//его мнимой части. Это значение fi
//будет присвоено второму аргументу процедуры по окончании вызова
double minAxeXcrossVal(double r,double& fi);
};//class polinomComplexRoot
//*************************************************************************
Текст файла polynomComplexRoot.cpp
Содержимое
//*************************************************************************
#include <math.h>
#include <polynomComplexRoot.h>
#include <polynomRealRoots.h>
const double cPI=3.14159265358979323846;
polinomComplexRoot::polinomComplexRoot(int _degree,double* _kf)
{
degree=_degree;errorCode=0;
//предварительная инициализация
kf=0;ck=0;sk=0;rpw=0;ki=0;cosRootsArray=0;
//отбраковка неприемлемых значений коэффициентов исходного полинома
if(_kf[0]==0){errorCode=1;return;}
if(_kf[degree]==0){errorCode=2;return;}
if(degree<2){errorCode=3;return;}
kf=new double[1+degree];
ki=new double[1+degree];
cosRootsArray=new double[1+degree];
rpw=new double[degree+1];
ck=new int*[1+degree];
sk=new int*[1+degree];
for(int i=0;i<=degree;i++)
{
ck[i]=new int[1+degree];
sk[i]=new int[1+degree];
}
//отбраковка исходного полинома, имеющего вещественные корни
polynomRealRoots(degree,_kf,kf,errorCode);
if(errorCode>0){errorCode=4;return;}
for(int i=0;i<=degree;i++)kf[i]=_kf[i]/_kf[0];
for(int i=0;i<=degree;i++)
for(int j=0;j<=degree;j++)
{ck[i][j]=0;sk[i][j]=0;}
//коэффициенты косинусных полиномов для представления
//кратных синусов и косинусов по формулам
//cos(n*x)=ck[n,0]+ck[n,1]*cos(x)+ck[n,2]*cos^2(x)+...+ck[n,n]*cos^n(x)
//sin(n*x)=sin(x)*(sk[n,0]+sk[n,1]*cos(x)+sk[n,2]*cos^2(x)+...+sk[n,n]*cos^n(x))
ck[1][1]=1;
sk[1][0]=1;
//расчёт ck и sk по рекуррентным формулам
//здесь np1=n+1
for(int n=1,np1=2;n<degree;n=np1,np1++)
for(int k=0;k<=np1;k++)
{//реализация рекуррентных формул
//ck[n+1,k]=ck[n,k-1]+sk[n,k-2]-sk[n,k];
//sk[n+1,k]=sk[n,k-1]+ck[n,k];
if(k>=1)ck[np1][k]+=ck[n][k-1];
if(k>=2)ck[np1][k]+=sk[n][k-2];
if(k>=1)sk[np1][k]+=sk[n][k-1];
if(k<=n){ck[np1][k]-=sk[n][k];sk[np1][k]+=ck[n][k];}
}//реализация рекуррентных формул
return;
}//constructor
polinomComplexRoot::~polinomComplexRoot()
{
if(kf)delete[] kf;
if(ki)delete[] ki;
if(cosRootsArray)delete[] cosRootsArray;
if(rpw)delete[] rpw;
if(ck)
{
for(int i=0;i<=degree;i++)delete[] ck[i];
delete[] ck;
}
if(sk)
{
for(int i=0;i<=degree;i++)delete[] sk[i];
delete[] sk;
}
}//destructor
int polinomComplexRoot::run(double& rootRe,double& rootIm)
{
rootRe=0;rootIm=0;
if(errorCode>0)return errorCode;
//верхняя rup и нижняя rdn границы поиска для r
double fidn=0,rdn=0,fiup=0,rup=1;
//удваиваем rup пока оно недостаточно велико
for(;minAxeXcrossVal(rup,fiup)>0;)rup+=rup;
for(;;)
{//цикл деления пополам интервала (rdn, rup)
double fit,rt=0.5*(rdn+rup);
if(rt==rdn||rt==rup)break;
if(minAxeXcrossVal(rt,fit)>0){rdn=rt;fidn=fit;}else {rup=rt;fiup=fit;}
}//цикл деления пополам интервала (rdn, rup)
//формальный выбор для выдачи результата одного из двух
//практически одинаковых решений (rdn, fidn) или (rup, fiup)
//будет вычислен модуль исследуемого полинома в каждой из этих двух точек
//и в качестве результата решения будет выдана та из этих точек,
//которой соответствует вычислительно меньшее значение этого модуля
double minmod; //минимальное значение модуля полинома
bool mindn=true; //минимум достигнут в точке с суффиксом dn
for(int c=0;c<2;c++)
{//контрольный расчёт в точках up и dn
double rc,fic;
if(c==0){rc=rdn;fic=fidn;}
else {rc=rup;fic=fiup;}
//rec - вещественная часть исследуемого полинома в пробной точке
//imc - мнимая часть исследуемого полинома в пробной точке
double rec=kf[degree]*cos(degree*fic),
imc=kf[degree]*sin(degree*fic);
for(int i=degree-1;i>0;i--)
{//gorner
rec=rc*rec+kf[i]*cos(i*fic);
imc=rc*imc+kf[i]*sin(i*fic);
}//gorner
rec=rc*rec+kf[0];
imc=rc*imc;
//mc - квадрат модуля исследуемого полинома в пробной точке
double mc=rec*rec+imc*imc;
if(c==0)minmod=mc;
else if(mc<minmod)
{//точка up лучше точки dn
minmod=mc;
mindn=false;
}//точка up лучше точки dn
}//контрольный расчёт в точках up и dn
//формирование результата
if(mindn)
{//выбор точки dn в качестве результата
rootRe=rdn*cos(fidn);
rootIm=rdn*sin(fidn);
}//выбор точки dn в качестве результата
else
{//выбор точки up в качестве результата
rootRe=rup*cos(fiup);
rootIm=rup*sin(fiup);
}//выбор точки up в качестве результата
return errorCode;
}//run
//основная рабочая процедура
//при заданном r находит минимальное значение вещественной части
//исследуемого полинома от аргумента r*exp(i*fi)
//при том значении fi, которое обеспечивает равенство нулю его мнимой части
//это значение fi будет присвоено второму аргументу процедуры по окончании вызова
double polinomComplexRoot::minAxeXcrossVal(double r,double& fi)
{
//предварительно формируем вспомогательный массив rpw[k]=r^k
double rb=1;
for(int i=0;i<=degree;i++){rpw[i]=rb;rb*=r;}
//значение исследуемого полинома от вещественного аргумента r
rb=kf[0];for(int i=1;i<=degree;i++)rb+=rpw[i]*kf[i];
double rez=rb;fi=0;
//значение исследуемого полинома от вещественного аргумента -r
rb=kf[0];
for(int i=1,od=1;i<=degree;i++,od=1-od)if(od)rb-=rpw[i]*kf[i];else rb+=rpw[i]*kf[i];
//мы ищем минимальное значение абсциссы эпициклоиды
if(rb<rez){rez=rb;fi=cPI;}
//мнимая часть исследуемого полинома от комплексного аргумента,
//представленного параметрами r и fi, выражается так
//im=r*kf[1]*sin(fi)+r^2*kf[2]*sin(2*fi)+...+r^n*kf[n]*sin(n*fi)
//она будет представлена с участием некоторого полинома от cos(fi)
//коэффициенты этого полинома обозначены идентификатором ki
//im=sin(fi)*(ki[0]+ki[1]*cos(fi)+ki[2]*cos^2(fi)+...+ki[n]*cos^n(fi))
//коэффициенты ki выражаются через коэффициенты исследуемого полинома kf
//и коэффициенты ck и sk, вычисленные в конструкторе класса по формулам
//ki[0]=r*kf[1]*sk[1][0]+r^2*kf[2]*sk[2][0]+...+r^n*kf[n]*sk[n][0]
//ki[1]=r*kf[1]*sk[1][1]+r^2*kf[2]*sk[2][1]+...+r^n*kf[n]*sk[n][1]
//...
//ki[n]=r*kf[1]*sk[1][n]+r^2*kf[2]*sk[2][n]+...+r^n*kf[n]*sk[n][n]
for(int i=0;i<=degree;i++)
{//вычисление коэффициентов ki
rb=0;
for(int j=i+1;j<=degree;j++)rb+=(rpw[j]*kf[j]*sk[j][i]);
ki[i]=rb;
}//вычисление коэффициентов ki
//cosDegree это степень косинусного полинома, представленного коэффициентами ki
//страхуемся от возможности равенства нулю старших коэффициентов
int cosDegree=0,cosRootsCount=0;
for(int i=degree-1;i>0;i--)if(fabs(ki[i])>0){cosDegree=i;break;}
//интерпретируем ситуацию вырождения ki-полинома как внутреннюю ошибку
if(cosDegree<1){errorCode=5;return rez;}
//находим все вещественные корни ki-полинома
polynomRealRoots(cosDegree,ki,cosRootsArray,cosRootsCount);
//обследование найденных корней ki-полинома
for(int i=0;i<cosRootsCount;i++)if(fabs(cosRootsArray[i])<1)
{//расчёт fi и коррекция rez
double x=acos(cosRootsArray[i]),
im=0,re=kf[0];
//расчёт вещественной (re) и мнимой (im) части исследуемого полинома
//при очередном значении найденного корня
for(int j=1;j<=degree;j++)
{
re+=(kf[j]*rpw[j]*cos(j*x));
im+=(kf[j]*rpw[j]*sin(j*x));
}
//существенно ненулевое значение im интерпретируем как внутреннюю ошибку
if(fabs(im)>1e-6)errorCode+=6;
//мы ищем минимальное значение абсциссы эпициклоиды
if(re<rez){rez=re;fi=x;}
}//расчёт fi и коррекция rez
//интерпретируем невероятный случай fi=0 или fi=cPI
//как внутреннюю ошибку
if(fi==0||fi==cPI)errorCode+=7;
return rez;
}//minAxeXcrossVal
//*************************************************************************
Текст файла main.cpp
//*************************************************************************
//демонстрация расчёта комплексного корня полинома
#include <stdio.h>
#include <math.h>
#include <polynomComplexRoot.h>
int main()
{
//задание степени и коэффициентов исходного полинома
int degree=4;
//double kf[5]={24,24,12,4,1};
//double kf[5]={2,-2,3,-2,1};
double kf[5]={4,0,0,0,1};
//запуск процесса расчёта комплексного корня
double re,im;
int ret=polinomComplexRoot(degree,kf).run(re,im);
//распечатка результата расчёта корня
if(ret==0||ret>4)
{//успешное завершение процедуры расчёта корня
//распечатка результата расчёта корня
if(ret==0)printf("успешное решениеn");
else
{
printf("ПРЕДУПРЕЖДЕНИЕnбыли странные ситуацииn");
printf("возможно из-за недостаточной точности аппаратного представления вещественных чиселn");
}
printf("кореньВещт=%fnкореньМним=%fn",re,im);
//проверка достоверности найденного корня
//используется следующая формула для полинома от суммы аргументов:
//p0(x+y)=p0(x)+p1(x)*y+p2(x)*y^2/2!+...+pn*y^n/n!
//представляющая собой конечную сумму ряда Тейлора по приращению y
//для исходного полинома p0 в точке x
//здесь p1, p2, ... , pn - производные 1-го, 2-го, ... , n-го порядка от исходного полинома
//в тексте программы далее использован обратный порядок индексации исходного и производных полиномов
//там индекс полинома равен его степени
double** kfx=new double*[degree+1];
for(int i=0;i<=degree;i++)kfx[i]=new double[degree+1];
double* kfy=new double[degree+1];
for(int i=degree;i>=0;i--)
{//исходные присвоения
for(int j=0;j<=degree;j++)kfx[i][j]=0;
kfy[i]=0;
kfx[degree][i]=kf[i];
}//исходные присвоения
//расчёт коэффициентов производных полиномов
for(int i=degree;i>0;i--)
for(int j=i;j>0;j--)kfx[i-1][j-1]=kfx[i][j]*j;
double fact=1;
for(int i=0,dmi=degree;i<=degree;i++,dmi--)
{//расчёт коэффициентов полинома по y
//вычисляется по схеме Горнера значение производного полинома от аргумента re
kfy[i]=kfx[dmi][dmi];
for(int j=dmi-1;j>=0;j--)kfy[i]=re*kfy[i]+kfx[dmi][j];
kfy[i]/=fact;
fact*=(i+1);
}//расчёт коэффициентов полинома по y
//массив степеней мнимой единицы
const int ipw[4]={1,1,-1,-1};
double ypw=1;
//вещественная и мнимая части значения исходного полинома
//при значении комплексного аргумента re+i*im
double fre=0,fim=0;
for(int i=0,od=0;i<=degree;i++,od=1-od)
{//расчёт значения исходного полинома
if(od==0)fre+=(ypw*kfy[i]*ipw[i%4]);
else fim+=(ypw*kfy[i]*ipw[i%4]);
ypw*=im;
}//расчёт значения исходного полинома
//печать погрешности расчёта корня исходного полинома
//это модуль полинома в найденном корне,
//нормированный на значение свободного члена
printf("погрешность=%7.1en",sqrt(fre*fre+fim*fim)/kf[0]);
//заключительное освобождение занимаемой памяти
for(int i=0;i<=degree;i++)delete[] kfx[i];
delete[] kfx;
delete[] kfy;
}//успешное решение
if(ret>0)switch(ret)
{//печать краткой диагностики произошедшей ошибки
case 1:
printf("#ошибка 1:нулевое значение свободного члена исходного полиномаn");
break;
case 2:
printf("#ошибка 2:нулевое значение старшего коэффициента полиномаn");
break;
case 3:
printf("#ошибка 3:степень исходного полинома слишком малаn");
break;
case 4:
printf("#ошибка 4:исходный полином имеет вещественные корниn");
break;
default:printf("#код ошибки=%dn",ret);
}//печать краткой диагностики произошедшей ошибки
return 0;
}//main
//*************************************************************************
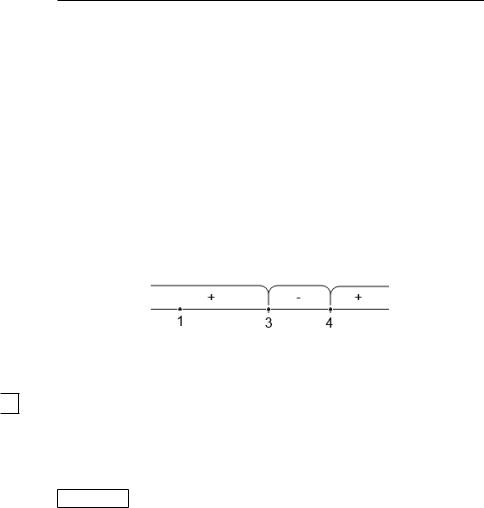
132 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
ными точками (рис. 24). Квадратный трехчлен ( 2 + + 1)
при всех вещественных сохраняет знак «+». Два корня –
3 и 4 – нечетной кратности, в них многочлен меняет знак. Таким образом, точки 3 и 4 разбивают вещественную ось на три промежутка знакопостоянства. Расставим на схеме (рис. 24) знаки и запишем ответ. Ответ включает подмножество, состоящее из изолированной точки 1, которая расположена внутри «знакоположительного» интервала.
Ответ: {1} [3; 4].
Рис. 24. Промежутки знакопостоянства из примера 7
Задачи к параграфу на с. 200, п. 27–28.
125 149 На протяжении всей истории развития человеческого общества развивалось и понятие «число». В ряде открытых европейскими путешественниками первобытных племен Африки и Океании люди знали только натуральные числа: 1, 2 и 3. Все, что больше, – это «много». Наверное, также обстояло дело с арифметикой и у наших далеких предков. Сейчас это может показаться смешным, но

|
§ 3.4. Комплексные корни многочлена |
133 |
такая числовая система вполне удовлетворяла потребности их общественной практики. Древние греки уже рассматривали не только натуральные числа, но и их отношения, т. е. положительные рациональные числа, а в школе Пифагора знали о существовании величин, которые нельзя измерить и
вэтой числовой системе. Так, диагональ единичного квадрата не может быть измерена рациональной дробью. Сейчас мы сказали бы, что уравнение 2 = 2 не имеет решения
на множестве рациональных чисел или не существует таких целых чисел и , что ( )2 = 2 . В средневековой Европе величины, не измеряемые отношением целых чисел,
называли иррациональными, т. е. «неразумными». Только
вXVI веке эти числа несколько реабилитировал Симон Стевин, внедривший в обиход десятичные дроби. Наконец, в XIX веке благодаря трудам Георга Кантора, Карла Вейерштрасса и Юлиуса Вильгельма Рихарда Дедекинда иррациональные числа получили строгое определение, а следовательно, прописку на числовой оси. Множество рациональных чисел, дополненное иррациональными, назвали множеством вещественных чисел. Оказалось, что иррациональные числа «заткнули» все дыры на числовой оси и теперь любая величина может быть измерена. На этом в истории развития «числа» можно было бы поставить жирную точку, если бы не одна беда. Еще Кардано при нахождении корней многочленов третьей степени, даже если они были вещественны-

134 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
√
ми, использовал вспомогательные величины вида + −1. Существование таких величин не укладывалось в традиционное мировоззрение, и сам Кардано считал их лишенными какого-либо смысла, однако совсем отказаться от их использования не получалось. Декарт также рассматривал их как
нечто нереальное, и с его легкой руки в XVI–XVII веках ве-
√
личины вида + −1 стали называть мнимыми. Впрочем, как мы заметили выше, тогда даже иррациональные числа еще «не добились равноправия» на вещественной оси да и на отрицательные нередко посматривали неодобрительно даже математики. И все-таки практическая польза по-
степенно теснила «эстетику». В XVIII веке Леонард Эйлер
√
ввел мнимую единицу = −1, а в XIX веке Карл Фридрих Гаусс доказал алгебраическую замкнутость множества комплексных чисел, т. е. чисел вида + . Последнее означает, что любой многочлен степени выше нулевой имеет хотя бы один комплесный корень. Если степень многочлена ( )
больше единицы и 1 его комплексный корень, то, разделив многочлен на линейный член ( − 1), мы получим многочлен степени на единицу меньшей (с. 102), который также должен иметь по крайней мере один комплексный корень. Продолжим процесс понижения степени многочлена до тех пор, пока в результате деления не получим многочлен нулевой степени 0. Теперь мы можем утверждать, что любой

|
§ 3.4. Комплексные корни многочлена |
135 |
многочлен -й степени имеет комплексных корней и
( ) = 0( − 1)( − 2) . . . ( − ).
Сейчас мнимую единицу определяют как некую величину (не являющуюся вещественным числом), для которой верно утверждение 2 = −1, а комплексное число как выражение вида + , где , . Если = + , то вещественное число = ( ) называют действительной частью, а = ( ) – мнимой частью.
Сразу сделаем два важных замечания. Иногда мнимую единицу определяют как решение уравнения 2 = −1. Такое определение некорректно, поскольку точно также решением будет и (− ). И второе. Поначалу сложилась практика в записи комплексного числа ставить отрицательное число под знак квадратного корня. Тогда
√ √ √ √
−1 · −1 = (−1)(−1) = 1 = 1.
Но, с другой стороны,
√√
−1 · −1 = · = 2 = −1.
|
Подобных недоразумений можно избежать, если, например, |
||||
|
√ |
√ |
|||
|
вместо |
−3 писать 3, т. е. не допускать записи отрица- |
тельного числа под корнем. Дело в том, что обычно сим-

|
136 |
ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА |
|
|
волом √ |
мы обозначаем арифметический квадратный ко- |
|
рень, определяемый как положительное вещественное число, квадрат которого равен подкоренному выражению. Данное определение исключает возможность нахождения под знаком квадратного корня отрицательного числа. В более широком смысле под квадратным корнем подразумевают решение уравнения 2 = . Уравнение имеет два корня. Определенный таким образом «корень» сложно использовать в выражениях.
Пусть 1 = 1 + 1 и 2 = 2 + 2. Тогда основные арифметические операции с комплексными числами определяются так:
1)1 ± 2 = ( 1 ± 2) + ( 1 ± 2);
2)1 2 = ( 1 + 1)( 2 + 2) = ( 1 2 − 1 2) + ( 1 2 + 2 1);
3)1 = 1 + 1 = ( 1 + 1)( 2 − 2) =2 2 + 2 ( 2 + 2)( 2 − 2)
|
= |
1 2 + 1 2 |
+ |
· |
2 1 − 1 2 |
. |
|
22 + 22 |
|||||
|
22 + 22 |
Имеет место равенство ( + ) = + . Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части:
( 1) = ( 2) и ( 1) = ( 2).

|
§ 3.4. Комплексные корни многочлена |
137 |
Иначе говоря, ( 1 = 2)&( 1 = 2). Отношение неравенства для комплексных чисел не определено. Теперь обобщим алгоритм нахождения корней квадратного трехчлена
2 + + (с. 59) на случай произвольного дискриминанта. Пусть ̸= 0. Тогда квадратный трехчлен имеет два комплексных корня. Дискриминант = 2 − 4 . Корни
√
|
± |
, если ≥ 0; |
|||
|
2 |
||||
|
± 2 − , если < 0. |
||||
|
1,2 = |
√ |
Таким образом, мы избегаем ситуаций, когда под знаком квадратного корня может оказаться отрицательное число.
Пример 1. Найти корни квадратного трехчлена 2 2+2 +3. 200
|
Решение. На с. 61 мы установили, что этот трехчлен не име- |
||||||||||||||||||
|
ет вещественных корней. Найдем комплексные: |
||||||||||||||||||
|
√ |
√ |
|||||||||||||||||
|
= 4 |
− |
24 = 20 < 0 |
= |
−2 ± 20 |
= |
−1 ± 5 |
. |
|||||||||||
|
− |
1,2 |
4 |
2 |
|||||||||||||||
|
Ответ: |
√ |
√ |
||||||||||||||||
|
1 = |
−1 − |
5 |
и 2 = |
−1 + 5 |
. |
|||||||||||||
|
2 |
||||||||||||||||||
|
2 |
||||||||||||||||||
|
Пример 2. Найти корни многочлена 2 3 + 2 |
+ 4 − 15. |
|||||||||||||||||
|
201 |
||||||||||||||||||
|
Решение. В примере на с. 116 мы разложили этот много- |
||||||||||||||||||
|
член на множители: |
2 3 + 2 + 4 − 15 = (2 − 3)( 2 + 5).

|
138 |
ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА |
|||||||||
|
Корни неполного квадратного трехчлена 2+5: 2,3 = ± √ |
. |
|||||||||
|
5 |
||||||||||
|
√ |
√ |
|||||||||
|
Ответ: 1 = 1, 5; 2 = − 5 и 3 = |
5. |
|||||||||
|
201 |
Пример 3. |
Найти корни многочленаа 2 4 + 3 +4 2 + +2. |
Решение. В примере на с. 120 мы разложили многочлен в произведение двух квадратных трехчленов:
2 4 + 3 + 4 2 + + 2 = (2 2 + + 2)( 2 + 1).
Рассмотрим первый квадратный трехчлен 2 2 + + 2.
|
√ |
. |
||
|
= 1 − 16 = −15 < 0 1,2 = |
−1± 15 |
||
|
4 |
Корни неполного квадратного трехчлена: 3,4 = ± .
Ответ:
√√
|
1 |
= |
−1 − |
15 |
; |
2 |
= |
−1 + |
15 |
; |
3 |
= |
− |
и |
4 |
= . |
|||
|
4 |
4 |
|||||||||||||||||
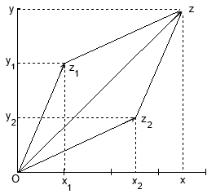
Комплексному числу + можно поставить в соответствие точку плоскости с координатами ( ; ). Таким образом, если раньше мы говорили о вещественной оси, то теперь можем говорить о комплексной плоскости. Комплексные числа образуют векторное пространство, базисом которого являются вещественная единица 1 и мнимая единица , и складываются по правилу сложения векторов (с. 136): если 1 = 1+ 1 и
2 = 2 + 2, то 1 + 2 = ( 1 + 2) + ( 1 + 2) (рис. 25). Также = + .
Для задания точки на плоскости, кроме декартовых прямо-
|
§ 3.4. Комплексные корни многочлена |
139 |
Рис. 25. Сумма комплексных чисел
угольных координат, в математике часто используют и так называемые полярные координаты. Причем в повседневной жизни последние нам гораздо привычней. Действительно, если человек в лесу спросит у вас: «Как пройти в Ольховку?», то что вы ответите? Назовете координаты квадрата, в котором находится село? Нет! Вы скажете, что «это в двух километрах на северо-западе», т. е. укажете направление и расстояние относительно вашего текущего местонахождения. Это и есть полярные координаты. Мы введем их, отталкиваясь от декартовых. Пусть – точка плоскости с кординатами ( ; ) (рис. 26). Проведем из начала коорди-
|
нат в точку радиус-вектор −−→. Пусть радиус-вектор |
|||||
|
– длина |
|||||
|
2 |
+ |
2 |
|||
|
образует с осью угол , а = |−−→|= |
|||||
|
вектора. Направление и расстояние |
образуют пару поляр- |
||||
|
√ |
ных координат ( ; ), задающих положение точки . Для
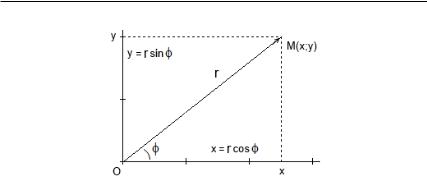
140 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Рис. 26. Тригонометрическое представление комплексного числа
всех точек плоскости, кроме начала координат, имеет место взаимнооднозначное соответствие между парами координат
( ; ) и ( ; ), задаваемое уравнениями
= · cos ;
= · sin .
|
Комплексное |
число можно представить в тригонометри- |
||||
|
ческой форме: |
|||||
|
= + = (cos + · sin ), |
|||||
|
где = | |= |
2 + 2 |
называют модулем, а = ( ) |
|||
|
– |
аргументом |
. Леонард Эйлер расширил область |
|||
|
√числа |
определения элементарных и ряда других функций на комплексную плоскость и установил тождество
= cos + sin ,
которое называют формулой Эйлера. Таким образом, в
теории функций комплексной переменной экспонен-
|
§ 3.4. Комплексные корни многочлена |
141 |
та выражается через тригонометрические функции и наоборот:
Отсюда еще одна форма представления комплексного числа
–экспоненциальная:
= + = (cos + · sin ) = = ln + .
Из формулы Эйлера следует интересное отношение
= −1.
На множестве вещественных чисел мы лишены возможности видеть эти связи, как человек, рассматривающий с берега моря живописные острова, не подозревает, что они всего лишь вершины сложной горной системы подводного царства. На комплексной плоскости «в порядке вещей» многое из того, что категорически запрещено на вещественной оси. Здесь существуют решения уравнений ( ) = 5, 2 = −3
и т. д. Конечно, и теперь мы рассматриваем комплексное число как некую абстракцию, но не в большей мере, чем число «три». Ведь числа «три» также в природе не существует! Естественно возникает вопрос: не придется ли для решения других уравнений, например 4 + 1 = 0, и даль-
142 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
ше расширять понятие «число». Оказывается, на множестве комплексных чисел любой многочлен, как с действительными, так и с комплексными коэффициентами, имеет корни. Однако вернемся к тригонометрической форме. Как найти аргумент и модуль комплексного числа? Если = + ,
√
то = | |= 2 + 2, а аргумет = ( ) можно определить, приняв во внимание, что (0; ), следующим образом (рис. 27):
|
( |
|||||||
|
= |
√ |
), |
если ≥ 0; |
||||
|
2+ 2 |
|||||||
|
, |
< 0. |
||||||
|
(√ 2+ 2 ) |
если |
||||||
|
− |
Рис. 27. Аргумент комплексного числа
202 Пример 4. Преобразовать комплексное число
= 2 + 2 в тригонометрическую форму.

|
§ 3.4. Комплексные корни многочлена |
143 |
||||||||||||||||||||||||||||||||||||||
|
Решение: |
√ |
√ |
√ |
√ |
|||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||
|
Ответ: |
2√2 |
cos ( |
). |
( |
) |
||||||||||||||||||||||||||||||||||
|
+ sin |
4 |
||||||||||||||||||||||||||||||||||||||
|
4 |
2 |
+ |
= 2 2 |
||||||||||||||||||||||||||||||||||||
|
= 2 + 2 = 2 |
2 |
2 |
cos 4 + sin 4 . |
||||||||||||||||||||||||||||||||||||
|
( |
) |
||||||||||||||||||||||||||||||||||||||
|
Пример 5. Преобразовать комплексное число |
202 |
||||||||||||||||||||||||||||||||||||||
|
= 3 + 4 в тригонометрическую форму. |
|||||||||||||||||||||||||||||||||||||||
|
Решение: | |= |
√ |
= 5 = 3 + 4 = 5 53 |
+ 54 |
. |
|||||||||||||||||||||||||||||||||||
|
32 + 42 |
|||||||||||||||||||||||||||||||||||||||
|
Ответ: 5(cos + · sin ), где = 53 . |
( |
) |
|||||||||||||||||||||||||||||||||||||
|
Пример 6. Преобразовать комплексное число = 5 − 7 |
202 |
||||||||||||||||||||||||||||||||||||||
|
в тригонометрическую форму. |
|||||||||||||||||||||||||||||||||||||||
|
Решение: |
√ |
√ |
|||||||||||||||||||||||||||||||||||||
|
√ |
5 |
−7 |
|||||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||
|
74(cos + |
sin ) |
= |
( |
) |
|||||||||||||||||||||||||||||||||||
|
| |= 5 + 7 = |
74 = 5 |
− 7 = |
74 √74 + √74 . |
||||||||||||||||||||||||||||||||||||
|
Ответ: |
√ |
· |
, где |
− |
5 |
. |
|||||||||||||||||||||||||||||||||
|
√ |
|||||||||||||||||||||||||||||||||||||||
|
74 |
|||||||||||||||||||||||||||||||||||||||
|
Операции сложения и вычитания комплексных чисел подчи- |
|||||||||||||||||||||||||||||||||||||||
|
няются правилу сложения и вычитания векторов (рис. 25). |
|||||||||||||||||||||||||||||||||||||||
|
Но формулы умножения и деления комплексных чисел вы- |
|||||||||||||||||||||||||||||||||||||||
|
глядят сложновато (с. 136). |
|||||||||||||||||||||||||||||||||||||||
|
Попробуем теперь выполнить эти операции с числами в три- |
|||||||||||||||||||||||||||||||||||||||
|
гонометрическом представлении. Пусть |
|||||||||||||||||||||||||||||||||||||||
|
1 = 1(cos + · sin ), |
2 |
= 2(cos + · sin ). |
Тогда 1 2 = 1 2(cos + · sin )(cos + · sin ) =
=1 2[(cos cos − sin sin )(cos sin + sin cos )] =
=| 1|| 2|(cos( + ) + sin( + )).

144 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются (рис. 28).
Рис. 28. Умножение комплексных чисел
Аналогично
|
1 |
= |
1 |
(cos + · sin ) |
= |
1 |
(cos + · sin )(cos − · sin ) |
= |
||||||||
|
2 |
2 |
(cos + · sin ) |
2 |
(cos + · sin )(cos − · sin ) |
|||||||||||
|
= |
| 1 |
| |
[cos( |
− |
) + sin( |
− |
)]. |
||||||||
|
| 2 |
| |
||||||||||||||
Следовательно,
| 1 2|= | 1|| 2|, ( 1 2) = ( 1) + ( 2),
|
2 |
= |
| 2 |
|, |
( 2 ) |
= ( 1) − ( 2). |
|||||
|
1 |
1 |
| |
1 |
|||||||
|
| |
||||||||||
В частности,
1
cos + · sin = cos − · sin .

|
§ 3.4. Комплексные корни многочлена |
145 |
Поскольку целая степень числа означает многократное произведение,
= [ (cos + · sin )] = (cos + · sin ).
Последнее тождество известно как формула Муавра. Отрицательная степень
− = [ (cos + · sin )]− = 1 (cos − · sin ).
|
Пример 7. Найти девятую степень числа cos + sin . |
202 |
||||||||||||||
|
Решение: |
6 |
6 |
|||||||||||||
|
9 |
|||||||||||||||
|
(cos |
+ sin |
) |
= cos |
9 |
+ sin |
9 |
= cos |
3 |
+ sin |
3 |
= − . |
||||
|
6 |
6 |
6 |
6 |
2 |
2 |
Ответ: − .
Пусть = (cos + · sin ) и требуется найти все решения
уравнения = (cos + · sin ).
(cos + sin ) = (cos( + 2 ) + · sin( + 2 ))
|
+ 2 |
||||||||||||
|
= , = + 2 |
= |
√ , = |
||||||||||
|
, |
||||||||||||
|
где k=0,1,. . . , n-1. Следовательно, |
). |
|||||||||||
|
0,1,··· −1 |
= √ (cos |
+ · sin |
||||||||||
|
+ 2 |
+ 2 |
146 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
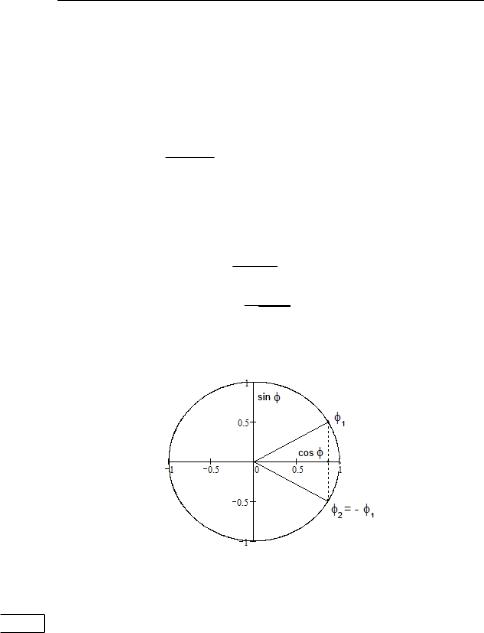
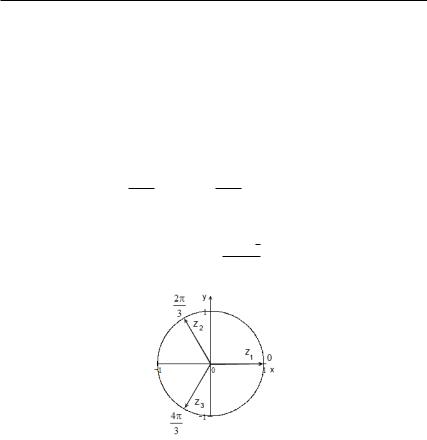
Если принимает значения 0, 1, . . . −1, то – принимает различных значений. В следующем параграфе нам понадобятся все кубические корни из 1, т. е. все решения уравнения
= 1. Представим вещественную единицу в тригонометрической форме: = cos 2 + · sin 2 . Тогда
= cos 23 + · sin 23 , где = 0, 1, 2.
Кубические корни из единицы показаны на диаграмме (рис. 29).
√
Таким образом, 1 = 1, 2,3 = −1±2 3 .
Рис. 29. Кубические корни единицы
|
202 |
Пример 8. |
Решить уравнение 3 |
= 5 + · 5. |
|||||||||||||||||
|
Решение: |
||||||||||||||||||||
|
√ |
√ |
|||||||||||||||||||
|
3 = 5√ |
( |
) |
= 5√ |
(cos |
+ 2 |
+ 2 |
), |
|||||||||||||
|
2 |
+ |
2 |
4 |
+ · sin |
4 |
|||||||||||||||
|
2 |
2 |
|||||||||||||||||||
|
2 |
2 |
3 |
3 |
где = 0, 1, 2. Подставляя поочередно в правую часть ра-
венства значения , получим
|
§ 3.4. Комплексные корни многочлена |
147 |
||||||||||||||||||||||||||||||||||
|
Ответ: |
|||||||||||||||||||||||||||||||||||
|
√3 |
|||||||||||||||||||||||||||||||||||
|
20 |
|||||||||||||||||||||||||||||||||||
|
1 = √6 50 |
(cos |
+ · sin |
) |
= |
[1 +3 |
√3 + · (−1 + √3)]; |
|||||||||||||||||||||||||||||
|
12 |
12 |
4 |
|||||||||||||||||||||||||||||||||
|
2 |
= √6 |
(cos 34 |
+ · sin |
4 |
) = |
2 (−1 + ) ; |
|||||||||||||||||||||||||||||
|
50 |
|||||||||||||||||||||||||||||||||||
|
3 |
√20 |
||||||||||||||||||||||||||||||||||
|
√3 |
|||||||||||||||||||||||||||||||||||
|
20 |
|||||||||||||||||||||||||||||||||||
|
3 = √6 50 |
(cos |
+ · sin |
) |
= |
[1 − |
√3 + · (−1 − √3)]. |
|||||||||||||||||||||||||||||
|
12 |
12 |
4 |
Прежде чем перейти к следующему вопросу, коротко коснемся проблемы графического представления многочлена, определенного на комплексной плоскости. Пусть дан многочлен с вещественными коэффициентами ( ) = 3 + 2 + +1
от комплексной переменной = + . Его график для действительных значений , т. е. для = , изображен на рис. 30г. Как видно на графике, многочлен имеет один вещественный корень = −1. Теперь рассмотрим комплексные значения = + . В таком случае и ( ) – комплексное число. Для построения графика функции, отображающей комплексную плоскость на комплексную плоскость, нам пришлось бы выйти в четырехмерное пространство, но мы поступим проще, рассмотрев отдельно графики [ ( )]
и [ ( )], т. е. графики действительной и мнимой частей функции ( ). Каждый график – это поверхность в трехмерном пространстве, а поверхность можно задать линиями уровня, как на географической карте. Такой график мы уже видели на рис. 13а (с. 73). График вещественной части
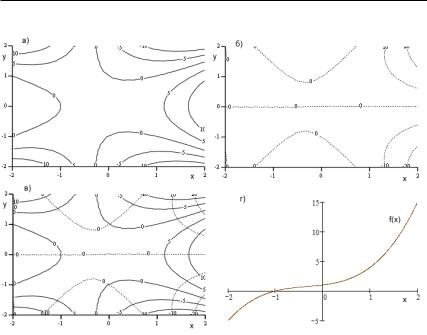
148 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Рис. 30. Графики многочлена 3 + 2 + + 1
( ) показан на рис. 30а, комплексной – на рис. 30б. Обратите внимание на нулевые линии уровня. На рис. 30б одна из таких линий задана уравнением = 0, поскольку действительным значениям соответствуют действительные значения функции. Корнями многочлена будут те значения , для которых одновременно [ ( )] = 0 и [ ( )] = 0, т. е. точки пересечения нулевых линий уровня, представленных на рис. 30а и 30б. На рис. 30в мы разместили оба графика на одной комплексной плоскости. Сплошные линии уровня соответствуют действительной, а пунктирные – комплексной
Решение уравнений с комплексными числами
Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.
Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = <0, 1, 2, 3, …n-1 >.
Пример 1. Найти все корни уравнения

Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:


Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = <0, 1, 2, 3>. Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:


Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:
Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.
Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:


Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.
Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.
После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.
Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.
Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.
Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.
Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.
Квадратное уравнение с комплексными корнями
Вы будете перенаправлены на Автор24
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Двучленным называется уравнение вида $x^ =A$.
Рассмотрим три случая:
Решить уравнение: $x^ <3>=8$.
Так как $A>0$, то $x_ =sqrt[<3>] <8>cdot left(cos frac<2kpi > <3>+icdot sin frac<2kpi > <3>right),, , , k=0. 2$.
При $k=0$ получаем $x_ <0>=sqrt[<3>] <8>cdot left(cos 0+icdot sin 0right)=sqrt[<3>] <8>=2$.
При $k=1$ получаем
[x_ <1>=sqrt[<3>] <8>cdot left(cos frac<2pi > <3>+icdot sin frac<2pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=-1+sqrt <3>cdot i.]
При $k=2$ получаем
[x_ <2>=sqrt[<3>] <8>cdot left(cos frac<4pi > <3>+icdot sin frac<4pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=-1-sqrt <3>cdot i.]
Решить уравнение: $x^ <3>=1+i$.
Готовые работы на аналогичную тему
Так как $A$ – комплексное число, то
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа:
[varphi =arg z=arctgfrac<1> <1>=arctg1=frac<pi > <4>]
Подставим полученные значения и получим:
Уравнение перепишем в виде:
При $k=0$ получаем $x_ <0>=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi /4> <3>+icdot sin frac<pi /4> <3>right)=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)=sqrt[<6>] <2>cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)$.
При $k=1$ получаем
При $k=2$ получаем
Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.
[D=2^ <2>-4cdot 1cdot 5=4-20=-16.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
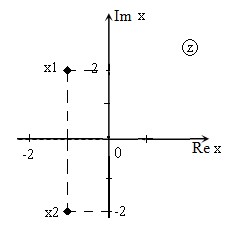
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.
Зная корни уравнения $x_ <1,2>=1pm 2i$, записать исходное уравнение.
Запишем уравнение следующим образом:
[x^ <2>-(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ <2>-x+2icdot x-x-2icdot x+1-4i^ <2>=0] [x^ <2>-2x+1+4=0] [x^ <2>-2x+5=0]
Следовательно, $x^ <2>-2x+5=0$ – искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Решить уравнение: $z^ <2>+(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.
Так как $D>0$, уравнение имеет два корня:
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
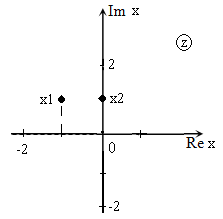
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 11 2021
![]()
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!
Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:


Выполним проверку того, что эти корни и права оказываются решением уравнения:


Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде:  .
.
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:
 ,
,  ,
,
 ,
,
 ,
,

В каждом случае получаем 2 сопряженных комплексных корня.
Решим квадратное уравнение  .
.
Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

 – сопряженные комплексные корни
– сопряженные комплексные корни
Т.о., у уравнения  есть 2 сопряженных комплексных корня:
есть 2 сопряженных комплексных корня:
 ,
,

Теперь можно решить любое квадратное уравнение!
У любого уравнения с многочленом n-ой степени  есть ровно n корней, некоторые из них могут быть комплексными.
есть ровно n корней, некоторые из них могут быть комплексными.
Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение z n = w, либо, записав в другом виде:  . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.
. Здесь n может принимать всякое натуральное значение, которое больше 1-цы.
В частности, при n = 2 получаем квадратный корень  .
.
У уравнения типа  есть ровно n корней z0, z1, z2, … zn-1, которые можно вычислить с помощью формулы:
есть ровно n корней z0, z1, z2, … zn-1, которые можно вычислить с помощью формулы:
 ,
,
где  – это модуль комплексного числа w,
– это модуль комплексного числа w,
φ – его аргумент,
а параметр k принимает значения:  .
.
Найдем корни уравнения:  .
.
Перепишем уравнение как:  .
.
В этом примере  ,
,  , поэтому у уравнения будет 2 корня: z0 и z1. Детализируем общую формулу:
, поэтому у уравнения будет 2 корня: z0 и z1. Детализируем общую формулу:
 ,
,  .
.
Далее найдем модуль и аргумент комплексного числа  :
:

Число w находится в 1-ой четверти, значит:

Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.
Детализируем еще немного общую формулу:
 ,
,  .
.
Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.
Подставляем в формулу значение k = 0 и получаем 1-й корень:
 .
.
Подставляем в формулу значение k = 1 и получаем 2-й корень:
 .
.
Ответ:  ,
, 
Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.
Часто вычисленные корни нужно изобразить геометрически:

Как выполнить чертеж?
Для начала на калькуляторе вычисляем, чему равен модуль корней  и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.
и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.
Далее берем аргумент 1-го корня  и вычисляем, чему равен угол в градусах:
и вычисляем, чему равен угол в градусах:
 .
.
Отмеряем транспортиром 45° и ставим на чертеже точку z0.
Берем аргумент 2-го корня  и переводим его тоже в градусы:
и переводим его тоже в градусы:  . Отмеряем транспортиром 165° и ставим на чертеже точку z1.
. Отмеряем транспортиром 165° и ставим на чертеже точку z1.
По этому же алгоритму ставим точку z2.
Видно, что корни располагаются геометрически правильно с интервалом  между радиус-векторами. Чертеж обязательно делать при помощи транспортира.
между радиус-векторами. Чертеж обязательно делать при помощи транспортира.
[spoiler title=”источники:”]
http://spravochnick.ru/matematika/kompleksnye_chisla_i_mnogochleny/kvadratnoe_uravnenie_s_kompleksnymi_kornyami/
http://www.calc.ru/Chisla-Izvlecheniye-Korney-Iz-Kompleksnykh-Chisel-Kvadratnoy.html
[/spoiler]
Комплексные корни
Решение уравнений
При решении многих задач в математике, физике, электротехнике часто возникает необходимость в решении уравнений с комплексными корнями, извлечении корней из комплексных чисел.
Пусть дано комплексное число z, из которого надо извлечь корень n. Для этого находим модуль |z| и аргумент (ф) комплексного числа.
Корень числа находим по формуле: ![]()
Результатом решения квадратных уравнений вида ах2 + by + с = 0 с комплексными коэффициентами являются комплексные корни 2-го порядка.
Для решения квадратного трехчлена необходимо вычислить дискриминант (D):
D = b2 — 4ac, затем найти корни, которые зависят от знака D. Квадратное уравнение имеет 2 корня.
- если D больше 0, уравнение имеет 2 вещественных корня;
- при D = 0 у уравнения 1 корень х = -b / 2а;
- при D меньше 0 — 2 мнимых корня (вещественных корней нет).
Общая формула: 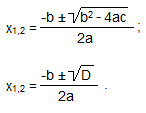
Любое уравнение вида ![]() имеет п комплексных корней. Часть из них, возможно и все, — действительные.
имеет п комплексных корней. Часть из них, возможно и все, — действительные.
Существует универсальный способ извлечения корней из любого комплексного числа.
Пусть дано уравнение ![]() , где w — комплексное число. Найти все n корней уравнения (z0, z1, z2, …z n-1) можно по формуле:
, где w — комплексное число. Найти все n корней уравнения (z0, z1, z2, …z n-1) можно по формуле: ![]()
|w| — модуль комплексного числа w, ф — его аргумент, k = 0, 1, 2, …n-1
С помощью онлайн калькулятора вы сможете быстро вычислять комплексные корни заданного многочлена.
