Что такое активное сопротивление катушки
Содержание
- 1 Катушка
- 2 Конструкция и разновидности
- 3 Принцип работы
- 4 Индуктивность
- 5 Активное сопротивление
- 6 Постоянный ток
- 7 Переменный ток
- 8 Замер сопротивления и формула расчета
- 9 Заключение
- 10 Видео по теме
Одной из наиболее важных радиотехнических деталей является катушка индуктивности. Статья раскроет тему, что такое активное сопротивление катушки. Также будет дана информация о назначении и принципе действия этого элемента, приведена формула расчета сопротивления.
Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.

Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.

Независимо от конструкции, все катушки работают по одному и тому же принципу.
Принцип работы
Катушка индуктивности работает только при прохождении электрического тока через набор витков обмотки. При подключении элемента к электрической цепи, по витку начинает двигаться ток. За счет взаимодействия провода с металлическим сердечником создается магнитный поток. Поток полностью пропорционален индуктивности катушки и величине тока. Величину магнитного потока можно рассчитать по следующей формуле: Ф=L×I.
Элементами формулы являются:
- «Ф» — величина магнитного потока.
- «L» — индукция.
- «I» — величина тока.

Количество витков влияет на величину ЭДС самоиндукции. Витки взаимодействуют не только с сердечником, но и между собой, что приводит к увеличению ЭДС.
В цепи переменного напряжения, величина ЭДС способна спровоцировать разность фаз напряжения и тока вплоть до 90 градусов.
Индуктивность
Индуктивностью катушки является способность к накапливанию электричества. Этот параметр зависит от:
- Числа витков.
- Сечения и длины провода.
- Конструктивных особенностей детали.
- От материала, длины, диаметра и формы сердечника.
- От расстояния между витками.
- Наличия экрана.
В радиоэлектронике не принято указывать значение индуктивности. Производители маркируют детали числом витков и указывают тип сердечника.
Активное сопротивление
Катушка индуктивности, не подключенная к электрической цепи, имеет только активное сопротивление.

Оно создается медным проводом и зависит от его длины, сечения. Активное сопротивление способно нарастать только после подключения в цепь. В этом случае процессы, протекающие внутри элемента, зависят от типа тока.
Постоянный ток
В подключенной к постоянному току катушке индуктивности создается магнитное поле. Его величина зависит от числа витков на сердечнике. При этом, ЭДС самоиндукции возникает при движении магнитного потока, который в зависимости от своей силы и скорости, выталкивает часть напряжения на поверхность обмотки.

За счет образования ЭДС, возникает эффект занижения нарастания тока в этой цепи. Ток, имея определенную силу, не способен нарасти мгновенно, так как на него действует сопротивление катушки. Постепенно преодолевая ограничение, ток плавно нарастает и достигает нормальных значений. Скорость такого переходного процесса рассчитывается с использованием следующих значений:
- «L» — индуктивность, генри;
- «R» — сопротивление электрической цепи, ом. Берется значение всей схемы с катушкой;
- «t» — время переходного процесса, сек.
Формула расчета выглядит следующим образом: t=L/R. В этой формуле также используется число витков элемента. Например, t=5×0.7/70=0.05 секунд, где 5 — число витков.
Для катушек индуктивности с первичной и вторичной обмоткой, ЭДС индуктивности протекает немного иным способом. Это различие создается за счет разницы сечений витков. В такой детали ЭДС не препятствует увеличению напряжения, а направляется вместе с прерванным током в одном направлении.
В трансформаторах первичная обмотка создает эффект сильного увеличения напряжения на контактах выхода. Этого удается достичь за счет изменения силы тока на первичной обмотке. Учитывая мгновенно изменение силы тока (одномоментное размыкание), во вторичной обмотке наводится импульс э.д.с амплитудой в десятки киловольт. Примером такого явления является катушка зажигания автомобиля. Ее магнитное поле позволяет достичь напряжения в тысячи вольт, несмотря на то, что сама она работает от аккумулятора с напряжением 12 вольт.
Переменный ток
Переменный ток сильно отличается от постоянного. Поэтому и его влияние на катушку индуктивности так же будет сильно отличаться. Помимо активного сопротивления, катушка подключенная к источнику переменному току, обладает еще и индуктивным.

Активное сопротивление не подключенной в цепь катушки зависит только от марки провода, его длины и сечения. При замере сопротивления отключенной от цепи катушки, тестер покажет только способность самого провода сопротивляться прохождению тока. По своей сути, активное сопротивление этого элемента будет равно 0 + подключенный резистор. При таком соотношении, катушка с ее 0 сопротивлением является идеальной. Для более точного измерения сопротивления в состоянии покоя, важно чтобы деталь была полностью отключена от цепи. При замере на схеме, сопротивление будет увеличено за счет параметров других радиодеталей.

Индуктивное сопротивление возникает только после подключения катушки в цепь переменного тока. Оно зависит от частоты тока и числа витков. Индуктивное сопротивление можно определить, используя простую формулу: XL=2×π×f×L. В данном выражении:
- «XL» — индуктивное сопротивление.
- «π» — число «пи», равное 3.14.
- «f» — частотная характеристика тока.
- «L» — индуктивность.
При прохождении переменного тока по виткам катушки, создается эффект вытеснения магнитными потоками доли токов. Это свойство схоже с влиянием постоянного тока. Главное отличие заложено в боковом вытеснении. Магнитное поле каждого витка оказывает давление на поле последующего витка. Таким образом происходит увеличение активного сопротивления.
Данный эффект увеличивается в зависимости от сечения провода, его проводимости и температуры. Эффект близости, сильно влияющий на увеличение активного сопротивления, снижают за счет подбора сечения обмоточного провода. Снижение эффекта близости недопустимо за счет увеличения расстояния между витками. Такой подход влияет на реактивное сопротивление и мощность магнитного поля.

В итоге активное сопротивление при подключении катушки к источнику переменного тока обладает следующими свойствами:
- Взаимодействует с параметрами индуктивного сопротивления.
- Способно занижать скорость магнитного потока.
- Создает сдвиг фаз напряжения и тока.
- При работе в условиях больших токов, активное сопротивление катушки увеличивает температуру самого компонента и всей цепи в целом. Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.
В электротехнике существует ряд разновидностей экранированных катушек индуктивности. Такие экран часто делают из стали или алюминия. Они необходимы для снижения воздействия магнитного поля на ближайшие элементы схемы. У экранов есть и обратная функция. С помощью них катушка защищает себя от воздействия смежных компонентов схемы. Таким образом производители могут уменьшить определенную часть помех. Воздействие магнитного поля неэкранированной катушки можно услышать, например, если поднести элемент к включенному радиоприемнику. У экрана есть и один существенный недостаток. Он сильно увеличивает активное сопротивление самой детали.
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.
- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.
- Прибор покажет только активное сопротивление обмотки.

При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
Z= 2×(R×R+XL×XL)
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Заключение
Расчет активного сопротивления катушки несет в себе большую практическую пользу. Радиолюбители и инженеры могут определить наименьший коэффициент сопротивляемости элемента, что помогает настроить частотные характеристики электронной аппаратуры.
Видео по теме
Для школьников.
В предыдущих статьях рассмотрены цепи переменного тока, содержащие только активное сопротивление и содержащие только емкостное сопротивление.
Сейчас рассмотрим случай, когда в цепи переменного тока находится только катушка индуктивности (индуктивное сопротивление), а активным и емкостным сопротивлениями цепи можно пренебречь.
Начнём с опыта, позволяющего понять, когда появляется и от чего зависит индуктивное сопротивление в цепи переменного тока.
Две маленькие одинаковые электрические лампочки подключались к источникам одинакового напряжения. Но одна (правая) подключалась к источнику постоянного тока (аккумуляторной батарее), а другая (левая) – к источнику переменного тока.
Лампочки светили одинаково, так как количество выделяющегося тепла не зависит от того, какой ток протекает по нитям лампочек (постоянный или переменный).
Затем к лампочкам последовательно подключили катушки индуктивности, сделанные из толстой медной проволоки, содержащей большое число витков. Внутри катушек находятся железные сердечники.
Катушками индуктивности называются катушки, имеющие большую индуктивность и малое активное сопротивление (изготовлены из толстой проволоки). Часто активным сопротивлением такой катушки можно пренебречь.
Опыт показал, что в случае постоянного тока лампочка горит ярко, а в случае переменного тока она светит тускло. Как это объяснить?
В случае постоянного тока лампочка горит ярко, потому что сопротивление катушки мало.
Но почему катушка индуктивности очень сильно ослабляет переменный ток? Продолжаем рассматривать опыт.
Если из катушки (рис. б) постепенно вытягивать железный сердечник, то нить лампочки будет накаляться всё сильнее. При полном вытягивании сердечника лампочка будет светить довольно ярко. Убрав железный сердечник, во много раз уменьшили индуктивность катушки, значит дело в индуктивности.
Так как сила переменного тока быстро меняется, то в катушке возникает ЭДС самоиндукции.
В цепи только с индуктивным сопротивлением приложенное к цепи напряжение в каждый момент времени равно и противоположно ЭДС самоиндукции.
ЭДС самоиндукции по правилу Ленца направлена так, что стремится препятствовать изменению тока, то есть оказывает току сопротивление. Чем больше индуктивность катушки, тем большая ЭДС самоиндукции в ней возникает, тем больше индуктивное сопротивление. Индуктивное сопротивление зависит ещё от частоты тока, чем больше частота, тем больше это сопротивление.
При нарастании тока ЭДС самоиндукции препятствует этому нарастанию, поэтому ток позже достигает максимума, чем в отсутствие самоиндукции.
При убывании тока ЭДС самоиндукции стремится поддерживать ток. Поэтому нулевые значения тока достигаются в более поздний момент, чем в отсутствие самоиндукции.
Таким образом, при наличие индуктивности ток отстаёт по фазе от тока в отсутствие индуктивности, а следовательно, отстаёт по фазе от своего напряжения.
Можно сказать так: из-за явления самоиндукции ток в катушке индуктивности не может меняться скачком и отстаёт от напряжения.
Чем больше частота тока, тем больше будет ЭДС самоиндукции, стремящейся противодействовать изменению тока и тем больше будет сопротивление переменному току.
Индуктивное сопротивление находится по формуле, которая получена теоретически и подтверждена опытом:
Напряжение на индуктивном сопротивлении (индуктивное напряжение) :
Ток в цепи, содержащей только индуктивность, равен отношению напряжения на зажимах источника к индуктивному сопротивлению цепи:
В цепи, содержащей только индуктивное сопротивление, напряжение опережает ток на четверть Т/4 периода (или ток отстаёт от напряжения на четверть периода):
Из рисунка видно, когда ток ещё только проходит через нулевое положение, напряжение уже проходит через максимум, то есть мгновенные значения напряжения и тока меняются согласно уравнениям:
Разность фаз между током и напряжением, равная “пи” пополам, величина отрицательная.
На следующем рисунке показано, как меняются во времени мгновенные значения тока, напряжения и мощности в цепи переменного тока, содержащей только индуктивное сопротивление:
Мгновенные значения мощности находятся через произведение мгновенных значений напряжения и тока, уравнения для которых записаны выше.
Видим, что мгновенная мощность в цепи, обладающей только индуктивностью, изменяется по синусоидальному закону с двойной частотой и имеет равные по модулю положительные и отрицательные значения.
В первую и третью части периода, когда ток в цепи растёт, мощность имеет положительное значение. В эти части периода магнитное поле вокруг электрической цепи усиливается за счёт энергии источника.
Убыванию тока соответствует отрицательное значение мощности. В эти части периода (второй и четвёртый) магнитное поле ослабевает, его энергия идёт обратно к источнику тока.
Таким образом, в цепи, содержащей только катушку индуктивности, происходит периодическая перекачка энергии от источника в энергию магнитного поля катушки индуктивности и возвращение её источнику.
Положительные и отрицательные значения мощности по модулю равны, поэтому средняя мощность за период в такой цепи равна нулю.
Эта мощность не расходуется во внешней части цепи, поэтому называется реактивной индуктивной мощностью:
Она образуется при работе электроприборов (трансформаторов, двигателей, электромагнитов и др., обладающих большой индуктивностью.)
Реактивная мощность в промышленных электрических цепях увеличивает нагрузку на провода и снижает коэффициент мощности цепи, поэтому реактивную нагрузку в электрической цепи на предприятиях снижают (об этом будет сказано в последующих статьях.)
Пример.
Катушка с индуктивностью 0,01 Гн включена в цепь переменного тока напряжением 120 В и частотой 50 Гц. Определить силу тока в катушке, индуктивное напряжение в ней и её реактивную мощность, если активным сопротивлением катушки можно пренебречь.
Используем формулы:
Ответ: 38,2 А; 120 В; 1460 Вт.
Из полученного ответа видим, что всё приложенное к катушке напряжение является индуктивным.
Итак, присутствие индуктивности в цепи переменного тока приводит к сдвигу фаз между током и напряжением в сети (колебания тока отстают от колебаний напряжения).
Емкостная мощность не совершает механической работы, не нагревает проводники.
Катушка индуктивности лишь периодически накапливает энергию магнитного поля и возвращает её обратно источнику тока.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Предыдущая запись : Конденсатор в цепи переменного тока. Емкостное сопротивление.
Следующая запись: Занятие 71. Последовательное соединение сопротивлений. Резонанс напряжений.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58 .
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Главная > Теория > Индуктивное сопротивление
Если подключить катушку индуктивности в цепь электротока переменного типа, то этот ток будет изменяться под влиянием непрерывного изменения электронапряжения. Такие изменения являются генераторами магнитного поля, которое убывает и возрастает периодами. Магнитное поле влияет на катушку, которая создает встречное электронапряжение, что препятствует изменению тока. Соответственно, ток протекает по цепи с постоянным противодействием, которое называется индуктивным сопротивлением.

Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Рассматривая примеры включения катушек в различные цепи мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:

Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление будет равно:
X_L = 2pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давай разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -varepsilon_L = Lfrac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + Lfrac{di}{dt}
Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = frac{X_L}{R}
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Итак, активное сопротивление катушки мы рассмотрели, давайте перейдем к следующему вопросу.
Формулы, зависимости и виды
Такое сопротивление напрямую зависит от значения индуктивности и частоты приложенного электрического напряжения. Поэтому индуктивное сопротивление представляется формулой:
XL=2π*f*L= ωL, где:
- XL – сопротивление индуктивного типа;
- π – математическая постоянная;
- ω – угловая частота (измеряется в радианах в секунду – рад/сек);
- L – индуктивность, которая измеряется в Генри (Гн);
- f – частота напряжения, измеряется в Герцах (Гц).
На заметку. Такая зависимость позволяет вывести из вышеприведенной формулы индуктивность или частоту.

Переменный электроток, проходя через проводниковый элемент, создает вокруг этого элемента переменное электромагнитное поле. Под воздействием этого поля в проводнике возникает электродвижущая сила противоположного направления, которая именуется ЭДС самоиндукцией. Противодействие, которое оказывает переменному электротоку ЭДС, называется реактивным индуктивным сопротивлением.
Следует учесть, что индуктивное сопротивление, зависящее от множества дополнительных факторов, имеет некоторые скрытые зависимости. Например, на нее влияет не только сила электротока в собственном проводниковом компоненте, но и в соседствующих проводах. Если увеличится расстояние между фазными проводами, то увеличится и сопротивление с одновременным снижением степени воздействия соседних проводов (в простейшей цепи такое явление можно продемонстрировать добавлением в цепь к катушке резисторов).
Во многих сферах энергетики применяется такое понятие, как индуктивное погонное сопротивление. Формула сопротивления такого вида выглядит следующим образом:
X0 = ω*(4,61g* (Dср/R) + 0,5μ)*10-4, где:
- ω – угловая частота;
- μ – магнитная проницаемость;
- Dср – среднее геометрическое расстояние между фазами ЛЭП;
- R – радиус провода.

Важно! Индуктивное погонное сопротивление полностью зависит от радиуса проводника в проводе, а не от его общего сечения. Когда такой радиус увеличивается, данная величина уменьшается.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину накопленной энергии катушки индуктивности:
W = frac{LI^2}{2}
Давайте переходить к вариантам соединения катушек между собой… Все расчеты мы будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0 и его необходимо учитывать при проведении любых расчетов.
Принцип работы катушки зажигания
Катушку зажигания на простом языке можно назвать обычным повышающим напряжение трансформатором. Её задача преобразовать низковольтное напряжение (6-15В) в высокое (20-30кВ). Она, как и трансформатор, состоит из двух обмоток — первичной и вторичной. Первичная низковольтная катушка состоит из небольшого количества витков, а вторичная из большего.
Но есть ещё один нюанс. Витки в катушке расположены определённым образом, что позволяет катушке, кроме индуктивности, иметь ещё и ёмкость. То есть, своего рода — колебательный контур.

При подаче тока в первичную обмотку в катушке генерируется магнитное поле. Наведенное напряжение генерируется в катушке путем самоиндукции. В момент воспламенения ток в катушке прерывается выходным каскадом (в старых системах — контактами прерывателя). Мгновенно сворачивающееся магнитное поле генерирует высокое индукционное напряжение в первичной обмотке. Оно трансформируется на вторичной обмотке катушки и преобразуется в соотношении — количество витков вторичной обмотки отнесенное к количеству витков первичной обмотки. В свече зажигания происходит высоковольтный разряд с ионизацией искрового промежутка и прохождением тока. Это продолжается, пока накопленная энергия не будет истрачена.
Эти все физические явления, наверное, мало кому интересны, поэтому давайте отвлечёмся и посчитаем, на мой взгляд, интересные факты. Сколько раз свеча зажигания «производит» искру за свой срок службы?
Количество искрообразований = «об/мин» умножить на «количество цилиндров» и всё это разделить на 2. Возьмём обычный 4-цилиндровый 4-тактный двигатель. Допустим, обороты двигателя составляют 3000 об/мин. Значит количество искрообразований = 3000 х 4/2 = 6000 искр / мин!
Свечи я меняю раз в 30000 км.
Если пройденное расстояние составляет 30 000 км со средней частотой вращения коленчатого вала двигателя 3000 об/мин при средней скорости 60 км/ч, то количество искрообразований составляет 45 000 000 на каждую свечу зажигания! Во как трудится катушка зажигания! Как Золушка, прям
Поэтому катушка зажигания вполне заслуженно может когда-нибудь устать и молча выйти из строя.
Последовательное соединение катушек индуктивности.

При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде бы все просто, проще некуда, но тут есть один важный момент. Данная формула справедлива только в том случае, если катушки расположены на на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:

Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация совсем другая. Возможно два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек — начало второй катушки подключается к концу первой. А второй вариант называют встречным включением — конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом «*«. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M — взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2medspace-medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу — уменьшается на ту же самую величину.
СОДЕРЖАНИЕ
В зависимости от назначения катушки индуктивности различают:
— контурные катушки (образующие совместно с конденсаторами колебательный контур);
— катушки связи (передающие высокочастотные колебания из одной цепи в другую);
— высокочастотные дроссели (катушки индуктивности, преграждающие путь токам высокой частоты).
По конструктивным признакам катушки могут быть разделены на цилиндрические, спиральные, тороидальные, однослойные, многослойные, с сердечником или без сердечника, экранированные, с постоянной или переменной индуктивностью.
На принципиальных электрических схемах рядом с условным графическим изображением катушки индуктивности помещают ее символическое буквенное обозначение (латинская прописная буква L) с порядковым цифровым (иногда буквенным) индексом. Значение индуктивности на схеме обычно не указывают (рис. 4.1).
| Катушка индуктивности | Катушка индуктивности с отводами | Катушки индуктивности с магнитопроводом (L6 — с медным) |
| Катушка индуктивности экранированная | Ферровариометр | Индуктивно связанные катушки (ВЧ трансформатор) |
Рис. 4.1. Обозначения катушек индуктивности на схемах
Дроссели имеют такое же графическое изображение, но обозначаются буквами Др.
Параллельное соединение катушек индуктивности.

При параллельном соединении катушек индуктивности также возможны три варианта:
- Магнитное поле одной катушки не пересекает витков второй катушки, тогда: frac{1}{L_0} = frac{1}{L_1} +frac{1}{L_2} или L_0 = frac{L_1L_2}{L_1 + L_2}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены согласно (как изображено на рисунке — то есть начала обеих катушек подключены к одному узлу). В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2medspace-medspace 2M}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены встречно. В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом мы и заканчиваем рассмотрение катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающие все эти элементы в разных комбинациях
Понятие импеданса используется в разных сферах науки. Существуют разные его формы: гидродинамический, артериальный (медицинский термин, состоит из статического и кинетического компонентов), используемый при измерении гидростатического давления. Есть и электрический импеданс, описывающий полное сопротивление цепного фрагмента. Электрику необходимо знать, от чего зависит и как вычисляется эта величина в однофазных и трехфазных цепях с трансформаторами тока и иными компонентами.
Импеданс описывает сопротивление всей цепи
Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.

Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
От чего зависит индуктивное сопротивление
Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.
Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.
Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.
Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.
На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.
Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.

Независимо от конструкции, все катушки работают по одному и тому же принципу.
Комбинирование импедансов
Основная статья: Последовательные и параллельные схемы
Общий импеданс многих простых сетей компонентов может быть рассчитан с использованием правил объединения импедансов последовательно и параллельно. Правила идентичны правилам комбинирования сопротивлений, за исключением того, что в целом числа сложные числа. Однако общий случай требует эквивалентные преобразования импеданса в дополнение к последовательному и параллельному.
Комбинация серий
Для компонентов, соединенных последовательно, ток через каждый элемент схемы одинаков; полный импеданс — это сумма импедансов компонентов.
Z экв = Z 1 + Z 2 + ⋯ + Z п { displaystyle Z _ { text {eq}} = Z_ {1} + Z_ {2} + cdots + Z_ {n} quad}
Или явно в реальном и воображаемом выражении:
Z экв = р + j Икс = ( р 1 + р 2 + ⋯ + р п ) + j ( Икс 1 + Икс 2 + ⋯ + Икс п ) { displaystyle Z _ { text {eq}} = R + jX = (R_ {1} + R_ {2} + cdots + R_ {n}) + j (X_ {1} + X_ {2} + cdots + X_ {n}) quad}
Параллельная комбинация
Для компонентов, соединенных параллельно, напряжение на каждом элементе схемы одинаковое; отношение токов через любые два элемента является обратной величиной их импедансов.
Следовательно, обратный полный импеданс является суммой обратных импедансов компонентов:
1 Z экв = 1 Z 1 + 1 Z 2 + ⋯ + 1 Z п { displaystyle { frac {1} {Z _ { text {eq}}}} = { frac {1} {Z_ {1}}} + { frac {1} {Z_ {2}}} + cdots + { frac {1} {Z_ {n}}}}
или, когда n = 2:
1 Z экв = 1 Z 1 + 1 Z 2 = Z 1 + Z 2 Z 1 Z 2 { displaystyle { frac {1} {Z _ { text {eq}}}} = { frac {1} {Z_ {1}}} + { frac {1} {Z_ {2}}} = { frac {Z_ {1} + Z_ {2}} {Z_ {1} Z_ {2}}}} Z экв = Z 1 Z 2 Z 1 + Z 2 { displaystyle Z _ { text {eq}} = { frac {Z_ {1} Z_ {2}} {Z_ {1} + Z_ {2}}}}
Эквивалентный импеданс Z экв { displaystyle Z _ { text {eq}}} можно рассчитать с точки зрения эквивалентного последовательного сопротивления р экв { displaystyle R _ { text {eq}}} и реактивное сопротивление Икс экв { displaystyle X _ { text {eq}}} .[11]
Z экв = р экв + j Икс экв р экв = ( Икс 1 р 2 + Икс 2 р 1 ) ( Икс 1 + Икс 2 ) + ( р 1 р 2 − Икс 1 Икс 2 ) ( р 1 + р 2 ) ( р 1 + р 2 ) 2 + ( Икс 1 + Икс 2 ) 2 Икс экв = ( Икс 1 р 2 + Икс 2 р 1 ) ( р 1 + р 2 ) − ( р 1 р 2 − Икс 1 Икс 2 ) ( Икс 1 + Икс 2 ) ( р 1 + р 2 ) 2 + ( Икс 1 + Икс 2 ) 2 { displaystyle { begin {align} Z _ { text {eq}} & = R _ { text {eq}} + jX _ { text {eq}} R _ { text {eq}} & = { гидроразрыв {(X_ {1} R_ {2} + X_ {2} R_ {1}) (X_ {1} + X_ {2}) + (R_ {1} R_ {2} -X_ {1} X_ {2 }) (R_ {1} + R_ {2})} {(R_ {1} + R_ {2}) ^ {2} + (X_ {1} + X_ {2}) ^ {2}}} X _ { text {eq}} & = { frac {(X_ {1} R_ {2} + X_ {2} R_ {1}) (R_ {1} + R_ {2}) — (R_ {1} R_ {2} -X_ {1} X_ {2}) (X_ {1} + X_ {2})} {(R_ {1} + R_ {2}) ^ {2} + (X_ {1} + X_ {2}) ^ {2}}} end {align}}}
Принцип работы
Катушка индуктивности работает только при прохождении электрического тока через набор витков обмотки. При подключении элемента к электрической цепи, по витку начинает двигаться ток. За счет взаимодействия провода с металлическим сердечником создается магнитный поток. Поток полностью пропорционален индуктивности катушки и величине тока. Величину магнитного потока можно рассчитать по следующей формуле: Ф=L×I.
Элементами формулы являются:
- «Ф» — величина магнитного потока.
- «L» — индукция.
- «I» — величина тока.

Количество витков влияет на величину ЭДС самоиндукции. Витки взаимодействуют не только с сердечником, но и между собой, что приводит к увеличению ЭДС.
В цепи переменного напряжения, величина ЭДС способна спровоцировать разность фаз напряжения и тока вплоть до 90 градусов.
Какие отличия
Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть. Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть
То есть, в окружающую среду полученная энергия не передается
Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.

Индуктивность
Индуктивностью катушки является способность к накапливанию электричества. Этот параметр зависит от:
- Числа витков.
- Сечения и длины провода.
- Конструктивных особенностей детали.
- От материала, длины, диаметра и формы сердечника.
- От расстояния между витками.
- Наличия экрана.
В радиоэлектронике не принято указывать значение индуктивности. Производители маркируют детали числом витков и указывают тип сердечника.
Активное сопротивление
Катушка индуктивности, не подключенная к электрической цепи, имеет только активное сопротивление.

Оно создается медным проводом и зависит от его длины, сечения. Активное сопротивление способно нарастать только после подключения в цепь. В этом случае процессы, протекающие внутри элемента, зависят от типа тока.
использованная литература
- Каллегаро, стр. 2
- Каллегаро, сек. 1.6
- Наука
, п. 18, 1888 г. - Оливер Хевисайд, Электрик
, п. 212, 23 июля 1886 г., перепечатано как
Электротехнические статьи, Том II
, стр. 64, Книжный магазин AMS, ISBN 0-8218-3465-7 - Кеннелли, Артур. Импеданс
(AIEE, 1893 г.) - Александр, Чарльз; Садику, Мэтью (2006). Основы электрических схем
(3, перераб.). Макгроу-Хилл. С. 387–389. ISBN 978-0-07-330115-0 . - Комплексный импеданс, Гиперфизика
- Горовиц, Пол; Хилл, Уинфилд (1989). «1». Искусство электроники
. Издательство Кембриджского университета. стр.31–32. ISBN 978-0-521-37095-0 . - Закон Ома переменного тока, Гиперфизика
- Горовиц, Пол; Хилл, Уинфилд (1989). «1». Искусство электроники
. Издательство Кембриджского университета. стр.32–33. ISBN 978-0-521-37095-0 . - Выражения параллельного импеданса, Гиперфизика
- ^ аб
Джордж Льюис-младший; Джордж К. Льюис старший и Уильям Ольбрихт (август 2008 г.). «Экономичная широкополосная схема измерения электрического импеданса и анализ сигналов для пьезоматериалов и ультразвуковых преобразователей».
Измерительная наука и технология
.
19
(10): 105102. Bibcode:2008MeScT..19j5102L. Дои:10.1088/0957-0233/19/10/105102. ЧВК 2600501. PMID 19081773.
Постоянный ток
В подключенной к постоянному току катушке индуктивности создается магнитное поле. Его величина зависит от числа витков на сердечнике. При этом, ЭДС самоиндукции возникает при движении магнитного потока, который в зависимости от своей силы и скорости, выталкивает часть напряжения на поверхность обмотки.

За счет образования ЭДС, возникает эффект занижения нарастания тока в этой цепи. Ток, имея определенную силу, не способен нарасти мгновенно, так как на него действует сопротивление катушки. Постепенно преодолевая ограничение, ток плавно нарастает и достигает нормальных значений. Скорость такого переходного процесса рассчитывается с использованием следующих значений:
- «L» — индуктивность, генри;
- «R» — сопротивление электрической цепи, ом. Берется значение всей схемы с катушкой;
- «t» — время переходного процесса, сек.
Формула расчета выглядит следующим образом: t=L/R. В этой формуле также используется число витков элемента. Например, t=5×0.7/70=0.05 секунд, где 5 — число витков.
Для катушек индуктивности с первичной и вторичной обмоткой, ЭДС индуктивности протекает немного иным способом. Это различие создается за счет разницы сечений витков. В такой детали ЭДС не препятствует увеличению напряжения, а направляется вместе с прерванным током в одном направлении.
В трансформаторах первичная обмотка создает эффект сильного увеличения напряжения на контактах выхода. Этого удается достичь за счет изменения силы тока на первичной обмотке. Учитывая мгновенно изменение силы тока (одномоментное размыкание), во вторичной обмотке наводится импульс э.д.с амплитудой в десятки киловольт. Примером такого явления является катушка зажигания автомобиля. Ее магнитное поле позволяет достичь напряжения в тысячи вольт, несмотря на то, что сама она работает от аккумулятора с напряжением 12 вольт.
Какие параметры есть у катушки
От того, где будет применяться индуктивный элемент и на какой частоте работать, зависит его исполнение. Имеются общие параметры:
- L – индуктивность;
- R пот – сопротивление потерь;
- Q – добротность;
- свой резонанс и паразитарная ёмкость;
- коэффициенты ТКИ и ТКД.
Индуктивность (коэффициент самоиндукции) L – это главная электрическая характеристика элемента, которая показывает количество накапливаемой дросселем энергии при передвижении тока. Величина энергии в катушки тем выше, чем больше её индуктивность. Единица измерений L – 1 Гн.
При взаимодействии тока и магнитного поля в обмотке возникают вредные явления. Они способствуют возникновению потерь, которые обозначают R пот. Формула потерь имеет вид:
R пот = rω + rd + rs + re.
Слагаемые формулы – это потери:
- rω – в проводах;
- rd – в диэлектрике;
- rs – в сердечнике;
- re – на вихревые токи.
В результате таких потерь импеданс индуктивного двухполюсника нельзя назвать целиком реактивным.
Добротность двухполюсника определяется по формуле:
Q = ω*L/R пот,
где ω*L = 2π*L – реактивное сопротивление.
При наматывании витков элемента между ними возникает ненужная ёмкость. Из-за этого дроссель превращается в колебательный контур с собственным резонансом.
ТКИ – показатель, описывающий зависимость L от Т0С.
ТКД – показатель, описывающий зависимость добротности от Т0С.
Информация. Изменение основных параметров индуктивного двухполюсника зависит от коэффициентов ТКИ, ТКД, а также от времени и влажности.
Переменный ток
Переменный ток сильно отличается от постоянного. Поэтому и его влияние на катушку индуктивности так же будет сильно отличаться. Помимо активного сопротивления, катушка подключенная к источнику переменному току, обладает еще и индуктивным.

Активное сопротивление не подключенной в цепь катушки зависит только от марки провода, его длины и сечения. При замере сопротивления отключенной от цепи катушки, тестер покажет только способность самого провода сопротивляться прохождению тока. По своей сути, активное сопротивление этого элемента будет равно 0 + подключенный резистор. При таком соотношении, катушка с ее 0 сопротивлением является идеальной. Для более точного измерения сопротивления в состоянии покоя, важно чтобы деталь была полностью отключена от цепи. При замере на схеме, сопротивление будет увеличено за счет параметров других радиодеталей.

Индуктивное сопротивление возникает только после подключения катушки в цепь переменного тока. Оно зависит от частоты тока и числа витков. Индуктивное сопротивление можно определить, используя простую формулу: XL=2×π×f×L. В данном выражении:
- «XL» — индуктивное сопротивление.
- «π» — число «пи», равное 3.14.
- «f» — частотная характеристика тока.
- «L» — индуктивность.
При прохождении переменного тока по виткам катушки, создается эффект вытеснения магнитными потоками доли токов. Это свойство схоже с влиянием постоянного тока. Главное отличие заложено в боковом вытеснении. Магнитное поле каждого витка оказывает давление на поле последующего витка. Таким образом происходит увеличение активного сопротивления.
Данный эффект увеличивается в зависимости от сечения провода, его проводимости и температуры. Эффект близости, сильно влияющий на увеличение активного сопротивления, снижают за счет подбора сечения обмоточного провода. Снижение эффекта близости недопустимо за счет увеличения расстояния между витками. Такой подход влияет на реактивное сопротивление и мощность магнитного поля.

В итоге активное сопротивление при подключении катушки к источнику переменного тока обладает следующими свойствами:
- Взаимодействует с параметрами индуктивного сопротивления.
- Способно занижать скорость магнитного потока.
- Создает сдвиг фаз напряжения и тока.
- При работе в условиях больших токов, активное сопротивление катушки увеличивает температуру самого компонента и всей цепи в целом. Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.
В электротехнике существует ряд разновидностей экранированных катушек индуктивности. Такие экран часто делают из стали или алюминия. Они необходимы для снижения воздействия магнитного поля на ближайшие элементы схемы. У экранов есть и обратная функция. С помощью них катушка защищает себя от воздействия смежных компонентов схемы. Таким образом производители могут уменьшить определенную часть помех. Воздействие магнитного поля неэкранированной катушки можно услышать, например, если поднести элемент к включенному радиоприемнику. У экрана есть и один существенный недостаток. Он сильно увеличивает активное сопротивление самой детали.
Конвертер величин
Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
Здесь
X
L — реактивное сопротивление катушки в омах (Ом),
Z
L — импеданс катушки в омах (Ом),
ω = 2πf
— угловая частота в рад/с,
f
— частота в герцах (Гц),
L
— индуктивность в генри (Гн),
j
— мнимая единица.
Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах.
Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.
Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике
В отличие от конденсаторов, которые препятствуют изменению напряжения
, приложенного к их обкладкам, катушки индуктивности препятствуют изменению
текущего в них тока
. В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.
В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока
. На них создается падение напряжения, прямо пропорциональное
скорости изменения тока
. Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие
реактивного сопротивления
. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.

L индуктивности и текущего через нее тока
I
от частоты
f
для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока
Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Если реальная катушка индуктивности подключена к источнику постоянного напряжения
, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения.
Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля.

/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму
Если к катушке индуктивности приложено переменное синусоидальное напряжение
, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла. В точке (
ωt
=
π
/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке
скорость изменения тока
максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или
π
/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.

Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте
. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности
X
L велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот). При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. С увеличением частоты импеданс катушек уменьшается.
Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.

Автор статьи: Анатолий Золотков
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.
- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.
- Прибор покажет только активное сопротивление обмотки.

При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
Z= 2×(R×R+XL×XL)
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Обобщенный импеданс в s-плоскости
Импеданс определяется как jω
может строго применяться только к цепям, которые управляются установившимся сигналом переменного тока. Понятие импеданса может быть расширено до цепи, запитанной любым произвольным сигналом, с помощью комплексная частота вместо того
jω
. Комплексная частота обозначается символом
s
и, как правило, является комплексным числом. Сигналы выражаются в терминах комплексной частоты с помощью Преобразование Лапласа из область времени выражение сигнала. Импеданс основных элементов схемы в этих более общих обозначениях следующий:
| Элемент | Выражение импеданса |
| Резистор | р { Displaystyle R ,} |
| Индуктор | s L { Displaystyle sL ,} |
| Конденсатор | 1 s C { displaystyle { frac {1} {sC}} ,} |
Для цепи постоянного тока это упрощает s
= 0. Для установившегося синусоидального сигнала переменного тока
s
=
jω
.
Активное сопротивление любого проводника определяется:
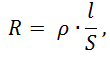
где ρ = 1,7∙10-8 Ом∙м – удельная проводимость материала (в данном случае – меди),
l – длина проводника, м,
S – площадь поперечного сечения проводника, м2.
Определим длину проводника. Для этого рассчитаем длину витка и умножим её на число витков. При этом длина витка будет равна длине окружности:
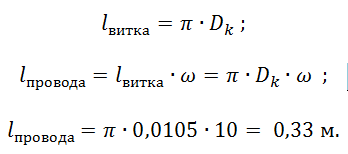
Определим площадь поперечного сечения проводника. В реальности проводник имеет круглое сечение, Maxwell же рассчитывает потери для всей области занятой катушкой, т.е. предполагается, что проводники полностью заполняют область. В случае, если необходим точный расчёт для катушек, намотанных проводом круглого сечения, каждый проводник катушки должен быть прорисован отдельным объектом.
Исходя из вышесказанного, будем условно считать, что катушка намотана проводником прямоугольного сечения. В этом случае площадь поперечного сечения проводника будет определяться:
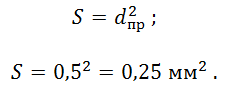
Определим сопротивление обмотки:
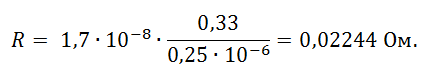
Построим геометрию модели из Примера 1 в 3D. Для этого нажимаем ПКМ на проекте модели 2D примера 1 и выбираем Create 3D Design. После чего модель будет автоматически преобразована в 3D.
1. Создадим сечение для задания возбуждения катушки.
Для этого выделим объект катушки и применим к нему операцию “сечение” (меню Modeler > Surface > Section, выбираем плоскость сечения YZ). Получим объект, состоящий из двух сечений. Для задания возбуждения необходимо одно сечение, поэтому разделим получившийся объект (меню Modeler > Boolean > Separate Bodyes). Второе сечение не нужно, и его можно удалить.
Последнему сечению назначим величину тока, равную 10 ампер-виткам (ПКМ по сечению > Assign Excitation > Current > Value), тип обмотки – распределённая (Stranded).
2. Задание граничных условий.
В 3D постановке задачи в Maxwell по умолчанию действует условие обнуления поля на границах модели. В отличии от 2D постановки задачи открытых границ (условие Balloon) в 3D нет. Поэтому расчётную область иногда приходится увеличивать до тех пор, пока результат расчёта модели не перестанет ощутимо изменяться.
Создадим область для расчёта: Create Region  (Создание региона), в открывшемся окне выберем Pad Individual Direction и по каждой оси отступим 40% от объектов модели:
(Создание региона), в открывшемся окне выберем Pad Individual Direction и по каждой оси отступим 40% от объектов модели:
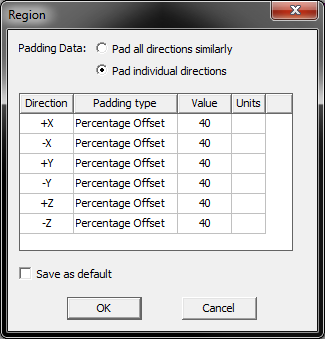
Граничные условия для модели не задаём, т.к. действует граничное условие по умолчанию (присваивается нулевая величина поля на границе расчётной модели).
3. Создание сетки элементов и задания на расчёт.
Далее – создаём сетку конечных элементов, предварительно выделив все объекты модели (Assign Mesh Operation > Inside Selection > Length Based… )
Создаём новое задание на расчёт с параметрами по умолчанию (ПКМ на Analysis > Add Solution Setup)
Запускаем задачу на расчёт.
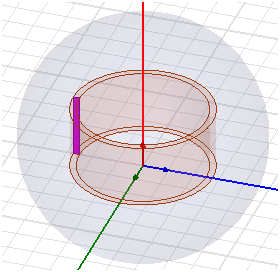
Рисунок П.2.1 – 3D модель рассчитываемой катушки
4. Расчёт омических потерь катушки.
Запустим калькулятор поля (ПКМ на Field Overlays > Calculator…)
В калькуляторе поля (Рисунок П.2.2), необходимо задать следующее выражение:
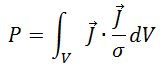
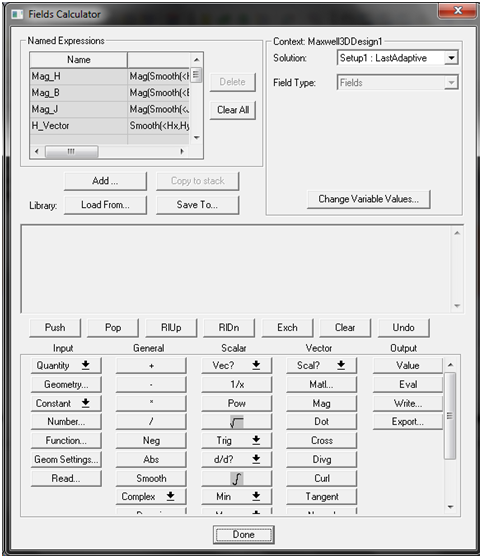
Рисунок П.2.2 – Калькулятор поля Maxwell
где V – объём, в котором рассчитываются потери (обмотка);
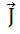 – вектор плотности тока в обмотке;
– вектор плотности тока в обмотке;
σ = 1/ρ = 58∙106 См/м – удельная проводимость материала (в данном случае – меди).
Запишем искомое выражение в калькуляторе поля, набрав следующую последовательность команд:
| Quantity > J | Выбираем вектор плотности тока |
| Push | Дублируем |
| Number > Scalar > Value 58000000 | Вводим величину удельной проводимости меди |
| / | Делим плотность тока на проводимость |
| Dot | Перемножаем |
| Geometry > Volume > Coil | Выбираем объём катушки (вместо Coil выбрать название катушки) |
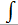 |
Интегрируем выражение по объёму. |
В строке выражений получится:
Scl : Integrate(Volume(Coil), Dot(<Jx,Jy,Jz>, /(<Jx,Jy,Jz>, 58000000)))
Получившееся выражение сохраняем в качестве переменной (Named Expression): PowerLoss (кнопка Add..)
Разделим получившиеся потери на квадрат тока ( I = 1 А ) в проводнике (выбираем PowerLoss в списке переменных > Copy to Stack > Eval > Number > Scalar > 1 > / (операция деления).
Получим результат: R = 0,022687 Ом.
Сравним с теоретическим результатом: R = 0,02244 Ом, погрешность составила: 0,1%.
Примечание: Нельзя забывать, что сечение электропроводящего материала в катушках, намотанных проводником круглого сечения, не будет соответствовать реальному сечению катушки. Поэтому нельзя в модели строить сечение катушек по реальным данным, т.к. это приведёт к уменьшению активного сопротивление катушки. В модели сечение катушки должно совпадать с сечением электропроводящего материала (медь, алюминий). Это сечение можно рассчитать, перемножив сечение провода на число витков в катушке.
Автор материалов: Drakon (С) 2014. Редактор: Админ
