|
V = λ * ν V — скорость λ — длина волны ν — частота |
Скорость волны в физике, теория и онлайн калькуляторы
Скорость волны
Определение скорости волны
Геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение, называют волновой поверхностью или фронтом волны.
Определение
Скорость перемещения фронта волны называется скоростью волны.
Если рассматривается одномерный случай гармонической волны, то уравнение волновой поверхности имеет вид:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Условию (1) в каждый момент времени соответствует только одна точка оси X c координатой, равной:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне вырождается в точку. Из выражения (2) видно, что волновые поверхности с течением времени перемещаются в веществе со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right).]
Для гармонических волн скорость движения поверхности волны совпадает со скоростью распространения волны. Скорость, определенная выражением (3) называют фазовой скоростью.
В случае гармонической волны скорость распространения энергии совпадает с фазовой скоростью волны.
Скорость волны зависима от среды и типа волны. Скорость волны не надо путать со скоростью колебания частиц среды в волне.
Фазовая скорость распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа.
Для определения скорости распространения продольных волн в газе используют формулу:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ – показатель адиабаты; $p$ – давление газа.
Фазовая скорость распространения продольных волн в твердом теле:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ – модуль Юнга вещества стержня.
Фазовая скорость распространения поперечных волн
Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Групповая скорость волн
Для диспергирующих волн помимо фазовой скорости волны следует использовать такое понятие как групповая скорость. Если фазовая скорость зависит от частоты и в среде распространяются волны сложного негармонического характера, то при помощи групповой скорости характеризуют распространение волн.
Групповой скоростью называют скорость движения группы (цуга) волн, которые создают в каждый момент времени локализованный в пространстве волновой пакет. Любая реальная волна является суперпозицией гармонических волн. Скорость с которой такая волна распространяется в веществе, имеющем дисперсию на равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тога фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
Задание: Какова скорость звука в азоте при температуре $T=$300 K? Считайте, что колебательные степени свободы молекул газа не возбуждаются.
Решение: Зная, что звук – продольная волна, за основу решения задачи примем формулу вычисления фазовой скорости продольной волны в газе:
[v=sqrt{frac{gamma p}{rho }}left(1.1right).]
Будем считать азот идеальным газом. Тогда используем уравнение Менделеева – Клапейрона:
[pV=frac{m}{mu }RTleft(1.2right),]
где $mu $ – молярная масса газа. Для азота она равна ${mu }_{N_2}=28cdot {10}^{-3}frac{кг}{моль}$; $R=8,31 frac{Дж}{мольcdot К}$ – универсальная газовая постоянная; $T$ – термодинамическая температура газа. Разделим обе части выражения (1.2) на объем:
[p=frac{rho }{mu }RTleft(1.3right),]
выразим отношение:
[frac{p}{rho }=frac{RT}{mu }left(1.4right),]
подставим полученное отношение в (1.1) скорость звука найдем как:
[v=sqrt{gamma frac{RT}{mu }}left(1.5right),]
где показатель адиабаты для идеального газа с пятью степенями свободы ($i$)молекулы равен:
[gamma =frac{i+2}{i}=frac{7}{5},]
так как молекула двух атомная имеет три степени свободы поступательного движения и две вращательного (рис.1).
Вычислим скорость звука в азоте:
[v=sqrt{frac{7}{5}cdot frac{8,31cdot 300}{28cdot {10}^{-3}}}approx 350 left(frac{м}{с}right).]
Ответ: $v=350frac{м}{с}$
Пример 2
Задание: Какова скорость распространения волны в упругой среде, если разность фаз точек, которые находятся на расстоянии $Delta x,$ равна $Delta varphi $
при частоте колебаний равной $nu $?
Решение: Рассмотрим уравнение одномерной плоской волны:
[s=A{cos left[omega t-kx+varphi right] }left(2.1right).]
где
[k=frac{2pi }{lambda }=frac{omega }{v}left(2.2right).]
Фазы колебаний двух точек в этой волне равны:
[{varphi }_1=omega t-kx_1+varphi ;; {varphi }_2=omega t-kx_2+varphi left(2.3right).]
Найдем их разность:
[Delta varphi =omega t-kx_2+varphi -left(omega t-kx_1+varphi right)=kleft(x_2-x_1right)=frac{omega }{v}Delta xleft(2.4right).]
Выразим циклическую частоту ($omega $) через частоту $nu $:
[omega =2pi nu left(2.5right).]
Выражение (2.4) преобразуем к виду:
[Delta varphi =frac{omega}{v} Delta x=frac{2 pi nu}{v} Delta xleft(2.6right).]
Из (2.6) выразим искомую скорость:
[v=frac{2 pi nu Delta x}{Delta varphi }(frac{м}{с}).]
Ответ: $v=frac{2 pi nu Delta x}{Delta varphi }frac{м}{с}$
Читать дальше: скорость движения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Помимо скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

где
v — скорость волны; T — период колебаний в волне; λ (греческая буква «ламбда») — длина волны.
Выбрав направление распространения волны за направление оси x и обозначив через y координату колеблющихся в волне частиц, можно построить график волны. График синусоидальной волны (при фиксированном времени t) изображен на рисунке 45. Расстояние между соседними гребнями (или впадинами) на этом графике совпадает с длиной волны λ.
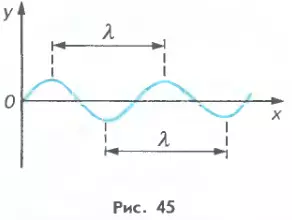
Формула (22.1) выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте, т. е. T = 1/ν, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
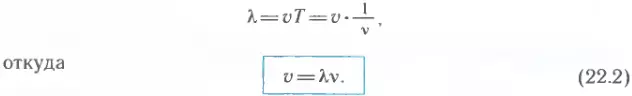
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
1. Что понимают под скоростью волны? 2. Что такое длина волны? 3. Как длина волны связана со скоростью и периодом колебаний в волне? 4. Как длина волны связана со скоростью и частотой колебаний в волне? 5. Какие из следующих характеристик волны изменяются при переходе волны из одной среды в другую: а) частота; б) период; в) скорость; г) длина волны?
Экспериментальное задание. Налейте воду в ванну и посредством ритмичных касаний воды пальцем (или линейкой) создайте на ее поверхности волны. Используя разную частоту колебаний (например, касаясь воды один и два раза в секунду), обратите внимание на расстояние между соседними гребнями волн. При какой частоте колебаний длина волны больше?

Если бросить камень в воду водоема, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.

Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λυTТак как период Т и частота v связаны соотношением T = 1 / v, то скорость волны: υ = λ / Т = λ v
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну: длина волны, скорость волны, период колебаний, частота колебаний.

Единицы измерения в системе СИ:
длина волны [λ] = 1 м скорость распространения волны [ v ] = 1м/с период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц

Абсолютно все в этом мире происходит с какой-либо скоростью. Тела не перемещаются моментально, для этого требуется время. Не являются исключением и волны, в какой бы среде они не распространялись.
Если вы бросите камень в воду озера, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется. Например, если вибрирующий железный лист засунуть концом в воду, то вода покроется рябью маленьких волн, однако скорость их распространения будет меньше, чем в железном листе.

Это несложно проверить даже в домашних условиях. Только не порежьтесь о вибрирующий железный лист. .
Длина волны
None Если зарисовать волну в виде рисунка или графика, то длиной волны будет являться расстояние между любыми ближайшими гребнями либо впадинами волны, либо между любыми другими ближайшими точками волны, находящимися в одинаковой фазе.
Так как длина волны это расстояние, пройденное ею, то и найти эту величину можно, как и любое другое расстояние, умножив скорость прохождения на единицу времени. Таким образом, длина волны связана со скоростью распространения волны прямо пропорционально. Найти длину волны можно по формуле:
λ=vT ,где λ длина волны, v скорость волны, T период колебаний.
А учитывая, что период колебаний обратно пропорционален частоте этих же колебаний: T=1⁄υ, можно вывести связь скорости распространения волны с частотой колебаний:
v=λυ .
[custom_ads_shortcode1]
Частота колебаний в разных средах
Частота колебаний волн не меняется при переходе из одной среды в другую. Так, например, частота вынужденных колебаний совпадает с частотой колебаний источника. Частота колебаний не зависит от свойств среды распространений. При переходе из одной среды в другую меняется лишь длина волны и скорость ее распространения.
Эти формулы справедливы как для поперечных, так и для продольных волн. При распространении продольных волн длина волны будет расстоянием между двумя ближайшими точками с одинаковым растяжением или сжатием. Она также будет совпадать с расстоянием, пройденным волной за один период колебаний, поэтому формулы будут полностью подходить и в этом случае.
[custom_ads_shortcode2]
Нужна помощь в учебе?
Предыдущая тема: Распространение колебаний в среде и волны: продольные и поперечные

Следующая тема: Источники звука и звуковые колебания: что это и как происходит
| Твитнуть | Нравится | Нравится |
Все неприличные комментарии будут удаляться.
Геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение, называют волновой поверхностью или фронтом волны. ОпределениеСкорость перемещения фронта волны называется скоростью волны.

Если рассматривается одномерный случай гармонической волны, то уравнение волновой поверхности имеет вид:
[Ф_s=omega t-kx+varphi left(1right),] где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Условию (1) в каждый момент времени соответствует только одна точка оси X c координатой, равной:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).] Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне вырождается в точку. Из выражения (2) видно, что волновые поверхности с течением времени перемещаются в веществе со скоростью:
![]()
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right).] Для гармонических волн скорость движения поверхности волны совпадает со скоростью распространения волны. Скорость, определенная выражением (3) называют фазовой скоростью. В случае гармонической волны скорость распространения энергии совпадает с фазовой скоростью волны.
Скорость волны зависима от среды и типа волны. Скорость волны не надо путать со скоростью колебания частиц среды в волне.
[custom_ads_shortcode3]
Фазовая скорость распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:
![]()
[v=sqrt{frac{K}{rho }}left(4right),] где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа. Для определения скорости распространения продольных волн в газе используют формулу:
None Фазовая скорость распространения продольных волн в твердом теле:
[v=sqrt{frac{E}{rho }}left(6right),] где $E$ – модуль Юнга вещества стержня.
[custom_ads_shortcode1]
Фазовая скорость распространения поперечных волн
Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:
[v=sqrt{frac{G}{rho }left(7right),}] где $G$ – модуль сдвига среды; $rho $ – плотность вещества. Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
[custom_ads_shortcode2]
Групповая скорость волн
Для диспергирующих волн помимо фазовой скорости волны следует использовать такое понятие как групповая скорость. Если фазовая скорость зависит от частоты и в среде распространяются волны сложного негармонического характера, то при помощи групповой скорости характеризуют распространение волн.

Групповой скоростью называют скорость движения группы (цуга) волн, которые создают в каждый момент времени локализованный в пространстве волновой пакет. Любая реальная волна является суперпозицией гармонических волн. Скорость с которой такая волна распространяется в веществе, имеющем дисперсию на равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой: [u=v-frac{dv}{dlambda }left(8right).] Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тога фазовая и групповая скорости равны и не зависят от длины волны.
[custom_ads_shortcode3]
Примеры задач с решением
None Решение: Зная, что звук – продольная волна, за основу решения задачи примем формулу вычисления фазовой скорости продольной волны в газе:

[v=sqrt{frac{gamma p}{rho }}left(1.1right).] Будем считать азот идеальным газом. Тогда используем уравнение Менделеева – Клапейрона:
[pV=frac{m}{mu }RTleft(1.2right),] где $mu $ – молярная масса газа. Для азота она равна ${mu }_{N_2}=28cdot {10}^{-3}frac{кг}{моль}$; $R=8,31 frac{Дж}{мольcdot К}$ – универсальная газовая постоянная; $T$ – термодинамическая температура газа. Разделим обе части выражения (1.2) на объем:
None [frac{p}{rho }=frac{RT}{mu }left(1.4right),] подставим полученное отношение в (1.1) скорость звука найдем как:

None [gamma =frac{i+2}{i}=frac{7}{5},] так как молекула двух атомная имеет три степени свободы поступательного движения и две вращательного (рис.1).
Вычислим скорость звука в азоте:
[v=sqrt{frac{7}{5}cdot frac{8,31cdot 300}{28cdot {10}^{-3}}}approx 350 left(frac{м}{с}right).] Ответ: $v=350frac{м}{с}$Пример 2Задание: Какова скорость распространения волны в упругой среде, если разность фаз точек, которые находятся на расстоянии $Delta x,$ равна $Delta varphi $ при частоте колебаний равной $nu $?

Решение: Рассмотрим уравнение одномерной плоской волны:
None [{varphi }_1=omega t-kx_1+varphi ;; {varphi }_2=omega t-kx_2+varphi left(2.3right).] Найдем их разность:
None [omega =2pi nu left(2.5right).] Выражение (2.4) преобразуем к виду:
![]()
None [v=frac{2 pi nu Delta x}{Delta varphi }(frac{м}{с}).] Ответ: $v=frac{2 pi nu Delta x}{Delta varphi }frac{м}{с}$Читать дальше: скорость движения.
None Скоростью волны называют скорость, с которой движется фронт волны. Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),] где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:

[x=frac{omega t+varphi -Ф_s}{k}left(2right).] Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
None Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны. Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
[custom_ads_shortcode1]
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как: [v=sqrt{frac{K}{rho }}left(4right),] где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение: [v=sqrt{frac{gamma p}{rho }}left(5right),] где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна: [v=sqrt{frac{E}{rho }}left(6right),] где $E$ – модуль Юнга вещества стержня.
[custom_ads_shortcode2]
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как: [v=sqrt{frac{G}{rho }left(7right),}] где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
[custom_ads_shortcode3]
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн. Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.

Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой: [u=v-frac{dv}{dlambda }left(8right).] Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
[custom_ads_shortcode1]
Примеры задач с решением
None Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
None [T=frac{t}{N} left(1.2right).] Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.] Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).] Ответ. $v=5frac{м}{с}$Пример 2Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды? Решение. Фазовую скорость движения волны найдем как:

None [T=frac{1}{nu }left(2.2right).] Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).] Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }] Максимальное значение скорости колебаний частиц в волне из (2.3) равно:

None [omega =2pi nu ,] тогда:
None [{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).] Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$Читать дальше: формула скорости свободного падения.
Источники:

- www.sites.google.com
- www.nado5.ru
- www.webmath.ru
- www.webmath.ru
Определение
Волна — это среда передачи энергии. Этот перенос происходит из-за какого-то возмущения (или колебания), которое распространяется от источника к месту назначения без чистого переноса материи.
Определение продольных волн
Волны, в которых частицы среды колеблются в направлении, параллельном направлению, в котором распространяется движение. Продольная всегда механическая и возникает вследствие последовательных сжатий (состояний максимальной плотности и давления) и расширений (состояний минимальной плотности и давления) среды. Примерами продольных являются волны, создаваемые пружиной, когда один из ее концов колеблется в том же направлении, что и пружина (рис. 1), и звуковые.

Определение поперечных волн
Волны, в которых частицы среды колеблются в направлении, перпендикулярном направлению, в котором распространяется движение. (Рис. 2)

Волны, возникающие в пруду с водой, на веревке, или электромагнитные являются примерами поперечных. На рисунке показана связь между сжатиями и расширениями продольной по отношению к гребням и впадинам поперечной.
Некоторые движения, такие как океанские и сейсмические волны, представляют собой комбинацию продольных и поперечных. Например, когда морская распространяется по поверхности воды, молекулы воды движутся почти по кругу, очерчивая ряд гребней и впадин.
Когда волна проходит, молекулы воды на гребнях движутся в ее направлении, а молекулы на впадинах движутся в противоположном направлении. Следовательно, после прохождения определенного числа полных волн смещения молекул воды не происходит.
Скорость поперечной волны
Вы когда-нибудь замечали, что в процессе настройки гитары колышек вращают, чтобы увеличить или уменьшить натяжение струны. При увеличении напряжения любой генерируемый в нем импульс будет иметь более высокую скорость распространения.
Но, поскольку не все струны имеют одинаковую толщину, указанная скорость также будет зависеть от этого фактора, так как чем больше толщина струны, тем меньше скорость распространения. Следовательно, можно утверждать, что скорость распространения по струне равна:
- Прямо пропорциональна его напряжению.
- Обратно пропорциональна толщине струны.
Для определения факторов, от которых зависит скорость распространения по струне, предположим, что на струну действует натяжение [F_{T}] и что в момент времени t 0 на ее конце действует сила в вертикальном направлении [F_{y}] чтобы заставить его колебаться, как показано на рисунке ниже.
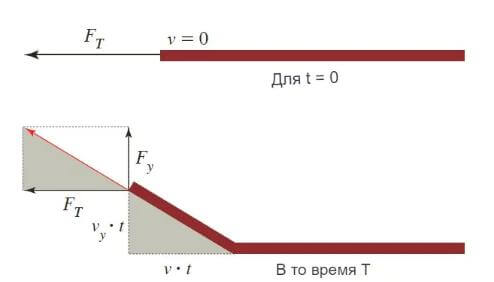
Масса движущихся частиц струны — это масса на единицу длины (м/л) или линейная плотность (м). Тогда v:
[begin{aligned}
&v^{2}=frac{F_{r}}{mu} \
&v=sqrt{frac{F_{r}}{mu}}
end{aligned}]
Распространение и скорость продольных и поперечных волн
Как вы уже знаете, механические волны передаются при взаимодействии близко расположенных друг к другу частиц. Например, без воды и ее частиц корабли не могли бы использовать сонар, а без частиц воздуха мы не могли бы услышать концерт, а летучие мыши не могли бы летать или охотиться в темноте. С другой стороны, другие типы волн, например, создаваемые солнечным светом, НЕ нуждаются в материальной среде для своей передачи. Солнечный свет достигает Земли после пересечения пустого пространства между двумя звездами. По этой причине нельзя сказать, что волна есть возмущение материального тела, а передача возмущения.
При распространении возмущений через какую-либо среду (землю, воздух, воду и т. д.) они не распространяются мгновенно повсюду, а требуют некоторого времени для перехода из одной точки в другую. Так, например, звук грома воспринимается дольше, чем дальше мы находимся от места, где происходит гроза.
Определение 2
Скорость распространения – это расстояние, проходимое возмущением, передаваемым волной, за заданное время. Скорость распространения зависит от материальной среды, в которой она распространяется. Таким образом, звук распространяется быстрее в воде, чем в воздухе, и быстрее в твердых телах, чем в жидкостях.
Формула
Мы можем рассчитать скорость, с которой распространяются волны, возникающие на поверхности пруда. Для этого нам нужно знать расстояние d между очагом или источником возмущения и точкой на поверхности воды, а также время, за которое возмущение достигает этой точки.
Зная эти значения, применяется следующее уравнение:
[v=frac{d}{t}]
Где:
v — скорость в метрах в секундах.
d — пройденное расстояние в метрах с.
t — время в секундах, за которое волна проходит это расстояние.
Нет времени решать самому?
Наши эксперты помогут!
Ключевые моменты
На основе вышесказанного, можно вывести основные особенности, а именно:
- Волны переносят энергию из одной точки в другую без чистого переноса материи.
- Поперечные имеют среду, колеблющуюся перпендикулярно направлению распространения, а продольные имеют среду, колеблющуюся параллельно направлению распространения.
- Есть четыре термина, характерных для определенных типов волн. Пики и впадины описывают поперечные. Сжатие и разрежение описывают продольные.
- Есть четыре термина, которые относятся к обоим типам: среда, длина, амплитуда и частота.
- Движение может состоять из поперечной и продольной составляющих.
Примеры 1 — 2
На графике показана поперечная волна. Какова ее длина?
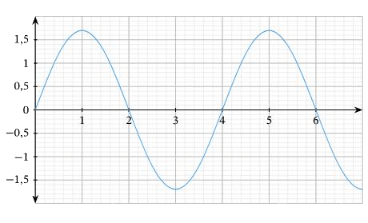
В основе этого вопроса лежат два навыка: с одной стороны, знание определения длины поперечной волны, а с другой стороны, интерпретация графиков.
Что касается первой точки, длина — это расстояние, пройденное за полный цикл. Это означает, что его можно рассматривать как расстояние между любой точкой и положением той же точки в следующем цикле. Например, расстояние между пиками равно длине, как и расстояние от пика до пика.
Теперь мы используем второй навык, чтобы прочитать расстояние от пика до пика на графике. Первая вершина находится над ориентиром 1, а вторая расположена над отметкой 5. Это дает нам расстояние от пика до пика 4.
Ответ: 4
На графике показана продольная волна, распространяющаяся вдоль пружины, и четыре кривые смещения во времени. Если положительное смещение соответствует сжатию пружины, то какой график правильно показывает изменение смещения со временем волны в пружине?
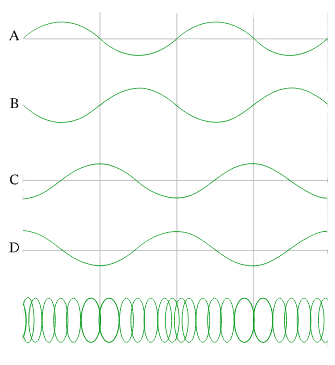
Этот вопрос основан на вашей способности понять идею представления продольной волны как поперечной волны. Нам нужно знать, как связать вершины поперечной волны с зонами сжатия продольной волны. Точно так же вы связываете впадины поперечной волны с областями разрежения продольной волны. Таким образом, правильным ответом будет D, так как пики совмещены с центрами областей сжатия, а впадины совмещены с центрами областей разрежения.
Ответ: D

