You should use conic sections. Say C1 is conic section of first ellipse and C2 is conic section of second ellipse. Then if C1 and C2 intersect then also their linear combination C3=C1+t.C2 must be intersecting. Choose t so that C3 is degenerate, that means det(C3)=0. This determinant leads to cubic equation for t. So you get up to 3 values of t. For each t evaluate C3. Since C3 is degenerate, it represents system of two lines (they can be equal). Calculate intersection of both lines with first ellipse and test if the intersection point is on second ellipse. This will give you all intersection points of the two ellipses (some results may be duplicated, but this should be easy to detect and avoid).
BTW, to simplify algebra, it is good idea to transform first ellipses so that one of them is in origin with axis on cartesian axis. Such ellipse is then x^2/a^2 + y^2/b^2 = 1 and conic section is very simple:
(b^2, 0, 0)
(0, a^2, 0)
(0, 0, -a^2.b^2)
|
1 / 1 / 0 Регистрация: 01.05.2017 Сообщений: 144 |
|
|
1 |
|
Точки пересечения двух эллипсов геометрическими преобразованиями17.02.2020, 21:33. Показов 1700. Ответов 15
привет
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
18.02.2020, 07:48 |
2 |
|
ведь после сжатия один эллипс перестает быть эллипсом. Сжатие эллипс переводит в эллипс всегда. Ну и читать труды, что вы цитируете, по-моему, очень вредно.
1 |
|
1 / 1 / 0 Регистрация: 01.05.2017 Сообщений: 144 |
|
|
18.02.2020, 08:21 [ТС] |
3 |
|
Сжатие эллипс переводит в эллипс всегда повернутый на угол эллипс при сжатии (другого эллипса) не превращается в эллипс
Ну и читать труды, что вы цитируете, по-моему, очень вредно почему?
0 |
|
630 / 435 / 219 Регистрация: 10.06.2016 Сообщений: 2,014 |
|
|
18.02.2020, 09:37 |
4 |
|
Не проще ли решить эту систему численно? Преобразования координат и сжатия все равно приведут к вычислительным ошибкам по точности.
0 |
|
3917 / 2473 / 524 Регистрация: 07.11.2019 Сообщений: 4,113 |
|
|
18.02.2020, 10:15 |
5 |
|
Мне кажется, проще перейти к однородным координатам. Тогда чтобы найти матрицу преобразования достаточно обращения матрицы 3×3 и умножения ее другую 3×3 матрицу. Все.
0 |
|
630 / 435 / 219 Регистрация: 10.06.2016 Сообщений: 2,014 |
|
|
18.02.2020, 10:17 |
6 |
|
u235, обращение, потом перемножение, столько арифметических операций….
0 |
|
3917 / 2473 / 524 Регистрация: 07.11.2019 Сообщений: 4,113 |
|
|
18.02.2020, 10:38 |
7 |
|
a= Добавлено через 5 минут Добавлено через 3 минуты
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
18.02.2020, 10:40 |
8 |
|
не превращается в эллипс Вот именно поэтому и не стоит читать малограмотные работы. Это столь же заразно, как короновирус.
2 |
|
3917 / 2473 / 524 Регистрация: 07.11.2019 Сообщений: 4,113 |
|
|
18.02.2020, 10:47 |
9 |
|
M еще нужно домножить на матрицу поворота чтобы окружность и центр второго эллипса выстроились по оси ox.
0 |
|
1471 / 826 / 140 Регистрация: 12.10.2013 Сообщений: 5,456 |
|
|
18.02.2020, 10:48 |
10 |
|
Не проще ли решить эту систему численно? Точно, минимум одной неизвестной. Параметрические эллипсы можно крутануть матрицей поворота. Разве вообще актуально мусолить такую ерунду.
1 |
|
u235 |
|
18.02.2020, 10:53
|
|
Не по теме: Советую книжку Роджерс Д., Адамс Дж. Математические основы машинной графики.
0 |
|
1 / 1 / 0 Регистрация: 01.05.2017 Сообщений: 144 |
|
|
18.02.2020, 20:11 [ТС] |
12 |
|
Советую книжку Роджерс Д., Адамс Дж. Математические основы машинной графики спасибо
не стоит читать малограмотные работы а что посоветуете? а еще вопрос. после сжатия как найти ось нового эллипса Миниатюры
0 |
|
3917 / 2473 / 524 Регистрация: 07.11.2019 Сообщений: 4,113 |
|
|
18.02.2020, 21:58 |
13 |
|
Зачем искать ось? Вам нужен его центр, чтобы повернуть эллипс вокруг начала координат…
0 |
|
1 / 1 / 0 Регистрация: 01.05.2017 Сообщений: 144 |
|
|
18.02.2020, 22:03 [ТС] |
14 |
|
но ведь в итоге чтобы найти точки пересечения нужны размеры осей эллипса
0 |
|
3917 / 2473 / 524 Регистрация: 07.11.2019 Сообщений: 4,113 |
|
|
18.02.2020, 22:07 |
15 |
|
Кстати, да.. ось нового не будет равна оси старого..
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
19.02.2020, 06:30 |
16 |
|
а что посоветуете? Для решения вашей задачи – как я понял надо решить систему из двух уравнений второго порядка с двумя неизвестными – существуют общие методы. Элементарное изложение можно найти например здесь С.Т. Завало. Элементарная алгебра. Изд-во “Просвещение”, М., 1964 г. Смотрите на странице 162 и далее, да и более ранние страницы стоит пролистать.
0 |
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Пересечение эллипсов
|
|
22/11/10 |
Можно ли найти точки пересечения двух произвольных эллипсов не численными методами?
|
|
|
|
|
Mitrius_Math |
Re: Пересечение эллипсов
|
|
22/05/09 |
Почитайте про результант многочленов (Винберг, Алгебра многочленов, с. 43 и далее, с. 101 и далее).
|
|
|
|
|
DDuMoH |
Re: Пересечение эллипсов
|
|
22/11/10 |
Дело в том, что алгебра многочленов это, конечно, хорошо, но результант всё-таки скорее имеет отношение к многочленам одной переменной – именно то, что меня интересует: способ получения такого многочлена, ну и последующее отыскание корней.
|
|
|
|
|
Mitrius_Math |
Re: Пересечение эллипсов
|
|
22/05/09 |
DDuMoH , так ведь многочлен от двух переменных можно рассматривать как многочлен от одной переменной, а вторую считать параметром. В той книге есть пример.
|
|
|
|
|
DDuMoH |
Re: Пересечение эллипсов
|
|
22/11/10 |
Mitrius_Math Параметр всмысле тригонометрической замены? У параметра должна быть задана область изменения так, чтобы описать исходную функцию(в нашем случае неявную). Насколько я знаю рекомендуемый учебник – суть ликбез по введению в алгебру первого курса с которой я худо бедно знаком. Вообще оставил пост в надежде на явный тычок в мою тупоголовость – вдруг сослепу не вижу какого-нибудь банального преобразования/замены переменных, приводящего к искомому уравнению 4ой степени.
|
|
|
|
|
ИСН |
Re: Пересечение эллипсов
|
||
18/05/06 |
Зачем, зачем Вам уравнение 4 степени? Его решать по формулам – это всё равно что не решать. Один чёрт, придётся делать численно. А численно можно делать и сразу эту систему, какая уж разница.
|
||
|
|
|||
|
armez |
Re: Пересечение эллипсов
|
|
09/06/12 |
Умножая первое уравнение на В принципе, эти выкладки эквивалентны приравниванию нулю результанта двух данных многочленов по переменной у с исключением переменной х. Развитие этой методики привело к появлению теории исключения.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
§ 18. Эллипс
Эллипсом называется
геометрическое место точек, для которых
сумма расстояний до двух фиксированных
точек плоскости, называемых фокусами,
есть постоянная величина, большая, чем
расстояние между фокусами. Постоянную
сумму расстояний произвольной точки
эллипса до фокусов принято обозначать
через 2а. Фокусы эллипса обозначают
буквами F1
и F2,
расстояние между ними — через 2с. По
определению эллипса 2а > 2с или а > с.
Пусть дан эллипс. Если оси декартовой
прямоугольной системы координат
выбраны так, что фокусы данного эллипса
располагаются на оси абсцисс
симметрично относительно начала
координат, то в этой системе координат
уравнение данного эллипса имеет вид
![]() ,
,
(1)
где b =
![]() ;
;
очевидно, a
b. Уравнение
вида (1) называется каноническим
уравнением эллипса.
При указанном выборе системы
координат оси координат являются осями
симметрии эллипса, а начало координат
— его центром симметрии (черт. 12). Оси
симметрии эллипса называются просто
его осями, центр симметрии — просто
центром. Точки, в которых эллипс пересекает
свои оси, называются его вершинами. На
черт. 12 вершины эллипса суть точки А’,
А, В’ и В.
Часто осями эллипса
называются также отрезки А’А
= 2а и В’В
= 2b;
вместе с тем отрезок
ОА = а называют
большой полуосью эллипса, отрезок ОВ=
b –
малой полуосью.
Если фокусы эллипса
расположены на оси Оу
(симметрично
относительно начала координат), то
уравнение эллипса имеет тот же вид (1),
во в этом случае b>
а; следовательно, если
мы желаем буквой а
обозначать большую
полуось, то в уравнении (1) нужно буквы
а и
b поменять
местами. Однако для удобства формулировок
задач мы условимся буквой а
всегда обозначать
полуось, расположенную на оси Ох,
буквой b
— полуось, расположенную
на оси Оу, независимо
от того, что больше, а
или b.
Если а
= b,
то уравнение (1)
определяет окружность, рассматриваемую
как частный случай эллипса. Число
![]()
где a – большая
полуось, называется эксцентриситетом
эллипса. Очевидно,
< 1 (для окружности
= 0). Если М (х;
у) — произвольная
точка эллипса, то отрезки F1М
= г1
и F2М
= r2
(черт. 12) называются
фокальными радиусами точки М.
Фокальные радиусы
могут быть вычислены по формулам r1
= а + х,
r 2
= а –
x.
Е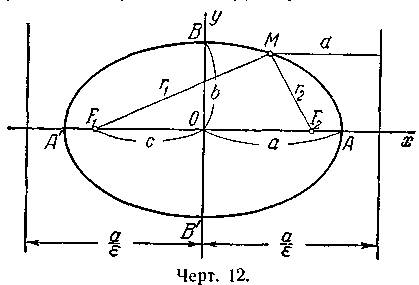 сли
сли
эллипс определён уравнением (1) и a
b, то
прямые
![]()
![]() (черт.
(черт.
12), называются директрисами эллипса
(если b >
а, то директрисы определяются
уравнениями
![]()
![]()
) .
Каждая директриса обладает следующим
свойством: если r –
расстояние произвольной
точки эллипса до некоторого фокуса,
d—расстояние
от той же точки до
односторонней с этим фокусом директрисы,
то отношение
![]()
есть постоянная
величина, равная эксцентриситету эллипса
![]()
Если две плоскости
и
образуют острый угол ,
то проекцией на
плоскость
окружности радиуса а,
лежащей на плоскости
,
является эллипс с большой
полуосью a;
малая полуось b
этого эллипса
определяется по формуле
b = a cos
(черт. 13).
Если круглый цилиндр имеет
в качестве
направляющей окружность радиуса b,
то в
сечении этого цилиндра
плоскостью, наклонённой к оси цилиндра
под острым углом ,
будет эллипс, малая
полуось которого
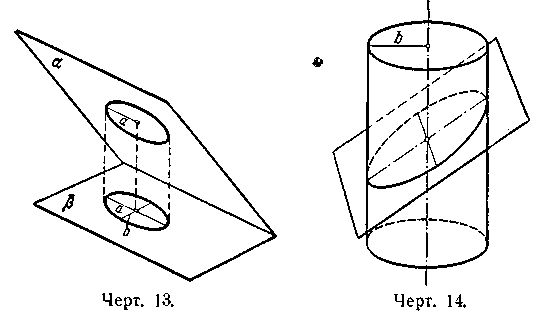
равна b;
большая полуось а
этого эллипса
определяется по формуле
(черт. 14).
![]()
444. Составить уравнение эллипса,
фокусы которого лежат на оси абсцисс,
симметрично относительно начала
координат, зная, кроме того, что:
1) его полуоси равны 5 и 2;
2) его большая ось равна 10,
а расстояние между фокусами 2с
= 8;
3) его малая ось равна 24, а расстояние
между фокусами 2с =10;
4) расстояние между его
фокусами 2с = 6 и
эксцентриситет
![]() ;
;
5) его большая ось равна 20,
а эксцентриситет
![]() ;
;
6) его малая ось равна 10, а
эксцентриситет
![]() ;
;
7) расстояние между его директрисами
равно 5 и расстояние между фокусами 2с
= 4;
8) его большая ось равна 8, а расстояние
между директрисами равно 16;
9) его малая ось равна 6, а расстояние
между директрисами равно 13;
10) расстояние между его
директрисами равно 32 и
![]() .
.
445. Составить уравнение эллипса,
фокусы которого лежат на оси ординат,
симметрично относительно начала
координат, зная, кроме того, что:
1) его полуоси равны соответственно 7 и
2;
2) его большая ось равна 10,
а расстояние между фокусами 2с
= 8;
3) расстояние между его
фокусами 2с = 24 и эксцентриситет
![]()
4) его малая ось равна 16, а
эксцентриситет
![]()
5) расстояние между его
фокусами 2с = 6 и расстояние между
директрисами равно 16![]()
6) расстояние между его
директрисами равно
![]()
и эксцентриситет
![]()
446. Определить полуоси каждого из
следующих эллипсов:
1)
![]() ;
;
2)
![]() ;
;
3)х2
+ 25у2
= 25;
4) х2
+ 5y2
= 15; 5) 4х2
+ 9у2
= 25; 6) 9х2
+ 25у2
= 1;
7) х2
+ 4у2
= 1;
8) 16х2
+ у2
= 16; 9) 25х2
+ 9у2
= 1;
10) 9х2
+ у2
= 1.
447. Дан
эллипс 9х2
+ 25у2
= 225. Найти: 1) его полуоси; 2) фокусы; 3)
эксцентриситет; 4) уравнения директрис.
448. Вычислить площадь четырёхугольника,
две вершины которого лежат в фокусах
эллипса
х2
+ 5у2
= 20,
а две другие совпадают с концами его
малой оси.
449. Дан
эллипс 9х2
+ 5у2
= 45. Найти: 1) его полуоси; 2) фокусы; 3)
эксцентриситет; 4) уравнения директрис.
450. Вычислить площадь четырёхугольника,
две вершины которого лежат в фокусах
эллипса
9х2
+ 5у2
= 1,
две другие совпадают с концами его малой
оси.
451.
Вычислить расстояние от фокуса
F(c;
0) эллипса
![]()
до односторонней с этим фокусом
директрисы.
452.
Пользуясь одним циркулем, построить
фокусы эллипса
![]() (считая,
(считая,
что изображены оси координат и задана
масштабная единица).
453. На
эллипсе
![]() найти
найти
точки, абсцисса которых равна — 3.
454.
Определить, какие из точек A1(—2;
3), А2(2;
—2), А3
(2; —4), А4(—1;
3), А5(—4;
—3), А6(3;
—1), А7(3;
—2), А8
(2; 1), А9(0;
15) и А10(0;
—16) лежат на эллипсе 8х2+5у2
= 77, какие внутри и
какие вне его.
455.
Установить, какие линии определяются
следующими уравнениями:
1)![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Изобразить эти линии на чертеже.
456.
Эксцентриситет эллипса
![]()
, фокальный радиус точки
М эллипса
равен 10. Вычислить расстояние от точки
М до
односторонней с этим фокусом
директрисы.
457.
Эксцентриситет эллипса
![]() ,
,
расстояние от точки М
эллипса до директрисы
равно 20. Вычислить расстояние от точки
М до
фокуса, одностороннего с этой директрисой.
458. Дана
точка М1
(2;
![]() )
)
на эллипсе
![]()
составить уравнения прямых, на которых
лежат фокальные радиусы точки M1.
459.
Убедившись, что точка М1
(— 4; 2,4) лежит на
эллипсе
![]() определить
определить
фокальные радиусы точки М1.
460.
Эксцентриситет эллипса
![]() ,
,
центр его совпадает с началом координат,
один из фокусов F(—2;
0). Вычислить расстояние от точки M1
эллипса с абсциссой, равной 2, до
директрисы, односторонней с данным
фокусом.
461.
Эксцентриситет эллипса
![]() ,
,
центр его совпадает с началом
координат, одна из директрис дана
уравнением х =16. Вычислить расстояние
от точки M1
эллипса с абсциссой,
равной – 4, до фокуса, одностороннего с
данной директрисой.
462.
Определить точки эллипса
![]() ,
,
расстояние которых
до правого фокуса равно 14.
463.
Определить точки эллипса
![]() ,
,
расстояние которых
до левого фокуса равно 2,5.
464. Через
фокус эллипса
![]()
проведён перпендикуляр
к его большой оси. Определить расстояния
от точек пересечения этого перпендикуляра
с эллипсом до фокусов.
465.
Составить уравнение эллипса, фокусы
которого расположены на оси абсцисс,
симметрично относительно начала
координат, если даны:
1) точка М1
(—2![]() ;
;
2) эллипса и его малая полуось b = 3;
2) точка M2
(2;—2)
эллипса и его большая полуось а = 4;
3) точки M1(4;_—
![]() )
)
и М2(2![]() ;
;
3) эллипса;
4) точка M1
(![]() ;
;
—1) эллипса и расстояние между его
фокусами 2с = 8;
5) точка М1
(2; —![]()
эллипса и его эксцентриситет
![]() ;
;
6) точка M1
(8; 12) эллипса и
расстояние r1
= 20 от неё до левого фокуса;
7) точка M1
(—![]() ;
;
2) эллипса и расстояние между его
директрисами равно 10.
4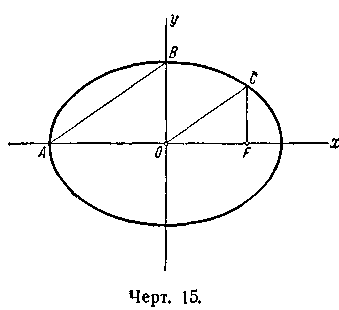 66.
66.
Определить эксцентриситет
эллипса, если:
1) его малая ось видна из фокусов под
углом в 60°;
2) отрезок между фокусами виден из вершин
малой оси под прямым углом;
3) расстояние между директрисами в
три раза больше расстояния между
фокусами;
4) отрезок перпендикуляра, опущенного
из центра эллипса на его директрису,
делится вершиной эллипса пополам.
467. Через
фокус F эллипса
проведён перпендикуляр к его большой
оси (черт. 15). Определить, при каком
значении эксцентриситета эллипса
отрезки
![]() и
и
![]()
будут параллельны.
468.
Составить уравнение
эллипса с полуосями a,
b и центром С(x0
; у 0),
если известно, что оси симметрии эллипса
параллельны осям координат.
469. Эллипс касается оси абсцисс в
точке А (3; 0) и оси ординат в точке
В (0; —4). Составить уравнение этого
эллипса, зная, что его оси симметрии
параллельны координатным осям.
470. Точка
С (— 3;
2) является центром эллипса, касающегося
обеих координатных осей. Составить
уравнение этого эллипса, зная, что его
оси симметрии параллельны координатным
осям.
471.
Установить, что каждое из следующих
уравнений определяет эллипс, и найти
координаты его центра С,
полуоси, эксцентриситет
и уравнения директрис:
1) 5х2
+ 9у2
— 30х + 18у + 9 = 0;
2) 16х2
+ 25у2
+ 32х — 100у — 284 = 0;
3) 4х2
+ 3у2
— 8х + 12у —32 = 0.
472. Установить, какие линии определяются
следующими уравнениями:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Изобразить эти линии на чертеже.
473. Составить уравнение эллипса,
зная, что:
1) его большая ось равна 26 и
фокусы суть F1
(—10; 0), F2
(14; 0);
2) его малая ось равна
2 и фокусы суть F1(—1;
—1), F2
(1; 1);
3) его фокусы суть F1
(2;
![]() )
)
, F2
(2;
![]() )
)
эксцентриситет
![]() ;
;
4) его фокусы суть F1
(l; 3), F2
(3; 1) и расстояние
между директрисами равно
![]() .
.
474.
Составить уравнение эллипса, если
известны его эксцентриситет
![]() ,
,
фокус F(-4; 1) и уравнение соответствующей
директрисы x – 5 = 0.
475.
Составить уравнение эллипса, если
известны его эксцентриситет
![]()
фокус F(—4;
1) и уравнение соответствующей директрисы
y + 3 = 0
476. Точка
А (— 3; — 5) лежит на эллипсе, фокус которого
F(—1;
—4), а соответствующая директриса дана
уравнением
х — 2 = 0.
Составить уравнение этого эллипса.
477.
Составить уравнение эллипса, если
известны его эксцентриситет
![]() ,
,
фокус F(3; 0)
и уравнение соответствующей директрисы
х + у — 1= 0.
478. Точка
M1
(2; —1) лежит на эллипсе, фокус которого
F(l; 0), а
соответствующая директриса дана
уравнением 2х — у — 10 = 0. Составить
уравнение этого эллипса.
479. Точка
M1
(3; —1) является концом малой оси эллипса,
фокусы которого лежат на прямой у +
6 = 0.Составить уравнение этого
эллипса, зная его эксцентриситет
![]() .
.
480. Найти
точки пересечения прямой х + 2у — 7 = 0 и
эллипса х2
+ 4у2
= 25.
481. Найти
точки пересечения прямой 3х + 10у —
25 = 0 и эллипса
![]()
482. Найти
точки пересечения прямой 3х — 4у — 40 = 0
и эллипса
![]()
483.
Определить, как расположена прямая
относительно эллипса: пересекает ли,
касается или проходит вне его, если
прямая и эллипс заданы следующими
уравнениями:
1) 2х—у —3 = 0, 2)
2х+у— 10 = 0,
![]()
![]()
3) 3х + 2у —20 = 0,
![]()
484.
Определить, при каких значениях m
прямая у = —k x
+ m: 1) пересекает эллипс
![]() ;
;
2) касается его; 3) проходит вне этого
эллипса.
485.
Вывести условие, при котором прямая y
= kx
+ m касается эллипса
![]()
486.
Составить уравнение касательной к
эллипсу
![]() в
в
его точке M1
(x1;
y1).
487.
Доказать, что касательные к эллипсу
![]()
проведённые в концах одного и того же
диаметра, параллельны. (Диаметром эллипса
называется его хорда, проходящая через
центр.)
488. Составить уравнения касательных
к эллипсу
![]()
параллельных прямой 3х + 2у + 7 = 0.
489. Составить уравнения касательных
к эллипсу
х2
+ 4у2
= 20,
перпендикулярных к прямой
2х —2у—13 = 0.
490. Провести касательные к эллипсу
![]()
параллельно прямой
4х —2у + 23 = 0
и вычислить расстояние d между ними.
491. На эллипсе
![]()
найти точку M1,
ближайшую к прямой
2х— 3у + 25 = 0,
и вычислить расстояние d от
точки M1
до этой прямой.
492. Из
точки А (![]() )
)
проведены касательные к эллипсу
![]()
Составить их уравнения.
493. Из точки С(10; —8) проведены
касательные к эллипсу
![]()
Составить уравнение хорды, соединяющей
точки касания.
494. Из точки Р(—16; 9) проведены
касательные к эллипсу
![]()
Вычислить расстояние d от точки Р до
хорды эллипса, соединяющей точки
касания.
495. Эллипс проходит через точку А
(4; —1) и касается прямой х + 4у—10 = 0.
Составить уравнение этого эллипса при
условии, что его оси совпадают с осями
координат.
496.
Составить уравнение эллипса, касающегося
двух прямых 3х—2у
— 20 = 0, х
+ 6у—
20 = 0, при условии, что его оси совпадают
с осями координат.
497. Доказать, что произведение
расстояний от центра эллипса до точки
пересечения любой его касательной с
фокальной осью и до основания
перпендикуляра, опущенного из точки
касания на фокальную ось, есть величина
постоянная, равная квадрату большой
полуоси эллипса.
498. Доказать, что произведение
расстояний от фокусов до любой
касательной к эллипсу равно квадрату
малой полуоси.
499. Прямая
х—у—
5 = 0 касается эллипса, фокусы которого
находятся в точках F1
(—3;
0) и F2 (3;
0). Составить уравнение этого эллипса.
500. Составить уравнение эллипса,
фокусы которого расположены на оси
абсцисс симметрично относительно начала
координат, если известны уравнение
касательной к эллипсу
3х+10у —25 = 0
и его малая полуось b
= 2.
501.
Доказать, что прямая, касающаяся эллипса
в некоторой точке М,
составляет равные углы
с фокальными радиусами F1M,
F2M
и проходит вне угла
F1MF2.
502. Из левого фокуса эллипса
![]()
под тупым углом
к оси Ох направлен
луч света. Известно, что tg
= — 2. Дойдя до эллипса, луч от него
отразился. Составить уравнение прямой,
на которой лежит отражённый луч.
503. Определить точки пересечения
двух эллипсов:
х2
+ 9у2
— 45 = 0, х2
+ 9у2
—6х —27 = 0.
504. Убедившись, что два эллипса
n2m2+
m2y2—
m2n2
= 0, m2x2
+ n2y2
— m2n2
= 0
(mn)
пересекаются в четырёх
точках, лежащих на окружности с центром
в начале координат, определить радиус
R этой
окружности.
505. Две
плоскости
и
образуют угол
= 300.
Определить полуоси эллипса, полученного
проектированием на плоскость
окружности радиуса R =10, лежащей на
плоскости .
506.
Эллипс, малая полуось которого равна
6, является проекцией окружности
радиуса R=12. Определить угол
между плоскостями,
в которых лежат эллипс и окружность.
507.
Направляющей круглого цилиндра является
окружность радиуса R = 8. Определить
полуоси эллипса, полученного в сечении
этого цилиндра плоскостью, наклонённой
к его оси под углом
= 30°.
508.
Направляющей круглого
цилиндра является окружность радиуса
R =
![]() .
.
Определить, под каким углом к оси цилиндра
нужно его пересечь плоскостью, чтобы в
сечении получить эллипс с большой
полуосью а
= 2.
509.
Равномерным сжатием
(или равномерным растяжением) плоскости
к оси абсцисс называется такое
преобразование точек

плоскости, при котором
произвольная точка М(х;
у)
перемещается в точку
М‘(х‘;
у‘)
(черт. 16) так, что
х‘
= х,
у‘
= qy,
где q>0 — постоянная, называемая
коэффициентом равномерного сжатия.
Аналогично определяется
равномерное сжатие плоскости к
оси Оу
при помощи уравнений
x’ = qx, y’ = y (черт. 17).
Определить, в какую линию преобразуется
окружность
х2
+ у2
= 25,
если коэффициент равномерного сжатия
плоскости к оси абсцисс
![]() q
q
=
![]() .
.
-
Коэффициент равномерного
сжатия плоскости к оси Оуз
равен
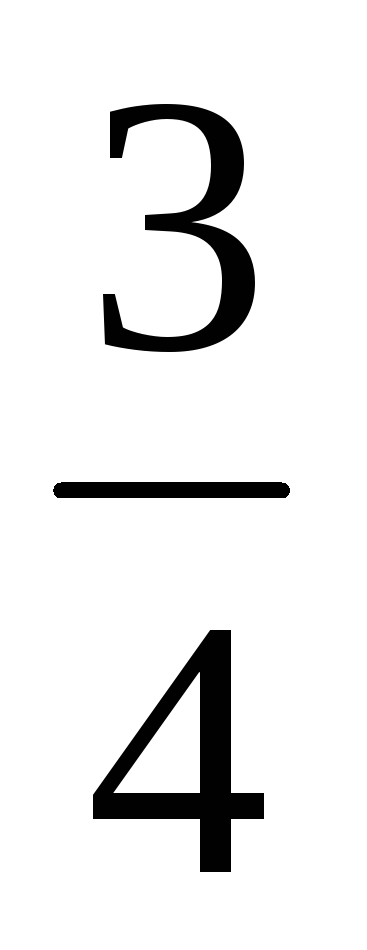 .
.
Определить уравнения линии, в которую
при таком сжатии преобразуется эллипс

511. Найти
уравнение линии, в которую преобразуется
эллипс
![]() при
при
двух последовательных равномерных
сжатиях плоскости к координатным
осям, если коэффициенты равномерного
сжатия плоскости к осям Ох
и Оу
равны соответственно
![]() и
и
![]() .
.
612.
Определить коэффициент
q
равномерного сжатия плоскости к оси
Ох,
при котором эллипс
![]()
преобразуется в эллипс
![]() .
.
613.
Определить коэффициент
q
равномерного сжатия
плоскости к оси Оу,
при котором эллипс
![]()
преобразуется в эллипс
![]() .
.
514.
Определить коэффициенты q1
и q2
двух последовательных равномерных
сжатий плоскости к осям Ох
и Оу,
при которых эллипс
![]()
преобразуется в окружность х2+у2=16.
Соседние файлы в папке kletenik_doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
От: |
e-Xecutor |
|
| Дата: | 22.10.03 13:13 | ||
| Оценка: |
Есть два эллипса.
Для простоты центр одного расположен в центре координат,
и оси совпадают с координатными.
А второй задан координатами центра, радиусами и углом поворота.
Нужно понять — пересекаются ли они.
Насколько я понимаю, всё сводится к решению уравнения 4-й степени.
Я даже помню, что есть такая формула Кордана.
Только самой формулы не помню ![]()
И найти не удалось (с ходу).
Соответственно вопросы:
1) может как-то проще/по другому можно?
2) кто помнит формулу Кордана? ![]()
Интересует аналитическое решение, численные методы не предлагать ![]()
|
|
От: |
Alglib |
|
| Дата: | 22.10.03 13:53 | ||
| Оценка: |
+1 |
Здравствуйте, e-Xecutor, Вы писали:
EX>Есть два эллипса.
EX>Для простоты центр одного расположен в центре координат,
EX>и оси совпадают с координатными.
EX>А второй задан координатами центра, радиусами и углом поворота.
EX>Нужно понять — пересекаются ли они.
EX>Насколько я понимаю, всё сводится к решению уравнения 4-й степени.
Почему четвертой? квадратное вроде уравнение должно получится?
а для четвертой, у меня вот здесь есть
Re[2]: Пересечение эллипсов
|
|
От: |
e-Xecutor |
|
| Дата: | 23.10.03 07:42 | ||
| Оценка: |
Здравствуйте, Alglib, Вы писали:
A>Здравствуйте, e-Xecutor, Вы писали:
EX>>Есть два эллипса.
EX>>Для простоты центр одного расположен в центре координат,
EX>>и оси совпадают с координатными.
EX>>А второй задан координатами центра, радиусами и углом поворота.
EX>>Нужно понять — пересекаются ли они.
EX>>Насколько я понимаю, всё сводится к решению уравнения 4-й степени.
A>Почему четвертой? квадратное вроде уравнение должно получится?
A>а для четвертой, у меня вот здесь есть
Не работает ссылка. Но я нашел тут: http://alglib.chat.ru/
![]()
А 4-й, вот почему:
Один эллипс задаётся вот так:
x(t)=w1*cos(t)
y(t)=h1*sin(t)
второй вот так:
x(t)=(w2*cos(t)+x0)*cos(a)-(h2*sin(t)+y0)*sin(a)
y(t)=(w2*cos(t)+x0)*sin(a)-(h2*sin(t)+y0)*cos(a)
если заменить sin(t) на X, а cos(t) на sqrt(1-X^2), и подставиться одно в другое,
получится уравнение типа:
x^2+C1*x*sqrt(x)+C2*x+C3*sqrt(x)+C4=0
из которого делается уравнение 4-й степени ![]()
Спасибо за ссылку.
Буду “копать” ![]()
Re[3]: Пересечение эллипсов
|
|
От: |
Alglib |
|
| Дата: | 23.10.03 08:48 | ||
| Оценка: |
EX>Не работает ссылка. Но я нашел тут: http://alglib.chat.ru/
EX>![]()
вроде проверял, но поскольку я сайт забросил, уже давно — вполне возможно![]()
если надо могу код на Паскале прислать.
EX>А 4-й, вот почему:
EX>Один эллипс задаётся вот так:
EX>x(t)=w1*cos(t)
EX>y(t)=h1*sin(t)
EX>второй вот так:
EX>x(t)=(w2*cos(t)+x0)*cos(a)-(h2*sin(t)+y0)*sin(a)
EX>y(t)=(w2*cos(t)+x0)*sin(a)-(h2*sin(t)+y0)*cos(a)
EX>если заменить sin(t) на X, а cos(t) на sqrt(1-X^2), и подставиться одно в другое,
EX>получится уравнение типа:
EX>x^2+C1*x*sqrt(x)+C2*x+C3*sqrt(x)+C4=0
EX>из которого делается уравнение 4-й степени ![]()
вообще получается система из двух уравнений второй степени, в принципе, и правда сводится к одному четвертой, но иногда удается обойтись квадратным.
а не проще решить два тригонометрических и посмотреть пересечение множеств решений одного и другого (сам не пробовал — так мысли в слух ![]() )
)
(w2*cos(t)+x0)*cos(a)-(h2*sin(t)+y0)*sin(a) = w1*cos(t)
(w2*cos(t)+x0)*sin(a)-(h2*sin(t)+y0)*cos(a) = h1*sin(t)
приводим к системе линейной относительно cos(t) и sin(t)
(w2*cos(a) — w1)*cos(t)-h2*sin(a)*sin(t) = y0*sin(a)-x0*cos(a)
(w2*sin(a) — h1)*cos(t)-h2*cos(a)*sin(t) = y0*cos(a)-x0*sin(a)
решаем, получаем
u=cos(t)
v=sin(t)
если u^2+v^2 != 1 — нет пересечения,
если u^2+v^2 = 1 — получаем точку пересечения?
Ногами не пинать, не проверял — исключительно схемотично![]()
Re[4]: Пересечение эллипсов
|
|
От: |
e-Xecutor |
|
| Дата: | 23.10.03 10:13 | ||
| Оценка: |
Здравствуйте, Alglib, Вы писали:
EX>>Не работает ссылка. Но я нашел тут: http://alglib.chat.ru/
EX>>![]()
A>вроде проверял, но поскольку я сайт забросил, уже давно — вполне возможно![]()
A>если надо могу код на Паскале прислать.
Буду признателен. Ибо вдалбливать это с 0-ля жутко неохота.
Точнее неохота потом глюки неделю ловить ![]()
EX>>А 4-й, вот почему:
EX>>Один эллипс задаётся вот так:
EX>>x(t)=w1*cos(t)
EX>>y(t)=h1*sin(t)
EX>>второй вот так:
EX>>x(t)=(w2*cos(t)+x0)*cos(a)-(h2*sin(t)+y0)*sin(a)
EX>>y(t)=(w2*cos(t)+x0)*sin(a)-(h2*sin(t)+y0)*cos(a)
EX>>если заменить sin(t) на X, а cos(t) на sqrt(1-X^2), и подставиться одно в другое,
EX>>получится уравнение типа:
EX>>x^2+C1*x*sqrt(x)+C2*x+C3*sqrt(x)+C4=0
EX>>из которого делается уравнение 4-й степени ![]()
A>вообще получается система из двух уравнений второй степени, в принципе, и правда сводится к одному четвертой, но иногда удается обойтись квадратным.
A>а не проще решить два тригонометрических и посмотреть пересечение множеств решений одного и другого (сам не пробовал — так мысли в слух ![]() )
)
A>(w2*cos(t)+x0)*cos(a)-(h2*sin(t)+y0)*sin(a) = w1*cos(t)
A>(w2*cos(t)+x0)*sin(a)-(h2*sin(t)+y0)*cos(a) = h1*sin(t)
A>приводим к системе линейной относительно cos(t) и sin(t)
A>(w2*cos(a) — w1)*cos(t)-h2*sin(a)*sin(t) = y0*sin(a)-x0*cos(a)
A>(w2*sin(a) — h1)*cos(t)-h2*cos(a)*sin(t) = y0*cos(a)-x0*sin(a)
A>решаем, получаем
A>u=cos(t)
A>v=sin(t)
A>если u^2+v^2 != 1 — нет пересечения,
A>если u^2+v^2 = 1 — получаем точку пересечения?
A>Ногами не пинать, не проверял — исключительно схемотично![]()
Пинать не буду, но не проканает ![]()
Там t разные с разных сторон от =.
поэтому как ни крути уравнение будет 4-й степени.
Это в общем-то коррелирует с потенциальным ответом:
точек пересечения двух эллипсов может быть 4,2 или 1 — ровно как и действительных решений уравнения 4-й степени.
Может есть какая либа на эту тему?
Re[5]: Пересечение эллипсов
|
|
От: |
Alglib |
|
| Дата: | 23.10.03 10:22 | ||
| Оценка: |
EX>>>Не работает ссылка. Но я нашел тут: http://alglib.chat.ru/
EX>>>![]()
A>>вроде проверял, но поскольку я сайт забросил, уже давно — вполне возможно![]()
A>>если надо могу код на Паскале прислать.
EX>Буду признателен. Ибо вдалбливать это с 0-ля жутко неохота.
EX>Точнее неохота потом глюки неделю ловить ![]()
куда кидать? там просто две процедуры, решения уравнения третьей и четвертой степени сюда вставлять много места займет![]()
и вот здесь еще посмотри.
EX>Пинать не буду, но не проканает ![]()
EX>Там t разные с разных сторон от =.
мдя…. чегой-то я совсем не того ….. ![]()
EX>поэтому как ни крути уравнение будет 4-й степени.
ну если покрутить может чего и получится? ![]()
EX>Это в общем-то коррелирует с потенциальным ответом:
EX>точек пересечения двух эллипсов может быть 4,2 или 1 — ровно как и действительных решений уравнения 4-й степени.
может еще быть ни одной или бесконечно много.
EX>Может есть какая либа на эту тему?
ну думаю наверное есть, только я не знаю где![]()
Re[6]: Пересечение эллипсов
|
|
От: |
e-Xecutor |
|
| Дата: | 23.10.03 11:23 | ||
| Оценка: |
Здравствуйте, Alglib, Вы писали:
EX>>>>Не работает ссылка. Но я нашел тут: http://alglib.chat.ru/
EX>>>>![]()
A>>>вроде проверял, но поскольку я сайт забросил, уже давно — вполне возможно![]()
A>>>если надо могу код на Паскале прислать.
EX>>Буду признателен. Ибо вдалбливать это с 0-ля жутко неохота.
EX>>Точнее неохота потом глюки неделю ловить ![]()
A>куда кидать? там просто две процедуры, решения уравнения третьей и четвертой степени сюда вставлять много места займет![]()
Кинь на xecutor@sendmail.ru плиз.
A>и вот здесь еще посмотри.
Мдя. Сишный код генерёный из фортрановского… Это дааа…
Мне проще будет из паскалевского в С перегнать ![]()
Re[7]: Пересечение эллипсов
|
|
От: |
Alglib |
|
| Дата: | 23.10.03 11:50 | ||
| Оценка: |
EX>Кинь на xecutor@sendmail.ru плиз.
лови
A>>и вот здесь еще посмотри.
EX>Мдя. Сишный код генерёный из фортрановского… Это дааа…
EX>Мне проще будет из паскалевского в С перегнать ![]()
а не надо искать легких путей![]()
Re[8]: Пересечение эллипсов
|
|
От: |
e-Xecutor |
|
| Дата: | 28.10.03 07:24 | ||
| Оценка: |
Здравствуйте, Alglib, Вы писали:
EX>>Кинь на xecutor@sendmail.ru плиз.
A>лови
A>>>и вот здесь еще посмотри.
EX>>Мдя. Сишный код генерёный из фортрановского… Это дааа…
EX>>Мне проще будет из паскалевского в С перегнать ![]()
A>а не надо искать легких путей![]()
В общем сенькаю веримачно ![]()
Заработало.
Re[9]: Пересечение эллипсов
|
|
От: |
Alglib |
|
| Дата: | 29.10.03 07:39 | ||
| Оценка: |
EX>В общем сенькаю веримачно ![]()
великом
EX>Заработало.
куль
Re[9]: Пересечение эллипсов
|
|
От: |
Vlad_ |
|
| Дата: | 11.09.08 11:14 | ||
| Оценка: |
Здравствуйте, e-Xecutor, Вы писали:
EX>Здравствуйте, Alglib, Вы писали:
EX>>>Кинь на xecutor@sendmail.ru плиз.
A>>лови
A>>>>и вот здесь еще посмотри.
EX>>>Мдя. Сишный код генерёный из фортрановского… Это дааа…
EX>>>Мне проще будет из паскалевского в С перегнать ![]()
A>>а не надо искать легких путей![]()
EX>В общем сенькаю веримачно ![]()
EX>Заработало.
Поделись плиз кодом. Та же задача стоит.
Re[9]: Пересечение эллипсов
|
|
От: |
TheBeard |
|
| Дата: | 12.09.08 11:53 | ||
| Оценка: |
Здравствуйте, e-Xecutor, Вы писали:
EX>Заработало.
Там еще, помнится, засада в стабильности решения. Из-зв возведения коэффициентов в большие степени вылезают нехилые погрешности, причем с геометрической точки зрения случаи выглядят невинно: небольшой эксцентриситет, почти перпендикулярные в месте пересечения контуры.
Есть на эту тему статья в Graphics Gems V: Herbison-Evans, Don, Solving Quartics and Cubics for Graphics, p. 3-15


- Переместить
- Удалить
- Выделить ветку
Пока на собственное сообщение не было ответов, его можно удалить.









 , второе – на
, второе – на  и вычитая одно из другого, получаем уравнение, линейное относительно х. Выражаем из него х через у (при этом выражение будет, вообще говоря, квадратичным по у) и подставляем в одно из данных уравнений. Так и получаем уравнение 4-й степени относительно у.
и вычитая одно из другого, получаем уравнение, линейное относительно х. Выражаем из него х через у (при этом выражение будет, вообще говоря, квадратичным по у) и подставляем в одно из данных уравнений. Так и получаем уравнение 4-й степени относительно у. 