Как найти центральную координату прямоугольника? [закрытый]
Я нарисовал прямоугольник. Я знаю его (x1,y1) верхние левые и (x2,y2) нижние правые координаты.. У меня тоже есть высота h и ширина W нарисованного прямоугольника.. Как найти координаты центра (x, y) ?
в настоящее время я использую следующую формулу.
Он дает правильную координату y, но не повезло в x.
3 ответов
Дайте мне знать ваш код.
центр x =
x + 1/2 ширины
Центр y =
y + 1/2 высоты
Если вы уже знаете ширину и высоту, вам нужен только один набор координат.
мы можем рассчитать, используя среднюю точку формулы линии,
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:

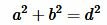 . . |
(1) |
Из равенства (1) найдем d:
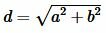 . . |
(2) |
Пример 1. Стороны прямоугольника равны  . Найти диагональ прямоугольника.
. Найти диагональ прямоугольника.
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя  в (2), получим:
в (2), получим:

Ответ: 
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac<large d> <large 2>) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac<large sqrt> <large 2>) | (4) |
Пример 2. Стороны прямоугольника равны  . Найти радиус окружности, описанной вокруг прямоугольника.
. Найти радиус окружности, описанной вокруг прямоугольника.
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя  в (4), получим:
в (4), получим:


Ответ: 
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
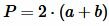 |
(5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны  . Найти периметр прямоугольника.
. Найти периметр прямоугольника.
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя  в (5), получим:
в (5), получим:

Ответ: 
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 |
(6) |
 |
(7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 |
(8) |
 |
(9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
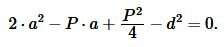 |
(10) |
Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул:
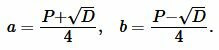 |
(12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
( frac< P><2>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна  , а периметр равен
, а периметр равен  . Найти стороны прямоугольника.
. Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим  ,
,  в (11):
в (11):

Подставляя значения  и
и  в первую формулу (12), получим:
в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения  и
и  в формулу, получим:
в формулу, получим:

Ответ:  ,
, 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Как точно определить центр круга?
Как найти центр начерченной окружности?
Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр.
Как найти центр окружности без измерений?
Надо просто отложить внутри окружности две любых линии (хорды), не параллельных друг другу. Провести перпендикулярные линии через середины этих хорд к противоположной точке на окружности. И снова пересечение этих двух будет являться центром.
Как при помощи циркуля найти центр окружности?
При помощи циркуля начертите две пересекающиеся окружности.
Центром первой окружности сделайте точку А, а второй окружности – точку В. Чертите окружности так, чтобы они пересекались наподобие диаграммы Венна.
Как найти центр окружности из уравнения?
Уравнение окружности ω (A; R) имеет вид (x – a)2 + (y – b)2 = R2, где a и b – координаты центра A окружности ω (A; R) .
Как найти центр круга при помощи линейки?
Воспроизвести ее совсем нетрудно: необходимо лишь положить линейку на круг в любом месте так, чтобы она пересекала окружность в двух местах, и провести карандашом прямую линию. Отрезок внутри окружности и будет хордой.
Как вычислить длину окружности?
Формула Чтобы найти длину окружности, нужно либо диаметр окружности умножить на π ≈ 3 , 1415926535 … , либо найти удвоенное произведение радиуса и числа . Здесь – это радиус заданной окружности, а – диаметр, π ≈ 3 , 1415926535 … .
Как рассчитать диаметр круга по длине окружности?
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
Как разделить окружность на 6 равных частей?
Как разделить окружность на 6 частей с помощью циркуля
(окружность красного цвета). Не изменяя радиуса, переносим ножку циркуля на окружность (точка 1) и чертим еще одну окружность. Получаем две точки пересечения черной и красной окружностей 6 и 2.
Как определить радиус?
R = D : 2, где D — диаметр. Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Что такое центр круга?
Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности.
Как найти середину тарелки?
Для того, чтобы найти центр, необходимо повернуть наш треугольник таким образом, чтобы его углы касались края нашей тарелочки. Точка пересечения двух прямых будет являться центром окружности. Все эти работы надо делать очень аккуратно.
[spoiler title=”источники:”]
http://matworld.ru/geometry/pryamougolnik.php
http://shnurovik.ru/kak-tochno-opredelit-tsentr-kruga
[/spoiler]
![]()
![]()
Очень просто – измеряем диаметр круга, строим вокруг нашей окружности равносторонний квадрат, со сторонами равными диаметру круга. Стороны квадрата пройдут по касательной к окружности. Далее делим этот квадрат по диагонали на четыре треугольника. В точке пересечения линий будет цент круга.

автор вопроса выбрал этот ответ лучшим
![]()
Galina7v7
[120K]
6 лет назад
Когда говорят о нахождении центра круга или окружности, то многие считают, что это просто, мол, проведи два диаметра.и всё.А как провести диаметр, если центра не видно.Но с помощью циркуля и простой линейки это сделать возможно.
Отмечаем на окружности(обрамляющей круг) четыре произвольных точки A,B,C,D,примерно располагающих на одном расстоянии друг от друга(это даже не важно).Из точек А и В произвольным радиусом провести засечки циркулем. Две точки А1 и В1-точки пересечения засечек, соединяем, и она точно лежит на диаметре круга.
Аналогично для точек С и Д получим точки С1 и Д1, соединяем их, и прямая С1Д1 тоже лежит на другом диаметре круга.Пересечение любых двух диаметров окружности даёт её центр, точку О.
И это один из верных способов построения центра круга и окружности.
![]()
Bokatashka
[22.4K]
8 лет назад
Чтобы найти середину круга нужно провести две хорды. У каждой из них найти середины и провести к ним перпендикулярные лучи. Точка пересечения этих лучей и будет центром круга.

Также центр круга можно найти при помощи циркуля. Для этого нужно провести горизонтальную линию от одной точки окружности до другой (отмечаем точки А и В):

При помощи циркуля начертить два одинаковых перекрывающихся круга с центрами в точках А и В.

Далее проводим вертикальную линию через точку, в которой круги пересекаются. Отмечаем на окружности точки C и D:

Для удобства стираем два вспомогательных круга и получаем такой рисунок:

Чертим ещё два одинаковых перекрывающихся круга с центрами в точках С и D:

Проводим горизонтальную линию через точки пересечения этих двух кругов. Отмечаем на окружности точки Е и F:

Стираем вспомогательные круги. Точка пересечения прямых СD и EF (назовём её точкой О) и будет искомой серединой круга.

Чтобы найти центр круга, достаточно провести диаметр и построить к нему перпендикуляр с помощью циркуля и линейки.
сначала проводим через круг линию (можно произвольно, но лично я для удобства провожу горизонтальную) и с помощью циркуля и линейки проводим перпендикулярную линию, которая делит нашу хорду и весь круг ровно пополам. Аналогично проводим перпендикуляр к уже полученному диаметру и находим центр круга. Ко всему прочему – мы еще разделили окружность на четыре ровные части.

Но бывает, что диаметр провести нельзя, так как есть только часть круга, тогда можно применить способ. который подходит практически везде:
в произвольном месте провести две хорды и через их центры провести перпендикуляры – в точке пересечения и будет центр

![]()
Грустный Роджер
[396K]
8 лет назад
Всех делов тут – вспомнить школьную геометрию. Два радиуса и хорда дают равнобедренный треугольник, в котором высота, опущенная на основание, делит его пополам.
Поэтому на окружности надо отметить три произвольные точки, и одну из них соединить с двумя другими. Это даст две хорды. Теперь делим эти хорды пополам и к каждой проводим перпендикуляр к середине – это стандартная школьная задачка на построение циркулем и линейкой. Точка пересечения перпендикуляров и будет центром круга.
![]()
Мне представляется достаточно простой способ нахождения центра окружности путем вписывания в нее прямоугольника. То есть проводим произвольную хорду и принимаем этот отрезок за одну сторону прямоугольника. Достраиваем сперва перпендикулярные стороны из точек пересечения хорды с окружностью, потом достраиваем противоположную параллельную сторону. Вся проблема – в проведении перпендикуляров, но и во всех остальных методах применяется тот же принцип построения. После получения такого прямоугольника проводим в нем диагонали и вуаля, точка их пересечения и будет центром окружности, ну а сами диагонали окажутся диаметрами.

![]()
Ксарфакс
[156K]
6 лет назад
Чтобы найти центр круга, можно отметить 2 любые точки на окружности и провести отрезок.
Затем нужно провести ещё один отрезок, имеющий такую же длину и параллельный первому отрезку.
Соединяем противоположные концы отрезков линиями, которые будут параллельными друг другу.
Таким образом, получится прямоугольник, который будет вписан в круг.
Центр пересечения его диагоналей и будет центром нашего круга.

![]()
Azamatik
[55.3K]
6 лет назад
Для этого берем треугольник (линейку) и проводим диаметр круга. Далее можно с помощью угольника провести такой же диаметр, перпендикулярный первой линии. Пересечение двух этих линий и будет центром (серединой) круга.
![]()
Ярослава Лещинская
[29.9K]
8 лет назад
Найти середину круга очень просто. Надо нарисовать круг и провести диаметр слева направо и сверху вниз, точка соединения линий и будет середина круга. Если круг уже вырезан, сложить его пополам и еще раз пополам, в точке соединений сгибов и будет середина круга.
Водяной
[7.5K]
8 лет назад
Проводим две не параллельные любые хорды. Каждую хорду делим пополам, известным всем способом, как делят отрезки при помощи циркуля и линейки. В точке пересечения разделивших хорды лучей получим центр окружности.
Как найти центральную координату прямоугольника? [закрытый]
Я нарисовал прямоугольник. Я знаю его (x1,y1) верхние левые и (x2,y2) нижние правые координаты.. У меня тоже есть высота h и ширина W нарисованного прямоугольника.. Как найти координаты центра (x, y) ?
в настоящее время я использую следующую формулу.
Он дает правильную координату y, но не повезло в x.
3 ответов
Дайте мне знать ваш код.
центр x =
x + 1/2 ширины
Центр y =
y + 1/2 высоты
Если вы уже знаете ширину и высоту, вам нужен только один набор координат.
Определить центр прямоугольника
Не знаю, как точно называется. Допустим, есть прямоугольник такого вида: 
Как определить его центр? Система координат декартова, координаты каждой вершины известны(x, y). Или подскажите, в какую сторону курить.
Должно работать для любого параллелепипеда:
Достаточно даже 2 противоположных вершин:
![]()
Всё ещё ищете ответ? Посмотрите другие вопросы с метками математика или задайте свой вопрос.
Site design / logo © 2022 Stack Exchange Inc; user contributions licensed under cc by-sa. rev 2022.6.10.42345
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Как найти центр прямоугольника
Я нарисовал прямоугольник. Я знаю его (x1, y1) верхний левый и (x2, y2) нижний правый координаты. У меня также есть высота h и ширина w рисованного прямоугольника. Как найти координаты центра (x, y)?
В настоящее время я использую следующую формулу.
Он дает правильную координату y, но не везет в x.

- Выберите вкладку “Главная” панель “Рисование” раскрывающийся список “Прямоугольник” Угол .
 найти
найти - Продолжайте нажимать клавишу пробела до тех пор, пока не появится курсор

Свойства
Зная стороны прямоугольника, можно вычислить все остальные его параметры, используя следующий ход действий. Периметр прямоугольника представляет собой удвоенную сумму его сторон, поэтому его можно сразу вычислить. P=2(a+b)
Площадь прямоугольника равна произведению его сторон, поэтому ее также можно найти сразу. S=ab
Диагонали в прямоугольнике являются конгруэнтными, каждая из них образует прямоугольный треугольник со сторонами прямоугольника. Из теоремы Пифагора каждая диагональ будет равна квадратному корню из суммы квадратов сторон прямоугольника. (рис. 56.1) d_1=d_2=√(a^2+b^2 )
Из этого же прямоугольного треугольника можно найти углы α и β при диагоналях, зная только стороны прямоугольника. Отношения катетов друг к другу дают тангенс или котангенс углов треугольника, поэтому α и β будут равны арктангенсу отношений сторон, а дальше значение в градусах можно найти, используя таблицы тангенсов. α=arc tan〖b/a〗 β=arc tan〖a/b〗
Углы γ и δ, образованные пересечением диагоналей, как видно из чертежа, через прямоугольный треугольник с полуосью, равны удвоенным значениям α и β соответственно. (рис.56.2) γ=2α δ=2β
Так как углы у прямоугольника все равны друг другу, вокруг него можно описать окружность. Центр окружности будет находиться в точке пересечения диагоналей, и следовательно, радиус описанной окружности будет равен половине диагонали. (рис.56.3) R=d/2=√(a^2+b^2 )/2
Нахождение центра окружности с помощью любого прямоугольного предмета
Простой способ найти центр круга с помощью любого прямоугольного объекта. Здесь мы используем чертежный треугольник 45-45-90, но подойдет любой угол, угол которого равен 90°, например угол листа бумаги.

Центр окружности находится в точке C, где пересекаются два диаметра.
На этой странице показано, как найти центр круга, используя любой прямоугольный объект. Этот метод работает в результате использования теоремы Фалеса в обратном порядке. Диаметр окружности образует прямой угол с любой точкой окружности. Поместив угол объекта под углом 90° на окружность, мы можем найти диаметр. Найдя два диаметра, мы установим центр их пересечения.
Почему это работает
Этот метод работает в результате теоремы Фалеса. Диаметр окружности образует прямой угол с любой точкой окружности. Верно и обратное: прямой угол на окружности должен отрезать диаметр. Найдя два диаметра, мы найдем центр их пересечения.
Download Article
Download Article
Finding the center of a circle can help you perform basic geometric tasks like finding the circumference or area. There are several ways to find the center point! You can draw crossed lines, you can draw overlapping circles, or you can use a straightedge and ruler.
Things You Should Know
- Measure out and draw a set of crossed lines inside of a circle to pinpoint the center.
- Sketch two separate sets of overlapping circles to identify the exact center point.
- Draw a square snugly around the circle. Sketch an “X” between all 4 corners of the square to find the circle’s center.
-

1
Draw a circle. Use a compass, or trace any circular object. The size of the circle does not matter. If you’re finding the center of an existing circle, then you don’t need to draw a new circle.
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store![1]
- A geometry compass is a tool specifically designed to draw and measure circles. Buy one in a school or office supply store![1]
-

2
Sketch a chord between two points. A chord is a straight line segment that links any two points along the edge of a curve.[2]
Name the chord AB.- Consider using a pencil to sketch your lines. This way, you can erase the marks once you’ve found the center. Draw with a light touch so that it’ll be easier to erase.
Advertisement
-

3
Draw a second chord. This line should be parallel and equal in length to the first chord that you drew. Name this new chord CD.[3]
-

4
Make another line between A and C. This third chord (AC) should stretch through the center of the circle – but you will need to draw one more line to find the exact center point.
-

5
Join B and D. Draw one final chord (BD) across the circle between Point B and Point D. This new line should cross over the third chord (AC) that you drew.
-

6
Find the center. If you have drawn straight and accurate lines, then the center of the circle lies at the intersection of the crossed lines AC and BD.[4]
Mark the center point with a pen or pencil. If you only want the center point marked, then erase the four chords that you drew.
Advertisement
-

1
Draw a chord between two points. Use a ruler or straightedge to draw a straight line inside the circle, from one edge to another. The points that you use don’t matter. Label the two points A and B.
-

2
Use a compass to draw two overlapping circles. The circles should be the exact same size. Make A the center of one circle, and B the center of the other. Space the two circles so that they overlap like a Venn diagram.
- Draw these circles in pencil, not pen. The process will be simpler if you are able to erase these circles later on.
-

3
Draw a vertical line through the two points at which the circles intersect. There will be a point at the top and a point at the bottom of the “Venn diagram” space created between the overlap of the circles. Use a ruler to make sure that the line protrudes straight through these points. Finally, label the two points (C and D) at which this new line crosses the rim of the original circle. This line marks the diameter of the original circle.
-

4
Erase the two overlapping circles. This should clear up your work space for the next step of the process. Now, you should have a circle with two perpendicular lines running through it. Do not erase the center points (A and B) of these circles! You will be drawing two new circles.
-

5
Sketch two new circles. Use your compass to draw two equal circles: one with the point C at its center, and one with the point D. These circles, too, should overlap like a Venn diagram. Remember: C and D are the points at which the vertical line intersects the main circle.
-

6
Draw a line through the points at which these new circles intersect. This straight, horizontal line should cut through the overlap space of the two new circles. This line is the second diameter of your original circle, and it should be exactly perpendicular to the first diameter line.
-

7
Find the center. The intersection point of the two straight diameter lines is the exact center of the circle! Mark this center point for reference. If you want to clean up the page, feel free to erase the diameter lines and the non-original circles.
Advertisement
-

1
Draw two straight, intersecting tangent lines onto the circle. The lines can be completely random. However, the process will be easier if you make them roughly square or rectangular.[5]
-

2
Translate both of the lines to the other side of the circle. You will end up with four tangent lines forming a parallelogram or a rough rectangle.
-

3
Draw the diagonals of the parallelogram. The point where these diagonal lines intersect is the circle’s center.
-

4
Check the accuracy of the center with a compass. The center should be on target as long as you didn’t slip while translating the lines or when drawing the diagonals. Feel free to erase the parallelogram and diagonal lines.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
How do you find the center of a circle if you’re only given the equation?

David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

Academic Tutor
Expert Answer
-
Question
How do you find the center of the circle if you’re only given the endpoints of the diameter?

David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.

Academic Tutor
Expert Answer
-
Question
In the first method, what do I do if the chords are of different lengths?

It’s not easy to construct parallel chords of equal length. In practice, it would be a process of trial and error until you get the chords you need. But the real goal here is to find the center of a circle, and here’s a way to do it without worrying about equal and parallel chords: (1) draw any two or more chords; (2) perpendicularly bisect each chord (using either a compass or a ruler and right triangle; (3) the perpendicular bisectors will intersect at the circle’s center.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
You can also find the center of a circle by mathematically “completing the square.”[6]
This is useful if you are given a circle equation, but you aren’t working with a physical circle. -
Try using graph paper instead of blank or ruled paper. It might help to have the perpendicular lines and boxes for guidance.
-
If you have right angled square, place the corner anywhere along the circumference. Draw the 2 lines that intersect the circumference. Draw a line between those 2 points. Repeat on any other point on the circle. Where the lines intersect is the centrepoint.
Advertisement
-
A straightedge is not the same as a ruler. A straightedge can be any straight and even surface, but a ruler shows measurements. You can turn a straightedge into a functional ruler by marking it with inch or centimeter increments.
-
In order to find the true center of a circle, you must use a geometric compass and a straightedge.
Advertisement
Things You’ll Need
- Pencil
- Paper
- Straightedge
- Geometric compass
- Grid paper
References
About This Article
Article SummaryX
To find the center of a circle, start by drawing a straight line between 2 points on the circle. Don’t worry about trying to draw the straight line so it’s in the center — anywhere on the circle will do. Then, draw a second straight line that’s parallel to the first line on the opposite side of the circle. Next, draw a diagonal line from the first end of the first line to the opposite end of the second line. Repeat with the other two ends so that you’ve drawn an “X.” The point where the lines intersect is the center of the circle! If you want to learn how to draw overlapping circles to find the center, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 753,213 times.
Reader Success Stories
-

“I had a circular piece of wood that was a circular tabletop that I wanted to use for something else. I needed to…” more
