Лабораторная
работа 3
Изучение адсорбции пав на границе водный раствор – воздух
Краткая
теория:
Явление адсорбции
всегда связано с границей раздела фаз.
Адсорбция
может происходить
на любой поверхности раздела фаз:
«жидкость –
газ», «твердое
тело – газ»,
«твердое
тело – раствор»,
«жидкость –
жидкость».
Вещество, на
поверхности которого происходит
адсорбция, называется адсорбентом,
а поглощаемое вещество – адсорбтивом
или адсорбатом.
Состояние, в котором находится вещество
на границе раздела фаз в поверхностном
слое, существенно отличается от его
состояния в объеме фазы. Например, в
случае однокомпонентной двухфазной
системы «вода – водяной пар» (рис.7)
межмолекулярные силы, действующие на
молекулу воды, расположенную в объеме
фазы, распределены равномерно со стороны
соседних молекул. Молекулы, находящиеся
на поверхности раздела фаз, испытывают
действие межмолекулярных сил в большей
степени со стороны жидкой фазы и почти
не взаимодействуют с молекулами
газообразной фазы. Так как в газовой
фазе молекул газообразного вещества
намного меньше в единице объема и к тому
же они находятся на больших расстояниях
друг от друга, а следовательно и силы
Ван-дер-Ваальса здесь ничтожны малы.
Поэтому каждая отдельная молекула на
поверхности жидкости обладает большей
энергией по сравнению с энергией молекулы
в объеме фазы («глубинной»). Она находится
в неравновесном состоянии и стремится
втянуться в объем жидкости. Суммарный
избыток энергии всех молекул поверхностного
слоя, отнесенный к единице поверхности
раздела фаз, называется поверхностным
натяжением.
Поверхностное
натяжение обычно обозначают буквой σ
и измеряют
в Дж/м2
или Н/м, поскольку поверхностное натяжение
можно представить как силу, действующую
на единицу длины.
Поверхностное
натяжение s
есть
величина, измеряемая энергией Гиббса,
приходящейся на единицу площади
поверхностного слоя. Оно численно равно
работе, которую необходимо совершить
против сил межмолекулярного взаимодействия
для образования единицы поверхности
раздела фаз при постоянной температуре
(рис.7).
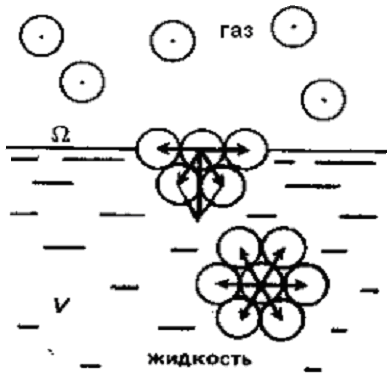
Рис.7.
![]()
(3.1)
Концентрирование
вещества на поверхности раздела фаз
называется адсорбцией.
Жидкость или твёрдое тело, на поверхности
которого происходит адсорбция называется
адсорбентом,
а вещество, образующее поверхностный
слой (адсорбирующийся газ или растворённое
вещество) – адсорбатом.
Количество
адсорбированного вещества обычно
определяется избытком вещества на
границе фаз по сравнению с равновесным
количеством. Избыток
вещества в молях, отнесенный к 1 см2
(или 1м2)
поверхности – называют адсорбцией.
Обозначают адсорбцию чаще всего буквой
Г и
рассчитывают по формуле:
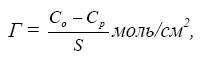
где
Со
и Ср
– начальная
и равновесная концентрации растворенного
вещест-
ва,
моль; S –
поверхность адсорбента, см2.
Адсорбция
по Гиббсу
– это избыток адсорбата в адсорбционном
слое, выражается в моль/см2.
Количественно связь между
величиной адсорбции и изменением
поверхностного натяжения с концентрацией
раствора d σ/ dC дается адсорбционным
уравнением Гиббса (1878 г.):
![]()
для
растворённых веществ (3.2)
![]()
для
адсорбции газов или паров (3.3)
где
С
– объёмная концентрация растворённого
вещества в моль/л, Р
– парциальное давление адсорбирующегося
газа в атм., К
– универсальная газовая постоянная
равная 8,31107
эргмоль-1град-1,
Т
– абсолютная температура в К,
![]()
– поверхностная активность (характеризует
способность вещества изменять
поверхностное натяжение).
Зависимость
адсорбции Г
от равновесной концентрации С
или давления Р
при постоянной температуре называется
изотермой
адсорбции.
Все
вещества по их воздействию на поверхностное
натяжение воды можно разделить на три
группы (рис.8):
1.
Поверхностно-активные
вещества (ПАВ)
понижают поверхностное натяжение
растворителя (sр.р<s0),
g>0.
Поверхностно-активными
веществами являются органические
соединения, молекулы которых имеют
дифильное строение, т.е. они содержат в
молекулах одновременно гидрофобную и
гидрофильную группы. В качестве
гидрофобной группы обычно выступает
углеводородный радикал, содержащий 10
– 18 углеродных атомов, чаще всего
линейного строения. К гидрофильным
группам могут относиться группы: –СООН,
–СООNа, –SО3Nа,
–ОН, –NН2
и др. Поэтому
такие молекулы называются дифильными,
т.е. обладающими двойным сродством
одновременно и с полярной, и неполярной
фазами. Если гидрофобные группы не
растворяются в воде и стараются
«оттолкнуться» от нее, то гидрофильные
группы, наоборот, легко взаимодействуют
с ней. В связи с этим молекулы
поверхностно-активных веществ
располагаются на границе раздела фаз
(в поверхностном слое) таким образом,
что гидрофильные группы направлены к
воде и растворены в ней, а гидрофобные
– выталкиваются из нее. Дифильные
молекулы ПАВ схематически на рисунках
чаще всего изображают в виде круглой
головки (гидрофильной части) с хвостиком
(гидрофобной, углеводородной частью):
о/////
или
○—
Тогда расположение
молекул ПАВ на границе раздела фаз можно
изобразить следующими образом
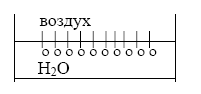
Дифильные молекулы,
попадая в воду, на границе раздела фаз
ориентируются полярными группами
(гидрофильными) в воду, а неполярными
углеводородными радикалами (гидрофобными)
в воздух, так как сродство их с газообразной
фазой больше, чем с водой. Интенсивность
межмолекулярных сил в газе невелика, и
поэтому газ или пар условно можно считать
неполярной фазой.
2.
Поверхностно-инактивные
вещества (ПИВ)
незначительно повышают поверхностное
натяжение растворителя (sр.р
>s0),
g<0
(неорганические кислоты, основания,
соли, глицерин, a-аминокислоты
и др).
3.
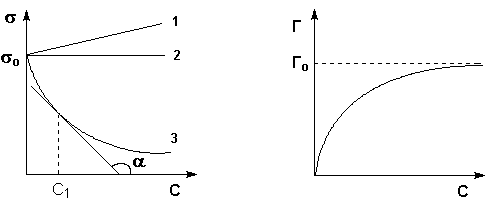
Рис.8.
Изотермы
поверхностного натяжения и
адсорбции
растворов ПАВ (3), ПНВ (2) и ПИВ (1)
3.
Поверхностно-неактивные вещества (ПНВ)
практически не изменяют поверхностного
натяжения растворителя (sр.р
=s0),
g=0 (по отношению к воде веществами
являются сахароза и ряд других).
Правило Дюкло –
Траубе: в
любом гомологическом ряду при малых
концентрациях удлинение углеродной
цепи на одну группу СН2
увеличивает поверхностную активность
в 3 –
3,5 раза:
![]()
(3.4)
Объяснение правила
Траубе с точки зрения молекулярно-кинетической
теории, данное Ленгмюром, позволяет
уточнить представление о структуре
адсорбционного слоя. Адсорбированные
молекулы ПАВ прочно связаны с водой
полярными, гидрофильными группами
–СООН, –ОН,
–NН2, –СN и
др., а углеводородные радикалы – слабее,
и до тех пор, пока концентрация мала,
молекулы находятся в «лежачем» положении
на границе фаз. К этому случаю и применимо
правило Траубе, так как увеличение длины
углеводородной цепи молекулы ПАВ влияет
на поверхностное натяжение. При увеличении
концентрации ПАВ происходит сжатие
адсорбционного слоя, углеводородные
радикалы отрываются от воды и принимают
наклонное положение к поверхности
раздела, а при максимально возможной
адсорбции молекулы располагаются
перпендикулярно поверхности раздела,
образуя так называемый «частокол»
Ленгмюра. Поэтому естественно предположить,
что максимальная адсорбция Г∞,
значение которой находится графически
из экспериментальных данных, определяется
именно размерами полярной группы и
адсорбированный слой при этом
мономолекулярен.
Отсюда можно вычислить и площадь So,
приходящуюся на одну полярную группу
в адсорбированном слое:
![]()
где
NA
– число
Авогадро.
Толщина адсорбционного
слоя l∞
рассчитывается
исходя из значения максимально возможной
адсорбции Г∞,
молярной массы М
и ρ
плотности
растворов ПАВ:
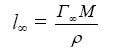
Поверхностное
натяжение жидкостей определяют с помощью
прибора
Ребиндера
(рис.9).
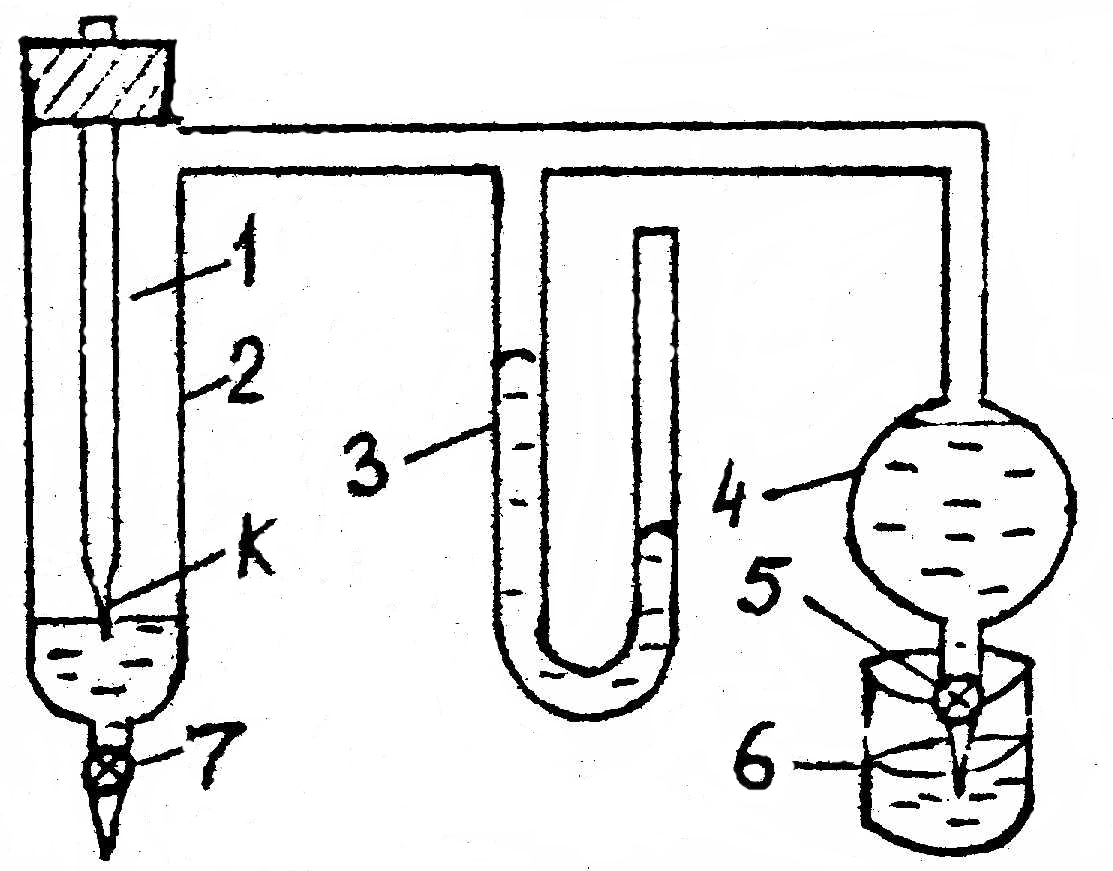
Рис.9.
Прибор для определения поверхностного
натяжения
где
1 – трубка с капилляром К, который
погружается в жидкость не более чем на
1 мм; 2 – пробирка с исследуемой жидкостью,
заканчивающаяся зажимом 7; 3 – манометр;
4 – аспиратор с водой; заканчивающийся
зажимом 5; 6 – сливной стакан.
Для
двух жидкостей с различными значениями
поверхностного натяжения существует
зависимость:
![]()
(3.5)
где
σ0
– поверхностное натяжение воды
(растворителя) в дн/см (Приложение 6), σ
– поверхностное натяжение добавленного
вещества (ПАВ, ПИВ, ПНВ) в дн/см, Р0
и Р
– соответствующие им избытки давления
над внешним давлением при проскоке
пузырька.
Цель
работы:
По
результатам определения поверхностного
натяжения раствора ПАВ построить
изотерму адсорбции ПАВ на поверхности
воды.
Оборудование:
Прибор для определения поверхностного
натяжения, два химических стаканчика,
штатив.
Реактивы:
Поверхностно-активное вещество,
дистиллированная вода, фильтровальная
бумага.
Порядок
работы:
-
Получить
у лаборанта прибор для определения
поверхностного натяжения (см. рис. 9).
Проверить, достаточно ли плотно
закрываются пробками пробирка 2 и
аспиратор 4, а также, хорошо ли заполнен
манометр (уровень воды в нём должен
составлять три четверти от его высоты,
и в воде не должно быть пузырьков
воздуха). -
Закрепить
прибор в штативе и тщательно промыть
пробирку 2 и трубку 1 дистиллированной
водой. -
С
помощью воронки залить дистиллированную
воду в аспиратор 4 и плотно закрыть его
пробкой. -
В
чистую пробирку 2 налить немного
дистиллированной воды и плотно закрыть
пробирку со вставленной в неё трубкой
с капилляром. При этом конец капилляра
должен быть погружён в воду на 1 мм. -
При
медленном выливании воды из аспиратора
4 через зажим 5 убедиться в том, что на
конце капилляра образуются пузырьки
воздуха, которые проскакивают через
жидкость в пробирке 2. При этом разность
Р
между атмосферным давлением и давлением
внутри прибора максимальна. -
Определить
максимальный h1
и минимальный h2
уровень воды в коленах манометра при
проскоке пузырьков через жидкость. Эти
измерения произвести не менее трёх раз
и записать их в таблицу 6. Из этих данных
найти средние значения ħ1
и ħ2
и максимальную разность давлений Р0
по формуле:
Р0
= ħ1
– ħ2
мм водн.ст.
-
Через
нижнюю трубку вылить воду из пробирки
2, выдуть воду из капилляра К и осушить
его с помощью фильтровальной бумаги.
Промыть пробирку 2 и капилляр К исследуемым
раствором ПАВ, затем налить его в
пробирку 2 и измерить давление Р,
при котором отрывается пузырёк воздуха,
как это делалось для воды.
Концентрации
растворов ПАВ, поверхностные натяжения
которых надо определить, указаны в
таблице 6.
Измерения
начинать с наиболее разбавленного
раствора и закончить наиболее
концентрированным. Тогда изменение
концентрации раствора ПАВ за счёт
оставшихся в растворе капель жидкости
будет минимальным. Рассчитать максимальную
разность давлений Р
для всех концентраций растворов ПАВ по
формуле:
Р
= ħ1
– ħ2
мм вод.ст.
Результаты
измерений и расчётов записать в рабочую
тетрадь.
-
Используя
формулу:
![]()
(3.6)
где
Р0
– давление, полученное для воды,
σ0
– поверхностное натяжение воды,
Р
– давление для раствора ПАВ данной
концентрации,
определить
поверхностные натяжения σ
растворов ПАВ и записать их значения в
таблицу 5.
-
Построить
изотерму поверхностного натяжения –
график зависимости σ
раствора ПАВ от его концентрации, как
показано на рис.2 в масштабе: по оси σ
10 эрг/см2
– 5 см,
а по оси С
0,05 моль/л
– 1 см.
Таблица
5.
t
= °С
|
Концентрация |
h1, |
h2, |
Р, мм |
σ, |
|
0 |
||||
|
0,05 |
||||
|
0,1 |
||||
|
0,2 |
||||
|
0,3 |
||||
|
0,5 |
-
Из
изотермы поверхностного натяжения
рассчитать величины поверхностных
активностей ∆σ/∆С
для шести указанных в таблице концентраций
ПАВ и записать полученные значения в
таблицу 6а. -
Рассчитать
величины адсорбции ПАВ в зависимости
от его концентрации в растворе по
формуле:
![]()
,
используя значения
∆σ/∆С
записать результаты расчёта в таблицу
6.
Таблица
6.
-
С,
моль/л
Г,
моль/см20,05
0,1
0,2
0,3
0,4
0,5
-
Построить
изотерму адсорбции ПАВ на поверхности
воды. Для этого по оси абсцисс отложить
концентрацию раствора С,
а по оси ординат – адсорбцию Г. -
(По усмотрению
преподавателя)
Вычисление величины предельной
(максимальной) адсорбции – Гmax
Предельная
(максимальная) адсорбция соответствует
полному насыщению поверхностного слоя.
Для определения Гmax
преобразуют
уравнение Ленгмюра:
![]()
где
Гmax
– величина
предельной (максимальной) адсорбции, В
– постоянная,
характеризующая сродство адсорбируемого
вещества к поверхности адсорбента.
Разделим единицу
на обе части этого уравнения, тогда:
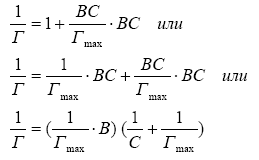
То есть получим
уравнение прямой, проходящей через
начало координат 1/Г
и 1/С
(рис.10).
Отрезок,
отсекаемый прямой ОА на оси ординат,
равен 1/ Гmax
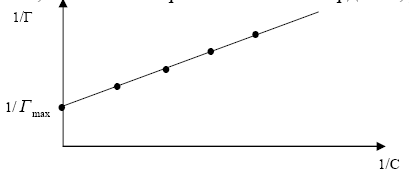
Рис. 10. График
для определения величины Гmax
Определив из
графика значение предельной адсорбции,
рассчитать площадь, приходящуюся на
одну молекулу S0
и толщину
адсорбционного слоя l.
Вопросы
к работе 3
-
В чём заключаются
особенности поверхностного (пограничного)
слоя? -
От каких факторов
зависит поверхностное натяжение
жидкостей? -
Что называется поверхностной активностью,
что является её количественной мерой?
Приведите примеры поверхностно-активных
и поверхностно-неактивных веществ. -
В чём отличие
физической адсорбции от химической? -
Как ориентируются молекулы ПАВ в
насыщенном адсорбционном слое? -
Какие параметры
измеряются при определении поверхностного
натяжения методом Ребиндера? Для чего
необходимо проводить опыт с дистиллированной
водой? -
Как рассчитать
поверхностное натяжение водных растворов
ПАВ на основании полученных значений
давлений? Как определить поверхностную
активность исследованных веществ? -
Нарисуйте на одном
графике изотермы поверхностного
натяжения масляной, уксусной и пропионовой
кислот. -
Во сколько раз
поверхностная активность метанола
отличается от поверхностной активности
пропанола при условии равенства
концентраций их растворов. -
В качестве
противоядия при отравлениях метанолом
применяют этанол. Почему? -
Приведите примеры гидрофильных и
гидрофобных групп в молекулах -
Какие вещества лучше адсорбируются на
гидрофобных поверхностях (ПАВ или ПИВ)?
Почему? Приведите примеры этих пар
адсорбант-адсорбат. -
Как зависит количество адсорбированного
вещества от его концентрации? -
Как изменяется адсорбция с повышением
температуры? -
Изобразите
адсорбцию молекул ПАВ на границе раздела
“уголь – вода”. -
Уравнение Гиббса
для адсорбции. Поясните значение
входящих в него величин. -
Указать, какие из
перечисленных ниже веществ уменьшают,
какие увеличивают, а какие не изменяют
поверхностное натяжение воды: C3H7OH,
KOH,
C6H12O6(фруктоза),
NaCl,
H2SO4,
CH3COONa,
Na2SO4,
HCOOH,
C6H12O6(глюкоза). -
Приведите два
способа уменьшения поверхностного
натяжения воды.
Задачи к работе
3
-
Рассчитайте
поверхностную активность раствора ПАВ
с концентрацией 0,075 М
при 298 К,
если адсорбция равна 710-10
моль/см2
(R=8.31107 эрг/моль). -
Рассчитать величину
адсорбции на границе раздела жидкость
– газ в растворе концентрации 0,2 моль/л
при температуре 27оС,
если поверхностная активность равна
(-50) единиц, R = 8.31107 эрг/(мольК).
Указать, к какому типу – поверхностно-активное,
поверхностно-инактивное или
поверхностно-нейтральное – следует
отнести растворённое вещество? -
Определите тип
адсорбции при растворении в воде серной
кислоты, если концентрация серной
кислоты в воде 2,33 моль/л, поверхностное
натяжение раствора 75,20 Дн/см,
поверхностное натяжение воды 73,05 Дн/см,
t=18°С. -
Определите тип
адсорбции при растворении в воде
ацетона, если концентрация ацетона в
воде 29 г/л, поверхностное натяжение
раствора 59,4 Дн/см, поверхностное
натяжение воды 73,49 Дн/см, t=15°С. -
Сравните
поверхностную активность пропионовой
и масляной кислот в водных растворах
в данном интервале концентраций, если
известно:
|
Кислота |
С, моль/л |
σ, Дн/см |
|
пропионовая |
0,0312 |
69,5 |
|
0,0625 |
67,7 |
|
|
масляная |
0,0312 |
65,8 |
|
0,0625 |
60,4 |
-
Поверхностное
натяжение водного раствора, содержащего
поверхностно-активное вещество (ПАВ)
в концентрации 0,056 моль/л, при 293 К
равно 4,33 Дн/см. Вычислите величину
адсорбции ПАВ из раствора с концентрацией
0,028 моль/л при 293 К. -
С увеличением
концентрации раствора изомасляной
кислоты с 0,125 моль/л до 0,250 моль/л
его поверхностное натяжение снизилось
с 55,1 Дн/см до 47,9 Дн/см, а у раствора
изовалериановой кислоты – с 43,2 Дн/см
до 35,0 Дн/см. Сравните величины
адсорбции веществ в данном интервале
концентраций. -
Вычислите, во
сколько раз изменится величина адсорбции
масляной кислоты из водного раствора
с ростом концентрации по экспериментальным
данным (Т=298 К):
|
С102, |
0,78 |
1,56 |
12,5 |
25,0 |
|
σ, Дн/см |
70,0 |
69,1 |
55,1 |
47,9 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Свободная поверхностная энергия самопроизвольно может только уменьшаться, что проявляется в уменьшении либо поверхности раздела фаз, либо межфазного (поверхностного) натяжения. Поверхностное натяжение может уменьшаться в результате самопроизвольного перераспределения компонентов системы между объемами фаз a и b и поверхностью их раздела. В поверхности раздела фаз будут преимущественно концентрироваться те компоненты, которые способны уменьшать избыточную свободную поверхностную энергию. Это явление получило название «адсорбция». Количественно мерой адсорбции служит избыток вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же слое в объеме фазы. Этот избыток обычно относят к единице площади поверхности (или к единице массы адсорбента). Такая адсорбция называется гиббсовской и обозначается буквой Гi. Поверхностный избыток является алгебраической величиной. Если он положителен, то вблизи поверхности данный компонент присутствует в избытке, если отрицателен, то концентрация компонента на поверхности фазы ниже, чем в ее объеме .
Рассмотрим распределение в системе i -го компонента, предполагая, что это вещество способно понижать поверхностное натяжение. В соответствии с уравнением (1.1.6) число молей n вещества i-го компонента в системе определяется как 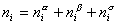 .
.
Количество вещества в обеих фазах составляет
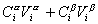 . (1.1.81)
. (1.1.81)
где Сa, Сb– концентрация вещества в фазах a, b.
Количество вещества на поверхности раздела фаз 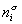 , избыточное по отношению к объемам фаз Va и Vb, оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны,
, избыточное по отношению к объемам фаз Va и Vb, оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны, 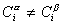 .
.
Учитывая уравнение (1.1.81) ,
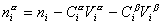 . (1.1.82)
. (1.1.82)
Разделив выражение (1.1.82) на площадь поверхности раздела фаз А, можем определить гиббсовскую адсорбцию:
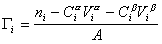 . (1.1.83)
. (1.1.83)
Фундаментальным уравнением физической химии поверхностей является взаимосвязь между адсорбцией и межфазным натяжением, которую можно определить экспериментально при одновременном изменении многих факторов. Остановимся на системах, в которых адсорбция протекает при постоянной температуре. Связь между адсорбцией и межфазным натяжением при постоянной температуре T называется изотермой адсорбции, фундаментальное уравнение которой известно как уравнение Гиббса. Рассмотрим его вывод.
При небольшом обратимом изменении энергии системы dU с учетом формулы (1.1.4) можем написать
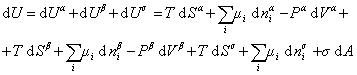 , (1.1.84)
, (1.1.84)
где U – полная внутренняя энергия системы; Ua, Ub, Us– внутренняя энергия фаз aиb и поверхности их раздела; Pa, Pb – давление в фазах aиb; m – химический потенциалi-того компонента; Sa, Sb, Ss – энтропия фаз a иb и их поверхности раздела; s – поверхностное натяжение.
Поскольку из курса химической термодинамики известно, что
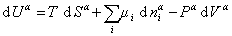 (1.1.85)
(1.1.85)
и
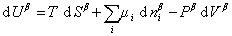 , (1.1.86)
, (1.1.86)
то
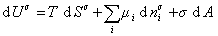 . (1.1.87)
. (1.1.87)
Если энергию, энтропию и количество компонентов увеличивать от нуля до некоторого определенного значения при постоянстве температуры T, площади поверхности раздела фаз A и количестве вещества на этой поверхности 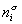 , то уравнение (1.1.87) переходит в общее уравнение
, то уравнение (1.1.87) переходит в общее уравнение
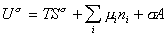 , (1.1.88)
, (1.1.88)
дифференцирование которого приводит к выражению
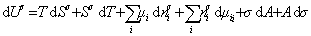 . (1.1.89)
. (1.1.89)
Сравнивая его с уравнением (1.1.88), получаем

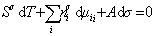 . (1.1.90)
. (1.1.90)
В расчете на единицу поверхности
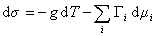 , (1.1.91)
, (1.1.91)
где 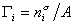 – гиббсовская адсорбция;
– гиббсовская адсорбция; 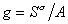 – удельная энтропия поверхностного слоя.
– удельная энтропия поверхностного слоя.
При постоянной температуре
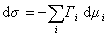 . (1.1.92)
. (1.1.92)
Для двухкомпонентной системы
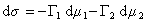 , (1.1.93)
, (1.1.93)
где индекс 1 относится к растворителю, а индекс 2 – к растворенному веществу.
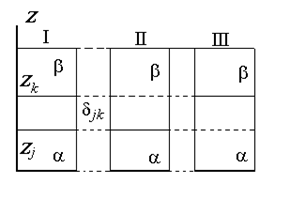 Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)
Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)
Разделяющая поверхность Гиббса может быть проведена так, чтобы обратилась в нуль адсорбция любого наперед заданного компонента, но только одного, как это показано на рис. 1.15.
Расстояние между двумя плоскостями (разделяющими поверхностями), одна из которых соответствует условию Гj = 0, а другая – Гk = 0, обозначим dkj:
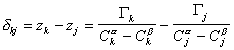 , (1.1.94)
, (1.1.94)
где Гk, Гj– избытки  рассматриваемых компонентов в поверхностном слое ; Cka, Ckb, Cja, Cjb – концентрация компонентов k и j в фазах a и b; zk, zj – координаты разделяющей поверхности.
рассматриваемых компонентов в поверхностном слое ; Cka, Ckb, Cja, Cjb – концентрация компонентов k и j в фазах a и b; zk, zj – координаты разделяющей поверхности.
Поскольку значения Г1 в уравнении (1.1.93) определены относительно произвольно выбранного положения разделяющей плоскости, то ее можно расположить так, чтобы избыток растворителя в поверхностном слое был равен нулю ( Г1 = 0).
Тогда
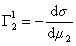 , (1.1.95)
, (1.1.95)
где верхний индекс 1 означает, что для выбранной поверхности раздела Г1=0.
Учитывая зависимость химического потенциала от активности растворенного вещества
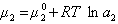 , (1.1.96)
, (1.1.96)
получаем после дифференцирования уравнения (1.1.96)
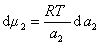 , (1.1.97)
, (1.1.97)
где 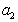 – активность растворенного вещества.
– активность растворенного вещества.
Поэтому, подставляя уравнение (1.1.97) в уравнение (1.1.95), получаем
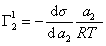 . (1.1.98)
. (1.1.98)
Из уравнения (1.1.98) следует, что если 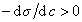 , то адсорбция положительна, а при
, то адсорбция положительна, а при 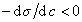 возникает дефицит растворенного вещества на разделяющей поверхности .
возникает дефицит растворенного вещества на разделяющей поверхности .
Поскольку 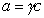 , где g – коэффициент активности, который для разбавленных растворов стремится к единице, то
, где g – коэффициент активности, который для разбавленных растворов стремится к единице, то 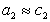 и
и
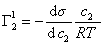 . (1.1.99)
. (1.1.99)
Уравнение (1.1.99) представляет собой наиболее употребляемую форму изотермы адсорбции Гиббса, причем так как рассматривается адсорбция именно растворенного вещества, индексы при адсорбции и концентрации опускают, т.е.
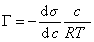 . (1.1.100)
. (1.1.100)
Исследования показывают, что существуют такие вещества, растворение которых приводит к резкому снижению поверхностного натяжения раствора. Эти вещества называют поверхностно-активными. В соответствии с уравнением Гиббса адсорбция их всегда положительна, т.е. концентрация в поверхностном слое выше объемной концентрации. По предложению Ребиндера мера поверхностной активности обозначается первой буквой фамилии Гиббса. Обычно используют значения поверхностной активности в бесконечно разбавленных растворах
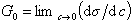 . (1.1.101)
. (1.1.101)
К классу поверхностно-активных веществ (ПАВ) относятся жирные кислоты и их соли (мыла), сульфокислоты, их соли, спирты, алкилсульфоэфиры и др. Если 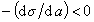 , то Г< 0 (адсорбция отрицательна). Поверхностное натяжение растворов этих веществ на границе с воздухом выше, чем на границе с чистым растворителем (водой). Такие вещества называют поверхностно-инактивными. К ним относятся минеральные соли, основания, кислоты и низшие органические кислоты.
, то Г< 0 (адсорбция отрицательна). Поверхностное натяжение растворов этих веществ на границе с воздухом выше, чем на границе с чистым растворителем (водой). Такие вещества называют поверхностно-инактивными. К ним относятся минеральные соли, основания, кислоты и низшие органические кислоты.
Очевидно, что если 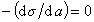 , то Г= 0 (адсорбция не происходит). Такое вещество называют поверхностно-инертным. Вещество, поверхностно-активное на одной границе раздела фаз, может быть неактивным на другой и наоборот. Приведенное выше деление веществ с соответствующими параметрами справедливо для границы водный раствор – воздух. На других границах данные вещества могут вести себя иначе.
, то Г= 0 (адсорбция не происходит). Такое вещество называют поверхностно-инертным. Вещество, поверхностно-активное на одной границе раздела фаз, может быть неактивным на другой и наоборот. Приведенное выше деление веществ с соответствующими параметрами справедливо для границы водный раствор – воздух. На других границах данные вещества могут вести себя иначе.
В 1978 г. Дюкло и Траубе сформулировали эмпирическое правило: в гомологическом ряду поверхностно-активных веществ поверхностная активность и адсорбция возрастают при переходе к каждому последующему члену гомологического ряда примерно в 3,2 раза. Однако это правило справедливо только для весьма разбавленных растворов и исключает три первых члена гомологического ряда. Математически это правило может быть записано
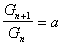 или
или 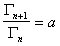 , (1.1.102)
, (1.1.102)
где n – число атомов углерода в углеводородной цепочке;
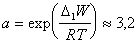 . (1.1.103)
. (1.1.103)
Зависимость поверхностной активности от числа метиленовых групп в углеводородной цепочке ПАВ выражается уравнением
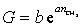 или
или 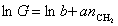 , (1.1.104)
, (1.1.104)
где 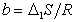 ;
; 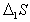 , D1W- изменение энтропии и работа переноса одного моля метиленовых групп из раствора на поверхность.
, D1W- изменение энтропии и работа переноса одного моля метиленовых групп из раствора на поверхность.
Свободно от недостатков правила Дюкло – Траубе эмпирическое уравнение Шишковского (1909 г.), устанавливающее зависимость поверхностного натяжения раствора от его концентрации:
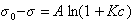 , (1.1.105)
, (1.1.105)
где А – постоянная для всего гомологического ряда, не зависящая от природы ПАВ; при температуре 20°С 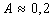 ; K – постоянная, характеризующая увеличение поверхностной активности при переходе к каждому последующему члену гомологического ряда;
; K – постоянная, характеризующая увеличение поверхностной активности при переходе к каждому последующему члену гомологического ряда; 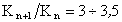 .
.
Замечательно, что это уравнение, полученное на основании обобщения экспериментальных данных, оказалось очень точным и применимым практически для всех ПАВ в широкой области концентраций растворов. Если концентрация ПАВ достаточно велика и следовательно Kc>>1, то единицей в уравнении Шишковского (1.1.105 ) можно пренебречь, тогда
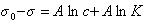
или
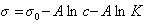 . (1.1.106)
. (1.1.106)
Обозначим постоянной В постоянные при изотермических условиях величины 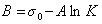 , тогда
, тогда
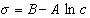 . (1.1.107)
. (1.1.107)
Следовательно, при относительно высокой концентрации растворов ПАВ их поверхностное натяжение должно уменьшаться экспоненциально с увеличением концентрации.
Уравнение (1.1.107) может быть получено непосредственно из уравнения изотермы адсорбции Гиббса:
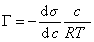 .
.
При достаточно высокой концентрации растворенного вещества адсорбция достигает предела , т.е. Г = Гmax , поэтому
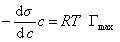 , (1.1.108)
, (1.1.108)
где при постоянной температуре правая часть представляет собой постоянную величину и может быть обозначена RT Гmax = A. Следовательно,
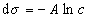 ,
,
откуда после интегрирования получаем
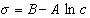 . (1.1.109)
. (1.1.109)
Таким образом, уравнение Шишковского может быть выведено из уравнения Гиббса, так как уравнения (1.1.107) и (1.1.109) идентичны. Точность уравнения Шишковского связана с тем, что в нем уже заложено условие насыщения адсорбционного слоя.
Если уравнение Шишковского в форме
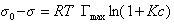 (1.1.110)
(1.1.110)
продифференцировать
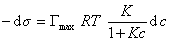 , (1.1.111)
, (1.1.111)
и подставить в уравнение Гиббса величину
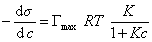 , (1.1.112)
, (1.1.112)
то уравнение изотермы адсорбции примет вид
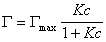 . (1.1.113)
. (1.1.113)
В такой форме уравнение изотермы адсорбции носит название изотермы Ленгмюра. Американский ученый И. Ленгмюр в 1917 г. развил представление о мономолекулярной адсорбции и на основании молекулярно- кинетической теории получил уравнение (1.1.113) .
Уравнение Шишковского позволяет определить предел адсорбции (при Kc>>1), так как в таком случае это уравнение принимает вид
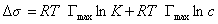 . (1.1.114)
. (1.1.114)
Построив график 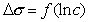 , как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.
, как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.
Понимание адсорбционных процессов имеет чрезвычайно важное значение, так как они лежат в основе многих процессов, протекающих на границе раздела фаз, например крашения, отмывания загрязнений, отделки текстильных материалов и т.д., т.е. в основе всех коллоидно -химических процессов на границе жидкость–газ.
Связь между величиной адсорбции, концентрацией ПАВ и изменением поверхностного натяжения дает фундаментальное уравнение адсорбции Гиббса. Для -компонентной системы оно имеет вид [c.14]
Изменение поверхностного натяжения водных растворов при наличии в них ПАВ обусловлено, как известно, адсорбцией ПАВ на границе между раствором и газом (воздухом). Именно на явлении адсорбции, а не на изменении натяжения основано практическое применение ПАВ, хотя эти два явления тесно связаны, в частности, уравнением изотермы адсорбции Гиббса. В связи с этим далее будет подразумеваться, что по-верхностно-активное вещество — это вещество, которое адсорбируется на границе раздела фаз. Акцент на адсорбции, а не на изменении натяжения, необходим потому, что адсорбция в принципе всегда может быть измерена, тогда как измерение натяжения возможно только на границе двух флюидных фаз (жидкость—газ и жидкость 1— жидкость 2). Натяжение же на границе твердого вещества с любой флюидной фазой не может быть измерено, следовательно, эффективность ПАВ не [c.795]
Слабое эмульгирование может быть получено с любым ПАВ, т. е. с любым соединением, которое понижает поверхностное натяжение между двумя жидкостями. Последнее связано с адсорбцией ПАВ на межфазной поверхности и влияет как на легкость диспергирования при получении эмульсии, так и на скорость разрушения жидкой пленки между каплями. Согласно некоторым взглядам, существенным фактором стабилизации является эластичность пленки. Ниже изложена хорошо известная теория этого явления Марангони и Гиббса . [c.84]
В растворах стремление к уменьшению свободной поверхностной энергии проявляется преимущественно в понижении поверхностного натяжения путем адсорбции поверхностно-активных веществ из раствора на поверхности раздела. Количественно связь между адсорбцией и понижением поверхностного натяжения определяется уравнением Гиббса (IV.6). Изменение поверхностного натяжения с концентрацией растворов выражается уравнением Шишковского (IV.9), а изменение поверхностной активности в гомологическом ряду — правилом Траубе. [c.89]
Связь между адсорбцией и понижением поверхностного натяжения, т. е. двухмерным давлением ps = 0(, — Ср, описывается уравнением Гиббса [c.46]
При физической адсорбции связь между уменьшением поверхностного натяжения адсорбента Отг, удельной адсорбцией Г и давлением адсорбата р описывается термодинамическим уравнением Гиббса [2] [c.32]
Количественная связь между адсорбцией и изменением поверхностного натяжения выражается уравнением Гиббса [c.287]
Уравнение, устанавливающее связь между всеми параметрами процесса адсорбции — величиной поверхностного натяжения а, концентрацией компонента с в одной из фаз, его адсорбцией Г, было выведено Дж. Гиббсом в 1876 г. Оно является общим термодинамическим уравнением, справедливым для любых составов и природы поверхности раздела фаз.Уравнение Гиббса— одно из важнейших уравнений, описывающих поверхностные явления. [c.207]
Связь между изменением поверхностного натяжения и изменением заряда межфазной границы может быть получена термодинамическим путем. С этой целью удобно характеризовать заряженный компонент (например, ионы, которые адсорбируются на межфазной поверхности) его электрохимическим потенциалом [х. Если ограничиться случаем, когда этот компонент находится только на межфазной границе, то произведение цйп (п — количество заряженного компонента в молях или грамм-ионах) будет равно электростатической работе заряжания единицы площади поверхности при адсорбции на ней йп молей заряженного компонента, несущих электрический заряд ск/. Эту электрическую работу можно, очевидно, представить как где ф — электрический потенциал поверхности, так что [c.99]
В условиях физической монослойной адсорбции, когда исключены какие-либо побочные процессы, в том числе и образование прочных пленок, адсорбция сначала пропорциональна равновесной концентрации, затем отстает от ее роста и, наконец, приходит к, насыщению, когда дальнейший рост концентрации не вызывает никаких изменений в адсорбционном слое. Одновременно с ростом адсорбции снижается поверхностное натяжение, степень и характер которого (снижение) зависят исключительно от величины адсорбции. Связь между адсорбцией и изменением поверхностного натяжения была количественно установлена работами Гиббса, Шишковского, Лангмюра и др. [c.23]
Роль растворителя в адсорбции также не может быть охарактеризована универсальными закономерностями. Большей частью соблюдается правило, что поглощение одного и того же вещества из разных растворителей обратно пропорционально его растворимости в них. Например отношение поглощения иода углем в сероуглероде, хлороформе и четыреххлористом углероде равно 4,5 2 1, а отношение растворимостей в них равно 1 1,8 4,8. Замечается также некоторый параллелизм между ростом поверхностного натяжения растворителя и ростом поглощения, что также можно поставить в связь с поверхностной активностью. [c.350]
ИССЛЕДОВАНИЕ СВЯЗИ МЕЖДУ ПОВЕРХНОСТНЫМ НАТЯЖЕНИЕМ И адсорбцией [c.107]
СВЯЗЬ МЕЖДУ АДСОРБЦИЕЙ И ПОВЕРХНОСТНЫМ НАТЯЖЕНИЕМ [c.141]
На поверхности, образующейся между двумя жидкостями, не смешивающимися между собой или обладающими ограниченной взаимной растворимостью, существуют соотношения, аналогичные рассмотренным. Поверхностное натяжение на поверхности раздела между двумя жидкостями обычно значительно меньше, чем на поверхности раздела между жидкостью и газом. Но и в этом случае действуют силы, стремящиеся уменьшить изобарный потенциал как путем уменьшения поверхности, так и путем понижения поверхностного натяжения, что происходит в результате адсорбции соответствующих компонентов в поверхностном слое. Это имеет место и в системе из двух компонентов, и при растворении в них третьего вещества (рис. 131). Все эти явления приобретают большое значение в случае тонкого диспергирования одной жидкости в другой, в особенности в коллоидных системах, в связи с огромным увеличением поверхности. [c.365]
Как известно, с повышением температуры поверхностное натяжение чистых жидкостей понижается, что связано с уменьшением сил когезии — молекулярного сцепления в жидкости вследствие увеличения среднего расстояния между молекулами. Ослабление взаимодействия между молекулами растворителя должно приводить к уменьшению работы адсорбции и, следовательно, поверхностной активности в соответствии с уравнением (43). Действительно, показано, например, что поверхностная активность натриевых солей жирных кислот (мыл) снижается с повышением температуры [5]. Вместе с тем известно, что в гомологических рядах ПАВ величина р при повышении температуры уменьшается (Р 1), т. е. при этом сглаживается различие в поверхностной активности соседних гомологов. [c.23]
Сравнивая (11.29), (11.33) с (11.34) и (II. 35), видим, что существует четкая связь между величиной адсорбции и поверхностным натяжением. [c.35]
В основе электрокапиллярных измерений лежит уравнение, выражающее связь между поверхностным натяжением а, избытком ПАВ (адсорбцией) в поверхностном слое Г п зарядом q поверхиости электрода [c.310]
Используя связь между величиной адсорбции и поверхностной активностью, можно подойти к характеристикам так называемых поверхностно-активных веществ (см. 6), но прежде следует обратиться к положениям, показывающим количественную зависимость между поверхностным натяжением растворов и их концентрацией. Такая зависимость была выражена на примере водных растворов еще в 1909 г. русским ученым Шишковским. Им было предложено эмпирическое уравнение для зависимости поверхностного натяжения от концентрации в водных растворах предельных жирных кислот [c.192]
Для интерпретаций явлений адсорбции на границе раствор — газ весьма существенно установить связь между избытком адсорбированного вещества в поверхностном слое Г, концентрацией по-верхностно-активного вещества в растворе с и поверхностным натяжением а на границе раствор — газ. Эта связь для разбавлен- [c.120]
Связь между поверхностным натяжением и адсорбцией определяется уравнением Гиббса, которое является одним нз основных в области поверхностных явлений. Для его вывода рассмотрим следующий вообралоемый процесс. Над жидкостью, помещенной в прямоугольном сосуде, имеется два отделения, содержащие практически нерастворимый в жидкости газ (рис. Х.7). В левом отделении концентрация газа С, а в правом С+ДС. Соответственно жидкость в обоих отделениях имеет различные значения а. [c.227]
Между поверхностным натяжением и адсорбцией есть связь, описываемая уравнением Гиббса, являющимся одной из основ всей области поверхностных явлений. Чтобы понять физический смысл этой связи, рассмотрим сначала следующий простой случай. Пусть над жидкой поверхностью имеются два отделения, (рис. ХУ.8), в которых находится некоторое газообразное веще- [c.311]
Связь между избыточным количеством вещества, приходящимся на единицу новерхности, — адсорбцией Г моль/см — и способностью вещества снижать поверхностное натяжение ст разбавленных растворов описывается уравнением Гиббса в следующей форме [c.73]
Наличие электрической компоненты изменяет свободную поверхностную энергию а, численно равную поверхностному натяжению , что весьма существенно, например, при изучении адсорбции, а также процессов разряда и осаждения ионов на электродах. Поэтому изучение связи между а и параметрами ДЭС существенно для электрохимии. [c.193]
Между поверхностным натяжением и адсорбцией есть связь, описываемая уравнением Гиббса, являющимся одной из основ всей области поверхностных явлений. [c.407]
Величины адсорбции компонентов раствора Г, и поверхностное натяженне связаны между собой фундаментальным адсорбционным уравнением Гиббса [c.10]
Найдем связь между величиной адсорбции Г и поверхностным натяжением а . Следуя Гиббсу, будем рассматривать поверхностный слой как новую фазу. Пусть N1 — избыток концентрации -той компоненты в этой фазе. Тогда изменение свободной энергии фазы есть [1 ] [c.443]
В общем распределения компонентов с,(х) около границы неизвестны, и поэтому прямые вычисления их избытков и адсорбций по Гиббсу невозможны. Фактически приведенные выше соотношения представляют интерес только как определения понятий поверхностный избыток и адсорбция по Гиббсу и ряда других избыточных экстенсивных (зависящих от размера системы) функций гетерогенной системы. К числу таковых, наравне с адсорбцией, относятся избыток энергии Гиббса и избыток энтропии. Прикладное значение величин гиббсовской адсорбции и других избытков состоит в том, что они могут быть связаны между собой и с экспериментально определяемыми величинами с помощью термодинамических уравнений, и, таким образом, искомая термодинамическая функция, например изотерма адсорбции, может быть выражена через другую, доступную экспериментальному определению термодинамическую функцию, например изотерму поверхностного натяжения. [c.551]
Высоцкий и Шаля (111) высказали предположение, что влияние адсорбированных катионов металлов промывной жидкости на пористую структуру силикагеля не ограничивается облегчением агрегации мицелл и укреплением скелета гидрогеля. Адсорбция катионов влечет за собой, по мнению этих авторов, уменьшение стягивающего действия капиллярных сил, зависящих не только от поверхностного натяжения интермицеллярной жидкости, но также и от интенсивности смачивания ею мицелл. Свое заключение они основывают на обнаруженной ими связи между структурой силикагеля и теплотами гидратации катионов чем меньше теплота гидратации в ряду исследованных ими катионов Н” > Са ” > Na” > К” , тем более крупнопористым получается силикагель, тем меньше его поверхность. [c.30]
Связь между поверхностным натяжением, адсорбцией ПАВ и его концентрацией в растворе устанавливает фундаментальное уравнение адсорбции Гиббса. Для /-компонентного раствора оно имеет вид [c.99]
Современные взгляды на эмульсии вообще, и на битумные эмульсии – в частности, базируются на теории адсорбционной оболочки, выдвинутой в 1913 году Банкрофтом. Подробно эта теория рассмотрена в упоминавшемся раннее труде Клейтона , мы же лишь кратко остановимся на-основных ее положениях.Учение об эмульсиях, созданное Банкрофтом, основано на более ранней теории поверхностного натяжения Доннана – в той ее части, где утверждается, что изменения поверхностного натяжения на поверхности раздела масло – вода протекает параллельно с изменением электрического потенциала… и возможно здесь играет роль избирательная адсорбция ионов . В понимании Доннана и его последователей эмульгированные шарики масла окружены очень вязкой или даже желатинообразной оболочкой , которая препятствует их слиянию. Эти оболочки появляются благодаря адсорбции, которая происходит при понижении поверхностного натяжения на границе масло – вода, т.е. эмульгирование тесно связано с низким поверхностным натяжением между маслом и эмульгатором . Льюис, Эллис и другие исследователи расширили теорию поверхностного натяжения, связав ее с адсорбцией, электрическим зарядом и коагуляцией. Пикеринг в 1910 году важнейшим фактором эмульгирования (помимо высокой вязкости и низкого поверхностного натяжения) назвал присутствие тонко раздробленных, нерастворимых в дисперсионной среде частиц, которые обволаки- [c.14]
Вопрос о возможности прп , екг ть уравнение типа уравнения Лэнгмюра к адсорбции на границе жидкость — пар представляет значительный интерес. Уравнение Гиббса указывает на связь меж ду поверхностным натяжением и концентрацией, но эта связь вы ражена в дифференциальной фор -, е п для интегрирования требу ется знание вида функции о = /(с]. Еще в начале XX в. Шишков ский, изучая поверхностное натяжение растворов жирных кислот показал, что между концеитрацие раствора и поверхностным натяжением а существует завнснн -ность, которую можно выразить уравнением [c.275]
Другие теории адсорбции органических веществ ira электродах отличаются от теории Фрумкина либо видом уравне ия состояния, передающего связь между поверхностным натяжением и поверхностной концентрацией, либо типом изотермы адсорбции, описывающей зависимостз поверхностной концентрации органического вещества от его концентрации в объеме. Кроме того, в теории Фрумкина в качестве параметра, характеризующего электрическое состояние электрода, выбран потенциал. По Парсонсу, Деванатхаиу и ряду других ученых, таким параметром должен быть не потенциал, а заряд поверхности электрода. [c.248]
Примером иоверхностно-инактивных веществ по отношению к воде являются неорганические соли, которые сильно гидратируются. Они взаимодействуют с водой сильнее, чем молекулы воды между собой. Вследствие этого они имеют отрицательную адсорбцию Г С 0. При добавлении неорганических солей к воде поверхностное натяжение повышается. Но в связи с тем что адсорбция отрицательна, увеличение концентрации в поверхностном слое отстает от роста ее в объеме. Поэтому поверхностное натяжениг раствора с увеличением концентрации иоверхностно-инактивных веществ растет очень медленно (см. рис. 11.6). [c.41]
Сущность работы. Уравнение Гиббса (13) определяет связь между поверхностным натяжением раствора и его концентрацией. Поэтому, измеряя при постоянной температуре поверхностное натяжениё растворов какого-либо ПАВ, обладающих известными, но различными концентрациями, можно получить функцию 0=1 (с). Из этой функции можно рассчитать адсорбцию Г и ее связь с концентрацией раствора, т. е. получить другую функцию Г = ф(с). Таким образом, экспериментальное определение поверхностного натяжения растворов ПАВ различной концентрации позволяет построить две изотермы а) поверхностного натяжения б) адсорбции. [c.41]
В случае легкоподвижной границы раздела дисперсной фааы и дисперсионной среды (пены и эмульсии) условие равенства нулю скорости течения жидкости на поверхности раздела, определяющее применимость уравнения Рейнольдса, кожет на выполняться, и утоньшение пленки будет происходить с большей скоростью. Однако в пенных и эмульсионных пленках, стабилизированных адсорбционными слоями ПАВ, условия вытекания жидкости приближаются к условиям вытекания из зазора между твердыми поверхностями даже и тогда, когда молекулы ПАВ не образуют сплошной твердообразной пленки. Это связано с тем, что при значениях адсорбции ПАВ меньших предельной Гта движение поверхности жидкости приводит к переносу части молекул ПАВ адсорбционного слоя из центральных участков пленки на периферийные участки, пр1илегающие к каналам Гиббса — Плато. В результате значение адсорбции в центре пленки уменьшается, а на периферии увеличивается, что обусловливает возникновение градпента поверхностного натяжения (градиента двухмерного давления) вдоль поверхности пленки, т. е. проявляется упомянутый выше эффект Марангони — Гиббса. Этот градиент поверхностного натяжения может в значительной степени уравновешивать стремление гра.ничных слоев жидкой пленки к вытвйанию п-ри этом поверхность приобретает как бы твердообразные свойства и устанавливается режим течения, описываемый уравнением Рейнольдса (IX—24). [c.256]
В то же время, для некоторых классов органических соединений (например, серусодержащих), не обнаружено связи между понижением ими поверхностного натяжения на ртутп и защитными свойствами по отношению к железу, т. е. адсорбция этих соединений зависит не только от свойств адсорбирующихся частиц, но и от химической природы металла. Было установлено также, что серусо-держащие соединения на железе хемосорбируются. Таким образом, для химически адсорбирующихся ингибиторов перенос данных электрокапиллярных измерений на ртути на реально корродирующие металлы затруднителен. Причины различий в адсорбционном поведении некоторых ингибиторов на ртути и на корродирующих металлах рассмотрены в [19]. По мнению А. Н. Фрумкина, перенос данных, полученных на ртути, на другие металлы должен осуществляться с большей осторожностью. [c.23]
Скорость зародышеобразования можно существенно изменять введением в раствор различных примесных добавок, в первую очередь добавок поверхностно-активных веществ. Общепринято, что действие этих веществ связано с их адсорбцией на поверхности субмикрозародышей, препятствующей дальнейшему росту зародышей. Кроме того, они изменяют поверхностное натяжение а между раствором и поверхностью зародыша, увеличивая работу образования зародыша. [c.363]
