Помогите с ДЗ по физике
Ученик
(122),
на голосовании
7 лет назад
Голосование за лучший ответ
Галя Автомат
Ученик
(108)
4 года назад
Помогите с ДЗ по физике
1. Определить цену деления шкалы амперметра и силу тока, которую он показывает.
2. Найдите силу тока в каждом разветвлении и общую во всей цепи.
3. Какое напряжение должен показывать вольтметр?
4. Вычислите общее сопротивление всего разветвления.
5. Начертите схему цепи с теми же сопротивлениями, включенными последовательно, и вычислите величину общего сопротивления при этом соединении.
6. Вычислите силу тока при последовательном соединении.
На прошлом уроке мы рассмотрели последовательное соединение проводников. При нем сила тока на всех участках цепи одинакова ($I = I_1 = I_2 = … = I_n$), а сопротивление всей цепи складывается из сопротивлений всех проводников, составляющих ее ($R = R_1 + R_2 + … + R_n$). Напряжение (подобно сопротивлению) всей цепи рассчитывается сложением напряжений на концах всех элементов, составляющих такую электрическую цепь ($U = U_1 + U_2 + … + U_n$).
На данном уроке мы рассмотрим другой вид соединения проводников — параллельный. Так мы подсоединяли вольтметр, когда измеряли напряжение на каком-либо участке цепи. Сейчас же мы рассмотрим закономерности для силы тока, сопротивления и напряжения в цепи для такого типа соединения.
Параллельное включение элементов в электрическую цепь
Какое соединение проводников называют параллельным?
Соберем электрическую цепь с таким соединением. Цепь будет состоять из источника тока, ключа и двух электроламп. Электролампы включены в цепь параллельно (рисунок 1).
Схема этой электрической цепи изображена на рисунке 2.
На схеме обозначены две точки A и B. Важный момент:
При параллельном соединении все входящие в него проводники одним своим концом присоединяются к точке A, а вторым концом — к другой точке B.
Так мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества параллельно подключенных в цепь проводников между точками A и B.
Напряжение в цепи при параллельном соединении проводников
Вольтметр подсоединяется в цепь параллельно. Взгляните на рисунок 3.
Можно ли сказать, что мы измеряем напряжение только на одной из ламп? Нет. Получается, что одновременно мы измеряем напряжения и на одной, и на другой лампе. Мы приходим к следующему заключению.
Напряжение на участке цепи AB и на концах всех параллельно соединенных проводников одно и то же:
$U = U_1 = U_2 = … = U_n$.
Значит, напряжение — это электрическая величина, которая одинакова для всех проводников, соединенных параллельно.
По этой причине в быту и технике очень удобно применять параллельный тип соединения проводников. Почему?
Во-первых, в таком случае все потребители электроэнергии изготавливаются в расчете на одну и ту же величину напряжения. Во-вторых, если исключить из цепи один потребитель, то другие продолжат работать. Цепь останется замкнутой.
Сила тока в цепи при параллельном соединении проводников
Теперь рассмотрим, что происходит с силой тока при параллельном подключении.
Взгляните на рисунок 4, а. В точке B ток разветвляется на два тока: $I_1$ и $I_2$.
Эти два тока сходятся снова в точке A. По смыслу этот момент очень похож на разветвление реки (рисунок 4, б) на два потока воды, которые через какое-то расстояние вновь сходятся в одно русло.
Как выражается сила тока в цепи до ее разветвления через силы токов в отдельных ветвях разветвления?
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках:
$I = I_1 + I_2 + … + I_n$.
Сопротивление в цепи при параллельном соединении проводников
Перейдем к сопротивлению. При параллельном соединении можно представить все проводники как один. Этот один проводник будет явно больше в диаметре, чем каждый из них по отдельности. Получается, что площадь поперечного сечения проводника как бы увеличивается при таком соединении.
Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Чем больше поперечное сечение, тем меньше сопротивление.
Значит, общее сопротивление цепи уменьшается. Оно становится меньше сопротивления каждого из проводников, которые входят в такую электрическую цепь.
В цепи на рисунке 1 у нас две одинаковые лампы с сопротивлениями $R_1$. Общее сопротивление цепи $R$ будет в два раза меньше сопротивления каждой лампы: $R = frac{R_1}{2}$.
Общее сопротивление цепи при параллельном соединении проводников рассчитывается по формуле:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2} + … + frac{1}{R_n}$.
Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
Очевидно, что чем больше проводников будет в разветвлении, тем меньше будет общее сопротивление цепи.
Пример параллельного соединения проводников
Взгляните на рисунок 5. Здесь изображена часть схемы электрической цепи. Здесь параллельно включены электрические лампы, нагревательные приборы и электродвигатель.
Где может использоваться такая схема соединения?
Например, в жилых помещениях. В точках A и B провода вводятся в квартиру.
Также в наших квартирах все стандартные розетки находятся под одинаковым напряжением в $220 space В$. Большинство производителей техники изготавливают приборы как раз под это напряжение.
Использовать параллельное подключение к одной и той же цепи очень удобно, поскольку в нее могут быть включены самые разные потребители энергии (рисунок 6).
Благодаря такому способу подключения, выключая свет в своей квартире, мы не выключаем его и у наших соседей. Любые электроприборы могут работать независимо от подключения или отключения в сеть других.
На практике также часто можно увидеть смешанное соединение проводников. В таких цепях присутствует и последовательный тип соединении, и параллельный.
Пример задачи
В осветительную сеть комнаты включены две электрические лампы, сопротивления которых равны $200 space Ом$ и $300 space Ом$. Напряжение в сети составляет $120 space В$. Определите силу тока в каждой лампе, силу тока в проводящих проводах (то есть силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.
Подразумевается, что лампы подключены в сеть параллельно. Запишем условие задачи и решим ее.
Дано:
$R_1 = 200 space Ом$
$R_2 = 300 space Ом$
$U = 120 space В$
$I_1 — ?$
$I_2 — ?$
$I — ?$
$R — ?$
Решение:
Запишем закон Ома для участка цепи с первой лампой:
$I_1 = frac{U_1}{R_1}$.
Значение сопротивления нам известно. Что с напряжением на этом участке?
Так как лампы подсоединены параллельно, то напряжение на каждой будет равно напряжению во всей цепи:
$U_1 = U_2 = U = 120 space В$
Тогда мы можем рассчитать силу тока в каждой лампе.
Сила тока в первой лампе:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{120 space В}{200 space Ом} = 0.6 space А$.
Сила тока во второй лампе:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{120 space В}{300 space Ом} = 0.4 space А$.
Сила тока до разветвления будет равна сумме сил этих двух токов в лампах:
$I = I_1 + I_2$,
$I = 0.6 space А + 0.4 space А = 1 space А$.
Общее сопротивление цепи мы можем определить двумя способами.
Способ №1
Используя закон Ома для участка цепи, состоящего из двух параллельно соединенных ламп:
$I = frac{U}{R}$,
$R = frac{U}{I}$,
$R = frac{120 space В}{1 space А} = 120 space Ом$.
Способ №2
Используя формулу для расчета сопротивления при параллельном соединении проводников:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{200 space Ом} + frac{1}{300 space Ом} = frac{5}{600 space Ом} = frac{1}{120 space Ом}$.
Отсюда, $R = frac{1}{frac{1}{120 space Ом}} = 120 space Ом$.
При решении этой задачи мы убедились, что общее сопротивление цепи меньше сопротивления каждого из параллельно подключенных проводников: $R < R_1 < R_2$.
Ответ: $I_1 = 0.6 space А$, $I_2 = 0.4 space А$, $I = 1 space А$, $R = 120 space Ом$.
Упражнения
Упражнение №1
Два проводника сопротивлением $10 space Ом$ и $15 space Ом$ соединены параллельно и подключены к напряжению в $12 space В$. Определите силу тока в каждом проводнике и силу тока до разветвления.
Дано:
$R_1 = 10 space Ом$
$R_2 = 15 space Ом$
$U = 12 space В$
$I_1 — ?$
$I_2 — ?$
$I — ?$
Показать решение и ответ
Скрыть
Решение:
Напряжение будет одинаковое как во всей цепи, так и на концах каждого из двух проводников.
Запишем закон Ома для первого проводника и рассчитаем силу тока в нем:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{12 space В}{10 space Ом} = 1.2 space А$.
То же самое сделаем для второго проводника:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{12 space В}{15 space Ом} = 0.8 space А$.
Сила тока до разветвления в цепи будет равна сумме сил тока в каждом проводнике:
$I = I_1 + I_2$,
$I = 1.2 space А + 0.8 space А = 2 space А$.
Ответ: $I_1 = 1.2 space А$, $I_2 = 0.8 space А$, $I = 2 space А$.
Упражнение №2
Почему бытовые приборы в помещении необходимо соединять параллельно?
Потому что бытовые приборы рассчитаны на то же напряжение, которое подается от городской сети — $220 space В$. При параллельном соединении это напряжение будет одинаковым на всех участках цепи.
Также параллельное соединение позволяет включать и выключать приборы независимо друг от друга, что невозможно при последовательном соединении.
Упражнение №3
Три потребителя с сопротивлениями $20 space Ом$, $40 space Ом$ и $24 space Ом$ соединены параллельно. Напряжение на концах этого участка цепи равно $24 space В$. Определите силу тока в каждом потребителе, общую силу тока в участке цепи и сопротивление участка цепи.
Дано:
$R_1 = 20 space Ом$
$R_2 = 40 space Ом$
$R_3 = 24 space Ом$
$U = 24 space В$
$I_1 — ?$
$I_2 — ?$
$I_3 — ?$
$I — ?$
$R — ?$
Показать решение и ответ
Скрыть
Решение:
Напряжение на концах этого участка цепи будет равно напряжению на концах каждого потребителя, так как они соединены параллельно: $U_1 = U2 = U_3 = U = 24 space В$.
Используя закон Ома для участка цепи, рассчитаем силу тока на каждом потребителе электроэнергии.
Для первого потребителя:
$I_1 = frac{U}{R_1}$,
$I_1 = frac{24 space В}{20 space Ом} = 1.2 space А$.
Для второго потребителя:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{24 space В}{40 space Ом} = 0.6 space А$.
Для третьего потребителя:
$I_3 = frac{U}{R_3}$,
$I_3 = frac{24 space В}{24 space Ом} = 1 space А$.
Сила тока до разветвления в цепи будет равна сумме сил тока в каждом потребителе электроэнергии:
$I = I_1 + I_2 + I_3$,
$I = 1.2 space А + 0.6 space А + 1 space А = 2.8 space А$.
Теперь используем закон Ома, представляя участок цепи с тремя потребителями как единый участок цепи:
$I = frac{U}{R}$,
$R = frac{U}{I}$,
$R = frac{24 space В}{2.8 space А} approx 8.6 space Ом$.
Ответ: $I_1 = 1.2 space А$, $I_2 = 0.6 space А$, $I_3 = 1 space А$, $I = 2.8 space А$, $R approx 8.6 space Ом$.
Упражнение №4
Два проводника имеют сопротивления, равные $5 space Ом$ и $500 space Ом$. Почему при последовательном соединении этих проводников их общее сопротивление будет больше $500 space Ом$, а при параллельном соединении меньше $5 space Ом$?
При последовательном соединении проводников общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников.
Общее сопротивление при последовательном соединении:
$R = R_1 + R_2 = 5 space Ом + 500 space Ом = 505 space Ом$.
Это значение действительно больше, чем $500 space Ом$.
При параллельном соединении общее сопротивление мы рассчитываем следующим образом:
$frac{1}{R} = frac{1}{R_1} + frac{1}{R_2}$,
$frac{1}{R} = frac{1}{5 space Ом} + frac{1}{500 space Ом} = frac{101}{500 space Ом}$,
$R = frac{1}{frac{101}{500 space Ом}} = frac{500 space Ом}{101} approx 5 space Ом$.
Согласитесь, что $5 space Ом$ намного меньше, чем $500 space Ом$.
Можно посмотреть на этот вопрос и с другой стороны. Сопротивление рассчитывается по формуле $R = frac{rho l}{S}$. Оно прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения.
При последовательном соединении проводников мы можем сказать, что длина проводника увеличивается. Значит, увеличивается и сопротивление. Общее сопротивление будет больше, чем сопротивление каждого отдельного проводника.
А при параллельном соединении увеличивается площадь поперечного сечения. Значит, сопротивление будет уменьшаться. Получается, что общее сопротивление такой цепи будет меньше сопротивления каждого из проводников.
Упражнение №5
На рисунке 7 изображена схема смешанного соединения проводников, сопротивления которых: $R_1 = 4 space Ом$, $R_2 = 6 space Ом$, $R_3 = 12 space Ом$, $R_4 = 2 space Ом$. Амперметр показывает силу тока $1 space А$. Определите напряжение между точками В и С и силу тока в каждом проводнике.
Дано:
$R_1 = 4 space Ом$
$R_2 = 6 space Ом$
$R_3 = 12 space Ом$
$R_4 = 2 space Ом$
$I_3 = 1 space А$
$U — ?$
$I_1 — ?$
$I_2 — ?$
$I_4 — ?$
Показать решение и ответ
Скрыть
Решение:
Амперметр подсоединен последовательно с проводником $R_3$. Он показывает силу тока $I_3 = 1 space А$. Это сила тока после разветвления.
Используя закон Ома для этого проводника, рассчитаем напряжение на его концах:
$I_3 = frac{U_3}{R_3}$,
$U_3 = I_3R_3$,
$U_3 = 1 space А cdot 12 space Ом = 12 space В$.
Так как проводники $R_3$ и $R_2$ подключены в цепь параллельно, то напряжение на каждом из этих проводников будет равно напряжению на участке цепи, который их включает. Это и есть напряжение между точками B и C:
$U = U_3 = 12 space В$.
По закону Ома рассчитаем силу тока на проводнике $R_2$:
$I_2 = frac{U}{R_2}$,
$I_2 = frac{12 space В}{6 space Ом} = 2 space А$.
Теперь мы можем рассчитать силу тока до его разветвления — на проводниках $R_1$ и $R_4$. При этом $I_1 = I_4 = I$, потому что эти проводники включены в цепь последовательно. Это значит, что сила тока в любом участке такой цепи будет одинаковой. В нашем случае на проводнике $R_1$ и $R_4$.
Рассчитаем эту силу тока, используя величины, полученные с параллельно соединенных проводников. Сила тока до разветвления будет равна сумме сил тока в каждом проводнике после разветвления:
$I = I_2 + I_3$,
$I = 1 space А + 2 space А = 3 space А$.
Ответ: $U = 12 space В$, $I_1 = I_4 = I = 3 space А$, $I_2 = 2 space А$, $I_3 = 1 space А$.
Закон Ома
Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).
Онлайн калькулятор
Найти силу тока
Напряжение: U = В
Сопротивление: R = Ом

Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:
Сила тока на этом участке I = 12 /2= 6 А
Найти напряжение
Сила тока: I = A
Сопротивление: R = Ом

Формула
Пример
Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:
Напряжение на этом участке U = 6⋅2 = 12 В
Найти сопротивление
Напряжение: U = В
Сила тока: I = A
Формула
Пример
Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:
Электрическое сопротивление на этом участке R = 12 /6 = 2 Ом
Закон Ома для полной цепи
Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Онлайн калькулятор
Найти силу тока
ЭДС: ε = В
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
Сила тока I = 12 /4+2 = 2 А
Найти ЭДС
Сила тока: I = А
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:
ЭДС ε = 2 ⋅ (4+2) = 12 В
Найти внутреннее сопротивление источника напряжения
Сила тока: I = А
ЭДС: ε = В
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r =
Формула
Пример
Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:
Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом
Найти сопротивление всех внешних элементов цепи
Сила тока: I = А
ЭДС: ε = В
Внутреннее сопротивление источника напряжения: r = Ом
Сопротивление всех внешних элементов цепи: R =
Формула
Пример
Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:
Закон Ома для участка цепи. Закон Джоуля — Ленца. Работа и мощность электрического тока. Виды соединения проводников.
В электрической цепи происходит преобразование энергии упорядоченного движения заряженных частиц в тепловую. Согласно з-ну сохранения энергии работа тока равна количеству выделившегося тепла.
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:
Работа и мощность электрического тока.
Работа электрического тока:
Мощность электрического тока (работа в единицу времени):
В электричестве иногда применяется внесистемная единица работы — кВт . ч (киловатт-час).
1 кВт . ч = 3,6 . 10 6 Дж.
Виды соединения проводников.
Последовательное соединение.

1. Сила тока во всех последовательно соединенных участках цепи одинакова:
I1=I2=I3=. =In=.
2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке:
U=U1+U2+. +Un+.
3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка:
R=R1+R2+. +Rn+.
Если все сопротивления в цепи одинаковы, то:
R=R1 . N
При последовательном соединении общее сопротивление увеличивается (больше большего).
Параллельное соединение.
1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках.
2. Напряжение на всех параллельно соединенных участках цепи одинаково:
U1=U2=U3=. =Un=.
3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению):
Если все сопротивления в цепи одинаковы, то:
При параллельном соединении общее сопротивление уменьшается (меньше меньшего).
4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках:
5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
6. Т.к. силы тока во всех участках одинаковы, то: U1:U2. Un. = R1:R2. Rn.
Для двух резисторов: — чем больше сопротивление, тем больше напряжение.
4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках:
A=A1+A2+. +An+.
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках:
P=P1+P2+. +Pn+.
6. Т.к. напряжения на всех участках одинаковы, то:
Для двух резисторов: ![]() — чем больше сопротивление, тем меньше сила тока.
— чем больше сопротивление, тем меньше сила тока.
Закон Ома

Физика — наука эмпирическая. Ее основные законы вытекают из практического опыта и частенько много лет не имеют теоретических обоснований. Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.
Электрические явления люди наблюдали сотни лет. Но никак не связывали между собой заряженность потертого янтаря и молнию. Только на исходе XVIII столетия электричество стали внимательно исследовать. В 1795 году Алессандро Вольта изобрел «вольтов столб», химическую батарею, и обнаружил появление тока в проводнике, соединяющем ее полюса. Сферы применения электричества стремительно множились, и появилась острая необходимость в расчетных формулах для инженеров. Эту задачу решали многие ученые, но первым сформулировал главную формулу электротехники именно Георг Ом. Он ввел в обиход понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи.
7
Какой энергией будет обладать эта
батарея конденсаторов при потенциале, указанном на карточке?
8
Какой собственной частотой будет
обладать колебательный контур, составленный из данной батареи конденсаторов и
катушки, величина индуктивности которой указана на карточке?
Вариант 1
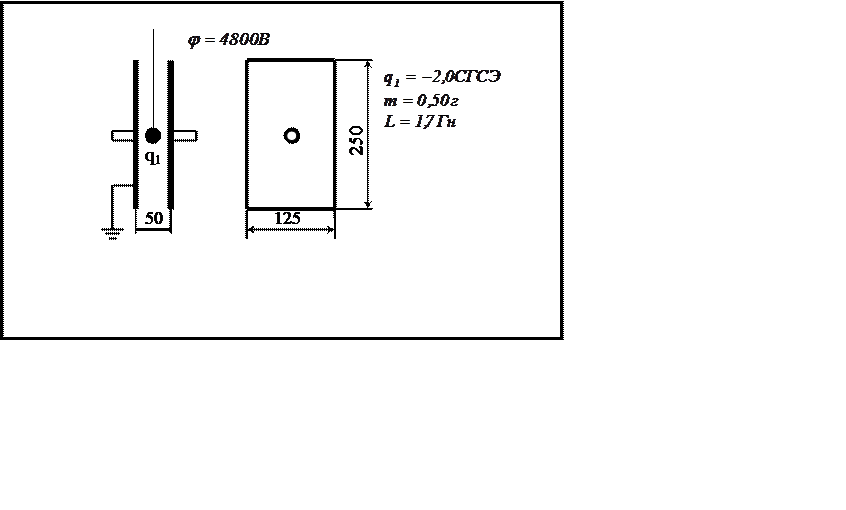 |
Вариант 2
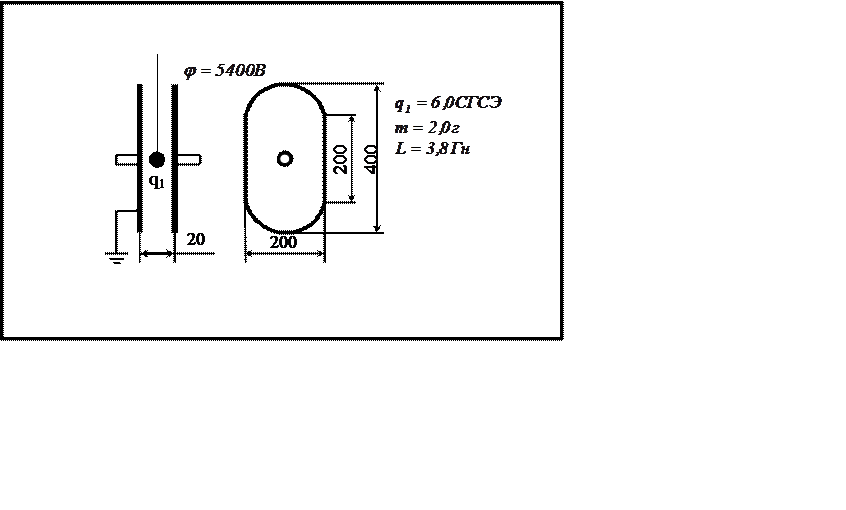 |
Вариант 3
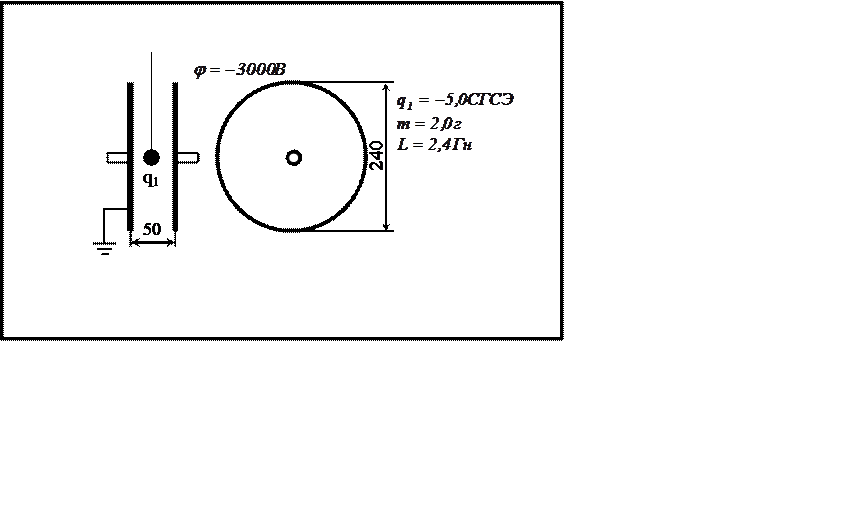 |
Вариант 4
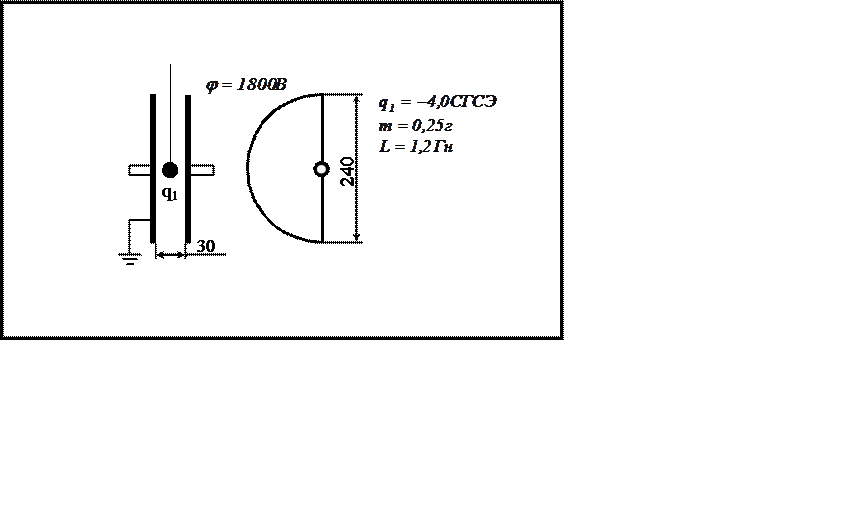
Вариант 5
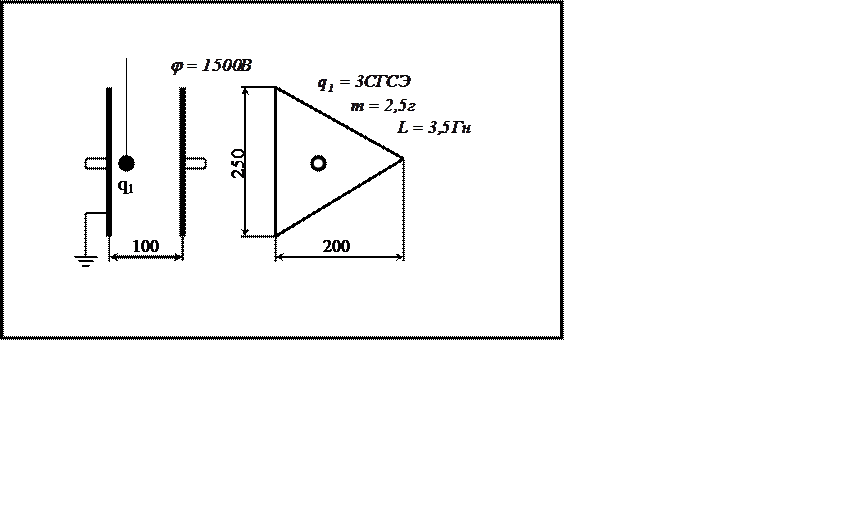 |
Вариант 6
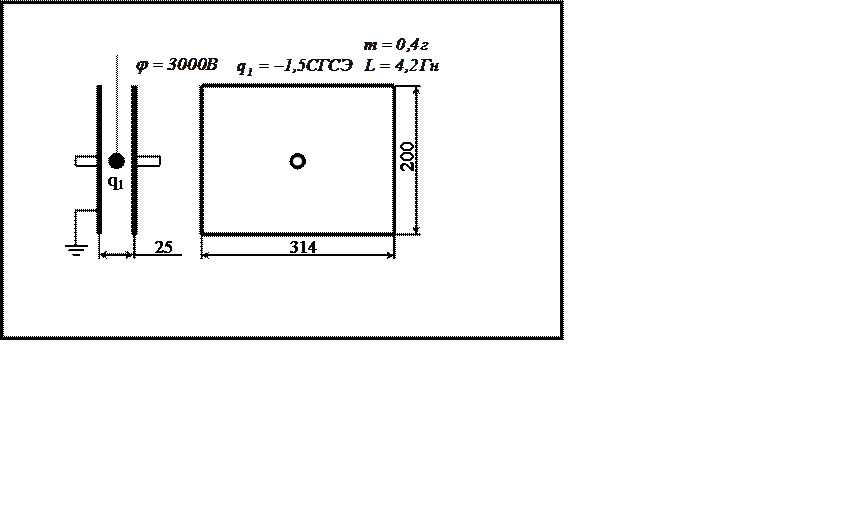
Вариант 7
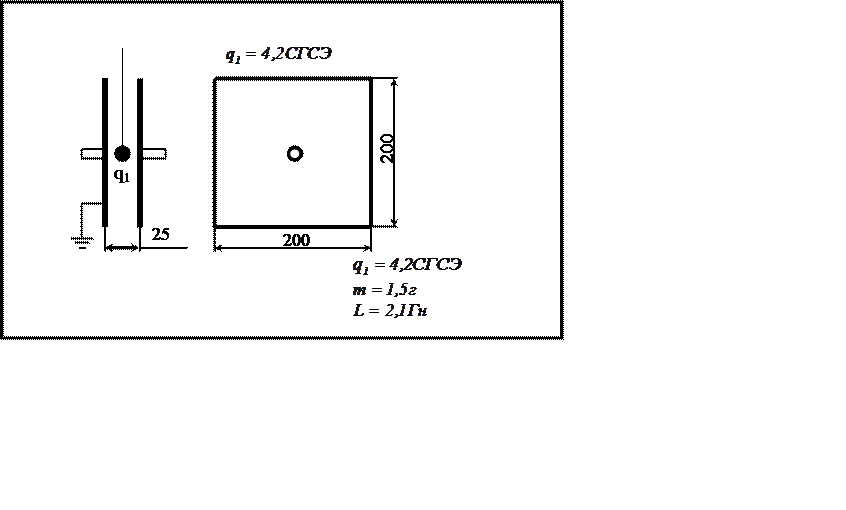 |
Вариант 8
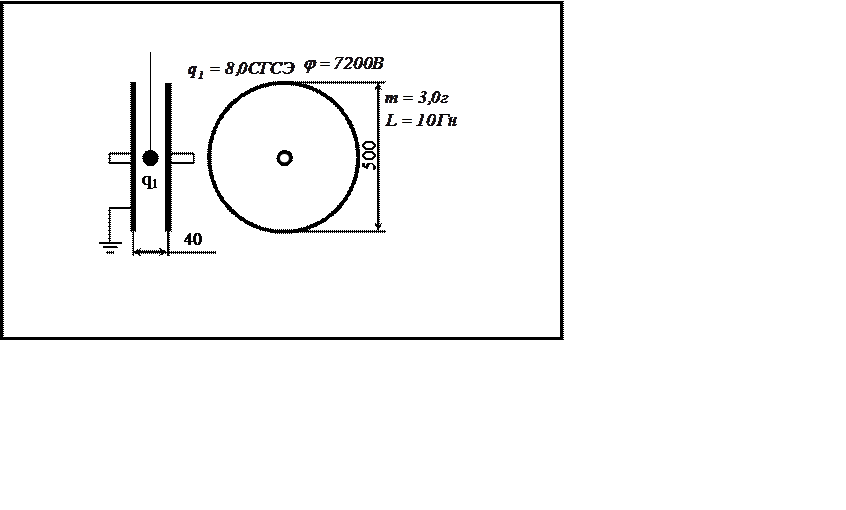 |
Вариант 9
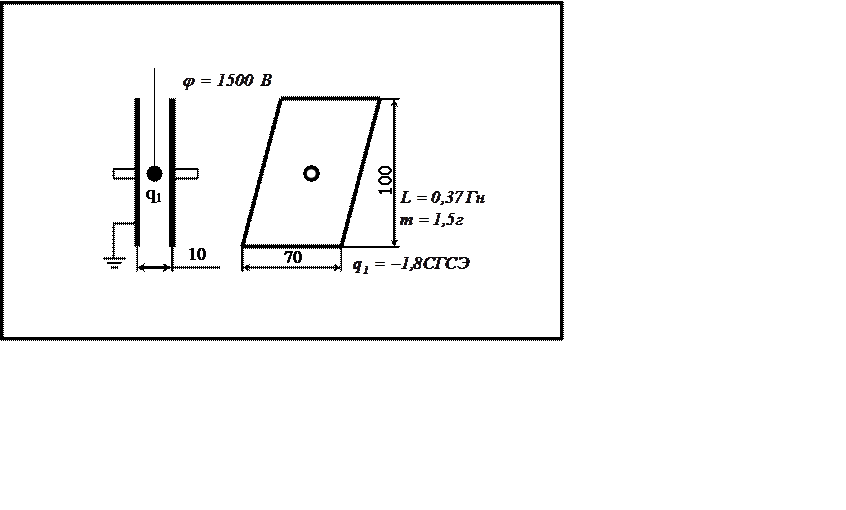 |
Вариант 10
 |
Вариант 11
 |
![]()
Вариант12
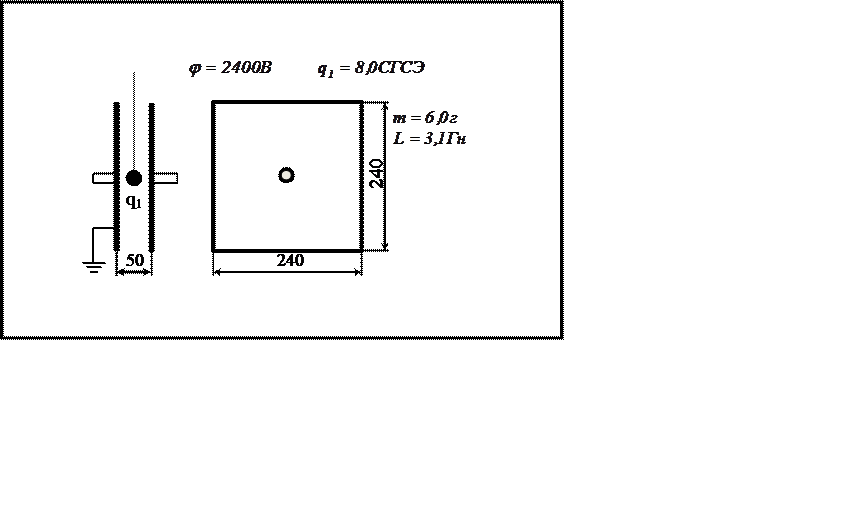 |
Конденсаторы
Образец решения
Вариант3
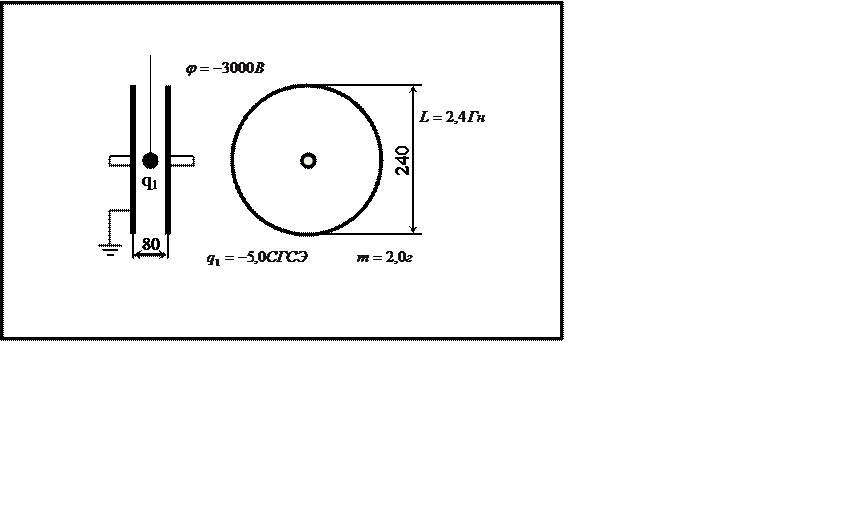 |
1
Активная площадь
пластины:
![]()
![]()
![]()
2
Электроемкость конденсатора:
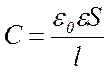
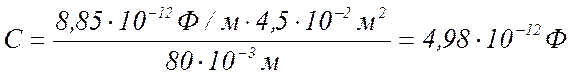
3
Напряженность электрического поля
между пластинами:
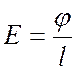
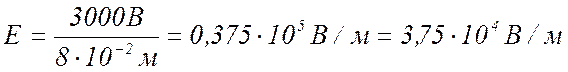
4
Заряд на пластине:
![]()
![]()
5
Сила действующая на шарик:
![]()
![]()
![]()
6
При соединении параллельно 100
подобных конденсаторов в батарею, у которых будет уменьшено расстояние между
пластинами до 0,1 мм и заполнено слюдой:
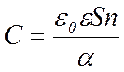
![]()
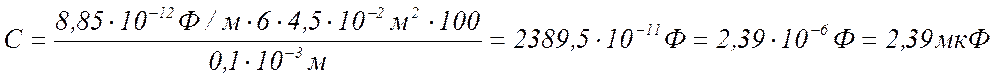
7
Потенциальная энергия такой
батареи:
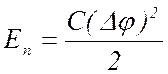
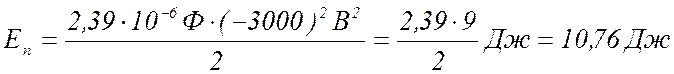
8
Контур, cоставленный из
данной батареи конденсаторов и индуктивности 2,4 Гн, указанной на карточке,
будет иметь собственную частоту: 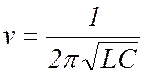
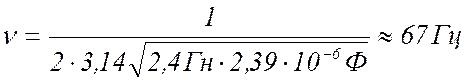
Параллельное соединение проводников
На рисунке изображена схема электрической цепи, на
которой соединены параллельно несколько резисторов и амперметр. Используя
показания амперметра и величину сопротивления резисторов, которые указаны в
карточке, выполните задания ответьте на вопросы.
1
Определите цену деления шкалы
амперметра и силу тока, которую он показывает.
2
Найдите силу тока в каждом
разветвлении и общую во всей цепи.
3
Какое напряжение должен показывать
вольтметр?
4
Вычислите общее сопротивление
всего разветвления.
5
Начертите схему цепи с теми же
сопротивлениями, включенными последовательно, и вычислите величину общего
сопротивления при этом соединении.
6
Вычислите силу тока при последовательном
соединении.
Вариант 1
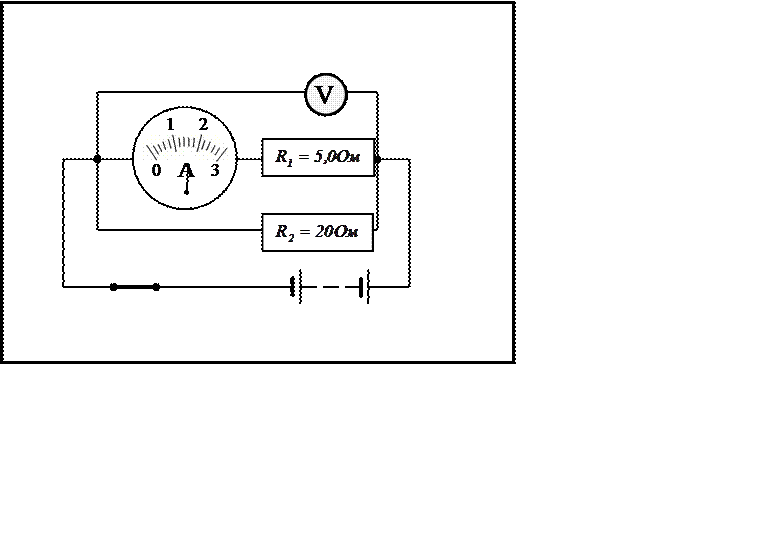 |
Вариант 2
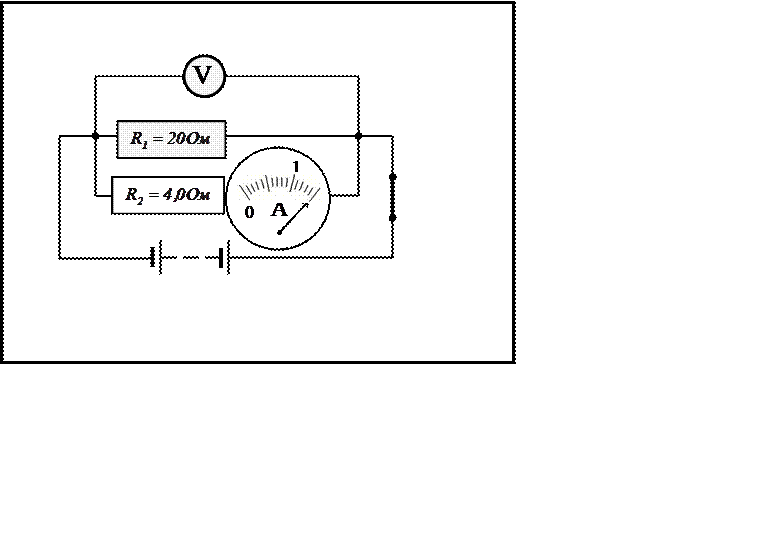 |
Вариант 3
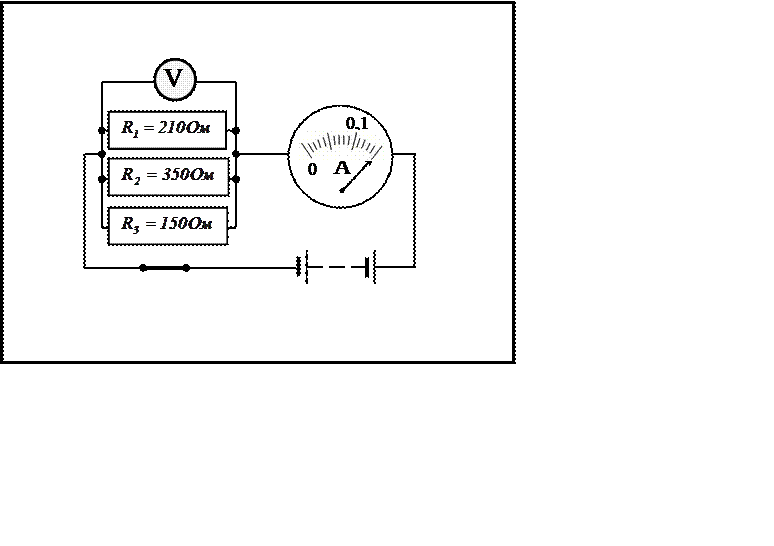 |
Вариант 4
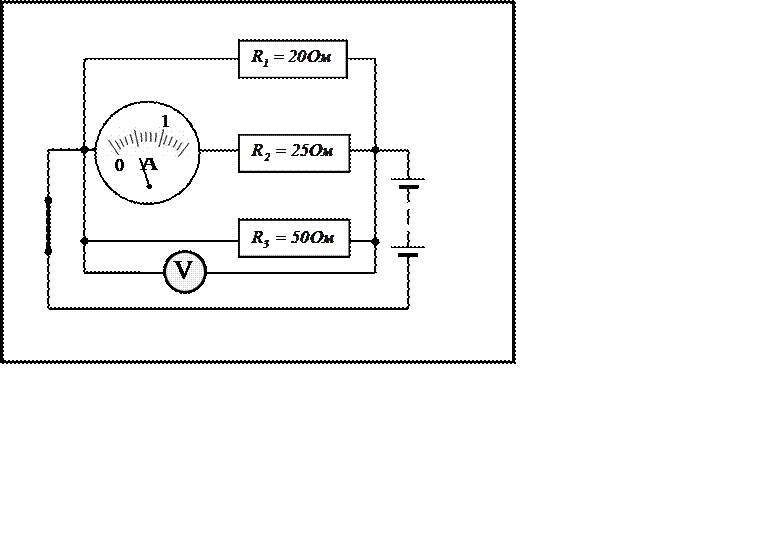 |
Вариант 5
 |
Вариант 6
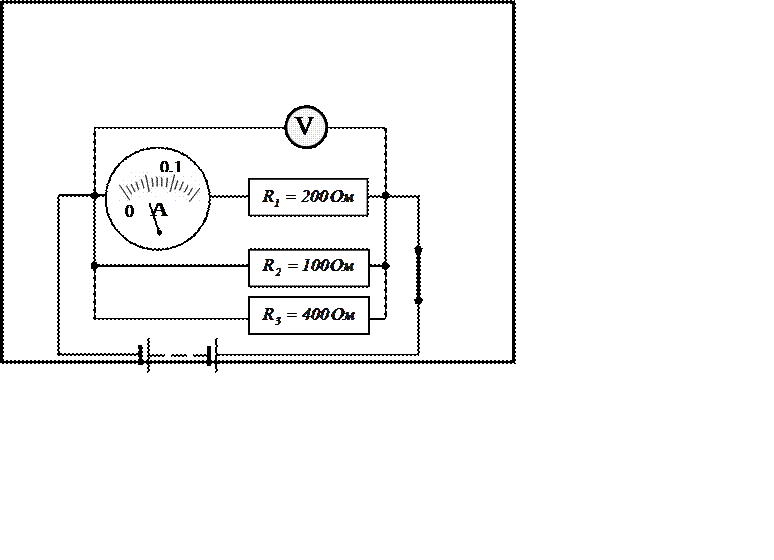 |
Вариант 7
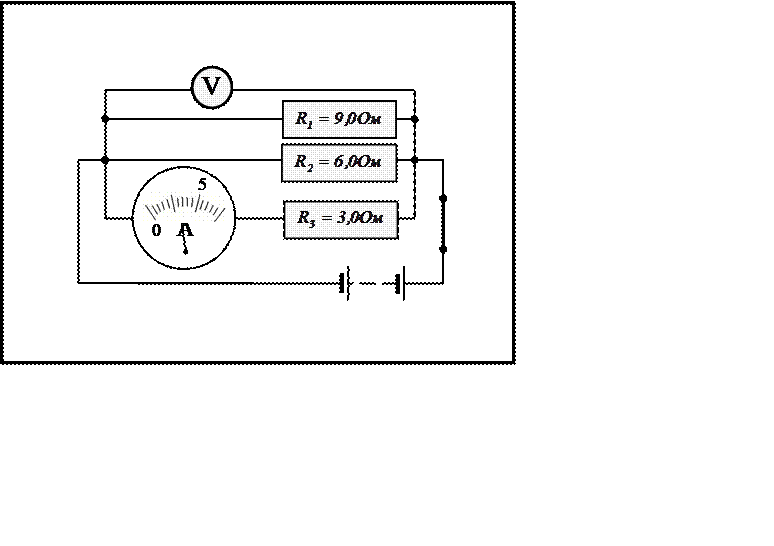 |
Вариант 8
 |
Вариант 9
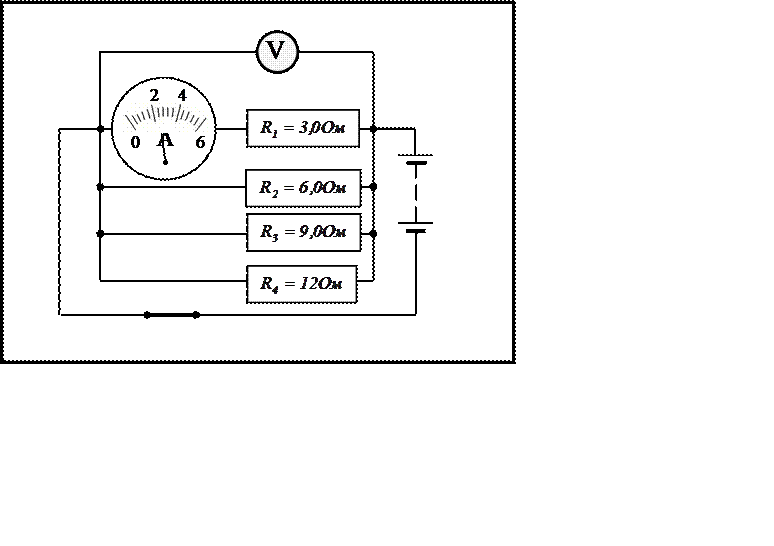 |
Вариант 10
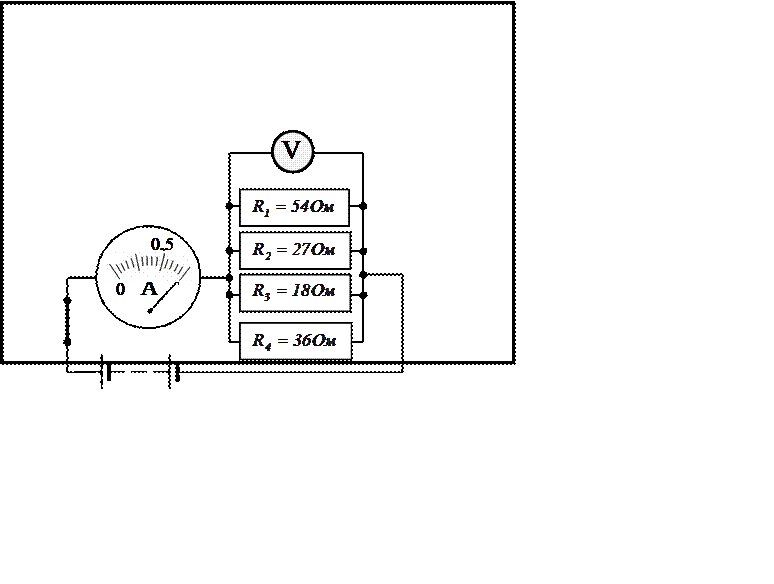 |
Вариант 11
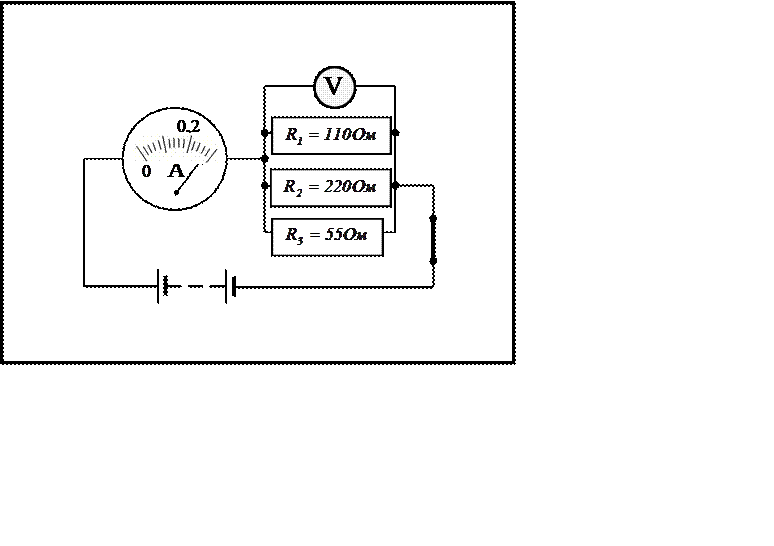 |
Вариант 12
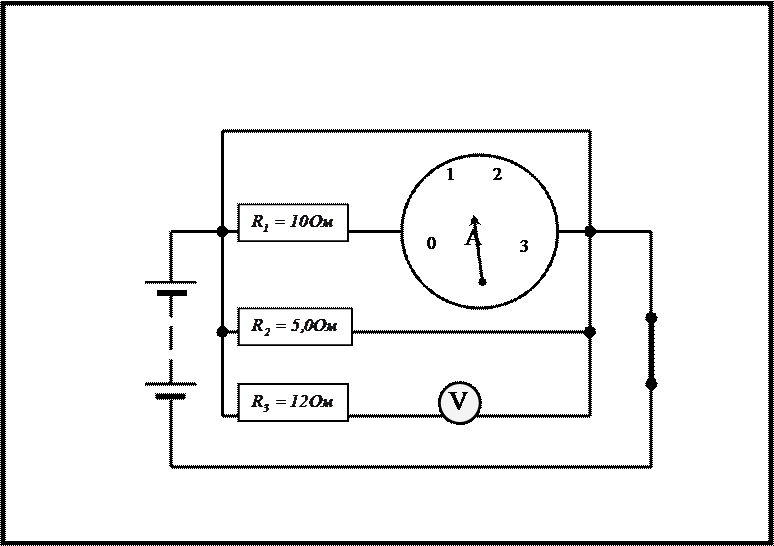 |
![]()
Параллельное соединение проводников
Образец решения
Вариант 7
На рисунках карточек приведены схемы параллельного
соединения проводников, величина сопротивления которых указана. Крупное
условное изображение амперметра несет на себе шкалу со стрелкой, показывающей
силу тока в каком-либо разветвлении или во всей цепи. Для питания цепи служит
батарея аккумуляторов с ничтожно малым сопротивлением. На вольтметре,
подключенном к общим точкам разветвления цепи, шкала не нанесена.
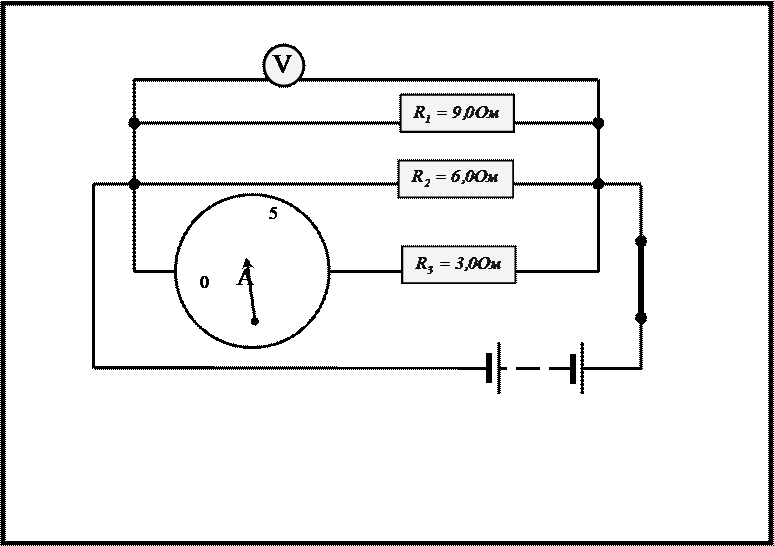 |
![]()
1
Цена деления шкалы амперметра –
0,5А
2
Сила тока:
в третьей
ветви (по амперметру) ![]()
во второй
ветви
![]() ,
, ![]() ,
, ![]() ;
;
в первой
ветви
![]() ,
, ![]() .
.
общая ![]() ,
, ![]() .
.
3
Напряжение: ![]()
![]() ,
, ![]() .
.
4
Сопротивление всего разветвления:
![]()
![]()
![]()
Расчет общего сопротивления иногда
проще производить, вычисляя общую проводимость в цепи:
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
 Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
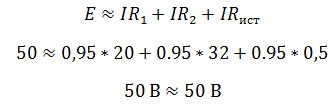
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
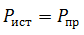
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
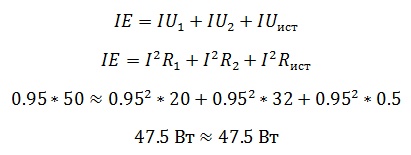
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах 
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
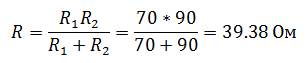
А затем напряжение

Зная напряжения, найдем токи, протекающие через резисторы
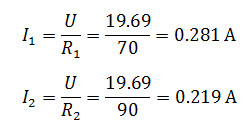
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
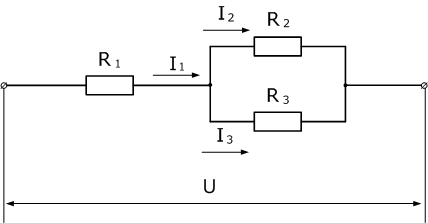
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи
 Отсюда мощность, выделяемая на R1
Отсюда мощность, выделяемая на R1
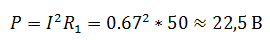 Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
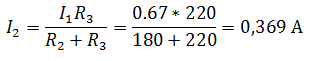
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
![]()
Таким образом производится расчет простых цепей постоянного тока.
