Нахождение длины вектора, примеры и решения
Длина вектора – основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
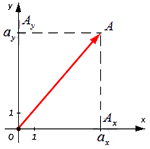
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
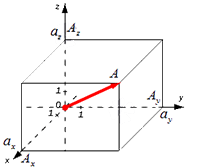
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → – 3 · j → + 5 · k → , где i → , j → , k → – орты прямоугольной системы координат.
Дано разложение вектора a → = 4 · i → – 3 · j → + 5 · k → , его координаты равны a → = 4 , – 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( – 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x – a x ; b y – a y ) значит, его длина может быть определена по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B – 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x – a x ) 2 + ( b y – a y ) 2 : A B → = ( – 3 – 1 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( – 3 – 1 ; 1 – 3 ) = ( – 4 ; 1 – 3 ) ; A B → = ( – 4 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 . –
Ответ: A B → = 20 – 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 = ( 5 – 0 ) 2 + ( 2 – 1 ) 2 + ( λ 2 – 2 ) 2 = 26 + ( λ 2 – 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 – 2 ) 2 = 30 26 + ( λ 2 – 2 ) 2 = 30 ( λ 2 – 2 ) 2 = 4 λ 2 – 2 = 2 и л и λ 2 – 2 = – 2 λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 – 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 – 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x – a x ) 2 + ( b y – a y ) 2 или A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Длина вектора — основные формулыВремя чтения: 16 минут Основные понятия вектораДля того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов. Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа». Вектор — это отрезок с определённой длиной и направлением. Графическое изображение вектора – отрезок который имеет указание направления в виде стрелки. Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой. Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные. Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения. Как найти длину вектораМодуль вектора а будем обозначать Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор На взятой системе координат, от её начала отложим вектор Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу: Когда вектор Чтобы рассчитать длину Чтобы найти модуль вектора используем ранее приведённую формулу
Ответ: Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО – диагональ прямоугольного параллелепипеда), поэтому из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA Ответ: Длина вектора через координаты точек начала и концаРанее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца. Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор При этом формула вычисления длины вектора Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1) Решение Ответ: Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2)) В первую очередь представим длину вектора в виде формулы. Длина вектора по теореме косинусовТак как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов. К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере. Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow). В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим: Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров. длина вектора формула для трёхмерного пространства; длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости. Существует также формула длины вектора перемещения: ( left|vec В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора. Применение векторов в других сферахПонятие и вычисление вектора важно не только в математике, но и других науках:
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор. [spoiler title=”источники:”] http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html [/spoiler] |
Elena Schatz
Высший разум
(140343)
13 лет назад
Решение:
Для нахождения длин сторон треугольника воспользуемся формулой нахождения расстояния между двумя данными точками
s = ((x2 – x1)^2+(y2-y1)^2)^(1/2)
где (x1,y1) и (x2, y2) – это координаты начала и конца отрезка.
Елена Гужвенко
Гений
(53581)
13 лет назад
Найти координаты векторов, образующих каждую сторону:
АВ=(х2-х1; у2-у1)
АС и АД аналогично.
Найти длины векторов |AB|=корень из суммы квадратов соответствующих координат векторов
Удачи!
Дядя ВаняПрофи (959)
13 лет назад
Спасибо большое… но не могли бы Вы немного по подробнее…
я не совсем понял… пожалуйста )))
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Раздел V.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
В раздел включены
задачи, которые рассматриваются в теме
«Аналитическая геометрия на плоскости
и в пространстве»: составление различных
уравнений прямых на плоскости и в
пространстве; определение взаимного
расположения прямых на плоскости,
прямых, прямой и плоскости, плоскостей
в пространстве; изображение кривых
второго порядка. Необходимо отметить,
что в данном разделе представлены задачи
экономического содержания, при решении
которых применяются сведения из
аналитической геометрии на плоскости.
При решении задач
аналитической геометрии целесообразно
воспользоваться учебными пособиями
следующих авторов: Д.В. Клетеника, Н. Ш.
Кремера, Д.Т. Письменного В.И. Малыхина,
т.к. в данной литературе рассматривается
более широкий круг задач, которые можно
использовать для самостоятельной
подготовки по данной теме. Применение
аналитической геометрии к решению
экономических задач изложено в учебных
изданиях М.С. Красса и В.И. Ермакова.
Задача 5.1. Даны
координаты вершин треугольника АВС.
Необходимо
а) написать
уравнения сторон треугольника;
б) написать
уравнение высоты треугольника проведенной
из вершины С
к стороне АВ
и найти ее длину;
в) написать
уравнение медианы треугольника,
проведенной из вершины В
к стороне АС;
г) найти углы
треугольника и установить его вид
(прямоугольный, остроугольный,
тупоугольный);
д) найти длины
сторон треугольника и определить его
тип (разносторонний, равнобедренный,
равносторонний);
е) найти координаты
центра тяжести (точка пересечения
медиан) треугольника АВС;
ж) найти координаты
ортоцентра (точка пересечения высот)
треугольника АВС.
К каждому из
пунктов а) – в) решения сделать рисунки
в системе координат. На рисунках
обозначить соответствующие пунктам
задачи линии и точки.
Данные к условию
задачи, соответствующие вариантам:
|
1)
2)
3)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17) 18) |
4)
5)
6)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29) 30) |
Пример 5.1
Даны координаты
вершин треугольника АВС:
![]() .
.
Необходимо а) написать уравнения сторон
треугольника; б) написать уравнение
высоты треугольника проведенной из
вершины С
к стороне АВ
и найти ее длину; в) написать уравнение
медианы треугольника, проведенной из
вершины В
к стороне АС;
г) найти длины сторон треугольника и
определить его тип (разносторонний,
равнобедренный, равносторонний); д)
найти углы треугольника и установить
его вид (прямоугольный, остроугольный,
тупоугольный); е) найти координаты центра
тяжести (точка пересечения медиан)
треугольника АВС;
ж) найти координаты ортоцентра (точка
пересечения высот) треугольника АВС.
Решение
а)
Для каждой стороны треугольника известны
координаты двух точек, которые лежат
на искомых линиях, значит уравнения
сторон треугольника – уравнения прямых,
проходящих через две заданные точки
|
|
(5.1) |
где
![]()
и
![]()
соответствующие координаты точек.
Таким образом,
подставляя в формулу (5.1) координаты
соответствующих прямым точек получаем
![]() ,
,
![]() ,
,
![]() ,
,
откуда после
преобразований записываем уравнения
сторон
![]() ,
,
![]() ,
,
![]() .
.
На рис. 7 изобразим
соответствующие сторонам треугольника
![]()
прямые.
Ответ:
![]() ,
,
![]() ,
,
![]() .
.
|
Рис. 7 |
б)
Пусть
![]()
– высота, проведенная из вершины
![]()
к стороне
![]() .
.
Поскольку
![]()
проходит через точку
![]()
перпендикулярно вектору
![]() ,
,
то составим уравнение прямой по следующей
формуле
|
|
(5.2) |
где
![]()
– координаты вектора перпендикулярного
искомой прямой,
![]()
– координаты точки, принадлежащей этой
прямой. Найдем координаты вектора,
перпендикулярного прямой
![]() ,
,
и подставим в формулу (5.2)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найдем длину высоты
CH
как расстояние от точки
![]()
до прямой
![]()
|
|
(5.3) |
где
![]()
– уравнение прямой
![]() ,
,
![]()
– координаты точки
![]() .
.
В предыдущем пункте
было найдено
![]() .
.
Подставив данные
в формулу (5.3), получим
![]() ,
,
На рис. 8 изобразим
треугольник и найденную высоту СН.
Ответ:
![]() .
.
|
Р |
в)
медиана
![]()
треугольника
![]()
делит сторону
![]()
на две равные части, т.е. точка
![]()
является серединой отрезка
![]() .
.
Исходя из этого, можно найти координаты
![]()
точки
![]()
|
|
(5.4) |
где
![]()
и
![]()
– координаты соответственно точек
![]()
и
![]() ,
,
подставив которые в формулы (5.4), получим
![]() ;
;
![]() .
.
Уравнение медианы
![]()
треугольника
![]()
составим как уравнение прямой, проходящей
через точки
![]()
и
![]()
по формуле (5.1)
![]() ,
,
![]() .
.
Ответ:
![]()
(рис. 9).
|
Р |
г)
Длины сторон треугольника найдем как
длины соответствующих векторов, т.е.
![]() ,
,
![]() ,
,
![]() .
.
Стороны
![]()
и
![]()
треугольника
![]()
равны, значит, треугольник является
равнобедренным с основанием
![]() .
.
Ответ:
треугольник
![]()
равнобедренный с основанием
![]() ;
;
![]() ,
,
![]() .
.
д)
Углы треугольника
![]()
найдем как углы между векторами,
исходящими из соответствующих вершин
данного треугольника, т.е.
![]() ,
,
![]() ,
,
![]() .
.
Поскольку треугольник
равнобедренный с основанием
![]() ,
,
то
![]() ,
,
![]()
Углы между векторами
вычислим по формуле (4.4), для которой
потребуются скалярные произведения
векторов
![]() ,
,
![]() .
.
Найдем координаты
и модули векторов, необходимых для
вычисления углов
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Подставляя
найденные данные в формулу (4.4), получим
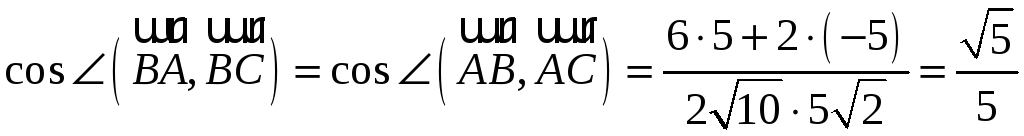 ,
,
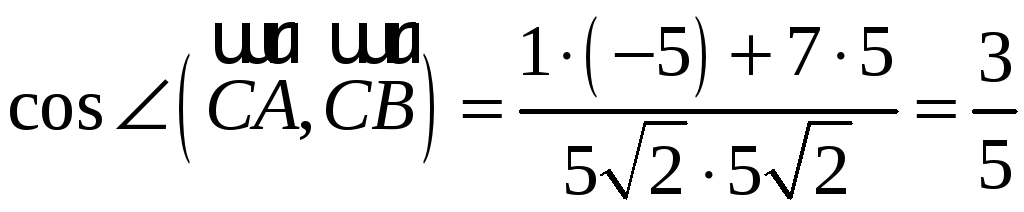 ,
,
Поскольку значения
косинусов всех найденных углов
положительны, то треугольник
![]()
является остроугольным.
Ответ:
треугольник
![]()
остроугольный;
![]() ,
,
![]() ,
,
![]() .
.
е)
Пусть
![]()
– центр тяжести треугольника
![]() ,
,
тогда координаты
![]()
точки
![]()
можно найти, по формулам (5.5)
|
|
(5.5) |
где
![]() ,
,
![]()
и
![]()
– координаты соответственно точек
![]() ,
,
![]()
и
![]() ,
,
следовательно,
![]() ,
,
![]() .
.
Ответ:
![]()
– центр тяжести треугольника
![]() .
.
ж) Пусть
![]()
– ортоцентр треугольника
![]() .
.
Найдем координаты точки
![]()
как координаты точки пересечения высот
треугольника. Уравнение высоты
![]()
было найдено в пункте б).
Найдем уравнение высоты
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Поскольку
![]() ,
,
то решение системы
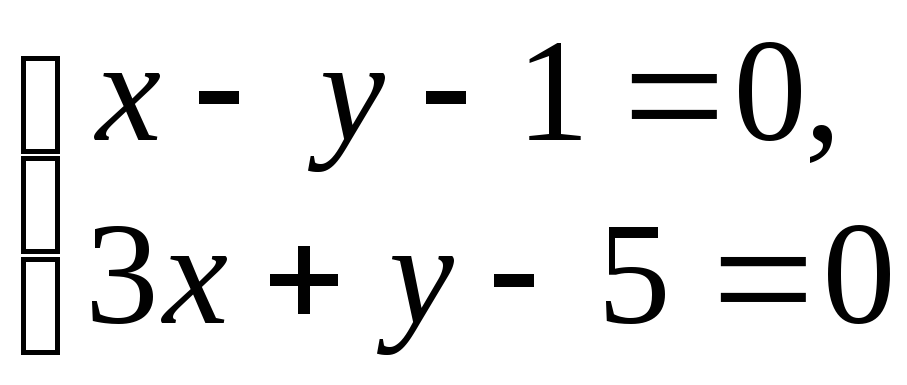
является координатами
точки
![]() ,
,
откуда находим
 .
.
Ответ:
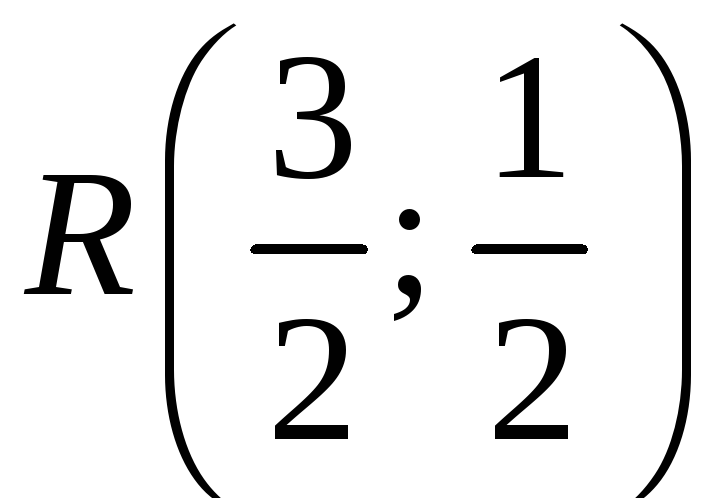
– ортоцентр треугольника
![]() .
.
Задача 5.2.
Фиксированные издержки на предприятии
при выпуске некоторой продукции
составляют F
руб. в месяц, переменные издержки – V0
руб. за
единицу продукции, при этом выручка
составляет R0
руб. за единицу изготовленной продукции.
Составить функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Данные к условию
задачи, соответствующие вариантам:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
![]() ;
;
22)
![]() ;
;
23)
![]() ;
;
24)
![]() ;
;
25)
![]() ;
;
26)
![]() ;
;
27)
![]() ;
;
28)
![]() ;
;
29)
![]() ;
;
30)
![]() .
.
Пример 5.2
Фиксированные
издержки на предприятии при выпуске
некоторой продукции составляют
![]()
руб. в месяц, переменные издержки –
![]()
руб. за единицу
продукции, при этом выручка составляет
![]()
руб. за единицу
изготовленной продукции. Составить
функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Решение
Вычислим совокупные
издержки на производстве при выпуске
q
единиц некоторой продукции
![]() .
.
Если будет продано
q
единиц продукции, то совокупный доход
составит
![]() .
.
Исходя из полученных
функций совокупного дохода и совокупных
издержек, найдем функцию прибыли
![]() ,
,
![]() ,
,
![]() .
.
 Точка
Точка
безубыточности – точка, в которой
прибыль равна нулю, или точка, в которой
совокупные издержки равны совокупному
доходу
![]() ,
,
![]() ,
,
откуда находим
![]()
– точка безубыточности.
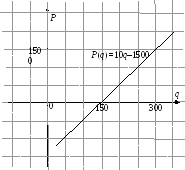
Для построения
графика (рис. 10) функции прибыли найдем
еще одну точку
![]() .
.
Рис. 10
Ответ:
функция прибыли
![]() ,
,
точка безубыточности
![]() .
.
Задача 5.3. Законы
спроса и предложения на некоторый товар
соответственно определяются уравнениями
p=pD(q),
p=pS(q),
где p
– цена на товар, q
– количество товара. Предполагается,
что спрос определяется только ценой
товара на рынке pС,
а предложение – только ценой pS,
получаемой поставщиками. Необходимо
а) определить
точку рыночного равновесия;
б) точку равновесия
после введения налога, равного t.
Определить увеличение цены и уменьшение
равновесного объема продаж;
в) найти субсидию
s,
которая приведет к увеличению объема
продаж на q0
ед. относительно изначального
(определенного в пункте а));
г) найти новую
точку равновесия и доход правительства
при введении налога, пропорционального
цене и равного N%;
д) определить,
сколько денег будет израсходовано
правительством на скупку излишка при
установлении минимальной цены, равной
p0.
К каждому пункту
решения сделать рисунок в системе
координат. На рисунке обозначить
соответствующие пункту задачи линии и
точки.
Данные к условию
задачи, соответствующие вариантам:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
![]() ;
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Определение
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать  .
.
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор  имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора
имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора  , через известные нам координаты aₓ и aᵧ.
, через известные нам координаты aₓ и aᵧ.
На взятой системе координат, от её начала отложим вектор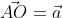 В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
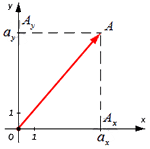
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
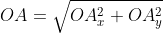
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 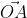 получаем
получаем
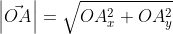
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор  дан в формате разложения по координатным векторам
дан в формате разложения по координатным векторам 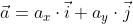 , то вычислить его можно по той же формуле
, то вычислить его можно по той же формуле  , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат
, в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат  , в данной системе координат.
, в данной системе координат.
Пример
Чтобы рассчитать длину  = (3, √x), расположенного в прямоугольной системе координат.
= (3, √x), расположенного в прямоугольной системе координат.
Необходимо:
Чтобы найти модуль вектора используем ранее приведённую формулу

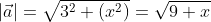
Ответ: 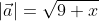
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор  =(aₓ ; aᵧ ; a
=(aₓ ; aᵧ ; a )
)
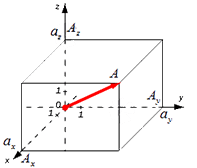
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому
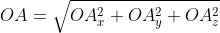
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA =a
=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
, а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
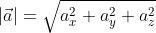
Пример
Необходимо узнать длину вектора ( left|vec{a}right|=2*vec{i}+3*vec{j}+4*vec{k} ), в котором ( vec{i}, vec{j}, vec{k} ), орты.
Решение
Получается, что дан вектор ( left|vec{a}right| ) с координатами (2; 3; 4)
Применив выведенную ранее формулу получим
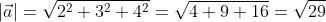
Ответ: 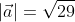
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор  имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
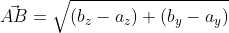
При этом формула вычисления длины вектора  для трёхмерного пространства, с координатами
для трёхмерного пространства, с координатами 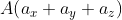 и
и 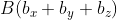 ), будет следующей:
), будет следующей:
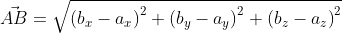
Пример
Для прямой системы координат, найти длину вектора ( overrightarrow{AB}) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
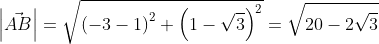
Существует второй вариант решения, где формулы применяются по очереди:
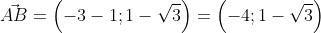
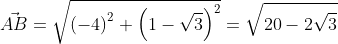
Ответ: 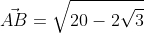
Пример
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
Решение
В первую очередь представим длину вектора в виде формулы.
( left|vec{AB}right|=sqrt{left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2})
(=sqrt{left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2} = sqrt{26 + left ( lambda^2 -2right )^2})
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
(
sqrt{26+left(lambda^2-2right)^2}=sqrt{30}
)
(
26+left(lambda^2-2right)^2=30
)
(
left(lambda^2-2right)^2=4
)
(
lambda^2-2=2
)
или
(
lambda^2-2=-2
)
(
lambda_1=-2, lambda_2=2, lambda_3=0.
)
Ответ: (
lambda_1=-2, lambda_2=2, lambda_3=0.
)
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow{AB}) и (overrightarrow{AC}) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow{BC} ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Пример
Даны длины двух векторов ( overrightarrow{AK}) и ( overrightarrow{AM}) 2 и 4 соответственно, а угол между ними равен ( frac{pi}{3} ) . необходимо найти длину ( overrightarrow{KM}).
Решение
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
(
KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac{pi}{3})
(=2^2+4^2-2cdot2cdot4cdotcosfrac{pi}{3})
(=4+16-16cosfrac{pi}{3})
(=20-8=12
)
Получается (KM=sqrt{12}
)
Ответ: (
left|overrightarrow{KM}right|=sqrt{12}
)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
Первая формула это ( left|overrightarrow{a}right|=sqrt{a_x^2+a_y^2}. ), для плоскости
( left|overrightarrow{a}right|=sqrt{a_x^2+a_y^2+a_z^2} )
длина вектора формула для трёхмерного пространства;
( left|vec{AB}right|=sqrt{left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2})
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vec{AB}right|=sqrt{left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2}) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vec{S}right|=sqrt{ s_x^2+s_y^2}) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.

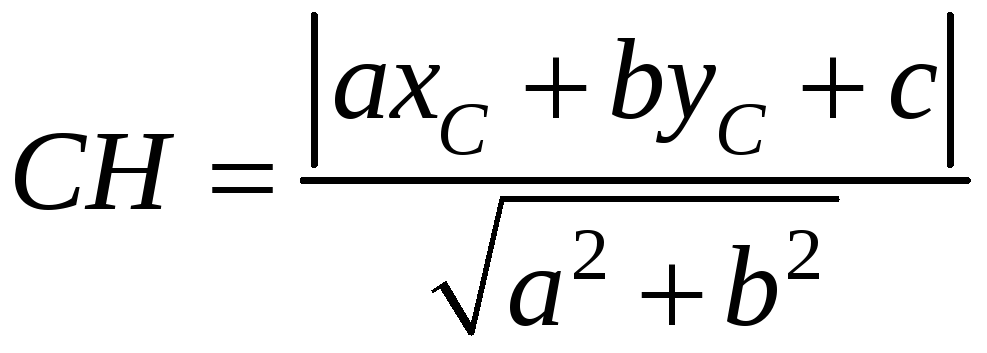 ,
, ис.
ис.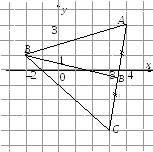 ис.
ис.