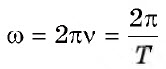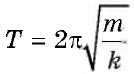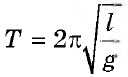Как найти кгц в задачах

Успешное решение данного типа задач предполагает знание технологии обработки и кодирования звука.

Рассмотрим решение задачи А8 из демонстрационной версии ЕГЭ 2012:

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 0.2 Мбайт       2) 2 Мбайт       3) 3 Мбайт       4) 4 Мбайт

Решение:

Зная частоту дискретизации и глубину кодирования легко найдем объем памяти, который занимает 1 секунда записи:

16000 Гц * 24 бит=384000 бит или 48000 байт или 46,875 Кбайт.

Так как в минуте 60 секунд, то минутная запись займет 60 сек * 46,875 Кбайт = 2 812,5 Кбайт или около 2,75 Мбайт. Правильный ответ 3.

Рассмотрим решение задачи А8 из демонстрационной версии ЕГЭ 2013:

Производится одноканальная (моно) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 4 минуты, её результаты записываются в файл, сжатия данных не производится. Какая из приведённых ниже величин наиболее близка к размеру полученного файла?

1) 44 Мбайт       2) 87 Мбайт       3) 125 Мбайт       4) 175 Мбайт

Решение:

Решение аналогично предыдущему. Учитывая, что 32 бита = 4 байта найдем, что одна секунда записи потребует 48000 * 4 байта = 192 000 байт памяти или 187,5 Кбайт. В 4-х минутах 240 секунд, соответственно объем файла будет равен 187,5Кбайт * 240 сек =45 000 Кбайт или около 43,95 Мб. Следовательно, правильный ответ 1.

Дополнение

В комментариях Arni попросил рассмотреть задачу на нахождение времени. Давайте рассмотрим 🙂 Пусть это будет задача А8 из тренировочной работы (вариант ИНФ1601):

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. В результате был получен файл размером 60 Мбайт, сжатие данных не производилось. Какая из перечисленных ниже величин наиболее близка по времени, к течение которого производилась запись?
1) 1 мин.           2) 2 мин.           3) 3 мин.           4) 4 мин.

Решение:

Все очень просто. Частота дискретизации показывает, что за 1 секунду происходит 32000 замеров уровня сигнала, при этом для каждого такого замера требуется 32 бита. 32 бита = 4 байта. Получается, что 1 секунда одноканальной записи потребует 32000 * 4 байта = 128 000 байт памяти. Так как у нас запись четырёхканальная, то получим, что секунда такой записи займет уже 128 000 * 4 = 512 000 байт.

Также известно, что весь файл занимает 60 Мбайт. Значит, чтобы найти время записи, надо 60 Мбайт разделить на 512 000 байт. Приведем эти числа к одной единице измерения:

60 Мбайт = 60 * 1024 = 61 440 Кбайт.

512 000 байт = 512 000 / 1024 = 500 Кбайт.

А теперь разделим:

61 440 Кбайт / 500 Кбайт и получим 122,88 секунды. Ближе всего к этому значению 2 минуты (120 секунд). Правильный ответ 2.

Автор:

Решение задач на кодирование звуковой информации

Введение

Данное электронное пособие содержит группу
задач по теме «Кодирование звуковой информации». Сборник задач разбит на типы
задач исходя из указанной темы. Каждый тип задач рассматривается с учетом дифференцированного
подхода, т. е. рассматриваются задачи минимального уровня (оценка «3»), общего
уровня (оценка «4»), продвинутого уровня (оценка «5»). Приведенные задачи взяты
из различных учебников (список прилагается). Подробно рассмотрены решения всех задач,
даны методические рекомендации для каждого типа задач, приведен краткий
теоретический материал. Для удобства пользования пособие содержит ссылки на
закладки.

Типы задач:

1. Размер цифрового аудиафайла (моно и
стерео).

2. Определение качества
звука.

3. Двоичное кодирование звука.

При решении задач учащиеся опираются на следующие
понятия:

Временная дискретизация – процесс, при котором, во время
кодирования непрерывного звукового сигнала, звуковая волна разбивается на
отдельные маленькие временные участки, причем для каждого такого участка
устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала,
тем громче звук.

Глубина звука  (глубина кодирования) – количество бит на кодировку
звука.

Уровни громкости  (уровни сигнала) – звук может иметь различные уровни
громкости. Количество различных уровней громкости рассчитываем по формуле N=
2^I  где I – глубина звука.

Частота
дискретизации – количество измерений уровня входного сигнала в
единицу времени (за 1 сек). Чем больше частота дискретизации, тем точнее
процедура двоичного кодирования. Частота измеряется в герцах (Гц). 1 измерение
за 1 секунду -1 ГЦ.

1000
измерений за 1 секунду 1 кГц. Обозначим частоту дискретизации буквой D. Для кодировки выбирают одну из трех
частот: 44,1 КГц, 22,05 КГц, 11,025 КГц.

Считается, что диапазон
частот, которые слышит человек, составляет от 20 Гц до 20 кГц.

Качество двоичного кодирования – величина, которая определяется
глубиной кодирования и частотой дискретизации.

Аудиоадаптер (звуковая плата) – устройство, преобразующее
электрические колебания  звуковой частоты в числовой двоичный код при вводе
звука и обратно (из числового кода в электрические колебания) при воспроизведении
звука.

Характеристики аудиоадаптера: частота дискретизации и
разрядность регистра.).

Разрядность регистра –число бит в регистре
аудиоадаптера. Чем больше разрядность, тем меньше погрешность каждого
отдельного преобразования величины электрического тока в число и обратно. Если
разрядность равна I, то при измерении входного сигнала может быть получено 2^I =N различных значений.

Размер цифрового моноаудиофайла  ( A)
измеряется по формуле:

A=D*T*I/8, где D –частота дискретизации (Гц), T – время звучания или записи звука, I разрядность регистра
(разрешение). По этой формуле размер измеряется в байтах.

Размер цифрового стереоаудиофайла  ( A)
измеряется по формуле:

A=2*D*T*I/8, сигнал записан для двух колонок, так
как раздельно кодируются левый и правый каналы звучания.

Учащимся полезно выдать таблицу 1, показывающую, сколько Мб будет
занимать закодированная одна минута звуковой информации при разной частоте
дискретизации:

1. Размер
цифрового файла

Уровень «3»

1. Определить размер (в
байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при
частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен.  ([1],
стр. 156, пример 1)

Решение:

Формула
для расчета размера (в байтах) цифрового аудио-файла: A=D*T*I/8.

Для перевода в байты полученную величину
надо разделить на 8 бит.

22,05 кГц =22,05
* 1000 Гц  =22050 Гц

A=D*T*I/8 = 22050
х 10 х 8 / 8 = 220500 байт.

Ответ: размер
файла  220500 байт.

2. Определить объем памяти
для хранения цифрового аудиофайла, время звучания которого составляет две
минуты при частоте дискретизации 44,1 кГц и разрешении 16 бит.  ([1], стр. 157,
№88)

Решение:

A=D*T*I/8. – объем памяти для хранения
цифрового аудиофайла.

44100 (Гц) х 120 (с) х 16 (бит) /8 (бит) =
10584000 байт= 10335,9375 Кбайт= 10,094 Мбайт.

Ответ: ≈ 10 Мб

Уровень «4»

3. В
распоряжении пользователя имеется память объемом 2,6 Мб. Необходимо записать
цифровой аудиофайл с длительностью звучания 1 минута. Какой должна быть частота
дискретизации и разрядность?  ([1], стр. 157, №89)

Решение:

Формула
для расчета частоты дискретизации и разрядности: D* I =А/Т

(объем
памяти в байтах) : (время звучания в секундах):

2, 6
Мбайт= 2726297,6 байт

D* I =А/Т= 2726297,6 байт: 60 = 45438,3 байт

D=45438,3 байт : I

 Разрядность
адаптера может быть 8 или 16 бит. (1 байт или 2 байта). Поэтому частота
дискретизации может быть либо  45438,3 Гц = 45,4 кГц ≈ 44,1
кГц –стандартная характерная частота дискретизации, либо 22719,15 Гц = 22,7
кГц ≈ 22,05 кГц – стандартная характерная частота дискретизации

Ответ:

4.  Объем свободной памяти на
диске — 5,25 Мб, разрядность звуковой платы — 16. Какова длительность звучания
цифрового аудиофайла, записанного с частотой дискретизации 22,05 кГц?  ([1],
стр. 157, №90)

Решение:

Формула для расчета
длительности звучания: T=A/D/I

(объем памяти в байтах)
: (частота дискретизации в Гц) : (разрядность звуковой платы в байтах):

5,25 Мбайт = 5505024 байт

5505024 байт: 22050 Гц
: 2 байта = 124,8 сек
Ответ: 124,8 секунды

5. Одна минута записи
цифрового аудиофайла занимает на диске 1,3 Мб, разрядность звуковой платы — 8.
С какой частотой дискретизации записан звук?  ([1], стр. 157, №91)

Решение:

Формула для расчета
частоты дискретизации : D =А/Т/I

(объем памяти в байтах) : (время записи в
секундах) : (разрядность звуковой платы в байтах)

1,3 Мбайт = 1363148,8 байт

1363148,8 байт  : 60 : 1 = 22719,1 Гц

Ответ: 22,05 кГц

6. Две минуты записи
цифрового аудиофайла занимают на диске 5,1 Мб. Частота дискретизации — 22050
Гц. Какова разрядность аудиоадаптера?  ([1], стр. 157, №94)

Решение:

Формула для расчета разрядности: (объем
памяти в байтах) : (время звучания в секундах): (частота дискретизации):

5, 1 Мбайт= 5347737,6 байт

5347737,6 байт: 120 сек : 22050 Гц= 2,02
байт =16 бит

Ответ: 16 бит

7. Объем свободной памяти на диске — 0,01 Гб,
разрядность звуковой платы — 16. Какова длительность звучания цифрового
аудиофайла, записанного с частотой дискретизации 44100 Гц?  ([1], стр. 157,
№95)

Решение:

Формула для расчета
длительности звучания T=A/D/I

(объем памяти в байтах) : (частота
дискретизации в Гц) : (разрядность звуковой платы в байтах)

0,01 Гб = 10737418,24 байт

10737418,24 байт : 44100 : 2 = 121,74 сек
=2,03 мин
Ответ: 20,3 минуты

8. Оцените информационный объем
моноаудиофайла длительностью звучания 1 мин. если “глубина”
кодирования и частота дискретизации звукового сигнала равны соответственно:
а) 16 бит и 8 кГц;
б) 16 бит и 24 кГц.

 ([2],
стр. 76, №2.82)

Решение:

а).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 8 000 = 128000 бит = 16000 байт = 15,625 Кбайт/с
2) Информационный объем звукового файла длительностью 1 минута равен:
15,625 Кбайт/с х 60 с = 937,5 Кбайт

б).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 24 000 = 384000 бит = 48000 байт = 46,875 Кбайт/с
2) Информационный объем звукового файла длительностью 1 минута равен:
46,875 Кбайт/с х 60 с =2812,5 Кбайт = 2,8 Мбайт

Ответ: а) 937,5 Кбайт; б) 2,8 Мбайт

Уровень «5»

Используется таблица 1

9. Какой объем памяти
требуется для хранения цифрового аудиофайла с записью звука высокого качества
при условии, что время звучания составляет 3 минуты?  ([1], стр. 157, №92)

Решение:

Высокое качество звучания достигается при
частоте дискретизации 44,1КГц и разрядности аудиоадаптера, равной 16.
Формула для расчета объема памяти: (время записи в секундах) x (разрядность
звуковой платы в байтах) x (частота дискретизации):
180 с х 2 х 44100 Гц = 15876000 байт = 15,1 Мб
Ответ: 15,1 Мб

10. Цифровой аудиофайл
содержит запись звука низкого качества (звук мрачный и приглушенный). Какова
длительность звучания файла, если его объем составляет 650 Кб?  ([1], стр. 157,
№93)

Решение:

Для мрачного и
приглушенного звука характерны следующие параметры: частота дискретизации — 11,
025 КГц, разрядности аудиоадаптера — 8 бит (см. таблицу 1). Тогда T=A/D/I.
Переведем объем в байты: 650 Кб = 665600 байт

Т=665600 байт/11025 Гц/1
байт ≈60.4 с

Ответ:
длительность звучания равна 60,5 с

11.  Оцените информационный
объем высокачественного стереоаудиофайла длительностью звучания 1 минута, если
“глубина” кодирования 16 бит, а частота дискретизации 48 кГц.   ([2],
стр. 74, пример 2.54)

Решение:

Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 48 000 х 2 = 1 536 000 бит = 187,5 Кбайт (умножили на 2, так как
стерео).

Информационный объем звукового файла длительностью 1 минута
равен:
187,5 Кбайт/с х 60 с ≈ 11 Мбайт

Ответ: 11 Мб

Ответ: а) 940 Кбайт; б) 2,8 Мбайт.

12.
 Рассчитайте
время звучания моноаудиофайла, если при 16-битном кодировании и частоте
дискретизации 32 кГц его объем равен:
а) 700 Кбайт;
б) 6300 Кбайт

 ([2], стр. 76, №2.84)

Решение:

а).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 32 000 = 512000 бит = 64000 байт = 62,5 Кбайт/с
2) Время звучания моноаудиофайла объемом 700 Кбайт равно:
700 Кбайт : 62,5 Кбайт/с = 11,2 с

б).
1) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 32 000 = 512000 бит = 64000 байт = 62,5 Кбайт/с
2) Время звучания моноаудиофайла объемом 700 Кбайт равно:
6300 Кбайт : 62,5 Кбайт/с = 100,8 с = 1,68 мин

Ответ: а) 10 сек; б) 1,5
мин.

13. Вычислить, сколько байт информации занимает на
компакт-диске одна секунда стереозаписи (частота 44032 Гц, 16 бит на значение).
Сколько занимает одна минута? Какова максимальная емкость диска (считая
максимальную длительность равной 80 минутам)?  ([4], стр. 34, упражнение №34)  

Решение:

Формула для расчета объема памяти A=D*T*I:
(время записи в секундах) * (разрядность звуковой платы в байтах) * (частота
дискретизации). 16 бит -2 байта.
1) 1с х 2 х 44032 Гц = 88064 байт (1 секунда стереозаписи на компакт-диске)
2) 60с х 2 х 44032 Гц = 5283840 байт (1 минута стереозаписи на компакт-диске)
3) 4800с х 2 х 44032 Гц = 422707200 байт=412800 Кбайт=403,125 Мбайт (80 минут)

Ответ: 88064 байт (1 секунда), 5283840 байт (1 минута), 403,125 Мбайт (80 минут)

2. Определение качества звука.

Для определения качества звука надо найти частоту
дискретизации и воспользоваться таблицей №1

256 (2⁸)
уровней интенсивности сигнала -качество звучания радиотрансляции,
использованием 65536 (2¹⁶)  уровней интенсивности сигнала – качество
звучания аудио-CD. Самая качественная частота соответствует музыке, записанной
на компакт-диске. Величина аналогового сигнала измеряется в этом случае
44 100 раз в секунду.

Уровень «5»

13. Определите
качество звука (качество радиотрансляции, среднее качество, качество аудио-CD)
если известно, что объем моноаудиофайла длительностью звучания в
10 сек. равен:
а) 940 Кбайт;
б) 157 Кбайт.

 ([2], стр. 76,
№2.83)

Решение:

а).
1) 940 Кбайт= 962560 байт = 7700480 бит
2) 7700480 бит : 10 сек = 770048 бит/с
3) 770048 бит/с : 16 бит = 48128 Гц –частота дискретизации – близка к самой
высокой 44,1 КГц
Ответ: качество аудио-CD

б).
1) 157 Кбайт= 160768 байт = 1286144 бит
2) 1286144 бит : 10 сек = 128614,4 бит/с
3) 128614,4 бит/с : 16 бит = 8038,4 Гц
Ответ: качество радиотрансляции

Ответ: а) качество CD; б) качество
радиотрансляции.

14.  Определите длительность
звукового файла, который уместится на гибкой дискете 3,5”.
Учтите, что для хранения данных на такой дискете выделяется 2847 секторов
объемом 512 байт.
а) при низком качестве звука: моно, 8 бит, 8 кГц;
б) при высоком качестве звука: стерео, 16 бит, 48 кГц.

 ([2],
стр. 77, №2.85)

Решение:

а).
1) Информационный объем дискеты равен:
2847 секторов х 512 байт = 1457664 байт = 1423,5 Кбайт
2) Информационный объем звукового файла длительностью в
1 секунду равен:
8 бит х 8 000 = 64 000 бит = 8000 байт = 7,8 Кбайт/с
3) Время звучания моноаудиофайла объемом 1423,5 Кбайт равно:
1423,5 Кбайт : 7,8 Кбайт/с = 182,5 с ≈ 3 мин

б).
1) Информационный объем дискеты  равен:
2847 секторов х 512 байт = 1457664 байт = 1423,5 Кбайт
2) Информационный объем звукового файла длительностью в
1 секунду равен:
16 бит х 48 000 х 2= 1 536 000 бит = 192 000 байт = 187,5 Кбайт/с
3) Время звучания стереоаудиофайла объемом 1423,5 Кбайт равно:
1423,5 Кбайт : 187,5 Кбайт/с = 7,6 с

Ответ: а) 3 минуты; б) 7,6
секунды.

3. Двоичное кодирование звука.

При решении задач пользуется следующим теоретическим
материалом:

Для того, чтобы кодировать звук,
аналоговый сигнал, изображенный на рисунке,

плоскость разбивается
на вертикальные и горизонтальные линии. Вертикальное разбиение –это
дискретизация  аналогового сигнала (частота измерения сигнала), горизонтальное
разбиение  – квантование по уровню. Т.е. чем мельче сетка – тем
качественнее приближен аналоговый звук с помощью цифр. Восьмибитное квантование
применяется для оцифровки обычной речи (телефонного разговора) и радиопередач
на коротких волнах. Шестнадцатибитное – для оцифровки музыки и УКВ
(ультро-коротко-волновые) радиопередач.

Уровень «3»

15.  Аналоговый звуковой
сигнал был дискретизирован сначала с использованием 256 уровней интенсивности
сигнала (качество звучания радиотрансляции), а затем с использованием 65536
уровней интенсивности сигнала (качество звучания аудио-CD). Во сколько раз
различаются информационные объемы оцифрованного звука?   ([2], стр. 77, №2.86)

Решение:

Длина
кода аналогового сигнала с использованием 256 уровней интенсивности сигнала
равна 8 битам, с использованием  65536 уровней
интенсивности сигнала равна 16 битам. Так как длина кода одного сигнала 
увеличилась вдвое, то информационные объемы оцифрованного звука  различаются в
2 раза.

Ответ: в
2 раза.

Уровень
«4»

16. Согласно
теореме Найквиста—Котельникова, для того чтобы аналоговый сигнал можно было
точно восстановить по его дискретному представлению (по его отсчетам), частота
дискретизации должна быть как минимум вдвое больше максимальной звуковой
частоты этого сигнала.

·        
Какова должна быть
частота дискретизации звука, воспринимаемого человеком?

·        
Что должно быть больше:
частота дискретизации речи или частота дискретизации звучания симфонического
оркестра?

 Цель: познакомить учащихся с
характеристиками аппаратных и программных средств работы со звуком. Виды
деятельности: привлечение знаний из курса физики (или работа со справочниками).  ([3], стр. ??, задача 2)

Решение:

Считается, что
диапазон частот, которые слышит человек, составляет от 20 Гц до 20 кГц. Таким
образом, по теореме Найквиста—Котельникова, для того чтобы аналоговый сигнал
можно было точно восстановить по его дискретному представлению (по его
отсчетам), частота дискретизации должна быть как минимум вдвое больше
максимальной звуковой частоты этого сигнала. Максимальная звуковая
частота которую слышит человек -20 КГц, значит, аппаратура и программные
средства должны обеспечивать частоту дискретизации не менее 40 кГц, а точнее
44,1 КГц. Компьютерная обработка звучания симфонического оркестра предполагает
более высокую частоту дискретизации, чем обработка речи, поскольку диапазон
частот в случае симфонического оркестра  значительно больше.

Ответ: не меньше 40 кГц, частота
дискретизации симфонического оркестра больше.

Уровень»5»

17. На
рисунке изображено зафиксированное самописцем звучание 1 секунды речи.
Закодируйте его в двоичном цифровом коде с частотой 10 Гц и длиной кода 3 бита.
 ([3], стр. ??, задача 1)

Решение:

Кодирование с частотой 10 Гц означает, что
мы должны измерить высоту звука 10 раз за секунду. Выберем равноотстоящие
моменты времени:

Длина кода в
3 бита означает 2³ = 8 уровней квантования. То есть в качестве
числового кода высоты звука в каждый выбранный момент времени мы можем задать
одну из следующих комбинаций: 000, 001, 010, 011, 100, 101, 110, 111. Их всего
8, следовательно, высоту звука можно измерять на 8 «уровнях»:

«Округлять» значения высоты звука будем до
ближайшего нижнего уровня:

Используя
данный способ кодирования, мы получим следующий результат (пробелы поставлены
для удобства восприятия): 100 100 000 011 111 010 011 100 010 110.

Примечание.
Целесообразно обратить внимание
учащихся на то, насколько неточно код передает изменение амплитуды. То есть
частота дискретизации 10 Гц и уровень квантования 2³ (3 бита)
слишком малы. Обычно для звука (голоса) выбирают частоту дискретизации 8 кГц,
т. е. 8000 раз в секунду, и уровень квантования 2⁸ (код длиной 8
бит).

Ответ: 100
100 000 011 111 010 011 100 010 110.

18. Объясните, почему уровень
квантования относится, наряду с частотой дискретизации, к основным
характеристикам представления звука в компьютере. Цели: закрепить
понимание учащимися понятий «точность представления данных», «погрешность
измерения», «погрешность представления»; повторить с учащимися двоичное
кодирование и длину кода. Вид деятельности: работа с определениями понятий.  ([3], стр. ??, задача 3)

Решение:

В геометрии, физике, технике есть понятие
«точность измерения», тесно связанное с понятием «погрешность измерения». Но
есть еще и понятие «точность представления». Например, про рост человека
можно сказать, что он: а) около. 2 м, б) чуть больше 1,7
м, в) равен 1 м 72 см, г) равен 1 м 71
см 8 мм. То есть для обозначения измеренного роста можно использовать 1, 2, 3
или 4 цифры.
Так же и для двоичного кодирования. Если для записи высоты звука в конкретный
момент времени использовать только 2 бита, то, даже если измерения были точны,
передать можно только 4 уровня: низкий (00), ниже среднего (01), выше среднего
(10), высокий (11). Если использовать 1 байт, то можно передать 256 уровней.
Чем выше уровень квантования, или, что то же самое, чем больше битов
отводится для записи измеренного значения, тем точнее передается это значение.

Примечание. Следует отметить, что измерительный инструмент
тоже должен поддерживать выбранный уровень квантования (длину, измеренную
линейкой с дециметровыми делениями, нет смысла представлять с точностью до
миллиметра).

Ответ: чем
выше уровень квантования тем точнее передается звук.

Литература:

[1] Информатика. Задачник-практикум в 2 т. /Под ред. И.Г. Семакина, Е.К.
Хеннера: Том 1. – Лаборатория Базовых Знаний, 1999
г. – 304 с.: ил.

 [2] Практикум по информатике и информационным технологиям. Учебное пособие
для общеобразовательных учреждений / Н.Д. Угринович, Л.Л. Босова, Н.И.
Михайлова. – М.: Бином. Лаборатория Знаний, 2002. 400 с.: ил.

 [3] Информатика в школе: Приложение к журналу «Информатика и образование».
№4 — 2003. — М.: Образование и Информатика, 2003. — 96 с.: ил.

[4] Кушниренко А.Г., Леонов А.Г., Эпиктетов М.Г. и др. Информационная
культура: одирование информации. Информационные модели. 9-10
класс: Учебник для общеобразовательных учебных заведений. — 2-е изд. — М.:
Дрофа, 1996. — 208 с.: ил.

[5] Гейн А.Г.,
Сенокосов А.И. Справочник по информатике для школьников. — Екатеринбург:
«У-Фактория», 2003. — 346. с54-56.  

1. Общие сведения

2. Пример задания

3. Советы учителям и ученикам 

4. Задачи для самостоятельного решения

5. Дополнение. Некоторые сведения о цифровой звукозаписи.

6.  Решения задач с сайта ege.yandex.ru

7. История

1. Общие сведения

Сложность: базовая.

Примерное время решения (для тех, кто будет выполнять часть 2):  2 минуты

Тема: Создание и обработка графической и мультимедийной информации

Подтема: Цифровая звукозапись

Что проверяется: Умение оценивать количественные характеристики процесса записи звука.

Краткие теоретические сведения: Поскольку данный тип задания является новым в КИМ ЕГЭ, приведем (пока без обоснования, обоснование ниже) математическую модель процесса звукозаписи:

N = k * F * L *T                                              (1)

где

• • N – размер файла (в битах) , содержащего запись звука;
• • k –  количество каналов записи (например, 1 – моно, 2 – стерео, 4 – квадро и т.д.);
• • F – частота дискретизации (в герцах), т.е. количество значений амплитуды звука фиксируемых за одну секунду;
• • L – разрешение, т.е. число бит, используемых для хранения каждого измеренного значения;
• • T – продолжительность звукового фрагмента (в секундах).

 Как может выглядеть задание?  Например, так:  Заданы значения всех требуемых параметров процесса звукозаписи, кроме одного. Требуется оценить значение оставшегося параметра, например, размер файла или продолжительность звукового фрагмента.

Пример условия:

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

Варианты ответов:

1) 0,2 Мбайт

2) 2 Мбайт

3) 3 Мбайт

4) 4 Мбайт

2. Пример задания 

2.1. Условие задачи.

Задача 2012-А8-1.

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 0,2 Мбайт            2) 2 Мбайт            3) 3 Мбайт            4) 4 Мбайт

2.2. Решение. 

Приводим исходные данные к размерности биты-секунды-герцы и проводим расчеты по формуле (1):

Дано:

k = 1, т.к. одноканальная (моно) звукозапись;

F = 16 кГц = 16 000 Гц;

L = 24;

T = 1 мин = 60 с.

Найти N  

Подставляем значение известных параметров в формулу (1)

N = 1*16000*24*60 =(16*1000)* (8*3) * (4*15)=

              = 2⁴*(2³*125)*(2³*3)* )*(2²* 15) = 2¹²*5625 (бит)=

               = 2¹²*5625 бит = (2¹²*5625)/2³ байт = 2⁹*5625 байт =

              = (2⁹*5625)/ 2²⁰ Мбайт =  5625/2¹¹ Мбайт = 5625/2048 Мбайт.

Число 5625/2048 находится между числами 2 и 3. При этом оно ближе к 3, чем к 2, т.к. 3 * 2048 – 5625 < 1000; 5625 – 2 * 2048 > 1000.

Правильный вариант ответа: №3 (3 Мбайт)

Замечание. Другая идея решения приведена в п.3.3

3. Советы учителям и ученикам 

3.1  Какие знания/умения/навыки нужны ученику, чтобы решить эту задачу 

1) Не следует «зазубривать» формулу (1). Ученик, представляющий суть процесса цифровой звукозаписи, должен быть способен самостоятельно её сформулировать.

2) Необходимо умение записывать значения параметров в требуемой размерности, а также элементарные арифметические навыки, в т.ч. оперирование со степенями двойки.

3.2. Рекомендации для учителей: как разбирать задачу с учениками

Эти рекомендации – не догма, а попытка сделать выводы из собственного опыта. Ждем комментариев и Ваших рекомендаций.

А. Сильные ученики. 

1. Скорее всего, они и так решат эту задачу.

2. Можно дать задание ученикам проверить формулу (1) на практике, записывая в файл звук с микрофона. При этом следует учесть, что она справедлива только в том случае, если записываемая информация не подвергается сжатию (формат WAV (PCM) без сжатия). Если используются аудиоформаты со сжатием (WMA, MP3), то объем получившегося файла будет по понятным причинам существенно меньше расчетного.  Для экспериментов с цифровой звукозаписью можно использовать свободно распространяемый аудиоредактор Audacity (http://audacity.sourceforge.net/).

3. Целесообразно подчеркнуть концептуальную общность растрового представления звука и изображения, являющихся разновидностями одного и того же процесса приближенного представления непрерывного сигнала последовательность коротких дискретных сигналов, т.е.  оцифровывания на основе дискретизации. В случае растрового изображения производится двумерная дискретизизация яркости в пространстве, в случае звука – одномерная дискретизация по времени. И в том, и в другом случае повышение частоты дискретизации (количества пикселей или звуковых отсчетов) и/или увеличение количества битов для представления одного отсчета (разрядность цвета или звука) ведет к повышению качества оцифровки, при одновременном росте размера файла с цифровым представлением. Отсюда – необходимость сжатия данных.

4. Желательно упомянуть об альтернативных способах оцифровки звука – запись «партий» инструментов в MIDI-формате. Здесь уместно провести аналогию с растровым и векторным представлением изображений.

Б. Не столь сильные ученики. 

1. Необходимо обеспечить усвоение соотношения (1). Рекомендуется дать задания типа «Как изменится объем файла, если время записи звучания увеличить/уменьшить в p раз? »,

«Во сколько раз можно увеличить/уменьшить продолжительность записи, если максимальный размер файла увеличить/уменьшить в p раз? », «Как изменится объем файла, если количество бит для записи одного значения  увеличить/уменьшить в p раз?» и т.д.

2. Необходимо  убедиться, что учащиеся свободно оперируют размерностями, знают, что в Мбайте 2²³ бит и т.д.

3. Необходимо  убедиться, что учащиеся достаточно арифметически грамотны, свободно владеют устным счетом со степенями двойки (умножение, деление, выделение сомножителей, представляющих собой 2ⁿ).

4. Придумывайте свои подходы и пробуйте их.

3.3. Полезный прием.

В подобных задачах часто возникают степени двойки. Перемножать и делить степени проще, чем произвольные числа: умножение и деление степеней сводится к сложению и вычитанию показателей.

Заметим, что числа 1000 и 1024 отличаются менее, чем на 3%, числа 60 и 64 отличаются менее, чем на 7%. Поэтому можно поступить так. Провести вычисления, заменив 1000 на 1024 = 2¹⁰ и 60 на 64 = 2⁶, используя преимущества операций со степенями. Ближайший к полученному числу ответ и будет искомым. Можно после этого перепроверить себя, проведя точные вычисления. Но можно учесть, что общая погрешность вычислений при нашем приближении не превышает 10%. Действительно, 60*1000 = 60000; 64*1024=65536;

60000 > 0.9 * 65536 = 58982.4

Таким образом, правильный результат умножений по формуле (1) немного больше, чем 90% от полученного приближенного результата. Если учет погрешности не меняет результата – можно не сомневаться в ответе.

Пример. (ege.yandex.ru, вариант 1).

Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 30 Мбайт               2) 60 Мбайт               3) 75 Мбайт               4) 90 Мбайт

Решение. Размер записи в битах равен

2*16*1000*32*12*60

С учетом замены 1000 на 1024=2¹⁰ и 60 на 64=2⁶ получим:

2¹*2⁴*2¹⁰*2⁵*3*2²*2⁶=3*2²⁸

Как известно, 1 Мбайт = 2²⁰ байт = 2²³ бит. Поэтому 3*2²⁸ бит = 3*32 = 96 Мбайт. Уменьшив это число на 10%, получим 86.4 Мбайт. В обоих случаях ближайшей величиной является 90 Мбайт.

Правильный ответ: 4

3.4. Рекомендации для учеников: как решать подобные задачи

1. Прочитайте условие задачи. Выразите неизвестный параметр через известные. Особое внимание обратите, на размерность известных параметров. Она должна быть – биты-секунды-герцы (напомним, что 1 Гц = с^-1). При необходимости, приведите значения параметров к нужной размерности, так же как это делается в задачах по физике.

2. Проводите вычисления, стараясь выделять степени двойки.

3. Обратите внимание, что в условии требуется выбрать наиболее подходящий ответ, поэтому высокая точность  вычислений до знаков после запятой не требуется. Как только стало ясно, какой из вариантов ответов наиболее близок к вычисляемому значению, вычисления следует прекратить. Если расхождение со всеми вариантами ответов очень велико (в разы или на порядок), то вычисления надо перепроверить.

Удачи!

4. Задачи для самостоятельного решения

4.1. Клоны задачи 2012-А8-1.

Ниже приведены еще четыре варианта задачи 2012-А8-1.

А) Производится одноканальная (моно) звукозапись с частотой дискретизации 32 кГц и 24-битным разрешением. Запись длится 15 секунд, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 1,5 Мбайт 2) 3 Мбайт 3) 6 Мбайт 4) 12 Мбайт

Б) Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 24-битным разрешением. Запись длится 30 секунд, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 1,5 Мбайт 2) 3 Мбайт 3) 6 Мбайт 4) 12 Мбайт

В)  Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 2 Мбайт 2) 4 Мбайт 3) 8 Мбайт 4) 16 Мбайт

Г)  Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 4 минуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 2 Мбайт 2) 4 Мбайт 3) 8 Мбайт 4) 16 Мбайт

Правильные ответы:

А:1; Б:3; В:3; Г:4.

4.2. Задача 2012-А8-2(обратная к предыдущей).

A) Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением.  Результаты записываются в файл, размер которого не может превышать 8 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

Б) Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением.  Результаты записываются в файл, размер которого не может превышать 8 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

В) Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и 8-битным разрешением.  Результаты записываются в файл, размер которого не может превышать 2,5 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

Г) Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и 16-битным разрешением.  Результаты записываются в файл, размер которого не может превышать 5 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

Правильные ответы:

А:3; Б: 4 ; В: 1; Г:1 .

5.Дополнение. Некоторые сведения о цифровой звукозаписи.

Распространение звука в воздухе можно рассматривать как распространение колебаний давления. Микрофон преобразует колебания давления в колебания электрического тока. Это аналоговый непрерывный сигнал. Звуковая плата обеспечивает дискретизацию входного сигнала от микрофона. Это делается следующим образом – непрерывный сигнал заменяется последовательностью измеренных с определенной точностью значений.

Пример:

График аналогового сигнала:

 

  Дискретное представление этого же сигнала (41 измеренное значение):

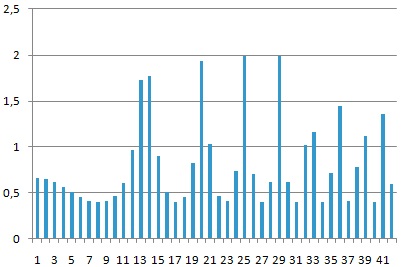
Дискретное представление этого же сигнала (161 измеренное значение, более высокая частота дискретизации):

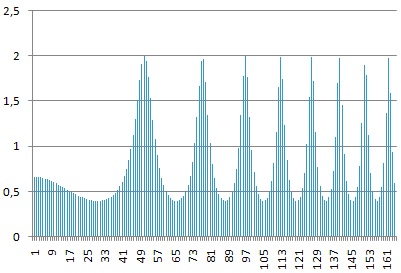
Видно, что чем выше частота дискретизации, тем выше качество приближенного (дискретного) сигнала. Кроме частоты дискретизации, на качество оцифрованного сигнала влияет количество двоичных разрядов, отводимых для записи каждого значения сигнала. Чем больше бит отводится под каждое значение, тем более точно можно оцифровать сигнал.

Пример 2-х битного представления этого же сигнала (двумя разрядами можно пронумеровать только 4 возможных уровня величины сигнала):

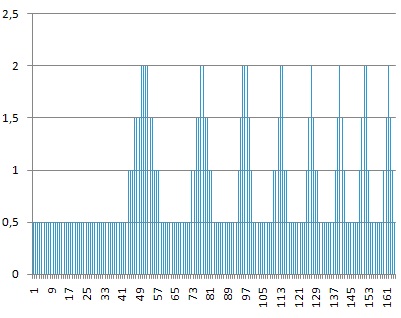
Теперь можно выписать зависимость для размера файла с оцифрованным звуком

размер_файла = (количество_значений,_фиксируемых_за_1_секунду)*

*( количество_двоичных_разрядов_для_записи_одного_значения )*

*(число_секунд_записи).

Учитывая возможность одновременной записи звука с нескольких микрофонов (стерео-, квадро- запись и т.д.), что делается для усиления реалистичности при воспроизведении, получаем формулу (1).

При воспроизведении звука цифровые значения преобразуются в аналоговые. Электрические колебания, передаваемые на динамики, преобразуются ими снова в колебания давления воздуха.

Задачи на Механические колебания с решениями

Формулы, используемые на уроках «Задачи на Механические колебания».

Название величины	Обозначение	Единица измерения	Формула
Амплитуда колебаний	A	м
Период колебаний	T	с	T = 1 / v ; T = t / N
Частота колебаний	v	Гц	v = 1 / T ; v = N / t
Число колебаний за какое-то время	N		N = t /T ; N = vt
Время	t	с	t = NT ; t = N / v
Циклическая частота колебаний	ω	Гц
Период колебаний пружинного маятника	T	c
Период колебаний математического маятника	T	c
Уравнение гармонических колебаний			x(t) = Asin(ωt+φ0)

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.
 Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

---

Задача № 2.
 На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

---

Задача № 3.
 Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

---

Задача № 4.
 Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

---

Задача № 5.
 Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с².

---

Задача № 6.
 Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

---

Задача № 7.
 Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

---

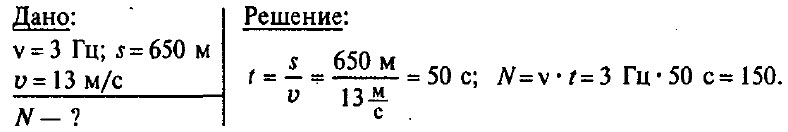
Задача № 8.
 Гармоническое колебание описывается уравнением 
 Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

---

Задача № 9.
 Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π² = 9,87.)

---

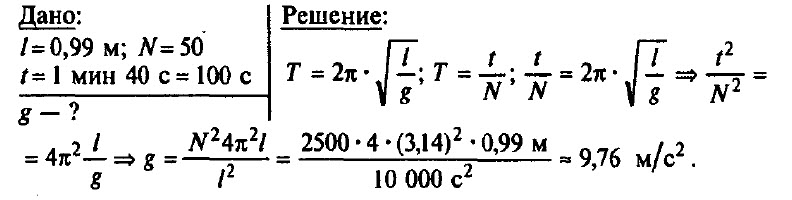
Задача № 10.
  ОГЭ
 Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

---

Задача № 11.
   ЕГЭ
 Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

---

Краткая теория для решения Задачи на Механические колебания.

---

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на 
• Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Решение задач на кодирование звуковой информации.

1. Теоретическая часть

При решении задач учащиеся опираются на следующие понятия:

 Временная дискретизация – процесс, при котором, во время кодирования непрерывного звукового сигнала, звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала, тем громче звук.

Глубина звука (глубина кодирования) – количество бит на кодировку звука.

Количество различных уровней громкости рассчитываем по формуле N= 2I , где I – глубина звука.

Частота дискретизации – количество измерений уровня входного сигнала в единицу времени (за 1 сек). Чем больше частота дискретизации, тем точнее процедура двоичного кодирования. Частота измеряется в герцах (Гц).

 Качество двоичного кодирования – величина, которая определяется глубиной кодирования и частотой дискретизации.

Разрядность регистра – число бит в регистре аудио адаптера. Чем больше разрядность, тем меньше погрешность каждого отдельного преобразования величины электрического тока в число и обратно. Если разрядность равна I, то при измерении входного сигнала может быть получено 2I =N различных значений.

1. Практическая часть. Разбор и решение задачи.

Задача 1. Оцените информационный объём цифрового звукового стерео файла длительностью 20 секунд при глубине кодирования 16 бит и частоте дискретизации 10000 Гц?  Результат представить в Кбайтах, округлить до сотых.

         При решении таких задач надо не забывать следующее:

Что  моно – 1 канал, стерео – 2 канала

Дано: I = 16 бит t = 20 сек η =10000 Гц	I – разрядность звуковой карты, t – время звучания аудиофайла, η – частота дискретизации	Решение: V =2· I · η ·t V = 2* 16 * 10000*20 = 6400000 бит 6400000/8 = 800000 байт 800000/1024 = 781,25 Кбайт Ответ:V(Инфор.) = 781,25 Кбайт
Найти: V(информационный объём)-?

Задача 2. Определить размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит.

Дано: I = 8 бит=1 байт t = 10 сек η = 22,05 кГц = 22,05 * 1000 Гц = 22050 Гц	I – разрядность звуковой карты, t – время звучания аудиофайла, η – частота дискретизации	Решение: V(Инфор.) =  I · η ·t V(Инфор.) =  22050 *10 *1 = 220500 байт Ответ: V(Инфор.) = 220500 байт
Найти: V(информационный объём)-?

Задача 3. Объем свободной памяти на диске — 5,25 Мб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 22,05 кГц?

Дано: I = 16 бит = 2 байт V(Инфор.) = 5,25Мб = 5505024 байт η = 22,05 кГц =22,05 * 1000 Гц =22050 Гц		Решение: V(Инфор.) =  I · η ·t t = V(Инфор.)/( η · I) t = 5505024/( 22050 *2 = 124,8 сек Ответ: t = 124,8 секунды
Найти: t-?