| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
центр:frac{y^2}{25}-frac{x^2}{9}=1
-
центр:frac{(x+3)^2}{25}-frac{(y-4)^2}{9}=1
-
центр:4x^2-9y^2-48x-72y+108=0
-
центр:x^2-y^2=1
- Показать больше
Описание
Пошаговый расчет центра гиперболы по заданному уравнению
hyperbola-center-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Practice, practice, practice
Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
The step by step workout for how to find what is the center, axis, eccentricity & asymptotes of a hyperbola.workout :
step 1 Address the formula input parameter and values
x0 = 5
y0 = 4
a = 5
b = 4
step 2 Apply x, y, a & b values in F (x, y) formula
F(x, y) = (x0 + √a² + b² , y0)
= (5 + √5² + 4² , 4)
= (5 + √25 + 16 , 4)
= (5 + √41 , 4)
= (5 + 6.4031 , 4)
F(x, y)= 11.4031, 4
step 3 Apply x, y, a and b values in F’ (x, y)
F’ (x, y) = (x0 – √a² + b² , y0)
= (5 – √5² + 4² , 4)
= (5 – √25 + 16 , 4)
= (5 – √41 , 4)
= (5 – 6.4031 , 4)
F’ (x, y)= -1.4031, 4
step 4 Apply a and b values in eccentricity formula
Eccentricity = √a² + b²
= √5² + 4²
= √41
Eccentricity = 6.4031
step 5 Apply the values a, b, x0, y0 in asymptotes H’L formula
Asymptotes H’L = b/ax + (y0 – b/ax0)
= 4/5x + (4 – 4/55)
= 0.8x + (4 – (0.8 x 5))
= 0.8x + (4 – (4))
Asymptotes H’L = 0.8x + 0
step 6 Apply the values a, b, x0, y0 in asymptotes L’H formula
Asymptotes L’H = -b/ax + (y0 + b/ax0)
= 4/5x + (4 + 4/55)
= -0.8x + (4 – (-0.8 x 5))
= -0.8x + (4 – (-4))
Asymptotes L’H = -0.8x + 8
Как найти центр гиперболы по уравнению
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac ), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac ) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
 гипербола, где k y≠0 это вторая асимптота.
гипербола, где k y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы. 
Пример №2:
$$y=frac -1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Дробь (color >) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1): 

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1): 

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат. 
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞). 

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: База знаний, Уроки Tag: Гипербола Leave a comment
Гиперболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению
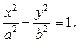 (25)
(25)
где  .
.
Параметры гиперболы:
Точки F1(–c, 0), F2(c, 0), где 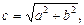 называются фокусами гиперболы, при этом величина 2с (с > a > 0) определяет междуфокусное расстояние. Точки А1(–а, 0), А2(а, 0) называются вершинами гиперболы, при этом А1А2 = 2а образует действительную ось гиперболы, а В1В2 = 2b – мнимую ось (В1(0, –b), B2(0, b)), О – центр гиперболы.
называются фокусами гиперболы, при этом величина 2с (с > a > 0) определяет междуфокусное расстояние. Точки А1(–а, 0), А2(а, 0) называются вершинами гиперболы, при этом А1А2 = 2а образует действительную ось гиперболы, а В1В2 = 2b – мнимую ось (В1(0, –b), B2(0, b)), О – центр гиперболы.
Величина 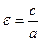 называется эксцентриситетом гиперболы, она характеризует меру «сжатости» гиперболы;
называется эксцентриситетом гиперболы, она характеризует меру «сжатости» гиперболы;
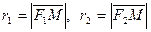 – фокальные радиусы гиперболы (точка М принадлежит гиперболе), причем r1 = a + εx, r2 = –a + εx для точек правой ветви гиперболы, r1 = – (a + εx), r2 = – (–a + εx) – для точек левой ветви;
– фокальные радиусы гиперболы (точка М принадлежит гиперболе), причем r1 = a + εx, r2 = –a + εx для точек правой ветви гиперболы, r1 = – (a + εx), r2 = – (–a + εx) – для точек левой ветви;
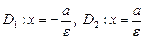 – директрисы гиперболы;
– директрисы гиперболы;
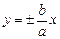 – уравнения асимптот.
– уравнения асимптот.
Для гиперболы справедливо: ε > 1, директрисы не пересекают границу и внутреннюю область гиперболы, а также обладают свойством 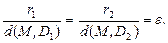
Говорят, что уравнение
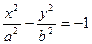 (26)
(26)
задает уравнение гиперболы, сопряженной данной (рис. 20). Его можно записать также в виде
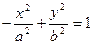 .
.
В таком случае ось 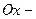 мнимая, фокусы лежат на оси
мнимая, фокусы лежат на оси 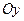 . Все остальные параметры определяются аналогично как для гиперболы (25).
. Все остальные параметры определяются аналогично как для гиперболы (25).
Точки гиперболы обладают важным характеристическим свойством: абсолютное значение разности расстояний от каждой из них до фокусов есть величина постоянная, равная 2a (рис. 19).
Для параметрического задания гиперболы в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на гиперболе, и положительным направлением оси Ox:
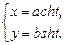
Пример 1. Привести уравнение гиперболы
к каноническому виду, найти еепараметры, изобразить гиперболу.
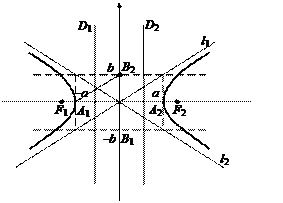
Решение. Разделим левую и правую части заданного уравнения на 144: 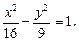 Из последнего уравнения непосредственно следует: a = 4, b = 3, c = 5, O(0, 0) – центр гиперболы. Фокусы находятся в точках F1(–5, 0) и F2(5, 0), эксцентриситет ε = 5/4, директрисы D1 и D2 описываются уравнениями D1: x = –16/5, D2: x = 16/5, асимптоты l1 и l2 имеют уравнения
Из последнего уравнения непосредственно следует: a = 4, b = 3, c = 5, O(0, 0) – центр гиперболы. Фокусы находятся в точках F1(–5, 0) и F2(5, 0), эксцентриситет ε = 5/4, директрисы D1 и D2 описываются уравнениями D1: x = –16/5, D2: x = 16/5, асимптоты l1 и l2 имеют уравнения 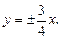
Сделаем чертеж. Для этого по осям Ox и Oy симметрично относительно точки (0, 0) отложим отрезки А1А2 = 2а = 8 и В1В2 = 2b = 6 соответственно. Через полученные точки А1(–4, 0), А2(4, 0), В1(0, –3), В2(0, 3) проведем прямые, параллельные координатным осям. В результате получим прямоугольник (рис. 21), диагонали которого лежат на асимптотах гиперболы. Строим гиперболу

Для нахождения угла φ между асимптотами гиперболы воспользуемся формулой
 .
.
 ,
,
откуда получаем 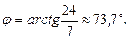
Пример 2. Определить тип, параметры и расположение на плоскости кривой, уравнение которой
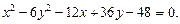
Решение. С помощью метода выделения полных квадратов упростим правую часть данного уравнения:
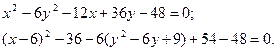
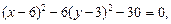
которое делением на 30 приводится к виду
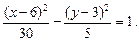
Это уравнение гиперболы, центр которой лежит в точке 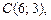 действительная полуось –
действительная полуось – 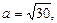 мнимая полуось –
мнимая полуось – 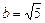 (рис. 22).
(рис. 22).
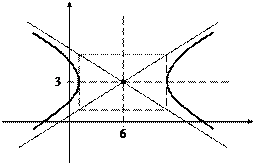
Пример 3. Составить уравнение гиперболы, сопряженной относительно гиперболы 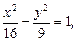 определить ее параметры и сделать чертеж.
определить ее параметры и сделать чертеж.
Решение.Уравнение гиперболы, сопряженной данной, –
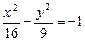 или
или 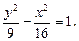
Действительная полуось b = 3, мнимая – а = 4, половина междуфокусного расстояния 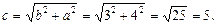 Вершинами гиперболы служат точки B1(0, –3) и В2(0, 3); ее фокусы находятся в точках F1(0, –5) и F2(0, 5); эксцентриситет ε = с/b = 5/3; директрисы D1 и D2 задаются уравнениями D1: y = –9/5, D2: y = 9/5; уравнения
Вершинами гиперболы служат точки B1(0, –3) и В2(0, 3); ее фокусы находятся в точках F1(0, –5) и F2(0, 5); эксцентриситет ε = с/b = 5/3; директрисы D1 и D2 задаются уравнениями D1: y = –9/5, D2: y = 9/5; уравнения 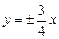 являются уравнениями асимптот (рис. 23).
являются уравнениями асимптот (рис. 23).
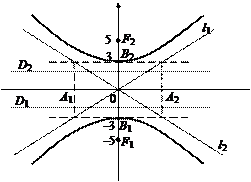
Заметим, что для сопряженных гипербол общими элементами являются вспомогательный «прямоугольник» и асимптоты.
Пример 4. Написать уравнение гиперболы с полуосями a и b (a > 0, b > 0), если известно, что ее главные оси параллельны координатным осям. Определить основные параметры гиперболы.
Решение. Искомое уравнение можно рассматривать как уравнение гиперболы 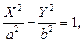 которое получается в результате параллельного переноса старой системы координат на вектор
которое получается в результате параллельного переноса старой системы координат на вектор 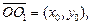 где (x0, y0) – центр гиперболы в «старой» системе координат. Тогда, используя соотношения между координатами произвольной точки М плоскости в заданной и преобразованной системах
где (x0, y0) – центр гиперболы в «старой» системе координат. Тогда, используя соотношения между координатами произвольной точки М плоскости в заданной и преобразованной системах
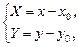
получим уравнение гиперболы
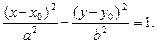
Определим параметры. Центр гиперболы определяет точка O¢(x0; y0), а значит, действительная ось задается уравнением x = x0,а мнимая – уравнением y = y0. Ее вершинами являются точки 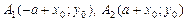 , а асимптотами являются прямые
, а асимптотами являются прямые 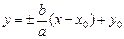 . Половина междуфокусного расстояния
. Половина междуфокусного расстояния 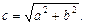 Тогда фокусы гиперболы находятся в точках
Тогда фокусы гиперболы находятся в точках 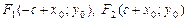 , эксцентриситет
, эксцентриситет
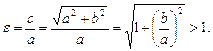
Директрисы D1 и D2 задаются уравнениями
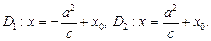
Пример 5.Написать уравнение гиперболы, имеющей вершины в фокусах эллипса 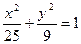 , а фокусы – в вершинах этого эллипса.
, а фокусы – в вершинах этого эллипса.
Решение.Уравнение 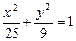 означает, что фокусами эллипса являются точки
означает, что фокусами эллипса являются точки 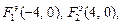 а вершины, лежащие на главной оси, находятся в точках
а вершины, лежащие на главной оси, находятся в точках 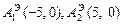 (так как
(так как 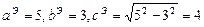 ).
).
Тогда для искомой гиперболы известно, что
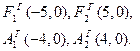
Значит, основные параметры гиперболы есть:
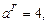
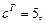
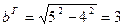 .
.
Используя данную информацию, приходим к уравнению гиперболы
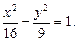
Задания для самостоятельного решения
Дата добавления: 2014-12-16 ; Просмотров: 6979 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Определение 7.2. Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой.
Замечание 7.2. Говоря о разности расстояний, подразумевают, что из большего расстояния вычитается меньшее. Это значит, что на самом деле для гиперболы постоянным является модуль разности расстояний от любой ее точки до двух фиксированных точек. #
Определение гиперболы аналогично определению эллипса. Различие между ними лишь в том, что для гиперболы постоянна разность расстояний до фиксированных точек, а для эллипса — сумма тех же расстояний. Поэтому естественно, что у этих кривых много общего как в свойствах, так и в используемой терминологии.
Фиксированные точки в определении гиперболы (обозначим их F1 и F2) называют фокусами гиперболы. Расстояние между ними (обозначим его 2с) называют фокальным расстоянием, а отрезки F1M и F2M, соединяющие произвольную точку M на гиперболе с ее фокусами, — фокальными радиусами.
Вид гиперболы полностью определяется фокальным расстоянием |F1F2| = 2с и значением постоянной величины 2а, равной разности фокальных радиусов, а ее положение на плоскости — положением фокусов F1 и F2.
Из определения гиперболы следует, что она, как и эллипс, симметрична относительно прямой, проходящей через фокусы, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 7.7). Первую из этих осей симметрии называют действительной осью гиперболы, а вторую — ее мнимой осью. Постоянную величину а, участвующую в определении гиперболы, называют действительной полуосью гиперболы.
Середина отрезка F1F2, соединяющего фокусы гиперболы, лежит на пересечении ее осей симметрии и поэтому является центром симметрии гиперболы, который называют просто центром гиперболы.
Для гиперболы действительная ось 2а должна быть не больше, чем фокальное расстояние 2с, так как для треугольника F1MF2 (см. рис. 7.7) справедливо неравенство ||F1M| — |F2M| | ≤ |F1F2|. Равенство а = с выполнено только для тех точек M, которые лежат на действительной оси симметрии гиперболы вне интервала F1F2. Отбрасывая этот вырожденный случай, далее будем предполагать, что а 2а. Согласно замечанию 7.2, гипербола состоит из тех точек M(х; у), для которых | |F1M| — — |F2M| | = 2а. Выберем прямоугольную систему координат Oxy так, чтобы центр гиперболы находился в начале координат, а фокусы располагались на оси абсцисс (рис. 7.8). Такую систему координат для рассматриваемой гиперболы называют канонической, а соответствующие переменные — каноническими.
В канонической системе координат фокусы гиперболы имеют координаты F1(c; 0) и F2(—с; 0). Используя формулу расстояния между двумя точками, запишем условие ||F1M| — |F2M|| = 2а в координатах |√((х — с) 2 + у 2 ) — √((х + с) 2 + у 2 )| = 2а, где (x; у) — координаты точки M. Чтобы упростить это уравнение, избавимся от знака модуля: √((х — с) 2 + у 2 ) — √((х + с) 2 + у 2 ) = ±2а, перенесем второй радикал в правую часть и возведем в квадрат: (х — с) 2 + у 2 = (х + с) 2 + у 2 ± 4а √((х + с) 2 + у 2 ) + 4а 2 . После упрощения получим —εх — а = ±√((х + с) 2 + у 2 ), или
√((х + с) 2 + у 2 ) = |εх + а| (7.7)
где ε = с/а. Возведем в квадрат вторично и снова приведем подобные члены: (ε 2 — 1)х 2 — у 2 = с 2 — а 2 , или, учитывая равенство ε = с/а и полагая b 2 = c 2 — a 2 ,
x 2 /a 2 — y 2 /b 2 = 1 (7.8)
Величину b > 0 называют мнимой полуосью гиперболы.
Итак, мы установили, что любая точка на гиперболе с фокусами F1(с;0) и F2(—с; 0) и действительной полуосью а удовлетворяет уравнению (7.8). Но надо также показать, что координаты точек вне гиперболы этому уравнению не удовлетворяют. Для этого мы рассмотрим семейство всех гипербол с данными фокусами F1 и F2. У этого семейства гипербол оси симметрии являются общими. Из геометрических соображений ясно, что каждая точка плоскости (кроме точек, лежащих на действительной оси симметрии вне интервала F1F2, и точек, лежащих на мнимой оси симметрии) принадлежит некоторой гиперболе семейства, причем только одной, так как разность расстояний от точки до фокусов F1 и F2 меняется от гиперболы к гиперболе. Пусть координаты точки M(х; у) удовлетворяют уравнению (7.8), а сама точка принадлежит гиперболе семейства с некоторым значением ã действительной полуоси. Тогда, как мы доказали, ее координаты удовлетворяют уравнению Следовательно, система двух уравнений с двумя неизвестными
имеет хотя бы одно решение. Непосредственной проверкой убеждаемся, что при ã ≠ а это невозможно. Действительно, исключив, например, x из первого уравнения:
после преобразований получаем уравнение
которое при ã ≠ а не имеет решений, так как . Итак, (7.8) есть уравнение гиперболы с действительной полуосью а > 0 и мнимой полуосью b = √(с 2 — а 2 ) > 0. Его называют каноническим уравнением гиперболы.
Вид гиперболы. По своему виду гипербола (7.8) заметно отличается от эллипса. Учитывая наличие двух осей симметрии у гиперболы, достаточно построить ту ее часть, которая находится в первой четверти канонической системы координат. В первой четверти, т.е. при x ≥ 0, у ≥ 0, каноническое уравнение гиперболы однозначно разрешается относительно у:
у = b/a √(x 2 — а 2 ). (7.9)
Исследование этой функции y(x) дает следующие результаты.
Область определения функции — ив этой области определения она непрерывна как сложная функция, причем в точке x = а она непрерывна справа. Единственным нулем функции является точка x = а.
Найдем производную функции y(x): y'(x) = bx/a√(x 2 — а 2 ). Отсюда заключаем, что при x > а функция монотонно возрастает. Кроме того, , а это означает, что в точке x = a пересечения графика функции с осью абсцисс существует вертикальная касательная. Функция y(x) имеет вторую производную y” = —ab(x 2 — а 2 ) -3/2 при x > а, и эта производная отрицательна. Поэтому график функции является выпуклым вверх, а точек перегиба нет.
Указанная функция имеет наклонную асимптоту, это вытекает из существования двух пределов:
Наклонная асимптота описывается уравнением y = (b/a)x.
Проведенное исследование функции (7.9) позволяет построить ее график (рис. 7.9), который совпадает с частью гиперболы (7.8), содержащейся в первой четверти.
Так как гипербола симметрична относительно своих осей, вся кривая имеет вид, изображенный на рис. 7.10. Гипербола состоит из двух симметричных ветвей, расположенных по разные
стороны от ее мнимой оси симметрии. Эти ветви не ограничены с обеих сторон, причем прямые у = ±(b/a)x являются одновременно асимптотами и правой и левой ветвей гиперболы.
Оси симметрии гиперболы различаются тем, что действительная пересекает гиперболу, а мнимая, будучи геометрическим местом точек, равноудаленных от фокусов, — не пересекает (поэтому ее и называют мнимой). Две точки пересечения действительной оси симметрии с гиперболой называют вершинами гиперболы (точки A(a; 0) и B(—a; 0) на рис. 7.10).
Построение гиперболы по ее действительной (2a) и мнимой (2b) осям следует начинать с прямоугольника с центром в начале координат и сторонами 2a и 2b, параллельными, соответ-ственно, действительной и мнимой осям симметрии гиперболы (рис. 7.11). Асимптоты гиперболы являются продолжениями диагоналей этого прямоугольника, а вершины гиперболы — точками пересечения сторон прямоугольника с действительной осью симметрии. Отметим, что прямоугольник и его положение на плоскости однозначно определяют форму и положение гиперболы. Отношение b/a сторон прямоугольника определяет степень сжатости гиперболы, но вместо этого параметра обычно используют эксцентриситет гиперболы. Эксцентриситетом гиперболы называют отношение ее фокального расстояния к действительной оси. Эксцентриситет обозначают через ε. Для гиперболы, описываемой уравнением (7.8), ε = c/a. Отметим, что если эксцентриситет эллипса может принимать значения из полуинтервала [0,1) (значение 0 соответствует предельному варианту эллипса — окружности), то эксцентриситет гиперболы всегда попадает в интервал (1, + ∞).
Построим прямоугольник с центром в начале системы координат Oxy и сторонами 2a, 2b, параллельными осям абсцисс и ординат соответственно. Проведем прямые y = (b/a)x и y = — (b/a)x, на которых лежат диагонали прямоугольника. Существует две гиперболы, соответствующие построенному прямоугольнику (рис. 7.12). Первая из них описывается каноническим уравнением (7.8), а вторая — уравнением
x 2 /a 2 — y 2 /b 2 = -1. (7.10)
Вторую гиперболу называют сопряженной по отношению к первой, а уравнение (7.10) — каноническим уравнением сопряженной гиперболы. Действительная и мнимая оси первой гиперболы являются соответственно мнимой и действительной осями сопряженной гиперболы, а асимптоты у них общие.
Пример 7.2. Найдем каноническое уравнение гиперболы по ее действительной полуоси a = 4 и фокальному расстоянию 2с = 10. Построим гиперболу и определим координаты ее вершин, фокусов и уравнения асимптот.
Так как действительная полуось a гиперболы известна, то, чтобы найти каноническое уравнение гиперболы, достаточно определить мнимую полуось b. Поскольку с = 5, b = √(с 2 — а 2 ), то b = √(5 2 — 4 2 ) = 3. Итак, искомое уравнение имеет вид x 2 /4 2 — y 2 /3 2 = 1. Построим прямоугольник,соответствующий заданной гиперболе (рис. 7.13). Продолжим его диагонали до асимптот ги-перболы и построим саму гиперболу. Уравнениями асимптот являются у = ±3x/4, вершины находятся в точках (±4; 0), а фокусы совпадают с точками (±5; 0).
Геометрические свойства. Геометрические свойства гиперболы во многом повторяют свойства эллипса. Вернемся к формуле (7.7). Она эквивалентна каноническому уравнению гиперболы и дает выражение для длины фокального радиуса F2M ее точки M(х; у):
|F2M| = √((х + с) 2 + у 2 ) = ±(εх + a) (7.11)
где знак плюс соответствует правой ветви гиперболы, а знак минус — левой.
Аналогично можно получить формулу для длины другого фокального радиуса, если при выводе канонического уравнения гиперболы перед первым возведением в квадрат в правую часть равенства перенести не второй, а первый квадратный радикал. При этом вместо (7.7) получим εх — a = ±√((х — с) 2 + у 2 ) , откуда
|F1M| = √((х — с) 2 + у 2 ) = ±(εх — a) (7.12)
где, как и в (7.11), знак плюс соответствует правой ветви гиперболы, а знак минус — левой. Каждое из уравнений (7.11), (7.12) является уравнением гиперболы.
Гипербола не проходит через свои фокусы (при 0 2 /c = (c 2 — a 2 )/c = b 2 /c
Гипербола также имеет и оптическое свойство, аналогичное оптическому свойству эллипса. Оно состоит в том, что лучи, вышедшие из одного фокуса, после отражения от ближайшей ветви гиперболы распространяются так, будто вышли из другого фокуса (рис. 7.15).
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Построение графика
дробно-линейной функции (гиперболы).
Если вам нужно просто построить график любой функции, то для этого у нас есть отдельная программа.
Эта математическая программа для построения графика дробно-линейной функции (гиперболы) сначала делает преобразование вида
$$ y= frac ; rightarrow ; y= frac +q $$
а затем последовательно строит графики функций:
$$ y= frac<1> $$
$$ y= frac $$
$$ y= frac +q $$
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода дробно-линейной функции, рекомендуем с ними ознакомиться.
В качестве переменной можно использовать только x
Все остальные буквы недопустимы.
При вводе можно использовать только целые числа.
Калькулятор гиперболических функций
u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f n
u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f u0438u043bu0438 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c – u044du0442u043e u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c u0447u0438u0441u0435u043b, u0442u0430u043au0430u044f, u0447u0442u043e u0440u0430u0437u043du0438u0446u0430 u043cu0435u0436u0434u0443 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du044bu043cu0438 u0447u043bu0435u043du0430u043cu0438 u043fu043eu0441u0442u043eu044fu043du043du0430. u0420u0430u0437u043du0438u0446u0430 u0437u0434u0435u0441u044c u043eu0437u043du0430u0447u0430u0435u0442 u0432u0442u043eu0440u043eu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043cu0438u043du0443u0441 u043fu0435u0440u0432u044bu0439. n
u041eu043fu0440u0435u0434u0435u043bu0435u043du0438u0435: u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f – u044du0442u043e u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c u0432u0438u0434u0430 $$ a_1, \ a_1+d, \ a_1+2d, \ a_1+3d, \ a_1+4d. $$ n
u0415u0441u043bu0438 u043fu0435u0440u0432u044bu0439 u0447u043bu0435u043d $ a_1 $ u0438 u043eu0431u0449u0430u044f u0440u0430u0437u043du043eu0441u0442u044c $ d $ u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u0438u0437u0432u0435u0441u0442u043du044b, u0442u043e u043cu043eu0436u043du043e u0432u044bu0447u0438u0441u043bu0438u0442u044c u043bu044eu0431u043eu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438.: $$ a_1 \ a_2 = a_1+d \ a_3 = a_2+d=a_1+2d \ a_4=a_3+d=a_1+3d \ . $$ n
u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f u0444u043eu0440u043cu0443u043bu044b n
n-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 u043cu043eu0436u0435u0442 u0431u044bu0442u044c u043fu043eu043bu0443u0447u0435u043d u0434u043eu0431u0430u0432u043bu0435u043du0438u0435u043c (n – 1) u0440u0430u0437u043du043eu0441u0442u0435u0439 u043a u043fu0435u0440u0432u043eu043cu0443 u0447u043bu0435u043du0443 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438. n
u041eu0431u0449u0430u044f u0444u043eu0440u043cu0443u043bu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438: $$ a_n = a_1+d*(n-1) $$ where n – n-u044bu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438, $ a_1 $ – u043fu0435u0440u0432u044bu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438, d – u0440u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438. n
u0437u0430u0434u0430u043du0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c ($ a_n $), u0433u0434u0435 $a_1 = 0$ u0438 $d = 2$.
u041du0430u0439u0434u0438u0442u0435 10-u0439 u044du043bu0435u043cu0435u043du0442 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ a_n = a_1 + d(n-1) = \implies a_ <10>= 0 + 2 * (10 -1) = 2*9 = 18 $$ n
u0420u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 n
u0420u0430u0437u043du043eu0441u0442u044c (d, u0448u0430u0433, u0440u0430u0437u043du0438u0446u0430 u0432 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438) – u044du0442u043e u0440u0430u0437u043du0438u0446u0430 u043cu0435u0436u0434u0443 u0441u043bu0435u0434u0443u044eu0449u0438u043c u0438 u043fu0440u0435u0434u044bu0434u0443u0449u0438u043c u0447u043bu0435u043du0430u043cu0438 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438.
u0415u0441u043bu0438 u043eu0431u0449u0430u044f u0440u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043fu043eu043bu043eu0436u0438u0442u0435u043bu044cu043du0430, u0442u043e u0442u0430u043au0430u044f u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c u043du0430u0437u044bu0432u0430u0435u0442u0441u044f u0432u043eu0437u0440u0430u0441u0442u0430u044eu0449u0430u044f u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f , u0435u0441u043bu0438 u0440u0430u0437u043du0438u0446u0430 u043eu0442u0440u0438u0446u0430u0442u0435u043bu044cu043du0430u044f, u0442u043e u0443u0431u044bu0432u0430u044eu0449u0430u044f u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f . n
u0420u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u0444u043eu0440u043cu0443u043bu044b n
u0420u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043cu043eu0436u043du043e u0440u0430u0441u0441u0447u0438u0442u0430u0442u044c u043fu043e u0441u043bu0435u0434u0443u044eu0449u0438u043c u0444u043eu0440u043cu0443u043bu0430u043c: $$ d = a_ – a_n $$
- d – u0440u0430u0437u043du043eu0441u0442u044c
- n – n-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ d = \frac$$
- m – m-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ d = \frac<2*\frac-2a_1>$$
- S – u0441u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 n
u0421u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 n
u0421u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 – u044du0442u043e u0440u0435u0437u0443u043bu044cu0442u0430u0442 u0441u043bu043eu0436u0435u043du0438u044f u0432u0441u0435u0445 u0447u043bu0435u043du043eu0432 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043fu043eu0434u0440u044fu0434. $$ S_n = \displaystyle\sum_^ a_i = n=<2a_1 + d(n-1) \over 2>n=n $$ n
u0421u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u0444u043eu0440u043cu0443u043bu044b:
$$ S_n = n* \left(\frac<2>\right) $$ $$ S_n = \frac<2>*(2a+d*(n-1)) $$ “,”meta_title”:”u041au0430u043bu044cu043au0443u043bu044fu0442u043eu0440 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438″,”meta_keyword”:”u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f, u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438, u0441u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438, u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f u0444u043eu0440u043cu0443u043bu044b, u0440u0435u0448u0435u043du0438u0435 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438″,”meta_description”:”u0412 u043cu0430u0442u0435u043cu0430u0442u0438u043au0435 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f u0438u043bu0438 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c – u044du0442u043e u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c u0447u0438u0441u0435u043b, u0442u0430u043au0430u044f, u0447u0442u043e u0440u0430u0437u043du0438u0446u0430 u043cu0435u0436u0434u0443 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du044bu043cu0438 u0447u043bu0435u043du0430u043cu0438 u043fu043eu0441u0442u043eu044fu043du043du0430. u0420u0430u0437u043du0438u0446u0430 u0437u0434u0435u0441u044c u043eu0437u043du0430u0447u0430u0435u0442 u0432u0442u043eu0440u043eu0439 u043cu0438u043du0443u0441 u043fu0435u0440u0432u044bu0439.”,”translations”:[<“id”:367,”conversion_id”:184,”locale”:”en”,”title”:”Arithmetic sequence”,”url”:”Arithmetic-progression”,”abbreviation”:”au2099″,”summary”:”
With this calculator find the nth term of arithmetic sequence, calculate common difference, sum of arithmetic sequence.
What is arithmetic sequence? n
Arithmetic sequence (algebraic) or arithmetic progression is a list of numbers (progression members) in which each number, starting from the second, is obtained from the previous one by adding to it a constant number d known as common difference . n
Definition: An arithmetic sequence is a sequence of the form $$ a, \ a+d, \ a+2d, \ a+3d, \ a+4d. $$ n
If the first term a and common difference d of the arithmetic sequence are known, then it is possible to calculate any member of the arithmetic sequence: $$ a_1 \ a_2 = a_1+d \ a_3 = a_2+d=a_1+2d \ a_4=a_3+d=a_1+3d \ . $$ n
How to find the arithmetic sequence? n
The nth term of the arithmetic sequence can be obtained by adding (n u2212 1) differences to the first term of the progression. n
The general formula of the arithmetic sequence: $$ a_n = a+d*(n-1) $$ where n – is the nth term of an arithmetic sequence, a – is the first member of the sequence, d – is the common difference. n
given an arithmetic sequence ($ a_n $), where a = 0 and d = 2.
Find the 10th element of an arithmetic sequence $$ a_n = a + d(n-1) = \implies a_ <10>= 0 + 2 * (10 -1) = 2*9 = 18 $$ n
What is the common difference in arithmetic sequence? n
The common difference-(d, step, progression difference) is the difference between the next and the previous term of the arithmetic sequence.
If the common difference of the arithmetic sequence is positive, then such a sequence called increasing arithmetic sequence , if the difference is negative, then decreasing arithmetic sequence . n
How to find common difference in arithmetic sequence? n
The common difference of the arithmetic sequence can be calculated using the following formulas: $$ d = a_ – a_n $$
- d – common difference
- n – nth term of arithmetic sequence $$ d = \frac$$
- m – m-th term of arithmetic sequence $$ d = \frac<2*\frac-2a>$$
- S – sum of arithmetic sequence
- a – first element of arithmetic sequence n
What is sum of arithmetic sequence? n
The sum of an arithmetic progression is the result of the addition of all terms in a row. $$ S_n = \displaystyle\sum_^ a_i = n=<2a_1 + d(n-1) \over 2>n=n $$ n
Arithmetic sequence sum formula:
$$ S_n = n* \left(\frac<2>\right) $$ $$ S_n = \frac<2>*(2a+d*(n-1)) $$ “,”meta_title”:”Arithmetic sequence calculator”,”meta_keyword”:”arithmetic sequence, arithmetic progression, arithmetic progression calculator, arithmetic progression definition, arithmetic progression formula, arithmetic sequence calculator”,”meta_description”:”Arithmetic progression (algebraic) is a sequence of numbers (progression members) in which each number, starting from the second, is obtained from the previous one by adding to it a constant number d (step, or progression difference).”>,<“id”:368,”conversion_id”:184,”locale”:”ru”,”title”:”u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f”,”url”:”Arifmeticheskaya-progressiya”,”abbreviation”:”au2099″,”summary”:”
u0421 u043fu043eu043cu043eu0449u044cu044e u044du0442u043eu0433u043e u043au0430u043bu044cu043au0443u043bu044fu0442u043eu0440u0430 u043du0430u0439u0434u0438u0442u0435 n-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438, u0432u044bu0447u0438u0441u043bu0438u0442u0435 u0440u0430u0437u043du043eu0441u0442u044c, u0441u0443u043cu043cu0443 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438.
u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f n
u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f u0438u043bu0438 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c – u044du0442u043e u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c u0447u0438u0441u0435u043b, u0442u0430u043au0430u044f, u0447u0442u043e u0440u0430u0437u043du0438u0446u0430 u043cu0435u0436u0434u0443 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du044bu043cu0438 u0447u043bu0435u043du0430u043cu0438 u043fu043eu0441u0442u043eu044fu043du043du0430. u0420u0430u0437u043du0438u0446u0430 u0437u0434u0435u0441u044c u043eu0437u043du0430u0447u0430u0435u0442 u0432u0442u043eu0440u043eu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043cu0438u043du0443u0441 u043fu0435u0440u0432u044bu0439. n
u041eu043fu0440u0435u0434u0435u043bu0435u043du0438u0435: u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f – u044du0442u043e u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c u0432u0438u0434u0430 $$ a_1, \ a_1+d, \ a_1+2d, \ a_1+3d, \ a_1+4d. $$ n
u0415u0441u043bu0438 u043fu0435u0440u0432u044bu0439 u0447u043bu0435u043d $ a_1 $ u0438 u043eu0431u0449u0430u044f u0440u0430u0437u043du043eu0441u0442u044c $ d $ u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u0438u0437u0432u0435u0441u0442u043du044b, u0442u043e u043cu043eu0436u043du043e u0432u044bu0447u0438u0441u043bu0438u0442u044c u043bu044eu0431u043eu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438.: $$ a_1 \ a_2 = a_1+d \ a_3 = a_2+d=a_1+2d \ a_4=a_3+d=a_1+3d \ . $$ n
u0410u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f u0444u043eu0440u043cu0443u043bu044b n
n-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 u043cu043eu0436u0435u0442 u0431u044bu0442u044c u043fu043eu043bu0443u0447u0435u043d u0434u043eu0431u0430u0432u043bu0435u043du0438u0435u043c (n – 1) u0440u0430u0437u043du043eu0441u0442u0435u0439 u043a u043fu0435u0440u0432u043eu043cu0443 u0447u043bu0435u043du0443 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438. n
u041eu0431u0449u0430u044f u0444u043eu0440u043cu0443u043bu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438: $$ a_n = a_1+d*(n-1) $$ where n – n-u044bu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438, $ a_1 $ – u043fu0435u0440u0432u044bu0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438, d – u0440u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438. n
u0437u0430u0434u0430u043du0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c ($ a_n $), u0433u0434u0435 $a_1 = 0$ u0438 $d = 2$.
u041du0430u0439u0434u0438u0442u0435 10-u0439 u044du043bu0435u043cu0435u043du0442 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ a_n = a_1 + d(n-1) = \implies a_ <10>= 0 + 2 * (10 -1) = 2*9 = 18 $$ n
u0420u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 n
u0420u0430u0437u043du043eu0441u0442u044c (d, u0448u0430u0433, u0440u0430u0437u043du0438u0446u0430 u0432 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438) – u044du0442u043e u0440u0430u0437u043du0438u0446u0430 u043cu0435u0436u0434u0443 u0441u043bu0435u0434u0443u044eu0449u0438u043c u0438 u043fu0440u0435u0434u044bu0434u0443u0449u0438u043c u0447u043bu0435u043du0430u043cu0438 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438.
u0415u0441u043bu0438 u043eu0431u0449u0430u044f u0440u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043fu043eu043bu043eu0436u0438u0442u0435u043bu044cu043du0430, u0442u043e u0442u0430u043au0430u044f u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u044c u043du0430u0437u044bu0432u0430u0435u0442u0441u044f u0432u043eu0437u0440u0430u0441u0442u0430u044eu0449u0430u044f u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f , u0435u0441u043bu0438 u0440u0430u0437u043du0438u0446u0430 u043eu0442u0440u0438u0446u0430u0442u0435u043bu044cu043du0430u044f, u0442u043e u0443u0431u044bu0432u0430u044eu0449u0430u044f u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au0430u044f u043fu0440u043eu0433u0440u0435u0441u0441u0438u044f . n
u0420u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u0444u043eu0440u043cu0443u043bu044b n
u0420u0430u0437u043du043eu0441u0442u044c u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043cu043eu0436u043du043e u0440u0430u0441u0441u0447u0438u0442u0430u0442u044c u043fu043e u0441u043bu0435u0434u0443u044eu0449u0438u043c u0444u043eu0440u043cu0443u043bu0430u043c: $$ d = a_ – a_n $$
- d – u0440u0430u0437u043du043eu0441u0442u044c
- n – n-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ d = \frac$$
- m – m-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ d = \frac<2*\frac-2a_1>$$
- S – u0441u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 n
u0421u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 n
u0421u0443u043cu043cu0430 u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 – u044du0442u043e u0440u0435u0437u0443u043bu044cu0442u0430u0442 u0441u043bu043eu0436u0435u043du0438u044f u0432u0441u0435u0445 u0447u043bu0435u043du043eu0432 u043fu0440u043eu0433u0440u0435u0441u0441u0438u0438 u043fu043eu0434u0440u044fu0434. $$ S_n = \displaystyle\sum_^ a_i = n=<2a_1 + d(n-1) \over 2>n=n $$ n
[spoiler title=”источники:”]
http://www.math-solution.ru/math-task/graph-frac-lin
http://owlcalculator.com/ru/kalykulyatory-po-algebre/Giperbolicheskie-funkcii
[/spoiler]
- m – m-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ d = \frac<2*\frac-2a_1>$$
- m – m-th term of arithmetic sequence $$ d = \frac<2*\frac-2a>$$
- m – m-u0439 u0447u043bu0435u043d u0430u0440u0438u0444u043cu0435u0442u0438u0447u0435u0441u043au043eu0439 u043fu043eu0441u043bu0435u0434u043eu0432u0430u0442u0435u043bu044cu043du043eu0441u0442u0438 $$ d = \frac<2*\frac-2a_1>$$
Как находить координаты центра симметрии гиперболы?
Анастасия Прохорова
Ученик
(116),
закрыт
3 месяца назад
Как находить координаты центра симметрии гиперболы?
Например y=2x-1/x (х в знаменателе,остальное в числителе)
Зызя
Гуру
(4997)
4 месяца назад
Привести к каноническому виду:
xy = 2x – 1;
x (2-y) = 1;
x = x’+y’, 2-y = x’-y’;
x’² – y’² = 1.
Центр симметрии х’ = у’ = 0, то есть х = 0, у = 2.
0x1е78 = 7800Гений (96106)
4 месяца назад
Бедная Василиночка, никто тебя не лайкает, все К. А. лайкают 🙁
К. А.
Просветленный
(37632)
Коржо́, значит ответ понравился.
И в чем проблема, пролайкай сам себя, это же твой аккаунт)))
Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и
есть величина постоянная
, меньшая расстояния
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Фокальное свойство гиперболы
Точки и
называются фокусами гиперболы, расстояние
между ними — фокусным расстоянием, середина
отрезка
— центром гиперболы, число
— длиной действительной оси гиперболы (соответственно,
— действительной полуосью гиперболы). Отрезки
и
, соединяющие произвольную точку
гиперболы с ее фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение , где
, называется эксцентриситетом гиперболы. Из определения
следует, что
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
(3.50)
Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и
. Для произвольной точки
, принадлежащей гиперболе, имеем:
Записывая это уравнение в координатной форме, получаем:
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:
где , т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство гиперболы). Здесь
и
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса и директрисы
(рис.3.41,а) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса
и директрисы
:
Уравнение гиперболы в полярной системе координат
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид
, где
— фокальный параметр гиперболы.
В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке
, принадлежащий прямой
, но не содержащий точки
(рис.3.41,б). Тогда для произвольной точки
, принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение гиперболы имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замены
:
что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы,
для эллипса).
Геометрический смысл коэффициентов в уравнении гиперболы
Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения:
. Следовательно, вершины имеют координаты
. Длина отрезка, соединяющего вершины, равна
. Этот отрезок называется действительной осью гиперболы, а число
— действительной полуосью гиперболы. Подставляя
, получаем
. Длина отрезка оси ординат, соединяющего точки
, равна
. Этот отрезок называется мнимой осью гиперболы, а число
— мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.
Замечания 3.10.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).
2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).
Для равносторонней гиперболы, описываемой уравнением (т.е. при
), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат
(рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид
(гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).
В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами
Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем
3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.
Действительно, если точка принадлежит гиперболе
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат той же гиперболе.
Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.
4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму гиперболы. Чем больше
, тем шире ветви гиперболы, а чем ближе
к единице, тем ветви гиперболы уже (рис.3.43,а).
Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника:
. Учитывая, что
и
, получаем
Чем больше , тем больше угол
. Для равносторонней гиперболы
имеем
и
. Для
угол
тупой, а для
угол
острый (рис.3.43,а).
6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и
называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы
приводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет гиперболу с центром в точке
, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение
определяет сопряженную гиперболу с центром в точке
.
Параметрическое уравнение гиперболы
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где — гиперболический косинус, a
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .
Пример 3.21. Изобразить гиперболу в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось,
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя
в уравнение гиперболы, получаем
Следовательно, точки с координатами и
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет ; фокальныи параметр
. Составляем уравнения асимптот
, то есть
, и уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

